2. 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室,山东 青岛 266071;
3. 海底科学与探测技术教育部重点实验室,山东 青岛 266100;
4. 中国地质调查局青岛海洋地质研究所,山东 青岛 266071
弹性波方程逆时偏移是实现多波地震资料深度域成像的有效工具,目前多分量地震资料逆时偏移领域的研究现状是:(1)弹性波的延拓算法与成像方法已趋于成熟[1-4],相关技术基本能够满足工业需求。如基于交错网格的弹性波正向和逆时延拓技术[5-6],逆时偏移的边界反射压制技术[7-9],纵横波解耦技术和矢量横波的标量合成技术[10],以及纵横波成像技术等均达到或正在接近工业应用水准;(2)由层间反射引起的逆时偏移噪声的压制问题得到了初步解决[11-13];(3)炮点弹性波场随机边界重构技术已经具备了工业应用价值[14];(4)弹性波逆时偏移GPU并行计算技术已达到了工业应用水准[15-16];(5)纵横波角度域共成像点道集(ADCIG)提取技术正在成为研究热点[17-18];(6)纵横波速度建模技术已在工业生产中崭露头角[19-21];(7)多分量地震资料保幅逆时偏移技术取得了进展[22-23]。
上述工作对于推动多分量地震联合逆时偏移技术的发展具有重要意义,但总体上说,目前的技术还不能满足工业应用的需求,主要表现在:(1)现有技术假定多分量地震数据中的各个分量具有相同的地震频谱,而实际上,野外多分量数据中的Z分量往往具有更高的主频和更宽的频带;(2)即使不考虑各分量之间的频谱差异,现有技术也仍然存在许多难题需要克服,包括逆时偏移震源子波的设置、速度模型的建立、偏移噪声的进一步压制、纵横波的保幅解耦、宽频数据的延拓方法、矢量横波的标量合成以及纵横波保幅成像方法等;(3)基于复杂各向异性理论的弹性波逆时偏移技术严重滞后于工业需求;(4)现有的并行计算方法存在随机边界噪声干扰。
本文在简要介绍多分量地震逆时偏移算法原理的基础上,结合弹性波逆时偏移技术的发展现状和工业需求,分析并给出该技术进入工业应用所必须解决的技术难题。
1 弹性波逆时偏移的基本原理弹性波逆时偏移将多分量地震记录当作弹性波场的边值问题[1]来处理,由计算机实现炮点波场的正向延拓和接收点波场的逆时延拓,并在延拓过程中采用相应的算法实现纵横波的成像。其输入数据一般为未经坐标旋转的三分量炮集,输出数据一般包括反射纵波成像结果、P-SV转换横波成像结果和SH波成像结果。
弹性波逆时偏移的基本原理为:假定地下介质由一系列绕射点组成,地面、海底或井中接收到的三分量记录为各绕射点产生的纵横绕射波场在接收点处的叠加响应,其中各绕射点纵横绕射波的产生时间为炮点波场的主能量到达该点的时间[24],绕射点产生的纵横绕射波振幅取决于该点的反射系数[25],由此可通过求取各绕射点产生纵横绕射波的时间和该时刻的纵横波振幅来确定地下各绕射点的空间位置和反射系数,实现地下介质的纵横波成像。实际成像过程一般由以下几部分组成:(1)炮点波场的正向延拓和重构;(2)接收点波场的逆时延拓;(3)炮、检波场延拓过程中的纵横波解耦与横波的标量化处理;(4)提高成像精度的处理与计算;(5)纵横波成像。
工业界目前对弹性波逆时偏移技术的要求主要有二:(1)地下构造的纵横波准确成像;(2)纵横波偏移结果的振幅能够指示岩石岩性。但现有的技术还不能满足上述要求,以下通过弹性波逆时偏移技术中一些难点问题的分析来说明现有方法与技术的局限并探讨今后该技术的研究重点。
2 现有弹性波逆时偏移技术的局限与今后的研究重点探讨本文认为,欲满足工业需求并进入实际生产,弹性波逆时偏移技术至少应在以下几方面取得突破。
2.1 分量之间的频率一致性处理技术或粘弹逆时偏移技术现有的多分量地震技术往往假定震源只激发纵波,各接收点接收到的纵横波是地下波阻抗界面对入射波进行反射或转换的产物。因此在多分量资料逆时偏移时也将炮点波场设置为一个纵波源,此时如果采用弹性理论进行多分量资料的偏移处理,则算法自动隐含了一个假设:X、Y、Z三个分量具有相同的子波与频谱。而事实上,实测三分量地震记录的频谱存在巨大差异,Z分量记录的频谱宽、主频高,X和Y两个水平分量记录的频谱窄、主频低[26]。这种实际情况与理论假设的背离降低了现有弹性波逆时偏移技术解决实际问题的能力。
解决这一问题的思路主要有三:(1)采用标量理论对各分量分别进行逆时偏移[27]并成像,即偏移处理前首先对三分量数据进行纵、横波解耦得到反射纵波分量和转换横波分量,然后利用常规标量算法进行反射纵波分量的逆时偏移,对于转换横波分量,则仍以标量理论为基础,分别利用纵波速度、纵波方程和横波速度、横波方程进行炮点波场正向延拓和接收点波场逆时延拓,其成像方法与反射纵波类似。(2)研发新技术进行分量之间的子波与频率一致性校正,使校正后的各分量具有尽可能一致的子波与频谱,此时的数据自动满足了弹性波逆时偏移所隐含的假设条件,但目前为止,还尚未见到这一领域研究成果的报道;(3)研发基于粘弹理论[28]的多分量联合逆时偏移技术解决各分量频谱不一致的问题。野外多分量地震勘探中各分量所包含的反射和转换波均来源于同一震源,说明这种分量之间的频谱和子波不一致性并不是由激发源的不同所引起的,而是由地层对不同频率的纵波和横波的吸收、衰减不一致引起的[29],由此推断,如果在弹性波逆时偏移过程中能够采用适当方法消除或补偿这种吸收、衰减影响,则分量之间的频谱和子波不一致问题将自动得到解决。
上述第一种思路具有如下优点:(1)可借鉴成熟的单分量地震波场逆时偏移技术,简化处理流程;(2)纵、横波独立成像,效率高。主要缺陷为:(1)用两个或三个标量波场等效三分量矢量地震波场,偏移结果无法准确描述弹性波的矢量特征;(2)它假定分离后的单分量波场中不包含其他类型的波,这对纵横波的分离精度提出了很高的要求;(3)由于采用不同频谱和类型的子波对纵横波进行分别处理,导致纵、横波偏移结果具有不同的分辨率,影响后期的纵横波联合解释与反演;(4)无法解决复杂各向异性问题,由于各向异性介质中纵横波是耦合在一起的,理论上不存在一个显式的横波方程,即使是近似方程,目前学术界也只是在TI介质中的准纵波方程推导方面取得了一些初步成果[30-31],而在准横波方程领域尚未取得具有工业应用价值的成果,因此基于标量理论的逆时偏移技术在解决各向异性问题方面缺乏横波方程的支撑,无法应用。
本文认为第二、三种思路应当是今后弹性波逆时偏移领域的研究重点,理由如下:(1)可以避开第一种思路的缺陷,无需在偏移前进行纵横波分离并可以解决各向异性问题,同时也能使纵横波具有相同的分辨率;(2)矢量场处理,在理论上更具保幅性;(3)理论基础更为坚实。第一种思路在解决各向异性问题时需要一个准横波方程,而目前为止学术界还没有推导出一个可用的各向异性准横波方程,同时目前的各向异性介质准纵波方程也只是对弹性波方程的一种近似,其精度和振幅保真性还有提升空间,而弹性波方程则不存在理论近似问题,它在对应的理论假设下是严谨的。
第二、三种思路的难点在于:(1)研发一种新的技术实现分量之间的子波与频率一致性校正存在巨大的研究难度;(2)现有的粘弹理论需要进一步发展才能从根本上解决多分量联合逆时偏移中各分量频谱不一致的问题。例如地层对地震波的吸收应该是地震波频率的函数[32-33],而现有粘弹理论往往假定粘弹系数与频率无关。
2.2 震源子波对逆时偏移的影响机理与震源子波设置技术多分量地震波场的联合逆时偏移常通过炮点波场与接收点波场的互相关来实现,其中炮点波场的计算需要给定速度模型和震源子波,震源子波的类型、形态以及频宽等决定炮点波场的诸多属性[29],而炮点波场的属性又会显著影响多分量地震资料联合逆时偏移的成像结果,因此震源子波是决定多分量数据逆时偏移成像效果的关键因素之一。问题的关键是:震源子波对多分量地震数据逆时偏移的影响机理到底是什么?怎么消除或降低这种影响?
通过简单模型的逆时偏移处理测试可得到以下结论:多分量数据逆时偏移中的震源子波不仅影响纵横波成像结果的分辨率,而且对构造的成像精度也有影响。相同条件下,当震源子波与地震记录的子波一致时,构造的成像位置最准确,当二者不一致时,即使是水平反射界面的成像结果也会出现明显误差[34-35],表现为:①界面位置不准确;②成像结果的频率与三分量记录的频率差别大,偏移剖面的分辨率变差。
目前业界在震源子波对逆时偏移的影响机理的研究还基本处于感性认识阶段,尚未上升到理论高度。因此,要想实现多分量数据的高精度联合逆时偏移,必须深入研究震源子波对多分量地震数据逆时偏移的影响机理,在此基础上给出偏移子波的设置方法或子波影响的消除方法。
2.3 宽频数据的延拓技术海洋多波地震中的OBS、OBN数据往往具有宽频特征,常规有限差分法对宽频数据进行延拓时会产生严重的数值频散问题[36],进而给偏移结果带来构造假象并降低偏移结果的保真性。
目前业界对数值频散的压制思路主要有三:(1)提高差分精度,包括更高阶的有限差分格式、紧致高阶有限差分算法等[5, 37]。这类方法存在差分阶数的瓶颈效应,当差分阶数达到一定程度时,进一步提高差分阶数对数值频散压制效果的提升有限,同时差分阶数的提高也会使得截断边界的处理复杂化,同时会增加并行处理中的通信负担,降低效率;(2)减小网格剖分步长,这类方法会增加存储量,同时也可能引起差分算法的稳定性问题;(3)采用通量校正技术(FCT)压制数值频散[6],但FCT校正会导致波场振幅损失、降低保真度。
此外,上述三种方法只注重压制由空间差分引起的数值频散,没有考虑由时间差分引起的数值频散压制问题,因此,进一步提高宽频多分量资料逆时偏移效果需要同时考虑如何降低由空间和时间差分引起的数值频散。近年来,国内外在这一领域取得了一些积极成果[38-39],这些成果已经在地震波正演中得到了应用,但如何将之应用于宽频多分量资料的逆时偏移中,需进一步研究。
2.4 纵横波解耦和矢量横波的标量合成技术各向同性情况下,Helmholtz波场解耦技术[40]能将弹性波场分解为一个标量纵波和一个矢量横波,而多分量地震资料联合逆时偏移中常用的互相关成像条件要求参与互相关计算的横波必须以标量的形式输入,这要求在对转换横波进行成像前必须先进行矢量横波的标量化处理[10]。横波的标量化处理需要求取各成像点处不同时刻炮点纵波场和接收点横波场的传播方向,目前的求取方法主要有极化向量法和坡印廷矢量法两类,其中极化向量法假设波只在炮检连线所在的平面内传播,故该方法只适用于简单模型情况。速度-应力方程的坡印廷矢量法只能求取混合波场的传播信息,不能求取纯纵波或纯横波的传播信息,基于速度-胀缩-旋转弹性波方程可分别求得纯纵波和纯横波的传播信息[41],但无法准确求取当空间某点存在多组纵横波时的波场传播信息;同时,当存在弹性参数突变时,入射到该位置的纵波会瞬间产生4个波(反射波、透射波、反射转换波、透射转换波),加上入射波此时波的传播方向至少有5个,坡印廷矢量法只能求出一个方向或两个方向,这个方向是多个波的传播方向的综合效应,因此利用坡印廷矢量法进行矢量横波的标量合成存在较大误差。
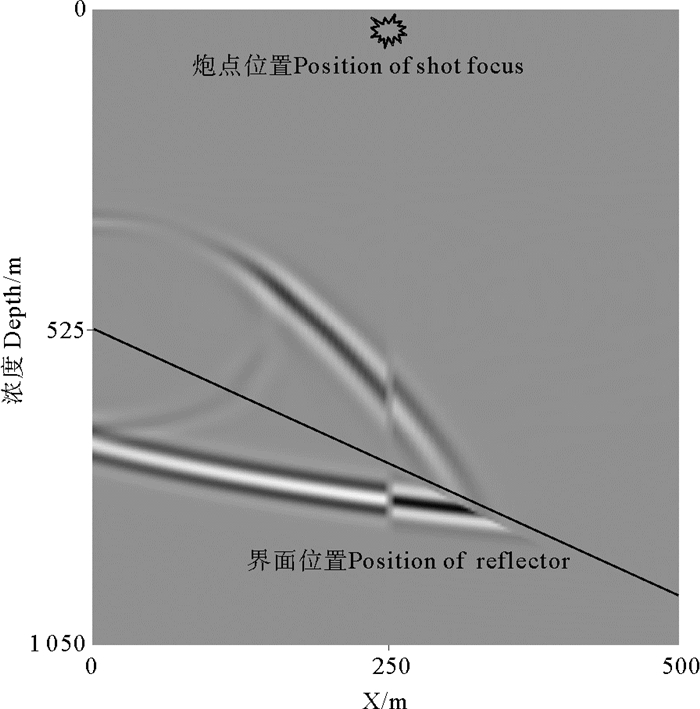
图 1为倾斜地层介质中极化向量法合成横波快照,合成结果存在极性反转现象,说明这种方法无法解决复杂构造问题。
|
图 1 极化矢量法求取的标量横波快照 Fig. 1 Scalar S-wave with polarization vector method |
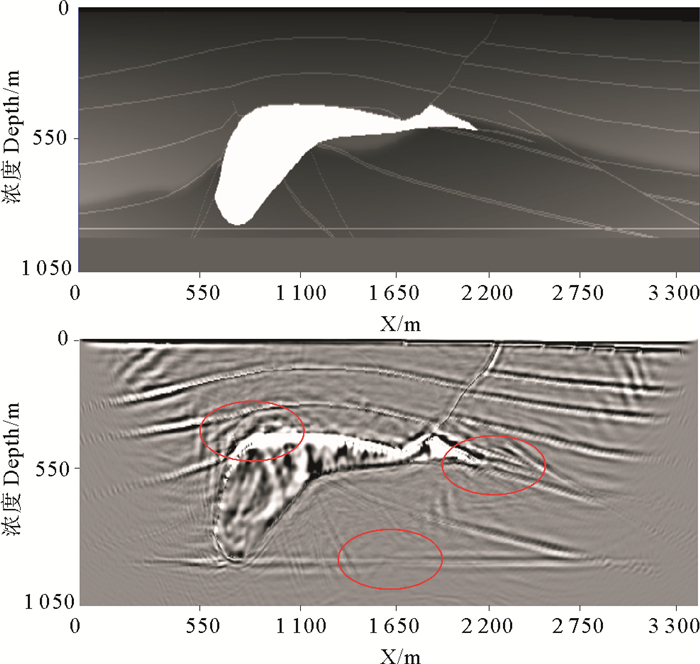
图 2为利用坡印廷矢量法进行横波的标量处理并最终得到的盐丘切片模型的转换横波偏移叠加剖面,椭圆区域部分出现同相轴破碎、断裂现象(红色椭圆内),说明坡印廷矢量法同样不适用于复杂构造问题。
|
图 2 盐丘切片速度模型及PS波偏移叠加剖面 Fig. 2 Velocity model of salt mound and RTM stack profile of PS-wave |
各向异性介质中,由于纵波的偏振方向不再与其传播方向平行,横波的偏振方向也不再与其传播方向垂直,Helmholtz解耦技术无法准确分离出准纵波和准横波,因此必须研究新方法实现准纵横波的解耦,其次才能考虑横波的标量合成问题。
以横向各向同性(TI)介质为例,其纵横波解耦方法有两类,一类是根据TI介质中各种类型的波的相速度推导相应的波动方程[42-44],目前的研究还主要集中在对纯qP波方程的声学近似阶段,研究成果无法应用于弹性波逆时偏移领域。另一类是利用TI介质中各种类型波的偏振方向对弹性波场进行滤波[40];其主要做法是将空间域波场转换至波数域,波数域波场中包含了沿波数指示方向传播的平面波振幅和相位信息。由于沿同一方向传播的qP波,qSV波和SH波的偏振方向是相互垂直的,因此可以利用这一性质设计矢量滤波算子,该算子的功能是只让一种性质的波通过,阻止其他两种波通过;将该矢量滤波算子与波数域中的三分量数据相乘,即可得到标量化的qP波,qSV波和SH波。
上述第二类方法可以同时解决纵横波解耦和横波的标量合成问题,但存在以下问题:(1)平面波假设无法准确描述弹性波中超过奈奎斯特波数的高波数成分,如qSV波的尖点和固液分界面处透射横波的突然消失等;(2)分离保真性需要进一步提高,目前所谓的保幅分离方法[45]只能做到使波场分离结果与原弹性波的极性保持一致,而无法做到分离结果与弹性波场在振幅和相位上完全一致;(3)现有的分离方法以模型为驱动,对各向异性模型的依赖性过高,而逆时偏移时往往无法提供一个准确的各向异性模型,限制了其实际应用。因此以数据为驱动的保幅波场分离算发将是进一步研究工作的方向。
2.5 纵横波子波拉伸校正技术逆时偏移子波拉伸是指偏移后纵、横波在垂向(深度)上的子波延续长度和频率随地震波速度和反射角变化,造成角度域共成像点道集(ADCIG)中不同入射角的地震道具有不同频谱的现象[46]。逆时偏移的子波拉伸不是由于偏移算法的误差引起的,而是因视角不同引起的,属几何效应,它随着入射角的增大而增大[47]。对于海洋多分量地震中的OBN和OBS资料来说,由于包含了丰富的大偏移距信息,子波拉伸对纵横波成像结果的影响尤其严重。
子波拉伸对偏移结果的影响主要有三:(1)降低偏移结果中大反射角的纵横波频率;(2)增加拾取剩余速度的难度。速度建模时由于大反射角信息对速度的敏感性远强于小反射角信息,因此大反射角信息可有效增加拾取剩余速度的确定性,但现有的逆时偏移技术对大反射角信息具有较强的破坏性,无法用于速度建模;(3)影响后续纵横波AVA/AVO反演的精度。现有技术为避免波场拉伸对偏移叠加剖面的影响往往直接将大反射角数据的成像结果直接切除,而这些被切除的大反射角信息又恰恰是纵横波的AVA/AVO反演所急需的,因此如果能对大反射角信息进行适当校正以消除波场拉伸的影响,则能使得叠前反演道集中的信息更全面,提高纵横波反演精度。
目前解决这一问题的思路有三种:(1)先偏移后压缩,即先采用常规偏移方法得到拉伸后的偏移结果,然后利用一些针对性技术对已经拉伸的数据进行压缩,这种思路一般认为逆时偏移的波场拉伸和动校正拉伸具有相似特征,故可利用或改进动校拉伸校正方法对偏移后的大入射角数据进行压缩;(2)先压缩后偏移,即在偏移前先对地震炮记录进行时间上的压缩,然后再偏移成像;(3)在逆时偏移的过程中进行拉伸校正。对于第一种思路,由于逆时偏移后大入射角信息已经遭到损失或破坏,拉伸校正试图恢复已经破坏或损失的信息,很难达到理想效果;对于第二种思路,由于在偏移前压缩地震记录会破坏地震数据原来的动力学特征,而逆时偏移本身又无法恢复这些动力学信息,因此这种思路必然以降低偏移结果的保真性为代价,同时这种思路在操作上也存在巨大困难;第三种思路具有理论的先天优势,但存在内存消耗大、精度低的缺陷。
目前业界对逆时偏移子波拉伸校正算法的研究还集中在标量声波逆时偏移领域,其中最具代表性的成果是Zhu[48]等和杨佳佳[49]等在声波方程逆时偏移中的拉伸校正算法。但对于弹性波方程,由于校正需要首先求取纵横波的反射角等信息,而现有方法只能求取耦合波场的传播角度,因此弹性波逆时偏移中的纵横波子波拉伸技术将是今后的研究重点。
2.6 不连续数据的逆时偏移技术现有的弹性波逆时偏移技术假设接收点波场是连续的,OBC勘探和陆上多分量地震勘探资料基本满足这一假设,但OBN、OBS等勘探中的海底节点往往稀疏,道间距较大,共炮点记录的连续性差,这与逆时偏移的基本假设相悖。常规逆时偏移方法处理稀疏数据时往往产生大量的绕射干扰,这些绕射在偏移叠加剖面上又表现出线性干扰特征,降低了偏移结果的横向分辨率并产生虚假构造。在偏移前进行地震数据内插可以在一定程度上减少这些干扰[50],例如国内外目前热点研究的5D插值[51]大多针对此问题。但对于低信噪比资料,叠前道间内插往往给炮集引入新的虚假信息,降低偏移成像质量。因此,要想从根本上解决这一问题,还必须在波场延拓理论或成像方法上取得突破,消除不连续数据逆时偏移中的绕射噪声,保证成像精度。
2.7 随机边界噪声的压制技术三维弹性波逆时偏移常采用随机边界策略[14]来重构炮点波场,实现炮、检波场的并行延拓并降低I/O成本。随机边界策略的基本思路为:首先在模型空间外镶嵌若干层具有随机弹性参数的网格组成新的计算区域,其次在整个区域内进行炮点波场的正向延拓并记录下最后时刻所有网格点的波场值,最后利用所记录的波场值进行炮点波场的逆时重构实现炮、检波场的并行延拓。
由于随机边界不涉及波的衰减,故炮点波场的延拓过程是可逆的,说明用某一时刻的波场值重构其他时刻的波场值在理论上是可行的,并且当随机边界层数足够时其重构的波场也是精确的,但实际应用中,考虑到计算效率等问题,随机边界的厚度有限,且随机边界的本质是一种散射而非衰减方法,随机速度点产生的散射波在有限的孔径内很难完全聚焦,从而给纵横波偏移结果带来虚假信息,尤其对浅部地层的成像造成严重干扰。因此,如何更合理地设置随机边界的弹性参数也是进一步提高弹性波逆时偏移成像精度的一个重要研究内容。
2.8 多分量地震资料的各向异性逆时偏移技术由于纵横波对地层各向异性具有不同的响应,多波地震勘探在理论上更能解决各向异性地层的勘探问题,这也是该技术得到工业界重视的主要原因之一,因此研究基于各向异性理论的多分量地震资料逆时偏移技术具有重要的工业应用价值。
弹性波的各向异性逆时偏移技术在总体思路和实现过程上与各向同性技术并无本质性区别,但由于纵横波在这两种介质中的传播机理不同,各向同性逆时偏移中部分环节的思路与方法不再适用于各向异性问题,主要表现在:(1)基于各向同性理论的Helmholtz技术不能直接用于各向异性介质中的纵横波解耦;(2)纵横波子波拉伸校正所需的入射角和反射角信息、波场成像所需的沿不同方向传播的纵横波无法用各向同性算法准确得到;(3)横波三叉区的处理与成像没有可借鉴的思路与方法。
引起上述第一个差异的根本原因在于各向异性介质中地震波的传播方向与偏振方向不平行(或垂直),因此无法利用波的传播方向信息求取偏振方向,同时由于目前业界正着力研究的波数域矢量滤波技术[44]在本质上是一种模型驱动技术,对各向异性模型的依赖性过高,也不利于弹性波逆时偏移应用,故各向异性介质中纵横波的高精度解耦方法就成为了逆时偏移中的难题。对于第二个差异,理论上可以通过坡印廷矢量求取炮、检波场的传播方向[52],并进一步利用这些方向求取偏移拉伸校正和波场分解所需的信息,但各向异性介质中弹性波的坡印廷矢量仍然只代表混合波场的传播方向,无法准确求取同一成像点同一时刻多种波的传播方向。横波三叉区对弹性波逆时偏移结果的影响在于:在对炮、检波场中的横波成分进行互相关成像时,三叉区的存在会造成偏移剖面产生虚假同相轴。
因此,在多分量地震资料的各向异性逆时偏移领域迫切需要展开的研究工作应当包括以下内容:(1)数据驱动的各向异性介质纵横波解耦方法;(2)各向异性纵横波传播方向求取方法;(3)逆时偏移中横波三叉区的处理方法。
3 结语本文首先简要介绍了弹性波逆时偏移的基本原理,在此基础上归纳了目前多分量地震逆时偏移技术所遇到的部分理论与技术难题,并分析了产生这些技术难题的原因以及当前的解决方案并给出了今后研究方向的初步建议。综合以上,本文认为,当前和今后在弹性波逆时偏移领域的研究重点应当至少包括文章给出的八个问题,但是这里值得注意的一点是,本文在总结过程中没有考虑弹性参数模型的建立问题,而这一问题又是弹性波逆时偏移技术应用前必须解决的,弹性参数模型建立中的相关技术和难点问题需要另文讨论。此外,多分量地震资料的成像处理是一个系统工程,不能只靠多分量逆时偏移这一个环节来解决问题,还应当包括去噪、静校正、反褶积和弹性参数建模等诸多环节,只有把各个环节都合理解决才有可能最终解决纵横波的成像问题。
| [1] |
Chang W F, McMechan G A. Elastic reverse-time migration[J]. Geophysics, 1987, 52(10): 1365-1375. DOI:10.1190/1.1442249
(  0) 0) |
| [2] |
Chang W F, McMechan G A. 3D elastic pre-stack reverse-time depth migration[J]. Geophysics, 1994, 59(4): 597-609. DOI:10.1190/1.1443620
(  0) 0) |
| [3] |
何兵寿, 张会星. 多分量波场的矢量法叠前深度偏移技术[J]. 石油地球物理勘探, 2006, 41(4): 369-374. HE Bing-Shou, ZHANG Hui-Xing. Vector pre-stack depth migration of multi-component wavefield[J]. Oil Geophysical Prospecting, 2006, 41(4): 369-374. DOI:10.3321/j.issn:1000-7210.2006.04.003 (  0) 0) |
| [4] |
Du Q Z, Gong X F, Zhu Y T, et al. PS Wave Imaging in 3D Elastic Reverse-Time Migration[C]. 2012 SEG Annual Meeting[s.l.]: Society of Exploration Geophysicists, 2012. https://www.researchgate.net/publication/278915575_3D_PS-wave_imaging_with_elastic_reverse-time_migration
(  0) 0) |
| [5] |
杜启振, 李宾, 侯波. 横向各向同性介质紧致交错网格有限差分波场模拟(英文)[J]. Applied Geophysics, 2009(1): 42-49. DU Qi-Zhen, LI Bin, HOU Bo. Numerical modeling of seismic wavefields in transversely isotropic media with a compact staggered-grid finite difference scheme[J]. Applied Geophysics, 2009(1): 42-49. (  0) 0) |
| [6] |
Book D L, Boris J P, Hain K. Flux-corrected transport Ⅱ: Generalizations of the method[J]. Journal of Computational Physics, 1975, 18(3): 248-283.
(  0) 0) |
| [7] |
Higdon R L. Absorbing boundary conditions for difference approximations to the multidimensional wave equation[J]. Mathematics of Computation, 1986, 47(176): 437-459.
(  0) 0) |
| [8] |
Hastings F D, Schneider J B, Broschat S L. Application of the perfectly matched layer (PML) absorbing boundary condition to elastic wave propagation[J]. The Journal of the Acoustical Society of America, 1996, 100(5): 3061-3069. DOI:10.1121/1.417118
(  0) 0) |
| [9] |
任志明, 刘洋. 一阶弹性波方程数值模拟中的混合吸收边界条件[J]. 地球物理学报, 2014, 57(2): 595-606. REN Zhi-Ming, LIU Yang. Numerical modeling of the first-order elastic equations with the hybrid absorbing boundary condition[J]. Chinese Journal of Geophysics, 2014, 57(2): 595-606. (  0) 0) |
| [10] |
Du Q Z, Zhu Y, Ba J. Polarity reversal correction for elastic reverse time migration[J]. Geophysics, 2012, 77(2): S31-S41. DOI:10.1190/geo2011-0348.1
(  0) 0) |
| [11] |
郭鹏, 何兵寿, 郭敏. 基于坡印廷矢量的声波方程叠前逆时偏移成像条件[J]. 煤炭学报, 2011, 36(8): 1290-1295. GUO Peng, HE Bing-Shou, GUO Min. Acoustic equation pre-stack reverse-time migration imaging condition based on Poynting vector[J]. Journal of China Coal Society, 2011, 36(8): 1290-1295. (  0) 0) |
| [12] |
Chen T, He B S. A normalized wavefield separation cross-correlation imaging condition for reverse time migration based on Poynting vector[J]. Applied Geophysics, 2014, 11(2): 158-166. DOI:10.1007/s11770-014-0441-5
(  0) 0) |
| [13] |
丁亮, 刘洋. 基于归一化波场拆分互相关成像条件的叠前逆时偏移成像方法[J]. 石油地球物理勘探, 2012, 47(3): 411-419. DING Liang, LIU Yang. Pre-stack reverse-time migration based on normalized wavefield decomposition cross-correlation imaging condition[J]. Oil Geophysical Prospecting, 2012, 47(3): 411-419. (  0) 0) |
| [14] |
Clapp R G. Reverse Time Migration with Random Boundaries[C]. 79th Annual International Meeting.[s.l.]: SEG Expanded Abstracts, 2009. https://www.researchgate.net/publication/242554950_Reverse_time_migration_with_random_boundaries
(  0) 0) |
| [15] |
刘红伟, 李博, 刘洪, 等. 地震叠前逆时偏移高阶有限差分算法及GPU实现[J]. 地球物理学报, 2010, 53(7): 1725-1733. LIU Hong-Wei, LI Bo, LIU Hong. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation[J]. Chinese Journal of Geophysics, 2010, 53(7): 1725-1733. DOI:10.3969/j.issn.0001-5733.2010.07.024 (  0) 0) |
| [16] |
Shi Y, Ke X. 3D VSP Reverse Time Migration Using GPU Acceleration[C]. Beijing: High PERFORMANCE Computing, 2016: 24-25.
(  0) 0) |
| [17] |
Sava P C, Fomel S. Angle-domain common-image gathers by wavefield continuation methods[J]. Geophysics, 2003, 68(3): 1065-1074. DOI:10.1190/1.1581078
(  0) 0) |
| [18] |
杨佳佳.多分量地震波逆时偏移的关键技术研究[D].青岛: 中国海洋大学, 2015. YANG Jia-Jia. Research of Multi-components Seismic Wave Reverse-time Depth Migration[D]. Qingdao: Ocean University of China. 2015. http://cdmd.cnki.com.cn/Article/CDMD-10423-1015712709.htm (  0) 0) |
| [19] |
Parekh C P, Lewis O J. Full-waveform Inversion for High-resolution Velocity Model Building Offshore Trinidad[C].[s.l.]: 78th EAGE Conference and Exhibition, 2016. https://www.slb.com/services/seismic/geophysical-processing/velocity-modeling/full-waveform-inversion.aspx
(  0) 0) |
| [20] |
王连坤, 方伍宝, 段心标, 等. 全波形反演初始模型建立策略研究综述[J]. 地球物理学进展, 2016, 31(4): 1678-1687. WANG Lian-Kun, FANG Wu-Bao, DUAN Xin-Biao. Review of full waveform inversion initial model building strategy[J]. Progress in Geophysics, 2016, 31(4): 1678-1687. (  0) 0) |
| [21] |
崔永福, 彭更新, 吴国忱, 等. 全波形反演在缝洞型储层速度建模中的应用[J]. 地球物理学报, 2016, 59(7): 2713-2725. CUI Yong-Fu, PENG Geng-xin, WU Guo-Chen. Application of full waveform inversion velocity model-building technology for the fractured-vuggy reservoir[J]. Chinese Journal of Geophysics, 2016, 59(7): 2713-2725. (  0) 0) |
| [22] |
Deng F, McMechan G A. True-amplitude pre-stack depth migration[J]. Geophysics, 2007, 72(3): S155-S166. DOI:10.1190/1.2714334
(  0) 0) |
| [23] |
杨佳佳, 栾锡武, 方刚, 等. 基于保幅波场分离的弹性波逆时偏移方法研究(英文)[J]. Applied Geophysics, 2016, 3: 008. YANG Jia-Jia, LUAN Xi-Wu, FANG Gang. Elastic reverse-time migration based on amplitude-preserving P-and S-wave separation[J]. Applied Geophysics, 2016, 3: 008. (  0) 0) |
| [24] |
Claerbout, J. F. Toward a unified theory of reflector mapping[J]. Geophysics, 1971, 36(3): 467-481. DOI:10.1190/1.1440185
(  0) 0) |
| [25] |
Zhi L, Chen S, Li X. Joint AVO inversion of PP and PS waves using exact Zoeppritz equation[C]. //SEG Technical Program Expanded Abstracts 2013. Beijing: Society of Exploration Geophysicists, 2013: 457-461. https://www.researchgate.net/publication/269043019_Joint_AVO_Inversion_of_PP_and_PS_waves_using_exact_Zoeppritz_equation
(  0) 0) |
| [26] |
赵邦六. 多分量地震勘探在岩性气藏勘探开发中的应用[J]. 石油勘探与开发, 2008, 35(4): 397-409. ZHAO Bang-Liu. Application of multi-component seismic exploration in the exploration and production of lithologic gas reservoirs[J]. Petroleum Exploration and Development, 2008, 35(4): 397-409. DOI:10.3321/j.issn:1000-0747.2008.04.002 (  0) 0) |
| [27] |
Dankbaar J W M. Separation of P-and S-waves[J]. Geophysical Prospecting, 1985, 33(7): 970-986. DOI:10.1111/gpr.1985.33.issue-7
(  0) 0) |
| [28] |
杨午阳.粘弹性波动方程保幅偏移技术研究[D].北京: 中国地质科学院, 2004. YANG Wu-Yang. Amplitude-Preserved Migration with Viscoelastic Wave Equations[D]. Beijing: Chinese Academy of Geological Sciences, 2004. http://cdmd.cnki.com.cn/Article/CDMD-82501-2007213435.htm (  0) 0) |
| [29] |
陆基孟. 地震勘探原理(上 下册)[M]. 北京: 中国石油大学出版社, 1993. LU Ji-Meng. The Principle of Seismic Exploration[M]. Beijing: Chinese University of Petroleum Press, 1993. (  0) 0) |
| [30] |
Duveneck E, Milcik P, Bakker P M, et al. Acoustic VTI wave equations and their application for anisotropic reverse-time migration[M]//SEG Technical Program Expanded Abstracts 2008. Beijing: Society of Exploration Geophysicists, 2008: 2186-2190.
(  0) 0) |
| [31] |
Fletcher R P, Du X, Fowler P J. Reverse time migration in tilted transversely isotropic (TTI) media[J]. Geophysics, 2009, 74(6): WCA179-WCA187. DOI:10.1190/1.3269902
(  0) 0) |
| [32] |
Wang Y. Q analysis on reflection seismic data[J]. Geophysical Research Letters, 2004, 31(17): 159-180.
(  0) 0) |
| [33] |
李振春, 王清振. 地震波衰减机理及能量补偿研究综述[J]. 地球物理学进展, 2007, 22(4): 1147-1152. LI Zhen-Chun, WANG Qing-Zhen. A review of research on mechanism of seismic attenuation and energy compensation[J]. Progress in Geophysics, 2007, 22(4): 1147-1152. DOI:10.3969/j.issn.1004-2903.2007.04.021 (  0) 0) |
| [34] |
杨仁虎, 常旭, 刘伊克. 叠前逆时偏移影响因素分析[J]. 地球物理学报, 2010, 53(8): 1902-1913. YANG Ren-Hu, ChANG Xu, LIU Yi-Ke. The influence factors analyses of imaging precision in Pre-stack reverse migration[J]. Chinese Journal of Geophysics, 2010, 53(8): 1902-1913. DOI:10.3969/j.issn.0001-5733.2010.08.016 (  0) 0) |
| [35] |
牟海波, 何兵寿. 地震波逆时偏移中的层位校正与去噪方法[J]. 中国煤炭地质, 2016, 28(4): 71-75. MOU Hai-Bo, HE Bing-Shou. Imaging horizon correction and denoising method in seismic wave reverse-time migration[J]. Coal Geology of China, 2016, 28(4): 71-75. DOI:10.3969/j.issn.1674-1803.2016.04.15 (  0) 0) |
| [36] |
Liang W Q, Wang Y F, Yang C C. Comparison of numerical dispersion in acoustic finite-difference algorithms[J]. Exploration Geophysics, 2014, 46(2): 206-212.
(  0) 0) |
| [37] |
董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 2000, 43(3): 411-419. DONG Liang-Guo, MA Zai-Tian, CAO Jing-Zhong. A study on stability of the staggered-grid high-order difference method of first-order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 43(3): 411-419. DOI:10.3321/j.issn:0001-5733.2000.03.015 (  0) 0) |
| [38] |
吴国忱, 王华忠. 波场模拟中的数值频散分析与校正策略[J]. 地球物理学进展, 2005, 20(1): 58-65. WU Guo-Chen, WANG Hua-Zhong. Analysis of numerical dispersion in wave field simulation[J]. Progress in Geophysics, 2005, 20(1): 58-65. DOI:10.3969/j.issn.1004-2903.2005.01.012 (  0) 0) |
| [39] |
唐怀谷, 何兵寿. 一阶声波方程时间四阶精度差分格式的伪谱法求解[J]. 石油地球物理勘探, 2017(1): 71-80. TAMG Huai-Gu, HE Bing-Shou. Pseudo spectrum method of first-order acoustic wave equation finite-difference schemes with fourth-order time difference accuracy[J]. Oil Geophysical Prospecting, 2017(1): 71-80. (  0) 0) |
| [40] |
Dellinger J, Etgen J. Wave-field separation in two-dimensional anisotropic media[J]. Geophysics, 1990, 55(7): 914-919. DOI:10.1190/1.1442906
(  0) 0) |
| [41] |
HG Tang, BS He, HB Mou. P- and S-wave energy flux density vectors[J]. Geophysics, 2016, 81(6): T357-T368. DOI:10.1190/geo2016-0245.1
(  0) 0) |
| [42] |
Chu C, Macy B K, Anno P D. An Accurate and Stable Wave Equation for Pure Acoustic TTI Modeling[C].[s.l.]: Seg Technical Program Expanded, 2011: 179-184. https://www.researchgate.net/publication/268453787_An_accurate_and_stable_wave_equation_for_pure_acoustic_TTI_modeling
(  0) 0) |
| [43] |
Pestana R C, Ursin B, Stoffa P L. Separate P-and SV-Wave Equations for VTI Media[C].[s.l.]: Seg Technical Program Expanded, 2011: 163-167. https://www.researchgate.net/publication/268453955_Separate_P-_and_SV-wave_equations_for_VTI_media
(  0) 0) |
| [44] |
Xu S, Zhou H. Pure Quasi-P Wave Calculation in Anisotropic Media[C].[s.l.]: Seg Technical Program Expanded, 2014: 3887-3891. https://www.researchgate.net/publication/301396806_Pure_quasi-P_wave_calculation_in_anisotropic_media
(  0) 0) |
| [45] |
Yan J, Sava P. Elastic wave mode separation for tilted transverse isotropy media[J]. Geophysical Prospecting, 2012, 60(1): 29-48. DOI:10.1111/gpr.2012.60.issue-1
(  0) 0) |
| [46] |
Xu S, Chauris H, Lambare G., et al. Common angle image gather-A strategy for imaging complex media[J]. Geophysics, 2001, 66(6): 1877-1892. DOI:10.1190/1.1487131
(  0) 0) |
| [47] |
Canning A, Malkin A. Removing NMO/Migration Stretch Effects for Improved AVO Analysis[C].[s.l.]: 7th International Conference & Exposition on Petroleum Geophysics, 2008, 366-370.
(  0) 0) |
| [48] |
Zhu X F, McMechan G A. Stretch-free migration imaging condition[J]. Geophysics, 2013, 78(4): s 203-s 210. DOI:10.1190/geo2012-0519.1
(  0) 0) |
| [49] |
杨佳佳, 何兵寿, 陈婷. 逆时深度偏移中的子波拉伸校正[J]. 石油地球物理勘探, 2016(1): 135-140. YANG Jia-Jia, HE Bing-Shou, Chen Ting. Wavelet stretch correction for reverse-time migration[J]. Oil Geophysical Prospecting, 2016(1): 135-140. (  0) 0) |
| [50] |
陈可洋, 范兴才, 吴清岭, 等. 提高逆时偏移成像精度的叠前插值处理研究与应用[J]. 石油物探, 2013, 52(4): 409-416. CHEN Ke-Yang, FAN Xing-Cai, WU Qing-Ling. Seismic wave pre-stack interpolation processing for improving the precision of reverse-time migration and its application[J]. Geophysical Prospecting for Petroleum, 2013, 52(4): 409-416. DOI:10.3969/j.issn.1000-1441.2013.04.011 (  0) 0) |
| [51] |
Chiu S K, Davidson M, Yan Y, et al. 5D anti-aliasing interpolation: Application on an unconventional shale play[C]. Beijing: 2013 SEG Annual Meeting. Society of Exploration Geophysicists, 2013.
(  0) 0) |
| [52] |
Yoon K, Marfurt K J. Reverse-time migration using the Poynting vector[J]. Exploration Geophysics, 2006, 37(1): 102-107. DOI:10.1071/EG06102
(  0) 0) |
2. Evaluation and Detection Technology Laboratory of Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China;
3. Key Lab of Submarine Geosciences and Prospecting Techniques Ministry of Education, Qingdao 266100, China;
4. China Geological Survey Qingdao Institute of Marine Geology, Qingdao 266071, China
 2019, Vol. 49
2019, Vol. 49

