2. 中国海洋大学物理海洋教育部重点实验室, 山东 青岛 266100;
3. 青岛海洋科学与技术试点国家实验室,山东 青岛 266237
南半球中纬度上空盛行着风暴轴,它代表了天气尺度瞬变涡动最强烈的区域,又对应大尺度环流的西风急流,在中纬度天气和气候系统中扮演着重要的角色。从天气系统来讲,中纬度天气尺度瞬变涡动与每日的气旋和反气旋活动密切相关,这些气旋和反气旋的频繁活动为局地区域带来大量降水,并导致冷空气爆发[1-2]。因此,风暴轴的异常变化能够影响局地风、云、降水等天气过程,进而影响中纬度天气系统的发展,对未来天气系统的异常变化具有重要意义。从气候系统来讲,中纬度大气承担着将热量从副热带输送到极区的任务,在南北纬40°左右达到极值,约占到总热量输运的90%。而在这些大气向极热量输运中,瞬变涡动输运约占70%,其中天气尺度瞬变涡动输运约占总涡动输运的50%[3-4]。同时,天气尺度瞬变涡动与行星尺度的时间平均流之间存在共生关系,即风暴轴的异常变化伴随着行星尺度气流的异常变化。两者相互作用对中纬度大气低频变异至关重要[5-6]。因此,风暴轴强度和位置的系统性变化将导致中纬度天气和气候发生重大改变。
Cayan等[7]认为,在年际尺度内中纬度海表面温度异常(Sea Surface Temperature Anomalies; SSTAs)被认为是对大气强迫的响应。对于年际到年代际尺度,很多基于模式的研究已证实中纬度的海洋-大气反馈是维持气候低频变化的重要过程[8]。特别是天气尺度涡动沿着风暴轴迁移在调节大尺度大气环流对中纬度SSTAs的相当正压响应中扮演着重要的角色。大气斜压不稳定是风暴轴形成和发展的一个主要原因。根据大气线性斜压不稳定理论,风暴轴中瞬变涡动被认为是斜压不稳定波在垂直剪切的西风平流中扰动增长的表现,其最大增长率(涡动强度)与平均经向温度梯度(根据热成风关系等同于平均西风垂直剪切)和静力稳定度的倒数成正比[9]。根据该理论,我们可以如下理解:由于瞬变涡动在强斜压不稳定区域中将平均有效位能转换为涡动运动能得以发展,发展的瞬变涡动同时也将大量热量向极输运,进而减弱了平均经向温度梯度,减弱了大气背景场的斜压不稳定度,不利于风暴轴的形成和维持,因此需要有外部的能量持续输入从而维持斜压不稳定,巩固风暴轴的发展。在最近十几年中,越来越多的证据表明,风暴轴和下垫面海洋存在相互作用,特别是在中纬度海洋锋区,绝大多数的风暴轴形成和能量获取都出现在海表面温度梯度大值区或者其下游[10],同时在风暴轴极值区的上游存在大气强斜压不稳定[11]。模式研究进一步表明,中纬度海洋锋区两侧提供的感热存在差异(向赤道增强,向极地减弱),对维持大气近表层经向温度梯度和斜压性至关重要,进而维持了风暴轴的发展[12-15]。值得注意的是,北半球的风暴轴具有显著的季节变化,其强度在冬季最强、夏季最弱;位置在冬季偏南、夏季偏北。而南半球的风暴轴则全年盛行。很多研究指出,南半球夏季(12月~次年2月)和冬季(6~8月)的风暴轴强度和结构差异较小,其空间特征与背景的西风急流季节变化一致[16-17]。以往研究更多围绕中纬度海洋如何维持风暴轴气候平均态开展工作,而关于不同季节内海温变异如何影响风暴轴变化的研究和讨论较少。鉴于此,本文将重点探讨南半球中纬度海温变异对不同季节风暴轴影响的差异性,并对大气斜压性和斜压能量转换进行诊断,研究和理解风暴轴不同响应的动力过程。
1 资料和方法本文研究所采用的水平风速、气温、表面风应力等气象数据来源于20世纪大气再分析数据集第二套版(Twentieth-Century Reanalysis dataset version 2;20CRv2)[18]。20CRv2是一套综合性全球大气环流数据集,其时间覆盖范围为1871—2011年,可提供的时间分辨率为6 h、日平均和月平均,水平分辨率为2°×2°,垂向分辨率为24层。20CRv2以HadISST1.1中的月平均SST和海冰分布数据作为下边界驱动条件,并且采用集合卡曼滤波数据同化方法仅仅同化了天气尺度的地面和海平面气压观测数据。因此,本文研究所采用的SST数据来源于哈德莱中心海冰和海表面温度数据集(Hadley Centre Global Sea Ice and Sea Surface Temperature;HadISST)中的全球月平均SST数据[19]。HadISST的时间覆盖范围为1870年至今,空间分辨率为1°×1°。为保证资料一致,所有资料的时间均取为1951—2000年。
风暴轴的表征方法主要有两种,即拉格朗日方法和欧拉方法。考虑到欧拉方法的易操作性以及本文研究侧重于风暴轴的群体变化特征,参照Blackmon对风暴轴的定义[20],本文用2~8 d带通滤波对南半球的对流层中不同层级变量场瞬变扰动方差或协方差来表征风暴轴。具体的风暴轴表征量如下:(ⅰ)250 hPa经向风速方差(〈v′v′〉);(ⅱ)850 hPa涡动热量经向通量(〈v′T′〉)。南半球风暴轴大值分布在30°S~60°S[11],因此分析区域选择30°S以南。作者利用基于傅里叶变换(Fourier transform;FFT)设计的滤波器对相应的日平均气象数据进行2~8 d带通滤波以提取出与天气尺度瞬变涡动相关的扰动。值得一提的是,Chang[21]和Trenberth[22]指出,一个较窄的带通滤波频段(如2~6 d)可能会扭曲斜压波的传播特征。因此本文采用较宽(2~8 d)的滤波频段以使这种可能性最小化。
由于本文的研究重点是中纬度海洋与风暴轴之间的局地相互作用,考虑到ENSO能够通过“大气桥”显著影响热带外海洋和大气[23],因此在进行EOF和回归分析前,本文去除了SST场与风暴轴场(Storm Track,以下简称为ST场)中的ENSO线性影响部分。根据Frankignoul和Sennéchael[24],本文采用季节变化的回归系数来去除ENSO影响。方法如下:设SST场和ST场中每一格点的时间序列分别为SST(t)和ST(t),通过多元回归方法得到ENSO对SST(t)和ST(t)的线性影响部分,即SSTENSO(t)=α1N1(t)+α2N2(t)+α0和STENSO(t)=β1N1(t)+β2N2(t)+β0。其中N1(t)和N2(t)为热带太平洋(20°S~20°N)SST异常场的前两个主成分,从SST(t)和ST(t)分别减去SSTENSO(t)和STENSO(t),从而去除ENSO线性影响。对于月平均数据而言,考虑到ENSO的季节锁相特征以及热带外海洋对ENSO的滞后响应,本文进一步处理方法如下:将SST和ST场中每一格点以及每一自然月的时间序列分别采用滞后n个月(取n等于0~4中使回归复相关系数平方最大的值)回归和同期回归的方法投影到N1(t)和N2(t)上,从而得到12个月的回归系数αi(t),βi(t),(i=1~2, t=1~12);为了减小样本误差,我们对回归系数αi(t),βi(t)作3个月的滑动平均,从而得到季节变化的回归系数。
2 南半球风暴轴对不同季节海温变异的响应特征作者在本文中展示了以2~8 d带通滤波的850 hPa涡动热量经向通量〈v′T′〉来表征风暴轴的分析结果。选择该风暴轴表征量主要基于两个原因:〈v′T′〉对于高层大气西风动量的向下传递以维持低层大气西风具有重要作用;异常的〈v′T′〉与海-气边界层中的异常温度和热通量有密切关系。瞬变涡动对大气响应(由SST异常直接诱导形成)的调整作用被称为“涡动反馈机制”,其可以使中纬度大气能够产生相当正压结构的响应[8]。实际上,本文也分析了带通滤波的250 hPa经向风速方差〈v′v′〉异常与SST异常之间的耦合关系,得到了相似的研究结果。
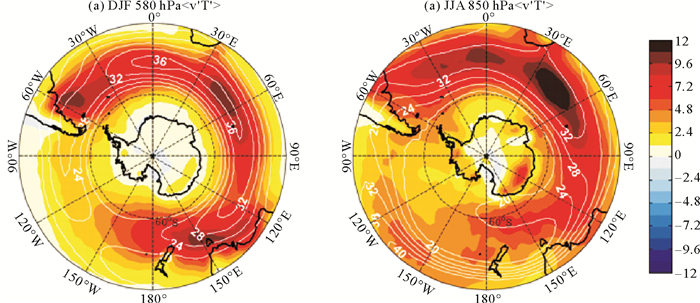
2.1 南半球风暴轴季节差异图 1为大气对流层低层风暴轴(850 hPa, 〈v′T′〉)月平均的空间分布,风暴轴振幅表征了涡动热量极向热通量。在夏季(12月~次年2月)和冬季(6~8月),风暴轴的大值区域与西风急流位置(250 hPa纬向风)表现了很好的一致性[25]。在北半球,风暴轴仅在冬季(12月~次年2月左右)得到显著强化[10, 20];而在南半球,风暴轴全年都保持充沛的能量,从南大西洋向东延伸,只是在南半球冬季强度稍强,经向和纬向的扇面幅度稍宽。从局部特征来看,不同大洋上空的风暴轴空间特征存在差异:(1)风暴轴峰值出现在南印度洋西部上空,全年维持在8 K·m·s-1以上,其强度在冬季大于夏季;(2)南大西洋的风暴轴虽然也全年盛行,相比南印度洋强度稍弱,在夏季时,大值区出现在南大西洋中西部,而在冬季时,大值区出现在南大西洋中东部;(3)风暴轴在南太平洋则呈现了明显的季节变化,夏季,风暴轴在澳大利亚东南延伸达到最强,峰值在8 K·m·s-1以上,冬季,风暴轴强度明显减弱。值得注意的是:虽然风暴轴在南半球中纬度三个大洋上空的空间特征存在差异,但由于南大洋无大陆阻隔,在分析和讨论南半球中纬度风暴轴时,仍将其作为一个整体来看。
|
( (填色部分代表〈v′T′〉,单位K·m·s-1); 白线代表250 hPa纬向风速,间隔为4 m·s-1。Shading, 〈v′T′〉, K·m·s-1) in (a)summertime(December, January and February, DJF) and(b)wintertime(June to August, JJA); Superimposed on 250 hPa zonal wind (white contours) with an interval of 4 m·s-1. ) 图 1 南半球(a)夏季(12月~次年2月平均)和(b)冬季(6~8月平均)的850 hPa风暴轴气候平均态 Fig. 1 Climatology of 850 hPa poleward heat flux associated with synoptic-scale eddies in summer(a) and winter(b) over the southern hemisphere |
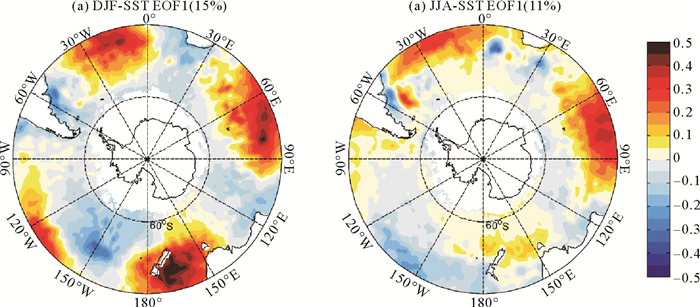
为了得到南半球SST不同季节主要模态,本文利用HadISST对1951—2000年南半球中纬度SST(30°S~60°S)异常场进行EOF分解(已经去掉季节循环和趋势项),南半球夏季和冬季SST主要模态呈现在图 1中,方差贡献分别为15%和11%。南大洋夏季SST异常场EOF分解第一模态空间特征表现为三极型暖异常(见图 2(a)):三个显著的暖异常中心分别出现在南大西洋中部、南印度洋中部和南太平洋西部,主要分布在30°S~50°S之间,其最大值出现在南太平洋中心(靠近新西兰),振幅达到0.6 K;同时在南太平洋中部,经向上存在两个较弱的偶极子异常(110°W~165°W)。相比于夏季,南大洋冬季SST异常场EOF第一模态的振幅则较弱,其空间特征表现为:两个暖异常分别出现在南大西洋中部和南印度洋中部,而出现在夏季的南太平洋暖异常中心几乎消失;同时,可以看到南大西洋的暖异常中心在经向上范围更窄,主要沿30°S~40°S分布,而南太平洋中部全部由振幅较弱的冷异常取代,在南太平洋向极一侧为较弱的正异常。从EOF时间系数来看,南半球夏季对比冬季,其对应的SST时间系数呈现出显著的年际变化特征,同时叠加上一些低频变率(见图 3(a), (b))。从功率谱分析[26]结果可以看到,夏季SST第一模态存在显著4年的年际周期,同时存在7~9年较弱的年代际周期;冬季SST第一模态时间系数则不存在显著的年际变化。这里值得注意,ENSO主要的影响在之前已经去除,因此由ENSO遥相关主导的年际变化信号并不存在于上文中的SST。
|
(方差贡献分别为15%,11%。The two modes account for 15% and 11 % of the total variance, respectively. ) 图 2 南半球中纬度(30°S~60°S)(a)夏季和(b)冬季SST(去掉ENSO影响,季节循环和趋势)的EOF1(单位:K) Fig. 2 EOF 1 of(a)DJF and (b)JJA mean midlatitude sea surface temperature(SST) anomalies (from 30°S to 60°S, K) with ENSO impacts, seasonal cycle and trend removed |
当时间尺度在季节或季节尺度以上时,如果中纬度海洋能够显著影响上空大气变化,那么协方差应当在海洋超前大气或两者同期时达到最大[27]。因此,本文将850 hPa风暴轴(〈v′T′〉)分别同期回归到夏季和冬季的SST标准化时间系数,以了解不同季节中纬度海温变异是如何影响风暴轴变化的。

|
(两条虚线分别表示80%和90%的置信度线。Dashed lines indicate the 80% and 90% confidence level. ) 图 3 (a) SST第一模态对应的标准化时间序列、(b)夏季和(c)冬季SST第一模态时间序列的功率谱分析 Fig. 3 (a) Normalized time coefficients of SSTderived from the corresponding first EOF mode、power spectrum of SST time coefficients in (b) DJF and (c) JJA, respectively, derived from the first EOF mode |
图 4(a)展示了夏季850 hPa涡动热量极向热通量〈v′T′〉与SST第一模态时间系数的回归系数空间分布场。〈v′T′〉异常的空间分布场(涂色部分)呈现了沿着40°S~60°S纬向条带状的向极正异常分布。其中,通过95%显著性检验的区域主要在南大西洋和南太平洋,最大值出现在南太平洋西部。而在冬季的回归系数空间分布场中(见图 4(b)),可以看到风暴轴正异常主要分布在南大西洋中部至南印度洋。较之夏季(见图 4(a)),该正异常分布的纬度较低,而并非极向强化;同时,南太平洋西部完全由风暴轴的负异常取代。对照图 1中〈v′T′〉季节平均的气候平均态表明,夏季和冬季SSTA都能够显著影响到风暴轴变化(也可对照图 4a中等值线),表现特征不同:在南半球夏季,中纬度海盆尺度SST三极子型暖异常可以使风暴轴出现向极增强,大气低层涡动活动显著加强。风暴轴变化振幅较大区域集中在南太平洋洋西南部。在南半球冬季,南大西洋低纬度的暖异常和南印度洋中部的暖异常,可以使局地的风暴轴增强,大气低层涡动活动加强;同时,南太平洋中西部较弱SSTA偶极子出现,使得局地的风暴轴减弱。

|
(涂色代表风暴轴异常(K·m·s-1),黑色等值线表示风暴轴气候平均态,间隔为2 K·m·s-1。斜线区域表示超过95%的统计置信度水平。Colors are for 〈v′T′〉 (K·m·s-1)anomalies and contours are for 〈v′T′〉 corresponding climatology with an interval of 0.2 K·m·s-1.Hatching areas indicate statistical significance at the 95% confidence level. ) 图 4 (a) 夏季和(b)冬季平均风暴轴(850 hPa)回归到对应季节SST EOF1标准化时间序列 Fig. 4 Regression of the 〈v′T′〉 at 850 hPa averaged in (a) DJF and (b)JJA against the corresponding SST EOF1 normalized time coefficients |
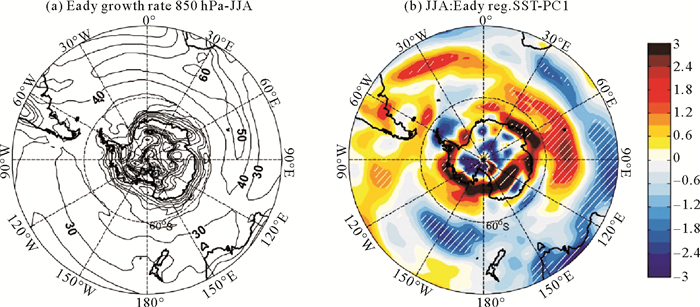
关于大气斜压理论与风暴轴关系的研究早有开展,Eady[9]风暴轴发展和形成的一个主导因素是由于大气斜压不稳定,它为瞬变涡动的发展提供了斜压“源泉”[1]。因此,为了解风暴轴对SST异常的响应动力过程,本文中对干燥大气的斜压不稳定性分析采用了大气最大Eady增长率σEady(Maximum Eady growth rate)作为指标。根据文献[28],σEady具体计算方法如下:
| $ {\sigma _{{\rm{Eady}}}} = 0.31g{N^{ - 1}}{T^{ - 1}}\left| {\frac{{\partial T}}{{\partial y}}} \right|。$ |
其中:T是气温;N是Brunt-Väisälä频率,N2=-ρg2θ-1(∂θ/∂p); ρ=PRd-1θ-1(P0/P)Rd/Cp, P0=1 000 hPa;θ是平均位温度。
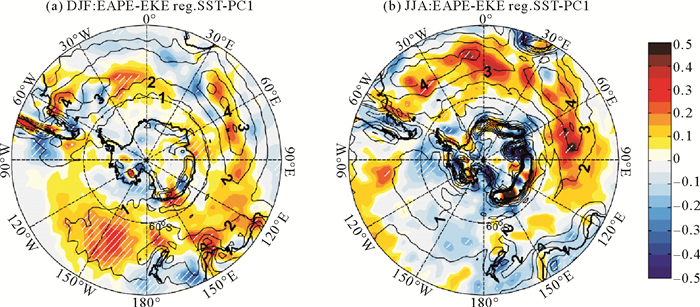
另外,Chang等[29]指出,涡动运动从时间平均流获取斜压能量的有效性受到了大气瞬变涡动结构和非绝热加热等因素主导。本文也计算了大气局地斜压能量转换(Baroclinic energy conversion;BCEC),包含两部分为:平均有效位能(Mean available potential energy;MAPE)向涡动有效位能(Eddy available potential energy;EAPE)的转换。涡动有效位能向涡动运动能(Eddy kinetic energy;EKE)的转换。根据Cai等[30]具体计算方法如下:
| $ \begin{array}{l} BCEC\left( {MAPE\;to\;EAPE} \right) = \\- {C_1}{\left( {\frac{{{P_0}}}{P}} \right)^{\frac{{{R_d}}}{{{C_p}}}}}{\left( { - \frac{{d\theta }}{{dp}}} \right)^{ - 1}}\left( {\overline {u'T'} \frac{{\partial \overline T }}{{\partial x}} + \overline {vT'} \frac{{\partial \overline T }}{{\partial y}}} \right), \\ BCEC\left( {EAPE\;to\;EKE} \right) = - {C_1}\overline {w'T'} 。\end{array} $ |
其中:C1=(P0/P)CvCpRd/g; P0=1 000 hPa;Rd, u, v, w, θ, Cp(Cv)分别表示干空气的气体常数、纬向速度、经向速度、垂向速度、位温、干空气定压(定容)比热容。表示2~8 d带通滤波的瞬变扰动,表示时间平均。
本文将850 hPa和σEady大气斜压能量转换分别回归到夏季和冬季的SST第一模态标准化时间系数。回归分析结果表明,南半球中纬度海盆尺度SST异常能够向极加强(或减弱)大气对流层斜压性,这很可能进一步导致相应的风暴轴活动对应变化。在南半球夏季,从图 5(b)中可以看到,对流层低层(850 hPa)的σEady在其气候平均位置(见图 5(a))的南部(45°S以南)显著增大,从南大西洋至南太平洋沿纬向向西延伸,表明对流层低层的斜压性向极移动并加强,其中最大正异常位于南太平洋中西部,而在气候平均位置的北部,呈现了向赤道方向的减弱。冬季的σEady回归分析结果也与作者猜想一致(见图 6),即在南大西洋和南印度洋出现了显著增强,其振幅稍大于夏季的异常响应,最大值出现在南印度洋中部;同时,在南太平洋中西部σEady呈现了显著减小,表明该区域对流层低层的斜压性向极移动并减弱。对比风暴轴回归系数分布(见图 4),可以清楚地看到σEady异常响应的分布与风暴轴变化呈现很好的一致性。
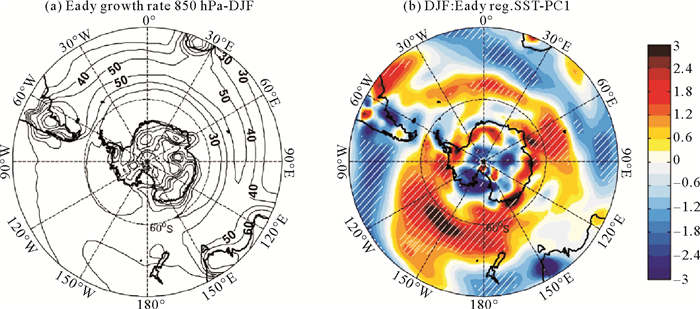
|
(斜线区域表示超过95%的统计置信度水平。Hatching areas indicate statistical significance at the 95% confidence level. ) 图 5 (a) 夏季最大Eady增长率(单位:×10-2 d-1)气候平均态(850 hPa)及(b)夏季平均最大Eady增长率回归到SST EOF1标准化时间序列 Fig. 5 (a)Climatology of the Eady growth rate(×10-2 d-1) at 850 hPa in DJF and (b) regression of the Eady growth rate at 850 hPa averaged in DJF against the corresponding SST EOF1 normalized time coefficients |
由于对流层斜压性的增强(减弱)能够提供更多(更少)的斜压能量给瞬变涡动,因此斜压性的上述变化很可能是使风暴轴活动增强(减弱)的一个重要原因。事实上,BCEC的诊断分析证实了斜压涡动能够从平均气流中获取更多的有效位能。从图 7和8中可以看到,对不同季节SSTA的响应,在夏季时MAPE向EAPE的转换以及EAPE向EKE的转换均在南半球中纬度显著增强,最大值同样出现在南太平洋中西部,表明风暴轴活动加强;冬季MAPE向EAPE的转换以及EAPE向EKE的转换在南大西洋和南印度洋中部显著增加,在南太平洋中西部减小,分别表明局地风暴轴活动加强和减弱。本文作者注意到,虽然在南半球极锋急流北侧由很大σEady负异常占据,局地的风暴轴活动却并未表现出一致的变化。这种南北两侧的差异一定程度上反应了风暴轴对赤道方向SST变化的非线性响应,也一定程度体现了湿过程对部分气旋发展壮大的重要性。
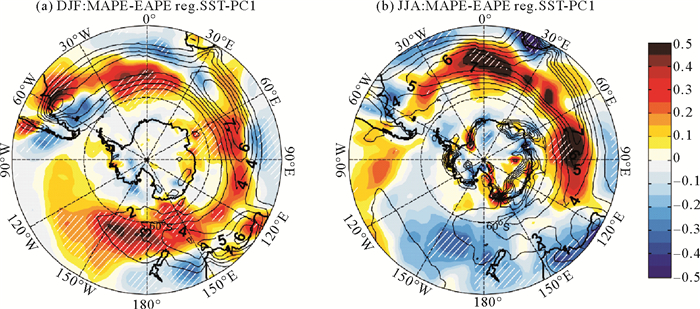
|
(涂色部分代表MAPE到EAPE转换异常(单位:W·m-2),黑色等值线表示MAPE到EAPE转换气候平均,间隔为1 W·m-2。斜线区域表示超过95%的统计置信度水平。Colors are for MAPE to EAPE anomalies (W·m-2)and contours are for the MAPE to EAPE corresponding climatology with an interval of 1 W·m-2 Hatching areas indicate statistical significance at the 95% confidence level. ) 图 7 (a) 夏季和(b)冬季平均MAPE到EAPE转换(850 hPa)回归到SST EOF1标准化时间序列 Fig. 7 (a)Climatology of MAPE to EAPE of at 850 hPa in DJF and (b) regression of MAPE to EAPE at 850 hPa averaged in DJF against the corresponding SST EOF1 normalized time coefficients |
4 结论
本文重点揭示了南半球冬夏季中纬度海表温度异常通过影响大气斜压性,进而来影响风暴轴变化的季节差异。主要结论如下:
(1) 南半球中纬度SST冬夏季主模态存在季节差异:南半球夏季SST第一模态表现为三极子型SST暖异常,SST暖异常分别在南大西洋、南印度洋中部和南太平洋西部,该模态存在显著4年的年际变化周期;南半球冬季SST第一模态表现为暖异常分布在南大西洋中部(较窄)、南印度洋中部,在南太平洋中西部出现弱偶极子型SST异常,该模态不存在显著的年际变化周期。
(2) 南半球中纬度SST变化能显著影响到风暴轴活动。夏季时,三极子型SST暖异常能够使对流层低层涡动活动增强,体现在850 hPa涡动热量极向热通量(〈v′T′〉)向极增加,其增强最显著的区域出现在南太平洋西部;冬季时,南大西洋、南印度洋的SST暖异常,与南太平洋中西部的弱偶极子型SST异常,分别能够在局地增强和减弱对流层低层涡动活动,体现在〈v′T′〉增强和减弱。
(3) 大气斜压性和斜压能量转换的诊断分析结果表明,南半球中纬度SST主模态表现的海盆尺度暖(冷)异常能够使对流层低层斜压性出现向极增强(减弱),同时大气斜压能量转换表现出一致性加强(减弱),这很可能导致相应的风暴轴活动加强(减弱)。
| [1] |
Chang E K M, FU Y. Interdecadal variations in northern hemisphere winter storm track intensity[J]. J Climate, 2002, 15: 642-658. DOI:10.1175/1520-0442(2002)015<0642:IVINHW>2.0.CO;2
(  0) 0) |
| [2] |
Field P R, Wood R. Precipitation and cloud structurein midlatitude cyclones[J]. J Climate, 2007, 20: 233-254. DOI:10.1175/JCLI3998.1
(  0) 0) |
| [3] |
Trenberth K E, Caron J M. Estimates of meridional atmosphereand ocean heat transports[J]. J Climate, 2001, 14: 3433-3443. DOI:10.1175/1520-0442(2001)014<3433:EOMAAO>2.0.CO;2
(  0) 0) |
| [4] |
Trenberth K E, Stepaniak D P. Covariability of components of poleward atmospheric energy transports on seasonal and interannual timescales[J]. J Climate, 2003, 16: 3691-3705. DOI:10.1175/1520-0442(2003)016<3691:COCOPA>2.0.CO;2
(  0) 0) |
| [5] |
Lau KM, Sheu P J, Kang I S. Multiscale low-frequency circulation modes in the global atmosphere[J]. J Atmos Sci, 1994, 51(9): 1169-1193. DOI:10.1175/1520-0469(1994)051<1169:MLFCMI>2.0.CO;2
(  0) 0) |
| [6] |
Kug J S, Jin F F, Par JH, et al. A general rule for synoptic-eddy feedback onto low-frequency flow[J]. Clim Dyn, 2010, 35: 1011-1026. DOI:10.1007/s00382-009-0606-8
(  0) 0) |
| [7] |
Cayan D. Latent and sensible heat flux anomalies over the Northern Oceans: The connection to monthly atmospheric circulation[J]. J Climate, 1992, 5: 354-369. DOI:10.1175/1520-0442(1992)005<0354:LASHFA>2.0.CO;2
(  0) 0) |
| [8] |
Kushnir Y, Robinson W A, Blade I, et al. Atmospheric GCM response to extratropical SST anomalies: Synthesis and evaluation[J]. J Climate, 2002, 15: 2233-2256. DOI:10.1175/1520-0442(2002)015<2233:AGRTES>2.0.CO;2
(  0) 0) |
| [9] |
Eady E T. Long waves and cyclone waves[J]. Tellus, 1949, 1: 33-52.
(  0) 0) |
| [10] |
Nakamura H, Sampe T, Tanimoto Y, et al. Observed associations among storm tracks, jet streams and midlatitude oceanic fronts. Earth's climate: The ocean-atmosphere interaction[J]. Geophys Monogr, 2004, 147: 329-346.
(  0) 0) |
| [11] |
Nakamura H, Shimpo A. Seasonal variations in the southern hemisphere storm tracks and jet streams as revealed in a Reanalysis Dataset[J]. J Climate, 2004, 17: 1828-1844. DOI:10.1175/1520-0442(2004)017<1828:SVITSH>2.0.CO;2
(  0) 0) |
| [12] |
Nakamura H, Shimpo A, Goto A, et al. On the importance of midlatitude oceanic frontal zones for the mean state and dominant variability in the tropospheric circulation[J]. Geophys Res Lett, 2008, 22: 880-904. DOI:10.1029/2008GL034010
(  0) 0) |
| [13] |
Hotta D, Nakamura H. On the significance of sensible heat supply from the ocean in the maintenance of mean baroclinicity along storm tracks[J]. J Climate, 2011, 24: 3377-3401. DOI:10.1175/2010JCLI3910.1
(  0) 0) |
| [14] |
Ogawa F, Nakamura H, Nishii K, et al. Dependence of the climatological axial latitudes of the tropospheric westerlies and storm tracks on the latitude of an extratropical oceanic front[J]. Geophys Res Lett, 2012, 39: L05804.
(  0) 0) |
| [15] |
Small R J, Tomas R A, Bryan FO. Storm track response to ocean fronts in a global high-resolution climate model[J]. Climate Dyn, 2014, 43: 805-828. DOI:10.1007/s00382-013-1980-9
(  0) 0) |
| [16] |
Trenberth K E. Observed southern hemisphere eddy statistics at 500mb: Frequency and spatial dependence[J]. J Atmos Sci, 1981, 38: 2585-2605. DOI:10.1175/1520-0469(1981)038<2585:OSHESA>2.0.CO;2
(  0) 0) |
| [17] |
Trenberth K E. Seasonality in southern hemisphere eddy statistics at 500[J]. J Atmos Sci, 1982, 39: 2507-2520. DOI:10.1175/1520-0469(1982)039<2507:SISHES>2.0.CO;2
(  0) 0) |
| [18] |
Compo G P, Coauthors. The twentieth century reanalysis project[J]. Quart J Roy Meteor Soc, 2011, 137: 1-28.
(  0) 0) |
| [19] |
Rayner N A, Parker D E, Horton E B, et al. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century[J]. J Geophys Res, 2003, 108: 4407. DOI:10.1029/2002JD002670
(  0) 0) |
| [20] |
Blackmon M L, Wallace J M, Lau N C, et al. An observational study of the northern hemisphere wintertime circulation[J]. J Atmos Sci, 1977, 34: 1040-1053. DOI:10.1175/1520-0469(1977)034<1040:AOSOTN>2.0.CO;2
(  0) 0) |
| [21] |
Chang E K M. Downstream development of baroclinic waves asinferred from regression analysis[J]. J Atmos Sci, 1993, 50: 2038-2053. DOI:10.1175/1520-0469(1993)050<2038:DDOBWA>2.0.CO;2
(  0) 0) |
| [22] |
Trenberth K E. Storm tracks in the southern hemisphere[J]. J Atmos Sci, 1991, 48: 2159-2178. DOI:10.1175/1520-0469(1991)048<2159:STITSH>2.0.CO;2
(  0) 0) |
| [23] |
Alexander M A, Blade I, Newman M, et al. The atmospheric bridge: The influence of ENSO teleconnections on air-sea interaction over the global oceans[J]. J Climate, 2002, 15: 2205-2231. DOI:10.1175/1520-0442(2002)015<2205:TABTIO>2.0.CO;2
(  0) 0) |
| [24] |
Frankignoul C, Sennéchael N. Observed influence of North Pacific SST anomalies on the atmospheric circulation[J]. J Climate, 2007, 20: 592-606. DOI:10.1175/JCLI4021.1
(  0) 0) |
| [25] |
Zhang L, Gan B, Wu L, et al. Seasonal dependence of coupling between storm tracks and sea surface temperature in the southern Hemisphere Midlatitudes: A statistical assessment[J]. J Climate, 2018, JCLI-D-17-0196.1.
(  0) 0) |
| [26] |
Mann M E, Lees J M. Robust estimation of background noise and signal detection in climatic time series[J]. Climatic Change, 1996, 33: 409-445. DOI:10.1007/BF00142586
(  0) 0) |
| [27] |
Frankignoul C. Sea surface temperature anomalies, planetary waves and air-sea feedback in the middle latitudes[J]. Rev Geophys, 1985, 23: 357-390. DOI:10.1029/RG023i004p00357
(  0) 0) |
| [28] |
Lindzen R S, Brian F, Tung K K. The concept of wave overreflection and its application to baroclinic instability[J]. J Atmos Sci, 1980, 37(1): 44-63. DOI:10.1175/1520-0469(1980)037<0044:TCOWOA>2.0.CO;2
(  0) 0) |
| [29] |
Chang E K M. GCM and observational diagnoses of the seasonal and interannual variations of the Pacific storm track during the cool season[J]. J Atmos Sci, 2001, 58: 1784-1800. DOI:10.1175/1520-0469(2001)058<1784:GAODOT>2.0.CO;2
(  0) 0) |
| [30] |
Cai M, Yang S, Van den Dool H M, et al. Dynamical implications of the orientation of atmospheric eddies: A localenergetics perspective[J]. Tellus, 2007, 59A: 127-140.
(  0) 0) |
2. Physical Oceanography Laboratory, CIMST, Ocean University of China, Qingdao 266100, China;
3. Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao 266237, China
 2020, Vol. 50
2020, Vol. 50