2. 国家海洋局第一海洋研究所, 山东 青岛 266061;
3. 青岛大学物理科学学院, 山东 青岛 266071
海洋盐度是描述海洋物理性质的基本参数, 是影响海洋动力环境和海-气相互作用的一个关键因子[1]。盐度遥感卫星SMOS(Soil Moisture and Ocean Salinity)发射之前, 海面盐度数据获取依赖于现场观测手段, 数据主要集中于近海和航路附近。Argo计划的实施一定程度上改善了实测数据空间覆盖的问题, 但Argo观测网中浮标的分布密度的平均距离为3°×3°, 而且Argo浮标完成一个剖面的测量需约10 d时间, 其测量数据的时空分辨率较低[2]。自1970年代, 研究者开展了一系列现场和机载实验, 研究利用遥感手段实现海洋盐度观测的可能, 为基于星载平台的海表盐度遥感测量积累了经验[3-7]。
盐度遥感卫星SMOS和Aquarius的入轨运行, 使人类获得了从太空监测海洋表面盐度的能力[8-9]。SMOS和Aquarius盐度卫星在数天内即可覆盖全球海域, 为海洋科学研究提供了长时间序列、高时空分辨率和覆盖率的盐度遥感数据。SMOS和Aquarius均工作于L波段, 其对海表盐度变化的敏感性为0.2~0.8 K。
亮温中与海表盐度变化相关的部分仅有数K[10]。星载盐度计观测亮温数据中除了与海表盐度有关的平静海面亮温之外, 还包括了粗糙海面亮温辐射。粗糙海面辐射亮温是辐射计观测角、极化状态、风速风向、风浪谱、泡沫覆盖率等参量的复杂函数。粗糙海面亮温辐射与海表盐度无关, 相当于盐度信息提取中的“噪声”。针对星载盐度计SMOS和Aquarius数据精度验证研究表明, 粗糙海面亮温是盐度反演的一个重要误差源, 需要进行校正[11-12]。
自1970年代Thomann[3]开展L波段微波辐射计观测盐度变化实验以来, 研究者发展了若干理论模型和经验模型以描述L波段粗糙海面辐射特性, 主要包括理论模型和经验模型两类。理论模型主要有双尺度模型(Two-Scale Model, TSM)和小斜率近似(Small Slope Approximation, SSA)模型[13], 其计算过程复杂, 难以直接用于星载盐度计数据处理。经验模型主要采用一些现场观测实验获得的数据, 获得粗糙海面亮温信号与风速、风向、波高等参量的经验关系, 建立描述粗糙海面辐射特性的地球物理模型函数(Geophysical Model Function, GMF)[14-15], 其模型的准确度受到实验区域、周期等现场观测条件的限制, 数据的代表性难以保证。星载盐度计发射入轨后, 又有研究者基于星载盐度计亮温发展了一些新的粗糙海面辐射模型[16-17]。这些模型建立过程中均使用了NCEP再分析产品提供风场数据, 但再分析数据时空分辨率相对较低, 难以获得与盐度计观测时空同步的风场信息。为了解决这一问题, 本文选择星载扫描微波辐射计WindSat与星载盐度计Aquarius进行匹配, 以发展粗糙海面辐射模型。WindSat与Aquarius两颗卫星的降交点地方时仅相差7min, (6:00和6:07);轨道倾角仅相差0.7°(98°和98.7°), 且地面足印面积相当, 相似的轨道参数保证了两者数据的有效匹配; 而且WindSat作为全极化微波辐射计, 可测量风速、风向、SST等参数, 提供与Aquarius观测时空同步的海气参量。最终本文利用Aquarius和WindSat匹配数据, 建立了一个L波段粗糙海面辐射参数化模型, 进而将其用于海表盐度反演, 并将反演结果与Argo浮标实测数据进行了比较。
1 数据与方法 1.1 数据与时空匹配(1) Aquarius数据。研究中使用的Aquarius数据是L2级SCI数据产品(V3.0), 提取了Aquarius辐射计观测的大气层顶(Top of Atmosphere, TOA)亮温数据。TOA亮温是对辐射计天线温度TA(Antenna Temperature)进行RFI、法拉第旋转以及天线方向图等校正后获得的, 其包含了粗糙海面、宇宙天体以及大气等微波辐射的贡献。为防止陆地及海冰对亮温数据的污染, 研究中剔除了陆地或海冰占视场面积大于0.1%的数据。
(2) WindSat数据。WindSat是美国海军实验室NRL(Naval Research Laboratory)于2003年发射的世界上第一颗星载全极化微波辐射计, 用于验证全极化微波辐射计的风场反演能力。WindSat数据采用RSS(Remote Sensing System)提供的最新版本(V7.01)数据产品; 其空间分辨率为25 km, 数据产品中包括SST、中/低频通道反演的10m风速、水汽和云液水含量、雨率、风向以及全天候(All-Weather)风速产品[18]。
(3) 海面有效波高数据。前期有研究者发现, 粗糙海面辐射/散射信号除了受海面风场影响之外, 还受到海面波浪的影响[16-17]。本文在发展粗糙海面地球物理函数模型过程中, 采用了Aquarius L2数据产品中所包含的有效波高数据, 其数据来源于NOAA WaveWatch-3模型的有效波高产品。Aquarius地面处理系统将有效波高数据通过时空插值, 获得Aquarius盐度计扫描位置的有效波高值。
(4) 海面盐度数值模式数据。为了保证数据的独立性, 建立辐射参数化模型过程中没有采用Aquarius盐度计的反演结果, 而是采用Aquarius L2数据产品中包含的HYCOM(Hybrid Coordinate Ocean Model)模式提供的海面盐度数据。
(5) NCEP再分析数据。NCEP再分析数据由美国国家大气研究中心(National Center for Atmospheric Research, NCAR)提供, 时空分辨率分别为6 h和1°, 数据格式为GRIB格式, 包含压强、温度、湿度和高度剖面数据。NCEP剖面数据的层数为26层, 其中大气压1000至900百帕每25百帕为一层, 900至100百帕每50百帕为一层, 100百帕到10百帕每10~30百帕为一层。
(6) 数据时空匹配。研究中分别提取了WindSat升轨和降轨的SST、观测经纬度和时间等信息。采用的时空窗口为25 km和1 h, 在60°S~60°N范围内对Aquarius和WindSat数据进行了匹配, 要求Aquarius观测位置周围4个WindSat网格点的数据均为有效反演, 并将WindSat数据线性插值到Aquarius观测位置上, 对2012年5322轨的Aquarius数据与WindSat数据进行了匹配实验, 获得匹配数据共1749253组。Aquarius和WindSat的匹配数据可覆盖全球海域, 平均匹配率约40%。
NCEP再分析数据与Aquarius遥感数据的匹配采用时空双线性插值方法, 将NCEP大气剖面插值到Aquarius扫描位置, 用于大气辐射亮温的计算。
1.2 粗糙海面发射率提取由辐射传输理论可知, Aquarius测量的大气层顶(TOA, Top of Atmosphere)亮温数据可以表示为:
| $ \begin{gathered} {T_B} = {T_{BU}} + \tau {T_s}({\varepsilon _{flat}} + {\varepsilon _{rough}}) + \hfill \\ \tau (1-({\varepsilon _{flat}} + {\varepsilon _{rough}}))({T_{BD}} + \tau \cdot{T_{COS}}), \hfill \\ \end{gathered} $ | (1) |
其中:TBU为大气上行辐射亮温; TBD为大气下行辐射亮温; τ为大气透射率, 以上三项可利用NCEP大气剖面数据结合Liebe大气辐射模型计算, 该模型可适用于1~1 000 GHz频率范围内的大气辐射计算[19]; Tcos为宇宙背景辐射和天体辐射, 根据Aquarius盐度反演算法ATBD文档取为3 K[20]; Ts为海表温度, 由WindSat微波辐射计提供; εflat为平静海面发射率, 可由海水介电常数模型进行计算; εrough为粗糙海面发射率。本文采用WindSat观测的SST数据和HYCOM盐度数据, 结合Klein-Swift[21]模型计算平静海面发射率, 进而可通过下式提取H/V极化粗糙海面发射率εrough, (2)式中TB为星载盐度计测量亮温, 其他参数的意义与(1)式相同。
| $ {\varepsilon _{rough}} = \frac{{\frac{{{T_B}-{T_{BU}}}}{\tau }-({T_{BD}} + \tau \cdot{T_{COS}})}}{{{T_s}-({T_{BD}} + \tau \cdot{T_{COS}})}} - {\varepsilon _{flat}}。$ | (2) |
利用(2)式提取的无雨条件下的粗糙海面发射率, 通过分析粗糙海面发射率与风速、相对风向和有效波高的统计关系, 建立描述粗糙海面发射率的参数化模型。
研究中的风速范围取2~25 m/s, 间隔1 m/s。风速下限没有取到0值的原因在于, 辐射计/散射计能直接观测的是海面粗糙度而不是海面风速, 当风速较低时海面粗糙度变化不明显, 所以辐射/散射计在低风速时测量精度不高。风向范围为0~360°、间隔10°。目前散射计和全极化微波辐射计提取风向的精度约20°, 取20°以下的风向间隔意义不大。有效波高的取值范围为0~10 m, 间隔1 m。因此, 形成24×36×11共9 504个网格, 将1 749 253组数据按照其风速、风向和有效波高数据, 存放到相应数据网格中并进行了平均, 剔除了网格内数据量少于5个的网格点。最终获得了在各种海气条件下, L波段粗糙海面发射率平均值, 并将其表示为与相对风向的余弦函数关系:
| $ \begin{gathered} \Delta {e_p}\left( {ws, wd, swh} \right) = {e_{p0}}\left( {ws, swh} \right) + {e_{p1}}\left( {ws, swh} \right){\text{cos}}\varphi + \hfill \\ {e_{p2}}\left( {ws, swh} \right){\text{cos}}2\varphi \hfill \\ \end{gathered} $ | (3) |
其中Δe为粗糙海面发射率; p为极化状态, epi(i=0, 1, 2)为各种风速、有效波高条件下的拟合系数。epi为风速和有效波高的函数, 当风速和有效波高数据已知时, 可通过查表的方式确定各阶拟合系数epi, 进而计算海表发射率。
2 L波段粗糙海面辐射特性分析 2.1 海面辐射与风场的关系本文对各种海面有效波高条件下提取的粗糙海面发射率进行了平均, 获得了粗糙海面发射率与海面风速和风向的关系。结果表明, 粗糙海面发射率中包含了海面风向信息, 且随着海面风速的增大, 粗糙海面发射率对风向的依赖也更为明显。当风速低于10 m/s时, 风向引起的粗糙海面发射率变化小于0.000 3, 相当于0.1K的亮温变化; 当风速达到15 m/s时, 风向引起的粗糙海面发射率变化可达0.003, 相当于1K的亮温变化, 是低风速时的10倍。相对于辐射计百K量级的亮温数据, 风向对亮温的影响较小, 因此双极化微波辐射计并不适合风向提取。
|
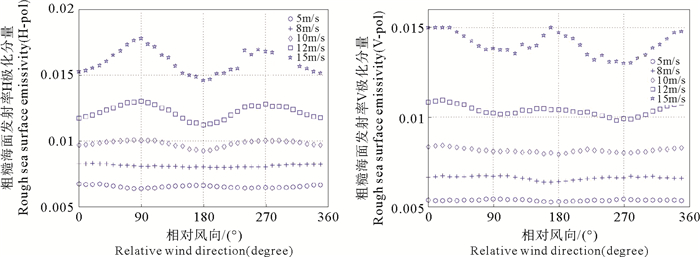
图 1 粗糙海面发射率与相对风向的关系(左:H极化; 右:V极化) Fig. 1 Relationship of emissivityand relative wind direction (left:H-pol; right:V-pol) |
由上图可知, H/V极化海面发射率对海面风向响应存在差别。对于H极化分量, 在10 m/s以下较低风速条件时, 顺风向的海面发射率高于侧风向发射率, 即存在正的顺风-侧风各向异性(Positive upwind-crosswind asymmetry, PUC); 而风速高于10 m/s时, 顺风向的海面发射率低于侧风向发射率, 即存在负的顺风-侧风各向异性(Negative upwind-crosswind asymmetry, NUC); V极化对风向的响应与H极化相反, 即在低风速下存在NUC现象, 而在高风速下存在PUC现象。这种H/V海面发射率对风向的不同响应, 与其他学者的研究结果吻合[16, 22]。同时, 15 m/s以上的高风速下提取的粗糙海面发射率曲线噪声大于低风速情况。这是由于15 m/s以上的高风速数据明显少于较低风速的数据, 其仅相当于5 m/s风速时数据的1/6左右, 因此, 高风速条件下提取的粗糙海面发射率数据噪声较大。
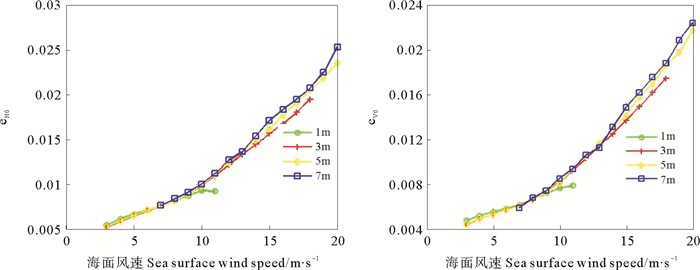
图 2为各种有效波高条件下, 0阶拟合系数ep0随海面风速的变化关系。不难发现当风速在7 m/s以下时, ep0受有效波高影响较小; 当风速上升时, 各曲线有分离的趋势, 说明有效波高的影响在增大。在各波高条件下, 各拟合系数均随着风速的增大而上升。
|
图 2 系数ep0与海面风速的关系(左:H极化; 右:V极化) Fig. 2 Relationship of coefficients ep0and surface wind speed (left:H-pol; right:V-pol) |
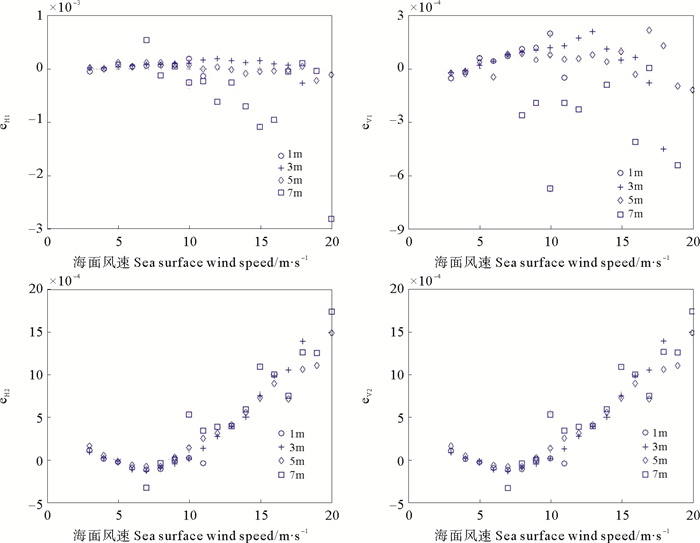
图 3为不同海面有效波高条件下海面发射率一阶和二阶拟合参数eH1, 2和eV1, 2随海面风速的变化曲线。图中可见, 由于5 m以上有效波高的数据量少, 其拟合参数偏离了其他条件下的拟合系数, 这在eH1和eV1图线中尤为明显。
|
图 3 ep1, p2系数与风速的关系(左:H极化; 右:V极化) Fig. 3 Relationship of coefficients ep1, p2 and surface wind speed (left:H-pol; right:V-pol) |
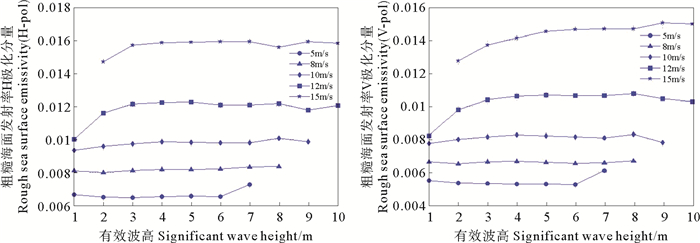
海面波浪同样影响海面粗糙度, 进而影响星载微波辐射计观测数据。本文利用提取的粗糙海面发射率和后向散射系数, 在0~360°风向范围内进行了平均, 以研究不同风速条件下, 粗糙海面辐射特性对海面有效波高的响应特性。图 4为粗糙海面发射率与有效波高的关系。可以看出, 海面有效波高的取值范围受海面风速影响, 在5 m/s的较低风速条件下, 海面波高没有7 m以上的数据; 在15 m/s高风速条件下, 海面波高没有2 m以下的数据。在相同的海面有效波高条件下, H/V极化粗糙海面发射率均随着风速的增大而上升; 且随着风速的增大, 海面发射率增大的也更快。在海面风速一定的条件下, 粗糙海面发射率随有效波高增大有增大的趋势, 但并不明显。
|
图 4 不同风速下海面发射率与有效波高的关系(左:H极化; 右:V极化) Fig. 4 Relationship of emissivity and wave height under different wind speeds(left:H-pol; right:V-pol) |
利用上面建立的GMF模型, 由海面亮温数据中提取平静海面亮温贡献:
| $ TB_{P, flat}^{obs} = {\text{ }}T{B_{P, surf}}-\Delta {e_{P, rough}}*SST。$ | (4) |
TBP, flatobs 上标obs代表从Aquarius观测数据中提取的平静海面亮温, 将提取的平静海面亮温代入以下的代价函数:
| $ \begin{gathered} {\chi ^2} = \frac{{{{(TB_H^{obs}-TB_H^{sim}(f, {\theta _i}, SST, SSS))}^2}}}{{{\sigma _{{T_{BH}}}}^2}} + \hfill \\ \frac{{{{(TB_V^{obs}-TB_V^{sim}(f, {\theta _i}, SST, SSS))}^2}}}{{{\sigma _{{T_{BV}}}}^2}} 。\hfill \\ \end{gathered} $ | (5) |
其中:TBPsim为采用Klein-Swift海水介电模型结合菲涅尔公式计算的平静海面亮温; f为电磁波频率, 取1.4GHz; θi为Aquarius波束一观测角, 取29.36°; SST为海表温度, 采用WindSat测量结果; SSS为HYCOM海表盐度初猜值; σTBH和σTBV为权重因子, 取为亮温噪声等效温度(NEDT)0.1 K。利用Levenberg-Marquardt非线性迭代方法, 不断调整海表盐度值使代价函数收敛, 进而输出海表盐度反演结果。
3.2 盐度反演结果误差分析本文利用±5d、±50 km的时空窗口对反演结果与Argo数据进行匹配, 得到无雨条件下匹配数据14 926组, 对盐度反演误差进行了统计分析。
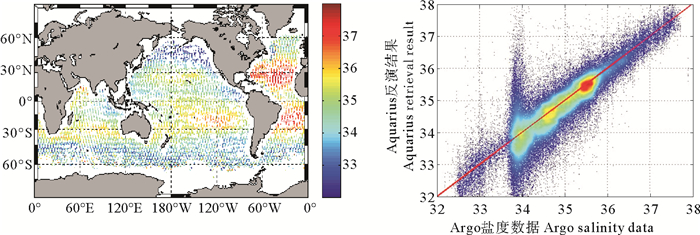
图 5为利用本文发展的参数化模型反演的海表盐度分布, 可见反演结果与海面盐度的空间分布特征吻合。赤道南北副热带海域存在着2个高盐水域, 盐度值在35以上, 大西洋海域的盐度高于太平洋海域; 赤道海域海表盐度明显低于副热带海域; 总体而言盐度随纬度呈马鞍形双峰分布。由散点图可知, 盐度反演误差主要分布于-1~1范围内; 与Argo数据相比反演结果存在约-0.1的系统误差, 标准差为0.48, 相关系数为0.89。海表盐度较高时反演误差较小, 34以下低盐区域的反演精度较低。自2011年6月Aquarius发射入轨以来, 有若干研究者采用盐度现场数据对Aquarius在全球[23-25]以及印度洋[26]、中国南海[27]等海域的精度进行了检验, 这些工作表明Aquarius反演结果与现场数据比较的标准差0.38~0.62, 与本文的结果相当。
|
图 5 盐度反演值分布(左)和盐度反演值与Argo数据的比较(右) Fig. 5 Spatial distribution of retrieved salinity(left), scatter plot of retrieved salinity and in-situ data(right) |
|
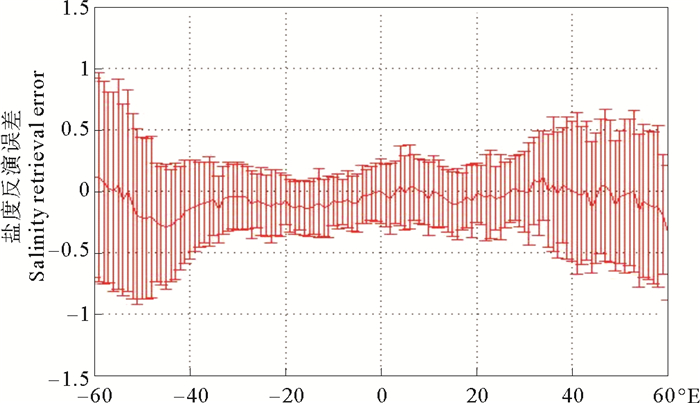
图 6 盐度反演平均偏差和±1倍标准差的纬度分布 Fig. 6 Latitudinal distribution of value of ΔSSS±1 standard deviation |
本文在纬度60°S~60°N范围内, 按1°间隔统计了盐度反演平均偏差及标准差数据。可见盐度反演偏差在高纬度较大, 特别是在南北半球西风带区域; ±40°之内的低纬度海域盐度反演标准差优于0.4。
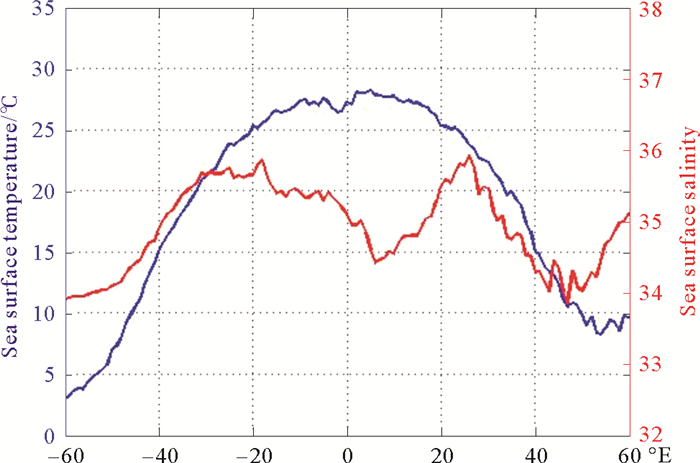
下图是Argo测量的海表温度、盐度随纬度的分布曲线。由图可知, 34psu海表盐度主要分布区域为南北纬40°以上的南大洋西风带和北太平洋海域, 该区域海面温度一般不高于15℃; 同时该区域常年受西风带影响, 海面波高和风速较大。数值模拟的结果表明, L波段亮温对海面盐度的敏感性随SST的增大而增大[28-29], 因此该海域较低的海表面温度, 降低了L波段亮温对盐度的敏感度, 从而导致该海域反演误差较大; 另外本文发展的参数化粗糙海面辐射模型在高风速下误差大于低风速, 也导致40°以上海域的反演误差较大。
|
图 7 Argo测量的海面盐度与温度的纬度分布 Fig. 7 Latitudinal distribution of SST/SSS from Argo |
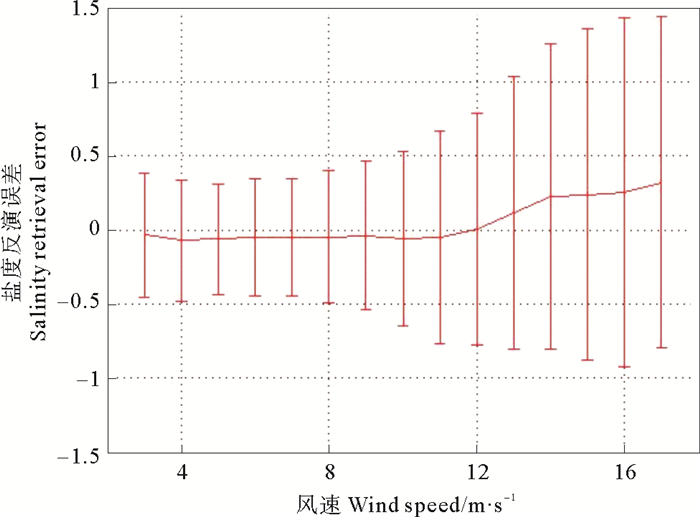
为进一步分析海面风速对反演结果的影响, 在2~20 m/s风速范围内按1 m/s风速间隔对盐度反演误差与风速关系进行了统计。如图 8所示, 在海面风速4~10 m/s范围内, 盐度反演算法偏差基本为0, 标准差约0.3~0.5范围内, 表明此时粗糙海面模型准确的描述了海面亮温对风速的响应。当风速高于10 m/s时, 平均偏差和标准差均随风速的增大而增大, 风速每增大1 m/s, 平均偏差约增大0.06, 标准差约增大0.1, 表明本文发展的粗糙海面模型在高风速下性能有待完善。反演结果的正偏差说明粗糙海面模型高估了风致粗糙海面亮温, 导致计算的平静海面亮温过低, 进而高估了海面盐度值。此外当风速小于4 m/s时, 盐度反演的标准差略大于4 m/s以上风速的情况。产生这种现象可能的原因在于, 本文用于盐度精度验证的Argo浮标的盐度测量深度为5 m, 而星载盐度计测量的是海表 1 cm处的盐度值; 当海表风速较小时, 风致海水垂直混合作用较小, 盐度垂向梯度较大, 从而导致反演结果与Argo盐度值差异较大。另外微波辐射计在低风速条件下观测风速精度下降, 影响了海面辐射GMF模型的精度, 也是导致盐度误差增大的原因。
|
图 8 反演误差与风速的关系 Fig. 8 Mean value of ΔSSS ±1 standard deviationas function of wind speed |
本文利用Aquarius和WindSat微波辐射计匹配数据, 发展了一种描述粗糙海面L波段微波辐射的参数化模型, 基于该模型分析了粗糙海面在不同风速、风向和波高条件下的辐射特性, 发现粗糙海面辐射H极化分量在10 m/s以下风速时, 存在正的顺风-侧风各向异性(PUC), 而风速高于10 m/s时, 存在负的顺风-侧风各向异性(NUC); 粗糙海面辐射V极化分量变化特征与H极化相反; 在海面风速一定的条件下, 粗糙海面发射率随有效波高增大有增大的趋势。进而利用该模型进行了海表盐度反演, 并利用Argo实测数据对反演结果进行了检验, 发现反演结果的平均偏差为-0.1, 标准差为0.48, 低纬度海域反演结果优于中高纬度海域, 反演结果受到海表温度和风速等条件的影响。结果表明, 本文发展的参数化模型可以比较准确的描述12m/s以下风速条件下的粗糙海面辐射, 但在高风速条件下对粗糙海面亮温存在高估, 反演误差可超过1。
致谢 感谢美国国家航空航天局、Remote Sensing System (RSS)、美国国家海洋和大气管理局(NOAA)为本文提供数据支持。
| [1] |
Font J, Camps A, Borges A, et al. SMOS:The Challenging Sea Surface Salinity Measurement From Space[J]. Proceedings of the IEEE, 2010, 98(5): 649-665. DOI:10.1109/JPROC.2009.2033096
(  0) 0) |
| [2] |
Yueh S H, Tang W, Fore A G. Validation of Aquarius sea surface salinity with in situ measurements form Argo floats and moored buoys[J]. Journal of Geophysical Research:Oceans, 2014, 119(9): 6171-6189. DOI:10.1002/2014JC010101
(  0) 0) |
| [3] |
Thomann G C. Remote measurement of salinity in an estuarine environment[J]. Remote Sensing of Environment, 1973(2): 249-259.
(  0) 0) |
| [4] |
Wilson J W, Simon H Y, Steven J D, et al. Passive active Land S-band(PALS)microwave sensor for ocean salinity and soil moisture measurement[J]. IEEE Trans Geosci Remote Sensing, 2001, 39(5): 1039-1049. DOI:10.1109/36.921422
(  0) 0) |
| [5] |
Goodberlet M A, Swift CT, Kevin K P, et al. Microwave remote sensing of coastal zone salinity[J]. Journal of Coastal Research, 1997, 13(2): 363-372.
(  0) 0) |
| [6] |
Wilson J W, Simon H Y, Steve JD, et al. High-stability L-band radiometer measurements of salt water[J]. IEEE Trans Geosci Remote Sensing, 2004, 42(9): 1829-1835. DOI:10.1109/TGRS.2004.833393
(  0) 0) |
| [7] |
Burrage DM, Heron ML, Hacker JM, et al. Structure and influence of tropical river plumes in the Great Barrier Reef:application and performance of an airborne sea surface salinity mapping system[J]. Remote Sensing of Environment, 2003, 85: 204-220. DOI:10.1016/S0034-4257(02)00206-7
(  0) 0) |
| [8] |
Font J, Camps A, Borges A, et al. SMOS:The Challenging Sea Surface Salinity Measurement From Space[J]. Proceedings of the IEEE, 2010, 98(5): 649-665. DOI:10.1109/JPROC.2009.2033096
(  0) 0) |
| [9] |
Vine D, Lagerloef G, Torrusio S. Aquarius and Remote Sensing of Sea Surface Salinity from Space[J]. Proceedings of the IEEE, 2010, 98(5): 688-703. DOI:10.1109/JPROC.2010.2040550
(  0) 0) |
| [10] |
王进, 张杰, 王晶. 基于ARGO浮标数据的星载微波辐射计Aquarius数据产品质量评估[J]. 海洋学报, 2015, 37(3): 46-53. Wang J, Zhang J, Wang J. Quality assessment of spaceborne microwave radiometer Aquarius data product based on ARGO buoy data[J]. Haiyang Xuebao, 2015, 37(3): 46-53. (  0) 0) |
| [11] |
Boutin J, Martin N, Yin X. First Assessment of SMOS Data Over Open Ocean:Part Ⅱ—Sea Surface Salinity[J]. IEEE Trans Geosci Remote Sens, 2012, 50(5): 1662-1675. DOI:10.1109/TGRS.2012.2184546
(  0) 0) |
| [12] |
Fore A.G, Yueh S.H, Tang W. Aquarius Wind Speed Products:Algorithms and Validation[J]. IEEE Trans Geosci Remote Sens, 2014, 52(5): 2920-2927. DOI:10.1109/TGRS.2013.2267616
(  0) 0) |
| [13] |
SMOS Team. SMOS L2 OS Algorithm Theoretical Baseline Document(SO-TN-ARG-GS-0007)[J]. IFREMER, 2013, 33-36.
(  0) 0) |
| [14] |
Hollinger J P. Passive microwave measurements of sea surface roughness[J]. IEEE Trans Geosci Elec, 1997, 9(3): 165-169.
(  0) 0) |
| [15] |
Camps A, Font J, Vall-llossera M, et al. WISE 2000 and 2001 field experiments in support of SMOS mission:Sea surface L-Band brightness temperature observations and their application to sea surface salinity retrieval[J]. IEEE Trans Geosci Remote Sens, 2004, 42(4): 804-823. DOI:10.1109/TGRS.2003.819444
(  0) 0) |
| [16] |
Yueh S H, Tang W, Fore A G, et al. L-Band Passive and Active Microwave Geophysical Model Functions of Ocean Surface Winds and Applications to Aquarius Retrieval[J]. IEEE Trans Geosci Remote Sens, 2013, 51(9): 4619-4632. DOI:10.1109/TGRS.2013.2266915
(  0) 0) |
| [17] |
Meissner T, Wentz F J, Ricciardulli L. The emission and scattering of L-band microwave radiation from rough ocean surfaces and wind speed measurements from the Aquarius sensor[J]. Journal of Geophysical Research:Oceans, 2014, 119(9): 6499-6522. DOI:10.1002/2014JC009837
(  0) 0) |
| [18] |
Meissner T, Wentz F J. Wind-vector retrievals under rain with passive satellite microwave radiometers[J]. IEEE Trans Geosci Remote Sens, 2009, 47(9): 3065-3083. DOI:10.1109/TGRS.2009.2027012
(  0) 0) |
| [19] |
Liebe H. MPM-An atmospheric millimeter-wave propagation model[J]. International Journal of Infrared and Millimeters Waves, 1989, 10(6): 631-650. DOI:10.1007/BF01009565
(  0) 0) |
| [20] |
Wentz F J, Le Vine D. Aquarius Salinity Retrieval AlgorithmAlgorithm Theoretical Basis Document[R]. RSS Technical Report 082912, 2012.
(  0) 0) |
| [21] |
Klein L A, Swift C T. An Improved Model for the Dielectric Constant of Sea Water at Microwave.Frequencies[J]. IEEE Trans Geosci Remote Sens, 1997, 25(1): 104-111.
(  0) 0) |
| [22] |
Yueh S H, Tang W, Fore A G. Aquarius Geophysical Model Function and Combined Active Passive Algorithm for Ocean Surface Salinity and Wind Retrieval[J]. Journal of Geophysical Research:Oceans, 2014, 119(8): 5360-5379. DOI:10.1002/2014JC009939
(  0) 0) |
| [23] |
Ebuchi N, Abe H. Evaluation of Sea Surface Salinity Oobserved by Aquarius[C]. IGASS 2012, 5767-5769.
(  0) 0) |
| [24] |
Drucker R, Riser S C. Validation of Aquarius Sea Surface Salinity with Argo:Analysis of Error Due to Depth of Measurement and Vertical Salinity Stratification[J]. Journal of Geophysical Research:Oceans, 2014, 119(7): 4626-2637. DOI:10.1002/2014JC010045
(  0) 0) |
| [25] |
Vine D L, Dinnat E P, Meissner T, et al. Status of Aquarius/SAC-D and Aquarius Salinity Retrievals[J]. IEEE Trans Geosci Remote Sens, 2015, 26(5): 1-15.
(  0) 0) |
| [26] |
Ratheesh S, Sharma R, Sikhakolli R. Assessing Sea Surface Salinity Derived by Aquarius in the Indian Ocean[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(4): 719-722. DOI:10.1109/LGRS.2013.2277391
(  0) 0) |
| [27] |
王新新, 杨建洪, 赵冬至, 等. Aquarius/SAC-D卫星盐度数据在中国南海的准确度评估[J]. 热带海洋学报, 2013, 32(5): 23-28. Wang X, Yang J, Zhao D, et al. Assessment of Aquarius/SAC-D salinity data accuracy in the South China Sea[J]. Journal of Tropical Ocanography, 2013, 32(5): 23-28. (  0) 0) |
| [28] |
齐震, 魏恩泊, 刘淑波. 粗糙海面L和C波段的代价函数多参量遥感反演分析[J]. 海洋科学, 2012, 36(1): 100-107. Q iZ, Wei E, Liu S. Rough sea surface cost function retrieval models for L and C band[J]. Marine Sciences, 2012, 36(1): 100-107. (  0) 0) |
| [29] |
Qi Z, Wei E. Analysis of cost functions for retrieving sea surface salinity[J]. Journal of Ocean University of China, 2012, 11(2): 147-152. DOI:10.1007/s11802-012-1872-3
(  0) 0) |
2. The First Institute of Oceanography, SOA, Qingdao 266061, China,;
3. College of Physics, Qingdao University, Qingdao 266071, China
 2018, Vol. 48
2018, Vol. 48


