2. 中国海洋大学山东省海洋工程重点实验室,山东 青岛 266100
近年来,风电场的建设向深远海区域逐渐拓展,浮式风机基础是深远海风机安装的主要结构形式。浮式基础在海洋环境中受到风、浪、流的作用会产生多自由度的复杂运动,风机与浮式基础之间的耦合运动会影响整个结构的完整性与安全性,导致风机的推力和功率产生周期性波动,影响发电效率[1]。因此,需要利用风机运动模拟装置开展关于风载荷如何影响风机运动、发电效率,以及风机与浮式基础间的相互作用的研究。
国内外学者对于浮式风机运动模拟试验装置展开了一系列相关研究。Bayati等[2]提出的“Hexafloat”运动平台可以模拟浮式风机在海上受到波浪流力的作用下产生的多自由度运动,为风机设计和性能评估提供依据;Belloli等[3]进行了浮式风机半物理模型(Hardware in the loop)风洞试验,探究了非定常空气动力学以及风机控制器与平台动力学间的相互作用;Ferrari等[4]提出了一种用于六自由度试验平台运动综合的遗传算法,对六自由度平台几何参数进行优化;Giberti等[5]设计了一种用于模拟海上浮式风机和船舶多自由度运动的装置,可以考虑不同的设计需求;张浩[6]改进了基于Hexaglide的风洞模型支撑系统的驱动布置方式和平台铰接点位置,并进行驱动力仿真分析;谭兴强[7]根据风洞试验的需求,设计了一种6-PUS并联机器人用于模拟风机平台运动,得到了驱动力曲线,证明了机构的刚度满足支撑系统需要。然而,现有的研究往往聚焦于运动模拟装置,没有考虑运动模拟装置与风机的耦合及系统响应,模拟运动与风机实际运动差别较大。
为此,本文给出了用于风洞试验的海上浮式风机的运动模拟装置的设计,对其运动学进行了分析,基于Kane方程建立了风机—运动模拟装置的动力学模型,并对装置模拟风机浮式基础完成2种单自由度运动进行数值计算。在多体动力学软件中模拟浮式基础的多自由度耦合运动,对不同风载荷下的浮式风机-运动模拟装置系统进行动力学仿真,得到风机-运动模拟装置系统的动力学响应。
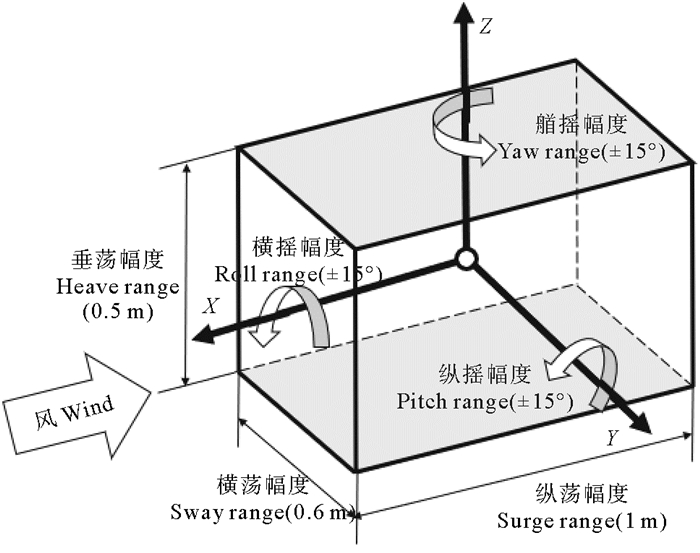
1 装置设计 1.1 构型选择参考Matha[8]对于3种不同形式的海上浮式风机在FAST软件中的模拟结果,考虑风机浮式基础可能出现的极限位移及最大加速度,确定了需要运动模拟装置提供的运动幅度。表 1为模拟装置需要提供的运动幅度,图 1显示了需要模拟装置达到的工作空间。
|
|
表 1 模拟装置运动幅度 Table 1 Motion range of simulator |
|
图 1 工作空间 Fig. 1 Desired workspace |
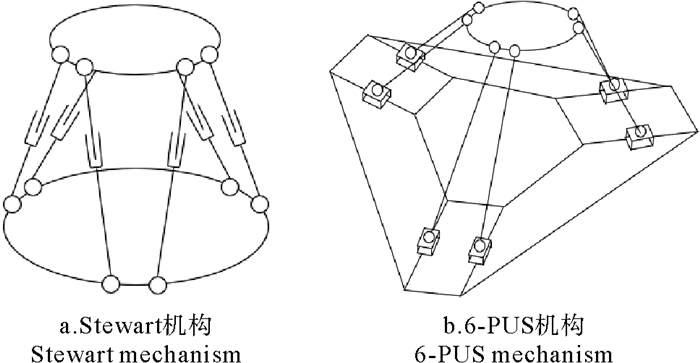
常见的运动模拟装置构型包括Stewart机构和6-PUS机构(见图 2)等,这两种机构均可模拟六自由度运动,但支链周向布置使得工作空间关于中心对称,作动器在支链上使得运动时惯性较大。
|
图 2 运动模拟装置常用构型 Fig. 2 Common configurations of motion simulator |
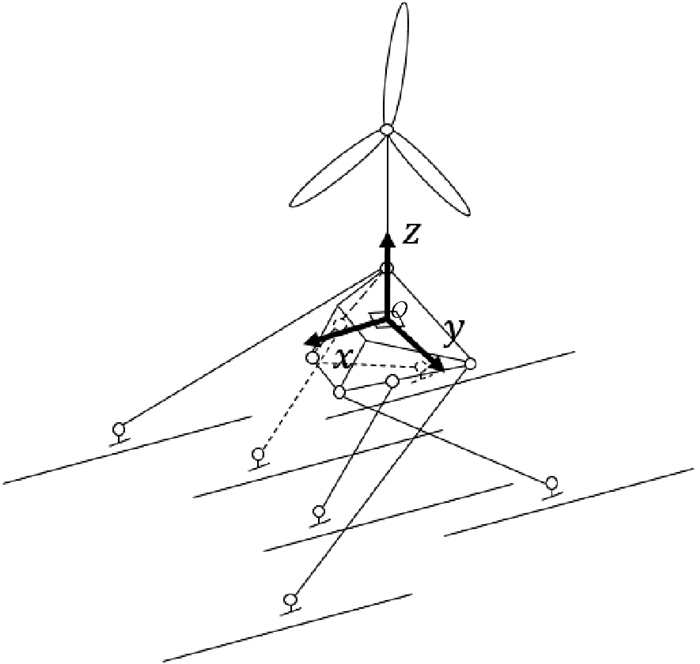
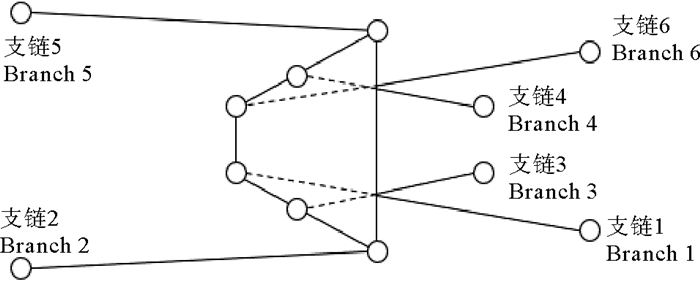
根据模拟装置所需提供的运动幅度,结合浮式风机风洞实验需要,选择如图 3所示的6-PSS构型作为运动模拟装置的基本结构:6根导轨并行,每条支链由最下端的滑块驱动,滑块和上平台均通过球铰和定长杆连接,通过控制滑块在导轨上的移动,带动连杆和上平台运动,实现风机的六自由度运动,图 4表示滑块及连杆分布情况。除了具有并联机构共有的无累计误差、承载能力强、动态性能好等特性,文献[2]对平行导轨六自由度并联机构用于风机运动模拟平台的优势进行如下总结:
|
图 3 运动模拟装置简图 Fig. 3 Brief of simulator |
|
图 4 滑块及连杆布置情况 Fig. 4 Layout of sliders and rods |
(1) 工作空间中心低,为风机模型保留更大的自由空间,有利于减小比例效应及堵塞效应对于试验的影响;
(2) 工作空间的主要方向和风向一致,可以模拟浮式风机的大幅纵荡运动;
(3) 驱动装置全部固定在机架上,可以控制负载质量与移动质量间的比例,减少支链间的干扰,使系统具有较好的动态特性。
1.2 尺寸设计浮式风力机模型设计参考5MW-NREL[9]风力发电机参数,根据Froude缩放方法进行缩放,选择比例系数λL=1/60,风机的移动(纵荡、横荡和垂荡)使用上述比例尺量进行缩放,时间轴按λt=
|
|
表 2 风机—运动模拟装置设计参数 Table 2 Parameters of FOWT-motion simulator |
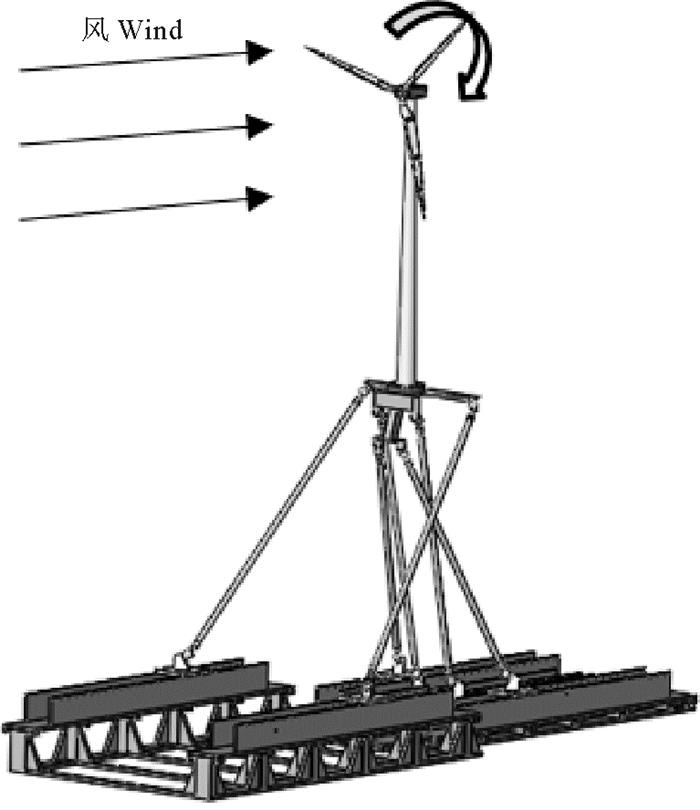
|
图 5 搭载风机模型的运动模拟装置 Fig. 5 Motion simulator with FOWT model |
以初始动平台的质心处为原点,建立固定坐标系{O0-x0y0z0}和连体坐标系{Op-xpypzp},用xiS、yiS、ziS(i=1, 2, …, 6)表示6个滑块在固定坐标系中的位置坐标,xiD、yiD、ziD(i=1, 2, …, 6)表示6个球铰在连体坐标系中的坐标,xiD(0)、yiD(0)、ziD(0)(i=1, 2, …, 6)表示球铰在固定坐标系的坐标[10],坐标系坐标轴方向定义如图 3所示,滑块1、滑块2、滑块3所在导轨与滑块6、滑块5、滑块4所在导轨分别关于连体坐标系O-xz平面对称。
空间转动采用卡尔丹角描述,刚体对固定参考系的任意转动,先绕x轴转α角,再绕新的y轴转β角,最后绕新的z轴转γ角,刚体转动的方向余弦矩阵为:
| $[\mathit{\boldsymbol{A}}] = \left[ {\begin{array}{*{20}{c}} {\cos \beta \cos \gamma }&{ - \cos \beta \sin \gamma }&{\sin \beta }\\ {\sin \alpha \sin \beta \cos \gamma + \cos \alpha \sin \gamma }&{ - \sin \alpha \sin \beta \sin \gamma + \cos \alpha \cos \gamma }&{ - \sin \alpha \cos \beta }\\ { - \cos \alpha \sin \beta \cos \gamma + \sin \alpha \sin \gamma }&{\cos \alpha \sin \beta \sin \gamma + \sin \alpha \cos \gamma }&{\cos \alpha \cos \beta } \end{array}} \right]{\rm{。}}$ | (1) |
选取整个机构的广义坐标为{q}={x, y, z, α, β, γ},式中: x, y, z为动平台质心在固定坐标系中的3个平动位移;α, β, γ为动平台在固定坐标系的3个卡尔丹角。6个球副在固定坐标系中的位置可以描述为:
| $\left[ {\begin{array}{*{20}{l}} {x_i^{D(0)}}\\ {y_i^{D(0)}}\\ {z_i^{D(0)}} \end{array}} \right] = [\mathit{\boldsymbol{A}}]\left[ {\begin{array}{*{20}{l}} {x_i^D}\\ {y_i^D}\\ {z_i^D} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} x\\ y\\ z \end{array}} \right], (i = 1, 2, 3, 4, 5, 6){\rm{。}}$ | (2) |
令六根连杆长度为li,根据球副位置关系有:
| ${l_i} = \sqrt {{{\left( {x_i^S - x_i^{D(0)}} \right)}^2} + {{\left( {y_i^S - y_i^{D(0)}} \right)}^2} + {{\left( {z_i^S - z_i^{D(0)}} \right)}^2}}{\rm{。}} $ | (3) |
可求得6个滑块在固定坐标系中的位置:
| $x_i^S = x_i^{D(0)} + k\sqrt {l_i^2 - {{\left( {y_i^S - y_i^{D(0)}} \right)}^2} - {{\left( {z_i^S - z_i^{D(0)}} \right)}^2}} {\rm{。}}$ | (4) |
进一步可以得到滑块速度表达式:
| $\dot x_i^S = \dot x_i^{D(0)} + k\frac{{\left( {y_i^S - y_i^{D(0)}} \right)\dot y_i^{D(0)} + \left( {z_i^S - z_i^{D(0)}} \right)\dot z_i^{D(0)}}}{{\sqrt {l_i^2 - {{\left( {y_i^S - y_i^{D(0)}} \right)}^2} - {{\left( {z_i^S - z_i^{D(0)}} \right)}^2}} }}{\rm{。}}$ | (5) |
式中:当i=1, 3, 4, 6时,k=-1;当i=2, 5时,k=1。通过以上分析,当上平台模拟运动给定,可以求得滑块所需的输入运动。
2.2 风载荷计算对风载荷进行分析时,可以将其分为平均风和脉动风,分别应用静力理论和动力理论进行近似处理[11]。
风力机受到的平均风载荷根据式(6)计算[12],脉动风可视为零均值的高斯随机过程,在频域内根据功率谱函数进行描述,常用谐波叠加、逆傅里叶变换等方法生成脉动风时程。为简化模型,脉动风载荷在数值计算及动力学模拟中被考虑为平均风载荷以正弦规律变化。
| ${F_{\rm{w}}} = 0.5{\rho _{\rm{ \mathsf{ α}}} }{\rm{A}}u_{{\rm{rel}}}^2{C_{\rm{T}}}\left( {{U_{\rm{r}}}} \right){\rm{。}}$ | (6) |
式中:ρα为空气密度;Α为叶轮扫略面积;urel为来风和风机的相对速度;CT(Ur)为推力系数,是相对风速的函数。
2.3 风机-运动模拟装置动力学方程建立参考文献[10]中的建模方法,根据Kane方程,风机-运动模拟装置的广义主动力与广义惯性力之和等于零,有
| $\mathit{\boldsymbol{f}} + {\mathit{\boldsymbol{f}}^*} = 0{\rm{。}}$ | (7) |
式中:f为系统受到的广义主动力;f*为系统受到的广义惯性力。广义主动力向量:
| ${\mathit{\boldsymbol{f}}} = {\mathit{\boldsymbol{J}}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{F}}} + {\mathit{\boldsymbol{J}}}_{\rm{C}}^{\rm{T}}{\mathit{\boldsymbol{G}}} + {\mathit{\boldsymbol{J}}}_{{\rm{f}}1}^{\rm{T}}{{\mathit{\boldsymbol{F}}}_{\rm{W}}}{\rm{。}}$ | (8) |
广义惯性力向量:
| ${{\mathit{\boldsymbol{f}}}^*} = {\mathit{\boldsymbol{J}}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{F}}}_{\rm{S}}^* + {\mathit{\boldsymbol{J}}}_{\rm{C}}^{\rm{T}}{\mathit{\boldsymbol{F}}}_{\rm{C}}^* + {\mathit{\boldsymbol{J}}}_{{\rm{f}}2}^{\rm{T}}{\mathit{\boldsymbol{F}}}_{\rm{f}}^* + {\mathit{\boldsymbol{J}}}_{\rm{ \mathsf{ ω} }} ^{\rm{T}}{\mathit{\boldsymbol{T}}}_{\rm{C}}^* + {\mathit{\boldsymbol{J}}}_{\rm{ \mathsf{ ω} }} ^{\rm{T}}{\mathit{\boldsymbol{T}}}_{\rm{f}}^*{\rm{。}}$ | (9) |
式中:JS为滑块的偏速度矩阵;F为滑块驱动力主矢矩阵;JC为动平台偏速度矩阵;G为重力主矢矩阵;Jf1为风机叶轮中心处的偏速度矩阵;FW为风力主矢矩阵;FS*为滑块惯性力矩阵;FC*为动平台惯性力矩阵;Jf2为风机质心处的偏速度矩阵;Ff*为风机惯性力矩阵;Jω为动平台偏角速度矩阵;TC*为动平台惯性力矩;Tf*为风机惯性力矩。
将式(8)、(9)中的相关矩阵写成带广义速度向量和广义加速度向量的形式,可得最终的简化方程
| $\begin{array}{l} \;\;\;\;\;\;\;\left( {{\mathit{\boldsymbol{J}}}_{\rm{S}}^{\rm{T}}m{{\mathit{\boldsymbol{J}}}_{\rm{S}}} + {\mathit{\boldsymbol{J}}}_{\rm{C}}^{\rm{T}}{\mathit{\boldsymbol{M}}}{{\mathit{\boldsymbol{J}}}_{\rm{C}}} + {\mathit{\boldsymbol{J}}}_{\rm{ \mathsf{ ω} }} ^{\rm{T}}{{\mathit{\boldsymbol{I}}}_{\rm{A}}}{{\mathit{\boldsymbol{J}}}_{\rm{ \mathsf{ ω} }} } + {\mathit{\boldsymbol{J}}}_{{\rm{i}}2}^{\rm{T}}{{\mathit{\boldsymbol{m}}}_{\rm{f}}}{{\mathit{\boldsymbol{J}}}_{{\rm{f}}2}} + {\mathit{\boldsymbol{J}}}_{\rm{ \mathsf{ ω} }} ^{\rm{T}}{{\mathit{\boldsymbol{I}}}_{\rm{f}}}{{\mathit{\boldsymbol{J}}}_{\rm{ \mathsf{ ω} }} }} \right)\\ \mathop {\mathit{\boldsymbol{q}}}\limits^{..} + \left( {{\mathit{\boldsymbol{J}}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{m}}}{{\mathit{\boldsymbol{J}}}_{\rm{S}}} + {\mathit{\boldsymbol{J}}}_{\rm{C}}^{\rm{T}}{\mathit{\boldsymbol{M}}}{{\dot J}_{\rm{C}}} + {\mathit{\boldsymbol{J}}}_{\rm{ \mathsf{ ω} }} ^{\rm{T}}{{\mathit{\boldsymbol{I}}}_{\rm{A}}}{{\dot J}_{\rm{ \mathsf{ ω} }} } + {\mathit{\boldsymbol{J}}}_{\rm{ \mathsf{ ω} }} ^{\rm{T}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}{{\mathit{\boldsymbol{I}}}_{\rm{A}}}{{\mathit{\boldsymbol{J}}}_{\rm{ \mathsf{ ω} }} } + {\mathit{\boldsymbol{J}}}_{{\rm{i}}2}^{\rm{T}}{{\mathit{\boldsymbol{m}}}_{\rm{f}}}{{\mathop {\mathit{\boldsymbol{J}}}\limits^. }_{{\rm{F}}2}}} \right.\\ \left. { + {\mathit{\boldsymbol{J}}}_{\rm{ \mathsf{ ω} }} ^{\rm{T}}{{\mathit{\boldsymbol{I}}}_{\rm{f}}}{{\dot J}_{\rm{ \mathsf{ ω} }} } + {\mathit{\boldsymbol{J}}}_{\rm{ \mathsf{ ω} }} ^{\rm{T}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}{{\mathit{\boldsymbol{I}}}_{\rm{f}}}{{\mathit{\boldsymbol{J}}}_{\rm{ \mathsf{ ω} }} }} \right)\mathop {\mathit{\boldsymbol{q}}}\limits^. = {\mathit{\boldsymbol{J}}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{F}}} + {\mathit{\boldsymbol{J}}}_{\rm{C}}^{\rm{T}}{\mathit{\boldsymbol{G}}} + {\mathit{\boldsymbol{J}}}_{{\rm{f}}1}^{\rm{T}}{{\mathit{\boldsymbol{F}}}_{\rm{w}}}{\rm{。}} \end{array}$ | (10) |
式中:m为滑块质量矩阵;M为动平台质量矩阵;IA为动平台过质心关于连体坐标系轴的惯性张量;
至此,当已知广义速度和广义加速度以及上部风机受到的风载荷,可通过计算得到各滑块驱动力。
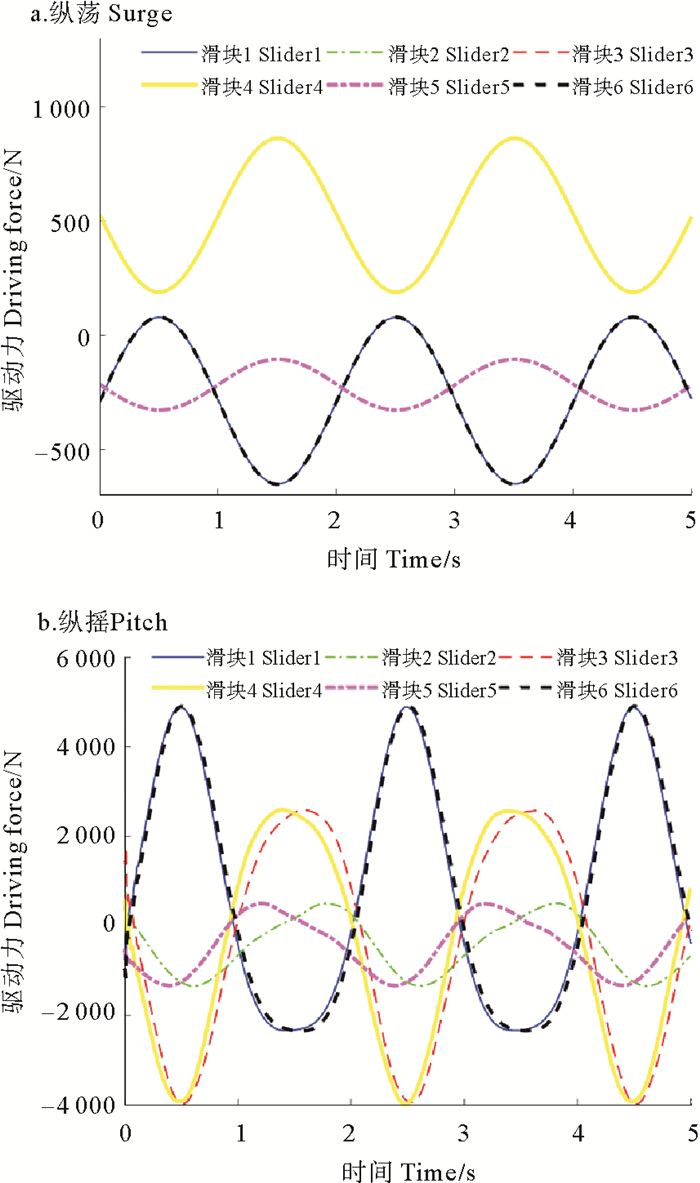
3 动力学仿真 3.1 运行工况算例波浪和风的联合作用对浮式风机纵荡及纵摇运动影响较大,根据上述建立的风机-运动模拟装置系统数学模型,对模拟风机完成纵荡和纵摇运动分别进行数值计算。工况选取纵荡振幅50 mm,纵摇振幅10°,频率0.5 Hz。在风机叶轮中心处施加恒定50 N的风力,纵荡、纵摇运动得到的滑块驱动力分别如图 6a、b所示。
|
图 6 滑块驱动力 Fig. 6 The driving force of the slider |
根据图 6,当运动模拟装置模拟风机作纵荡或纵摇运动时,对称导轨上的滑块驱动力大小及变化规律完全相同或在一定程度上相似,具体表现为:当模拟纵荡运动时,对称导轨上的滑块驱动力(如:滑块3、4)大小及变化相同;当模拟纵摇运动时,对称导轨上的滑块驱动力大小相等,变化周期相同,但相位角存在一定差异,滑块2驱动力与滑块5驱动力相位差最大,滑块1驱动力与滑块6驱动力相位差最小。浮式风机在波、浪、流作用下产生的是不规律的耦合运动,需进一步研究模拟浮式基础实际运动时,模拟装置各支链驱动力的大小及变化规律。
3.2 动力学仿真浮式风机在海洋环境中受到的风载荷可分为平均风和脉动风,平均风周期大于结构自振周期,作用相当于静载荷;脉动风变化周期往往和结构自振周期较接近,应作为动荷载处理[13]。
对风机-运动模拟装置系统进行动力学仿真,以期得到在风机受到不同风载荷情况下,模拟平台实现耦合运动时滑块需提供的驱动力,按照以下步骤仿真:
(1) 根据给定海浪条件,在ANSYS Workbench中计算OC3-Hywind单桩型风机[14]浮式基础在给定条件下的时域响应,作为模拟平台的运动。
(2) 对动平台施加驱动,得到6个滑块的速度曲线,将得到的速度作为输入,分别施加在对应的六个滑块上,仿真得到滑块的驱动力变化曲线。
(3) 对风机受到不同风载荷情况下的运动模拟系统进行仿真,对比驱动力变化。
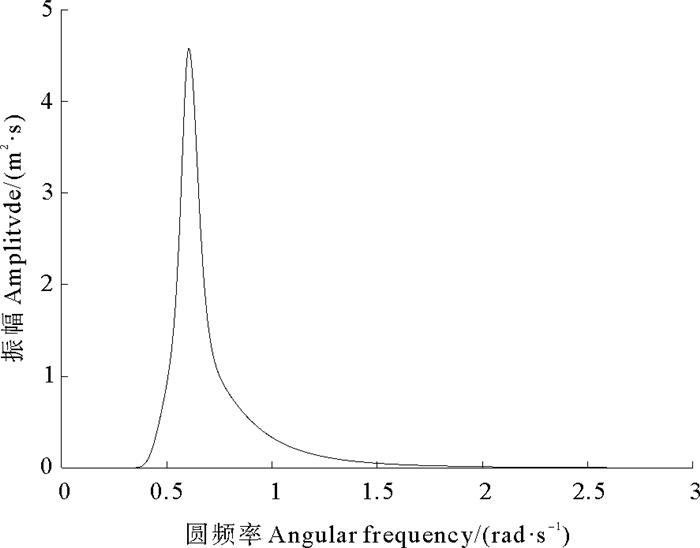
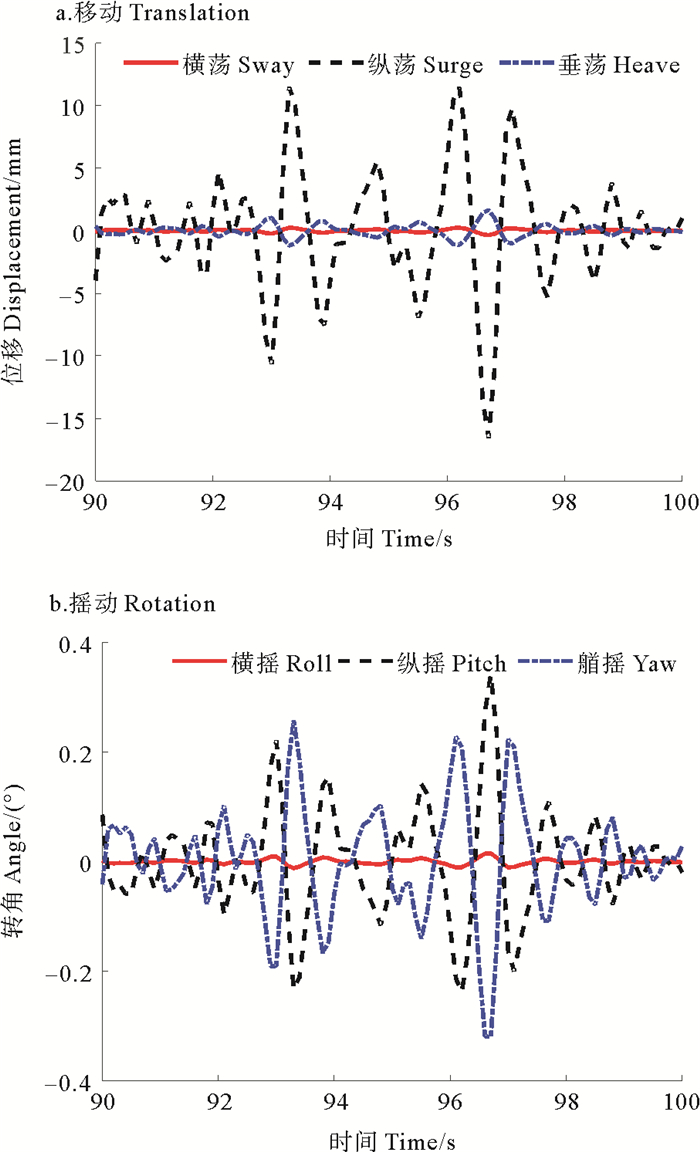
给定有效波高3.66 m,周期9.7 s,图 7表示给定海况下的JONSWAP海浪谱。计算OC3-Hywind单桩型风机浮式基础在波浪流作用下的时域响应,并根据选取的比例因子进行缩放如图 8所示。给定运动模拟装置上平台运动所需的各滑块位移如图 9。仿真得到不同风载荷作用下各滑块驱动力结果如图 10。
|
图 7 JONSWAP海浪谱 Fig. 7 JONSWAP spectrum |
|
图 8 浮式基础六自由度运动 Fig. 8 6-DOF motion of floating foundation |
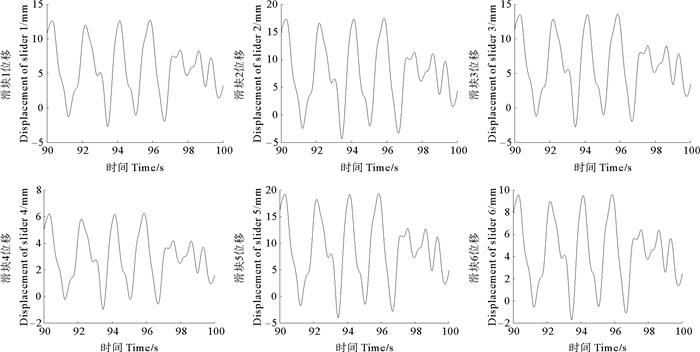
|
图 9 滑块位移 Fig. 9 Displacements of slider |
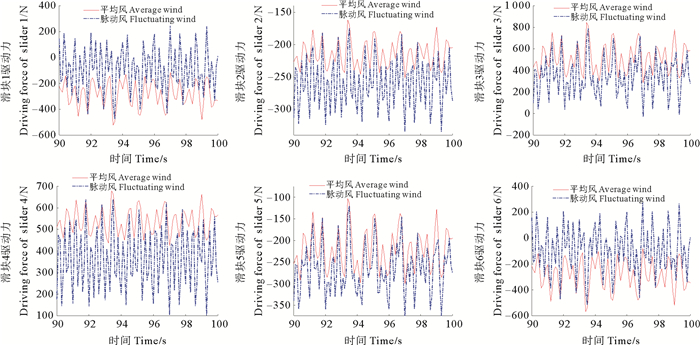
|
图 10 不同风载荷下各滑块驱动力 Fig. 10 Driving force with different wind load |
由图 8可知,浮式风机在海洋环境中的运动以纵荡、纵摇和艏摇为主。
根据图 9显示,尽管数值有所差异,各滑块位移曲线变化相似,这使上平台和风机在滑块的驱动下产生以纵荡、纵摇、艏摇为主的六自由度耦合运动。图 10可以看出,和风机受平均风载荷下的滑块驱动力比较,脉动风载荷使滑块驱动力峰值增大,变化周期缩短,要求的加速度增大。不同支链滑块驱动力差距较大,根据选取海况下风机及浮式基础的运动而言,滑块3及滑块4所在支链需提供的驱动力变化范围及驱动力峰值最大。应根据需要模拟的运动计算驱动力范围为各支链选择合适的驱动器。
4 结论本文对基于6-PSS并联机构的海上浮式风机试验的运动模拟装置进行动力学研究,基于Kane方法建立了风机-运动模拟装置系统动力学模型,并用数值方法对运动装置的运动和受力进行了求解,得到以下结论:
(1) 当运动模拟装置模拟风机纵荡或纵摇运动时,对称导轨上的滑块在驱动力数值和变化趋势上相同或存在一定相似,具体表现为纵荡运动时对称导轨上滑块的驱动力完全相同,纵摇运动时对称导轨上滑块的驱动力存在一定相位差;
(2) 风载荷的变化将导致驱动力产生数值及周期变化,具体表现在当受到脉动风载荷时,驱动单元需提供的驱动力变化幅度增大,变化频率加快;
(3) 运动模拟装置各支链所需提供的驱动力存在较大差异,就模拟选取海况下风机及浮式基础的运动而言,支链3和支链4需要提供更大的驱动力。
| [1] |
王强, 廖康平, 马庆位, 等. 海上浮式风机耦合运动响应的研究[C]//第十九届中国海洋(岸)工程学术讨论会论文集(上). 重庆: 中国海洋工程学会, 2019: 249-253. Wang Q, Liao K P, Ma Q W, et al. Study on coupled motion response of floating offshore wind turbine[C]// Proceedings of the 19th China Marine (Shore) Engineering Symposium. Chongqing: China Marine Engineering Society, 2019: 249-253. (  0) 0) |
| [2] |
Bayati I, Belloli M, Ferrari D, et al. Design of a 6-DoF robotic platform for wind tunnel tests of floating wind turbines[J]. Energy Procedia, 2014, 53: 313-323. DOI:10.1016/j.egypro.2014.07.240 (  0) 0) |
| [3] |
Belloli M, Bayati I, Facchinetti A, et al. A hybrid methodology for wind tunnel testing of floating offshore wind turbines[J]. Ocean Engineering, 2020, 210: 107592. DOI:10.1016/j.oceaneng.2020.107592 (  0) 0) |
| [4] |
Ferrari D, Giberti H. A genetic algorithm approach to the kinematic synthesis of a 6-DOF Parallel manipulator[C]//2014 IEEE Conference on Control Applications. Antibes: IEEE, 2014: 222-227.
(  0) 0) |
| [5] |
Giberti H, Ferrari D. A novel hardware-in-the-loop device for floating offshore wind turbines and sailing boats[J]. Mechanism and Machine Theory, 2015, 85: 82-105. DOI:10.1016/j.mechmachtheory.2014.10.012 (  0) 0) |
| [6] |
张浩. 六自由度并联风洞模型支撑系统机构优化[D]. 北京: 清华大学, 2011. Zhang H. Optimization of Design Parameters for a Six-DOF Parallel Wind Tunnel Model Positioning Mechanism[D]. Beijing: Tsinghua University, 2011. (  0) 0) |
| [7] |
谭兴强, 谢志江. 6_PUS并联支撑机器人柔性动力学研究[J]. 机械设计与制造, 2014(2): 133-135. Tan X Q, Xie Z J. Study on flexible dynamics of 6_PUS parallel support robot[J]. Machinery Design & Manufacture, 2014(2): 133-135. (  0) 0) |
| [8] |
Matha D. Model development and loads analysis of an offshore wind turbine on a tension leg platform with a comparison to other floating turbine concepts[R]. Golden, Colorado: National Renewable Energy Laboratory, 2009.
(  0) 0) |
| [9] |
Jonkman J, Butterfield S, Musial W, et al. Definition of a 5-MW reference wind turbine for offshore system development[R]. Golden, Colorado: National Renewable Energy Laboratory, 2009.
(  0) 0) |
| [10] |
赵海峰. 基于KANE方法的并联六自由度机构的动力学计算[J]. 计算力学学报, 2010, 28: 165-170. Zhao H F. Dynamic computation of the 6-DOF parallel mechanism based on kane method[J]. Chinese Journal of Computational Mechanics, 2010, 28: 165-170. (  0) 0) |
| [11] |
曾一非. 海洋工程环境[M]. 上海: 上海交通大学出版社, 2007. Zeng Y F. Marine Engineering Environment[M]. Shanghai: Shanghai Jiaotong University Press, 2007. (  0) 0) |
| [12] |
Nielsen F G, Hanson T D, Skaare B. Integrated dynamic analysis of floating offshore wind turbines[C]//Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering. Hamburg: ASME, 2006: OMAE2006-92291.
(  0) 0) |
| [13] |
Liu M Y, Chiang W L, Hwang J H, et al. Wind-induced vibration of high-rise building with tuned mass damper including soil-structure interaction[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6-7): 1092-1102. DOI:10.1016/j.jweia.2007.06.034 (  0) 0) |
| [14] |
Jonkman J. Definition of the floating system for phase Ⅳ of OC3[R]. Golden, Colorado: National Renewable Energy Laboratory, 2010.
(  0) 0) |
2. The Key Laboratory of Ocean Engineering of Shandong Province, Ocean University of China, Qingdao 266100, China
 2022, Vol. 52
2022, Vol. 52


