Nicholson果蝇模型
| $ x^{\prime}(t)=-\alpha x(t)+\beta x(t-\tau) \mathrm{e}^{-\gamma x(t-\tau)} $ | (1) |
是1980年数学家W. S. C. Gurney等[1]给出的, 目的是为了描述Nicholson有关果蝇数量周期振动的经典实验[2]。其中x(t)表示t时刻果蝇数量, α>0表示成虫的日均死亡率, β>0表示日均最大产卵率, 1/γ>0表示最大繁殖率下的果蝇数量, τ>0表示果蝇从出生到成熟的时间, 即传代时间。
对于生物种群, 除了常见的时间延迟现象, 脉冲影响也普遍存在, 例如种群的捕获或者补充, 同时, 现实生活中广泛存在的随机因素也影响模型的动力学性质。因此, 在模型(1)的基础上, 各种更符合实际的Nicholson果蝇模型被广泛研究。2010年, L. Berezansky等[3]收集了Nicholson果蝇模型发展30年来重要的代表性成果, 并提出了一些开放问题。2010年至今, 关于Nicholson果蝇模型的研究成果开始大量涌现, 例如正周期解的全局吸引性、概周期解的存在性、指数稳定性和零解稳定性等, 主要结果详见文献[4-11]。
但是,在诸多关于Nicholson果蝇模型中,对于脉冲和随机因素的考虑和研究较少,基于上述原因,本文将研究一类脉冲随机Nicholson果蝇模型的均方指数最终有界性。
1 预备知识在现实世界, 描述有关人口和生态问题的微分方程中, 系数和时滞通常是时变的, 再加之随机与脉冲因素的作用, 所以, 模型(1)自然被推广为如下脉冲随机Nicholson果蝇模型:
| $ \left\{ {\begin{array}{*{20}{c}} {{\rm{d}}x(t) = \left[ { - \alpha (t)x(t) + \sum\limits_{j = 1}^m {{\beta _j}} (t) \cdot } \right.}\\ {\left. {x\left( {t - {\tau _j}(t)} \right){{\rm{e}}^{ - {\gamma _j}(t)x\left( {t - {\tau _j}(t)} \right)}}} \right]{\rm{d}}t + }\\ \begin{array}{l} \sigma (t)x(t){\rm{d}}\omega (t), t \ne {t_k}, t \ge {t_0}\\ \Delta x\left( {{t_k}} \right) = {I_k}\left( {x\left( {t_k^ - } \right)} \right), k \in {{\bf{N}}}\\ x\left( {{t_0} + s} \right) = \phi (s), s \in [ - \tau , 0] \end{array} \end{array}} \right.。$ | (2) |
式中:α(t), βj(t), γj(t)和σ(t)均为连续函数且上、下确界为正常数;τj(t)(j=1, 2, …,m), 是非负连续有界函数;σ2(t)是噪声强度, ω(t)是定义在满足通常条件下的完全概率空间
记R+=[0, +∞), 令PC([-τ, 0], R+)为所有逐段右连续函数ϕ: [-τ, 0]→ R+组成的函数族, 且赋予范数
令
| $ \|\phi\|_{L^2}^2=E\left[\sup\limits _{-\tau \leqslant \theta \leq 0}|\phi(\theta)|^2\right] <\infty 。$ |
式中E表示随机过程的期望。
由Nicholson果蝇模型的实际意义, 只需考虑模型(2)的正解, 我们假设对于任何初始函数ϕ(s)∈
为叙述方便, 给出本文后面使用的记号如下:
| $ \begin{gathered} \alpha=\inf _{t \in \bf{R}^{+}}\{\alpha(t)\}, \beta_j=\sup _{t \in \bf{R}^{+}}\left\{\beta_j(t)\right\}, 1 \leqslant j \leqslant m, \\ \sigma^2=\sup _{t \in \bf{R}^{+}}\left\{\sigma^2(t)\right\}, \gamma_j=\inf _{t \in \bf{R}^{+}}\left\{\gamma_j(t)\right\}, 1 \leqslant j \leqslant m 。\end{gathered} $ |
定义1 模型(2)具有全局均方指数最终有界性, 是指如果存在常数λ>0, K>0和M>0, 对任何初始条件
| $ E\|x(t)\|^2 \leqslant K\|\phi\| \|_{L^2}^2 \mathrm{e}^{-\lambda\left(t-t_0\right)}+M, t \geqslant t_0 \text { 。} $ |
式中: M为模型(2)最终的一个界, λ为指数收敛率。
2 主要结果定理1 记
(H1)
(H2)
这里Tk=tk-tk-1≥τ。
则模型(2)是全局均方指数最终有界的, 且指数收敛率为
| $ M = \frac{\mathit{\Lambda }}{\rho }{{\rm{e}}^{\rho T}}\left( {\frac{1}{\xi } - \underline \eta } \right)\frac{\xi }{{\xi - 1}} + \frac{\mathit{\Lambda }}{\rho }\left( {{{\rm{e}}^{\rho T}} - 1} \right), $ |
式中:
证明 令Lyapunov泛函
| $ V(x(t))=x^2(t) 。$ |
应用
| $ \begin{gathered} \mathscr{L} V(x(t))=2 x(t)[-\alpha(t) x(t)+ \\ \left.\sum\limits_{j=1}^m \beta_j(t) x\left(t-\tau_j(t)\right) \mathrm{e}^{-\gamma_j(t) x\left(t-\tau_j(t)\right)}+\sigma^2(t) x^2(t)\right] 。\end{gathered} $ | (3) |
注意到
| $ \begin{aligned} & \mathscr{L} V(x(t)) \leqslant-2 \alpha x^2(t)+\sum\limits_{j=1}^m \frac{2 \beta_j}{\gamma_j \mathrm{e}} x(t)+\sigma^2 x^2(t) \leqslant \\ & \left(-2 \alpha+\sigma^2+\frac{m}{\mathrm{e}}\right) x^2(t)+\frac{1}{\mathrm{e}} \sum\limits_{j=1}^m\left(\frac{\beta_j}{\gamma_j}\right)^2= \\ & \rho x^2(t)+{\mathit{\Lambda}}, t \in\left(t_{k-1}, t_k\right], k \in {\bf{N}} 。\end{aligned} $ | (4) |
将(4)式乘以e-ρt可得
| $ \mathscr{L}\left(\mathrm{e}^{-\rho t} V(x(t))\right) \leqslant {\mathit{\Lambda}} \mathrm{e}^{-\rho t}, $ | (5) |
利用Itô公式和(5)式可得
| $ \begin{aligned} & E V(x(t)) \leqslant E V\left(x\left(t_{k-1}^{-}\right)\right) \mathrm{e}^{\rho\left(t-t_{k-1}\right)}-\frac{{\mathit{\Lambda }}}{\rho}\left[1-\mathrm{e}^{\rho\left(t-t_{k-1}\right)}\right] , \\ & t \in\left(t_{k-1}, t_k\right], k \in {\bf{N}}。\end{aligned} $ | (6) |
由条件(H1), 有
| $ V\left(x\left(t_k^{+}\right)\right) \leqslant \eta_k V\left(x\left(t_k\right)\right), k \in {\bf{N}} \text { 。} $ | (7) |
在(6)式中, 令k=1, 可得
| $ \begin{aligned} & \quad E V\left(x\left(t_k\right)\right) \leqslant E V\left(x\left(t_0\right)\right) \mathrm{e}^{\rho\left(t-t_0\right)}-\frac{{\mathit{\Lambda }}}{\rho}\left[1-\mathrm{e}^{\rho\left(t-t_0\right)}\right] ,\\ & t \in\left(t_0, t_1\right]。\end{aligned} $ | (8) |
由(7)、(8)式及条件Tk≥τ, 有
| $ \begin{gathered} E V\left(x\left(t_1^{+}\right)\right) \leqslant \eta_1 E V\left(x\left(t_1\right)\right) \leqslant \\ \eta_1 E V\left(x\left(t_0\right)\right) \mathrm{e}^{\rho\left(t-t_0\right)}-\frac{\eta_1 {\mathit{\Lambda }}}{\rho}\left[1-\mathrm{e}^{\rho\left(t-t_0\right)}\right], \end{gathered} $ | (9) |
由(6)及(9)式, 有
| $ \begin{aligned} & E V(x(t)) \leqslant E V\left(x\left(t_1^{+}\right)\right) \mathrm{e}^{\rho\left(t-t_1\right)}-\frac{{\mathit{\Lambda }}}{\rho}\left[1-\mathrm{e}^{\rho\left(t-t_1\right)}\right] \leqslant \\ & \eta_1 E V\left(x\left(t_0\right)\right) \mathrm{e}^{\rho\left(t-t_0\right)}+\frac{\eta_1 {\mathit{\Lambda }}}{\rho} \mathrm{e}^{\rho\left(t-t_0\right)}-\frac{\eta_1 {\mathit{\Lambda }}}{\rho} \mathrm{e}^{\rho\left(t-t_1\right)}+ \\ & \frac{{\mathit{\Lambda }}}{\rho} \mathrm{e}^{\rho\left(t-t_1\right)}-\frac{{\mathit{\Lambda }}}{\rho}, t \in\left(t_1, t_2\right]。\end{aligned} $ | (10) |
以此类推, 一般地, 可得
| $ \begin{array}{r} E V(x(t)) \leqslant \prod\limits_{i=1}^k \eta_i E V\left(x\left(t_0\right)\right) \mathrm{e}^{\rho\left(t-t_0\right)}+\sum\limits_{j=1}^k \sum\limits_{i=j}^k \eta_i \cdot \\ \frac{{\mathit{\Lambda }}}{\rho}\left[\mathrm{e}^{\rho\left(\left(t-t_{j-1}\right)\right.}-\mathrm{e}^{\rho\left(t-t_j\right)}\right]+\frac{{\mathit{\Lambda }}}{\rho} \mathrm{e}^{\rho\left(t-t_k\right)}-\frac{{\mathit{\Lambda }}}{\rho}, t \in\left(t_k, t_{k+1}\right]。\end{array} $ | (11) |
又因为ρ>0, ξ>1及条件(H2), 有
| $ 0 <\eta_k<\eta_k{ }^{{ }^{\rho T_k}}<\frac{1}{\xi}<1, k \in {\bf{N}}。$ | (12) |
结合(10)、(11)两式可得
| $ \begin{aligned} & E V(x(t)) \leqslant E V\left(x\left(t_0\right)\right)\left(\frac{1}{\xi}\right)^k \mathrm{e}^{\rho\left(t-t_k\right)}+ \\ & \sum\limits_{j=2}^k\left(\frac{1}{\xi}\right)^{k-j+1} \frac{{\mathit{\Lambda }}}{\rho} \mathrm{e}^{\rho\left(t-t_k\right)}\left(\frac{1}{\xi}-\eta_{j-1}\right)+ \\ & \frac{{\mathit{\Lambda }}}{\rho} \mathrm{e}^{\rho\left(t-t_k\right)}\left(\frac{1}{\xi}-\eta_k\right)+\frac{{\mathit{\Lambda }}}{\rho}\left(\mathrm{e}^{\rho\left(t-t_k\right)}-1\right) \leqslant \\ & E V\left(x\left(t_0\right)\right)\left(\frac{1}{\xi}\right)^k \mathrm{e}^{\rho\left(t-t_k\right)}+\frac{{\mathit{\Lambda }}}{\rho} \mathrm{e}^{\rho\left(t-t_k\right)}\left(\frac{1}{\xi}-{\underline \eta }\right) \sum\limits_{j=1}^k\left(\frac{1}{\xi}\right)^{j-1}+ \\ & \frac{{\mathit{\Lambda }}}{\rho}\left(\mathrm{e}^{\rho\left(t-t_k\right)}-1\right) \leqslant E V\left(x\left(t_0\right)\right)\left(\frac{1}{\xi}\right)^k \mathrm{e}^{\rho T}+ \\ & \frac{{\mathit{\Lambda }}}{\rho} \mathrm{e}^{\rho T}\left(\frac{1}{\xi}-{\underline \eta }\right) \frac{\xi}{\xi-1}+\frac{{\mathit{\Lambda }}}{\rho}\left(\mathrm{e}^{\rho T}-1\right), t \in\left(t_k, t_{k+1}\right]。\end{aligned} $ | (13) |
因为
| $ \begin{aligned} & \quad t-t_0=\left(t-t_k\right)+\left(t_k-t_{k-1}\right)+\cdots+\left(t_1-t_0\right) \leqslant \\ & (k+1) T, t \in\left(t_k, t_{k+1}\right], k \in {\bf{N}} 。\end{aligned} $ |
故, 有
| $ k \geqslant \frac{t-t_0}{T}-1, t \in\left(t_k, t_{k+1}\right], k \in {\bf{N}} { 。} $ | (14) |
结合(13)、(14)式, 可得
| $ \begin{aligned} & E V(x(t)) \leqslant E V\left(x\left(t_0\right)\right) \mathrm{e}^{-\frac{\ln \xi}{T}\left(t-t_0\right)} \xi \mathrm{e}^{\rho T}+ \\ & \frac{{\mathit{\Lambda }}}{\rho} \mathrm{e}^{\rho T}\left(\frac{1}{\xi}-\eta\right) \frac{\xi}{\xi-1}+\frac{{\mathit{\Lambda }}}{\rho}\left(\mathrm{e}^{\rho T}-1\right), t \geqslant t_0 。\end{aligned} $ | (15) |
从而, 有
| $ E\|x(t)\|^2 \leqslant K\|\phi\|_{L^2}^2 \mathrm{e}^{-\lambda\left(t-t_0\right)}+M, $ |
式中:
定理2 假设
证明 取Lyapunov泛函V(x(t))=x2(t), 由(4)式及ρ=0, 有
| $ L V(x(t)) \leqslant {\mathit{\Lambda }}, t \in\left(t_{k-1}, t_k\right], k \in {\bf{N}}。$ | (16) |
利用Itô公式可得
| $ \begin{aligned} & E V(x(t)) \leqslant E V\left(x\left(t_{k-1}^{+}\right)\right)+\left(t-t_{k-1}\right) {\mathit{\Lambda }}, \\ & t \in\left(t_{k-1}, t_k\right], k \in {\bf{N}} 。\end{aligned} $ | (17) |
在(17)式中取k=1, 得
| $ E V(x(t)) \leqslant E V\left(x\left(t_0\right)\right)+\left(t-t_0\right) {\mathit{\Lambda }}, t \in\left(t_0, t_1\right]。$ | (18) |
利用条件(H1)及(18)式可得
| $ \begin{gathered} E V\left(x\left(t_1^{+}\right)\right) \leqslant \eta_1 E V\left(x\left(t_1\right)\right) \leqslant \\ \eta_1 E V\left(x\left(t_0\right)\right)+\eta_1\left(t_1-t_0\right) {\mathit{\Lambda }} 。\end{gathered} $ | (19) |
联合(17)和(19)式, 有
| $ \begin{aligned} & \quad E V(x(t)) \leqslant E V\left(x\left(t_1^{+}\right)\right)+\left(t-t_1\right) {\mathit{\Lambda }} \leqslant \\ & \eta_1 E V\left(x\left(t_0\right)\right)+\eta_1\left(t_1-t_0\right) {\mathit{\Lambda }}+\left(t_1-t_0\right) {\mathit{\Lambda }}, t \in\left(t_1, \right. \\ & \left.t_2\right] \text { 。} \end{aligned} $ | (20) |
重复以上过程, 可得
| $ \begin{aligned} & E V(x(t)) \leqslant \prod\limits_{i=1}^k \eta_i E V\left(x\left(t_0\right)\right)+\sum\limits_{j=1}^k \sum\limits_{i=j}^k \eta_i(t- \\ & \left.t_{j-1}\right) {\mathit{\Lambda }}+\left(t-t_k\right) {\mathit{\Lambda }}, t \in\left(t_k, t_{k+1}\right]_{\circ} \end{aligned} $ | (21) |
由条件(H2)和ρ=0, 有
| $ \eta_k <\frac{1}{\xi}, k \in {\bf{N}}。$ | (22) |
联合(21)和(22)式, 得
| $ \begin{array}{r} E V(x(t)) \leqslant\left(\frac{1}{\xi}\right)^k E V\left(x\left(t_0\right)\right)+\sum\limits_{i=1}^k\left(\frac{1}{\xi}\right)^i T {\mathit{\Lambda }}+ \\ \left(t-t_k\right) {\mathit{\Lambda }} \leqslant\left(\frac{1}{\xi}\right)^k E V\left(x\left(t_0\right)\right)+\frac{T {\mathit{\Lambda }} \xi}{\xi-1}, t \in\left(t_k, t_{k+1}\right] \text { 。} \end{array} $ | (23) |
从而, 由(14)和(23)式, 得
| $ E V(x(t)) \leqslant E V\left(x\left(t_0\right)\right) \mathrm{e}^{-\frac{\ln \xi}{T}\left(t-t_0\right)} \xi+\frac{T {\mathit{\Lambda }} \xi}{\xi-1}, t \geqslant t_0 \text { 。} $ | (24) |
即
| $ E\|x(t)\|^2 \leqslant \xi\|\phi\|{ }_L^2 \mathrm{e}^{-\frac{\ln \hat{n}}{T}\left(t-t_0\right)}+\frac{T {\mathit{\Lambda }} \xi}{\xi-1}, t \geqslant t_0 。$ |
定理3 假设
证明 由ξ>1及条件(H2), 有
| $ \eta_k \mathrm{e}^{\rho T_k}<\frac{1}{\xi}<1, k \in {\bf{N}}。$ | (25) |
仍取Lyapunov泛函V(x(t))=x2(t), 类似(11)式的推导过程, 且注意到ρ < 0, 则有
| $ \begin{aligned} & E V(x(t)) \leqslant \prod\limits_{i=1}^k \eta_i \mathrm{e}^{\alpha T_i} E V\left(x\left(t_0\right)\right) \mathrm{e}^{\rho\left(t-t_k\right)}+ \\ & \sum\limits_{j=2}^k \sum\limits_{i=j}^k \eta_i \mathrm{e}^{\rho T_i\left(T-t_k\right)} \eta_{j-1}\left(1-\mathrm{e}^{\rho T_{j-1}}\right)+\eta_k \frac{{\mathit{\Lambda }}}{-\rho} \mathrm{e}^{\rho\left(t-t_k\right)}+ \\ & \frac{{\mathit{\Lambda }}}{-\rho}\left(1-\mathrm{e}^{\rho\left(t-t_k\right)}\right) \leqslant E V\left(x\left(t_0\right)\right)\left(\frac{1}{\xi}\right)^k \mathrm{e}^{\rho\left(t-t_k\right)}+ \\ & \frac{{\mathit{\Lambda }}}{-\rho} \mathrm{e}^{\rho\left(t-t_k\right)}-\bar{\eta} \sum\limits_{j=1}^k\left(\frac{1}{\xi}\right)^{j-1}\left(1-\mathrm{e}^{\rho T}\right)+\frac{{\mathit{\Lambda }}}{-\rho}\left(1-\mathrm{e}^{\rho\left(t-t_k\right)}\right) \leqslant \\ & E V\left(x\left(t_0\right)\right)\left(\frac{1}{\xi}\right)^k+\frac{{\mathit{\Lambda }}}{-\rho}\left(1-\mathrm{e}^{\rho T}\right)\left(\frac{\bar{\eta} \xi}{\xi-1}+1\right) \\ & t \in\left(t_k, t_{k+1}\right], \end{aligned} $ | (26) |
联合(14)和(26)式, 得
| $ \begin{aligned} & E V(x(t)) \leqslant E V\left(x\left(t_0\right)\right) \mathrm{e}^{-\frac{\ln \xi}{T}\left(t-t_0\right)} \xi+ \\ & \frac{{\mathit{\Lambda }}}{-\rho}\left(1-\mathrm{e}^{\rho T}\right)\left(\frac{\bar{\eta} \xi}{\xi-1}+1\right), t \geqslant t_0 。\end{aligned} $ | (27) |
即
| $ E\|x(t)\|^2 \leqslant \\ \xi\|\phi\|{ }_L^2 \mathrm{e}^{-\frac{\ln \xi}{T}\left(t-t_0\right)}-\frac{{\mathit{\Lambda }}}{\rho}\left(1-\mathrm{e}^{\rho T}\right)\left(\frac{\bar{\eta} \xi}{\xi-1}+1\right), t \geqslant t_0 。$ |
注1 由定理1和定理2, 因为ρ>0或ρ=0, 则无脉冲的模型(3)可能是无界的, 而这两个定理的结果说明, 一个无界的随机Nicholson模型在合适的脉冲控制率下能转变成一个有界的。
3 仿真实例例1 考虑模型(2), 其中的脉冲点为tk+1=tk+1, t0=0, k∈ N。且满足
| $ x\left(t_k^{-}\right)+I\left(x\left(t_k^{-}\right)\right)=x\left(t_k^{+}\right)=\mathrm{e}^{-1} x\left(t_k\right), $ |
则有
| $ \eta_k={\underline \eta }=\bar{\eta}=\mathrm{e}^{-2}, T_k=T=1 \text { 。} $ |
情形1 令
| $ \begin{aligned} & \alpha(t)=\sin t+\frac{4}{3}, m=2, \beta_1(t)=\beta_2(t)=\cos ^2 t+ \\ & 0.5, \tau_1(t)=\tau_2(t)=\gamma_1(t)=\gamma_2(t)=3-2 \sin ^2 t, \sigma(t)= \\ & \frac{2}{3}+\frac{1}{3} \cos t, \xi=1.5 。\end{aligned} $ |
则有
| $ \alpha=\frac{1}{3}, \beta_1=\beta_2=1.5, \gamma_1=\gamma_2=\tau=1, \sigma^2=1 \text { 。} $ |
可以验证
| $ \begin{gathered} \rho=\sigma^2-2 \alpha+\frac{m}{\mathrm{e}}=\frac{2}{\mathrm{e}}+\frac{1}{3}>0, \\ {\left[x\left(t_k^{-}\right)+I_k\left(x\left(t_k^{-}\right)\right)\right]^2 \leqslant \eta_k x^2\left(t_k\right), k \in {\bf{N}}, } \end{gathered} $ |
此情形下无脉冲和有脉冲影响的模型解的仿真图见图 1。
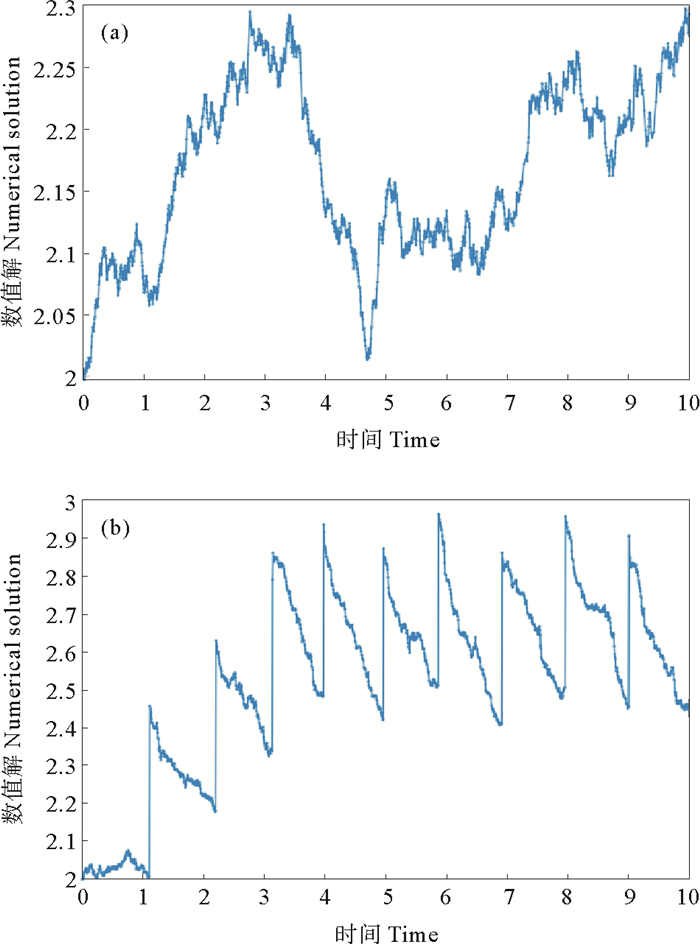
|
图 1 无脉冲情形(a)和脉冲情形(b)下模型(2)在情形1中的数值解 Fig. 1 Numerical solutions of model (2) in case 1 for the non-pulse case (a) and pulse case (b) |
由图 1可以看出, 在给定的参数下, 满足ρ>0, 模型(2)无脉冲的数值解无界, 加入脉冲条件的数值解是全局均方指数最终有界的,验证了注1。
情形2 令
| $ \alpha(t)=\cos ^2 t+\frac{3}{2 \mathrm{e}}, m=2, \beta_1(t)=\beta_2(t)=\sin t+1, \\ \tau_1(t)=\tau_2(t)=\gamma_1(t)=\gamma_2(t)=3-2 \sin t, \sigma(t)=\mathrm{e}^{-\frac{1}{2}}- \\ \frac{1}{5}+\frac{1}{5} \cos t, \xi=2 。$ |
则有
| $ \alpha=\frac{3}{2 \mathrm{e}}, \beta_1=\beta_2=1, \gamma_1=\gamma_2={ }_\tau=1, \sigma^2=\frac{1}{\mathrm{e}} 。$ |
可以验证
| $ \begin{gathered} \rho=0, \\ {\left[x\left(t_k^{-}\right)+I_k\left(x\left(t_k^{-}\right)\right)\right]^2 \leqslant \eta_k x^2\left(t_k\right), k \in {\bf{N}}, } \\ \ln \left(\xi \eta_k\right)+\rho T_k \approx-1.307 <0, \end{gathered} $ |
故定理2的条件均满足, 故由定理2的结论知, 模型(2)是全局均方指数最终有界的, 其收敛率为
此情形下无脉冲和有脉冲影响的模型解的仿真图见图 2。
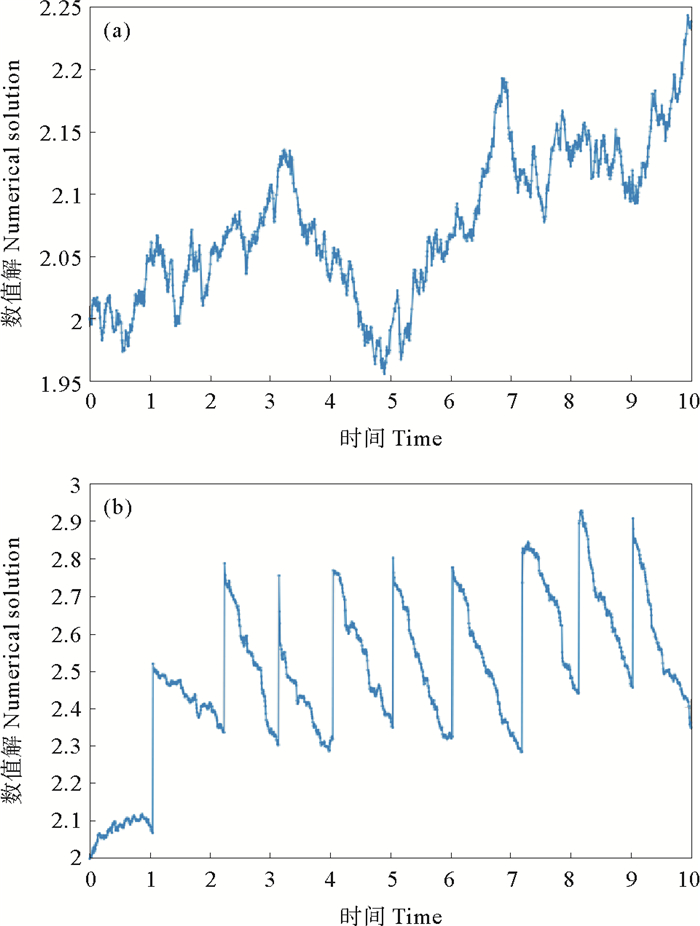
|
图 2 无脉冲情形(a)和脉冲情形(b)下模型(2)在情形2中的数值解 Fig. 2 Numerical solutions of model (2) in case 2 for the non-pulse case (a) and pulse case (b) |
由图 2可以看出, 在给定的参数下, 满足ρ=0, 模型(2)无脉冲的数值解无界,加入脉冲条件的数值解是全局均方指数最终有界的,验证了注1。
情形3 令
| $ \begin{aligned} & \alpha(t)=0.5+\sin ^2 t, m=2, \beta_1(t)=\beta_2(t)=\sin ^2 t+ \\ & 1.5, \tau_1(t)=\tau_2(t)=\gamma_1(t)=\gamma_2(t)=3-2 \sin t, \sigma(t)= \\ & \frac{1}{4}+\frac{1}{4} \cos t, \beta_1=\beta_2=1.5, \xi=2 。\end{aligned} $ |
则有
| $ \alpha=0.5, \gamma_1=\gamma_2=\tau=1, \sigma^2=0.25 \text { 。} $ |
可以验证
| $ \begin{gathered} \rho=\sigma^2-2 \alpha+\frac{m}{\mathrm{e}}=\frac{2}{\mathrm{e}}-0.75 \approx-0.014 <0, \\ {\left[x\left(t_k^{-}\right)+I_k\left(x\left(t_k^{-}\right)\right)\right]^2 \leqslant \eta_k x^2\left(t_k\right), k \in {\bf{N}}, } \\ \ln \left(\xi \eta_k\right)+\rho T_k \approx-1.321<0, \end{gathered} $ |
故定理3的条件均满足, 由定理3的结论知, 模型(2)是全局均方指数最终有界的, 其收敛率为
此情形下无脉冲和有脉冲影响的模型解的仿真图见图 3。
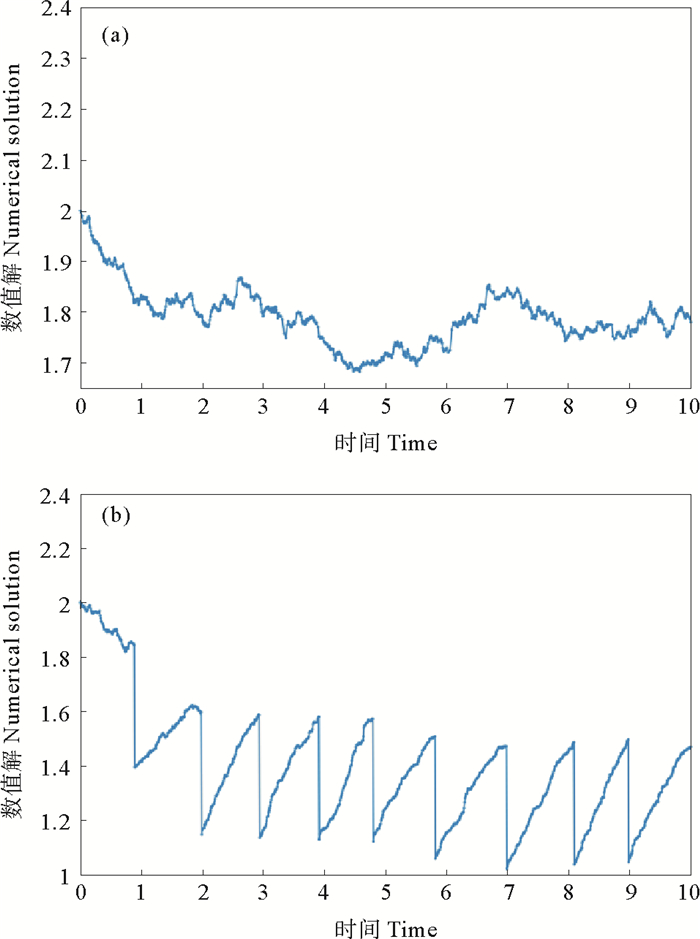
|
图 3 无脉冲情形(a)和脉冲情形(b)下模型(2)在情形3中的数值解 Fig. 3 Numerical solutions of model (2) in case 3 for the non-pulse case (a) and pulse case (b) |
由图 3可以看出, 在给定的参数下, 满足ρ < 0, 模型(2)无脉冲及有脉冲影响的数值解均为全局均方指数最终有界的。
4 结语本文讨论了一类有脉冲影响的随机Nicholson果蝇模型, 利用Lyapunov泛函、Itô公式及某些不等式技巧给出了该模型的均方指数最终有界的充分条件, 并估计了指数收敛率和最终的一个界,最后通过MATLAB仿真实验讨论了不同情形下脉冲对模型解的影响, 说明了本文所得结论的有效性。
| [1] |
Nicholson A J. An outline of the dynamics of animal populations[J]. Australian Journal of Zoology, 1954, 2(1): 9-65. DOI:10.1071/ZO9540009 (  0) 0) |
| [2] |
Gurney W S C, Blythe S P, Nisbet R M. Nicholson's blowflies revisited[J]. Nature, 1980, 287(5777): 17-21. DOI:10.1038/287017a0 (  0) 0) |
| [3] |
Berezansky L, Braverman E, Idels L. Nicholson's blowflies differential equations revisited: Main results and open problems[J]. Applied Mathematical Modelling, 2010, 34(6): 1405-1417. DOI:10.1016/j.apm.2009.08.027 (  0) 0) |
| [4] |
Liu B W. Permanence for a delayed Nicholson's blowflies model with a nonlinear density dependent mortality term[J]. Annales Polonici Mathematici, 2011, 101(2): 123-128. DOI:10.4064/ap101-2-2 (  0) 0) |
| [5] |
Hou X H, Lian D. New Results on periodic solutions of delayed Nicholson's blowflies models[J]. Electronic Journal of Qualitative Theory of Differential Equations, 2012, 24: 1-11. (  0) 0) |
| [6] |
Long F. Positive almost periodic solution for a class of Nicholson's blowflies model with a linear harvesting term[J]. Nonlinear Analysis: Real World Applications, 2012, 13(2): 686-693. DOI:10.1016/j.nonrwa.2011.08.009 (  0) 0) |
| [7] |
Shu H Y, Wang L, Wu J H. Global dynamics of Nicholson's blowflies equation revisited: Onset and termination of nonlinear oscillations[J]. Journal of Differential Equations, 2013, 255(9): 2565-2586. DOI:10.1016/j.jde.2013.06.020 (  0) 0) |
| [8] |
Deng K, Wu Y X. On the diffusive Nicholson's blowflies equation with distributed delay[J]. Applied Mathematics Letters, 2015, 50: 126-132. DOI:10.1016/j.aml.2015.06.013 (  0) 0) |
| [9] |
Yi T S, Zou X F. Global attractivity of the diffusive Nicholson blowflies equation with Neumann boundary condition: A non-monotone case[J]. Journal of Differential Equations, 2017, 245(11): 3376-3388. (  0) 0) |
| [10] |
Wang W T, Wang L Q, Chen W. Stochastic Nicholson's blowflies delayed differential equations[J]. Applied Mathematics Letters, 2018, 87: 20-26. (  0) 0) |
| [11] |
Abbas S, Niezabitowski M, Grace S R. Global existence and stability of Nicholson blowflies model with harvesting and random effect[J]. Nonlinear Dynamics, 2021, 103: 2109-2123. DOI:10.1007/s11071-020-06196-z (  0) 0) |
 2023, Vol. 53
2023, Vol. 53

