2. 中国地质大学(武汉) 海洋学院,湖北 武汉 430074
桩基础是海洋工程建设中常用的基础形式,海底滑坡是一种常见的地质灾害,其对桩基础的冲击可能直接导致桩基失效,进而危及上部结构安全。海底滑坡经过长距离流滑后,形态由最初的块状逐渐演变为流体状的泥流和浊流[1],常被视为特殊的非牛顿流体[2]。国内外多采用流体力学中传统的惯性拖曳力形式表达高速流滑体对构筑物的法向稳态冲击力[3-7](以下简称冲击力),但该表达形式显著低估了中低速流滑体的冲击力[8]。
近20年来,海底滑坡冲击构筑物的研究多集中在深海管线稳定性,Randolph和White[9]给出了冲击力的典型表达,即将海底管线截面受到的冲击力分解为拖曳力和承载力两部分:
| $ p=\frac{1}{2} C_{\mathrm{D}} \rho v^{2}+N_{\mathrm{C}} s_{\mathrm{u}}。$ | (1) |
式中:
| $ p=\frac{1}{2} C_{\mathrm{D}} \rho v^{2}+N_{\mathrm{C}} s_{\mathrm{u}}+C_{\gamma}\left(\rho-\rho_{\mathrm{w}}\right) g H。$ | (2) |
式中:Cγ为自重系数;ρw为水的密度;H为流滑体冲击管线时的初始高度。
流滑体冲击桩基础的试验和数值模拟数量有限。室内模型试验能够再现不同性质流滑体对单桩的冲击,但大都基于传统拖曳力形式总结冲击力表达式[13-14]。单治钢等[15]进行的流体动力学模拟考虑了流滑体的粘性、冲击速度和桩体直径,结果表明:如果流滑体高度远大于桩径,可合理忽略流滑体自重影响,即将该问题简化为二维平面应变问题,能够通过式(1)预测单位长度桩基础承受的冲击力。
当流滑体高度与桩径比值较小时,二维平面应变模拟不再适用,需按三维问题考虑,流滑体自由表面和自重的影响不能忽略。本文针对高度有限的流滑体,利用计算流体动力学软件Fluent建立三维模型,模拟不同粘性、速度和高度的流滑体对桩基的冲击过程,讨论流滑体自由表面和自重对冲击力的影响。对比已有的模型试验,验证数值模型的合理性。分析影响冲击力的主要因素,改进预测冲击力的表达式,并给出相关参数。
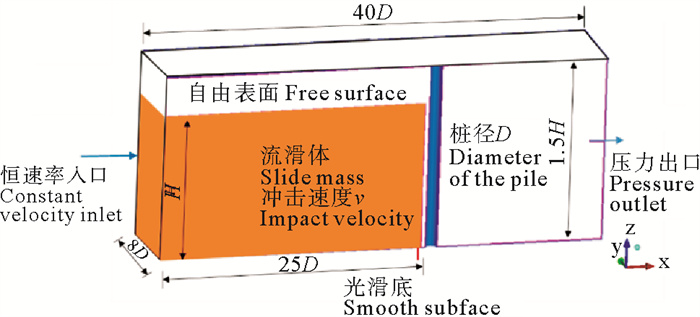
2 数值模型 2.1 有限体积模型和网格划分采用基于有限体积法的商业软件Fluent,建立流滑体与桩基相互作用的三维模型。为提高计算效率,考虑对称性,采用半模型进行分析(见图 1)。假设桩基为位置固定且完全粗糙的刚性结构,桩径为D;为避免边界效应,桩基与计算域左右侧面和背面的距离应足够大,取计算域宽为8D,滑坡体长为25D,其长度足以观察冲击过程中流变形态的变化,初始高度为H;为追踪流滑体上部自由表面的变化,取计算域高度为1.5H;底面光滑,左侧面由流滑体恒速率流入进口(高度为H)和大气压进口组成,流滑体通过进口时的速度等于冲击速度v;顶面和右侧面与外界联通,为大气压出口。
|
图 1 有限体积模型 Fig. 1 Finite volume model |
采用六面体单元生成网格,并在以桩基为中心的4D水平延展范围内加密网格,如图 2所示,桩基附近采用细网格,并且按比例向周围逐渐扩大。为减小计算结果对网格密度的依赖性,改变桩基周围的最小单元尺寸,分别取为0.05D、0.1D和0.2D。经过试算后,三种网格密度所得冲击力差别不超过4%。综合考虑计算效率与精度,以下计算中取桩基周围最小单元尺寸为0.1D。

|
图 2 网格划分 Fig. 2 Mesh generation |
当不考虑温度影响时,常用的非牛顿流体流变模型包括Bingham模型、幂律模型和Herschel-Bulkley (H-B)模型。长距离流滑体的特性表现为[16-17]:当应变速率足够小时,剪应力趋向零,流滑体的流动极易触发。因此本研究选择幂律流体描述流滑体的剪应力:
| $ \tau=K \dot{\gamma}^{n} 。$ | (3) |
式中:
参照已有研究[4],得到流滑体名义应变速率:
| $ \dot{\gamma}_{\mathrm{app}}=v / D 。$ | (4) |
结合式(3) 和(4) 得到幂律流体的名义剪应力:
| $ \tau_{\text {app }}=K \dot{\gamma}_{\mathrm{app}}{ }^{n}=K(v / D)^{n} \text { 。} $ | (5) |
幂律流体的雷诺数为:
| $ R e=\frac{\rho v^{2}}{\tau_{\mathrm{app}}}=\frac{\rho v^{2}}{K(v / D)^{n}}=\frac{\rho v^{2-n} D^{n}}{K} \text { 。} $ | (6) |
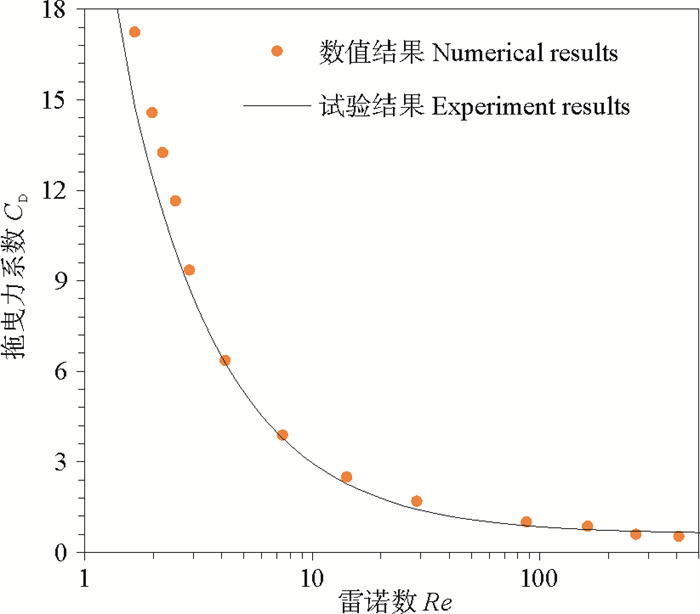
由于海底滑坡冲击管线的研究相对成熟,为验证幂律模型描述流滑体性质的可行性,故首先模拟海底滑坡冲击管线问题,与Zakeri等[5]的物理模型试验进行比较。管线直立于海床表面,轴线与流滑体冲击方向的夹角为90°,此时冲击情况与图 1类似。管线直径为50 mm,流滑体参数取值如表 1。按照该物理模型试验中的总结方式,将冲击力表达为纯拖曳力,Fluent模拟与试验得到的拖曳力系数如图 3所示。可以看出,当雷诺数Re>5时,二者基本吻合;当Re < 5时,数值结果略高,但误差在15%以内。这表明建立的数值模型是可靠的。
|
图 3 冲击管线的数值与试验结果对比 Fig. 3 Comparison between numerical and experiment results for the pipelines |
冯斌等[13]对冲击桩基础问题设计了物理模型试验,该试验没有采用幂律模型,而是采用H-B模型描述流滑体剪应力:
| $ \tau=\tau_{c}+K \dot{\gamma}^{n} 。$ | (7) |
式中,τc为屈服应力。H-B流体对应的雷诺数为:
| $ R e=\frac{\rho v^{2}}{\tau_{c}+K(v / D)^{n}}。$ | (8) |
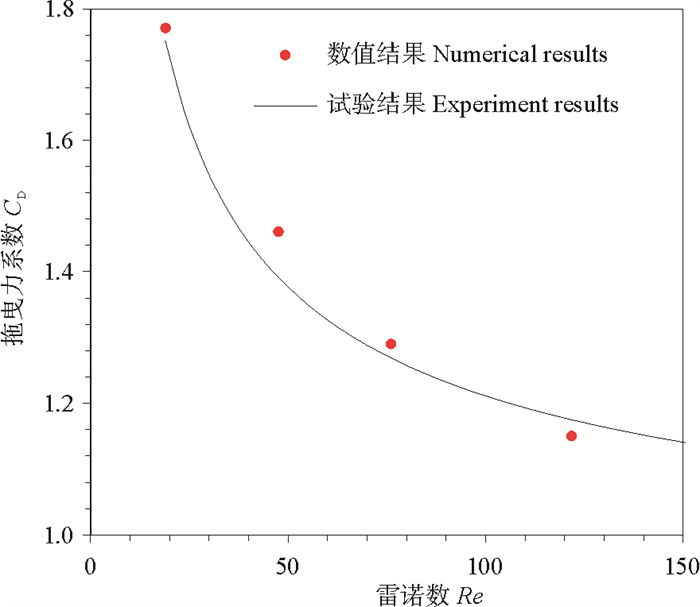
高岭土与石英砂混合而成的流滑体沿4°的斜坡滑动,冲击外径为32 mm的单桩,流滑体距离单桩200 mm。流滑体在斜坡上的初始速度与材料参数见表 2,为验证数值模型对桩基础冲击问题的可行性,Fluent模拟中相应采用H-B模型。按照纯拖曳力形式表达冲击力,Fluent模拟与试验拟合的拖曳力系数如图 4所示,二者吻合较好,相差不超过10%。这证明了建立的三维数值模型能够有效模拟桩体冲击问题。
|
图 4 冲击桩体的数值与试验结果对比 Fig. 4 Comparison between numerical and experiment results for the piles |
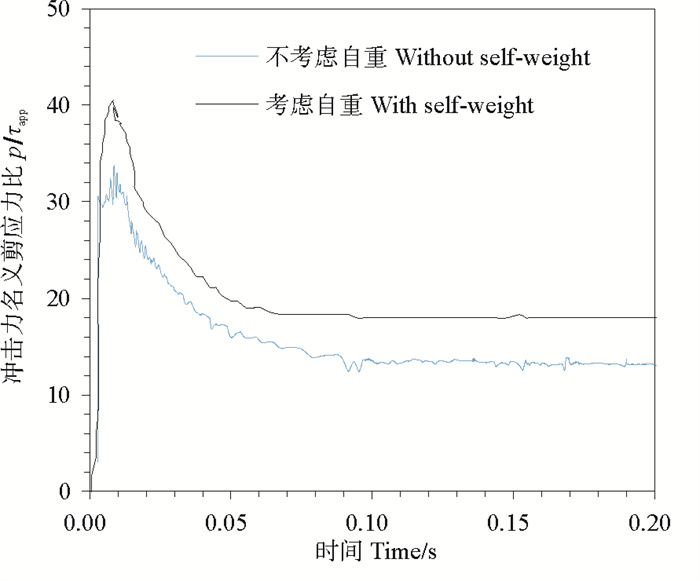
以
|
图 5 自重对冲击力的影响 Fig. 5 Influence of self-weight on impact forces |

|
图 6 考虑自重时的流滑体形态变化 Fig. 6 Geographical evolution of slide mass with self-weight |
改变流滑体的高度、密度、强度特性和冲击速度及桩径, 考虑自由表面和流沮体自重, 进行变动㕕数模拟。根据海底滑坡的实际条件[13,18], 取
根据式(2)中自重项的表达,可得到不同雷诺数对应的自重系数Cγ随H/D的变化(见图 7)。随着H/D增大,Cγ减小。在Re < 120的范围内,Cγ值离散程度不大,可将Cγ视为H/D的单值函数,拟合为:
| $ C_{\gamma}=0.23 e^{-0.23(H / D)} \text { 。} $ | (9) |
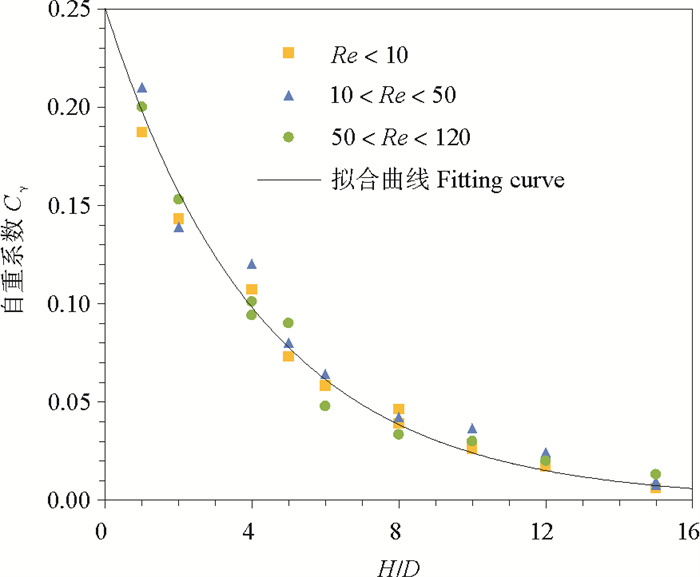
|
图 7 自重系数随H/D的变化 Fig. 7 Variation of self-weight coefficient with H/D |
文献[14]给出了不考虑流滑体自重时, 由平面应变模拟总结的流滑体冲击力为:
| $ p=0.38 \rho v^{2}+7.2 \tau_{\text {app }}。$ | (10) |
考虑流滑体自重时, 结合式(1) 和式(9), 按照式(2)得到桩体冲击力表达式为:
| $ p=F / H D=0.38 \rho v^{2}+7.2 \tau_{\mathrm{app}}+0.23 e^{-0.23(H / D)} \text {. }\\ \left(\rho-\rho_{\mathrm{w}}\right) g H 。$ | (11) |
式中三部分依次代表拖曳力项、承载力项和自重项。
5 冲击力表达式讨论针对性质已知的流滑体冲击, 当初始冲击速度改变时, 式(2)中各项占冲击力的比重随之改变。以下述工况为例: 流滑体
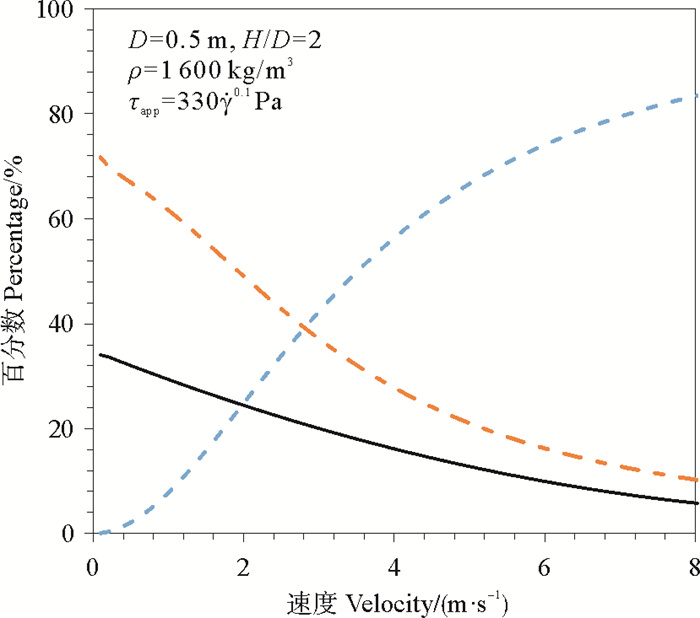
|
图 8 各部分对冲击力的影响 Fig. 8 Influence of items on impact forces |
随着桩基H/D的增大,考虑流滑体自重的三维冲击问题逐渐接近不考虑自重的平面应变问题。为考察流滑体平面应变解答的适用范围,流滑体参数取值同上,分析H/D= 1~20、Re=0.1~20时,自重项在冲击力中的占比变化,如图 9所示。由图 9 (a)可知,H/D=1~8的范围内,在低雷诺数下自重项的占比随着雷诺数增大而减小,H/D < 8时,占比在15%~35%之间,在Re达到20时,自重项占比均降到30%以下,但不可忽略;H/D=2和8时,占比基本相同,H/D=1时占比最小;由图 9 (b)可知,在H/D>8的范围内,H/D越大,自重项占比越小,且H/D>15时,占比小于15%。相同雷诺数下的自重项占比随H/D的变化如图 10所示,同一雷诺数下,当H/D增大时,自重项在冲击力中的占比先增大、后减小,且在H/D=4和5处占比最大,尤其是拟静力条件下(Re < 1),占比超过30%;当H/D=20时,在Re < 20的范围内,自重项占比均小于10%。由趋势可知,当H/D>20时,在宽广雷诺数范围内可以合理忽略流滑体自重的影响,采用平面应变表达式预测冲击力。
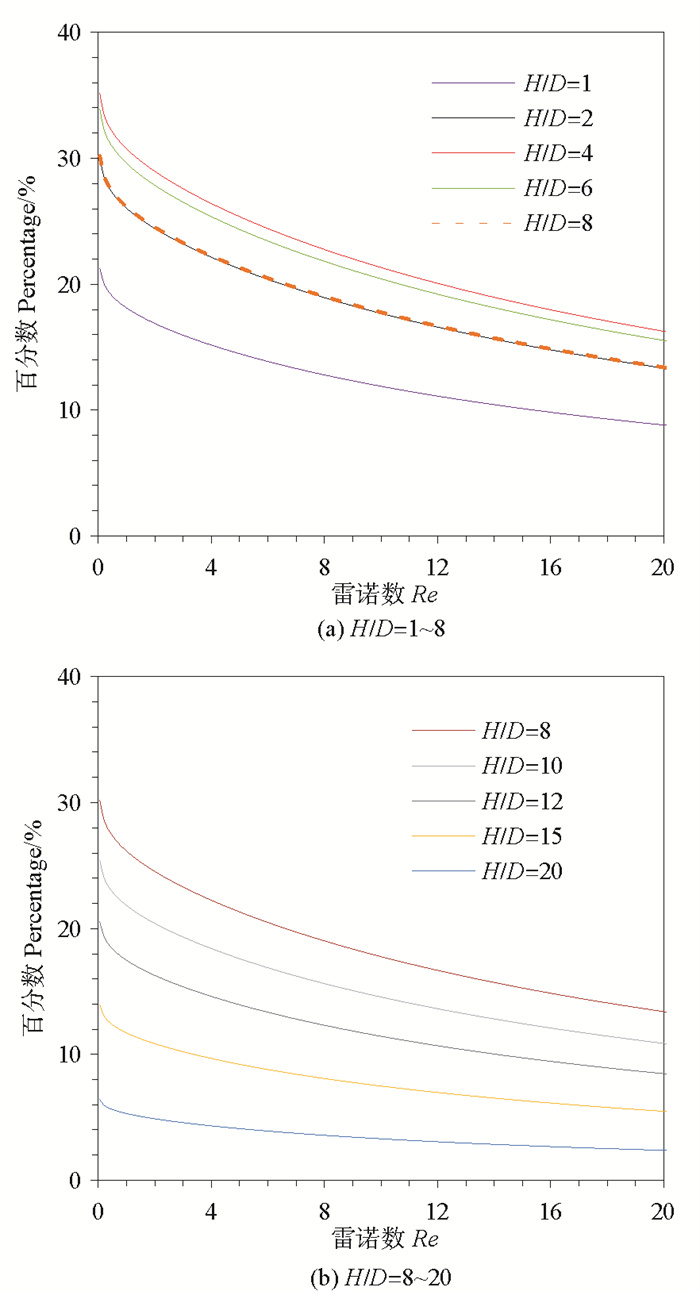
|
图 9 自重项对冲击力中贡献随雷诺数的变化 Fig. 9 Variation of self-weight item contribution to impact forces with Reynolds numbers |
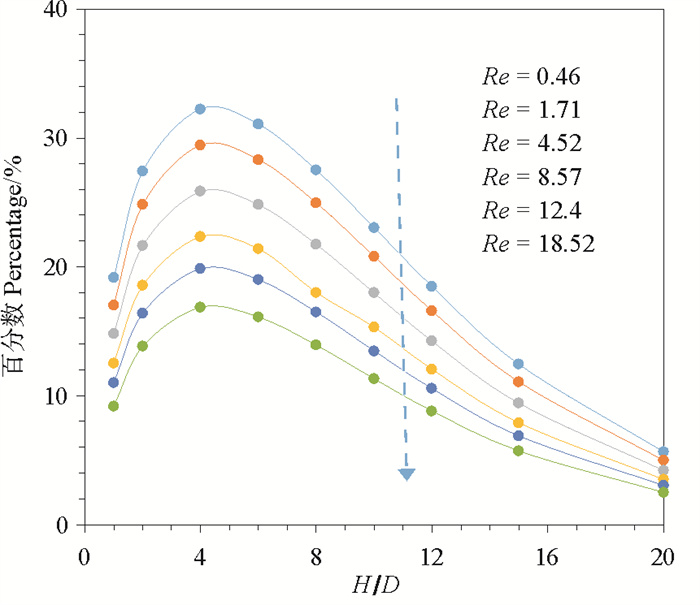
|
图 10 自重项对冲击力贡献随H/D的变化 Fig. 10 Variation of self-weight item contribution to impact forces with H/D |
用幂律流体描述近海滑坡发生后形成的流滑体,建立三维数值模型,采用有限体积法,模拟有限高度的流滑体对桩基的冲击。主要结论如下:
(1) 探究流滑体自由表面和自重对冲击力的影响,在已有平面应变冲击力表达式基础上,推导出了新的包含拖曳力项、承载力项和自重项的冲击力表达式。
(2) 对于有限高度的流滑体,自重系数随着H/D的增大而减小。当D=0.5 m时,在H/D>20范围内,冲击力的大小与平面应变的结果相近,可以忽略自重;否则应当考虑流滑体自重,按照提出的式(11)预测冲击力,当H/D=4或5时,自重项在冲击力中的占比最大。
| [1] |
Hampton M A, Lee H J, Locat J. Submarine landslides[J]. Reviews of Geophysics, 1996, 34(1): 33-59. DOI:10.1029/95RG03287 (  0) 0) |
| [2] |
O'Brien J S, Julien P Y. Laboratory analysis of mudflow properties[J]. Journal of Hydraulic Engineering, 1988, 114(8): 877-887. DOI:10.1061/(ASCE)0733-9429(1988)114:8(877) (  0) 0) |
| [3] |
White F M, Corfield I. Viscous Fluid Flow[M]. New York: Mc Graw-Hill, 2006.
(  0) 0) |
| [4] |
Zakeri A, Hraeg K, Nadim F. Submarine debris flow impact on pipelines-Part I: Experimental investigation[J]. Coastal Engineering, 2008, 55(12): 1209-1218. DOI:10.1016/j.coastaleng.2008.06.003 (  0) 0) |
| [5] |
Zakeri A. Submarine debris flow impact on suspended (free-span) pipelines: Normal and longitudinal drag forces[J]. Ocean Engineering, 2009, 36(6-7): 489-499. DOI:10.1016/j.oceaneng.2009.01.018 (  0) 0) |
| [6] |
Liu J, Tian J. Impact Forces of Submarine Landslides on Free-Span Pipelines[C]. American Society of Mechanical Engineers: The 33rd International Conference on Ocean, Offshore and Arctic Engineering, 2014: V06BT04A037.
(  0) 0) |
| [7] |
Liu J, Tian J, Yi P. Impact forces of submarine landslides on offshore pipelines[J]. Ocean Engineering, 2015, 95: 116-127. DOI:10.1016/j.oceaneng.2014.12.003 (  0) 0) |
| [8] |
王忠涛, 张宇, 杨庆, 等. 海底滑坡对管线冲击力的数值分析[J]. 岩土工程学报, 2019, 41(3): 567-573. Wang Z T, Zhang Y, Yang Q, et al. Numerical analysis for impact of submarine landslides on pipelines[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(3): 567-573. (  0) 0) |
| [9] |
Randolph M F, White D J. Interaction forces between pipelines and submarine slides-A geotechnical viewpoint[J]. Ocean Engineering, 2012, 48(7): 32-37. (  0) 0) |
| [10] |
Pazwash H, Robertson J M. Forces on bodies in Bingham fluids[J]. Journal of Hydraulic Research, 1975, 13(1): 35-55. DOI:10.1080/00221687509499719 (  0) 0) |
| [11] |
Imran J, Harff P, Parker G. A Numerical model of submarine debris flow with graphical user interface[J]. Computers & Geosciences, 2001, 27(6): 717-729. (  0) 0) |
| [12] |
Dong Y, Wang D, Randolph M F. Investigation of impact forces on pipeline by submarine landslide using material point method[J]. Ocean Engineering, 2017, 146: 21-28. DOI:10.1016/j.oceaneng.2017.09.008 (  0) 0) |
| [13] |
冯斌, 孙宏磊, 蔡袁强, 等. 海底滑坡对海洋单桩冲击压力试验研究[J]. 海洋工程, 2019, 37(6): 114-121. Feng B, Sun H L, Cai Y Q, et al. Experimental study of submarine landslide impact on offshore wind power piles[J]. Ocean Engineering, 2019, 37(6): 114-121. (  0) 0) |
| [14] |
李东黎, 晏鄂川, 冯斌, 等. 海底碎屑流对海洋桩的冲击[J]. 浙江大学学报(工学版), 2019, 53(12): 2342-2347. Li D L, Yan E C, Feng B, et al. Impact of submarine debris flow on offshore piles[J]. Journal of Zhejiang University (Engineering Science), 2019, 53(12): 2342-2347. DOI:10.3785/j.issn.1008-973X.2019.12.011 (  0) 0) |
| [15] |
单治钢, 李阳, 王栋, 等. 近海滑坡冲击桩体的数值模拟[J]. 中国海洋大学学报(自然科学版), 2021, 51(10): 115-120. Shan Z G, Li Y, Wang D, et al. Numerical simulation of the impact on piles by nearshore landslides[J]. Periodical of Ocean University of China, 2021, 51(10): 115-120. (  0) 0) |
| [16] |
Demars K R. Design of marine pipelines for areas of unstable sediment[J]. Transportation Engineering Journal, 1978, 104(1): 109-112. (  0) 0) |
| [17] |
Locat A, Leroueil S, Fortin A, et al. The 1994 landslide at Sainte-Monique, Quebec: Geotechnical investigation and application of progressive failure analysis[J]. Canadian Geotechnical Journal, 2015, 52(4): 1-15. (  0) 0) |
| [18] |
Jeong S W, Leroueil S, Locat J. Applicability of power law for describing the rheology of soils of different origins and characteristics[J]. Canadian Geotechnical Journal, 2009, 46(9): 1011-1023. DOI:10.1139/T09-031 (  0) 0) |
2. College of Marine Science and Technology, China University of Geosciences, Wuhan 430074, China
 2022, Vol. 52
2022, Vol. 52


