2. 中国海洋大学海底科学与探测技术教育部重点实验室,山东 青岛 266100
海水是良导体,当它在地磁场中运动时可以产生电流。根据毕奥-萨伐尔定律,海水中的感应电流会产生磁场。利用海水运动感应磁场可以研究海水的物理性质,比如研究复杂的海洋内波运动[1],记录复杂的海况等[2]。通过对地震引起海啸产生的磁场进行监测,可以实现海啸的提前预警[3-4]。但对于用海洋大地电磁测深法研究海底地质构造而言,海水运动感应磁场是海洋电磁测量中的主要噪声源,因而研究和分析海水运动电磁场的特征有助于海洋电磁数据的处理和解释[5]。
海水运动产生磁场的理论最早由法拉第提出,但是由于当时仪器水平的限制,无法直接观测到海水运动感应磁场。随着仪器水平的提高,探测到海水运动产生的磁场以后,人们开始探索磁场与海水运动之间的关系。通常采用法拉第电磁感应定律和麦克斯韦方程结合的方法求得海水运动产生的磁场。
当海水运动的速度场可以用解析式表达时, 比如海水表面重力波[6-7]和内波[1],可以通过直接求解麦克斯韦方程组获得解析速度场产生的磁场。但是,只有几种简单的海水运动形式的速度场具有解析表达式。有学者提出用格林函数[8]或者傅里叶积分[9]求解麦克斯韦方程,可以消除对速度场的限制,获得任意速度场的感应磁场。但是复杂的海水运动受到地形的影响,有时需要模拟海底地形起伏下海水运动产生的磁场[10]。当计算尺度较大的海水运动(如潮汐)感应磁场时,不得不考虑地球曲率和陆地边界的影响。Kuvshinov用数值方法获得了球坐标下潮汐产生的磁场[11]。
描述海水运动的地球流体动力学方程都是偏微分方程,除极个别情况外,很难求得其解析解。较为复杂的速度场一般都是通过数值方法计算得到的,这样获得的速度场是离散的。前人的工作主要是通过求解麦克斯韦方程组得到海水运动磁场的解析表达式。而这些解析表达式对于离散速度场不一定适用。为了计算与实际海水运动更为接近的速度场产生的磁场,本文从毕奥-萨伐尔定律出发,推导了二维海水运动离散速度场感应磁场的积分表达式,用高斯积分方法计算二维离散速度场感应磁场响应,并分析了海水运动频率、振幅和水深等对感应磁场的影响。
1 海水运动产生磁场的原理 1.1 海水运动产生的感应电流海水运动产生磁场的方式有很多,其中海水中感应电流产生的磁场比其他方式要大得多[10]。在本文中假定海水中的磁场主要是海水中的感应电流产生的。根据法拉第电磁感应定律,作为良导体的海水,运动切割地磁场可以产生感应电流:
| $ \mathit{\boldsymbol{j}} = \sigma \left( {\mathit{\boldsymbol{V}} \times \mathit{\boldsymbol{B}}} \right)。$ | (1) |
式中:σ为海水电导率,本文假定海水电导率是均匀的且为4 S·m-1,V为海水速度场,B为总地磁场。在本文中,我们假设地磁场为不随时间变化的恒定地磁场。由于海水运动产生的磁场远小于恒定地磁场,因而可以用恒定地磁场F代替总磁场B,式(1)变为如下形式:
| $ \mathit{\boldsymbol{j}} = \sigma \left( {\mathit{\boldsymbol{V}} \times \mathit{\boldsymbol{F}}} \right)。$ | (2) |
在已知海水速度场分布的情况下,通过上式可以得到海水中的感应电流分布。海水运动产生的感应电流,与海水电导率、海水运动速度和地磁场强度均呈正相关。获得海水中的电流分布后,利用毕奥-萨伐尔定律定理即可得到海水中感应电磁场的分布。
1.2 毕奥-萨伐尔定律毕奥-萨伐尔定律描述的是恒定电流在其周围产生的磁场。当电流缓慢随时间变化时,该定律也成立。于是,我们用毕奥-萨伐尔定律计算海水运动中感应电流产生的磁场,其具体计算式为:
| $ \mathit{\boldsymbol{B}}=\iiint{\frac{{{\mu }_{0}}}{4\text{ }\!\!\pi\!\!\text{ }}\frac{\mathit{\boldsymbol{j}}\times \mathit{\boldsymbol{r}}}{{{r}^{3}}}\text{d}x\text{d}y\text{d}z}。$ | (3) |
式中:μ0为真空中的磁导率;j是电流密度;r是计算点和电流之间的距离。在直角坐标系下,式(3)写成如下形式:
| $ \left\{ \begin{align} &{{B}_{x}}=\frac{{{\mu }_{0}}}{4\text{ }\!\!\pi\!\!\text{ }}\iiint{\frac{{{j}_{y}}{{r}_{z}}-{{j}_{z}}{{r}_{y}}}{{{r}^{3}}}\text{d}x\text{d}y\text{d}z} \\ &{{B}_{y}}=\frac{{{\mu }_{0}}}{4\text{ }\!\!\pi\!\!\text{ }}\iiint{\frac{{{j}_{z}}{{r}_{x}}-{{j}_{x}}{{r}_{z}}}{{{r}^{3}}}\text{d}x\text{d}y\text{d}z} \\ &{{B}_{z}}=\frac{{{\mu }_{0}}}{4\text{ }\!\!\pi\!\!\text{ }}\iiint{\frac{{{j}_{x}}{{r}_{y}}-{{j}_{y}}{{r}_{x}}}{{{r}^{3}}}\text{d}x\text{d}y\text{d}z}。\\ \end{align} \right. $ | (4) |
由上式可知,各个方向的磁场分量都由与其正交的两个方向的电流分量所产生。当已知海水中感应电流的分布时,即可计算海水运动感应电流产生的磁场。
2 二维海水运动磁场的计算 2.1 二维海水运动磁场方程当海水沿某一个水平方向传播时,可以看成是二维海水运动。简单的风浪、涌浪和内波都可以看成是二维海水运动。假设海水沿着水平方向x运动:
| $ \mathit{\boldsymbol{V}} = \left( {{V_x},0,{V_z}} \right)。$ | (5) |
式中:Vx和Vz分别为水流沿水平方向x和垂直方向z的运动速度。将(5)式代入(2)式,可以得到该速度场产生的感应电流:
| $ \mathit{\boldsymbol{j}} = \sigma \left( { - {V_z}{F_y},{V_z}{F_x} - {V_x}{F_z},{V_x}{F_y}} \right)。$ | (6) |
由上式可知,海水感应电流的各个分量分别由与其正交的海水速度分量与地磁场分量切割产生。由于二维海水运动的速度场与y无关,故其产生的感应电流也与y无关。于是,由式(4),可得
| $ \left\{ \begin{align} &{{B}_{x}}=\frac{{{\mu }_{0}}}{2\text{ }\!\!\pi\!\!\text{ }}\iint{\frac{{{j}_{y}}{{r}_{z}}}{r_{xz}^{2}}\text{d}x\text{d}z} \\ &{{B}_{y}}=\frac{{{\mu }_{0}}}{2\text{ }\!\!\pi\!\!\text{ }}\iint{\frac{{{j}_{z}}{{r}_{x}}-{{j}_{x}}{{r}_{z}}}{r_{xz}^{2}}\text{d}x\text{d}z} \\ &{{B}_{z}}=\frac{{{\mu }_{0}}}{2\text{ }\!\!\pi\!\!\text{ }}\iint{\frac{-{{j}_{y}}{{r}_{x}}}{r_{xz}^{2}}\text{d}x\text{d}z}。\\ \end{align} \right. $ | (7) |
式中:rxz为计算点在xz垂直面上的投影域和电流之间的距离。将式(6)代入式(7),得到二维海水运动产生的磁场积分表达式
| $ \left\{ \begin{align} &{{B}_{x}}=\frac{2{{\mu }_{0}}\sigma }{4\text{ }\!\!\pi\!\!\text{ }}\iint{\frac{\left( {{V}_{z}}{{F}_{x}}-{{V}_{x}}{{F}_{z}} \right){{r}_{z}}}{r_{xz}^{2}}\text{d}x\text{d}z} \\ &{{B}_{y}}=\frac{2{{\mu }_{0}}\sigma }{4\text{ }\!\!\pi\!\!\text{ }}\iint{\frac{{{V}_{x}}{{F}_{y}}{{r}_{x}}+{{V}_{z}}{{F}_{y}}{{r}_{z}}}{r_{xz}^{2}}\text{d}x\text{d}z} \\ &{{B}_{z}}=\frac{2{{\mu }_{0}}\sigma }{4\text{ }\!\!\pi\!\!\text{ }}\iint{\frac{-\left( {{V}_{z}}{{F}_{x}}-{{V}_{x}}{{F}_{z}} \right){{r}_{x}}}{r_{xz}^{2}}\text{d}x\text{d}z}。\\ \end{align} \right. $ | (8) |
当海水速度场可以用解析式表达时,计算(8)式的二维积分可以得到海水运动产生的磁场。但当速度场为离散值时,式(8)不能直接使用,需要用线性插值的方法得到速度场,再代入式(8)中求积分得到感应磁场。
2.2 离散速度场的计算假设二维离散速度场单元为不规则四边形,则其所产生的感应磁场为:
| $ \left\{ \begin{align} &{{B}_{x}}=\frac{2{{\mu }_{0}}\sigma }{4\text{ }\!\!\pi\!\!\text{ }}\iint_{Y}{\frac{\left( {{V}_{z}}{{F}_{x}}-{{V}_{x}}{{F}_{z}} \right){{r}_{z}}}{r_{xz}^{2}}\text{d}s} \\ &{{B}_{y}}=\frac{2{{\mu }_{0}}\sigma }{4\text{ }\!\!\pi\!\!\text{ }}\iint_{Y}{\frac{{{V}_{x}}{{F}_{y}}{{r}_{x}}+{{V}_{z}}{{F}_{y}}{{r}_{z}}}{r_{xz}^{2}}\text{d}s} \\ &{{B}_{z}}=\frac{2{{\mu }_{0}}\sigma }{4\text{ }\!\!\pi\!\!\text{ }}\iint_{Y}{\frac{-\left( {{V}_{z}}{{F}_{x}}-{{V}_{x}}{{F}_{z}} \right){{r}_{x}}}{r_{xz}^{2}}\text{d}s}。\\ \end{align} \right. $ | (9) |
上式中四边形的积分难以直接求解,其原因有二。首先四边形为不规则四边形,另外,只有四边形的四个顶点处的速度场已知。而计算二重积分时需要知道单元内的速度场。
本文使用线性形函数描述单元内速度变化。假设在四边形单元内海水运动速度是线性变化的,并可近似为
| $ \left\{ \begin{array}{l} {V_x} = {N_1}{V_{x1}} + {N_2}{V_{x2}} + {N_3}{V_{x3}} + {N_4}{V_{x4}}\\ {V_z} = {N_1}{V_{z1}} + {N_2}{V_{z2}} + {N_3}{V_{z3}} + {N_4}{V_{z4}}\\ x = {N_1}{x_1} + {N_2}{x_2} + {N_3}{x_3} + {N_4}{x_4}\\ z = {N_1}{z_1} + {N_2}{z_2} + {N_3}{z_3} + {N_4}{z_4}。\end{array} \right. $ | (10) |
式中:Vxi, 和Vzi, 分别是全球坐标系中四边形第i(i=1, 2, 3, 4)顶点上速度分量Vx, 和Vz, 的值。Ni为矩阵单元的形函数,其表达式为:[12]
| $ \left\{ \begin{array}{l} {N_1} = \frac{1}{4}\left( {1 - \xi } \right)\left( {1 + \eta } \right),{N_2} = \frac{1}{4}\left( {1 - \xi } \right)\left( {1 - \eta } \right)\\ {N_3} = \frac{1}{4}\left( {1 + \xi } \right)\left( {1 - \eta } \right),{N_4} = \frac{1}{4}\left( {1 + \xi } \right)\left( {1 + \eta } \right)。\end{array} \right. $ | (11) |
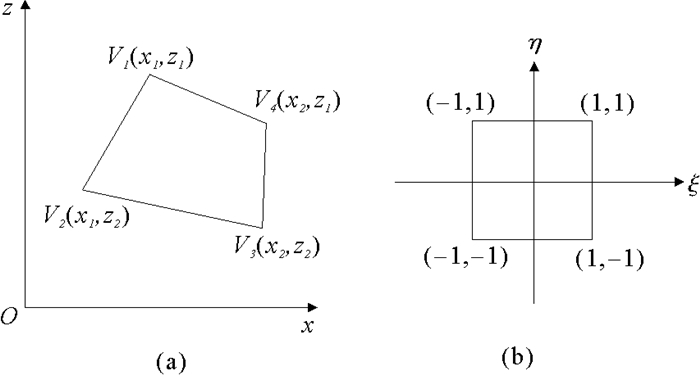
|
图 1 四边形子单元(a)和母单元(b) Fig. 1 (a)Quadrilateral original coordinate system (b) Transformed coordinate system |
对子面积单元ds=dxdz进行变换,根据雅可比变换有
| $ {\rm{d}}s = {\rm{d}}x{\rm{d}}z = \left| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial \xi }}\frac{{\partial z}}{{\partial \xi }}}\\ {\frac{{\partial z}}{{\partial \eta }}\frac{{\partial z}}{{\partial \eta }}} \end{array}} \right|{\rm{d}}\xi {\rm{d}}\eta = J\left( {\xi ,\eta } \right){\rm{d}}\xi {\rm{d}}\eta 。$ | (12) |
其中:J(ξ, η)是雅可比变换行列式。将式(11)和(12)代入式(10),得
| $ \left\{ \begin{array}{l} {B_x} = \frac{{{\mu _0}\sigma }}{{2{\rm{ \mathit{ π} }}}}\int_{ - 1}^1 {\int_{ - 1}^1 {\frac{{\sum\limits_{n = 1}^4 {{N_n}\left( {{V_{zn}}{F_x} - {V_{xn}}{F_z}} \right){r_z}} }}{{r_x^2 + r_z^2}}J\left( {\xi ,\eta } \right){\rm{d}}\xi {\rm{d}}\eta } } \\ {B_y} = \frac{{{\mu _0}\sigma }}{{2{\rm{ \mathit{ π} }}}}\int_{ - 1}^1 {\int_{ - 1}^1 {\frac{{\sum\limits_{n = 1}^4 {{N_n}\left[ {{V_{xn}}{F_y}{r_x} + {V_{zn}}{F_y}{r_z}} \right]} }}{{r_x^2 + r_z^2}}J\left( {\xi ,\eta } \right){\rm{d}}\xi {\rm{d}}\eta } } \\ {B_z} = \frac{{{\mu _0}\sigma }}{{2{\rm{ \mathit{ π} }}}}\int_{ - 1}^1 {\int_{ - 1}^1 {\frac{{\sum\limits_{n = 1}^4 {{N_n}\left( {{V_{xn}}{F_z} - {V_{zn}}{F_x}} \right){r_x}} }}{{r_x^2 + r_z^2}}J\left( {\xi ,\eta } \right){\rm{d}}\xi {\rm{d}}\eta } } 。\end{array} \right. $ | (13) |
其中:rx和rz是计算点P(xp, zp)到速度场单元的距离:
| $ \left\{ \begin{array}{l} {r_x} = {x_p} - x\\ {r_z} = {z_p} - z。\end{array} \right. $ | (14) |
各个速度场单元产生的感应磁场可以通过计算式(13)中的二重定积分得到。本文用高斯数值积分法
| $ \int\limits_{ - 1}^1 {\int\limits_{ - 1}^1 {f\left( {\xi ,\eta } \right){\rm{d}}\xi {\rm{d}}\eta } } = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{A_i}{A_j}f\left( {{\xi _i},{\eta _j}} \right)} } 。$ | (15) |
计算该二维积分。将式(15)代入式(13),得:
| $ \left\{ \begin{array}{l} {B_x} = \frac{{2{\mu _0}\sigma }}{{4{\rm{ \mathit{ π} }}}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{A_i}{A_j}\frac{{\sum\limits_{n = 1}^4 {{N_n}\left( {{V_{zn}}{F_x} - {V_{xn}}{F_z}} \right){r_z}} }}{{{{\left( {{r_x}} \right)}^2} + {{\left( {{r_z}} \right)}^2}}}J\left( {{\xi _i},{\eta _j}} \right)} } \\ {B_y} = \frac{{2{\mu _0}\sigma }}{{4{\rm{ \mathit{ π} }}}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{A_i}{A_j}\frac{{\sum\limits_{n = 1}^4 {{N_n}\left[ {{V_{xn}}{F_y}{r_x} + {V_{zn}}{F_y}{r_z}} \right]} }}{{{{\left( {{r_x}} \right)}^2} + {{\left( {{r_z}} \right)}^2}}}J\left( {{\xi _i},{\eta _j}} \right)} } \\ {B_z} = \frac{{2{\mu _0}\sigma }}{{4{\rm{ \mathit{ π} }}}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{A_i}{A_j}\frac{{\sum\limits_{n = 1}^4 {{N_n}\left( {{V_{xn}}{F_z} - {V_{zn}}{F_x}} \right){r_x}} }}{{{{\left( {{r_x}} \right)}^2} + {{\left( {{r_z}} \right)}^2}}}J\left( {{\xi _i},{\eta _j}} \right)} } 。\end{array} \right. $ | (16) |
在已知四边形单元顶点处速度值的情况下,通过上式可以计算海水运动产生的磁场。先求得各个速度单元所产生的磁场,然后再将所有速度单元产生的磁场叠加求和,即得到整个速度场产生的磁场。
3 毕奥-萨伐尔定律计算海水运动磁场的精度当从麦克斯韦方程组出发,推导海水运动产生的磁场所满足的微分方程时,海水中的感应电流为:
| $ \mathit{\boldsymbol{j}} = \sigma \left( {\mathit{\boldsymbol{E}} + \mathit{\boldsymbol{V}} \times \mathit{\boldsymbol{F}}} \right)。$ | (17) |
而用毕奥-萨伐尔定律方法计算海水运动感应磁场时,感应电流计算式(1)中不含σE项。这是因为毕奥-萨伐尔定律假设海水中的电流是恒定的,而σE是由于感应电流随时间变化而产生的二次场。那么,二次电流将对计算得到的磁场结果有多大影响呢?本文分别通过毕奥-萨伐尔定律方法解和麦克斯韦方程的方法计算海水速度场产生的磁场,对比两者之间的差别。
假设海水速度场为二维无限水深线性波浪[13]:
| $ \left\{ \begin{array}{l} {V_x} = - \frac{{kag}}{\omega }{e^{ - kz}}\sin \left( {\omega t - kx} \right)\\ {V_z} = \frac{{kag}}{\omega }{e^{ - kz}}\cos \left( {\omega t - kx} \right)。\end{array} \right. $ | (18) |
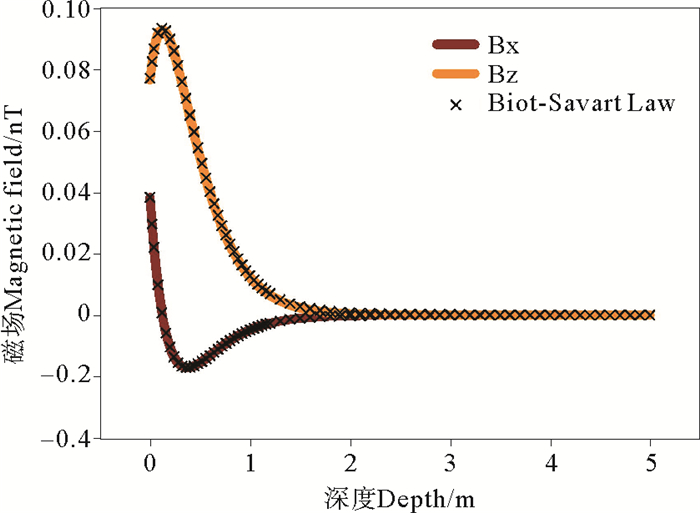
式中:k=ω2/g为波数;a为波浪的振幅;ω=2πf为角频率;g为重力加速度。假定波浪振幅为1 m,计算了频率分别为1和0.1 Hz,时间t=0时刻的沿垂直轴从海平面到300 m深处(0≤ z ≤300 m)的感应磁场如图 2和3所示。
|
图 2 1 Hz海浪产生的磁场 Fig. 2 Magnetic variations of 1 Hz wave |
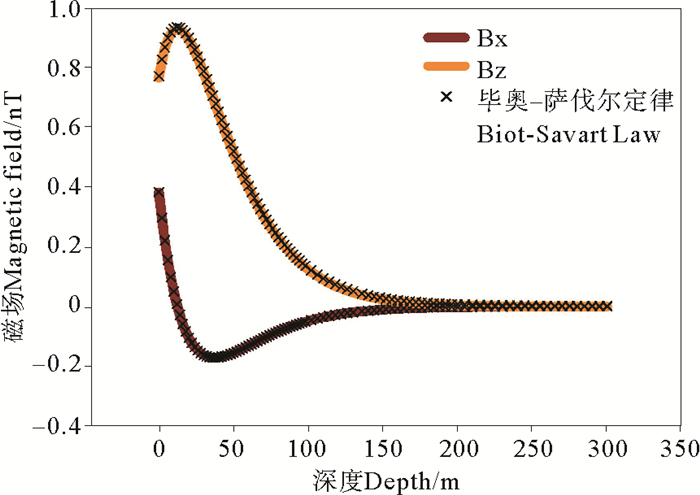
|
图 3 0.1 Hz海浪产生的磁 Fig. 3 Magnetic variations of 0.1 Hz wave |
虽然两种计算方法中所采用的感应电流不同(相差σE),但是利用两种计算方法得到的感应磁场几乎没有差别。即使当海水运动频率达到了1 Hz,用毕奥-萨伐尔定律方法计算的结果和用麦克斯韦方法得到方程的结果相差不大。由此可以得到这样的认识,当海水波动的频率小于1 Hz时,忽略感应电流中的σE项对计算结果影响不大。可见,用毕奥-萨伐尔定律计算海水运动产生的磁场是可行的,且精度较高。
4 海浪运动感应磁场特征分析下面分析海浪运动感应磁场在不同的海水运动频率、振幅和水深下的特征。上文中二维无限水深线性波浪产生的磁场只有Bx和Bz分量。与无限水深不同,有限水深海浪产生的磁场By分量不为零。为了研究海水运动频率、振幅和水深对感应磁场不同分量的影响,下面例子考虑二维有限水深海浪,其表达式为:[13]
| $ \left\{ \begin{array}{l} {V_x} = - \frac{{kag}}{\omega }\frac{{ch\left[ {k\left( {D - z} \right)} \right]}}{{chkD}}\sin \left( {\omega t - kx} \right)\\ {V_z} = \frac{{kag}}{\omega }\frac{{sh\left[ {k\left( {D - z} \right)} \right]}}{{chkD}}\cos \left( {\omega t - kx} \right)。\end{array} \right. $ | (19) |
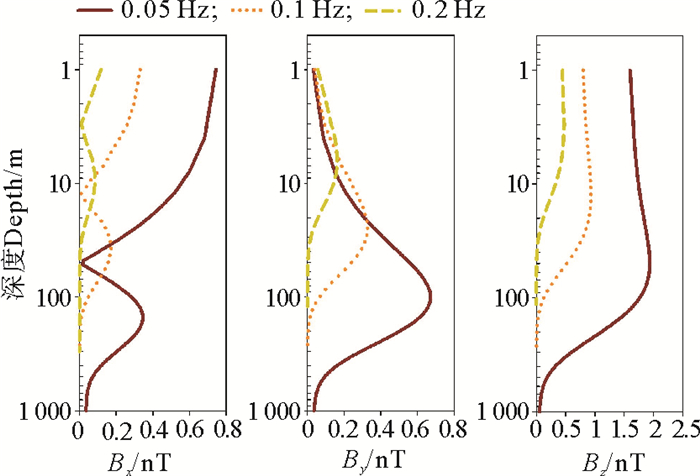
以有限水深二维线性波浪(19)为例,图 4为海水振幅为1 m,水深为300 m,频率分别是0.05、0.1和0.21 Hz的波浪产生的感应磁场。
|
图 4 0.05、0.1和0.2 Hz二维线性波浪产生的磁场 Fig. 4 Magnetic variations of 0.05, 0.1 and 0.2 Hz waves |
由图 4可知,频率较低的海水运动产生的磁场较大,Bx的零点、By和Bz的极大值点更深。当振幅一定时,频率越低的波浪流速越大,波长越长。因此海水运动的频率越低,产生的磁场就越大,随深度的增加衰减越慢,影响深度越大。
4.2 海水振幅对磁场的影响图 5为海水振幅分别为0.3、1和3 m,频率为0.1 Hz深度为300 m的波浪产生的磁场。

|
图 5 振幅分别为0.3、1和3 m波浪产生的磁场 Fig. 5 Magnetic variations of amplitudes are 0.3, 1 and 3 m waves |
由图 5可知,海水振幅越大,感应磁场越大。感应磁场极值点的位置不因海水振幅的变化而变化。将速度场方程式(18)带入磁场计算方程式(8),可将振幅a提到积分外,因此海水运动磁场与海水波动振幅的关系是线性的。
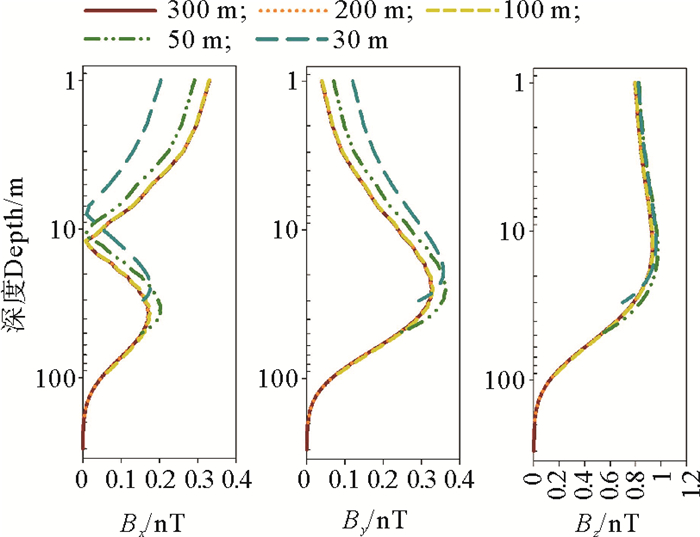
4.3 水深对磁场的影响由于本文的计算中,假设海底是绝缘的,电流只存在于海水中。因此,水深变化的影响是使速度场发生变化,进而影响其产生的磁场。图 6是水深分别为300、200、100、50和30 m,频率为0.1 Hz振幅为1 m时,二维线性波浪产生的磁场。
|
图 6 水深分别为300、200、100、50和30 m二维线性波浪产生的磁场 Fig. 6 Magnetic variations of depths are 300, 200, 100, 50 and 30 m waves |
由图 6可知,当水深从300 m减小到100 m时,感应磁场变化很小。但当深度从100 m减小到30 m时,Bx明显减小,By明显增大,而Bz只在海底附近处稍微减小。对于二维有限水深线性海浪,水深比较大时,波速不受水深影响,其产生的磁场也与水深无关。本例中,海水运动频率为时0.1 Hz,当水深大于100 m时,磁场便与水深无关。当水深较小时,水深的减小使波浪的垂直速度急剧减小,而水平速度变化不大。由于海水运动磁场的水平分量Bx和By主要受海水的垂直速度Vz影响,磁场的垂直分量Bz主要受水平速度Vx的影响。因此,的水深较小时,水深的变化主要影响水平方向的磁场,对垂向磁场影响不大。
5 结论本文介绍了利用毕奥-萨伐尔定律计算二维海水运动离散速度场感应磁场的新方法。本文所述方法的计算结果和通过解麦克斯韦方程方法的结果精度相同,表明用毕奥-萨伐尔定律计算海水运动产生的磁场是可行的,且精度较高。算例表明:
(1) 当海水振幅一定时,频率越低的海浪产生的磁场越大,影响深度也越大。
(2) 海浪的振幅与其产生的磁场呈正比。
(3) 水深较深时,海水运动产生的磁场不受水深影响。但水深较小时,水深减小使Bx减小,By增大,而对Bz影响较小。
| [1] |
Beal H T, Weaver J T. Calculations of magnetic variations induced by internal ocean waves[J]. Journal of Geophysical Research, 1970, 75: 6846-6852. DOI:10.1029/JC075i033p06846
(  0) 0) |
| [2] |
Lilley F E M, Hitchman A P, Milligan P R, et al. Sea-surface observations of the magnetic signals of ocean swells[J]. Geophysical Journal International, 2004, 159(2): 565-572. DOI:10.1111/gji.2004.159.issue-2
(  0) 0) |
| [3] |
Manoj C, Kuvshinov A, Neetu S, et al. Can undersea voltage measurements detect tsunamis?[J]. Earth Planets and Space, 2010, 62: 353-358. DOI:10.5047/eps.2009.10.001
(  0) 0) |
| [4] |
Toh H, Satake K, Hamano Y, et al. Tsunami signals from the 2006 and 2007 Kuril earthquakes detected at a seafloor geomagnetic observatory[J]. Journal of Geophysical Research: Solid Earth, 2011, 116: 1-10.
(  0) 0) |
| [5] |
张自力, 魏文博, 刘保华, 等. 海浪感应电磁场的理论计算[J]. 海洋学报, 2008, 30: 42-46. Zhang Zi-li, Wei Wen-bo, Liu Bao-hua, et al. Theoretical calculation of electromagnetic field generated by ocean waves[J]. Acta Oceanologica Sinica, 2008, 30: 42-46. DOI:10.3321/j.issn:0253-4193.2008.01.005 (  0) 0) |
| [6] |
Longuet-higgins M S. The electrical field induced by ocean currents and waves, with applications to the method of towed electrodes[J]. Deep Sea Research, 1954, 13(1): 1-37.
(  0) 0) |
| [7] |
Weaver J T. Magnetic variations associated with ocean waves and swell[J]. Journal of Geophysical Research, 1965, 70: 1921-1929. DOI:10.1029/JZ070i008p01921
(  0) 0) |
| [8] |
K M Bhatt. Motion Induced Noice in Marine Electromagnetic Data[D].[s.l.]: Institut für Geophysik Und Extraterrestrische Physik, 2011.
(  0) 0) |
| [9] |
Podney W. Electromagnetic fields generated by ocean waves[J]. Journal of Geophysical Research, 1975, 80: 2977-2990. DOI:10.1029/JC080i021p02977
(  0) 0) |
| [10] |
Sanford T B. Motionally induced electric and magnetic fields in the sea[J]. Journal of Geophysical Research, 1971, 76: 3476-3492. DOI:10.1029/JC076i015p03476
(  0) 0) |
| [11] |
Kuvshinov A V. Electromagnetic induction in the oceans and the anomalous behaviour of coastal C-responses for periods up to 20 days[J]. Geophysical Research Letters, 2005, 29: 359-365.
(  0) 0) |
| [12] |
徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994. Xu Shi-zhe. Finite Element Mettod in Geophysice[M]. Beijing: Science Press, 1994. (  0) 0) |
| [13] |
叶安乐, 李凤歧. 物理海洋学[M]. 青岛: 青岛海洋大学出版社, 1992. Ye An-le, Li Feng-qi. Physical Oceanography[M]. Qingdao: Qingdao Ocean University Press, 1992. (  0) 0) |
2. Ocean University of China, Key Lab of Submarine Geosciences and Prospecting Techniques of Ministry Education, Qingdao 266100, China
 2019, Vol. 49
2019, Vol. 49


