2. 山东省海洋工程重点实验室, 山东 青岛 266100;
3. 中国海洋大学海洋与大气学院, 山东 青岛 266100
伴随着对海洋环境保护日益重视和大规模海洋开发,各种无人海洋机器人如远程控制机器人(Remoted Operation Vehicle或ROV)、自治水下机器人(Automated Underwater Vehicle或AUV)、水面无人艇(Unmanned Surface Vessel或USV)等在海洋科学考察、海洋工程、海水养殖、军事等领域得到了广泛的应用。从能源供给角度来看以上传统的机动观测装置的能量供给大大限制了它们的长时间、大范围观测的能力。美国Liquid Robot公司开发了波浪能驱动的机动浮标产品Wave Glider,它利用波浪能垂荡运动的能量提供运动能量,该装置已经在海洋动物学、溢油泄漏检测、海平面升高等多领域得到应用,取得较好的效果[1]。
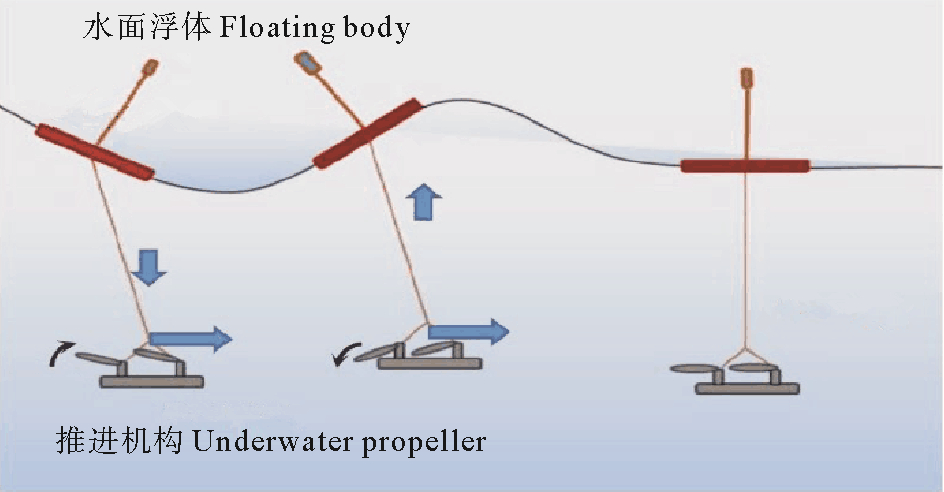
波浪能滑翔机(见图 1)由水面浮体、水下推进机构及连接两者的缆索组成,它的优点是不需要外界能量的供给,只需要从波浪的上下运动中获取能量来驱动探测机构的前进(见图 2),因此该类型的机构能够长期、大范围、经济灵活、可靠自主的进行海洋观测任务,在民用及军用领域都具有广泛的应用前景[2]。它的前进动力主要由翼片在流体作用下的被动摆动产生。Eslam等[3]分析了在固定雷诺数下理想推进模式下的翼片在不同垂荡和纵荡运动规律下的涡泄脱落情况;Triantafyllou等[4]研究了扑翼推进性能和翼片参数的关系;Silva等[5]基于雷诺平均纳维-斯托克(Reynolds Average Navier-Stokes,即RANS)方程和动网格技术,模拟了其水动力学性能;Politis等[6]利用边界元方法对波浪垂荡驱动激励下的翼片水动力学进行了研究,分析了翼片产生的推进力和涡泄状态;Bøckmann等[7]通过控制翼片的纵荡运动获得了更好的推进性能;刘鹏、胡合文等[8-9]基于RANS方程研究了串列扑翼推进的水动力学,发现翼间涡系干扰是导致推进性能差异的主要原因。贾丽娟、郑炳欢、李小涛等[10-12]利对翼片做了水动力定常计算分析,贾丽娟计算了翼型在不同来流速度、不同水翼间隔分布情况下的升阻比值,郑炳欢计算得出水翼的旋转角度为45°时水翼产生的水平推力达到极大值,李小涛对水面母船不同来流方向和不同吃水做静水阻力计算并与经验公式对比发现趋势相同,并对固定水翼在不同来流攻角下做了定常阻力计算。

|
图 1 波浪滑翔机 Fig. 1 Wave glider |
|
图 2 波浪滑翔机工作原理 Fig. 2 Operational mechanism |
本文基于有限体积法和Fluent软件,用雷诺平均Navier-Stokes方程(RANS),对开始运动阶段给定垂荡运动和摆动运动的推进装置翼片水动力学进行了分析和仿真,模拟了单个翼片、多翼片纵向阵列的压力分布、涡泄状况和推进动力,着重分析了翼片间距变化对推进力的影响作用。
1 波浪滑翔机推进装置翼片水动力学建模 1.1 波浪滑翔机推进装置翼片水动力学模型波浪滑翔机是依靠推进机构随浮体上下运动对翼片产生水动力来实现运动的,波浪滑翔机在启动、稳定运转和回收等过程的动态性能的各不相同。本文对该设备的启动阶段进行了研究,启动阶段是典型的非稳态流动或湍流问题。现有的湍流数值模拟的方法有三种:直接数值模拟(Direct Numerical Simulation, DNS),大涡模拟(Large Eddy Simulation, LES)和Reynolds平均方法(Reynolds Average Navier-Stokes, RANS)[13]。直接数值模拟可以获得湍流场的精确信息,是研究湍流机理的有效手段,需要较大的计算资源,限制了其应用范围。LES大涡模拟的计算量介于另外两者之间,相较于RANS方法,LES可以模拟更多的湍流大尺度运动,LES所用的湍流亚网格应力模型受边界的几何形状和流动类别的影响小。Reynolds平均方法只要设定合理的Reynolds应力模型,可以很容易地从RANS方程解出湍流的统计量。
对非稳态的N-S方程作时间演算,得到方程:
动量方程:
| $ \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{\partial {x_j}}} = {S_i} - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_i}}}\left( {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho \overline {{{\dot u}_i}{{\dot u}_j}} } \right)。$ | (1) |
湍流运动的连续性方程:
| $ \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial {x_i}}} = 0。$ | (2) |
其他变量输运方程:
| $ \frac{{\partial (\rho \varphi )}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}\varphi } \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left( {\Gamma \frac{{\partial \varphi }}{{\partial {x_j}}} - \rho \overline {{{\dot u}_j}\dot \varphi } } \right) + S。$ | (3) |
式中附加应力可记为
在Fluent计算中采用RNGK-ε模型,使得附加项与时均值联系起来,采用SIMPLE算法进行压力速度耦合来求解运算。
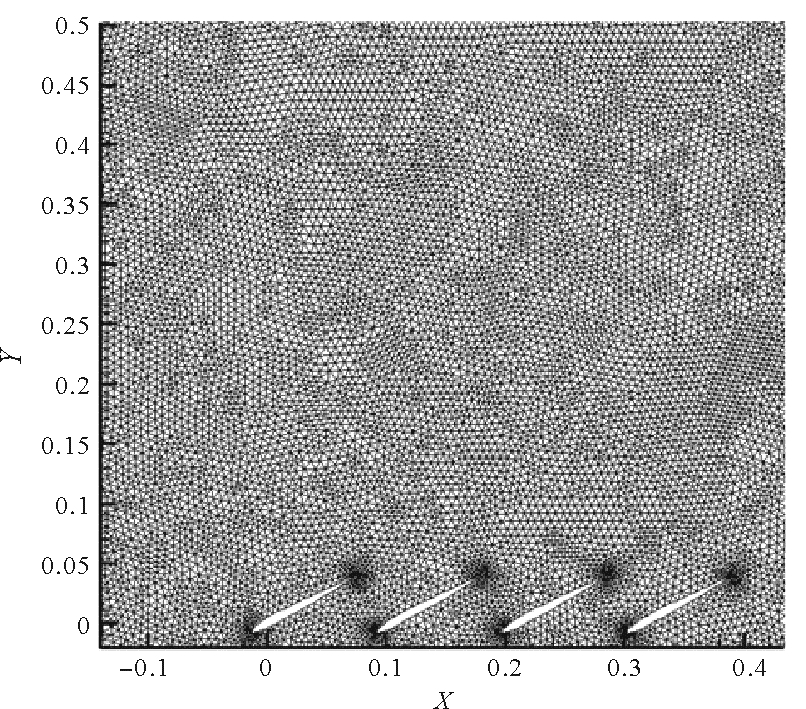
1.2 边界条件及参数设置计算中应用两方程的RNG K-ε模型,采用非平衡壁面函数法进行壁面修正,使用二维非结构划分整个流域,并采用动网格技术来保证翼片运动过程中的网格质量,翼片网格初始状态如图 3所示。
|
图 3 翼片初始姿态网格 Fig. 3 Mesh of fin in initial state |
对波浪滑翔机启动阶段进行分析,设定来流速度为0,对波浪滑翔机的工作原理和实验过程进行观察[8],估计翼片摆动的时间占整个运动周期的1/4,翼片的摆动规律设为:
| $ \begin{array}{l} 当t = \left( {0 - \frac{T}{8}} \right)时, \begin{array}{*{20}{c}} {Y = {y_0}\sin (2\pi ft), }\\ {A = {a_0}\sin (2\pi ft);} \end{array}\\ 当t = \left( {\frac{T}{8} - \frac{T}{2}} \right)时, \begin{array}{*{20}{c}} {Y = {y_0}\sin (2\pi ft), }\\ {A = 0;} \end{array}\\ 当t = \left( {\frac{T}{2} - \frac{{5T}}{8}} \right)时, \begin{array}{*{20}{c}} {Y = {y_0}\sin (2\pi ft), }\\ {A = {a_0}\sin (2\pi ft);} \end{array}\\ 当t = \left( {\frac{{5T}}{8} - T} \right)时, \begin{array}{*{20}{c}} {Y = {y_0}\sin (2\pi ft), }\\ {A = 0。} \end{array}\\ \begin{array}{*{20}{l}} {}\\ {} \end{array} \end{array} $ | (4) |
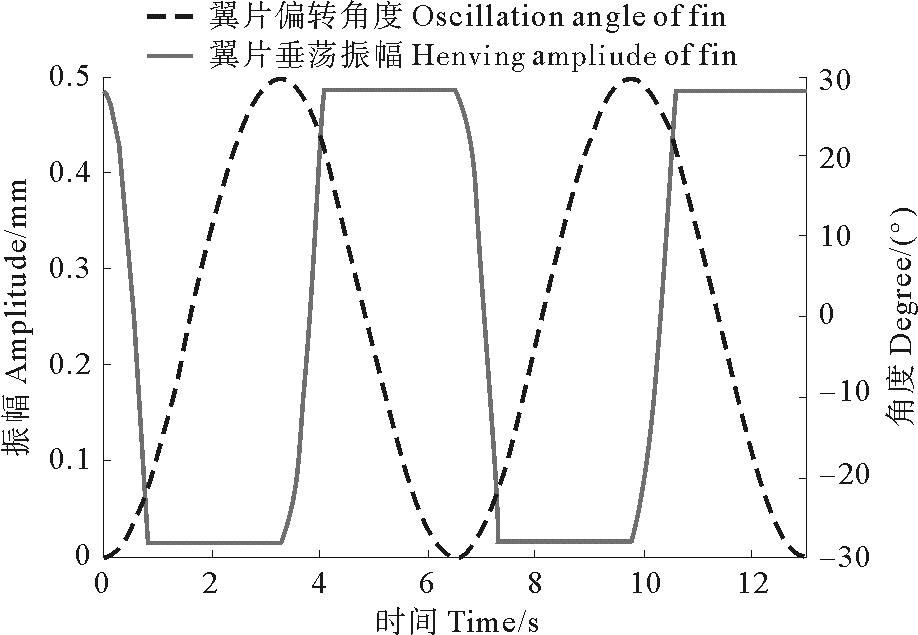
式中:T为运动周期;f为频率;Y为升沉运动的振幅;A为翼片的摆动角。运动规律通过Fluent中的用户定义函数(UDF)来定义,翼片运动规律如图 4所示。
|
图 4 翼片运动规律 Fig. 4 Motion of fin |
翼型采用NACA0008对称翼型,划分三角形网格。计算分析周期6.5 s,振幅0.5 m下翼片最大偏转角度为28°的受力情况。
在实际模拟假设:浮体对波浪完全响应,即驱动翼片运动周期等于波浪周期,升沉幅度等于波高;对波浪滑翔机启动阶段推进装置的翼片水动力学行为进行研究,通过控制翼片主动运动分析启动阶段的受力与流场。
波浪滑翔机理论计算中的水平推力系数Cx,竖直方向升力系数Cy,以及以翼片转轴为作用点的力矩系数Cm由相应的推力Fx,升力Fy和力矩M0沿翼片表面积积分确定:
| $ \begin{array}{l} Cx = \int\limits_s {\frac{{2{F_x}}}{{\rho {C_0}v_0^2}}{\rm{d}}s;} \\ Cy = \int\limits_s {\frac{{2{F_y}}}{{\rho {C_0}v_0^2}}{\rm{d}}s;} \\ Cm = \int\limits_s {\frac{{2{M_0}}}{{\rho {C_0}v_0^2}}{\rm{d}}s。} \end{array} $ | (5) |
式中:C0为翼片的特征长度;ρ为水的密度;V0为水流速度。
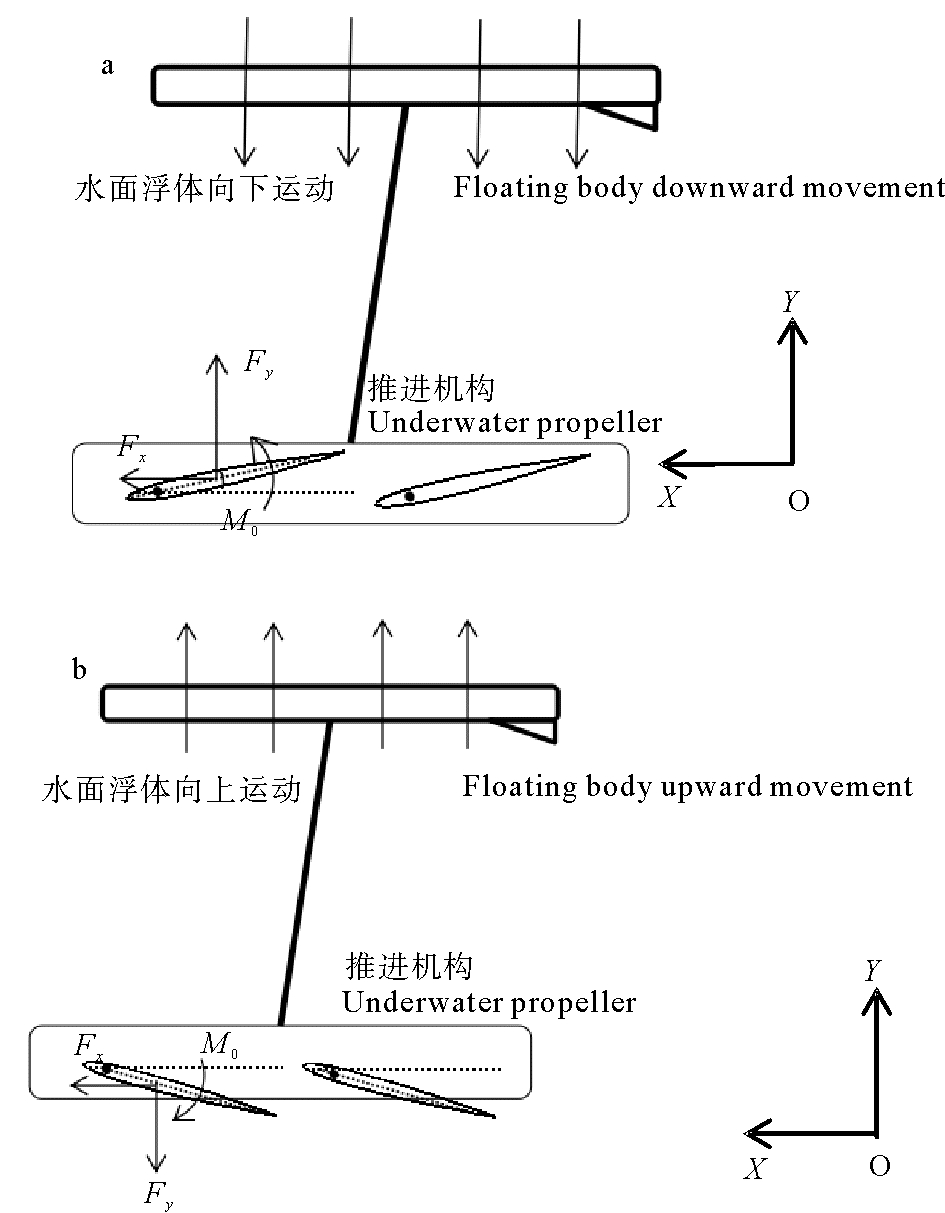
图 5(a)为水下推进机构随着上浮体在波浪激励下向下运动运动时翼片受力,可以看出翼片会产生一个向前进的推力。
|
((a.水面浮体向下运动Floating body downward movement;b.水面浮体向上运动Floating body upward movement)) 图 5 翼片工作原理 Fig. 5 Operational mechanism |
图 5(b)为水下推进机构随着上浮体在波浪激励下向上运动运动时翼片受力,可以看出翼片同样会产生一个向前进的推力使波浪滑翔机向前运动。
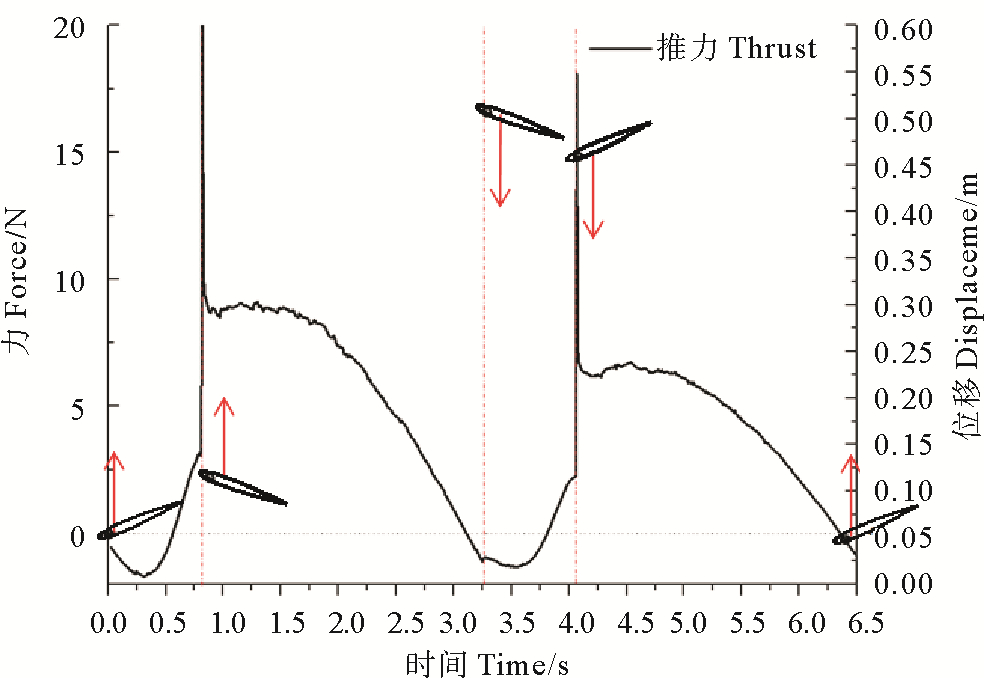
2 结果和分析 2.1 单片翼片水动力学分析图 6为单翼片在X方向所受到的驱动力变化曲线,可以看出在翼片偏转到最大角度时由于限位作用会产生推进力的突变。在启动阶段尚未达到稳定的运行状态时,前半个周期所产生的推进力大于后半个周期。翼片随着上浮体在波浪激励下上下运动时都可以产生向前的推进力。
|
图 6 单个翼片X方向驱动力 Fig. 6 thrust of single fin in X direction |
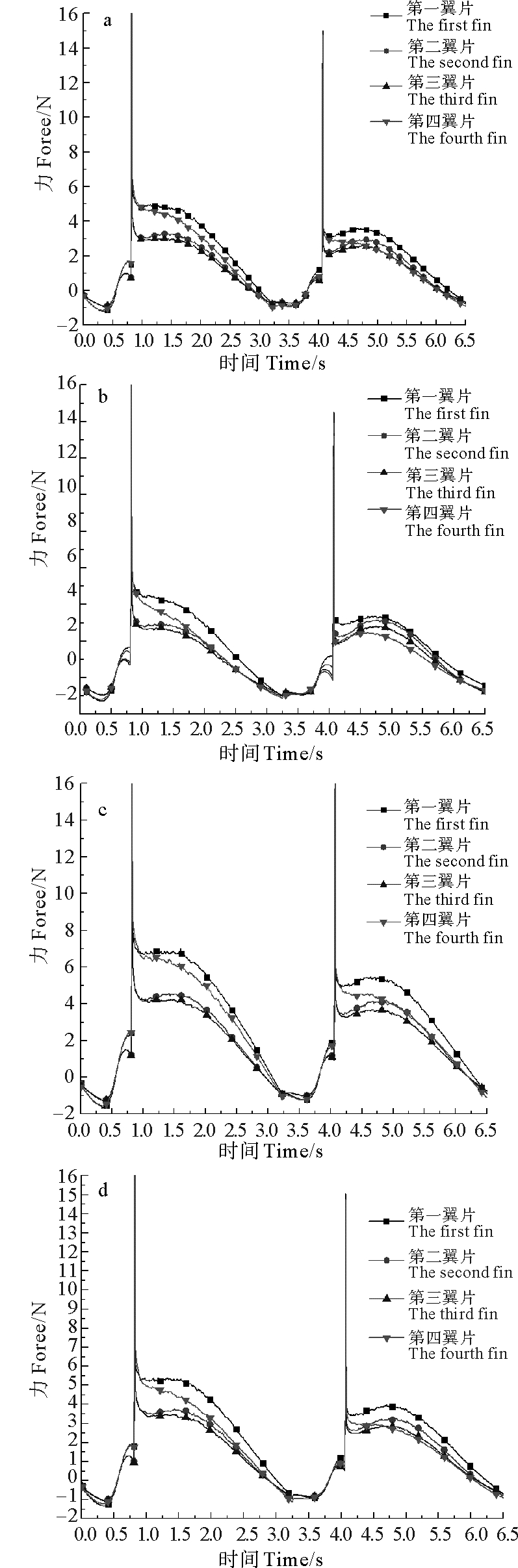
图 7为相同运动状态下5、10、15及20 mm间距下各翼片的受力情况。由图可见不同位置的翼片驱动力不同,表明翼片间的流场扰动对翼片的驱动力有较大的影响,不同间距下纵向阵列翼片的受力为最前端与最尾端翼片所产生的推进力均大于中间两翼片所产生的推进力。翼片驱动力变化规律同单翼片变化相同。
|
(a. 5 mm间距下翼片推进力Thrust of fin with distance of 5 mm; b. 10 mm间距下翼片推进力Thrust of fin with distance of 10 mm;c. 15 mm间距下翼片推进力Thrust of fin with distance of 15 mm;d. 20 mm间距下翼片推进力Thrust of fin with distance of 20 mm.) 图 7 不同间距下翼片推进力 Fig. 7 Thrust of fin with different distance |
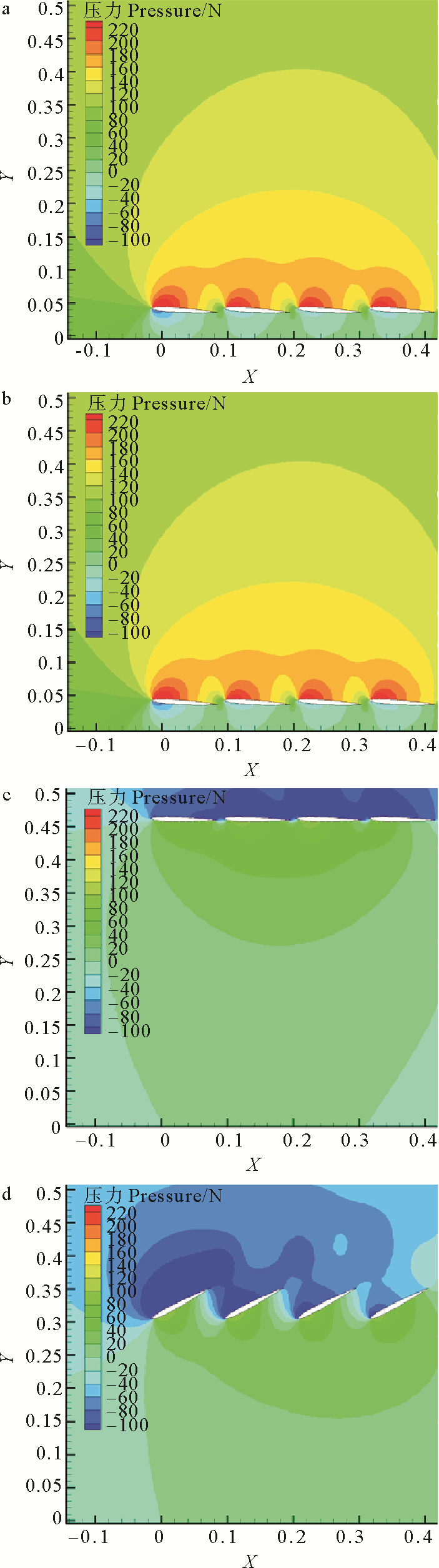
图 8为10 mm间距下不同时刻的压力分布情况,可知0~3.25 s这半个周期的压力差明显大于后半个周期,这是后半个周期幅值小于前半个周期的原因,在启动阶段产生的推进力大于稳定运行阶段。由10 mm间距下不同时刻的压力分布情况可以看出,不同翼片形成的前缘涡与尾涡相互影响较大,是导致不同位置翼片驱动力不同的原因。
|
(a. 0.6 s压力分布Pressure distribution of fin in 0.6 s;b. 1.4 s压力分布。Pressure distribution of fin in 1.4 s;c. 3.8 s压力分布Pressure distribution of fin in 3.8 s;d. 4.6 s压力分布Pressure distribution in of fin 4.6 s.) 图 8 翼片间距10 mm下不同时刻压力分布 Fig. 8 Pressure distribution of fin with distance of 10 mm in one period |
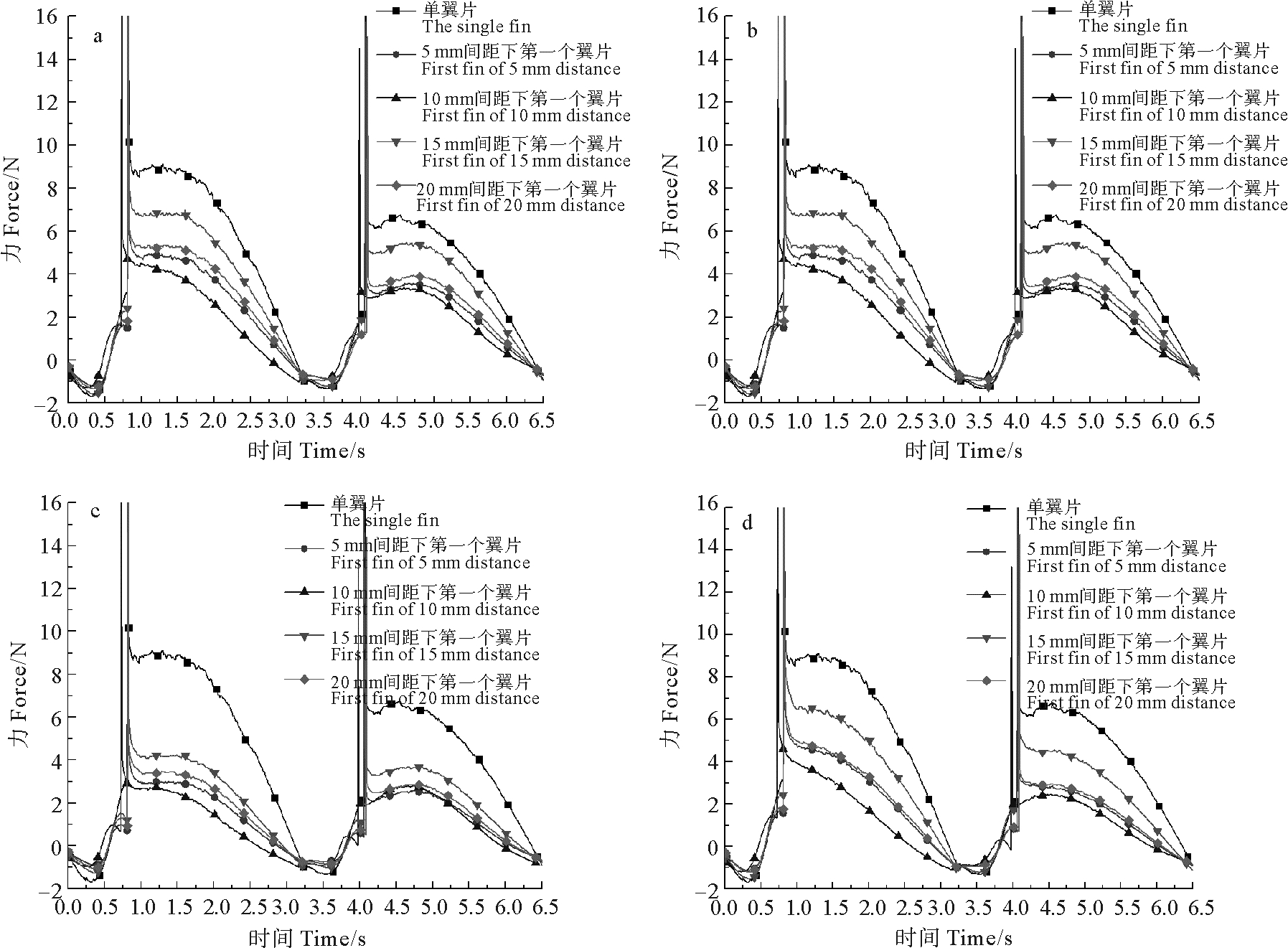
由图 9可以看出单独翼片所产生的推进力都大于阵列翼片所产生的推进力。15 mm间距时纵向阵列翼片所产生的推进力都大于5、10、20 mm间距时阵列翼片所产生的推进力。
|
(a.不同间距第一翼片与单翼片推力Compare thrust of single fin with first fin in different distance;b.不同间距第二翼片与单翼片推力Compare thrust of single fin with second fin in different distance;c.不同间距第三翼片与单翼片推力;Compare thrust of single fin with third fin in different distance;d.不同间距第四翼片与单翼片推力Compare thrust of single fin with fourth fin in different distance.) 图 9 单翼片推进力与不同间距纵向阵列翼片推力比较 Fig. 9 Compare thrust of single fin with array fin in different distance |
本文对波浪滑翔机在起始运动阶段推进装置的水动力学采用流体有限元进行了研究,得到如下结论:
(1) 对比一个运动周期内纵向阵列翼片内每个翼片所产生的推进力,单个翼片所产生的推进力均大于纵向阵列翼片中每个翼片的推进力,不同位置的翼片所产生的推进力不同。
(2) 对比纵向阵列翼片不同间距下各翼片所产生的推进力,首端与末端翼片所产生的推进力均大于中间翼片所产生的推进力。
(3) 对比纵向阵列翼片间距为5、10、15、20 mm下纵向阵列翼片的受力情况,发现在15 mm间距时翼片所产生的推进力更大。
(4) 翼片随着上浮体在波浪激励下向上及向下运动时都可以产生推进滑翔机运动的推进力。
| [1] |
Hine R, Willcox S, Hine G, et al. The wave glider: A wave-powered autonomous marine vehicle[C]. /Ocean 2009. Biloxi: IEEE Xplore, 2009: 1-6.
(  0) 0) |
| [2] |
Daniel T, Manley J, Trenaman N. The Wave Glider: Enabling a new approach to persistent ocean observation and research[J]. Ocean Dynamics, 2011, 61(10): 1509-1520. DOI:10.1007/s10236-011-0408-5
(  0) 0) |
| [3] |
Eslam Panah A, Buchholz J. Hydrodynamics of efficient propulsion in oscillating foils[C]. /APS Division of Fluid Dynamics Meeting. Portland, Oregon: APS Division of Fluid Dynamics Meeting Abstracts, 2010.
(  0) 0) |
| [4] |
Triantafyllou M S, Techet A H, Hover F S. Review of experimental work in biomimetic foils[J]. IEEE Journal of Oceanic Engineering, 2004, 29(3): 585-594. DOI:10.1109/JOE.2004.833216
(  0) 0) |
| [5] |
Silva L W A D, Yamaguchi H. Numerical study on active wave devouring propulsion[J]. Journal of Marine Science & Technology, 2012, 17(3): 261-275.
(  0) 0) |
| [6] |
Politis G, Politis K. Biomimetic propulsion under random heaving conditions, using active pitch control[J]. Journal of Fluids & Structures, 2014, 47(2): 139-149.
(  0) 0) |
| [7] |
Bøckmann E, Steen S. Experiments with actively pitch-controlled and spring-loaded oscillating foils[J]. Applied Ocean Research, 2014, 48: 227-235. DOI:10.1016/j.apor.2014.09.004
(  0) 0) |
| [8] |
刘鹏, 苏玉民, 刘焕兴, 等. 串列异步拍动翼推进性能分析[J]. 上海交通大学学报, 2014(4): 457-463. Liu P, Su Y M, Liu H X, et al. Propulsive performance analysis of tandem asynchronous flapping foil[J]. Journal of Shanghai Jiao Tong University, 2014(4): 457-463. (  0) 0) |
| [9] |
胡合文.波浪滑翔机的水动力分析[D].哈尔滨: 哈尔滨工程大学, 2015. Hu H W. Hydrodynamic Analysis of Wave Glider[D]. Harbin: Harbin Engineering University, 2015. (  0) 0) |
| [10] |
贾立娟.波浪动力滑翔机双体结构工作机理与动力学行为研究[D].天津: 国家海洋技术中心, 2014. Jia L J. Study of Operation Principle of Two-part Architecture and Dynamic Behavior of Wave glider[D]. Tianjin: Nation Ocean Technology Center, 2014. (  0) 0) |
| [11] |
Zheng B H, Xu C Y, Yao C L, et al. The effect of attack angle on the performance of wave glider wings[J]. Applied Mechanics & Materials, 2015, 727-728: 587-591.
(  0) 0) |
| [12] |
李小涛.波浪滑翔器动力学建模及其仿真研究[D].北京: 中国舰船研究院, 2014. Li X T. Dynamic Model and Simulation Study Based on The Wave Glider[D]. Beijing: China Ship Research and Development Academy, 2014. http://cdmd.cnki.com.cn/Article/CDMD-86201-1014069441.htm (  0) 0) |
| [13] |
王雄.圆孔射流近场湍流特性DNS与RANS、LES的对比研究[D].杭州: 浙江大学, 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1852909
(  0) 0) |
2. Key Lab of Ocean Engineering of Shandong Province, Qingdao 266100, China;
3. College of Oceanic and Atmospheric Sciences, Qingdao 266100, China
 2020, Vol. 50
2020, Vol. 50


