随着近海渔业资源的不断枯竭,通过建设人工鱼礁体来发展大规模的海洋牧场已成为一种有效的丰富渔业资源手段。
人工鱼礁体作为海洋牧场的重要组成部分,是通过在海中设置构造物,改善海域生态环境,营造海洋生物栖息的良好环境,为鱼类等提供繁殖、生长、索饵和庇敌的场所,实现保护、增殖和提高渔获量的目的。
Granneman等[1]通过对比加利福尼亚南部5组人工鱼礁体和天然鱼礁在集鱼效果方面的差异分析,发现人工鱼礁体和天然鱼礁在鱼类丰富度方面没有显著差异,但人工鱼礁体在鱼类密度和生物复杂程度方面趋于偏高。
Li等[2]通过数值模拟和PIV实验研究了5种不同来流速度和3种不同布置组合情况下圆管型人工鱼礁体周围的流场效应,并发现上升流和背涡流的强度和规模均随着礁体数量的增加而增强。
姜昭阳[3]基于CFD方法和PIV技术研究了单孔、多孔方型人工鱼礁体和梯型台人工鱼礁体各断面压力分布、流场效应和礁体的受力情况,发现由于方型和梯型台迎流面与来流方向夹角的差异,方型礁体对来流的阻力要强于梯型台礁体,所产生的流场范围相对梯型台人工鱼礁体较为广泛。
刘同渝[4]通过水槽和风洞实验研究了梯型台、半球型、三角锥体、堆叠式人工鱼礁体的流场效应,发现水流经过鱼礁体时会在其两侧形成上升流和背涡流,且上升流区范围约为鱼礁体的1/3,背涡流距礁体渐远渐弱;从流场效应看堆叠式人工鱼礁体最佳,梯型台人工鱼礁体次之。
庞运禧等[5]通过数值方法分别模拟了透空率为20%的箱型、梯型台、三棱体多孔空心人工鱼礁体在不同来流速度和布设工况下的流场过程。结果表明同种模拟工况下人工鱼礁体以90°摆放时形成的上升流和背涡流规模强度达到最大;单礁体时箱型鱼礁体产生的流场效应更佳。
马荍沣[6]等通过选取k-ε湍流模型的数值方法分别模拟了不同开口比的单体人工鱼礁,发现开口单体人工鱼礁的流场效应明显优于不开口的单体实心鱼礁,但开口不应过大,在单孔鱼礁情形下,开口比为0.04时流场效应最优。
由上述研究工作可知,国内外学者对人工鱼礁体的研究主要集中于单一开口比情况下人工鱼礁体周围流场形态随海流流速、鱼礁体形状、鱼礁体迎流角度等方面的变化,但对梯型台人工鱼礁体的研究及其流场效应随开口比和海底坡度的变化情况尚缺乏研究,而已有研究工作[7-8]表明鱼礁体开口比和海底坡度变化对上述流场特性有一定的影响。本文利用Fluent软件模拟了不同工况下梯型台人工鱼礁体流场过程,旨在探究鱼礁体流场效应受开口比和海底坡度变化的影响程度,为实际鱼礁体结构的设计提供参考。
1 数值模型及鱼礁体结构 1.1 控制方程假设鱼礁体附近的流场为粘性不可压缩流体的湍流运动,温度变化不大,因此能量方程可以忽略。
连续方程:
| $ \frac{\partial u_{i}}{\partial x_{i}}=0。$ | (1) |
动量方程:
| $ \frac{\partial u_{i}}{\partial t}+u_{j} \frac{\partial u_{i}}{\partial x_{j}}=-\frac{1}{\rho} \frac{\partial p}{\partial x_{i}}+\frac{\partial}{\partial x_{j}}\left[\nu \frac{\partial u_{i}}{\partial x_{j}}-\overline{u_{i}^{\prime} u_{j}^{\prime}}\right]+f_{i}。$ | (2) |
式中:ui(i=1,2,3)分别为x、y、z方向的雷诺平均速度;ρ为流体密度;p为压强;ν为运动粘性系数;fi为体积力。
1.2 湍流模型本文采用RNG κ-ε两方程湍流模型,该模型可以更好地处理高应变率及流线弯曲程度较大的流动;选用标准壁面函数法处理近壁区内及Re数较低的流动[9]。
湍动能κ方程:
| $ \frac{\partial(\rho \kappa)}{\partial t}+\frac{\partial\left(\rho \kappa u_{i}\right)}{\partial x_{i}}=\frac{\partial}{\partial x_{j}}\left(\alpha_{\kappa} \mu_{\mathrm{eff}} \frac{\partial \kappa}{\partial x_{j}}\right)+G_{\kappa}+\rho \varepsilon。$ | (3) |
湍流耗散率ε方程:
| $ \frac{{\partial (\rho \varepsilon )}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left( {{\alpha _\varepsilon }{\mu _{{\rm{eff}}}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right) + \frac{{C_{1\varepsilon }^*\varepsilon }}{\kappa }{G_\kappa } - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{\kappa }。$ | (4) |
其中:μeff=μ+μt;
其中:
湍动粘度系数:
经验常数:Cμ=0.084 5;
Prandtl数:ακ=αε=1.39;
热膨胀系数:β=0.012;
时均应变率:
鱼礁体4个侧面开口形式相同,开口比(φ)定义为鱼礁体迎流面在垂直于水流方向上开口的投影面积与迎流面投影面积之比[7]。图 1为开口型梯型台人工鱼礁体结构示意图。

|
图 1 梯型台人工鱼礁体结构示意图 Fig. 1 The sketch of trapezoidal artificial reef |
本文选取的梯型台人工鱼礁体下底面为3 m×3 m、上底面为1.8 m×1.8 m、高为2 m、开口比φ分别为0、0.1、0.2、0.3、0.4、0.5、0.6;海底坡度分别为θ1=0°、θ2=1.15°(tanθ2=1/50)、θ3=1.91°(tanθ3=1/30)、θ4=5.71°(tanθ4=1/10)的海域,为研究海底坡度的影响,分别考虑了θ5=10°、θ6=20°两个较大的坡度。设鱼礁体下底面长度为L,宽度为W,礁高为H,计算域设定长度为鱼礁体前4L、礁后6L、宽度为6W、高度为5H[10];加密区设定尺寸为5L×3W×3H[11];流速取值为0.8 m/s(见图 2)。

|
图 2 计算区域 Fig. 2 Computational domain |
本文所设定的初始边界条件:
(1) 入口边界设置为速度入口,来流速度为0.8 m/s,并设定边界上湍动能和湍动耗散率;
(2) 出口边界设置为自由出流;
(3) 计算域的两侧面设置为对称边界;
(4) 计算域的顶面设置为具有与入口水流相同速度的可移动壁面,剪切力为零,底面和鱼礁体表面设置为无滑移壁面。
2 模型可靠性验证 2.1 数学模型验证为了验证本文湍流模型、参数设置和网格划分的准确性,选择姜昭阳[3]建立的4个侧面均开有直径D=3.5 cm的圆形开口,壁厚为1.2 cm,上底面边长a=6 cm,下底面边长b=10 cm,礁高h=7 cm的梯型台人工鱼礁体进行数值模拟,如图 3所示。

|
图 3 梯型台人工鱼礁体 Fig. 3 Artificial reef of trapezoid platform |
本文使用ANSYS Workbench 【Mesh】模块对计算域进行四面体单元非结构化网格划分。数学模型中加密区网格尺寸为0.01 m,其他计算域网格尺寸为0.02 m,来流速度为0.212 3 m/s,表 1给出了模拟结果与姜昭阳[3]的PIV实验结果和数值模拟结果的对比。
|
|
表 1 礁体阻力结果对比 Table 1 Comparison of the results of resistance of the reef |
由表 1可知,本文的鱼礁体阻力数值模拟值与姜昭阳[3]PIV实验值较为接近,表明本文的数值模拟是可行的,结果是可信的。
2.2 网格收敛性验证为了减小在数值模拟中由网格尺寸所致影响,选取开口比为0.3的梯型台人工鱼礁体进行模拟。加密区网格尺寸为0.250 m,其他计算域网格分别为0.900、0.700、0.500、0.300 m,网格收敛性验证以礁体阻力系数为变量,结果如表 2所示。
|
|
表 2 不同网格尺寸模拟结果 Table 2 Simulated results with different gird sizes |
由表 2可得,当网格尺寸为0.500 m时,礁体阻力系数值较为稳定,网格收敛性较好。考虑计算效率,本文加密区网格尺寸设置为0.250 m,其他计算域网格尺寸设置为0.500 m。
3 数值结果基于上述模型,模拟了7种开口比、6种海底坡度梯型台人工鱼礁体周围水流场,并重点分析鱼礁体的上升流水平长度、最大高度、竖向最大速度和背涡流水平长度、水平宽度、最大高度的变化。
3.1 流场效应随开口比变化本研究中上升流区域定义为水流z方向速度与来流速度之比大于或等于5%的水域[12]。背涡流区域定义为水流x方向速度小于0的水域[13]。
图 4分别给出了来流速度为0.8 m/s时,7种不同开口比鱼礁体在海底坡度为0、y=1.5 m截面上的上升流区域分布图。图 5给出的是鱼礁体上升流体积与开口比的关系。由图 4、5可知:当开口比为0时,鱼礁体上升流体积最大。随着鱼礁体开口比的增大,来流受到鱼礁体开口的分流增多,上升流体积逐渐减小。通过最小二乘法拟合可得鱼礁体上升流体积(y)与开口比(φ)的关系式为:
| $ y=-268.9 \varphi+202.0。$ | (5) |

|
图 4 不同开口比鱼礁体y=1.5 m平面上升流区分布图 Fig. 4 The velocity contour diagrams of upwelling zone of reefs with different opening ratios in the plane of y=1.5 m |

|
图 5 鱼礁体上升流体积与开口比的关系 Fig. 5 The relation between the volume of upwelling and the opening ratio of the reef |
表 3中Hu-max/H为鱼礁体产生的上升流最大高度与礁高之比,Lu-max/L为上升流水平长度与礁长之比,Vz-max/V为上升流区竖直方向最大速度与来流速度之比。由表 3可知,随着鱼礁体开口比的增大,由于分流作用的影响,上升流最大高度和竖向最大速度均逐渐减小;当鱼礁体开口比为0.2时,其所产生的上升流最大高度约为鱼礁体高度的2.75倍,这与姜昭阳[3]得出的数模结果相近;而上升流水平长度呈现先增大后减小,当开口比为0.3时达到最大值;由于梯型台人工鱼礁体迎流面与水平来流存在一定夹角,阻水作用小于单孔方型人工鱼礁体,因此,鱼礁体迎流面对水平来流起到一定的加速作用,其所产生的上升流竖向最大速度大于单孔方型人工鱼礁体,对海底营养物质向上传输以及吸引鱼群具有积极的作用。
|
|
表 3 不同开口比变化对上升流特性参数的影响 Table 3 The influence of different opening ratios on the characteristic parameters of upwelling |
图 6给出的是来流速度为0.8 m/s时,7种开口比鱼礁体在y=0 m截面上的速度矢量分布。由图可知,开口比为0时,鱼礁体后方产生一个顺时针的漩涡,此区域一般称为背涡区,随着开口比的增大,漩涡逐渐消失;其他当开口比由0变化到0.1时,鱼礁体周围速度矢量分布较为复杂;当开口比大于0.4时,由于鱼礁体开口透水作用增强,速度矢量趋于平行,因而没有明显的背涡区。
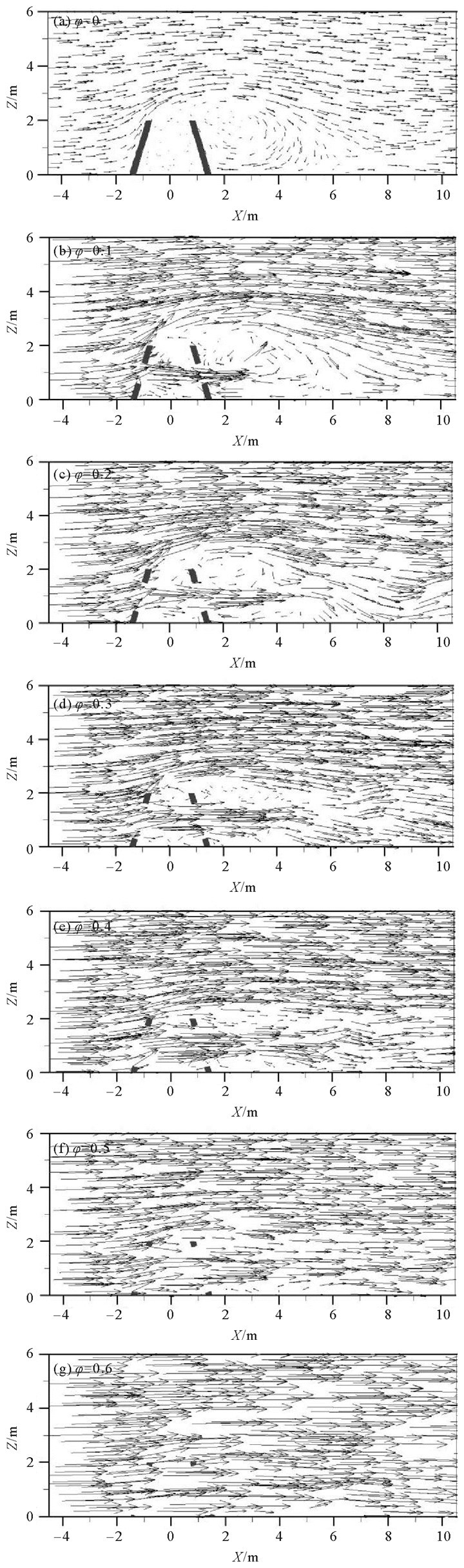
|
图 6 不同开口比鱼礁体y=0 m平面速度矢量分布 Fig. 6 The velocity vector diagrams of reefs with different opening ratios in the plane of y=0 m |
表 4中Hv-max/H为鱼礁体产生的背涡流最大高度与礁高之比,Lv-max/L为背涡流水平长度与礁长之比,Wmax/W为背涡流水平宽度与礁宽之比。当鱼礁体开口比为0.1时,其背涡流最大高度和水平宽度最大,水平长度略小于开口比为0时的值;当鱼礁体开口比为0时,其背涡流水平长度约为礁长的2.33倍,这与刘同渝[4]得出的背涡流水平长度为礁长的2~3倍相一致;随着鱼礁体开口比的增大,圆孔分流作用增强,其背涡流水平长度及水平宽度逐渐减小。
|
|
表 4 不同开口比变化对背涡流特性参数的影响 Table 4 The influence of different opening ratios on the characteristic parameters of the wake vortex |
海底坡度是人工鱼礁区选择的重要因素之一,它可影响鱼礁体周围的流场效应以及礁体的稳定性。通常人工鱼礁体投放的海域海底坡度为0~5°左右,本文为研究海底坡度对鱼礁体周围流场效应的影响选取开口比分别为0.1、0.3、0.5的梯型台人工鱼礁体,假定海底平坦,将鱼礁体放置于海底坡度分别为θ1=0°、θ2=1.15°(tanθ2=1/50)、θ3=1.91°(tanθ3=1/30)、θ4=5.71°(tanθ4=1/10)的海域,为研究海底坡度的影响,分别考虑了θ5=10°、θ6=20°两个较大的坡度。

|
图 7 海底坡度示意图 Fig. 7 The diagram of seafloor slope |
由表 5~10可得,在相同海底坡度下,上升流和背涡流特性参数与开口比的关系和上文保持一致;当鱼礁体开口比不变时,随着海底坡度的增加,鱼礁体产生的上升流最大高度、水平长度和竖向最大速度均逐渐增大;当开口比为0.5、海底坡度为5.71°时,对应的上升流最大高度约是海底坡度为0时的1.72倍,流场效应更佳;而鱼礁体产生的背涡流范围几乎不受海底坡度的影响。
|
|
表 5 开口比为0.1时不同海底坡度变化对上升流特性参数的影响 Table 5 The influence of different seafloor slopes on the characteristic parameters of upwelling at opening ratio of 0.1 |
|
|
表 6 开口比为0.3时不同海底坡度变化对上升流特性参数的影响 Table 6 The influence of different seafloor slopes on the characteristic parameters of upwelling at opening ratio of 0.3 |
|
|
表 7 开口比为0.5时不同海底坡度变化对上升流特性参数的影响 Table 7 The influence of different seafloor slopes on thecharacteristic parameters of upwelling at opening ratio of 0.5 |
|
|
表 8 开口比为0.1时不同海底坡度变化对背涡流特性参数的影响 Table 8 The influence of seafloor slopes on the characteristic parameters of the wake vortex at opening ratio of 0.1 |
|
|
表 9 开口比为0.3时不同海底坡度变化对背涡流特性参数的影响 Table 9 The influence of seafloor slopes on the characteristic parameters of the wake vortex at opening ratio of 0.3 |
|
|
表 10 开口比为0.5时不同海底坡度变化对背涡流特性参数的影响 Table 10 The influence of seafloor slopes on the characteristic parameters of the wake vortex at opening ratio of 0.5 |
本文利用Fluent软件中的RNG κ-ε湍流模型,模拟了7种开口比和6种海底坡度下梯型台人工鱼礁体周围的水流场,分析了其流场效应在不同开口比和海底坡度情况下的变化,得到了如下结论。本文研究结果可为人工鱼礁体的设计提供参考。
(1) 在海底坡度不变的情况下,梯型台人工鱼礁体产生的上升流体积、最大高度和竖向最大速度均随开口比的增大而减小;而上升流水平长度先增大后减小,当开口比为0.3时达到最大值;当开口比为0.1时,鱼礁体产生的背涡流范围最广,随着开口比的增大,背涡流范围逐渐减小。
(2) 在开口比不变的情况下,梯型台人工鱼礁体产生的上升流最大高度、水平长度和竖向最大速度均随海底坡度的增大而增大,且当开口比为0.5、海底坡度为5.71°时,其所对应的上升流最大高度约是海底坡度为0时的1.72倍,流场效应更佳;而背涡流范围几乎不受海底坡度的影响。
(3) 当开口比为0~0.6时,上升流体积(y)与开口比(φ)存在如下关系:
| $ y = - 268.9\varphi + 202.0{\rm{ }}({R^2} = 0.98)。$ |
(4) 当开口比为0.1、海底坡度为5.71°时,梯型台人工鱼礁体产生的上升流和背涡流范围较其他工况最广,流场效应最佳。
| [1] |
Granneman J E, Steele M A. Effects of reef attributes on fish assemblage similarity between artificial and natural reefs[J]. Ices Journal of Marine Science, 2015, 72(8): 2385-2397.
(  0) 0) |
| [2] |
Li J, Zhang Y X, Gong P H, et al. Numerical simulation and piv experimental study of the effect of flow fields around tube artificial reefs[J]. Ocean Engineering, 2017, 134: 96-104.
(  0) 0) |
| [3] |
姜昭阳.人工鱼礁水动力学与数值模拟研究[D].青岛: 中国海洋大学, 2009. Jiang Z Y. Numerical Simulation of Hydrodynamics for Artificial Reefs[D]. Qingdao: Ocean University of China, 2009. (  0) 0) |
| [4] |
刘同渝. 人工鱼礁的流态效应[J]. 水产科技, 2003(6): 43-44. Liu T Y. Flow regime effect of artificial reefs[J]. Fisheries Science and Technology, 2003(6): 43-44. (  0) 0) |
| [5] |
庞运禧, 李芳成, 李尧. 同透空率下多孔人工鱼礁流场效应的三维数值模拟研究[J]. 水资源与水工程学报, 2017, 28(2): 133-141. Pang Y X, Li F C, Li Y. Study on three-dimensional numerical simulation of flow field effect of multi-aperture artificial fish reef under identical penetration rate[J]. Journal of Water Resources and Water Engin eering, 2017, 28(2): 133-141. (  0) 0) |
| [6] |
马荍沣, 张瑞瑾, 席彦彬, 等. 开口比变化对人工鱼礁流场效应影响的评价[J]. 安徽农业科学, 2018, 46(5): 105-108. Ma F F, Zhang R J, Xi Y B, et al. Evaluation of the effect of opening ratio on the flow field effect of artificial reefs[J]. Anhui Agricultural Science, 2018, 46(5): 105-108. (  0) 0) |
| [7] |
邵万骏, 刘长根, 聂红涛, 等. 人工鱼礁的水动力学特性及流场效应分析[J]. 水动力学研究与进展, 2014, 29(5): 580-585. Shao W J, Liu C G, Nie H T, et al. Analysis of hydrodynamic characteristics and flow field around artificial reefs[J]. Chinese Journal of Hydrodynamics, 2014, 29(5): 580-585. (  0) 0) |
| [8] |
Düzbastilar F O, Sentürk U. Determining the weights of two types of artificial reefs required to resist wave action in different water depths and bottom slopes[J]. Ocean Engineering, 2009, 36: 900-913.
(  0) 0) |
| [9] |
王福军. 计算流体动力学分析-CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004. Wang F J. Computational Fluid Dynamics Analysis-Cfd Software Principles and Applications[M]. Beijing: Tsinghua University Press, 2004. (  0) 0) |
| [10] |
郑延璇, 关长涛, 宋协法, 等. 星体型人工鱼礁流场效应的数值模拟[J]. 农业工程学报, 2012, 28(19): 185-193. Zheng Y X, Guan C T, Song X F, et al. Numerical simulation on flow field around star artificial reefs[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(19): 185-193. (  0) 0) |
| [11] |
唐衍力, 龙翔宇, 王欣欣, 等. 中国常用人工鱼礁流场效应的比较分析[J]. 农业工程学报, 2017, 33(8): 97-103. Tang Y L, Long X Y, Wang X X, et al. S Comparative analysis on flow field effect of general artificial reefs in China[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(8): 97-103. (  0) 0) |
| [12] |
黄远东, 姜剑伟, 赵树夫. 方型人工鱼礁周围水流运动的数值模拟研究[J]. 水资源与水工程学报, 2012, 23(3): 1-3. Huang Y D, Jiang J W, Zhao S F. Study on numerical model of water flows past a square artificial reef[J]. Journal of Water Resources and Water Engineering, 2012, 23(3): 1-3. (  0) 0) |
| [13] |
Kim D, Woo J, Yoon H S, et al. Wake lengths and structural responses of Korean general artificial reefs[J]. Ocean Engineering, 2014, 92: 83-91.
(  0) 0) |
 2020, Vol. 50
2020, Vol. 50

