海洋浮游生物探测对于海洋生态研究和环境监测具有重要意义[1-2]。数字全息显微技术[3-5]作为一种光学测量方法,与传统的探测技术相比,可以实现浮游生物原位、实时、无损坏、快速、大视场、大景深、三维立体探测,因此,被广泛应用于海洋浮游生物的探测与研究。
目前,各种数字全息或数字全息显微系统已用于海洋浮游生物的原位探测,例如,英国阿伯丁大学的Watson等设计研制了水下全息照相系统HoloCAM[6],该系统成功应用于海洋浮游生物的实地探测,浮游生物的尺寸从几十微米到几十毫米不等,分辨率可达到50 μm。HoloCAM系统能够同时记录同轴和离轴全息图,通过分层再现,可以精确确定生物个体的大小、轮廓和相对位置。美国MIT的Loomis等DHI(Digital Holographic Imaging)系统搭载深海探测设备,拍摄记录了深海浮游生物的同轴全息图,分辨率可达到2.2 μm[7-8]。中国海洋大学的于佳团队[9]也成功将数字全息显微系统用于海洋浮游生物探测,分辨率可达到7.8 μm。
然而,以上对海洋浮游生物的探测也只是得到其二维平面图,在一定程度上很难反应物体的三维形貌特征,而三维形貌特征作为浮游生物识别归类和建立三维数据库的重要依据,对海洋生态环境检测和保护有着重要的意义。因此,本文通过对基于离轴菲涅尔数字全息显微的探测实验进行研究,记录浮游生物的全息图,全息图再现,通过改进的相位恢复方法,对相位畸变预消除,直接得到正确的相位信息,避免了后期复杂的相位补偿计算,从而对浮游生物三维形貌快速恢复。
1 相位畸变产生的原因及其矫正数字全息显微可分为无透镜傅里叶变换和预防大离轴菲涅尔全息[10],前者系统结构简单、紧凑,再现算法简单(只需要进行一次傅里叶变换),但成像分辨率不高。后者很好的解决了前者分辨率不高的缺点,在显微成像探测领域应用更广泛。因此本论文基于预防大离轴菲涅尔系统,对海洋浮游生物进行了表面形貌的三维重建研究。然而,在再现像的相位测量过程中,物体折射率不均匀以及系统景深对相位分布的影响,再现像产生相位畸变,相位畸变是指对全息图进行数字再现得到的再现像的相位分布,与被测物体实际相位分布之间的差异,本论文中研究的相位畸变包括一次畸变和二次相位畸变[11-12]。
1.1 一次相位畸变及其矫正在离轴菲涅尔数字全息图记录中,物光和参考光分别为O(x, y)、R(x, y),夹角为θ,参考光竖直和水平方向的夹角分别为α、β,参考光表达式如下:
| $ R\left( x, y \right)=\text{exp}\left[j2\pi (\frac{\text{cos}\alpha }{\lambda }x+\frac{\text{cos}\beta }{\lambda }y) \right]。$ | (1) |
全息图再现的过程中,若模拟原参考光再现,则需要在再现算法中非常准确的设置参考光的偏置角,然而这个角度较小无法直接测量。一般的再现算法不考虑这个偏置角度,直接模拟垂直照射的平面波进行再现,这样就出现了数值模拟的再现光不能准确的还原传统光学全息所用的再现光。因此,再现像的相位产生畸变,成为一次相位畸变。由具体的推算过程可以得到一次相位畸变因子离散化表达式如下:
| $ {{\mathit{\Phi }}_{1}}\left( m, n \right)=\text{exp}\left[j2\pi (\frac{\text{cos}\alpha }{\lambda }m\Delta {{x}_{i}}+\frac{\text{cos}\beta }{\lambda }n\Delta {{y}_{i}}) \right]。$ | (2) |
其中:m和n(m≥-N/2, n≤N/2-1)为再现像面的像素坐标;Δxi和Δyi为像平面的像素尺寸,其大小根据不同的再现算法而定。
一次相位畸变与参考光和物光夹角有关,实际实验中这一角度无法直接测量,针对这一问题,本论文提出一种改进的卷积再现算法,能准确设置再现光的偏置角度,达到矫正一次相位畸变的目的。具体的矫正步骤如下:
(1) 运行菲涅尔再现算法,设置不同的再现距离对全息图进行再现,得到一系列不同再现距离下的再现像,将这些像中的聚焦像的再现距离代入卷积再现算法中,作为全息图的再现距离。
(2) 角度定标。在卷积再现算法中引入带有偏置角度的参考光如式(1),α可通过图像处理软件(如Photoshop)的标尺功能读取图干涉条纹的倾斜度数得出,β是算法中的待测参数,运行卷积算法得到不同β角度下的再现图,当得到聚焦再现像时,α、β的值即为参考光准确的偏置角度。
(3) 得到准确的偏置角度后,利用卷积算法对同样实验条件下拍摄的其它全息图进行处理,提取再现像振幅图和无畸变的相位图。
该方法是在全息图聚焦位置和参物角都未知的情况下,首先运行菲涅尔算法找到聚焦位置,然后再利用卷积算法确定参考光的偏置角度。定标过程稍显繁琐,但是,参物角一旦确定,就可以在该条件下进行多次实验。因此,只需要进行一次定标实验,即可对相位畸变实现预消除,这相对于在后期对已经产生的相位畸变进行繁琐的相位畸变补偿计算,大大加快了相位恢复的速度。
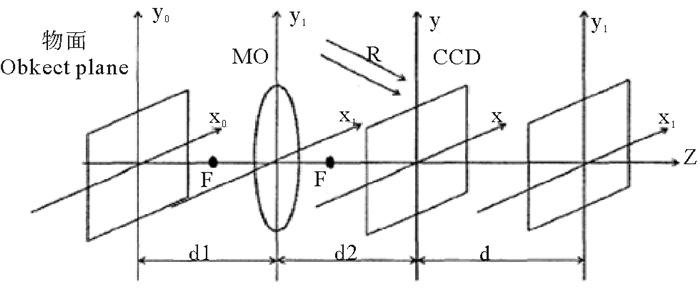
1.2 二次相位畸变及其矫正预放大离轴菲涅尔数字全息记录光路中,物平面和CCD平面加入了显微物镜(MO)用来放大被测样品的物光场。如图 1所示。
|
图 1 预放大离轴数字全息记录光路示意图 Fig. 1 Schematic of pre-magnificate off-axisl digital hologram recording system |
被测物经MO成像在CCD后面的像平面上,在CCD面接受的是放大的虚像,参考光在CCD面上发生干涉得到数字全息图。在MO成像过程中造成了二次相位畸变。二次相位畸变因子的表达式为:
| $ {{\mathit{\Phi }}_{2}}({{x}_{i}}, {{y}_{i}})=\text{exp}\left[\frac{jk}{\lambda {{d}_{2}}}\cdot \frac{{{d}_{1}}+{{d}_{2}}}{{{d}_{2}}}({{x}_{i}^{2}}+{{y}_{i}^{2}}) \right]。$ | (3) |
其中二次畸变因子只与MO的焦距和放大率有关,与参物夹角、记录距离等条件无关。
物光光路的显微物镜发出的球面波引起了二次相位畸变,那么在参考光的光路中引入一个发出等曲率球面波的显微物镜,就可以对相位畸变进行补偿。具体方法为:在物光光路不引入被测物的前提下,微调两个显微物镜,使得两束光的干涉条纹平行等间距分布。此时两束光等曲率面弯曲,从而达到消除二次相位因子的目的。
通过参物角定标和引入显微物镜,可以在相位畸变之前进行预消除,避免了后期繁琐的相位畸变矫正算法研究。
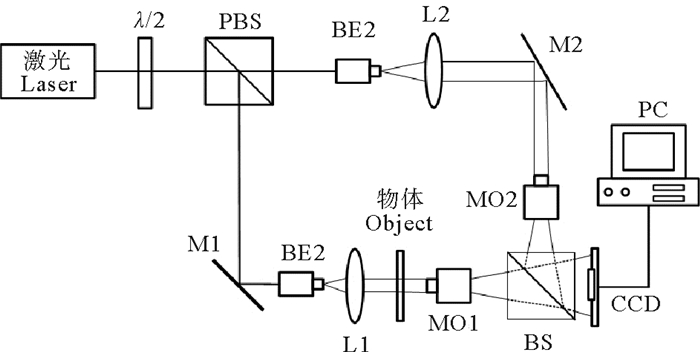
2 实验 2.1 实验系统简介如图 2为实验系统光路图,激光经过偏振分光棱镜(PBS)被分为物光和参考光两束,两束光分别经过扩束准直。通过PBS前的λ/2玻片调节两束光的光强比。物光和参考光分别被显微物镜1(MO1)和显微物镜2(MO2)放大经消偏振棱镜(BS)到达CCD,在CCD上发生干涉,记录下干涉条纹,具体实验设备参数见表 1。
|
图 2 实验系统光路示意图 Fig. 2 Schematic of hologram recording system |
|
|
表 1 实验系统设备参数 Table 1 Experiment system of the device parameters |
浮游生物分布探测和三维形貌重建之前,首先利用分辨率板对实验系统定标参数确定。
第一步:在参考光光路中引入相同参数的显微物镜,微调两个显微物镜的距离,使得CCD接受到等间距平行的干涉条纹,加入分辨率板拍摄全息图。
第二步:利用菲涅尔算法再现全息图,找到再现距离,本实验中分辨率板再现距离为d=12 cm时,再现图清晰、聚焦。
第三步:将再现距离以及β=43°(在图像处理软件中读取)代入卷积再现算法,设置不同的参物夹角α再现全息图,由结果可知偏置角为α=7.8°, β=43°时,得到居中、清晰的再现像。
通过偏置角度定标和引入等曲率弯曲参考光,对再现像相位畸变进行预矫正,从而避免了后期繁琐的后期算法研究。并且,将分辨率板换成其它被测物,进行同样的处理过程,可以得到被测物无相位畸变的再现像。偏置角度等实验参数不变的条件下,被测物更换为海洋浮游生物,进行三维形貌重建实验。
2.3 浮游生物三维形貌重建实验对浮游生物的三维形貌重建,基于其全息图再现像相位的准确恢复,需要进行相位畸变预矫正、相位提取和相位解包裹[13-15]三个步骤;进而对解包裹相位图三维视觉化从而实现浮游生物的三维形貌重建[16]。文章以桡足类和夜光虫为例(在山东省青岛市沙子口码头海水取样),对其进行表面形貌三维重建。
系统放大率12.3×记录单个桡足类浮游生物全息图。图 3(a)、(b)分别为记录全息图、再现距离d=62 mm的振幅再现图,由于桡足类有一定大小和厚度,整体无法同时聚焦在同一再现平面上,不同再现距离下桡足类的不同部位在焦,图 3(c)、(d)、(e)分为桡足类为:d=62 cm身体聚焦,d=56 cm触角聚焦,d=84 cm触须聚焦。

|
图 3 放大率12.3×桡足类全息图(左上)及其整体和不同部位的振幅再现图 Fig. 3 Recording image and amplitude reconstruction image of the whole body and different parts of copecod with 12.3× magnification |
桡足类不同再现距离下聚焦部分不同,然而前后一定范围内,再现像清晰度变化不大,可认为仍然在焦。因此,选取再现距离d=62 cm为桡足类聚焦距离。
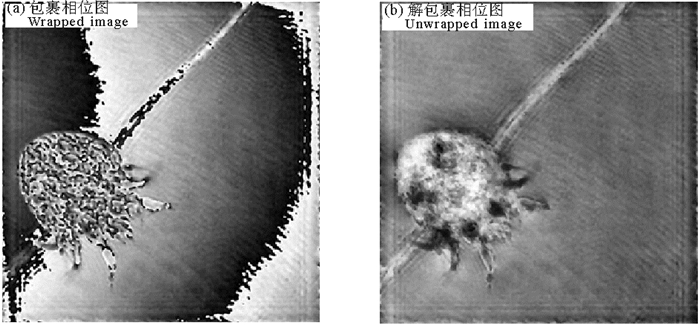
图 4(a)为聚焦距离d=62 cm处的相位包裹图,利用基于离散余弦变换法对包裹相位图进行相位解包裹,图 4(b)为解包裹相位图。
|
图 4 浮游生物的再现包裹相位图(左)和解包裹相位图(右) Fig. 4 Wrapped and Unwrapped phase reconstruction image of plankton |
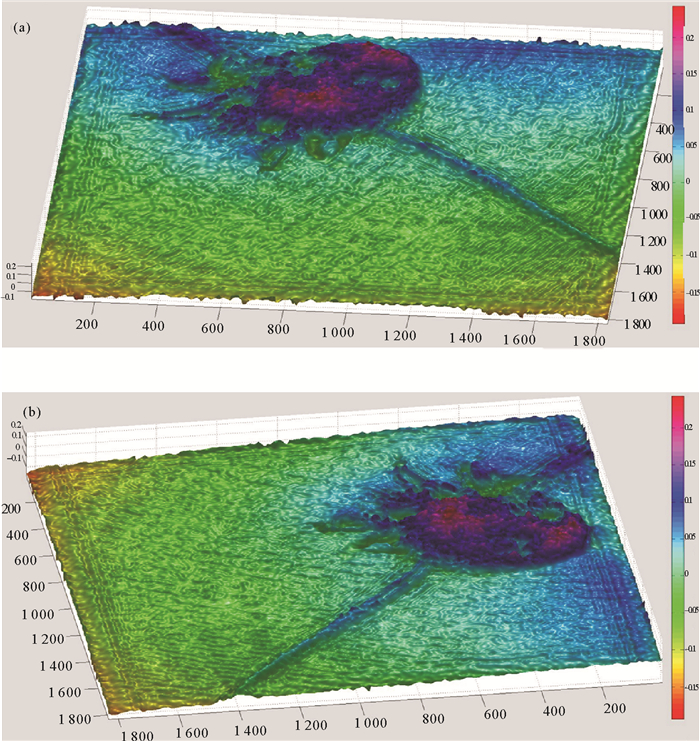
解包裹相位图为浮游生物的真实相位分布,相位图中物体每一点与基准面存在相位差,根据整体的相位分布可以得到物体的三维信息分布,在MATLAB中利用这些三维信息对桡足类进行三维重建,图 5为桡足类三维重建图。
|
图 5 桡足类浮游生物表面形貌三维重建图 Fig. 5 3D reconstruction image of copepods' surface profile |
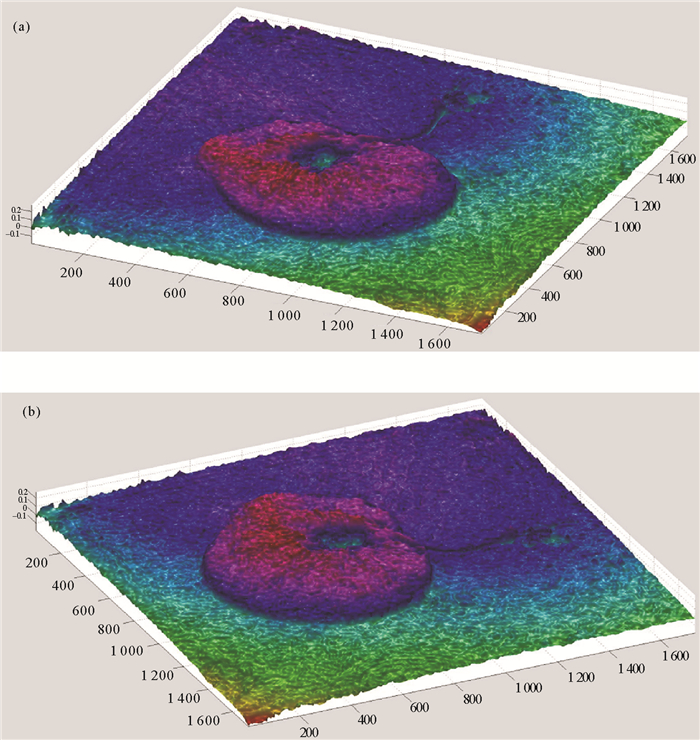
同理,夜光虫的三维形貌重建结果如图 6所示。
|
图 6 夜光虫表面形貌三维重建图 Fig. 6 3D reconstruction image of noctilucas |
浮游生物的厚度、透明度、以及内部结构的复杂程度等都会对相位解包裹的速度和准确性造成影响,进而影响物体三维重建的效果,由图 5和6可知,透明度高、内部结构相对简单的夜光虫,在相位畸变预矫正的基础上,三维重建图视觉效果相对较好。
解包裹相位图,如图 4(b),反应的是物体真实相位分布情况,物体上每一点与基准面都存在相位差,根据整体的相位分布可以得到物体的三维信息分布,从而对物体进行三维形貌重建。然而,该三维分布并不是物体表面形貌的实际高度分布,而只是物体相位与基准面的相对相位差分布,但该分布还是可以在一定程度上反映物体三维形貌信息的。
由图 3可知,系统放大率12.3×,桡足类身体线度约为191 μm×175 μm,触须约为330 μm×19 μm,触角约为106 μm×30 μm,最小线度均达到3.5 μm。即在放大率为12.3×,系统探测分辨率能达到3.5 μm。
4 结语本论文将预放大离轴菲涅尔数字全息系统与显微系统相结合,应用于海洋浮游生物表面形貌三维探测实验研究中。针对透射型浮游生物的细微结构和表面形貌,对于尺寸不同的桡足类(0.5~1 mm)和海藻类(100~500 μm)都实现了较好的探测效果,得到了三维化图像数据。由于采用改进的再现算法和全息图记录光路,对相位畸变进行预消除,简化了后期需要对再现像相位畸变进行繁琐的相位补偿计算,这有利于对海洋浮游生物进行实时探测和快速重建。
| [1] |
Davis C S, Thwaites F T, Gallager S M, et al. A three-axis fast-tow digital Video Plankton Recorder for rapid surveys of plankton taxa and hydrography[J]. Limnology and Oceanography: Methods, 2005, 3(2): 59-74. DOI:10.4319/lom.2005.3.59
(  0) 0) |
| [2] |
Goodman J W, Lawrence R W. Digital image formation from electronically detected holograms[J]. Applied Physics Letters, 1967, 11(3): 77-79. DOI:10.1063/1.1755043
(  0) 0) |
| [3] |
高本利, 顾济华, 周皓, 等. 预放大离轴菲涅耳数字全息显微技术[J]. 红外与激光工程, 2010(4): 706-710. Gao B L, Gu J H, Zhou H. Pre-magnified off-axis Fresnel digital holographic microscopy[J]. Infrared and Laser Engineering, 2010(4): 706-710. DOI:10.3969/j.issn.1007-2276.2010.04.027 (  0) 0) |
| [4] |
Sheng J, Malkiel E, Katz J. Digital holographic microscope for measuring three-dimensional particle distributions and motions[J]. Applied Optics, 2006, 45(16): 3893-3901. DOI:10.1364/AO.45.003893
(  0) 0) |
| [5] |
Garcia-Sucerquia J, Xu W, Jericho S K, et al. Digital in-line holographic microscopy[J]. Applied Optics, 2006, 45(5): 836-850. DOI:10.1364/AO.45.000836
(  0) 0) |
| [6] |
Hobson P R, Watson J. The principles and practice of holographic recording of plankton[J]. Journal of Optics A: Pure and applied optics, 2002, 4(4): S34. DOI:10.1088/1464-4258/4/4/362
(  0) 0) |
| [7] |
Yu Jia, Nie Yaru, Wang Tian, et al. Digital In-line Holographic Microscopy for in-situ Investigation of Marine Plankton[J]. Acta Laser Biology Sinica, 2014, 23(6): 547-552.
(  0) 0) |
| [8] |
赵洁, 王大勇, 王华英, 等. 用于微结构几何量测量的数字全息方法[J]. 红外与激光工程, 2008, 37: 173-176. Zhao J, Wang D Y, Wang H Y. Measurement of gemetrical parameters of microstructure with digital holography[J]. Infrared and Laser Engineering, 2008, 37: 173-176. DOI:10.3969/j.issn.1007-2276.2008.01.040 (  0) 0) |
| [9] |
王添, 于佳, 杨宇, 等. 数字全息显微测量中相位畸变的矫正方法[J]. 红外与激光工程, 2014, 43(11): 3615-3620. Wang T, Yu J, Yang Y. Correction method of phase distortion in digital holographic microscopy detection[J]. Infrared and Laser Engineering, 2014, 43(11): 3615-3620. DOI:10.3969/j.issn.1007-2276.2014.11.019 (  0) 0) |
| [10] |
张中恒.数字全息中再现像的相位畸变补偿[D].昆明: 昆明理工大学, 2014. Zhang Z H, Phase Distortion Compensation of Numerically Reconstructed Images in Digital Holography[D]. Kunming: Kunming University of Science and Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10674-1014349165.htm (  0) 0) |
| [11] |
马利红, 王辉, 金洪震, 等. 数字全息显微定量相位成像的实验研究[J]. 中国激光, 2012, 39(3): 209-215. Ma L H, Wang H, Jin H Z. Experiment study on quantitative phase imaging by digital holographic microscopy[J]. Chinese Journal of Lasers, 2012, 39(3): 209-215. (  0) 0) |
| [12] |
Cuche E, Marquet P, Depeursinge C. Simultaneous amplitude-contrast and quantitative phase-contrast microscopy by numerical reconstruction of Fresnel off-axis holograms[J]. Applied Optics, 1999, 38(34): 6994-7001. DOI:10.1364/AO.38.006994
(  0) 0) |
| [13] |
Schnars U, Jüptner W P O. Digital recording and numerical reconstruction of holograms[J]. Measurement Science and Technology, 2002, 13(9): R85. DOI:10.1088/0957-0233/13/9/201
(  0) 0) |
| [14] |
邸江磊, 赵建林, 范琦, 等. 数字全息显微术中重建物场波前的相位校正[J]. 光学学报, 2008, 28(1): 56-61. Di J L, Zhao J L, Fan Q. Phase correction of wavefront reconstruction in digital holographic microscopy[J]. Acta Optica Sinica, 2008, 28(1): 56-61. DOI:10.3321/j.issn:0253-2239.2008.01.011 (  0) 0) |
| [15] |
Itoh K. Analysis of the phase unwrapping algorithm[J]. Appl Opt, 1982, 21(14): 2470. DOI:10.1364/AO.21.002470
(  0) 0) |
| [16] |
王云新, 王大勇, 赵洁, 等. 基于数字全息显微成像的微光学元件三维面形检测[J]. 光学学报, 2011, 31(4): 109-114. Wang Y X, Wang D Y, Zhao J. 3D profile measurement for micro-optical component by using digital holographic microscopy[J]. Acta Optica Sinica, 2011, 31(4): 109-114. (  0) 0) |
 2019, Vol. 49
2019, Vol. 49


