2. 中水珠江规划勘测设计有限公司,广东 广州 510610
黄河流域水资源状况关系着社会发展及生态安全。降水是黄河流域水资源的主要来源,其时空分布与变化直接影响水资源的合理开发与利用,也是进一步研究水循环的基础[1-2]。研究降水量的分布特征及趋势预测,可为抗旱防涝提供依据,对了解降水趋势变化规律、保证农业、水利部门决策以及保障当地社会经济发展具有重要意义。
青海省作为黄河流域的发源省份,降水变化一直备受关注。戴虎德等[3]分析了黄河源头地区近50年降水及气温变化特点,并指出黄河源头年和四季平均气温呈上升趋势,地表蒸发量增大,而降水量无明显变化;白淑英等[4]研究了青海省近60年降水数据的空间分布特征及变化规律,指出降水分布呈现东多西少、南多北少的格局;王文等[5]利用黄河中上游24站夏季降水资料,提出基于EEMD的统计预报模型,提高了降水预报的精度。徐慧等[6]分析了青海省月降水异质性指数和降水集中性指数的区域分布及变化趋势,并指出季节性降水的增加有助于改善月降水分配的均匀性;王明常等[7]的研究发现,青海省极端降水事件及极端降水指数均呈上升趋势,且极端降水事件空间差异显著;刘晓琼等[8]的研究发现,在过去55年三江源地区总体降水量变化更趋向于青藏高原的降水变化,呈现弱增趋势。
青海省降水分析现有研究多采用降水距平分析、小波分析、Arcgis空间插值等方法进行降水空间分析,而对于时间尺度上的降水预测研究较少;在黄河流域降水研究方面,以上、中、下游分区研究居多,在单个省份的研究较少。为探讨青海省降水预测模型合理性以及丰富黄河流域研究内容,本文基于M-K检验、Pettitt检验、Morlet小波分析以及ARIMA模型等方法,采用青海省黄河流域31个气象站1956—2018年月值降水资料,重点探讨年、季降水变化特性以及降水预测变化的合理性,从而对当地水资源规划和管理做出指导。
1 区域概况与数据来源 1.1 区域概况青海省黄河流域位于青海省东部,地处95°39′E—103°06′E,32°43′N—39°08′N,包括龙羊峡以上的黄河源头和龙羊峡至寺沟峡的高山峡谷,地形复杂,海拔高度呈现出由西南向东北递减的特点,大部分海拔高程在3 000 m以上,平均气温为-6~9.2 ℃。气候属高原大陆性高寒气候,寒冷干燥,雨热同期。多年平均降水量在230~650 mm之间,区域地貌复杂多样。
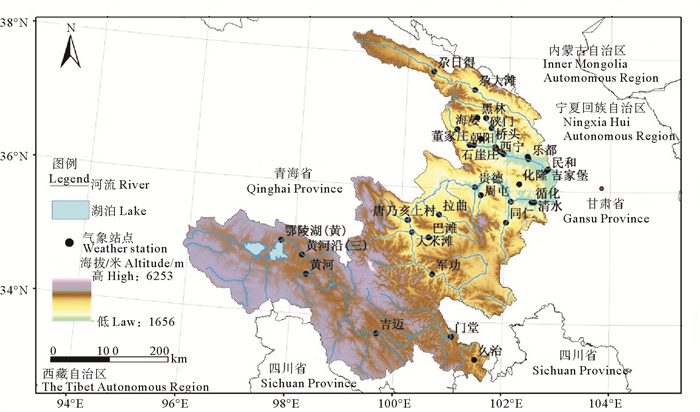
1.2 数据来源与处理本研究选取1956—2018年青海省黄河流域内31个气象站点的逐日降水数据。数据由中国气象科学数据共享服务网平台提供(http://data.cma.cn/),质量可靠,站点分布见图 1。首先利用Excel软件对青海省黄河流域31个气象站点近63年逐日降水数据进行初步处理,对于霜、雪、雾以及微量降水进行特殊处理、对于少量不观测或者无数据情况采用邻近日数据线性回归插值处理,从而计算各站点逐月降水数据;其次利用Arcgis软件采用修正反距离加权平方法[9]对31个气象站点月值降水数据进行空间差值处理,得到青海省黄河流域区域近63年逐月降水数据。
|
图 1 青海省黄河流域气象站点分布图 Fig. 1 Distribution map of meteorological stations in the Yellow River Basin of Qinghai Province |
Mann-Kendall检验法(简称M-K检验法)是世界气象组织(World Meteorological Organization, WMO) 推荐并广泛使用的非参数检验方法,目前被广泛应用于水文序列趋势变化及突变点检验[10-13]。在趋势变化方面,M-K检验能够剔除少数异常值,且数据不需要服从一定的分布,适用于一般数据序列趋势检验。在突变分析方面,M-K检验能够查找数据异常点,但有时会产生虚假突变点的情况,从而难以判断真正的突变位置[14]。本文采用M-K检验和Pettitt突变检验[15]两种方法来确定符合实际的突变时间及突变区域。
2.2 小波分析方法连续小波变换是应用最为广泛的变换方法之一,适合分析各评价因子的周期性变化,对原始数据要求较低,适用性好[16-18]。目前小波分析技术在水文学中的研究主要集中在水文序列多时间尺度分析和序列模拟预测两大方面[19-21]。本研究采用Morlet小波为母小波,进行多时间尺度的周期变换。
2.3 ARIMA模型差分自回归移动平均(Auto Regressive Integrated Moving Average, ARIMA)模型是由Box和Jenkins在20世纪70年代初提出的时间序列检测方法,简称ARIMA模型。ARIMA模型由3个重要参数(p, d, q)决定: p为自回归系数,表示序列滞后p阶;d为时间序列变为平稳时间序列需要进行的差分次数;q为滑动平均系数,表示误差项滞后q阶。ARIMA(p, d, q)模型已较为成熟,通过选择模型的参数和辨识模型的系数即可实现对时间序列的拟合,模型评价机制完善,预测效果较好。此外,ARIMA(p, d, q)模型具有建模简单,拟合效果好,短期预测误差小等优点,在水文时间序列的预测领域有广泛的应用[22-23]。
3 青海省黄河流域降水变化特性分析及预测 3.1 降水年内分配及年代变化特征分析将青海省黄河流域1956—2018年降水量按照月份为单位进行累加统计可得到表 1,季节划分按12月至次年2月为冬季,3—5月为春季,6—8月为夏季,9—11月为秋季。统计显示1956—2018年累计降水量达28 362 mm,其中,春季降水量占全年累计降水量的18.4%,夏季降水量占全年累计降水量的57.6%,秋季降水量占全年降水量的21.9%,冬季降水量占全年累计降水量的2.1%。此外,青海省黄河流域降水年内分配极不均匀,进入4月后降水逐渐增多,5—9月降水量占年降水量的84.3%左右。总体而言,青海省黄河流域具有年降水集中程度高,降水年内分配不均,丰枯季分明的特点。
|
|
表 1 青海省黄河流域年降水量月值统计结果 Table 1 Statistical results of monthly annual precipitation in the Yellow River Basin of Qinghai Province |
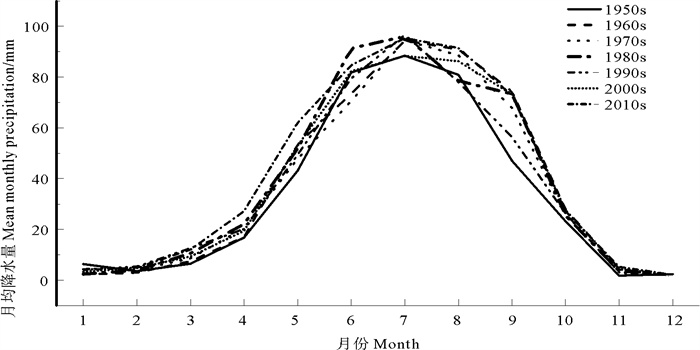
通过计算青海省黄河流域每个年代的月均降水量,绘制不同年代(20世纪50年代—21世纪20年代)降水变化(见图 2)。从图中可以看出,无论哪个年代,降水峰值均出现在7—8月,降水主要集中在4—10月。经统计分析发现,青海省黄河流域21世纪00年代与20世纪90年代相比,降水量下降了8%;而21世纪10年代与21世纪00年代相比,降水量上升了7%。整体来看,21世纪10年代降水量达到流域的顶峰。
|
图 2 青海省黄河流域降水量年代变化特征 Fig. 2 Time-varying characteristics of precipitation in the Yellow River Basin of Qinghai Province |
采用线性回归方法以及滑动平均方法对青海省黄河流域近63年降水时间序列进行线性趋势分析,线性方程的斜率为降水倾向率。同时采用M-K趋势分析方法对线性回归得到的趋势分析结果进行验证,以证实趋势预测结论的合理性。
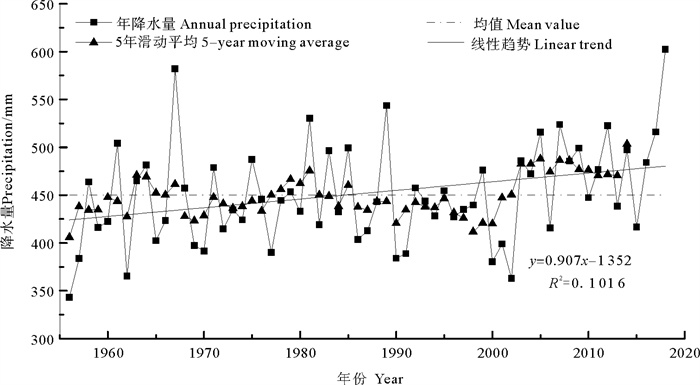
图 3显示了青海省黄河流域1956—2018年线性趋势、年降水量变化以及5年滑动平均过程,可以看出:(1)在95%置信区间下降水趋势函数为f(x)=0.907x-1 352,降水增长率为(9.01 mm/10 a),年降水量整体呈现出上升的波动趋势。(2)年降水量波动性变化较为明显,波动范围为343.30~602.36 mm,在1967、1989、2018年达到波峰,在1956、1962、2002年达到波谷,经历了偏枯-偏丰-正常-偏枯-偏丰5个阶段,年降水量最大值出现在2018年(602.36 mm),年降水量最小值出现在1956年(343.30 mm),最大值和最小值之比为1.75。(3)2014—2018年5年的平均降水量最大(503.27 mm),1956—1960年5年的平均降水量最小(405.90 mm),两者相差97.37 mm。
|
图 3 青海省黄河流域年降水量变化及5年滑动平均过程 Fig. 3 The process of annual precipitation change and 5-year moving average in the Yellow River Basin of Qinghai Province |
采用M-K突变检验方法对青海省黄河流域1956—2018年全年以及各季节分别计算统计量Z值(见表 2),可以看出,近63年以来青海省黄河流域年降水量呈现上升的变化趋势,这与线性回归方法分析结果一致。对于各季节降水量的变化趋势而言,春季和冬季降水统计量Z值均满足|z|≥1.96,说明上升趋势显著;夏季和秋季降水统计量Z值不满足|z|≤1.96,说明没有显著的上升趋势。
|
|
表 2 青海省黄河流域年及各季节降水M-K统计量Z值 Table 2 M-K statistic Z of annual and seasonal precipitation in the the Yellow River Basin of Qinghai Province |
简言之,通过线性回归方法和M-K方法分析青海省黄河流域1956—2018年降水时间序列可得出:青海省黄河流域年降水量有上升的变化趋势,即未来年降水量有增加的趋势;春季和冬季降水量有显著上升的趋势,而夏季和秋季降水量则无显著的上升趋势。
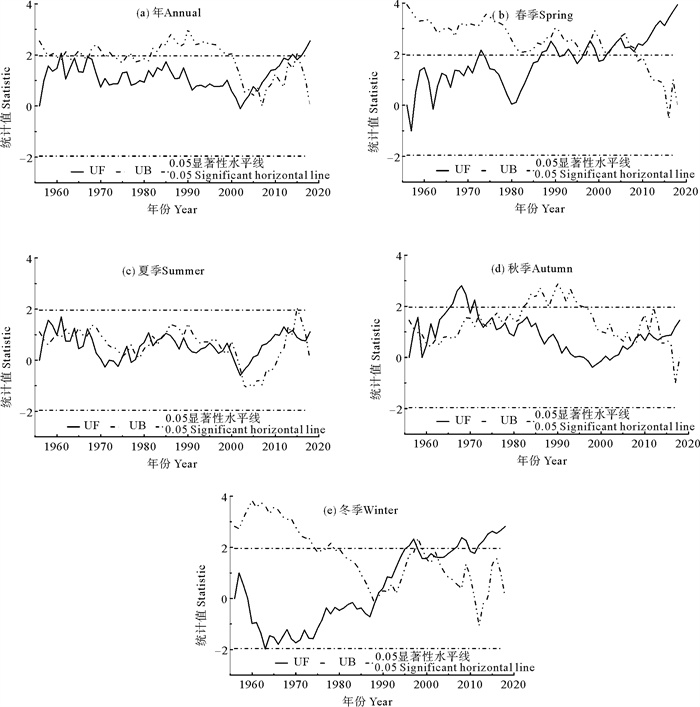
3.3 降水时间序列突变分析青海省黄河流域年及各季平均降水量M-K突变检验结果如图 4所示。结果表明,流域年及各季节平均降水的突变检验曲线均存在交汇点,依据图 4(a)可知,青海省黄河流域近63年降水序列M-K突变检验在0.05显著性水平下,UF统计量和UB统计量在2004年存在交点,说明2004年为年降水序列显著突变年份;依据图 4(b)、(c)、(d)、(e)可知,各季节多年平均降水M-K突变检验在0.05显著性水平下,UF统计量和UB统计量均存在多个交点情况,因此未明确真正的突变位置。
|
图 4 青海省黄河流域年及各季平均降水M-K检验结果 Fig. 4 M-K statistic of annual and seasonal mean precipitation in the Yellow River Basin of Qinghai Province |
结合Pettitt检验法对青海省黄河流域年及各季平均降水量的突变年份作进一步分析,其检验结果见表 3。其中,青海省黄河流域年降水统计量Umax=428,对应一级突变年为2004年,突变显著;春季和冬季平均降水量存在突变情况,通过了0.05水平的显著性检验,说明突变显著;夏季和秋季平均降水量未通过0.05水平的显著性检验,因此突变情况不显著;这与M-K突变检验结果相同。两种方法综合分析表明,青海省黄河流域历史年及各季节平均降水存在突变情况,且2004年为该流域大的降水转折年。
|
|
表 3 青海省黄河流域年及各季平均降水量Pettitt突变检验结果 Table 3 Inspection results of Pettitt abrupt change of annual and seasonal mean precipitation in the Yellow River Basin of Qinghai Province |
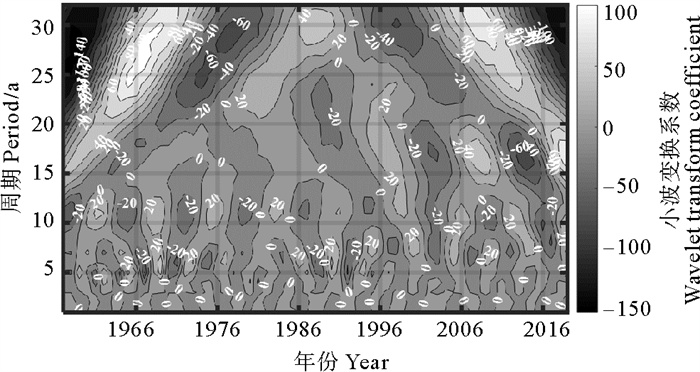
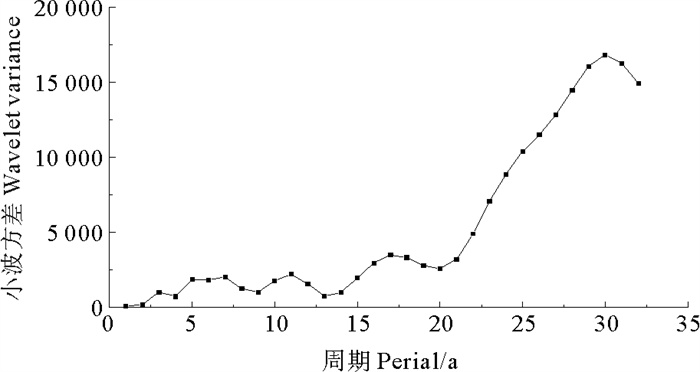
本文选用Morlet小波作为母小波对青海省黄河流域年降水时间序列进行周期分析,由于M-K检验得到2004年为降水序列突变年份,因此去除2004年的原始降水数据,进行插值处理得到新降水数据,并对时间序列进行距平处理和延拓处理。Morlet小波变换系数的实部反映了不同时间尺度下小波域内数据的波动特征,实部的正负取值交替反映了时间域内降水序列丰枯特征,小波方差则为小波系数的平方值在时间域上的积分,可以确定降水序列存在的多级主周期。据此,做出年降水序列小波系数等值线图(见图 5)和小波方差图(见图 6)。
|
图 5 青海省黄河流域年平均降水距平序列小波变换系数实部等值线图 Fig. 5 Isoline for the real components of wavelet transform coefficient chart for the annual mean precipitation anomaly in the Yellow River Basin of Qinghai Province |
|
图 6 青海省黄河流域年平均降水距平序列小波方差图 Fig. 6 Wavelet variance chart for the annual mean precipitation anomaly in the Yellow River Basin of Qinghai Province |
从图 5可以看出,青海省黄河流域年降水量在不同时间尺度表现出不同的周期变化和丰枯交替的变化过程,形成各种尺度正负相间的振荡中心,存在明显的年际变化和年代际变化。从上至下分析得出青海省黄河流域63年(1956—2018年)降水存在23~32 a,15~20 a,9~13 a以及4~6 a的周期变化规律。从23~32 a较大尺度分析,青海省黄河流域降水存在3个准振荡周期,1959年以前,1971—1977年和1996—2003均表现为枯水年,而1960—1970年,1978—1995年和2003—2015年表现为丰水年。青海省黄河流域降水在15~20 a尺度周期集中表现在1986年以后,存在3个准振荡周期,1988—1990年,2000—2005年和2013—2016年以后均表现为枯水年,而1991—1999年,2006—2012年和2016年以后均表现为丰水年。9~13 a和4~6 a的年际变化尺度具有全域性,丰枯交替频繁。不同时间尺度对应的降水结构有所不同,较大时间尺度的降水周期变化嵌套小时间尺度的降水变化,同一段时域内受多级周期影响。进一步结合图 6小波方差图确定降水序列存在的多级主周期,可以确定青海省黄河流域的降水序列存在四级主周期,即30、15、11和6 a时间尺度。
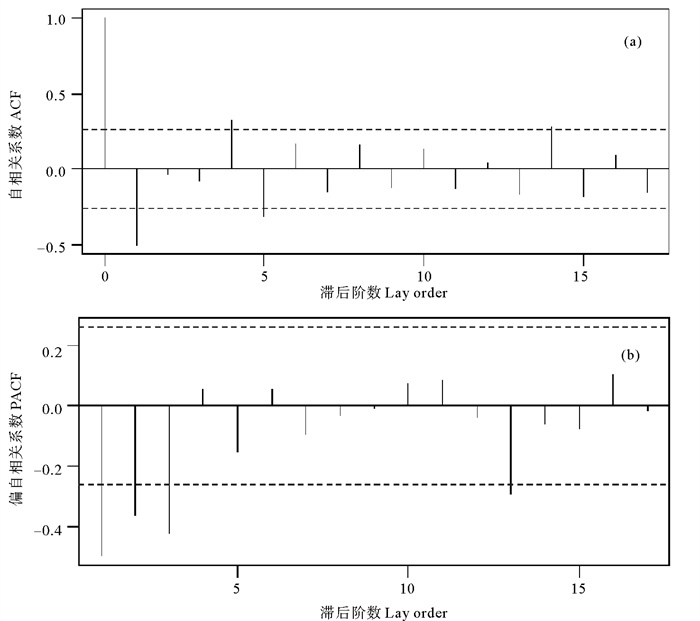
3.5 降水时间序列预测采用ARIMA模型对青海省黄河流域1956—2018年63年降水时间序列进行模型选择及降水预测,主要分为5个步骤:(1)序列的平稳化处理。根据ADF检验结果可知,此时间序列为非平稳序列,进行一阶差分后ADF检验结果显著,P-value=0.01 < 0.05,说明一阶差分处理后的序列为平稳序列,即ARIMA模型中的参数d取1。(2)绘制自相关图和偏自相关图。绘制一阶差分后平稳序列的自相关图(ACF图)和偏自相关图(PACF图)(见图 7)。(3)模型定阶。从PACF图中可以看出在5%的显著性水平下,偏自相关系数显著不为零的个数为3,之后趋于零,并呈现出拖尾现象,可以判断参数P值取3或者2(取2是因为最后一个显著超过0的阶数是由于偶然出现的);从ACF图中可看出,在5%的显著水平下,自相关系数显著为0的个数为5,可以判断参数q值取5或4(取4是因为最后一个显著超过0的阶数是由于偶然出现的)。因此,模型可初步确定为ARIMA(2, 1, 4)、ARIMA(2, 1, 5)、ARIMA(3, 1, 4)、ARIMA(3, 1, 5)。其中,ARIMA(3, 1, 4)模型的AIC值为672.38、ARIMA(2, 1, 5)模型的AIC值为674.15、ARIMA(3, 1, 4)模型的AIC值为674.22、ARIMA(3, 1, 5)模型的AIC值为676.15。由赤池信息准则(Akaike Information Criterion, AIC)可知,在一组可供选择的模型中选择最佳模型时,通常选择AIC值最小的模型。因此,最终选择ARIMA(2, 1, 4)为青海省黄河流域降水预测最佳模型。(4)模型的检验。对ARIMA(2, 1, 4)模型进行残差白噪声检验,残差的Ljung-Box检验结果中P-value=0.88>0.05, 说明模型的残差没用通过显著性检验,可以认为残差的自相关系数为零,ARIMA(2, 1, 4)模型能较好地拟合本序列。(5)模型的预测。本文采用ARIMA(2, 1, 4)模型对青海省黄河流域2019—2023年降水量进行预测,在95%置信区间下的2019—2023年降水量预测结果如表 4所示。
|
图 7 青海省黄河流域年降水量一阶差分序列ACF(a)和PACF(b)图 Fig. 7 ACF(a) and PACF(b) maps of the first difference series of annual precipitation in the Yellow River Basin of Qinghai Province |
|
|
表 4 95%置信区间下青海省黄河流域2019—2023年降水量预测结果 Table 4 Precipitation prediction results of the Yellow River Basin in Qinghai Province in 2019—2023 under 95% confidence interval |
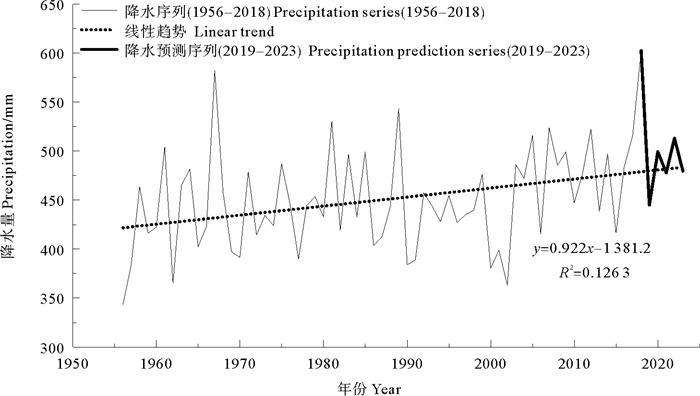
为验证ARIMA(2, 1, 4)模型对青海省黄河流域2019—2023年降水序列预测结果的合理性,本研究依旧采用线性回归方法及M-K趋势分析方法对青海省黄河流域1956—2023年降水序列进行趋势分析,其中,线性回归方法分析结果如图 8所示,可以看出,在95%置信区间下降水趋势函数为f(x)=0.922x-1 381.2,降水增长率为(0.922 mm/10 a),年降水量整体呈现出上升的波动趋势;通过M-K趋势检验法获得统计量Z值为3.08,满足|z|≥1.96,说明青海省黄河流域1956—2023年降水序列上升趋势显著。综上所述,可以看出3.5节中采用ARIMA(2, 1, 4)模型对青海省黄河流域2019—2023年降水序列预测结果符合3.2节中得出的青海省黄河流域年降水时间序列未来有增加趋势的结论。
|
图 8 青海省黄河流域1956—2023年降水时间序列趋势分析 Fig. 8 Tendency analysis of precipitation time series from 1956 to 2023 in the Yellow River Basin of Qinghai Province |
相较于青海省降水时空分布特性相关研究,本研究运用更为系统的包括降水分配、趋势、突变、周期以及预测在内的分析方法,并将趋势检验结果作为降水预测是否合理的一个度量标准,起到了双重验证的作用,丰富了青海省东南部地区降水特性的研究成果。相较于黄河流域降水特性相关研究,本研究仅选取青海省区域,研究范围更加精细化,且为黄河源区降水趋势预测提供了ARIMA(2, 1, 4)模型,可为水资源规划及农业发展做出参考。本研究在降水年内分配及趋势分析方面与白淑英等[4]研究结果大致相同;在降水周期分析方面与王玉娟等[24]研究略有差异,而降水趋势变化研究大致相同,这说明,不同的研究区域、研究时间和研究尺度都会导致降水量周期分析的差异。在降水预测方面,本研究只针对了单一变量的降水预测,可以考虑多气温、蒸发量、海拔高程等多因子对降水预测的影响。本研究利用M-K检验、Pettitt检验、小波分析等方法对青海省黄河流域1956—2018年降水量进行趋势、突变、周期分析,运用ARIMA(2, 1, 4)模型对青海省黄河流域2019—2023年降水量进行预测,并采用线性回归及M-K检验方法对预测趋势进行了合理验证。主要结论如下:
(1) 年降水序列表现为集中程度高、年内分配不均、丰枯季明显的特点,降水集中在夏秋两季,5—9月是降水多发期,预计未来该流域年降水量将处于偏丰或正常状态;1950s—2010s之间的任一年代,该流域月均降水均集中在4—10月,且月均降水量未来有上升的变化趋势。
(2) 年降水序列存在上升趋势,趋势函数为f(x)=0.907x-1 352,春、冬季降水量有显著上升的趋势,夏、秋季降水量无显著的上升趋势;2004年为该流域大的降水转折年,采用M-K检验与Pettitt检验两种方法对该流域进行突变识别效果优于单一使用M-K检验分析。
(3) 年降水序列存在23~32 a,15~20 a,9~13 a以及4~6 a的周期变化规律,且不同尺度的丰枯变化与降水丰枯分析较为吻合;降水序列的四级主周期分别对应30、15、11和6 a的时间尺度。
(4) ARIMA(2, 1, 4)模型能合理地对该流域未来5年降水序列进行预测,从而对当地水资源规划和管理做出指导。
| [1] |
张国胜, 李林, 时兴合, 等. 黄河上游地区气候变化及其对黄河水资源的影响[J]. 水科学进展, 2000(3): 277-283. Zhang G S, Li L, Shi X H, et al. Climatic changes over the upper Yellow River and its effects on water resources[J]. Advances in Water Science, 2000(3): 277-283. DOI:10.3321/j.issn:1001-6791.2000.03.009 (  0) 0) |
| [2] |
樊萍, 王得祥, 祁如英. 黄河源区气候特征及其变化分析[J]. 青海大学学报(自然科学版), 2004(1): 19-24. Fan P, Wang D X, Qi R Y. Climatic changes over the upper Yellow River and its effects on water resources[J]. Journal of Qinghai University(Natural Science Edition), 2004(1): 19-24. (  0) 0) |
| [3] |
戴虎德, 张元平. 黄河源头气候变化对生态环境的影响[J]. 干旱区资源与环境, 2012, 26(8): 141-147. Dai H D, Zhang Y P. Effect of climate change on the ecological environment in the source region of Yellow River[J]. Journal of Arid Land Resources and Environment, 2012, 26(8): 141-147. (  0) 0) |
| [4] |
白淑英, 史建桥, 相栋, 等. 近50年青海降水时空格局变化[J]. 干旱区资源与环境, 2013, 27(6): 148-153. Bai S Y, Shi J Q, Xiang D, et al. Spatiotemporal pattern change of precipitation in Qinghai in the last 50 years[J]. Journal of Arid Land Resources and Environment, 2013, 27(6): 148-153. (  0) 0) |
| [5] |
王文, 任冉, 李耀辉. 基于EEMD的黄河中上游夏季降水预报方法的研究[J]. 气象科学, 2014, 34(3): 261-266. Wang W, Ren R, Li Y H. Summer rainfall prediction in the upper and middle reaches of the Yellow River with EEMD method[J]. Journal of the Meteorological Sciences, 2014, 34(3): 261-266. (  0) 0) |
| [6] |
徐慧, 管蓓, 薛艳, 等. 青海省近50年降水集中性的时空变化特征研究[J]. 水电能源科学, 2015, 33(3): 6-9. Xu H, Guan B, Xue Y, et al. Spatio-temporal Variations of precipitation concentration in qinghai in recent 50 years[J]. Water Resources and Power, 2015, 33(3): 6-9. (  0) 0) |
| [7] |
张馨月, 邵晓华, 王明常, 等. 青海省近50年极端降水事件时空分布特征[J]. 世界地质, 2017, 36(3): 1015-1023. Zhang X Y, Shao X H, Wang M C, et al. Temporal and spatial distribution of extreme precipitation events in Qinghai Province in recent 50 years[J]. Global Geology, 2017, 36(3): 1015-1023. (  0) 0) |
| [8] |
刘晓琼, 吴泽洲, 刘彦随, 等. 1960-2015年青海三江源地区降水时空特征[J]. 地理学报, 2019, 74(9): 1803-1820. Liu X Q, Wu Z Z, Liu Y S, et al. Spatial-temporal characteristics of precipitation from 1960 to 2015 in the Three Rivers' Headstream Region, Qinghai, China[J]. Acta Geographica Sinica, 2019, 74(9): 1803-1820. (  0) 0) |
| [9] |
刘佳嘉. 变化环境下渭河流域水循环分布式模拟与演变规律研究[D]. 北京: 中国水利水电科学研究院, 2013. Liu J J. Distributed Simulation and Evolution Law of Water Cycle in the Weihe River Basin Under Changing Environment[D]. Beijing: China Institute of Water Resources & Hydropower Research(IWHR), 2013. (  0) 0) |
| [10] |
徐宗学, 张楠. 黄河流域近50年降水变化趋势分析[J]. 地理研究, 2006(1): 27-34. Xu Z X, Zhang N. Long-term trend of precipitation in the Yellow River basin during the past 50 years[J]. Geographical Research, 2006(1): 27-34. (  0) 0) |
| [11] |
Kendall M G. Rank Correlation Methods[M]. London: Charles Griffin, 1975.
(  0) 0) |
| [12] |
Hirsch R M, Slack J R. A non-parametric trend test for seasonal data with serial dependence[J]. Water Resource Research, 1984, 20(6): 727-732.
(  0) 0) |
| [13] |
张建云, 章四龙, 王金星, 等. 近50年来中国六大流域年际径流变化趋势研究[J]. 水科学进展, 2007(2): 230-234. Zhang J Y, Zhang S L, Wang J X, et al. Study on runoff trends of the six larger basins in China over the past 50 years[J]. Advances in Water Science, 2007(2): 230-234. (  0) 0) |
| [14] |
周园园, 师长兴, 范小黎, 等. 国内水文序列变异点分析方法及在各流域应用研究进展[J]. 地理科学进展, 2011, 30(11): 1361-1369. Zhou Y Y, Shi C X, Fan X L, et al. Advances in the research methods of abrupt changes of hydrologic sequences and their applications in drainage basins in China[J]. Progress in Geography, 2011, 30(11): 1361-1369. (  0) 0) |
| [15] |
Pettit A N. A non-parametric approach to the change-point problem[J]. Journal of the Royal Statistical Society: Series C (Applied Statistics), 1979, 28(2): 126-135.
(  0) 0) |
| [16] |
陆文秀, 刘丙军, 陈晓宏, 等. 珠江流域降水周期特征分析[J]. 水文, 2013, 33(2): 82-86. Lu W X, Liu B J, Chen X H, et al. Characteristics of precipitation period in Pearl River Basin[J]. Journal of China Hydrology, 2013, 33(2): 82-86. (  0) 0) |
| [17] |
刘博. 吉林省年降水量空间分布及周期变化规律分析[J]. 水电能源科学, 2018, 36(7): 1-4. Liu B. Spatial distribution and periodicity analysis of annual precipitation in Jilin Province[J]. Water Resources and Power, 2018, 36(7): 1-4. (  0) 0) |
| [18] |
冯文文, 柳凤霞, 钱会, 等. 气候变化背景下武功地区降水特征[J]. 水土保持研究, 2020, 27(2): 200-205. Feng W W, Liu F X, Qian H, et al. Characteristics of precipitation in Wugong Area under the background of climate change[J]. Research of Soil and Water Conservation, 2020, 27(2): 200-205. (  0) 0) |
| [19] |
王文圣, 丁晶, 向红莲. 小波分析在水文学中的应用研究及展望[J]. 水科学进展, 2002(4): 515-520. Wang wensheng, Ding Jing, Xiang Honglian. Application and prospect of wavelet analysis in hydrology[J]. Advance in Water Science, 2002(4): 515-520. (  0) 0) |
| [20] |
桑燕芳, 王中根, 刘昌明. 小波分析方法在水文学研究中的应用现状及展望[J]. 地理科学进展, 2013, 32(9): 1413-1422. Sang Y F, Wang Z G, Liu C M. Applications of wavelet analysis to hydrology: Status and prospects[J]. Progress in Geography, 2013, 32(9): 1413-1422. (  0) 0) |
| [21] |
王景才, 郭佳香, 徐蛟, 等. 近55年淮河上中游流域气候要素多时间尺度演变特征及关联性分析[J]. 地理科学, 2017, 37(4): 611-619. Wang J C, Guo J X, Xu J, et al. Multi-time scales change characteristics and relationship of meteorological variables in the upper and middle regions of the Huaihe River Basin in recent 55 years[J]. Scientia Geographica Sinica, 2017, 37(4): 611-619. (  0) 0) |
| [22] |
陈沪生, 周玉良, 周平, 等. 基于小波和ARIMA的黄山市年降水量分析及预测[J]. 南水北调与水利科技, 2019, 17(5): 50-55. Chen H S, Zhou Y L, Zhou P, et al. Analysis and prediction of annual precipitation in Huangshan City based on wavelet and ARIMA[J]. South-to-North Water Transfers and Water Science & Technology, 2019, 17(5): 50-55. (  0) 0) |
| [23] |
李智强, 邹红霞, 齐斌, 等. 基于EEMD-ARIMA的年降水预测拟合模型研究[J]. 计算机应用于软件, 2020, 37(11): 46-50+78. Li Z Q, Zou H X, Qi B, et al. A fitting model of annual precipitation precipitation based on eemd-arima[J]. Computer Applications and Software, 2020, 37(11): 46-50+78. (  0) 0) |
| [24] |
王玉娟, 祁栋林, 袁延得. 青海南部地区近57年降水变化及区域差异分析[J]. 青海环境, 2018, 28(3): 115-122+139. Wang Y J, Qi D L, Yuan Y D. Analysis of precipitation variations and regional differences in the southern part of Qinghai in recent 57 Year[J]. Journal of Qinghai Environment, 2018, 28(3): 115-122+139. (  0) 0) |
2. China Water Resources Pearl River Planning Survey and Design Co., Ltd., Guangzhou 510610, China
 2022, Vol. 52
2022, Vol. 52


