2. 中国海洋大学数学与科学学院,山东 青岛 266100;
3. 菏泽学院数学与统计学院,山东 菏泽 274000
1895年,科学家Korteweg和学生de-Vries在讨论液体表面的波动力学现象时,提出并引入了Korteweg de-Vries(KdV)方程,并给出了一个类似于孤立波的解析解, 即孤立波解[1],KdV方程也是最早发现具有孤立波解的方程。自此KdV方程进入了大家的视野,并且得到了广泛发展与应用。在许多物理问题中,KdV方程都是一个有用的近似,例如它可以用于描述浅水波的无损耗传播。
1965年,数学家Zabfsky与Krfskal[2]在不同的周期边界条件下对KdV方程进行了数值模拟,得出了不同条件下KdV方程的孤立波解,并推断出其所具有的特殊性质,即在传播过程中可以保持其波形不变,甚至发生碰撞之后其波形依然可以保持稳定。但在实际生活中,水体的情况并不是一成不变的,于是要考虑水体的这种变化,这时便引入了变系数KdV方程,它可以描述在海洋中地形、层结发生变化时内波的演化情形。近年来,关于变系数KdV方程的应用则成为学者研究的重点。
对于变系数KdV方程,宋等[3]运用行波法将其转化为常微分方程进行求解,包等[4]与Liu等[5]利用函数变换将其化为非线性微分方程再进行求解,蔡等[6]使用Hirota直接法求解方程, 张等[7]采用截断展开法对方程进行求解。本文介绍了一种数值解法,空间上应用差分法进行离散,时间上采用龙格库塔法进行求解。
1 变系数KdV方程本文考虑的是变系数无因次的KdV方程,其一般形式为:
| $ \frac{{\partial f}}{{\partial t}} + \alpha \frac{{\partial f}}{{\partial x}} + \frac{{{\partial ^3}f}}{{\partial {t^3}}} = 0。$ | (1) |
其中:α为待定的系数与实际水体情况有关,并且L1 < x < L2,0 < t < T,其中L1,L2及T为任意常数, 文中取L1=-500, L2=500, T=500、1 000、1 500。本文所选取的L1、L2及T均为无因次的,故无单位。
首先将方程进行网格划分,分为等大的矩形域,对于空间轴可以设空间步长

|
图 1 定义域划分结果 Fig. 1 Definition domain partition result |
龙格库塔法是一种用于解微分方程的显性计算方法,常用于一阶常微分方程的求解,至今已有一百多年的历史,并且已经发展的十分成熟。龙格库塔法也可以用于求解偏微分方程,且具有较高的精度,其中每一步的步长可以根据实际情况进行调整以提高计算精度,还可以调节代码来节约计算时间。经典的龙格-库塔法为[9]:
| $ \left\{ {\begin{array}{*{20}{c}} {{f_{n + 1}} = {f_n} + \frac{{h\left( {{k_1} + {k_2} + {k_3} + {k_4}} \right)}}{6}}\\ {{k_1}{\rm{ = }}y\left( {{t_n}, {f_n}} \right)}\\ {{k_2}{\rm{ = }}y\left( {{t_n} + \frac{h}{2}, {f_n} + \frac{{h{k_1}}}{2}} \right)}\\ {{k_3}{\rm{ = }}y\left( {{t_n} + \frac{h}{2}, {f_n} + \frac{{h{k_2}}}{2}} \right)}\\ {{k_4} = \left( {{t_n} + h, {f_n} + h{k_3}} \right)} \end{array}} \right.。$ | (2) |
其中:h为时间迭代步长;fn为原函数在网格点处迭代n次时的函数值;tn为第n次迭代的时间。本文中在时间上采用四阶龙格库塔法进行离散。
在空间上本文所使用的差分格式为向前差分法及中心差分法,其中对一阶偏导采用向前差分法进行离散,三阶偏导数则采用中心差分法进行离散。
中心差分法的形式为
一阶向前差分法的形式为
将以上两种差分格式带入变系数KdV方程,对方程进行离散,可得其空间部分为:
| $ \alpha {f_{i, j}}\frac{{{f_{i + 1, j}} - {f_{i, j}}}}{{\Delta x}} + \frac{{ - {f_{i - 2, j}} + 2{f_{i - 1, j}} - 2{f_{i + 1, j}} + {f_{i + 2, j}}}}{{2\Delta {x^3}}}。$ | (3) |
基本步骤可概括为[10]:
(1) 根据给定的初始条件及定义域划分后的每一点(xi, tj),求出方程在此点的函数值。
(2) 利用差分公式求出每一点的一阶及三阶偏导。
(3) 根据离散后的方程,对所有的点(xi, tj)先求出k1,再采用龙格库塔格式,依次求出k2、k3、k4。
(4) 对所有的点(xi, tj)求出fj,然后参考(3)中得到的k1、k2、k3、k4值,可以求出fj+1。
(5) 重复上述步骤继续迭代直至T。
4 数值求解算例 4.1 方程在不同条件下的解选取的初始条件为:
(1) 令
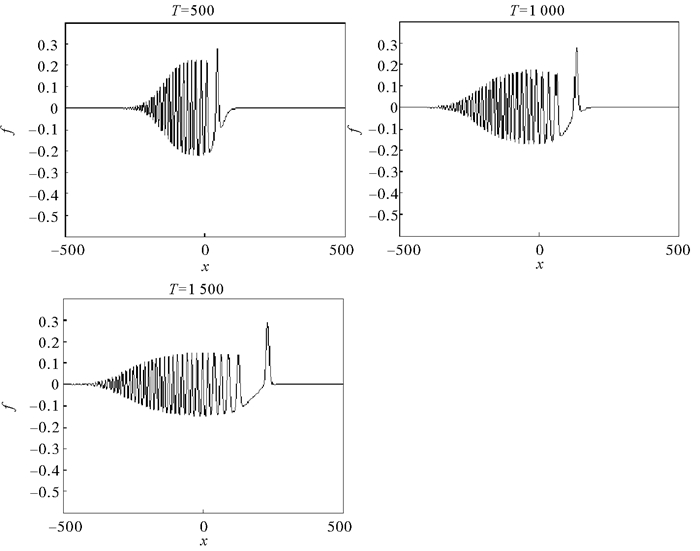
运用MATLAB进行编程并进行求解,得结果如图 2。
|
图 2 条件(1)下的结果 Fig. 2 Results under conditions (1) |
在计算过程中,α的值逐渐由-1变为1,变化趋势见图 3。随着α值的变化,孤立波的波形也发生了较大的变化,由一开始的下沉型内孤立波,逐渐转变为一个上凸型内孤立波,这个现象称之为内孤立波的极性转化[11]。这个现象在实际海洋中也有对应,即位于较深水域的下沉型内孤立波向近岸传播的过程中水深逐渐变浅,这时波形尾部会演化出孤立波子波列,即此孤立波受到浅水效应的影响,同时逐渐演变为上凸型的内孤立波[12];随着水深越来越浅,上凸型内孤立波幅度也逐渐增大,这体现了内波的频散特性。
|
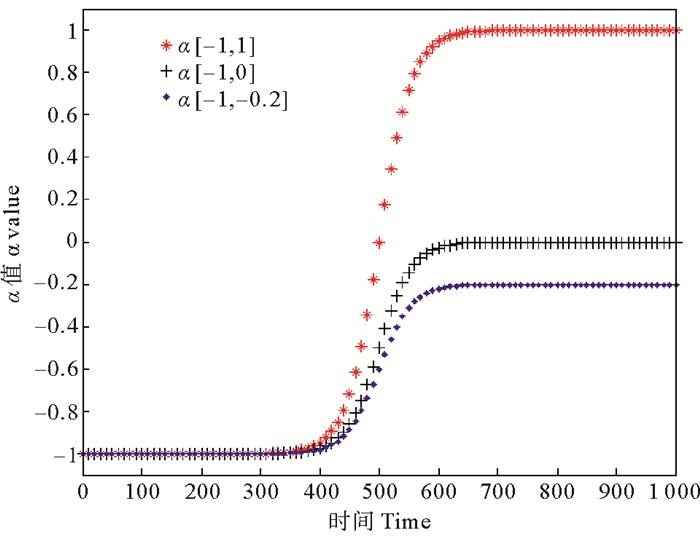
图 3 T=1 000时α的图像 Fig. 3 Images of α at T = 1 000 |
在这个变化过程中,因为α的值逐渐由-1变为1,即α的值会跨过零点,所以下沉型内孤立波的波谷会在α=0.5处时大幅度上升,波宽大幅度增加。然后在达到极性转化点时,波宽减小且波峰增加,在这个过程中完成由下沉型孤立波逐渐转变为一个上凸型内孤立波的过程。
(2) 令
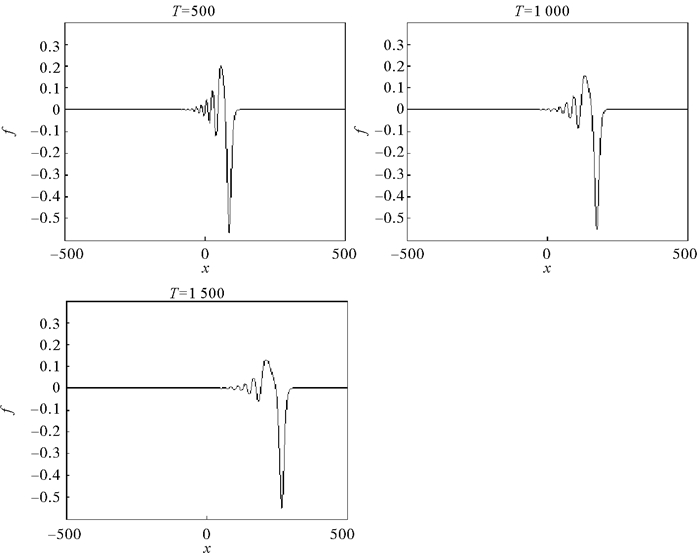
运用MATLAB进行编程并进行求解,得结果如图 4。
|
图 4 条件(2)下的结果 Fig. 4 Results under conditions (2) |
与上例不同,α的值逐渐由-1变为-0.2,在此过程中,变系数KdV方程的非线性项越来越接近零点,但是由于α值并没有越过零点,所以内孤立波并没有发生极性转化,所以主波形依然是下沉型内孤立波,但是随着α的值逐渐增大,内孤立波的尾波将会削弱,主波后的波形将会变得较为平滑,且时间跨度越大产生的尾波数量就会越少,正如上图所示。在α→-0.2时,内孤立波波形将会趋于稳定并变为一个全新的下沉型内孤立波。
(3) 令
运用MATLAB进行编程并进行求解,得结果如图 5。
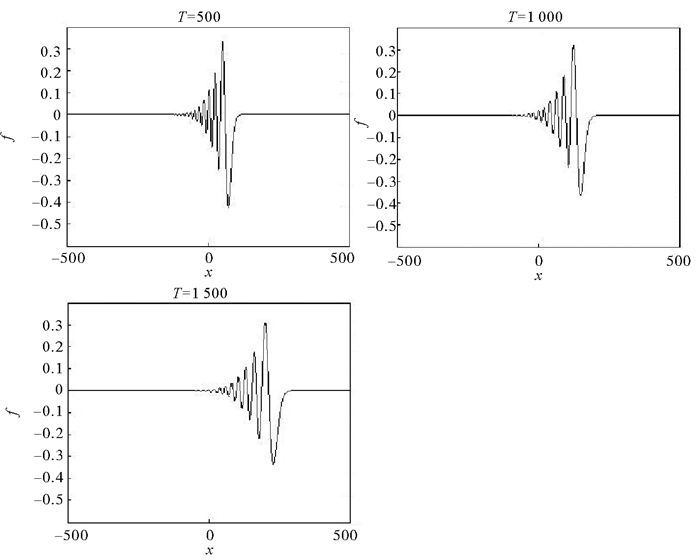
|
图 5 条件(3)下的结果 Fig. 5 Results under conditions (3) |
在这个条件下,当α的值逐渐接近0时,内孤立波的波形会如同条件(1)下的孤立波那样波宽减小且波峰增加,即内孤立波会在这个过程中被破坏。但是由于并没有跨过极性转化点,所以内孤立波波形将会在α→0时产生变化,更类似于一个线性周期波动。
4.2 α的变化情况在固定初始条件的情况下,T取1 000时,α的取值范围分别为[-1, 1]、[-1, 0]、[-1, -0.2],变化图像见图像3。
从α的变化中可以看到α的取值范围是与α0, α1有关的,而T的大小只决定了α值变化的速度。同理,可以选择不同的α0, α1的值,例如α0=-1, α1=0.5。这样可以得到更多的结果,更好的去进行结果分析。
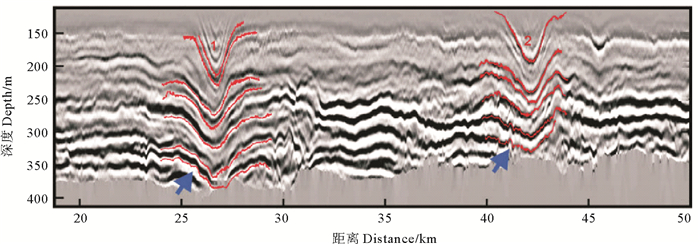
5 结果对比将方程离散并结合MATLAB进行编程求解,可得解如图 2、4、5,清楚地观察到孤立波随时间变化产生的波散现象,这正好体现了孤立波随时间变化而变化的理论特征,从理论上来说更加贴合实际。将结果对照图 6的实际海体中不同水深的孤立波,发现条件(1)与(2)的结果分别对应1、2两处,可得方程解与实际情况吻合度较高,结果具有较高的可信性,也在侧面说明方法的有效性。
结合图 5与图 2~4发现,在α的值逐渐由-1变为1时,内孤立波由一开始的下沉型逐渐转变为一个上凸型,这就代表着方程中频散项与非线性项由平衡到失衡然后又趋于平衡的过程;在α的值逐渐由-1变为-0.2时,由于没有跨过零点,内孤立波只是产生了波形变化而没有极性转换;而当α=0时显然是频散项与非线性项的不平衡点,此时内孤立波波形将会打乱同时转化为类线性波动。综上所述,内孤立波稳定的前提是方程中频散项与非线性项的相互抵消[13]。
6 结语本文主要讨论了对变系数KdV方程运用显格式差分方式进行数值求解的问题。在空间上,采用了中心差分法以及向前差分法进行离散,而在时间上,则采用四阶龙格库塔法进行离散。同时为了更好地研究孤立波的特性,分别选取了不同的α取值范围,分别考虑孤立波产生极性转换、类线性化及频散产生尾波等现象,以此展示内孤立波的特殊性质, 并将此数值模拟结果用于实际海洋中的内孤立波分析,更简洁明了地分析介绍了内孤立波的特性。与实际观测数据(见图 6)的对比,表明了变系数KdV方程可以用来解释海洋内孤立波的演化,以及分析内孤立波的物理特性。
| [1] |
王艳红, 王世勋. 一类KdV方程的精确解[J]. 信阳师范学院学报(自然科学版), 2010, 23: 492-494. Wang Y H, WANG S X. Exact solutions of a class of KdV equations[J]. Journal of Xinyang Teachers College(Natural Science Edition), 2010, 23: 492-494. DOI:10.3969/j.issn.1003-0972.2010.04.004 (  0) 0) |
| [2] |
Zabusky N J, Kruskal M D. Interaction of "Solitons" in a collisionless plasma and the recurrence of initial states[J]. Physical Review Letters, 1965, 15: 240-243.
(  0) 0) |
| [3] |
宋杨. 一类变系数偏微分方程的解法[J]. 佳木斯大学学报(自然科学版), 2013, 31: 786-787. Song Y. Solution of a class of variable coefficient partial differential equations[J]. Journal of Jiamusi University(Natural Science Edition), 2013, 31: 786-787. DOI:10.3969/j.issn.1008-1402.2013.05.044 (  0) 0) |
| [4] |
包永梅, 斯仁道尔吉. 变系数KdV方程的精确类孤子解[J]. 内蒙古大学学报(自然版), 2008, 39: 488-493. Bao Y M, Si R D E J. Exact soliton solutions of the variable coefficient KdV equation[J]. Journal of Inner Mongolia University (Natural Science Edition), 2008, 39: 488-493. (  0) 0) |
| [5] |
Liu X Q. Exact solutions of the variable coefficient kdV and sg type equations[J]. Applied Mathematics-A Journal of Chinese Universities, 1998, 13: 25-30. DOI:10.1007/s11766-998-0004-8
(  0) 0) |
| [6] |
蔡科杰.求解变系数Korteweg-de Vries(KdV)方程的两种方法的研究[D].北京: 北京邮电大学理学院, 2009. Cai K J. Study on Two Methods for Solving the Variable Coefficient Korteweg-de Vries (KdV) Eequation[D]. Beijing: School of Science, Beijing University of Posts and Telecommunications, 2009. (  0) 0) |
| [7] |
张解放, 陈芳跃. 截断展开法和广义变系数KdV方程新的精确类孤子解[J]. 物理学报, 2001, 50: 1648-1650. Zhang J F, Chen F Y. New exact soliton solutions of truncated expansion method and generalized variable coefficient KdV equation[J]. Acta Physica Sinica, 2001, 50: 1648-1650. (  0) 0) |
| [8] |
卜万奎, 徐慧. 差分方程理论的研究[J]. 菏泽学院学报, 2018, 40: 34-40. Bu W K, Xu X H. Research on the theory of difference equation[J]. Journal of Heze University, 2018, 40: 34-40. (  0) 0) |
| [9] |
冯建强, 孙诗一. 四阶龙格-库塔法的原理及其应用[J]. 数学学习与研究, 2017, 17: 3-5. Feng J Q, Sun S Y. The principle and application of the fourth-order Runge-Kutta method[J]. Mathematics Learning and Research, 2017, 17: 3-5. (  0) 0) |
| [10] |
蒋姝华, 黄伟祥, 朱三华. 经典R-K法在扩散方程数值求解中的尝试[J]. 广东水利电力职业技术学院学报, 2003(1): 45-46. Jiang Y H, Huang W X, Zhu S H. An attempt of the Classical R-K method for numerical solution of diffusion equations[J]. Journal of Guangdong Technical College of Water Resources and Electric Engineering, 2003(1): 45-46. DOI:10.3969/j.issn.1672-2841.2003.01.016 (  0) 0) |
| [11] |
李飞, 种劲松. 内波极性转变过程序列SAR图像仿真研究[J]. 遥感技术与应用, 2008(4): 451-456. Li F, Ji J S. Study on SAR image simulation of internal wave polarity transition process[J]. Remote Sensing Technology and Application, 2008(4): 451-456. (  0) 0) |
| [12] |
廖光洪.南海北部内潮与非线性内波: 观测与数值模拟研究[D].青岛: 中国海洋大学信息科学与工程学院, 2012. Liao G H. Internal and Nonlinear Internal Waves in the Northern South China Sea: Observation and Numerical Simulation[D]. Qingdao: School of Information Science and Engineering, Ocean University of China, 2012. (  0) 0) |
| [13] |
张扬, 李瑞杰, 郑金海. 波浪的非线性频散关系[J]. 水科学进展, 2004(4): 448-453. Zhang Y, Li R J, Zheng J H. The Nonlinear dispersion relation of waves[J]. Advances in Water Science, 2004(4): 448-453. DOI:10.3321/j.issn:1001-6791.2004.04.008 (  0) 0) |
| [14] |
拜阳, 宋海斌, 关永贤, 等. 利用地震海洋学方法研究南海东北部东沙海域内孤立波的结构特征[J]. 科学通报, 2015(60): 94-95. Bai Y, Song H B, Guan Y X, et al. Study on the structural characteristics of solitary waves in the Dongsha sea area in the northeastern South China Sea using seismic oceanography method[J]. Chinese Science Bulletin, 2015(60): 94-95. (  0) 0) |
2. School of Mathematics and Sciences, Ocean University of China, Qingdao 266100, China;
3. School of Mathematics and Statistics, Heze University, Heze 274000, China
 2020, Vol. 50
2020, Vol. 50