岬间海湾是一种典型的山地或者丘陵海湾,由岬角和海湾组成[1],湾内海岸根据动力成因可分为遮蔽段、过渡段和切线段。岬角通常是建造港口码头的优良场所,而过渡段和切线段海滩是休闲娱乐圣地。在岬湾半封闭系统中,海岸-海滩-沉积物补给量三个变量在长期的自然演化中会达到动态平衡,任何变量的改变(如岬角码头港口、防波堤等构筑物的建造)都影响到整个系统的平衡,造成海岸和海滩甚至海底沉积物的重新再分配。多年来世界各国人民抱着对美好生活的向往不断涌向海边,政府不得不修建新的海岸基础设施来满足社会需要。海岸和海滩的稳定直接影响到基础设施功能的发挥,也导致这一地带成为海岸学者和政府关注的重点。在岬湾系统的研究中,已发表的文献基于经验函数拟合法得到海岸平面平衡形态可用抛物线型、双曲线型、对数螺线型和椭圆型四种数学表达式来,研究人员根据实际岸线与这些经验关系式的拟合程度将岬湾海岸分为静态、动态或不稳定三种平衡态[2-6]。比如,程武风等通过岬湾平面模型与实际的差异关系分析了海南万宁岬湾海岸稳定性[7]; Silva G M D分析了不同时间尺度下岬角对岬湾内泥沙运移的影响,认为岬角引起了波浪的变化,控制着岬湾泥沙输运[8]; George利用Delft-3D和SWAN模拟分析了岬角形态对岬角处泥沙输运影响,得出了岬角形态、盛行波浪、底质粒径对泥沙运移起决定性作用[9]; 战超统计莱州湾东岸岬湾海岸60年来不同类型海岸带开发活动对海岸演化过程的影响,得到下游海岸线交替变化的规律[10]。随着社会经济的发展,越来越多的海岸被开发利用,防波堤向海伸出越来越远,形成新的人工岬角,极大地改变了岬湾的平面形状。在岬角变化情况下岬湾系统新的平衡状态将如何建立?厘清这种形态变化对下游海岸稳定性的影响,对保护海滩资源、优化岸线功能配置具有重要的现实意义。近年来,修建于南黄海西岸黄家塘湾的新青岛港为本文的研究提供了理想的研究场所。黄家塘湾是自然形成的岬角海湾,新青岛港在原岬角处修建了伸入海中1.9 km长的防波堤码头形成新的岬角。为研究岬角形状变化对湾内岸线的影响,本文通过卫星遥感影像提取了湾内新港口建造前、中、后的各段岸线平面位置,实地考查湾内岸线位置和侵蚀/堆积现状,在此基础了分析了湾内岸线的演化规律。
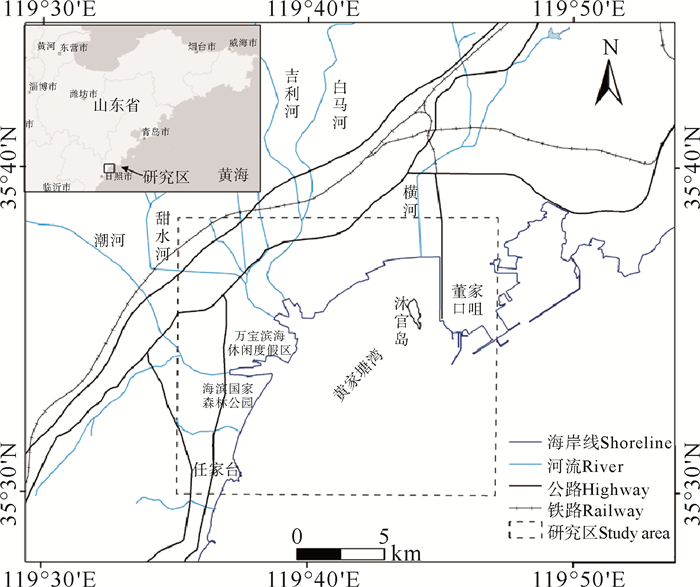
1 区域概况研究区域位于山东半岛日照-青岛之间的黄家塘湾(见图 1),由董家口嘴(港)和任家台咀两个基岩岬角围成。海湾湾口宽度14.5 km,朝向东南,海岸西南走向。湾内四条河流入形成三个入海河口。近年来由于河道整治和环境美化,沿河多级建坝蓄水挡沙,目前仅在汛期有少量径流入海,河口区无河流泥沙补给。研究区波浪以风涌混合浪为主,全年0.7 m以下波浪占比约80%,SE向波浪频率约59.52%[11]。研究区属于正规半日潮,潮差约为2.81 m,受黄海M2旋转潮波系统影响,近岸潮流以往复流为主,涨潮流向西南,落潮流向东北,涨潮流速大于落潮流速[12],沿岸流向西南。新青岛港于2009年开始动工修建,于2014年竣工投入运营,伸出于海中1.9 km且走向与下游岸线平行的防波堤于2012年建成。
|
图 1 研究区位置图 Fig. 1 Location of study areas |
本文分析的遥感数据来源于中国科学院计算机网络信息中心地理空间数据云平台(见表 1)[13],选取云量少、潮位低、年度时间较一致、清晰度高的图像,以Google Earth历史图像(彩色,最高分辨率0.5 m)[14]作为辅助,并于2017年10月进行了现场踏勘校准,确定了遥感影像上高潮线和人工岸线位置。然后对比现场调查结果,在ARCGIS环境下目视解译了2005—2017年研究区的多期岸线。然后参照美国地质调查局(USGS)提供的数字岸线分析方法(DSAS),在ARCGIS中向陆侧作各段平行于海岸走向的基线,以20 m间隔向海侧作垂直于基线的切线,其中过渡段作切线88条(见图 2,剖面号:1-88),切线段作切线263条(见图 2,剖面号:89-352)。通过两期切线剖面上的岸线移动距离除以间隔时间获得岸线变化速率,利用该段全部切线变迁速率之和除以切线总和得到岸段平均蚀积速率。利用得到的各剖面的岸线变化速率和各岸段平均速率数据分析了岬角改变前后岸线演化现状和变化机制。为了预测岬湾岸线的变化趋势,本文基于抛物线方程开发的Mepbay软件,计算岬角形态改变前后静态平衡岸线位置[15-16],对岸线稳定性进行了判别。
|
|
表 1 研究采用的遥感影像信息 Table 1 Remote sensing images used in the study |
|
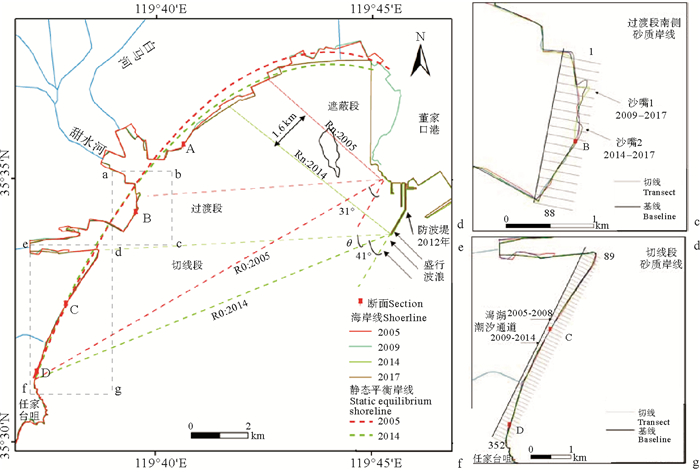
图 2 研究区岸线分区、分析断面和基于抛物线方程获得的岬角形状改变前后静态平衡岸线位置 Fig. 2 Thecoastline zone, analysis profiles and the static equilibrium position of the coastline during different time based on parabola equation |
根据成因,本文将研究区岬湾岸线平面形态分为切线段、遮蔽段和过渡段三个部分(见图 2)。切线段为靠近海岸下游岬角的直线段,一般呈线性且直接受波浪的作用; 遮蔽段是上岬角背后的掩护区,也是盛行波浪的波影区; 过渡段是位于两者之间的岸段[3],根据上述研究方法得到的各岸段平均蚀积速率见表 2,各断面的岸线蚀积速率如图 3所示。
|
|
表 2 各岸段平均蚀积速率统计表 Table 2 The statistical table of average erosion/deposition rate of each shore segment |
|
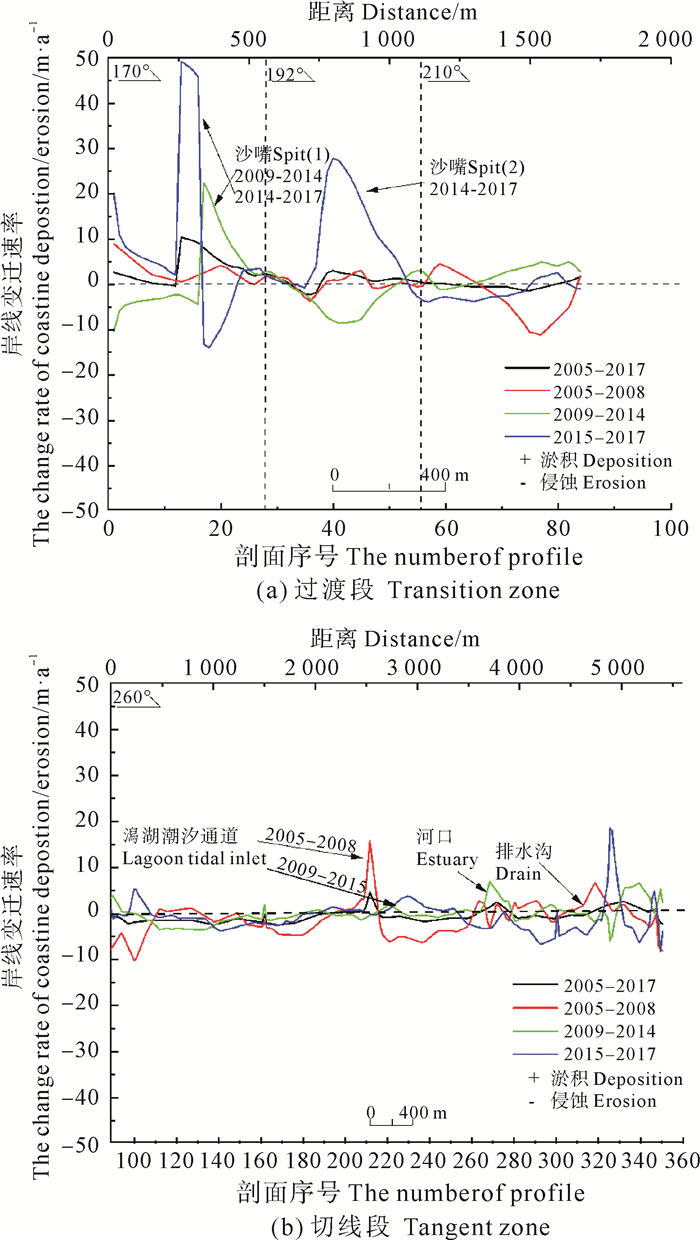
图 3 岸线侵蚀/淤积速率随剖面号的变化趋势 Fig. 3 The trend of erosion/deposition rate of coastline with profile number |
遮蔽段海岸线受人类活动影响很大。1990年代之前,遮蔽段形成了沙质海岸,1990年代初进行了大规模滩海养殖开发,挖沙筑池,或者填海造地,改变岸线属性全部形成人工岸线。遮蔽段海湾自然淤积的泥沙被人类挖沙活动抵消,2012年防波堤建成前后也未出现新的沙质岸线。
3.2 过渡段过渡段以白马河入海口分为南北两段。遥感影像显示河口北侧修建人工养殖池塘后曾发生泥沙堆积形成沙质岸线,至2005年时消失,海水进入到养殖池根部,以后再未出现淤积; 南侧人工养殖池塘于1992年修建后泥沙回淤,沿养殖池塘形成呈弧形向海凸出的沙质岸线,2005年前之岸线一直缓慢向外的淤涨。岬角形态改变过程中该段岸线发生明显的变化,表现为弧形岸线南段侵蚀,北段发生淤积,并在岸线转折处形成两处沙嘴。淤积面积大于蚀退面积,净淤积速率约为1.3 m/a。不同阶段的表现是:(1)岬角形状改变前(2005—2008年底),过渡段南段海岸处于动态平衡状态,侵蚀速率约为0.1 m/a,可以忽略。(2)岬角形状改变中(2009年初—2014年),北段海岸明显泥沙淤积形成了一处宽度约0.2 km的沙嘴,南段海岸发生侵蚀,岸段净淤积速率0.3 m/a。(3)岬角形态改变完成后(2015—2017年),过渡段北段海岸进一步淤积,原沙嘴向北发生迁移约0.2 km,形态更为狭长,弧形岸线凸出处又形成一新沙嘴,而南段海岸侵蚀加剧,岸段净淤积速率增加至5.1 m/a。
3.3 切线段切线段位于岬湾南侧的潮河河口至任家台岬角位置,长度约5.2 km。此处原为潮河入海开敞型河口,在波致沿岸流的作用下形成了NE向的水下沙坝。在二十世纪八十年代初沙坝堆积高出水面形成沙岛,后来沙岛连成一片形成水上沙坝、沙质岸线和半封闭的潟湖。沙坝北端一直沉积沿岸输沙,形成新淤陆地。澙湖被当地居民修建养殖池塘,顺着沙坝修建了沿海公路和防潮大堤。董家口岬角形状改变过程中该区产生了明显的变化。根据表 2岸段平均侵蚀/淤积统计和图 3(b)岸段每条切线上岸线侵蚀/淤积速率统计显示,切线段岸线在2005—2017年间的12年内海岸整体处于侵蚀状态,平均蚀退速率0.8 m/a。侵蚀速率自北向南逐渐减弱,至第312号切线(北起4.3 km处)岸线蚀退速率达到0,向南转为微淤积状态。其中岸线侵蚀最严重的地方发生在北侧第100号剖面处,海岸后退距离达到34 m。侵蚀段在泄洪口和原潟湖口出现异常,即口门发生小段淤积。三个时段变化各不相同。(1)岬角形态改变前(2005—2008年底),切线段整体处于侵蚀状态,平均侵蚀速率约为1.5 m/a,岸线自北向南逐渐由侵蚀转化为淤积,转换点位于第260号剖面(北起3.4 km)处,在泄洪口和原潟湖口处因岸线形状改变出现淤积状态。(2)岬角形态改变中(2009—2014年),切线段全段以侵蚀为主,平均侵蚀速率降至0.2 m/a。(3)岬角形态改变完成后(2015—2017年),切线段北侧侵蚀加剧,平均侵蚀速率达到1.0 m/a,而南段转为轻微淤积状态。
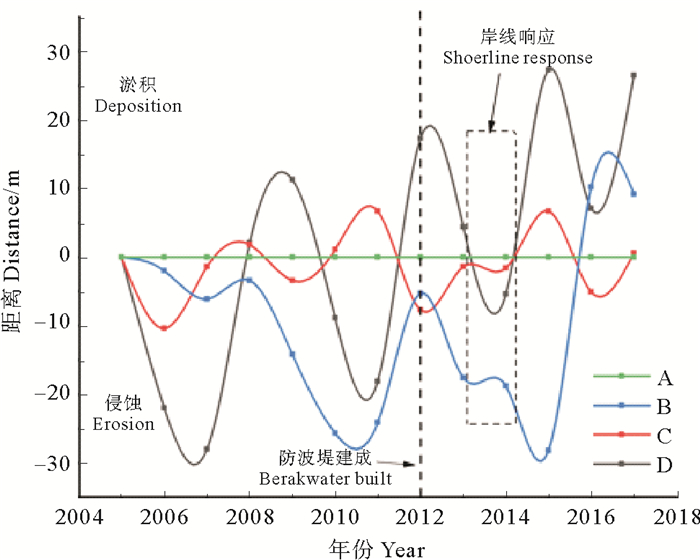
4 分析与讨论 4.1 岸线动态演化规律探讨上述调查结果已清晰地显示了岬角形状改变前后的岸线变化特征。为了进一步分析海岸地质作用发生的规律,本文根据海岸线的区域划分选择4条断面(位置见图 2)进行岸线位置的蚀积转化分析。其中A断面位于过渡段北人工岸线处,B断面位于过渡段海岸转折点,C、D断面分别位于切线段中部和南部。断面起点以2005年海岸线为基准,逐年统计切片交叉点岸线相对于2005年岸线的距离,得到每条断面岸线移动距离随时间的变化曲线(见图 4)。从图上可以看出,除位于过渡段人工岸线的A断面没有变化外,B、C、D断面沙质岸线均处于侵蚀淤积的动态变化中。在防波堤建成前,B断面处以侵蚀后退为主,C、D断面处于弱侵蚀状态。防波堤建设成后,B断面由侵蚀转向弱淤积,C断面依然处于弱侵蚀状态,D断面转向淤积。
|
图 4 各断面移动距离随时间的变化曲线(2005—2017) Fig. 4 Change curve of moving distance of each section with time (2005—2017) |
分析认为,研究区岬湾内虽有多条河流注入,但多年来河流中下游区域纷纷建坝拦沙,节节筑坝使得泥沙很少能到达河口区,2009年后入海口陆续修建的防潮坝彻底阻断了上游泥沙。而董家口嘴以北众多的小海湾阻挡了泥沙在该区SW向沿岸流的搬运,则研究区湾内已多年无沿岸泥沙补给。因此研究区在短时间尺度内可以被认为是一个封闭的系统,这样岸线的泥沙堆积来源的途径仅限于邻近海滩、或者海岸物质的侵蚀与搬运以及湾内泥沙的再悬浮。波致沿岸流和潮流产生的沿岸流成为该区海岸带泥沙搬运的主在动力。
岬角形状改变之前,在海湾切线段在盛行波浪斜向入射,形成平行于海岸的NE向波浪流,称之为波生沿岸流,导致切线段南段泥沙沿岸向NE向的移动而岸线侵蚀。而在区域性沿岸流作用下,过渡段北侧泥沙向SW向输运,两者共同作用,在切线段至过渡段岸段泥沙堆积形成新积岸线,并一直向外淤涨形成新的陆地。为保护海岸,当地栽种了防护林,这种海岸自然淤积现象被当地称为“人工生态修复的典型”。
岬角形状改变过程中,董家口防波堤逐渐向海伸出1.9 km,防波堤产生导流和新的挑流作用,工程施工导致岬角处泥沙被扰动在区域性南西向沿岸流作用下进入湾内,部分泥沙在各岸段重新分配,引起过渡段泥沙沉积量增加,切线段侵蚀速率降低。防波堤建成后,湾内动力环境逐渐达到新的平衡,C断面以南D断面处因任家台岬角的遮蔽作用岸线形成一定程度的淤积。当波生沿岸流到达C断面因湾口宽度变窄出现增强,导致C断面北侧岸线侵蚀,原坝头堆积沙体消失,2019年调查时海水已侵入到该处防潮大堤根部(见图 5)。当地曾于2015年1月在大风期间出现海岸数百米防潮堤垮塌的事故,对堤内安全构成威胁。而B断面所代表的过渡段受岬角改变影响较大,2017年现场调查发现B断面南侧发生了明显的侵蚀,出现沿岸侵蚀陡坎,已有沿岸防护林已倾伏到海中(见图 6),侵蚀泥沙落淤在B断面北侧形成向北延伸的沙嘴,B断面迅速由侵蚀转为淤积。可见,向海突出的新岬角改变了湾内的水动力条件,导致下游切线段波生沿岸流增强,海岸侵蚀加剧。

|
图 5 在切线段北部海水已侵入到防潮大堤根部(2019年) Fig. 5 The seawater has invaded the root of the embankment on the northern of coastline in the tangentsection(2019) |

|
图 6 B断面南侧的侵蚀现象,海岸防护林倾伏至海中(2017年) Fig. 6 The coast erosion occurredon the south side of section B, caused the coastal shelterbelts to collapsetoward the sea(2017 year) |
Silvester和夏益民通过对实验和原型海湾各形态要素与波浪要素之间的关系比较统计,拟合出满足海湾形态的函数曲线,以此作为静态平衡海湾的评判标准[17]。Hsu和Evans通过统计分析27个被认为是处于静态平衡的原型海湾和实验模型[4],提出了岬湾平面形态的抛物线方程(1),并提出了海岸稳定性判别方法:首先确定海湾盛行波向入射角,然后解析数学方程得到岬湾静态平衡岸线,将平衡岸线叠加在原有岸线上,通过分析平衡岸线和现有岸线的差异性判定海岸稳定性来预测未来岸线是否侵蚀或者淤积。根据模型,如果海湾的要素点落在曲线上,则为稳定海岸,如果低于/高于曲线则为不稳定海岸。
| $ R_{n} / R_{0}=C_{1}+C_{2} \times(\beta / \theta)+C_{3} \times(\beta / \theta)^{2}。$ | (1) |
式中:R0为控制线长度; Rn为任一条极半径; β为盛行波波峰线与控制线的岬角; θ为Rn与R0之间的极角; C1、C2、C3为27处海湾回归分析得到的参数,与β的四阶方程相关。
通过类比研究,本文选用抛物线方程对研究区岬角形态改变(建港)前后平面形态进行拟合,获得研究区2005和2014年的海岸平衡线方程(2)和(3),绘制其与实际岸线的位置如图 2所示。
| $ \begin{array}{r} 2005 \text { 年 }: R_{n} / 14272=0.043724+1.678879 \times \\ (31 / \theta)-0.1978 \times(31 / \theta)^{2} 。\\ \end{array} $ | (2) |
| $ \begin{array}{r} 2014 \text { 年 }: R_{n} / 13495=-0.00374+2.409548 \times \\ (41 / \theta)-0.34475 \times(41 / \theta)^{2}。\end{array} $ | (3) |
从图 2上可以看出,防波堤伸入引起岬角控制点向南移动,导致岬湾控制线Ro、盛行波向与控制线夹角β发生变化,导致静态平衡岸线位置发生变动,遮蔽段与过渡段分界线向南迁移了1.6 km。
根据静态平衡岸线判定海岸稳定性的依据,2005年切线段南部区域,实际岸线在静态平衡岸线后方,判定海岸淤积; 而中、北部实际岸线在静态平衡岸线前方,判定海岸侵蚀。与2005—2008年切线段岸线变迁规律相符合。岬角形态改变后形成新的静态平衡岸线,根据静态平衡岸线重新判定。2014年切线段南部区域,实际岸线在静态平衡岸线向陆位置,判定为海岸淤积,而中、北部实际岸线在静态平衡岸线更向海的位置,判定为海岸侵蚀,与2015—2017年切线段岸线的变迁规律趋势吻合。可以看出,该方法在切线段和稳定性判别是适用的。根据静态平衡线与现在岸线位置关系,切线段海岸平均需要蚀退9.7 m,才能与静态平衡岸线相吻合。切线段还将继续发生侵蚀,需引起管理部门的注意。
5 结论通过对岬角形状改变后湾内岸线演化规律的探讨,得出以下结论:
(1) 岬间海湾岬角形状改变对湾内岸线变迁将产生了一定程度的影响,其中影响最大是的过渡段,其次是切线段。
(2) 岬角形状改变过程中,工程建设导致岬角周围海底的泥沙被大量扰动,在SW向沿岸流作用下向湾内辐散,导致切线段泥沙沉积量增加,侵蚀速率降低。岬角形状改变完成后,NE向波致沿岸流加强,混沙向北输送至过渡段,致切线段北侧海岸侵蚀速率增加,过渡段淤积速率增加。
(3) 目前黄家塘岬湾内切线段北段海岸仍未形成新的动力平衡,海岸侵蚀可能后退9.7 m后达到稳定。湾内岸线发生变迁的动力机制来源于湾内切线段波生沿岸流增强。
| [1] |
童宵岭, 时连强, 夏小明, 等. 岬湾海滩沉积动力地貌研究[J]. 海洋地质前沿, 2011(10): 14-21. (  0) 0) |
| [2] |
Yasso, Warren E. Plan Geometry of headland-bay beaches[J]. The Journal of Geology, 1965, 73(5): 702-714. DOI:10.1086/627111
(  0) 0) |
| [3] |
Hsu J R C, Evans C. Parabolic bay shapes and applications[J]. Proceedings of the Institution of Civil Engineers, 1989, 87(2): 557-570.
(  0) 0) |
| [4] |
Dean R G. Equilibrium Beach profiles: Characteristics and applications[J]. Journal of Coastal Research, 1991, 7(1): 53-84.
(  0) 0) |
| [5] |
Bokuniewicz H J, Kraus N C, Munger S, et al. Monitoring incipient breaching at an artificial inlet: Georgica pond, New York[J]. Journal of Coastal Research, 2011, 59(59): 111-117.
(  0) 0) |
| [6] |
Pan Y, Kuang C P, Chen Y P, et al. A comparison of the performance of submerged and detached artificial headlands in a beach nourishment project[J]. Ocean Engineering, 2018, 159: 295-304. DOI:10.1016/j.oceaneng.2018.04.038
(  0) 0) |
| [7] |
程武风, 陈沈良, 胡进. 海南万宁岬湾海岸海滩稳定性研究[J]. 海洋工程, 2017, 35(1): 121-128. Cheng W F, Chen S L, Hu J. Stability of headland bay beaches on the east coast of Hainan Island[J]. The Ocean Engineering, 2017, 35(1): 121-128. (  0) 0) |
| [8] |
Silva G M D, Mousavi S M S, Jose F. Wave-driven sediment transport and beach-dune dynamics in a headland bay beach[J]. Marine Geology, 2012, 323-325: 29-46. DOI:10.1016/j.margeo.2012.07.015
(  0) 0) |
| [9] |
George D A, Largier J L, Storlazzi C D, et al. Currents, waves and sediment transport around the headland of Pt. Dume, California[J]. Continental Shelf Research, 2018, 171(1): 63-76.
(  0) 0) |
| [10] |
战超, 于君宝, 王庆, 等. 近60年莱州湾东部沙质海岸地貌的时空动态[J]. 海洋学报, 2017, 39(9): 90-100. Zhan C, Yu J B, Wang Q, et al. Spatial and temporal dynamics of sandy coastal geomorphology in the cast of Laizhou Bay over recent 60 years[J]. Acta Oceanologica Sinia, 2017, 39(9): 90-100. (  0) 0) |
| [11] |
高义磊.董家口港区总体规划的水动力分析[D].青岛: 中国海洋大学, 2012: 7-13. Gao Y L.The Hydrodnamics Analysis of the General Plan for Donjiakou Harbor Area[D]. Qingdao: Ocean University of China, 2012: 7-13. (  0) 0) |
| [12] |
王松涛, 印萍, 吴振. 山东日照海岸带地质[M]. 北京: 海洋出版社, 2014: 4-5. Wang S T, Yin P, Wu Z. Shandong Rizhao Coastal Geology[M]. Beijing: China Ocean Press, 2014: 4-5. (  0) 0) |
| [13] |
中国科学院计算机网络信息中心.地理空间数据云平台[EB/OL]. (2015-12-05)http://www.gscloud.cn. Computer Network Information Center, Chinese Academy of Sciences. Geospatial Data Cloud site[EB/OL]. (2015-12-05)http://www.gscloud.cn. (  0) 0) |
| [14] |
孙伟富, 马毅, 张杰, 等. 不同类型海岸线遥感解译标志建立和提取方法研究[J]. 测绘通报, 2011(3): 41-44. (  0) 0) |
| [15] |
Klein A H D F, Vargas A, André Luis Alice Raabe, et al. Visual assessment of bayed beach stability with computer software[J]. Computers & Geosciences, 2003, 29(10): 1249-1257.
(  0) 0) |
| [16] |
André L A, Raabe, Klein A H D F, Mauricio González, et al. MEPBAY and SMC: Software tools to support different operational levels of headland-bay beach in coastal engineering projects[J]. Coastal Engineering, 2010, 57(2): 213-226. DOI:10.1016/j.coastaleng.2009.10.008
(  0) 0) |
| [17] |
Hsu J R C, Silvester R. Closure to "static equilibrium bays: New relationships" by John R C Hsu, Richard Silvester and YiMin Xia(May, 1989, Vol. 115, No. 3)[J]. Joural of Waterway, Port, Coastal and Ocean Engineering, 1991, 117(2): 196-197. DOI:10.1061/(ASCE)0733-950X(1991)117:2(196.2)
(  0) 0) |
 2020, Vol. 50
2020, Vol. 50

