2. 中国海洋大学山东省海洋工程重点实验室,山东 青岛 266100;
3. 中海石油(中国)有限公司北京研究中心,北京 100028
海上风能资源丰富,近年来海上风电开发已成为新能源开发的热点,对于深远海风电的开发,往往优先考虑浮式平台基础,如现已大规模应用在Scotland海域的OC3-Hywind单点柱型(Spar)5 MW浮式风机平台。南海作为中国未来海上风电开发的主战场,同时也是内孤立波频发的海域。内孤立波具有振幅大、流速快等特点,这种强非线性波浪会对平台的安全运营产生威胁。
目前针对浮式结构物与内孤立波作用的荷载及运动响应特性研究,仍是海洋工程界面临的挑战性难题。以往的研究主要是将某一类内孤立波传播理论模型与Morison公式结合来研究浮式结构物的荷载动力响应,如Song等[1]将Morison公式与KdV(Korteweg-de Vries)理论结合研究了Spar平台的运动响应问题。尤云翔等[2]基于mKdV理论采用改进的Morison公式研究了两层流体中张力腿平台和半潜式平台的动力响应特性。马孟达[3]和黄文昊等[4]在考虑KdV、eKdV(Extend KdV)、MCC(Miya-Choi-Camassa)三类内孤立波理论的适用性条件后,分别建立了张力腿(TLP)平台、Spar平台的荷载理论模型,并在此基础上研究了结构物的运动响应特性。Cui等[5]通过开展系列模型实验,研究了一浮体在内波作用下的垂荡、纵荡和纵摇特点,同时指出系泊张力的幅值同内波振幅正相关。
在现有的文献中,计算结构物的内孤立波荷载主要是采用Morison公式,但其中采用的拖曳系数Cd和惯性力系数Cm值大部分是参考表面波来选取,其中会产生一定偏差。而计算流体力学(CFD)方法凭借在处理非线性波浪问题上具有的显著优势,开始逐渐应用在浮式结构与内波相互作用的研究中。文献[6-8]中采用CFD方法研究了Spar平台、TLP平台、半潜式平台的内波荷载特性,研究表明三类平台所受的水平力和垂向力主要由波浪力、黏性压差力和摩擦力组成,其中摩擦力与其他两种力相比可以忽略不计。Ding等[9]通过建立三维数值内波水槽,研究了不同浪向角下一小比尺半潜平台的整体受力情况及结构周围的复杂流场特性。需要指出的是,在这些文献中,往往只研究固定浮式结构物的荷载,并未考虑结构物的运动状态,无法准确得出结构物所受动态载荷。同时,对于实际工程中往往需要准确预报平台所受的内波动态荷载才能更好地评估平台运动响应特性,此时需要考虑到结构物对内波流场的影响,即考虑两者的耦合作用,并基于此开展内波作用下浮式平台的运动特性研究。
本文以CFD数值模拟方法,采用重叠网格技术以六自由度运动方式(6DOF)研究了一Spar型浮式风机平台在内孤立波作用下的运动特性。依据文献[10]给出的KdV、eKdV、MCC内孤立波理论的适用性条件,建立振幅及波形可控的内孤立波数值水槽。在此基础上,开展Spar平台与不同振幅、分层比下内孤立波的耦合作用机理研究,分析平台所受的水平动态载荷及纵、横荡特点;同时通过调整系泊的非线性刚度,模拟分析非线性系泊对平台纵荡的影响。
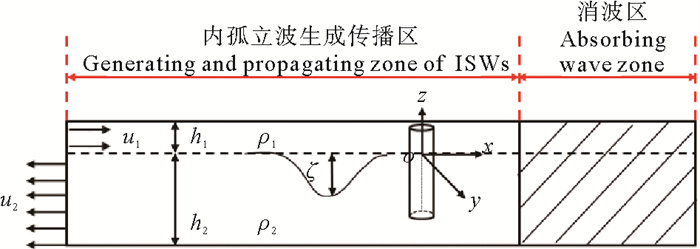
1 数值方法本文采用两层流体模式来研究内孤立波,建立如图 1所示的两层流体系统。设稳定分层的两层流体的总深度为H,上、下层深度分别为h1和h2,上、下层密度分别为ρ1和ρ2。建立直角坐标系oxyz,其中平面oxy位于未扰动的静止的分层界面上,oz轴与平台中心轴重合且垂直向上为正。内孤立波沿ox轴正向传播,ζ表示内孤立波界面位移。采用速度入口边界法生成内孤立波,并经过传播区形成稳定内孤立波后,研究Spar平台所受的内孤立波动态载荷及耦合运动特性。
|
图 1 内孤立波数值水槽示意图 Fig. 1 Schematic diagram of internal solitary wave numerical flume |
计算中假设流体为不可压黏性流,则结构物周围流场控制方程包括
连续性方程:
| $ \nabla \boldsymbol{U}=0 \text { 。} $ | (1) |
动量方程:
| $ \frac{\mathrm{D} \boldsymbol{U}}{\mathrm{D} t}=\boldsymbol{F}-\frac{1}{\rho} \nabla \boldsymbol{P}+v \nabla^2 \boldsymbol{U}。$ | (2) |
式中:▽为哈密顿算子;U为流体速度矢量;
设内孤立波界面位移为ζ,相速度为c,则上、下层流体层平均速度需要满足[10]:
| $ u_i=(-1)^i \frac{c \zeta}{h_i} 。$ | (3) |
式中:ui为分层流体水平流速;hi为分层流体深度;i为流体层数序号。
速度入口处上下层速度分别取u1和u2,采用体积分数(Volume fraction, VOF)模型追踪内孤立波的界面变化,消波方式采用阻尼消波和开渠边界相结合[11]的方式。
流场湍流模型采用的是标准RNG k-ε模型,壁面函数采用标准壁面函数,模型中湍动能k和湍流耗散率ε的方程为[12]:
| $ \begin{gathered} \frac{\partial}{\partial t}(\rho k)+\frac{\partial}{\partial x_j}\left(\rho u_j k\right)= \\ -\frac{2}{3} \rho k \frac{\partial u_k}{\partial x_j}+\frac{\partial}{\partial x_j}\left(\frac{\mu_{\mathrm{eff}}}{\sigma_k} \frac{\partial k}{\partial x_j}\right)+G_k-\rho \varepsilon 。\end{gathered} $ | (4) |
| $ \begin{gathered} \frac{\partial}{\partial t}(\rho \varepsilon)+\frac{\partial}{\partial x_j}\left(\rho u_j \varepsilon\right)= \\ -\left[\left(\frac{2}{3} C_{\varepsilon 1}-C_{\varepsilon 3}+\frac{2}{3} C_\mu C_\eta \frac{k \partial u_k}{\varepsilon \partial x_k}\right) \rho \varepsilon \frac{\partial u_k}{\partial x_k}+\right. \\ \left.\frac{\partial}{\partial x_j}\left(\frac{\mu_{\mathrm{eff}}}{\sigma_{\varepsilon}} \frac{\partial \varepsilon}{\partial x_j}\right)\right]+\rho \frac{\varepsilon}{k}\left[\left(C_{\varepsilon 1}-C_\eta\right) C_k-C_{\varepsilon 2} \rho \varepsilon\right] 。\end{gathered} $ | (5) |
式中: Gk为平均速度梯度产生的湍流动能;Cμ为模型修正系数;Cε1、Cε2和Cε3为耗散方程的经验参数,一般由试验确定或经验公式计算得到,式中各封闭常数为
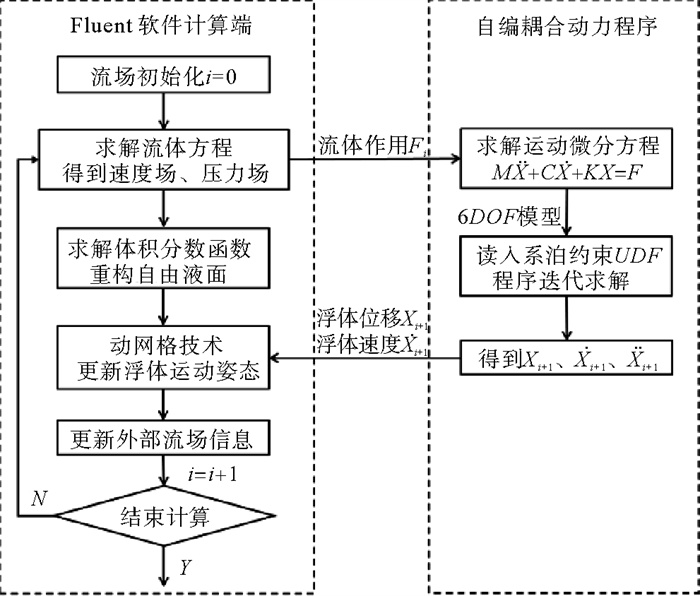
计算物体耦合运动时需要使用到动网格技术,对于大幅度偏移运动问题,使用重叠网格技术具有一定的优势,其在计算过程中能够保持网格质量不变,使流固耦合运动计算更稳定。流固耦合的实现过程是:每一时间步内,将CFD求解得到的外部激励及系泊约束代入到平台运动微分方程,求解得到平台下一步位移、速度及加速度,再将数据传递回Fluent,更新平台位置及流场信息,重复迭代计算(见图 2)。
|
图 2 耦合运动求解流程图 Fig. 2 Flow chart of the resolution of the fluid-structure interaction |
本文选取典型DTU 10 MW风机平台[13]作为研究对象,同时考虑到计算成本及计算效率采用1∶100的缩尺比,表 1给出了该Spar平台的主尺度。
|
|
表 1 Spar平台模型计算参数 Table 1 Calculation parameters of the Spar platform model |
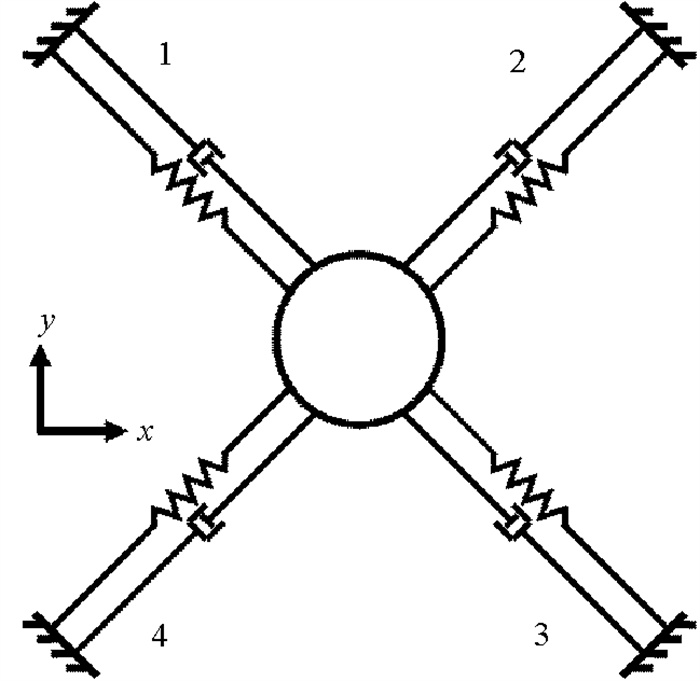
平台模型采用等效水平系泊提供回复力,系泊系统由4根线性弹簧组成,坐标轴建立在平台的重心位置,每根弹簧与坐标轴呈45°角,其布置方式如图 3所示。原型尺度下,系泊刚度2×105 N/m,预张力1.5×106 N,系泊系统阻尼比为0.08。
|
图 3 系泊布置方式示意图 Fig. 3 Layout of mooring system |
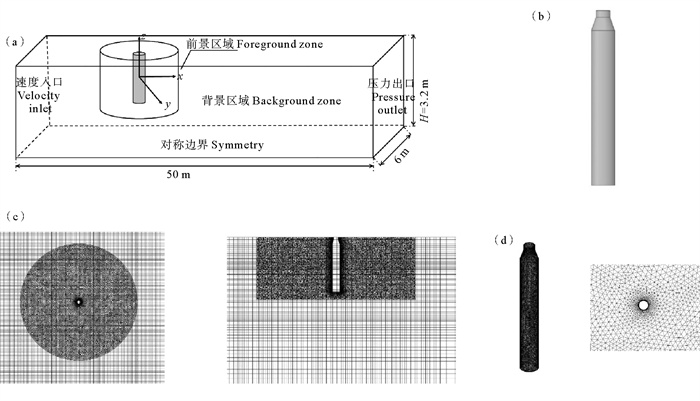
图 4给出了计算域整体网格划分。计算域分为背景网格和前景网格两部分,背景网格区域尺寸为50 m×6 m×3.2 m;前景网格区域尺寸为3.06 m×1.2 m。考虑多自由度运动时,尽量减少网格数量,同时保证计算精度,背景网格采用结构化网格,网格单元数量为131万;前景网格采用非结构化网格,对平台周围网格加密处理,网格单元数量为159万,两者组装后网格单元总数量为290万。
|
(((a)计算域和边界条件示意图Sketch of domain and boundary conditions;(b)浮式风机平台基础Spar model;(c)计算域整体网格划分Global mesh;(d)平台周围网格Local mesh) ) 图 4 计算域示意图及网格划分 Fig. 4 Sketch and mesh of the computational domain |
计算域左侧边界设为速度入口,通过UDF调整入口速度u;右侧为压力出口边界,给定出口静压力为0;上、下表面设为对称边界;在平台立柱表面,采用无滑移壁面;前景区域和背景区域之间采用重叠网格边界,2个计算域之间的数据传递主要采用界面耦合技术,通过插值方法实现重叠界面的数据交换。
2.4 数值模拟工况设置本文参照南海北部流花海域内孤立波实测数据[14],得出该海域水深在300~400 m,内孤立波振幅在30~100 m,主要以30~50 m为主。本文以此为依据,设计作业水深为320 m,典型下凹型内孤立波振幅为20~80 m。上层流体密度ρ1为998 kg/m3,下层流体密度ρ2为1 025 kg/m3,模拟不同内孤立波振幅a下平台的耦合运动,分析不同工况下平台的运动特点,具体计算工况见表 2。根据具体工况,需要采用适合的内孤立波理论模型,即根据文献[10]中确定的3类内孤立波理论KdV、eKdV、MCC的适用性条件,计算得到式(3)中的界面位移ζ。
|
|
表 2 数值模拟工况 Table 2 Computing cases of simulation |
为了生成稳定传播的内孤立波,首先需要校验本文所建内孤立波水槽的合理性,本文主要从内孤立波的生成传播特性、波形、最大波致流水平流速三方面进行说明。
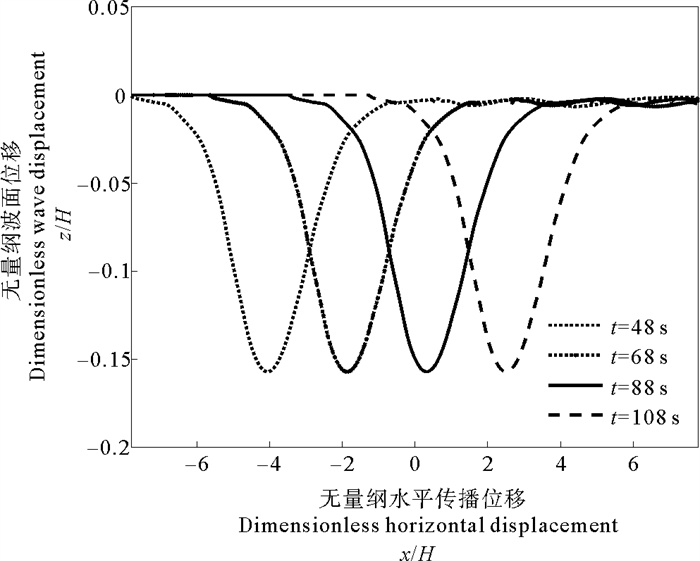
图 5给出了在h1∶h2=1∶3, a/H=0.156 3时,即B5工况下内孤立波的数值模拟结果,可以看出在内孤立波的传播过程中,内孤立波波形保持稳定不变,波高衰减很小。因此,本文所产生的内孤立波是稳定的。
|
图 5 内孤立波的传播特性 Fig. 5 Propagation characteristics of internal solitary waves |
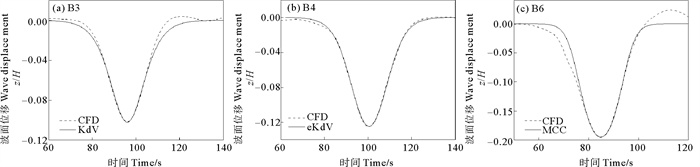
图 6分别给出了分层比h1∶h2=1∶3时3种工况下内孤立波数值模拟结果,工况B3的振幅水深比a/H=0.097 6,此时为弱非线性和弱色散性,采用KdV理论;工况B4的振幅水深比a/H=0.125,此时为中等非线性和弱色散性,采用eKdV理论;工况B6的振幅水深比a/H=0.194 7,此时为强非线性和弱色散性,采用MCC理论;从波形对比结果,可以看出CFD数值模拟结果分别与理论解拟合较好。因此,从波形结果也可以看出本文所采用的的数值造波方法是准确可靠的。
|
图 6 内孤立波波形对比 Fig. 6 Comparison of the numerical and theoretical results for internal solitary wave profile |
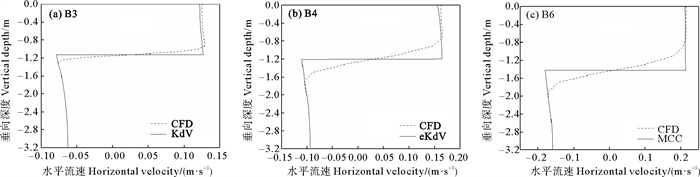
图 7同时给出了在工况B3、B4和B6下的最大波致流水平流速垂向分布,即波谷处的水平流速垂向分布,可以看出CFD数值模拟的上、下层流体水平瞬时速度与理论计算拟合较好,主要区别体现在两层流体界面与波谷间的过渡区域,与理论解在过渡区域速度突变不同,CFD很好地模拟出过渡区域速度渐变的过程,也为内波与结构物的耦合作用模拟提供合理的内波环境。
|
图 7 最大波致流水平流速对比 Fig. 7 Comparison of maximum wave induced horizontal velocity between numerical and theoretical results |
为方便陈述,本文分别定义Fx=Fx/ρ1gSxd、X=X/H、Y=Y/H为平台无因次内孤立波水平力、平台纵荡、平台横荡。其中Sx为平台迎流面积,d为平台吃水深度。
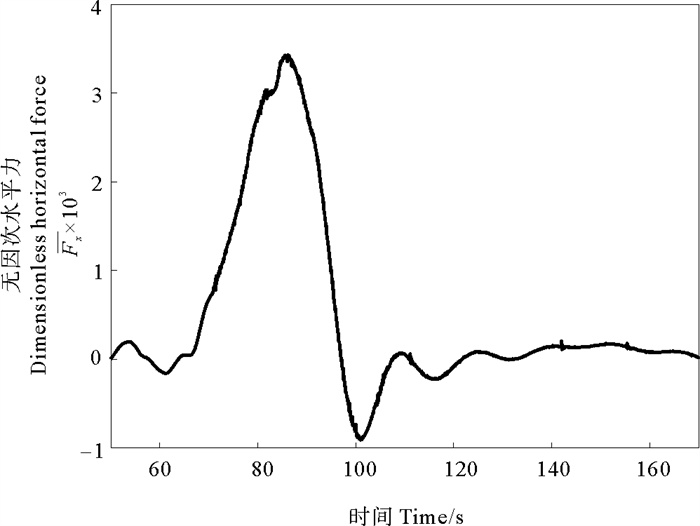
图 8给出了h1∶h2=1∶3, |a|/H=0.125时平台所受无因次水平力的时程变化曲线。结果表明,平台所受水平力在内孤立波波谷经过平台轴线的附近某个时刻达到峰值,随后逐渐减小,并且在内孤立波经过平台后,伴随着尾波列的作用会产生小幅的振荡。
|
图 8 h1∶h2=1∶3, |a|/H=0.125时平台所受水平力时程曲线图 Fig. 8 Time history of the horizontal force on the spar when h1∶h2=1∶3, |a|/H=0.125 |
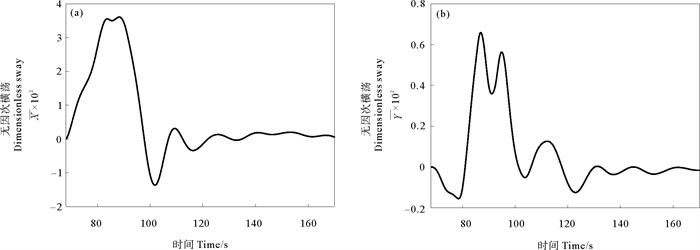
图 9给出了h1∶h2=1∶3, |a|/H=0.125时平台纵荡、横荡的时程曲线图。由图可知,平台会产生较大幅度的纵荡,其运动趋势与平台所受水平力基本一致,纵荡位移随着内孤立波的传播开始增大,在达到峰值后开始减小,当内孤立波经过平台后由于受尾波列的作用还会产生小幅振荡。同时在横向方向,平台还会产生小幅度的振荡,其运动峰值总要滞后于纵荡运动峰值,主要原因是平台横向运动的能量来源于纵荡方向的能量传递效应,且能量主要还是表现在纵荡方向。
|
图 9 h1∶h2=1∶3, |a|/H=0.125时平台纵荡(a)和横荡(b)时程曲线图 Fig. 9 Time history of Spar surge(a) and sway(b) when h1∶h2=1∶3, |a|/H=0.125 |
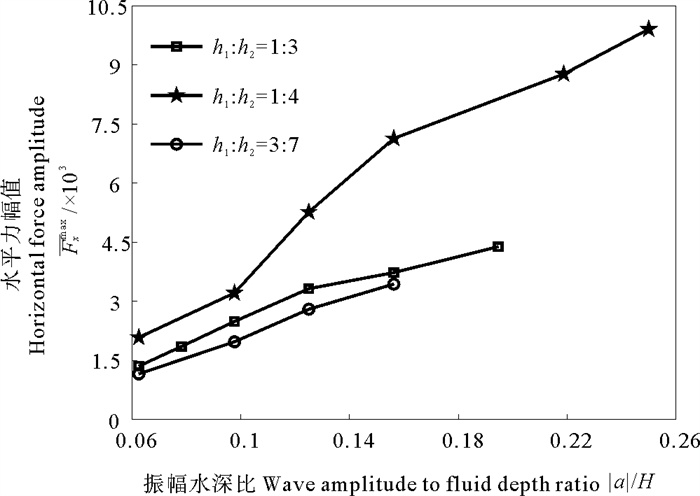
本节进一步探究了内孤立波作用下平台所受荷载及运动响应幅值的规律。图 10给出了水深比h1∶h2分别为1∶3、1∶4和3∶7时,平台所受的水平力峰值随波幅变化的情况。可以看出同一分层比下,随着内孤立波振幅水深比a/H的增大,水平力的峰值增大。同时从图中还可以发现,分层比对平台动态荷载幅值会产生影响,随着分层比的增大,即上层流体厚度变厚,同一振幅下水平载荷开始减小。
|
图 10 不同分层比下平台水平力幅值变化特性 Fig. 10 Variation characteristics of spar horizontal force amplitude at different layering ratios |
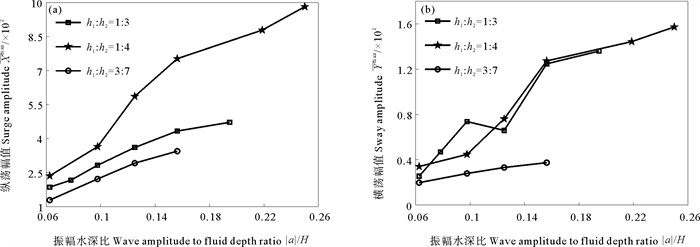
图 11则给出了3种分层比下平台纵荡和横荡幅值变化特性,平台的运动响应与其受力有关,同一水深比条件下,平台纵荡幅值随波幅的增大而增大,且增长幅度因分层比的不同而不同,同时随着分层比的增大,即流体分界面下移,下层流体厚度变小,此时根据其所受水平力特性,纵荡幅值减小;而横荡运动较为复杂,在分层比h1∶h2为1∶4或3∶7时,横荡峰值与波幅呈正相关,而在分层比h1∶h2为1∶3的条件下会出现拐点及局部最小值。
|
图 11 不同分层比下平台纵荡(a)与横荡(b)幅值变化特性 Fig. 11 Variation characteristics of Spar surge(a) and sway(b) amplitude at different layering ratios |
系泊系统对平台运动往往起着重要的作用,特别是对纵荡,为研究系泊刚度对平台纵荡运动影响,设定三维数值水槽模型参数为:上层水深h1=0.8 m;下层水深h2=2.4 m。
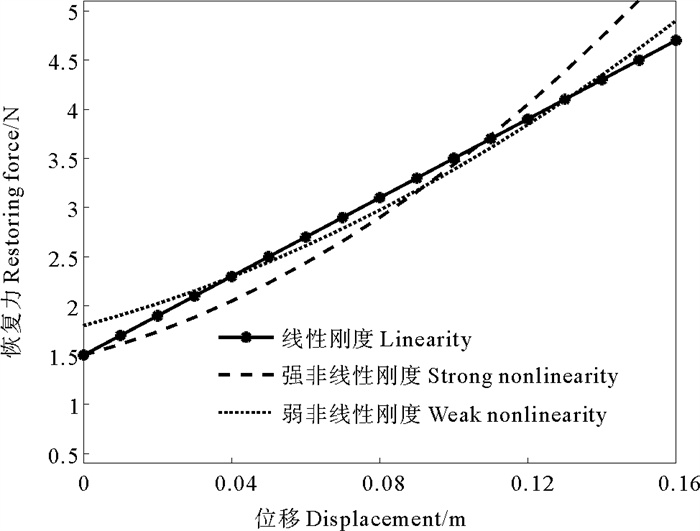
为了研究系泊系统刚度改变对平台纵荡的影响,对系泊系统刚度做出调整,选取了3种类型的系泊刚度,分别为线性刚度、强非线性刚度、弱非线性刚度,其位移恢复力曲线见图 12并采用表 3中的工况对其进行计算分析。
|
图 12 平台系泊位移恢复力曲线 Fig. 12 Displacement restoring force of mooring line |
|
|
表 3 调整系泊计算工况 Table 3 Computing cases of different mooring system |
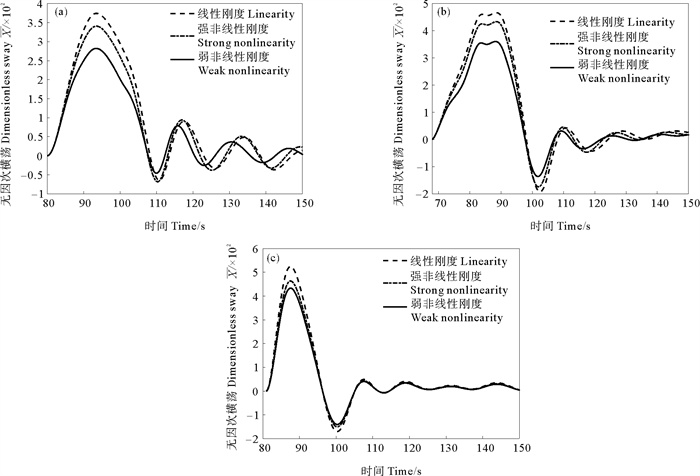
图 13给出了在分层比h1∶h2=1∶3时采用3种不同系泊刚度的平台纵荡历时曲线图,从图中可以看出在同一波幅下,平台的纵荡趋势一致,但非线性刚度对平台的纵荡运动峰值影响显著,平均峰值比线性刚度大20%左右,这主要是因为在平台运动的前期,线性刚度系泊给予结构的拉力要大于非线性系统所给予的拉力,因此系泊系统允许平台的运动位移量要小;同时还发现在非线性刚度下,弱非线性系统运动幅值要小于强非线性系统运动幅值,这是由于受流场及各自系泊系统的影响,两者对平台的运动影响程度不同。因此,由以上分析可知,系泊系统采用等效线性刚度弹簧时,往往会低估平台的纵荡幅值。
|
(((a)h1∶h2=1∶3, |a|/H=0.093 75;(b)h1∶h2=1∶3, |a|/H=0.125;(c)h1∶h2=1∶3, |a|/H=0.156 3) ) 图 13 调整系泊系统平台纵荡时历曲线 Fig. 13 Time history of Spar surge at different mooring system |
(1) 内孤立波作用下,平台会受到很大的突发性水平冲击荷载并表现出较大的水平偏移。当分层比h1∶h2=1∶4,振幅水深比|a|/H=0.125时,得到的最大波致流水平速度为2.5 m/s,与文献[15]中该海域观测到的最大波致流速相近,此时平台水平偏移量达到10%的水深。
(2) 随内孤立波振幅的增大,平台所受的水平力、纵荡、横荡峰值都呈增大的趋势。其中平台纵荡运动幅度较为明显,伴随小幅的横荡运动,且横荡峰值较纵荡滞后出现;随着上层流体厚度变厚,平台所受的水平力、纵荡幅值均减小。
(3) 调整系泊系统分析可知,平台纵荡运动趋势是一致,主要区别体现在纵荡幅值;相比于非线性系统,采用线性系泊系统会低估纵荡峰值平台约20%;同时在非线性系统下,弱非线性系统对平台的约束能力要优于强非线性系统。
研究表明,在中国南海北部海域进行海上风电开发时,需要充分考虑内孤立波对浮式风电平台的影响, 本文为内孤立波与浮式结构物耦合运动分析提供了一种新的手段。
| [1] |
Song Z J, Teng B, Gou Y, et al. Comparisons of internal solitary wave and surface wave actions on marine structures and their responses[J]. Applied Ocean Research, 2011, 33(2): 120-129. DOI:10.1016/j.apor.2011.01.003 (  0) 0) |
| [2] |
尤云祥, 李巍, 时忠民, 等. 海洋内孤立波中张力腿平台的水动力特性[J]. 上海交通大学学报, 2010, 44(1): 56-61. You Y X, Li W, Shi Z M, et al. Hydrodynamic characteristics of tension leg platform in ocean internal solitary waves[J]. Journal of Shanghai Jiaotong University, 2010, 44(1): 56-61. (  0) 0) |
| [3] |
马孟达, 尤云祥, 张新曙. 海洋内孤立波作用下张力腿平台动力响应特性[J]. 水动力学研究与进展A辑, 2016, 31(2): 135-144. Ma M D, You Y X, Zhang X S. Dynamic response characteristics of tension leg platform under isolated waves[J]. Journal of Hydrodynamics, Series A, 2016, 31(2): 135-144. (  0) 0) |
| [4] |
黄文昊, 尤云祥, 王旭, 等. 圆柱型结构内孤立波载荷实验及其理论模型[J]. 力学学报, 2013(5): 716-728. Huang W H, You Y X, Wang X, et al. Internal solitary wave load experiment and theoretical model of cylindrical structure[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013(5): 716-728. (  0) 0) |
| [5] |
Cui J, Dong S, Wang Z, et al. Experimental research on internal solitary waves interacting with moored floating structures[J]. Marine Structures, 2019, 67: 102641. DOI:10.1016/j.marstruc.2019.102641 (  0) 0) |
| [6] |
Wang X, Zhou J F, Wang Z, et al. A numerical and experimental study of internal solitary wave loads on semi-submersible platforms[J]. Ocean Engineering, 2018, 150: 298-308. DOI:10.1016/j.oceaneng.2017.12.042 (  0) 0) |
| [7] |
王旭, 林忠义, 尤云祥. 内孤立波与直立圆柱体相互作用特性数值模拟[J]. 哈尔滨工程大学学报, 2015, 36(1): 6-11. Wang X, Lin Z Y, You Y X. Numerical simulation of the interaction between internal solitary waves and a vertical cylinder[J]. Journal of Harbin Engineering University, 2015, 36(1): 6-11. (  0) 0) |
| [8] |
Wang X, Zhou J. Numerical and experimental study of internal solitary wave loads on tension leg platforms[J]. Journal of Hydrodynamics, 2021, 33(1): 93-103. DOI:10.1007/s42241-021-0015-y (  0) 0) |
| [9] |
Ding W, Ai C, Jin S, et al. 3D numerical investigation of forces and flow field around the semi-submersible platform in an internal solitary wave[J]. Water, 2020, 12(1): 208. DOI:10.3390/w12010208 (  0) 0) |
| [10] |
Cui J, Dong S, Wang Z. Study on applicability of internal solitary wave theories by theoretical and numerical method[J]. Applied Ocean Research, 2021, 111: 102629. DOI:10.1016/j.apor.2021.102629 (  0) 0) |
| [11] |
Zhu H, Wang L L, Tang H W. Large-eddy simulation of the generation and propagation of internal solitary waves[J]. Science China Physics, Mechanics & Astronomy, 2014, 57(6): 1128-1136. (  0) 0) |
| [12] |
Liu Y, Li H, Feng G. Simulation of inhalable aerosol particle distribution generated from cooking by Eulerian approach with RNG k-epsilon turbulence model and pollution exposure in a residential kitchen space[J]. Building Simulation, 2017, 10(1): 135-144. (  0) 0) |
| [13] |
Hou P, Hu W, Soltani M, et al. Optimized placement of wind turbines in large-scale offshore wind farm using particle swarm optimization algorithm[J]. IEEE Transactions on Sustainable Energy, 2015, 6(4): 1272-1282. (  0) 0) |
| [14] |
石新刚, 刘耀华, 兰志刚, 等. 南海北部流花海域内孤立波特征研究[J]. 热带海洋学报, 2013, 32(6): 22-27. Shi X G, Liu Y H, Lan Z G, et al. Study on the characteristics of solitary waves in Liuhua area in the northern South China Sea[J]. Journal of Tropical Oceanography, 2013, 32(6): 22-27. (  0) 0) |
| [15] |
Huang X, Chen Z, Zhao W, et al. An extreme internal solitary wave event observed in the northern South China Sea[J]. Scientific Reports, 2016, 6(1): 1-10. (  0) 0) |
2. Shandong Key Laboratory of Ocean Engineering, Ocean University of China, Qingdao 266100, China;
3. China National Offshore Oil Corporation Research Center, Beijing 100028, China
 2023, Vol. 53
2023, Vol. 53


