2. 青岛市海洋可再生能源重点实验室,山东 青岛 266100
作为一种储量巨大的清洁可再生能源,潮流能得到了各国科研人员的重视,出现了很多关于潮流能发电水轮机的研究。在实际海域中,影响潮流能水轮机获能的因素有很多,如地形、来流速度、来流方向、湍流等。其中,湍流对潮流能发电水轮机性能的影响主要有以下几点:第一,湍流对潮流能发电机组的获能效率和受力有影响;第二,不同湍流下的潮流能发电水轮机的尾流场有所不同[1]。
在实际的潮流能发电场布放海域中必然存在着湍流。Osalusi等[2]测定了英国Fall of Warness海域的湍流强度为7.9%~8.7%,在涨潮落潮时的湍流强度可达9.5%~10.3%;Milne等测量的英国Sound of Islay距离海底5 m处海域的湍流强度为12%~15%;Thomson等测量的美国Puget Sound海域的湍流强度为6.6%~9%。可见,世界上主要的潮流能资源区的湍流强度都较大。因此,研究湍流条件下潮流能发电水轮机性能及尾流特征是有必要的,多家研究机构进行了湍流对潮流能发电水轮机性能影响的研究。Mycek P等[3]在水槽中对工作在湍流强度分别为3%和15%两种工况下的直径为800 mm的潮流能发电水轮机获能系数和轴向力系数等进行了试验研究;Rose等[4]在实验室中用缩放比例为1/10的水轮机模型进行了湍流试验(原水轮机直径1.5 m),研究了不同来流速度下尾流场相关性能;Tedds等[5]主要研究了湍流条件下不同叶片数目、扭角情况下尾流形状。
上述研究主要从试验方面进行了湍流对潮流能发电水轮机的相关研究,本文主要从数值模拟方面进行湍流对潮流能发电水轮机相关性能影响的研究,通过设置不同的湍流强度,研究不同湍流强度对潮流能发电水轮机获能系数和轴向力系数以及尾流场性能的影响,从而为潮流能发电水轮机多机组阵列排布提供合理参考。
1 特征量介绍 1.1 湍流强度湍流强度(Ⅰ)简称湍流度或湍强,湍流是流体的一种流动状态。当流速很小时,流体分层流动,互不混合,称为层流;当流速增加到很大时,流线不再清楚可辨,流场中有许多小漩涡,层流被破坏,相邻流层间不但有滑动,还有混合。这时的流体作不规则运动,有垂直于流管轴线方向的分速度产生,这种运动称为湍流。实际水域中湍流强度可通过以下公式计算得到[6]:
| $ I = \frac{{\sqrt {\frac{1}{3}\left[ {{\sigma ^2}\left( u \right) + {\sigma ^2}\left( v \right) + {\sigma ^2}\left( w \right)} \right]} }}{{\sqrt {{u^2} + {v^2} + {w^2}} }} \times 100\% 。$ | (1) |
式中:I-湍流强度;σ-平方差;u-x方向水流速度(m·s-1);v-y方向水流速度(m·s-1);w-z方向水流速度(m·s-1)。
1.2 获能系数、轴向力系数分析水轮机特性时,表征水轮机水动力学性能的常用参数是功率系数、轴向力系数。其中功率系数直接关系到水轮机的发电效率;轴向力系数与潮流对支撑水轮机的轴向力有关系,主要用于对支撑结构进行设计和校核,对保证水轮机安全性和稳定性具有重要影响。功率系数和轴向力系数的表达式[8]为:
| $ {C_{\rm{p}}} = \frac{{{P_电}}}{{0.5\rho {V^3}{\rm{ \mathsf{ π} }}}}。$ | (2) |
| $ {C_{\rm{D}}} = \frac{F}{{0.5\rho {V^3}{\rm{ \mathsf{ π} }}}}{\rm{。}} $ | (3) |
式中:P电-水轮机实际功率;F-轴向力;ρ-水的密度;V—来流速度;R-水轮机半径。
在数值仿真中,可通过Fluent计算获得相应的转矩T,则水轮机功率为:
| $ {P_电} = T\omega 。$ | (4) |
式中ω—水轮机角速度。
2 数值建模 1.1 计算模型本文选用直径600 mm潮流能发电水轮机模型,翼型为NACA 63418,具体参数如表 1所示。
|
|
表 1 潮流能发电水轮机模型相关参数 Table 1 Related parameters of tial turbine model |
根据MATLAB生成的叶片翼型数据及转子的尺寸参数,在三维绘图软件中完成不同直径转子的水轮机建模,其三维模型如图 1所示。

|
图 1 水轮机转子三维模型 Fig. 1 3D model of tidal turbine rotor |
将潮流能发电水轮机三维模型导入到Gambit中进行网格划分(见图 2)。考虑到水轮机尾流场的充分扩展,流场域的尺寸选取为:长×宽×高=25D×5D×5D。水轮机采用三角形非结构面网格,旋转域和流场域均采用六面体非结构体网格。通过控制面网格、旋转域网格、流体域网格尺寸,实现了旋转域的局部加密,加密程度约为10倍网格加密,从而使模拟结果更精确。

|
图 2 网格划分 Fig. 2 Meshing |
水轮机的计算区域如图 3所示。水轮机中心距离入口为5D处,既提高了计算效率,节省了计算时间,同时又保证了计算准确性;为避免计算域上下边界对水轮机的干扰,选取上下边界距离水轮机中心2.5D;考虑尾流在水轮机后方大约20D处完全恢复,故出口边界在水轮机中心后方25D处[9]。

|
图 3 水轮机计算区域 Fig. 3 The area of computation about tidal turbine |
鉴于水为不可压缩液体及来流速度已知,设置进口边界为速度入口(Velocity inlet),出口边界条件为压力出口(Pressure outlet),水轮机叶片表面为无滑移的固壁条件(Wall);旋转域和流体域的类型都为流体(Fluid)。
1.3 湍流模型选择湍流模型的选择。假设流体为黏性不可压缩的液体,则流体运动方程为纳维-斯托克斯(N-S)方程,其三维流动连续性微分方程[10]为:
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \left( {\rho u} \right) = 0。$ | (5) |
式中:u-速度矢量(m·s-1);▽-拉普拉斯算子;ρ-流体密度(kg·m-3)。
鉴于Realizable模型已经广泛应用于旋转剪切流、包含有射流和混合流的自由流动、边界层流动,以及带有分离的流动,故本数值模拟选取Realizable模型[11],关于k和的输运方程如下:
| $ \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \frac{\partial }{{{x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} - \rho \varepsilon 。$ | (6) |
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \varepsilon {u_i}} \right) = \frac{\partial }{{{x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon}}}} \right)\frac{{\partial \varepsilon}}{{\partial {x_j}}}} \right]\\ \;\;\;\;\;\;\;\;\;\;\; + \rho {C_1}E\varepsilon - {C_2}\rho \frac{{{\varepsilon ^2}}}{{k + \sqrt {v\varepsilon } }}。\end{array} $ | (7) |
式中:k-湍流动能;ε-湍动耗散率;σk,σε-湍动能k和湍动耗散率对应的Prandtl数,σk =1.0,σε=1.2;xi、xj-位置坐标分量;ui-速度坐标分量;Gk-平均速度梯度引起的湍流动能k的产生项;μ-流体动力黏性系数。湍流黏性系数μ=ρCμk2/σε,Cμ-模型常数,C2=1.9。
3 数值模拟结果来流速度分别为0.4、0.6、0.8、1.0、1.2 m/s时不同湍流强度下(3%和15%)水轮机获能系数、轴向力系数和尾流场流速损失如图 4~6所示。

|
图 4 不同湍流强度时水轮机获能系数 Fig. 4 Cp of tidal turbine when turbulenceintensity is different |

|
图 5 不同湍流强度时水轮机轴向力系数 Fig. 5 CT of tidal turbine when turbulence intensity is different |
|
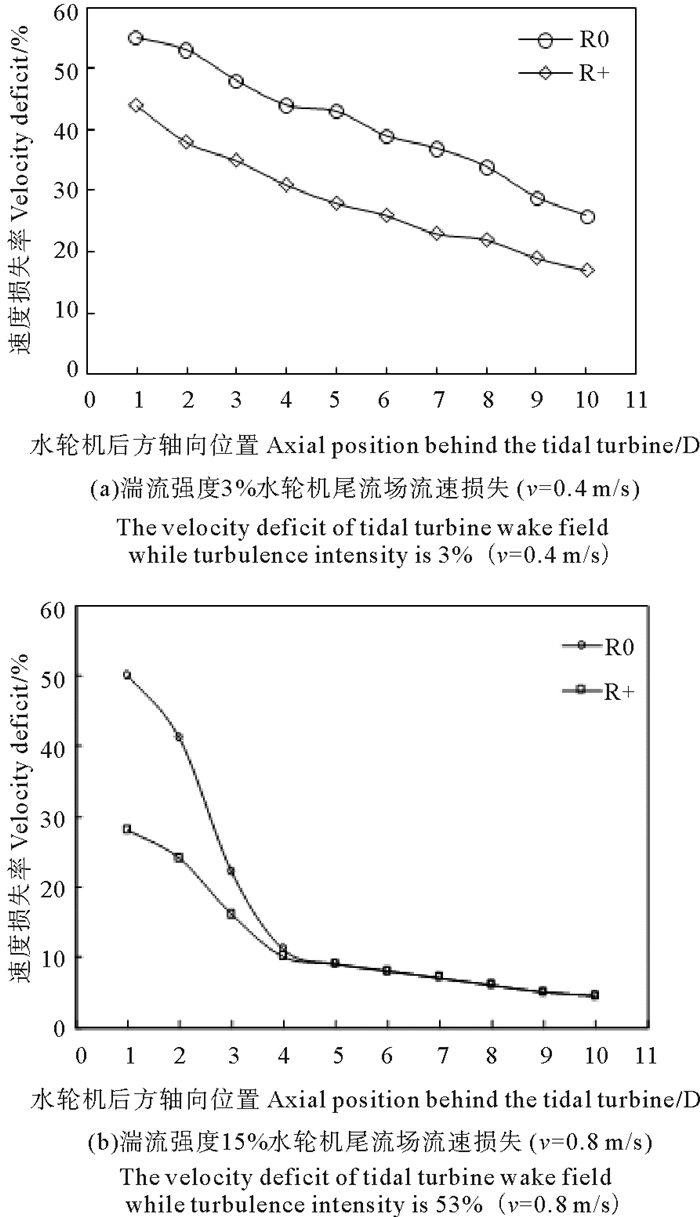
(尖速比为5,R0为水轮机中心,R+为水轮机半径。The tip speed ratio is 5, R0 represents the center of tidal turbine, R+ represents the radius of tidal turbine. ) 图 6 不同湍流强度时水轮机尾流场流速损失 Fig. 6 The velocity deficit of tidal turbine wake field while turbulence intensity is different |
如图 4所示,对两种湍流强度,当尖速比在3~6时水轮机获能系数较高;湍流强度为3%时各曲线更接近一条曲线,而湍流强度为15%时各曲线比较分散;对应每种来流速度下,湍流强度为3%时水轮机获能系数略高于湍流强度为15%时;获能系数随来流速度的增大而有所增加,来流速度为1.2 m/s时最大获能系数比来流速度为0.4 m/s时最大获能系数高10%左右。
如图 5所示,轴向力系数受湍流强度影响不是很大,相同来流速度下,湍流强度小,轴向力系数较大;对同一湍流强度下,来流速度大,轴向力系数较大,但来流速度为1.2 m/s时最大轴向力系数跟来流速度为0.4 m/s时最大轴向力系数差别不是很大。
如图 6所示,不同湍流强度时,水轮机后方相同位置处轴向速度损失不同,且湍流强度越小,水轮机后方轴向相同位置处速度损失越大;湍流强度为3%时,水轮机后方轴向10D位置处速度损失依然在20%左右,而对于湍流强度为15%时,在水轮机后方轴向5D处速度损失可达到10%,即尾流场速度恢复更快。
数值仿真中得到了相同来流速度下,不同湍流强度时水轮机后方尾流场速度云图及湍流强度云图,如图 7、8所示。

|
图 7 不同湍流强度尾流场速度云图对比图 Fig. 7 Cloud graphics of wake field velocity magnitude under different inlet flow turbulent intensity |
|
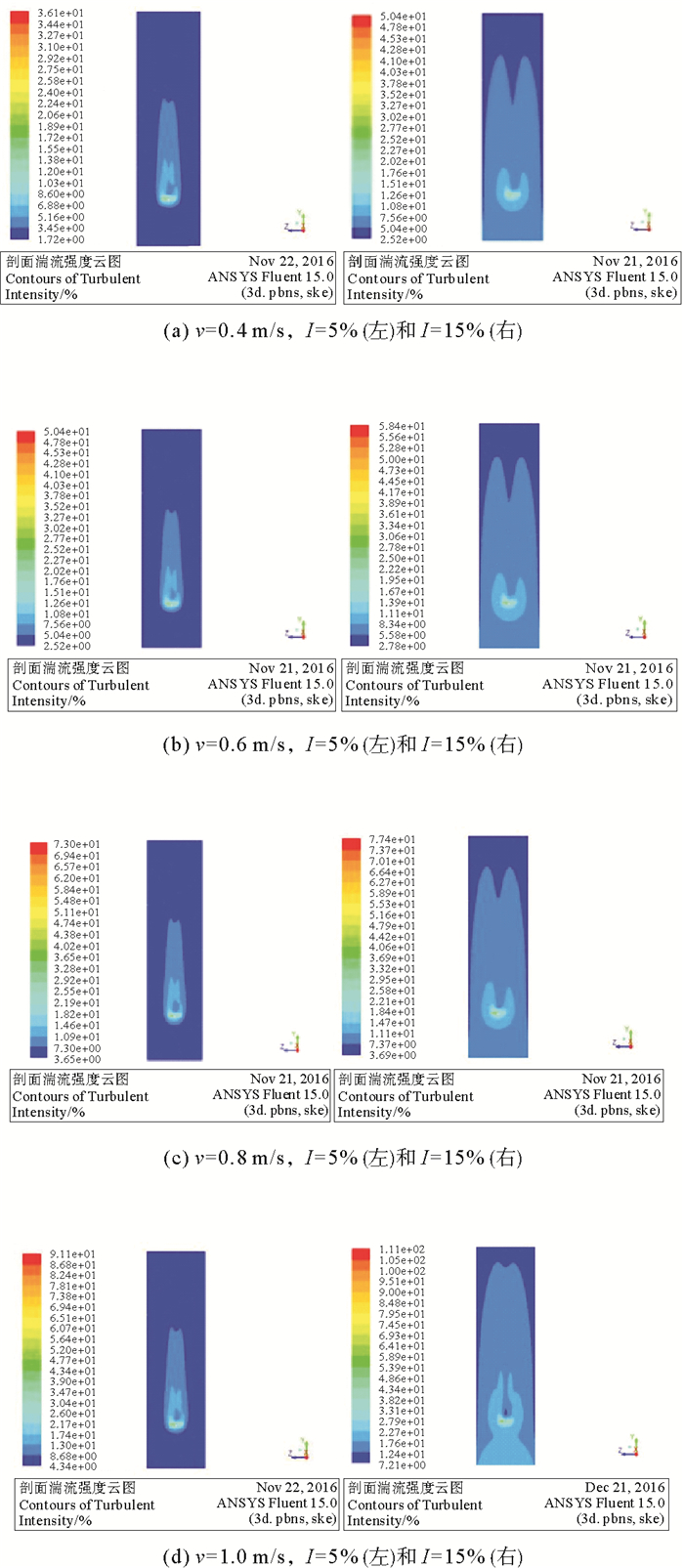
图 8 不同湍流强度尾流场湍流强度云图 Fig. 8 Cloud graphics of wake field turbulent intensity under different inlet flow turbulent intensity |
如图 7所示,相同来流速度时,湍流强度不同,尾流场长度也不同,且湍流强度越大,尾流场越小,即尾流场速度恢复越快,前排水轮机对后排水轮机影响更小。
如图 8所示,相同来流速度时,湍流强度不同,流过水轮机后尾流场湍流强度也不同,且湍流强度越大,尾流场轴向和径向影响范围越大。
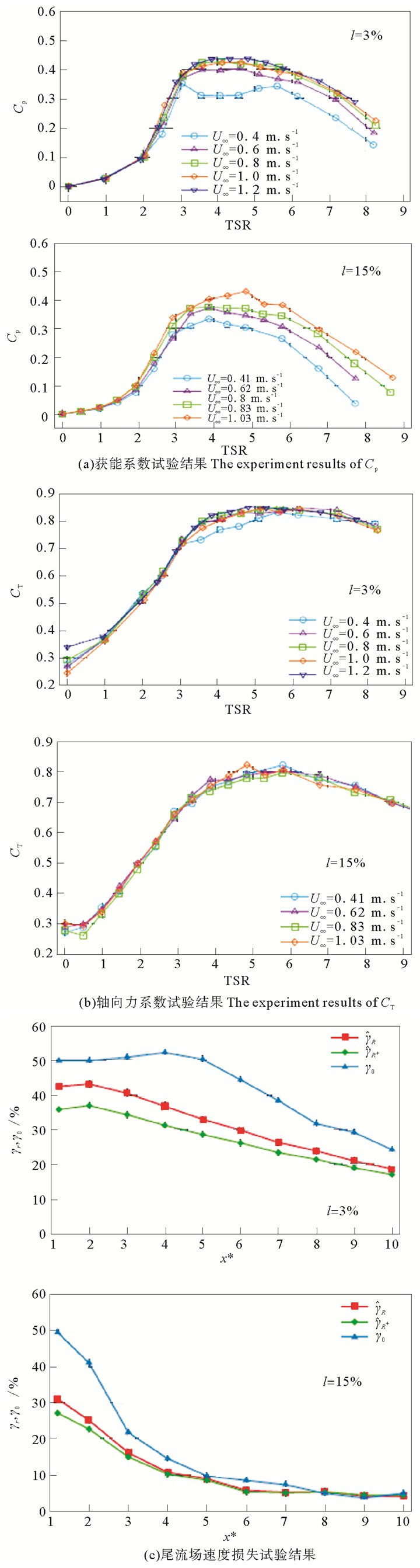
4 与相关文献的试验结果进行对比为了验证数值模拟结果的准确性,将模拟结果与文献[2]中的试验研究结果进行对比。文献[2]中Mycek P等[2]关于获能系数、轴向力系数和尾流场速度损失试验研究结果如图 9(a~c)所示。
|
图 9 Mycek P等[2]部分试验结果 Fig. 9 The experiment results of Mycek P |
将如图 4~6所示的不同湍流强度时水轮机获能系数、水轮机轴向力系数和水轮机尾流场流速损失与如图 9所示的文献[2]中Mycek P等的试验研究结果进行对比,两者的结果比较接近,变化趋势基本一致。可见,利用CFD软件对处于不同湍流强度下的潮流能发电水轮机性能进行数值模拟结果是可靠的。
5 结论及展望通过对数值模拟结果进行分析,并与相关文献[2]中的试验结果进行对比,两者结果比较符合,可以得到以下结论:
(1) 当来流速度相同时,湍流强度越大,水轮机获能系数越小;当湍流强度相同时,来流速度越大,获能系数越高。当存在湍流时,水轮机的获能效率降低,获能系数最大可降低10%左右。
(2) 湍流强度越大,水轮机轴向力系数略有减小;当湍流强度相同时,流速越大,轴向力系数也越大。
(3) 湍流强度越大,水轮机后方尾流场流速恢复越快,当湍流强度为3%时,水轮机后方轴向10D处只恢复到80%左右,而当湍流强度为15%时,水轮机后方轴向5D处即可恢复到90%左右。因此,湍流强度对第二排水轮机的排布位置具有明显的影响,湍流强度越大,适合安放第二排水轮机的前后间距越小。由于计算时间的原因以及与文献[2]对比的需要,数值模拟中只设置了两种典型的湍流强度。在后续研究中可对湍流强度进行进一步的细化,从而为湍流对潮流能发电水轮机的影响进行更加深入的研究。
| [1] |
Mycek P, Gaurier B, Germain G, et al. Experimental study of the turbulence intensity effects on marine current turbines behaviour. Part Ⅱ: Two interacting turbines[J]. Renewable Energy, 2014, 68(7): 876-892.
(  0) 0) |
| [2] |
Mycek P, Gaurier B, Germain G, et al. Experimental study of the turbulence intensity effects on marine current turbines behaviour. Part Ⅰ: One single turbine[J]. Renewable Energy, 214, 66(5): 729-746.
(  0) 0) |
| [3] |
Bahaj A S, Molland A F, Chaplin J R, et al. Power and thrust measurements of marine current turbines under various hydrodynamic flow conditions in a cavitation tunnel and a towing tank[J]. Renewable Energy, 2007, 32(3): 407-426. DOI:10.1016/j.renene.2006.01.012
(  0) 0) |
| [4] |
Rose S, Good A, Atcheson M, et al. Investigating experimental techniques for measurement of the downstream near wake of a tidal turbine[J]. Renewable Energy, 2013, 14(21): 87-88.
(  0) 0) |
| [5] |
Milne I A, Day A H, Sharma R N, et al. Blade loads on tidal turbines in planar oscillatory flow[J]. Ocean Engineering, 2013, 60(2): 163-174.
(  0) 0) |
| [6] |
Chen Y, Lin B, Lin J, et al. Effects of stream turbine array configuration on tidal current energy extraction near an island[J]. Computers & Geosciences, 2015, 77(C): 20-28.
(  0) 0) |
| [7] |
Blackmore T, Batten W M J, SBahaj A. Inlet grid-generated turbulence for large-eddy simulations[J]. International Journal of Computational Fluid Dynamics, 2013, 27(6-7): 307-315. DOI:10.1080/10618562.2013.819972
(  0) 0) |
| [8] |
宋晓鞠.复杂工况下潮流能水平轴水轮机水动力性能研究及叶片优化[D].浙江: 浙江工业大学, 2015. Song Xiaoju. The Research and Optimize of Blade or Tidal Current Turbine Working Complicated Conditions[D]. Zhejiang: Zhejiang University of Technology, 2015. (  0) 0) |
| [9] |
安佰娜.潮流能发电场尾流场数值模拟及其多机组影响规律研究[D].青岛: 中国海洋大学, 2012. Baina An. The Research of Tidal Turbine Arrays and the Simulation of Wake Field of Tidal Turbine Farm[D]. Qingdao: Ocean University of China, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10423-1012506303.htm (  0) 0) |
| [10] |
李玉柱, 贺五洲. 工程流体力学[M]. 北京: 清华大学出版社, 2006: 69-71. Li Yuzhu, He Wuzhou. Engineering Fluid Mechanics[M]. Beijing: Tsinghua University Press, 2006: 69-71. (  0) 0) |
| [11] |
刘臻, 史宏达, 刘芸. 应用Realizable k-ε湍流模型的振荡水翼绕流数值模拟研究[J]. 哈尔滨工程大学学报, 2008, 29(6): 628-634. Liu Zhen, Shi Hongda, liu Yun. Application of Realizable k -epsilon turbulence model of numerical simulation of flow around oscillating hydrofoil research[J]. Journal of Harbin Engineering University, 2008, 29(6): 628-634. DOI:10.3969/j.issn.1006-7043.2008.06.018 (  0) 0) |
2. Qingdao Marine Renewable Energy Key Laboratory, Qingdao 266100, China
 2019, Vol. 49
2019, Vol. 49

