2. 青岛地质工程勘察院, 山东 青岛 266071;
3. 山东省地矿局城市地质与地下空间资源重点实验室, 山东 青岛 266100;
4. 山东省海洋环境地质工程重点实验室, 山东 青岛 266100
地下水是重要的水资源之一,对人类生活和工农业生产至关重要。随着社会经济的快速发展,地下水污染问题越来越严重。为了对地下水资源进行科学的开发和管理,需要对地下水水质进行评价和预测。地下水水质评价的方法有单因子评价法、综合污染指数法[1]、层次分析法[2]、灰色系统评价法[3]、人工神经网络法[4]和模糊数学法[5]等。单因子评价法和综合污染指数法计算简单,使用便捷,但评价结果与真实水质状况有一定差异;层次分析法受人为因素影响较大,不能客观科学地进行评价;灰色系统法可对水质进行客观科学的评价,但构造函数复杂,操作不便;人工神经网络法通过自学习性进行水质评价,容易陷入局部极小,网络结构难以确定,且所需参数资料较多;基于地下水环境系统污染物质、水质类别划分的模糊性,国内外学者将模糊数学理论应用于水环境质量综合评价中,并成为国内外的研究热点[6-7]。传统模糊综合评价法采用超标法[8]确定权重,这种方法突出了实测浓度大的指标对水质的影响程度,而降低了一些低浓度指标的影响,会造成结果偏高,采用聚类权法[9]可弥补上述缺点,综合考虑所有指标实测值;传统模糊综合评价采用“取小取大法[10]”算子,容易造成信息丢失,利用“加权平均型”的“相乘相加法”算子[11],可充分考虑所有因素的影响,合理地对水质进行综合评价;传统模糊综合评价根据最大隶属度原则[12]确定评价对象的等级,存在一定的不适应性,利用级别特征值法[13]分析结果向量可解决不适性问题。
地下水水质预测常用的方法主要有:数值模型预测法[14]、灰色预测法[15]、人工神经网络预测法[16]和指数平滑法[17]。建立数值模型需要考虑的参数较多,且参数调整较为繁琐;灰色预测法精度依赖于监测数据的特点,对某时期水质指标波动较大的情况,预测结果较差;人工神经网络模型未进行水质因子的筛选,扩展了预测过程,使其复杂化;指数平滑法计算简单,所需观测值较少,适应性强,被广泛应用于水文学、环境科学等方面。
本文在权重确定、模糊算子的选择和评价等级判定三方面对传统模糊综合评价法进行了改进,利用改进的模糊综合评价法对大沽河地下水源地2002—2017年地下水水质进行质量评价。在此基础上采用指数平滑法预测大沽河地下水源地水质时空变化,为地下水资源管理规划提供依据。
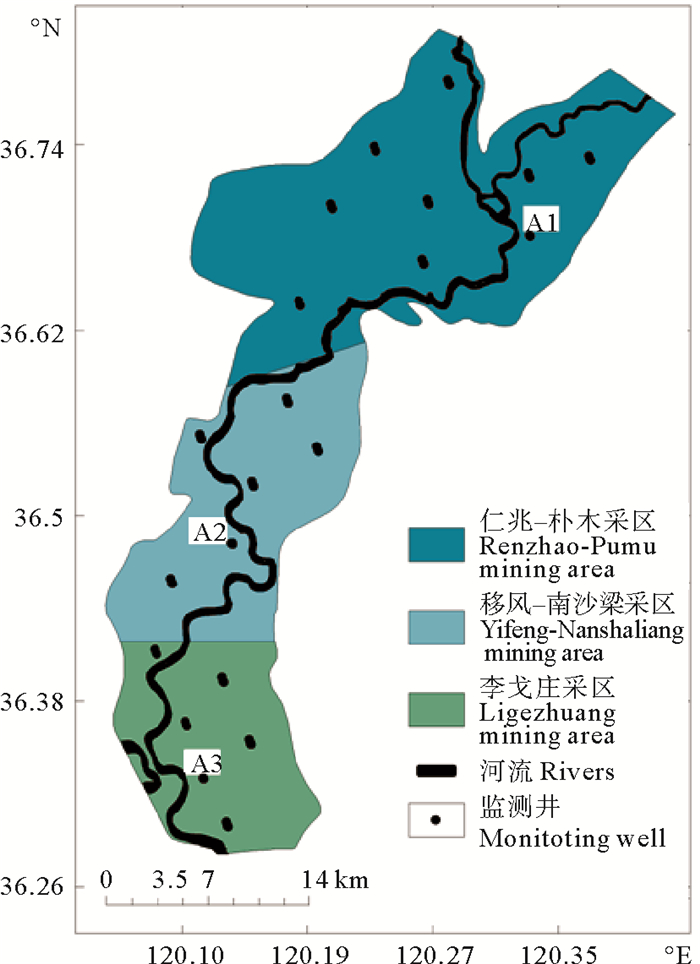
1 研究区的环境概况大沽河地下水水源地是青岛市主要的供水来源[18],位于大沽河流域的中下部,地理坐标为120°04′48″E~120°21′00″E,36°18′00″N~36°45′45″N,区域总面积460 km2(见图 1)。
|
图 1 青岛市大沽河地下水源地监测井位置图 Fig. 1 Location of monitoring wells in the Dagu River watershed in Qingdao |
研究区属于温带季风性气候,受海洋影响较大,具有较明显的海洋气候特征。多年平均气温为12 ℃,年温差小于50 ℃。降水量年际分布不均,多年平均降水量为650.5 mm,多年平均蒸发量为960.35 mm。
该区含水层由第四系冲积-冲洪积层下部的砂和砂砾石组成,属于潜水含水层,盖层以粘质砂土或砂质粘土为主,为地表补给地下水创造了条件;下覆底层主要是白垩系王氏组粉砂岩、砂砾岩和粘土岩,其透水性差,可以成为良好的隔水底板和边界,有助于储蓄地下水。含水层的平面形态在古河道的影响下呈狭长条带状,宽度为5~7 km,平均厚度为5.19 m,在纵向上,厚度从南到北呈下降趋势,在横向上,古河谷中心位置厚而两侧薄。
研究区地下水补给以大气降水补给为主,除此之外还有河流和橡胶坝入渗补给、侧向地下径流补给等;地下水排泄方式主要是人工开采和蒸发。
研究区中部和北部种植大量蔬菜作物,对施加的肥料(尤其是氨肥)吸收较少,加上畜禽养殖业发展带来的垃圾粪便下渗,造成地下水中硝酸盐污染严重;此外研究区内生产和生活产生的大量生活和工业污染物使Ca2+、Mg2+渗入地下水,而硝化作用引起地下水pH降低,从而促进Ca2+、Mg2+的溶解,使地下水中总硬度增加;研究区南部存在工业污染源,工业废水下渗入地下造成了地下水的污染。
本文以研究区2002—2017年监测井的地下水水质监测资料为原始数据(见图 1)。根据研究区水文地质条件和污染源分布的差异性,在3个开采区各取一个代表性监测点(A1、A2、A3监测点),进行了多年地下水水质评价,预测大沽河地下水源地未来的水质变化趋势。
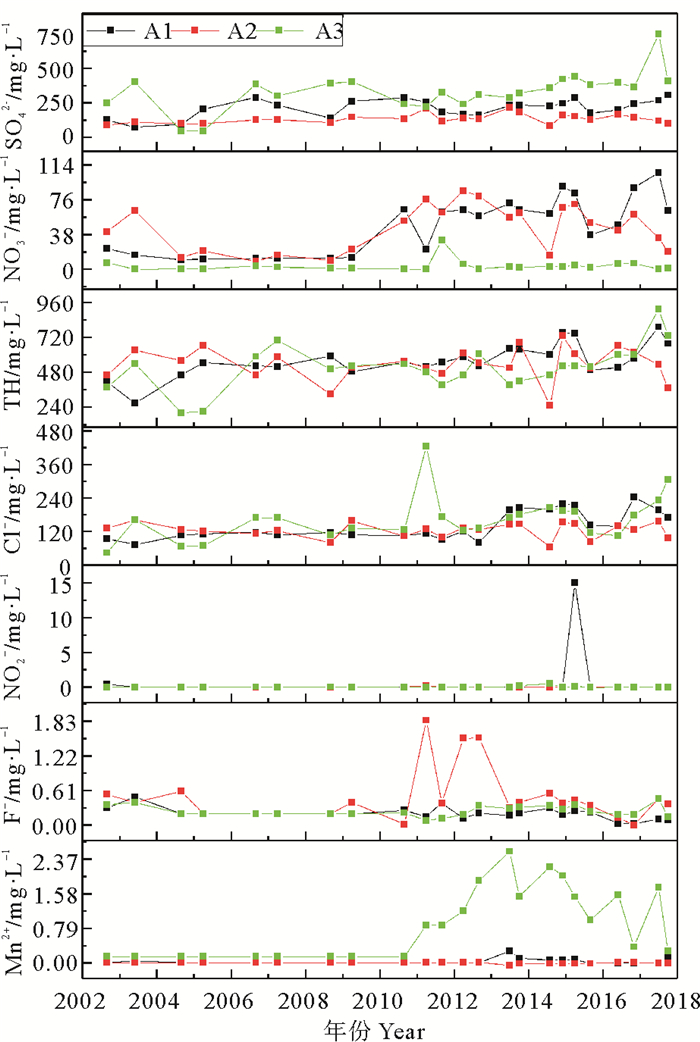
由于大沽河流域工农业活动以及海水入侵的影响,研究区地下水体部分水化学指标不断恶化[19]。本文选取超标严重且对水源地影响较大且各井位共有的指标作为评价指标,分别为硫酸盐、硝酸盐、总硬度、氯化物、亚硝酸盐、氟化物和锰离子[20]。在其中选取超标严重的硫酸盐、硝酸盐、总硬度和氯化物作为预测指标。水质监测资料由青岛市水环境监测中心提供(见图 2)。
|
图 2 大沽河水源地3个开采区典型监测井水质动态变化 Fig. 2 Dynamic changes of water quality in three typical monitoring wells in the Dagu River watershed |
依据地下水水质评价的模糊性和不确定性[21],本文采用模糊综合评价法对大沽河地下水质量进行评价。模糊综合评价是以隶属度描述评价指标的实测值和标准等级的关系,从而对水质所作的综合评价。其建模的主要步骤为[22]:①建立模糊评价因子集U和评价集V;②确定模糊评价矩阵R;③确定评价指标权重矩阵A;④进行评价等级的确定。
2.1.1 因子集和评价集因子集是影响评价结果的各个指标的集合,通常用U表示,根据前述水质污染指标的确定,因子集为:
| $ \mathit{\boldsymbol{U}} = \left\{ {{\rm{SO}}_4^{2 - },{\rm{NO}}_3^ - ,{\rm{TH}},{\rm{C}}{{\rm{l}}^ - },{\rm{NO}}_2^ - } \right\}。$ | (1) |
评价集是水质标准等级的集合,用V表示。本文以《地下水质量标准》(GB/T 14848-2017)为评价标准,所以评价集为:
| $ \mathit{\boldsymbol{V}} = \left\{ {{\rm{I}},{\rm{II}}, {\rm{III}} ,{\rm{IV}},{\rm{V}}} \right\}。$ | (2) |
式(2)中Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ分别代表《地下水质量标准》(GB/T 14848-2017)中的Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ类水。
2.1.2 模糊关系矩阵的建立根据“降半梯形”[23]的隶属函数确定各评价指标的隶属度,进一步得到评价对象的单因素隶属度矩阵R。
| $ \mathit{\boldsymbol{R}} = \left| {\begin{array}{*{20}{l}} {{r_{11}}}&{{r_{12}}}&{{r_{13}}}&{{r_{14}}}&{{r_{15}}}\\ {{r_{21}}}&{{r_{22}}}&{{r_{23}}}&{{r_{24}}}&{{r_{25}}}\\ {{r_{31}}}&{{r_{32}}}&{{r_{33}}}&{{r_{34}}}&{{r_{35}}}\\ {{r_{41}}}&{{r_{42}}}&{{r_{43}}}&{{r_{44}}}&{{r_{45}}} \end{array}} \right|。$ | (3) |
式(3)中rij为评价因子ui对评价等级vj的隶属度。
2.1.3 权重矩阵的确定根据各评价指标对地下水水质类别影响程度的不同,对各个指标赋予不同的权重值,建立权重矩阵A。权重越大表明指标对水质污染影响越大。
在地下水质评价中,确定权重的方法一般有首尾比率法[24]、超标法和聚类权法等,传统模糊综合评价采用超标法,其原理是根据指标实测值对于各级水质标准均值的超标情况计算权重,突出实测浓度大的指标对水质的影响,容易导致个别指标影响总体评价[9]。采用聚类权法可弥补以上缺陷,综合考虑了各个等级标准值间的差异和水样的实测值,使结果更加客观合理, 计算公式为:
| $ {a_{ij}} = \frac{{{C_i}/{S_{ij}}}}{{\sum\limits_{i = 1}^n {{C_i}} /{S_{ij}}}}\left( {i = 1,2,3,4;j = 1,2,3,4,5} \right)。$ | (4) |
式中:aij为评价因子ui对评价等级vj的权重;Ci为评价因子ui的实测值;Sij为评价因子ui在评价等级vj的标准值。
2.1.4 模糊算子的选择评价结果向量B是由模糊关系矩阵R和权重矩阵A作复合运算得到的,传统模糊综合评价采用“取小取大型”算子,本文使用“相乘相加法”算子进行改进,二者公式分别为:
| $ {b_j} = \vee \left( {{a_{ij}} \wedge {r_{ij}}} \right), $ | (5) |
| $ {b_j} = \sum\limits_{i = 1}^4 {{a_{ij}}} {r_{ij}}。$ | (6) |
式中:∧为取小运算;∨为取大运算;bj为评价对象对应等级vj的综合隶属度。
传统方法中的算子属于主因素决定型算子,在决定水质评价结果的因素较多时,各个aij值会很小,通过取小运算会“泯灭”了单因素隶属度信息,而利用“加权平均型”的“相乘相加法”算子,可充分考虑所有因素的影响,合理地对水质进行综合评价[13]。
2.1.5 评价等级的判定传统模糊综合评价根据最大隶属原则判定评价等级,但此方法有时不能使用,当
| $ {b_{\max }} \le 0.5。$ | (7) |
本文引入级别特征值法判定结果向量,即将评价结果向量B的各分量乘以相应等级的秩,求和得到评价对象的的相对位置,该法利用了全部隶属度信息,其判断结论更符合实际情况。,计算公式为:
| $ H = \frac{{\sum\limits_{j = 1}^5 {b_j^k} \times j}}{{\sum\limits_{j = 1}^5 {b_j^k} }}。$ | (8) |
式中:H为评价对象的级别特征值;j的含义及取值与公式(4)相同。
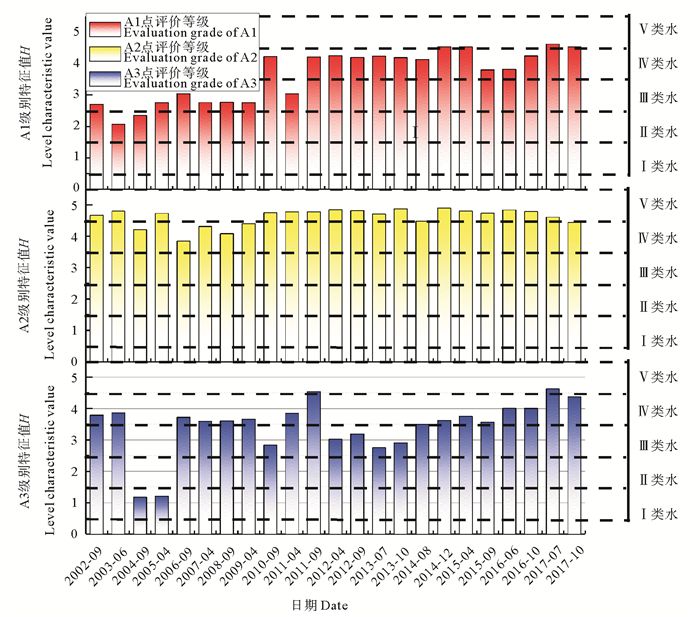
2.2 大沽河地下水源地水质评价和可靠性分析 2.2.1 地下水水质评价应用改进的模糊综合评价法对大沽河地下水水源地2002—2017年水质监测数据进行评价,得到级别特征值H,并进一步根据四舍五入法得到评价等级,评价结果见图 3。
|
图 3 大沽河水源地地下水质量评价结果图 Fig. 3 Evaluation results of groundwater quality in the Dagu River watershed |
由图可知,大沽河地下水源地仁兆-朴木采区(A1)2010年以前评价等级为Ⅱ类和Ⅲ类水,之后评价等级升高,超过地下水质量Ⅲ类标准,不能直接作为生活饮用水或其水源,说明该区水质状况较差并且在不断恶化,分析其原因为硝酸盐严重超标(2017年7月硝酸盐超过Ⅴ类标准2.52倍),相关部门要积极采取措施进行防治。
在大沽河地下水源地移风-南沙梁采区(A2),2002—2017年水质评价等级均较高,(Ⅳ类和Ⅴ类水),整体上评价等级值H高于仁兆-朴木采区(A1),说明该区地下水水质状况很差,主要是由于农业种植施加的氮肥下渗到地下水,引起硝酸盐的超标,造成了地下水的污染。
在大沽河地下水源地李戈庄采区(A3),2013年前水质评价等级波动较大,以Ⅱ类和Ⅳ类水居多,2014年后等级均为Ⅳ类和Ⅴ类水,且评价等级值H逐渐增大,说明近年来水质较差,分析原因为该区周围存在工业污染源,导致硫酸盐和氯化物浓度较高,但硝酸盐污染程度较低,整体水质状况变化不大。
2.2.2 评价模型的可靠性分析本文对传统模糊综合评价法进行了改进,使评价结果更加合理可靠。
在对大沽河地下水源地进行模糊综合评价中,部分监测井的最大隶属度小于0.5,不适用于传统模糊综合评价法,以大沽河水源地A1监测点2003年6月水质评价为例,归一化后的综合隶属度向量(0.147 5,0.373 4,0.455,0.024 1,0.0)中,最大隶属度为0.455,存在不适性问题。按照最大隶属度原则,该水质属于Ⅲ类水,但只考虑了最大隶属度的信息,本文采用级别特征值法得到的评价结果是Ⅱ类水,可以综合考虑所有隶属度的贡献,比传统方法更加合理可靠。
传统方法得到的评价结果为一固定的评价等级,对于等级相等的不同水样无法比较水质优劣,而改进的综合模糊评价法可克服此缺点。例如A2监测点,2016年11月和2017年7月水质评价等级均为Ⅴ类水,而改进方法得出其级别特征值分别为4.786和4.609,比较可知2017年7月水质更优,所以改进方法更具实用性。
从模糊综合评价结果来看,A2监测点所有评价等级均超过Ⅳ类水,水质状况最差,硝酸盐最高超过Ⅴ类水的2.52倍。实地调查显示该区蔬菜种植区占地最多,施加了大量氮肥,蔬菜对氮肥吸收率较低,而该区的水文地质条件有利于氮肥入渗,使大量氮肥渗入地下水,造成该区成为地下水污染最严重的区域。所以评价结果与实际污染状况相符合,进一步验证了本文使用的模糊综合评价模型的可靠性。
3 地下水水质变化的预测 3.1 地下水指数平滑预测模型采用指数平滑法进行大沽河地下水源地水质预测,指数平滑法是通过逐级计算平滑值构建预测模型的一种预测方法,在水质预测中的特点是既考虑了历年所有监测值对预测值的作用,又给予不同时期的监测值不同的权重,对近期数据给予较大的权重,远期数据给予较小的权重,
加强了近期数据对预测值的影响。指数平滑法预测水质的步骤为:平滑模型的确定、平滑模型构建、初始平滑值的确定、权系数的取值、水质预测。
本文以大沽河水源地3个开采区典型监测点的硫酸盐、硝酸盐、总硬度和氯化物为研究对象,首先依据2002—2015年实际监测值作为原始数据,对2016—2017年的水质指标进行短期预测,与实际监测值进行对比校正误差。在此基础上,预测未来十年(2019—2029年)地下水中水质指标的变化值。
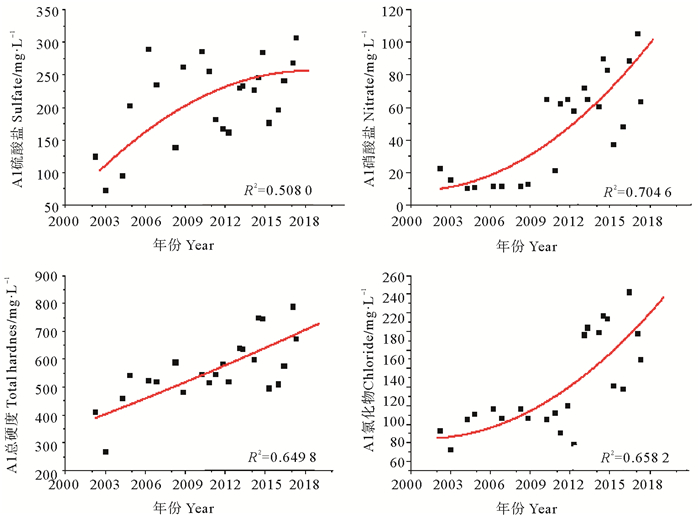
3.1.1 平滑预测模型的确定在地下水水质预测中,时间序列随着时间发展不断增加或减少,通过计算一次平滑值进行预测不够精确,需要进行二次平滑;若数据趋势为非线性时,要进行三次平滑[26]。本文对大沽河水源地三个监测点水质指标实测值进行曲线拟合,结果表明,二次曲线拟合效果较好(见图 4,5,6),所以本文选用三次指数平滑法进行预测模型的建立。
|
图 4 大沽河水源地A1点预测指标二次曲线拟合 Fig. 4 Conic fitting of the predicted index of A1 points in the Dagu River watershed |
|
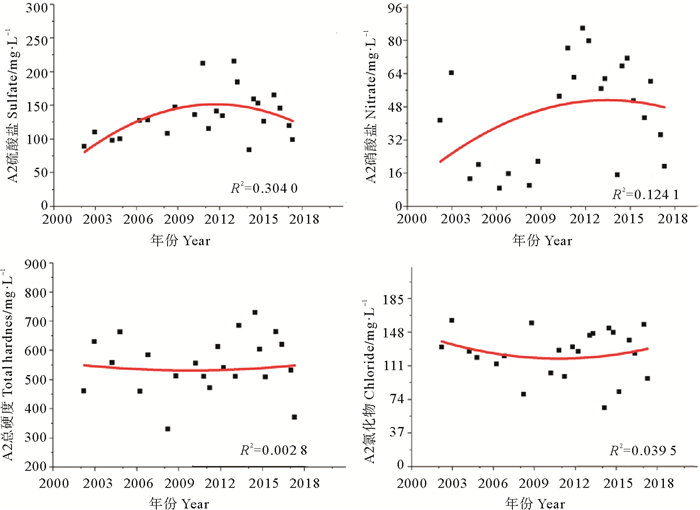
图 5 大沽河水源地A2点预测指标二次曲线拟合 Fig. 5 Conic fitting of the predicted index of A2 points in the Dagu River watershed |
|
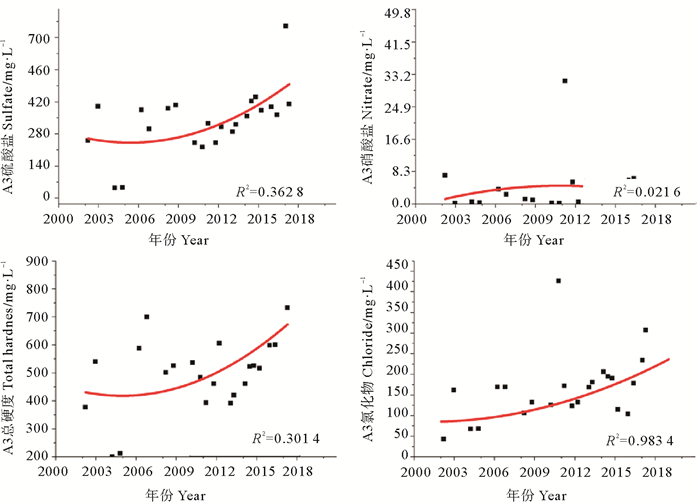
图 6 大沽河水源地A3点预测指标二次曲线拟合 Fig. 6 Conic fitting of the predicted index of A3 points in the Dagu River watershed |
首先给定一个权系数α,根据原始数据和前一级平滑值得到本级平滑值:
| $ {S_t} = \alpha {x_t} + \left( {1 - \alpha } \right){S_{t - 1}}。$ | (9) |
式中:St为t时刻的平滑值;xt为t时刻的实测值;St-1为t-1时刻的平滑值。
三次指数平滑值计算公式为:
| $ S_t^{\left( 1 \right)} = \alpha {x_t} + \left( {1 - \alpha } \right)S_{t - 1}^{\left( 1 \right)}, $ | (10) |
| $ S_t^{\left( 2 \right)} = \alpha S_t^{\left( 1 \right)} + \left( {1 - \alpha } \right)S_{t - 1}^{\left( 2 \right)}, $ | (11) |
| $ S_t^{\left( 3 \right)} = \alpha S_t^{\left( 2 \right)} + \left( {1 - \alpha } \right)S_{t - 1}^{\left( 3 \right)}。$ | (12) |
式中:St(1)、St(2)、St(3)分别为t时刻的第1次、第2次和第3次的平滑值。
根据上述计算得到的平滑值计算非线性预测模型参数,公式为:
| $ {a_t} = 3S_t^{\left( 1 \right)} - 3S_t^{\left( 2 \right)} + S_t^{\left( 3 \right)}, $ | (13) |
| $ {b_t} = \frac{a}{{2{{\left( {1 - \alpha } \right)}^2}}}\left[ {\left( {6 - 5a} \right)S_t^{\left( 1 \right)} - 2\left( {5 - 4a} \right)S_t^{\left( 1 \right)} + \left( {4 - 3a} \right)S_t^{\left( 3 \right)}} \right], $ | (14) |
| $ {c_t} = \frac{{{a^2}}}{{2{{\left( {1 - \alpha } \right)}^2}}}\left[ {S_t^{\left( 1 \right)} - 2S_t^{\left( 2 \right)} + S_t^{\left( 3 \right)}} \right]。$ | (15) |
式中at、bt、ct为模型参数,分别代表t时刻的期望值、线性增量、抛物线增量。
将模型参数代入非线性预测模型中即可进行水质预测,公式如下:
| $ {Y_{t + T}} = {a_t} + {b_t} * T + {c_t} * {T^2}。$ | (16) |
式中:T为t时刻到进行预测时刻的时间间隔;Yt+T为t+T时刻预测值。
3.1.3 起始平滑值的给定t时刻第i次平滑值Sti是由t-1时刻第i次平滑值Sit-1经过计算得到,而起始平滑值没有上一级平滑值,一般由经验给定,本文取起始监测值为起始平滑值[27]。
3.1.4 权系数α的取值α值决定了权数变化的快慢,对预测的合理性有直接影响。α的取值范围是0~1,取值一般由经验给定;若监测数据的时间序列波动很大,变化趋势明显,α值取较大的值;若时间序列变化较小,趋势稳定,α值在较小范围内取值[28]。根据经验选取的α值不够准确,本文使用试算法选取不同的α值,代入模型计算误差,从中选择误差最小时的α值,作为模型应用的α值。
3.1.5 指数平滑模型的验证预测结果存在误差,需要进行误差分析,从而验证指数平滑模型可靠性。每项评价指标的各个预测误差形成一个时间序列,判断该序列的随机性。若为随机序列,证明模型可靠;若不是随机序列,说明存在系统误差,则该模型预测结果不可靠。
判断时间序列是否有随机性的方法是卡方验证法。具体做法是:对于一组由n个误差值组成的时间序列,计算其前
| $ Q=n\sum\limits_{k=1}^{m}{r_{k}^{2}}。$ | (16) |
式中:rk为第k个自相关系数;m为自相关系数的个数,取
比较Q值与查表(卡方验证临界值表)得到的临界值x2。若Q值小于x2值,表示有95%置信度认为自相关系数与零没有显著性差异, 证明序列具有随机性,则该模型预测有效。
3.2 地下水源地水质预测和可靠性分析 3.2.1 预测模型可靠性分析本文选取2002—2015年的水质监测数据作为预测的初始资料,2015—2017年的监测数据作为误差验证的资料,原因是监测数据波动较大的情况多发生在2016年前(如A1点硝酸盐在2010年突增,氯化物在2013年增长幅度较大),而在2016—2017年水质指标的监测值变化趋势较稳定。在原始数据波动较大的情况下,利用趋势稳定的数据验证模型较为可靠,且预测准确率高。
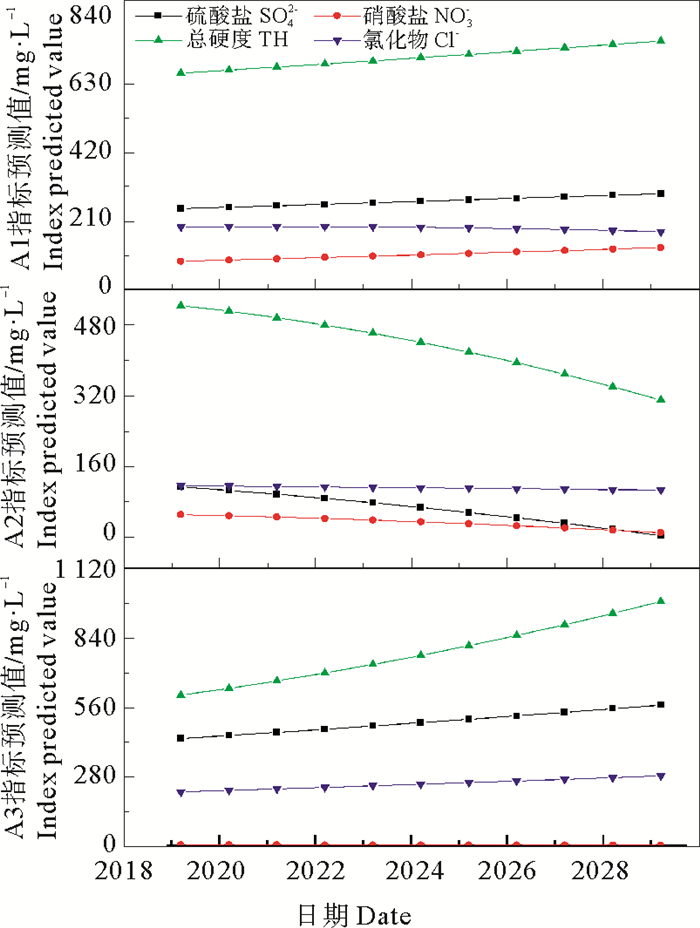
指数平滑模型预测结果见图 7,对2016—2017年预测结果进行验证,预测值及误差见图 8,根据卡方检验,查表得,自由度df=n-1=3,显著性水平α=0.05的临界值x2为7.815,计算得出的统计值Q值小于x2,所以有95%置信度认为误差值构成的时间序列是随机序列,预测误差为随机误差,该模型是可靠的,可应用于地下水水质预测。
|
图 7 大沽河水源地水质预测结果图 Fig. 7 Forecast results of water quality in Dagu River headwaters |
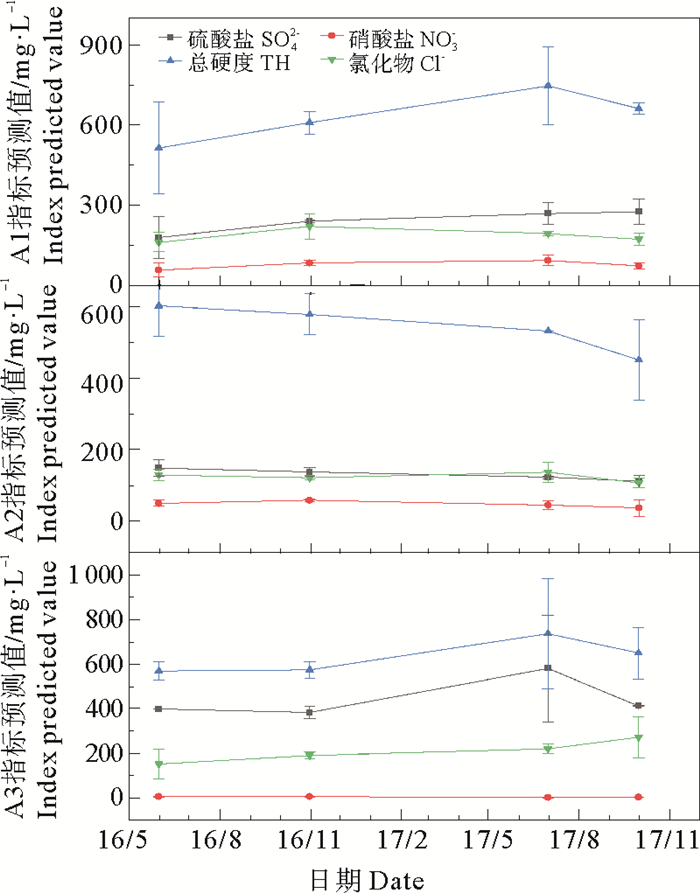
|
图 8 大沽河水源地2016—2017年预测误差图 Fig. 8 Forecast error chart of Dagu River water source in 2016—2017 |
指数平滑预测模型中误差产生的原因是多方面的。首先,地下水中物质在含水层中存在迁移和扩散的运动。在此过程中,物质和岩石系统的相互作用受环境影响,环境条件的突变对物质的扩散、吸收等有很大影响,而指数平滑法未能充分考虑突变情况,可能造成一定误差;另外,在本文预测时间序列中,2002—2010年监测频率为每年1次,2010—2017年监测频率为每年2次,监测时间间隔差异会对预测结果有一定影响。
3.2.2 地下水水质变化的预测由图 5可以看出,大沽河地下水源地仁兆-朴木采区(A1)除氯离子外其余各项水质指标浓度呈上升趋势,说明该区水质不断恶化且主要原因是硝酸盐和总硬度浓度的持续增加。移风-南沙梁采区(A2)各项水质指标浓度呈下降趋势,自2019年开始硫酸盐和氯离子浓度均优于Ⅱ类标准,硝酸盐浓度预测到2025年6月优于Ⅴ类标准,总硬度自2024年开始优于Ⅲ类标准,说明地下水水质不断优化。李戈庄采区(A3)硫酸盐、总硬度和氯化物浓度呈上升趋势,2019年硫酸盐和氯化物预测结果高于A2点,说明该区硫酸盐和氯化物污染加剧。
4 结论(1) 针对传统模糊综合评价存在的问题,本文对评价方法的关键环节进行了改进,在权重确定中,采用聚类权法弥补传统超标法的不足之处,提高了合理性;模糊算子选择“相乘相加法”算子,均衡兼顾所有因素,避免了信息丢失;使用级别特征值法分析结果向量,解决了最大隶属原则的不适性问题。
(2) 将改进的模糊综合评价应用于大沽河地下水源地水质评价中,结果表明,研究区水质状况较差,尤其是仁兆-朴木采区,2012年起均为Ⅳ类和Ⅴ类水,水质不断恶化,硝酸盐含量超标严重,主要是由于农业生产活动中施加的大量氮肥渗入地下,造成了地下水污染。评价结果与实际水质状况相符合,说明构建的改进模糊综合评价法是可靠的,可以应用于其他地区的地下水质量评价中。
(3) 采用指数平滑法进行地下水水质预测,使用试算法确定权系数,简便而有效。基于2002—2017年大沽河地下水质数据集,利用卡方检验验证预测方法的有效性,并对研究区未来10年水质进行了预测。结果表明,仁兆-朴木采区和李戈庄采区水质不断恶化,尤其是仁兆-朴木采区,硝酸盐浓度持续上升,应引起警惕。
| [1] |
Li R, Zou Z, An Y. Water quality assessment in Qu River based on fuzzy water pollution index method[J]. Journal of Environmental Sciences, 2016, 50(12): 87-92.
(  0) 0) |
| [2] |
Sutadian A D, Muttil N, Yilmaz A G, et al. Using the Analytic Hierarchy Process to identify parameter weights for developing a water quality index[J]. Ecological Indicators, 2017, 75: 220-233. DOI:10.1016/j.ecolind.2016.12.043
(  0) 0) |
| [3] |
Liu W, Wu C, Liu S, et al. Evaluating remanufacturing industry of China using an improved grey fixed weight clustering method-a case of Jiangsu Province[J]. Journal of Cleaner Production, 2017, 142(4): 2006-2020.
(  0) 0) |
| [4] |
Qaderi F, Babanejad E. Prediction of the groundwater remediation costs for drinking use based on quality of water resource, using artificial neural network[J]. Journal of Cleaner Production, 2017, 161(10): 840-849.
(  0) 0) |
| [5] |
Liu L, Zhou J, An X, et al. Using fuzzy theory and information entropy for water quality assessment in Three Gorges region, China[J]. Expert Systems with Applications, 2010, 37(3): 2517-2521. DOI:10.1016/j.eswa.2009.08.004
(  0) 0) |
| [6] |
Wang W, Xu D, Chau K, et al. Assessment of river water quality based on theory of variable fuzzy sets and fuzzy binary comparison method[J]. Water Resources Management, 2014, 28(12): 4183-4200. DOI:10.1007/s11269-014-0738-4
(  0) 0) |
| [7] |
Xu S, Wang T, Hu S. Dynamic assessment of water quality based on a variable fuzzy pattern recognition model[J]. International Journal of Environmental Research and Public Health, 2015, 12(2): 2230-2248. DOI:10.3390/ijerph120202230
(  0) 0) |
| [8] |
傅金祥, 陈喆, 马兴冠, 等. 改良模糊综合评价法在水质评价中的应用[J]. 环境工程, 2011, 29(6): 120-123. FU Jin-Xiang, CHEN Zhe, MA Xing-Guan, et al. Application of improved fuzzy comprehensive evaluation[J]. Environmental Engineering, 2011, 29(6): 120-123. (  0) 0) |
| [9] |
李录娟, 邹胜章. 不同权重确定方法对地下水质量评价的影响研究[J]. 人民长江, 2014(23): 98-102. LI Lu-Juan, ZOU Sheng-Zhang. Tudy of influence of different weight determining methods on groundwater quality assessment[J]. Yangtze River, 2014(23): 98-102. (  0) 0) |
| [10] |
赵和平. 环境综合评价模糊数学方法中4个算子的比较[J]. 环保科技, 2001, 7(3): 28-32. ZHAO He-Ping. Comparison of four operators in fuzzy mathematics method of environmental comprehensive evaluation[J]. Environmental Protection and Technology, 2001, 7(3): 28-32. (  0) 0) |
| [11] |
谢非, 张永祥, 任仲宇, 等. 改进的模糊综合评价法在地下水水质评价中的应用[J]. 水资源与水工程学报, 2014(3): 125-128. XIE Fei, ZHANG Yong-Xiang, REN Zhongyu, et al. Application of method of improved fuzzy comprehensive evaluation in assessment of groundwater quality[J]. Journal of Water Resources and Water Engineering, 2014(3): 125-128. (  0) 0) |
| [12] |
陈守煜. 工程模糊集理论与应用[M]. 北京: 国防工业出版社, 1998. CHEN Shou-Yu. Engineering Fuzzy Set Theory and Application[M]. Beijing: National Defense Industry Press, 1998. (  0) 0) |
| [13] |
马玉杰, 郑西来, 李永霞, 等. 地下水质量模糊综合评判法的改进与应用[J]. 中国矿业大学学报, 2009, 38(5): 143-148. MA Yu-Jie, ZHENG Xi-Lai, LI Yong-Xia, et al. Improvement and application of fuzzy synthetic evaluation of groundw ater quality[J]. Journal of China University of Mining & Technology, 2009, 38(5): 143-148. (  0) 0) |
| [14] |
Bauer P, Gumbricht T, Kinzelbach W. A regional coupled surface water/groundwater model of the Okavango Delta, Botswana[J]. Water Resources Research, 2006, 42(4): W4403.
(  0) 0) |
| [15] |
Kayacan E, Ulutas B, Kaynak O. Grey system theory-based models in time series prediction[J]. Expert Systems with Applications, 2010, 37(2): 1784-1789. DOI:10.1016/j.eswa.2009.07.064
(  0) 0) |
| [16] |
Cho K H, Sthiannopkao S, Pachepsky Y A, et al. Prediction of contamination potential of groundwater arsenic in Cambodia, Laos and Thailand using artificial neural network[J]. Water Research, 2011, 45(17): 5535-5544. DOI:10.1016/j.watres.2011.08.010
(  0) 0) |
| [17] |
Sbrana G, Silvestrini A. Aggregation of exponential smoothing processes with an application to portfolio risk evaluation[J]. Journal of Banking & Finance, 2013, 37(5): 1437-1450.
(  0) 0) |
| [18] |
岳玲莉, 高会旺, 乔飞, 等. 大沽河入海口污染物浓度多时间尺度变化特征分析[J]. 中国海洋大学学报(自然科学版), 2017, 47(6): 8-16. YUE Ling-Li, GAO Hui-Wang, QIAO Fei, et al. Multi-time scale variations of pollutants in the estury of dagu river[J]. Periodical of Ocean University of China, 2017, 47(6): 8-16. DOI:10.16441/j.cnki.hdxb.20160205 (  0) 0) |
| [19] |
张焘.青岛大沽河干流地下水主要污染物的污染预测[D].青岛: 中国海洋大学, 2014. ZHANG Tao. Prediction of Main Pollutants in Groundwater of Dagu River in Qingdao[D]. Qingdao: Ocean University of China, 2014. (  0) 0) |
| [20] |
方运海, 郑西来, 彭辉, 等. 基于模糊综合与可变模糊集耦合的地下水质量评价[J]. 环境科学学报, 2018(2): 546-552. FANG Yun-Hai, ZHENG Xi-Lai, PENG Hui, et al. Groundwater quality evaluation based on fuzzy synthetic evaluation and variable fuzzy sets[J]. Acta Scientiae Circumstantiae, 2018(2): 546-552. (  0) 0) |
| [21] |
田景环, 邱林, 柴福鑫. 模糊识别在水质综合评价中的应用[J]. 环境科学学报, 2005, 25(7): 950-953. TIAN Jing-Huan, QIU Lin, CHAI Fu-Xin. Application of fuzzy recognition in comprehensive evaluation of water quality[J]. Acta Scientiae Circumstantiae, 2005, 25(7): 950-953. (  0) 0) |
| [22] |
Lu X W, Li L Y, Kai L, et al. Water quality assessment of Wei River, China using fuzzy synthetic evaluation[J]. Environmental Earth Sciences, 2010, 60(8): 1693-1699. DOI:10.1007/s12665-009-0303-2
(  0) 0) |
| [23] |
杨浩, 张国珍, 杨晓妮, 等. 基于模糊综合评判法的洮河水环境质量评价[J]. 环境科学与技术, 2016(s1): 380-386. YANG Hao, ZHANG Guo-Zhen, YANG Xiao-Ni, et al. Comprehensive evaluation on water environment quality of the tao river based on fuzzy comprehensive method[J]. Environmental Science & Technology, 2016(s1): 380-386. (  0) 0) |
| [24] |
吴东杰, 王金生, 丁爱中. 地下水质量评价中两种确定指标权重方法的比较[J]. 工程勘察, 2006(7): 17-22. WU Dong-Jie, WANG Jin-Sheng, DING Ai-Zhong. Comparison of two methods for determining index weight in groundwater quality evaluation[J]. Engineering Investigation, 2006(7): 17-22. (  0) 0) |
| [25] |
陈守煜. 工程模糊集理论与应用[M]. 北京: 国防工业出版社, 1998: 6-11. CHEN Shou-Yu. Engineering Fuzzy Set Theory and Application[M]. Beijing: National Defense Industry Press, 1998: 6-11. (  0) 0) |
| [26] |
张建成, 智荣. 内蒙古林业总产值预测—基于马尔科夫修正的三次指数平滑预测模型[J]. 林业经济, 2018(3): 35-41. ZHANG Jian-Cheng, Zhi Rong. Prediction on total output value of forestry industry in inner mongolia—Based on three order exponential smoothing prediction model under markov correction[J]. Forestry Economics, 2018(3): 35-41. (  0) 0) |
| [27] |
张晓红. 应用指数平滑法建立城市工业三废排放量预测模型[J]. 环境工程学报, 1994(3): 77-80. ZHANG Xiao-Hong. An index smoothing method was used to establish the emission prediction model of urban industrial waste[J]. Journal of Evironmental Engineering, 1994(3): 77-80. (  0) 0) |
| [28] |
董骁雄, 陈云翔, 蔡忠义, 等. 基于粗糙集理论修正的后续备件指数平滑预测方法[J]. 系统工程与电子技术, 2018, 40(4): 833-838. DONG Xiao-Xiong, CHEN Yun-Xiang, CAI Zhong-Yi, et al. Residual prediction method of subsequent spare parts based on exponential smoothing method and rough set theory[J]. Systems Engineering and Electronics, 2018, 40(4): 833-838. (  0) 0) |
2. Qingdao Geo-engineering Exploration Institute, Qingdao 266071, China;
3. The Key laboratory of Urban Geology and Underground Space Resources, Shandong Provincial Bureau of Geology and Mineral Resources, Qingdao 266100, China;
4. The Key Laboratory of Marine Environment and Geological Engineering of Shandong Province, Qingdao 266100, China
 2020, Vol. 50
2020, Vol. 50


