潜堤淹没于水下,不影响海岸景观,具有抵御波浪、防止岸线侵蚀等作用。半圆型潜堤的堤身为半圆型拱圈,具有稳定性好、适用软弱基础,构件受力性能好等优点。借鉴Jarlan[1]提出的开孔沉箱结构,对半圆型潜堤进行表面开孔,可以加强其对波浪能量的耗散作用,有效降低结构承受的波浪力。
日本于1990年代初在宫崎港建成了半圆型开孔防波堤的试验段,Tanimoto和Takahashi[2]建议利用修正后的合田公式计算半圆型防波堤的波浪力。1997年,我国在天津港设计建成了半圆型防波堤,采用合田公式修正后的经验公式计算结构波浪力;随后,在长江口深水航道治理工程中修建了半圆型导堤,并基于5阶斯托克斯波的数学模型分析和物理模型试验,提出了适用于半圆型潜堤的结构波浪力计算公式[3]。一些学者通过物理模型试验和数值模拟对半圆型潜堤的水动力特性进行了深入研究。Dhinakaran等[4]试验研究了半圆型开孔潜堤在随机波作用下的反射系数、波浪爬高及受力特性,建议结构的最优开孔率为11%。Knoll等[5]利用钢筋网制作半圆型开孔潜堤模型,试验研究了结构在不规则波作用下的受力特性。Forbes和Schwartz[6]以及Forbes[7]在不同水深和弗劳德数下研究了均匀流通过半圆型潜堤时的流动特性。Kasem和Sasaki[8]通过数值求解粘性流体运动方程,研究了波浪对半圆型潜堤的作用。Yuan和Tao[9]将数值分析结果与模型试验结果进行对比分析,总结了不同淹没状态下半圆型潜堤的受力特性,提出结构波浪力的简化计算公式。
除上述模型试验和数值分析外,Liu和Li[10]利用多极子展开法建立了波浪对半圆型开孔潜堤作用的精确解析解,利用线性开孔边界条件[11]描述波浪通过开孔板的能量损失(压力损失)。多极子展开法由Ursell[12]首先应用于求解水波问题,具有收敛性好、计算速度快的优点,可用于流体对水平圆柱、圆球、椭圆球等结构作用的解析求解。Ursell[12]通过在流场中布置奇点,建立了极坐标系下拉普拉斯方程的奇异解,并在此基础上推导了不同边界条件下的速度势表达式。Thorne[13]进一步采用更为简洁的方法得到了Ursell的结果。Martin[14]给出多极子方法中满足收敛条件的结构物面方程。Linton和McIver[15]对多极子展开法进行了比较系统全面的总结。
Liu和Li[10]在解析研究中采用线性开孔边界条件,求解过程中无法直接考虑波高变化对开孔板处能量损失的影响。本文在Liu和Li[10]的研究基础上,进一步采用非线性压力损失边界条件[16-18],利用多极子展开法建立波浪对半圆型开孔潜堤作用的新解析解,深入分析半圆型潜堤的水动力特性。本文所建立的新解析解及相应的分析结果可为工程设计提供重要参考。
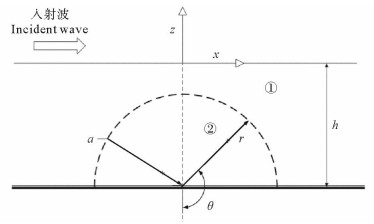
1 理论分析 1.1 控制方程和边界条件图 1为波浪对半圆型开孔潜堤作用的示意图。半圆型潜堤的半径为a,水深为h;波浪从左向右传播,波高为H,周期为T。以潜堤中垂线与静水面的交点为坐标原点,建立直角坐标系(x, o, z),以(0, -h)为原点建立极坐标系(r, θ),定义极轴垂直向下时θ=0。极坐标系与直角坐标系之间满足:rcosθ=-z+h,rsinθ=x。沿潜堤的半圆弧面将整个流域划分为两个部分,区域①为潜堤外部流场,区域②为潜堤内部流场。
|
图 1 波浪对半圆型开孔潜堤作用示意图 Fig. 1 Sketch of wave interaction with a submergedperforated semi-circular breakwater |
假定该流场内为无粘、无旋、不可压缩的理想流体,考虑线性规则波对结构的作用,速度势可以表示为:
| $ \Phi (x, z, t) = Re\left[ {\varphi (x, z){{\rm{e}}^{ - {\rm{i}}\omega t}}} \right]。$ | (1) |
其中:Re表示取实部;φ(x, z)表示与时间t无关的空间复速度势,
速度势满足拉普拉斯方程:
| $ \frac{{{\partial ^2}\varphi }}{{\partial {x^2}}} + \frac{{{\partial ^2}\varphi }}{{\partial {y^2}}} = 0。$ | (2) |
速度势还满足自由水面条件、水底条件和远场辐射条件:
| $ \frac{{\partial \varphi }}{{\partial z}} = 0, z = - h。$ | (3) |
| $ K\varphi + \frac{{\partial \varphi }}{{\partial z}} = 0, z = 0。$ | (4) |
| $ {\mathop {\lim }\limits_{x \to \pm \infty } \left( {\frac{\partial }{{\partial x}} \mp {\rm{i}}k} \right)\left( {\begin{array}{*{20}{c}} \varphi \\ {\varphi - {\varphi ^{\rm{I}}}} \end{array}} \right) = 0。} $ | (5) |
其中k为波数,满足K=ω2/g=ktanhkh(g为重力加速度);φI为入射波速度势,可以表示为:
| $ {\varphi ^{\rm{I}}} = - \frac{{{\rm{i}}\mathit{gH}}}{{2\omega }}\frac{{\cos \mathit{h}k(z + h)}}{{\cos \mathit{hkh}}}{{\rm{e}}^{{\rm{i}}kx}}。$ | (6) |
入射波速度势在极坐标系下可以表示为:
| $ {\varphi ^{\rm{I}}} = - \frac{{{\rm{i}}\mathit{gH}}}{{2\omega }}\frac{1}{{\cos \mathit{hkh}}}\left[ {\begin{array}{*{20}{c}} {\sum\limits_{n = 0}^\infty {\frac{{{{(kr)}^{2n}}}}{{(2n)!}}} \cos 2n\theta }\\ { + {\rm{i}}\sum\limits_{n = 1}^\infty {\frac{{{{(kr)}^{2n - 1}}}}{{(2n - 1)!}}} \sin (2n - 1)\theta } \end{array}} \right]。$ | (7) |
在潜堤的开孔半圆弧处,内外流场的法向速度连续:
| $ \frac{{\partial {\varphi _1}}}{{\partial r}} = \frac{{\partial {\varphi _2}}}{{\partial r}}, r = a。$ | (8) |
其中,下标1和2分别表示外部和内部流场内的变量。此外,流体运动满足非线性(二次)压力损失边界条件[16-18]:
| $ \begin{array}{l} {\varphi _2} - {\varphi _1} = - \frac{{8{\rm{i}}}}{{3{\rm{ \mathit{ π} }}\omega }}\frac{{1 - \varepsilon }}{{2\mu {\varepsilon ^2}}}\left| {\frac{{\partial {\varphi _2}}}{{\partial r}}} \right|\frac{{\partial {\varphi _2}}}{{\partial r}} - \\ \;\;\;\;\;\;\;\;\;2C\frac{{\partial {\varphi _2}}}{{\partial r}}, r = a。\end{array} $ | (9) |
其中:ε为半圆弧的开孔率(开孔面积与总面积的比值);μ为射流系数;C为开孔薄板的阻塞系数(Blockage coefficient)[19-20]。Molin[16]指出:通常情况下,射流系数μ在开孔率ε < 50%时约为0.3~0.4。Suh等[21]的研究表明,C可以表示为
| $ C = \frac{b}{{2\varepsilon }}。$ | (10) |
其中b为开孔薄板的厚度。
式(2)~(9)形成一个完整的边值问题,下面利用多极子展开方法进行求解。
1.2 速度势求解利用多极子展开法,流场中的复速度势可以写为对称解和反对称解之和。基于Liu和Li[10]的研究,区域①内的满足方程(2)~(5)的速度势φ1可以表示为:
| $ {\varphi _1} = {\varphi ^{\rm{I}}} + \frac{{ - {\rm{i}}gH}}{{2\omega }}\frac{1}{{\cos \mathit{hkh}}}\left[ {\begin{array}{*{20}{c}} {\sum\limits_{n = 1}^\infty {{a^{2n}}} c_n^ + \varphi _n^ + }\\ { + \sum\limits_{n = 1}^\infty {{a^{2n - 1}}} c_n^ - \varphi _n^ - } \end{array}} \right]。$ | (11) |
其中
| $ \varphi _n^ + = \frac{{\cos 2n\theta }}{{{r^{2n}}}} + \sum\limits_{m = 0}^\infty {A_{mn}^ + } {r^{2m}}\cos 2m\theta 。$ | (12) |
| $ \varphi _n^ - = \frac{{\sin (2n - 1)\theta }}{{{r^{2n - 1}}}} + \sum\limits_{m = 1}^\infty {A_{mn}^ - } {r^{2m - 1}}\sin (2m - 1)\theta 。$ | (13) |
| $ A_{mn}^ + = \frac{1}{{(2m)!(2n - 1)!}}\int_0^\infty {\frac{{(\mu + K){\mu ^{(2m + 2n - 1)}}{e^{ - \mu h}}}}{{\mu \sin h\mu h - K\cos \mathit{h\mu h}}}} {\rm{d}}\mu 。$ | (14) |
| $ \begin{array}{*{20}{l}} {A_{mn}^ - = \frac{1}{{(2m - 1)!(2n - 2)!}} \cdot }\\ {\int_0^\infty {\frac{{(\mu + K){\mu ^{(2m + 2n - 3)}}{e^{ - \mu h}}}}{{\mu \sin h\mu h - K\cos \mathit{h\mu h}}}} {\rm{d}}\mu 。} \end{array} $ | (15) |
上式中:cn+、cn-为未知待定系数;Amm+、Amm-中的积分路径从下方绕过奇点μ=k。
利用分离变量法,在区域②内满足方程(2)和(3)的速度势φ2可以写为:
| $ {\varphi _2} = - \frac{{{\rm{i}}gH}}{{2\omega }}\frac{1}{{\cos \mathit{hkh}}}\left[ {\begin{array}{*{20}{c}} {\sum\limits_{n = 0}^\infty {{r^{2n}}} d_n^ + \cos 2n\theta }\\ { + \sum\limits_{n = 1}^\infty {{r^{(2n - 1)}}} d_n^ - \sin (2n - 1)\theta } \end{array}} \right]。$ | (16) |
式中dn+、dn-为未知待定系数。
需要利用开孔半圆弧处的边界条件(8)和(9)来确定速度势中待定系数。根据Linton和McIver[15],利用加权积分和三角函数的正交性来求解待定系数的值。由于原速度势表达式为无穷级数,需要先取截断数M,使表达式变为有限项。将式(11)和(16)代入式(8)后,取正整数p=1, 2, 3,…,M,在式(8)两端分别乘以sin(2p-1)θ或cos2pθ,可以得到2M个方程;之后,在0.5π, 1.5π区间上对θ积分,消去θ及部分正交项,将方程简化。同理,将式(11)和(16)代入式(9)后,在式(9)两端分别乘以sin(2p-1)θ或cos2pθ,并在0.5π, 1.5π区间上对θ积分,可以再得到2M个方程。为使方程个数与待定系数相同,对式(9)在0.5π, 1.5π区间直接对θ积分,得到p=0时cos2pθ的加权方程。最后共得到以下4M+1个方程:
| $ \begin{array}{l} {\rm{i}}\frac{{{{(ka)}^{2p - 1}}}}{{(2p - 1)!}} - c_p^ - + \sum\limits_{n = 1}^M {{a^{2n + 2p - 2}}} c_n^ - C_{pn}^ - - \\ {a^{(2p - 1)}}d_p^ - = 0, p = 1, 2, 3, \cdots , M。\end{array} $ | (17) |
| $ \begin{array}{l} \frac{{{{(ka)}^{2p}}}}{{(2p)!}} - c_p^ + + \sum\limits_{n = 1}^M {{a^{2n + 2p}}} c_n^ + C_{pn}^ + - {a^{2p}}d_p^ + = 0\\ \;\;\;\;\;\;\;\;\;\;p = 1, 2, 3, \cdots , M。\end{array} $ | (18) |
| $ \begin{array}{*{20}{c}} {{a^{(2p - 1)}}d_p^ - \frac{{\rm{ \mathit{ π} }}}{2} - {\rm{ \mathit{ π} }}C \cdot (2p - 1) \cdot {a^{(2p - 2)}}d_p^ - = }\\ {\frac{{8{\rm{i}}}}{{3{\rm{ \mathit{ π} }}\omega }}\frac{{1 - \varepsilon }}{{2\mu {\varepsilon ^2}}}\int_{0.5{\rm{ \mathit{ π} }}}^{1.5{\rm{ \mathit{ π} }}} {\left| {\frac{{{\rm{i}}gH}}{{2\omega \cos \mathit{hkh}}} \cdot \frac{{\partial {{\varphi '}_2}}}{{\partial r}}} \right|} \frac{{\partial {{\varphi '}_2}}}{{\partial r}} \cdot \sin (2p - 1)\theta {\rm{d}}\theta }\\ {p = 1, 2, 3, \cdots , M。} \end{array}, $ | (19) |
| $ \begin{array}{l} \frac{{{{(ka)}^{2p}}}}{{(2p)!}}\frac{{\rm{ \mathit{ π} }}}{2} + c_p^ + \frac{{\rm{ \mathit{ π} }}}{2} + \sum\limits_{n = 1}^M {{a^{2n + 2p}}} c_n^ + C_{pn}^ + \frac{{\rm{ \mathit{ π} }}}{2} - \\ {a^{2p}}d_p^ + \frac{{\rm{ \mathit{ π} }}}{2} - {\rm{ \mathit{ π} }}C \cdot 2p \cdot {a^{(2p - 1)}}d_p^ + = \\ \frac{{8{\rm{i}}}}{{3{\rm{ \mathit{ π} }}\omega }}\frac{{1 - \varepsilon }}{{2\mu {\varepsilon ^2}}}\int_{0.5{\rm{ \mathit{ π} }}}^{1.5{\rm{ \mathit{ π} }}} {\left| {\frac{{{\rm{i}}gH}}{{2\omega \cos \mathit{hkh}}} \cdot \frac{{\partial {{\varphi '}_2}}}{{\partial r}}} \right|} \frac{{\partial {{\varphi '}_2}}}{{\partial r}} \cdot \cos 2p\theta {\rm{d}}\theta , \\ p = 0, 1, 2, \cdots , M。\end{array} $ | (20) |
其中:
| $ \left| {\frac{{\partial {{\varphi '}_2}}}{{\partial r}}} \right| = \left| {\begin{array}{*{20}{c}} {\sum\limits_{n = 1}^\infty 2 n \cdot {a^{2n - 1}}d_n^ + \cos 2n\theta }\\ { + \sum\limits_{n = 1}^\infty {(2n - 2)} \cdot {a^{(2n - 2)}}d_n^ - \sin (2n - 1)\theta } \end{array}} \right|。$ | (21) |
可以看出,式(19)和(20)中的
(1) 假设
(2) 将
(3) 利用新计算得到的
根据Liu和Li[10],多极子φn+和φn-的远场表达式为:
| $ {\varphi _n^ + \sim \frac{{{\rm{ \mathit{ π} i}}{k^{(2n - 1)}}\cos \mathit{hk}(z + h)}}{{2hN_0^2(2n - 1)!}}{{\rm{e}}^{ \pm {\rm{i}}kx}}, x \to \pm \infty 。} $ | (22) |
| $ {\varphi _n^ - \sim \pm \frac{{{\rm{ \mathit{ π} }}{k^{(2n - 2)}}\cos \mathit{hk}(z + h)}}{{2hN_0^2(2n - 2)!}}{{\rm{e}}^{ \pm {\rm{i}}kx}}, x \to \pm \infty 。} $ | (23) |
其中:N02=0.5[1+sinh2kh/(2kh)]。因此,反射系数CR和透射系数CT可以表示为:
| $ {C_R} = \left| {\begin{array}{*{20}{c}} {\sum\limits_{n = 1}^M {{a^{2n}}} c_n^ + \frac{{{\rm{i \mathit{ π} }}{k^{2n - 1}}}}{{2hN_0^2(2n - 1)!}}}\\ { - \sum\limits_{n = 1}^M {{a^{2n - 1}}} c_n^ - \frac{{{\rm{ \mathit{ π} }}{k^{2n - 2}}}}{{2hN_0^2(2n - 2)!}}} \end{array}} \right|。$ | (24) |
| $ {C_T} = \left| {\begin{array}{*{20}{c}} {1 + \sum\limits_{n = 1}^M {{a^{2n}}} c_n^ + \frac{{{\rm{i \mathit{ π} }}{k^{2n - 1}}}}{{2hN_0^2(2n - 1)!}}}\\ { - \sum\limits_{n = 1}^M {{a^{2n - 1}}} c_n^ - \frac{{{\rm{ \mathit{ π} }}{k^{2n - 2}}}}{{2hN_0^2(2n - 2)!}}} \end{array}} \right|。$ | (25) |
能量损耗系数CL=1-CR2-CT2。
根据线性伯努利方程,流场内任意点的动水压强可以写为:
| $ p(x, z) = i\rho \omega \varphi (x, z)。$ | (26) |
将动水压强沿结构物表面积分,可以得到波浪力。水平向波浪力为:
| $ {F_x} = {\rm{i}}\rho \omega \int\limits_{0.5{\rm{ \mathit{ π} }}}^{1.5{\rm{ \mathit{ π} }}} {\left[ {{\varphi _2}(a, \theta ) - {\varphi _1}(a, \theta )} \right]a\sin \theta {\rm{d}}\theta } 。$ | (27) |
垂向波浪力Fz包括两部分,即潜堤半圆弧面所受的力Fz1和底板所受的力Fz2:
| $ {F_z} = {F_{z1}} + {F_{z2}}; $ | (28) |
| $ {F_{z1}} = {\rm{i}}\rho \omega \int\limits_{0.5{\rm{ \mathit{ π} }}}^{1.5{\rm{ \mathit{ π} }}} {\left[ {{\varphi _2}(a, \theta ) - {\varphi _1}(a, \theta )} \right]a( - \cos \theta ){\rm{d}}\theta } 。$ | (29) |
| $ {F_{z2}} = - 2{\rm{i}}\rho \omega \int\limits_0^a {{\varphi _2}\left( {r, \frac{\pi }{2}} \right){\rm{d}}r} 。$ | (30) |
根据解析研究结果,确定截断数M后,可通过式(17)~(20)构成的非线性方程组求解速度势表达式中的展开系数,进而计算半圆型开孔潜堤在波浪作用下的各项水动力参数。随截断数M的增加,需要确认本文解析解是否能够收敛。表 1和2列出了无因次波数kh不同时,半径分别为a=0.6h和a=0.8h的半圆型开孔潜堤在不同截断数M下的反射系数CR。在算例中迭代精度取10-4,波高H=0.1h,开孔率ε=20%,开孔薄板的厚度b=0.03h,射流系数μ=0.35,阻塞系数C通过式(10)进行计算。可以看到,当M=6时CR在10-4的精度范围内达到收敛要求。因此,在后文计算中均取截断数M=6。
|
|
表 1 不同截断数M下潜堤反射系数CR计算结果(a=0.6h) Table 1 Reflection coefficient CR with different truncation numberM (a=0.6h) |
|
|
表 2 不同截断数M下潜堤反射系数CR计算结果(a=0.8h) Table 2 Reflection coefficient CR with different truncation numberM (a=0.8h) |
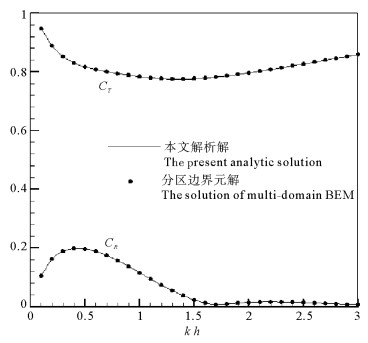
将本文解析解的水动力参数计算结果与Liu和Li[20]所建立的分区边界元方法的数值计算结果进行了对比。图 2给出了半圆型开孔潜堤的反射系数CR和透射系数CT在以上两种方法中的计算结果,计算条件为:半径a=0.7h,波高H=0.1h,开孔率ε=20%,板厚b=0.03h,射流系数μ=0.35。分区边界元方法中将流场边界离散为2 300个边界单元(直线段),计算结果收敛。图 2中曲线代表本文解析解的计算结果,点代表分区边界元方法的计算结果。可以看出:两种不同方法的计算结果一致,表明本文解析解的求解过程是正确的。
|
图 2 本文解析解与分区边界元解[20]的对比 Fig. 2 Comparison between the present analytic solution and the solution of multi-domain BEM[20] |
本节通过算例分析,研究半径a和开孔率ε这两个主要参数对半圆型开孔潜堤水动力特性的影响,计算条件为:板厚b=0.03h,射流系数μ=0.35,波高H=0.05h。
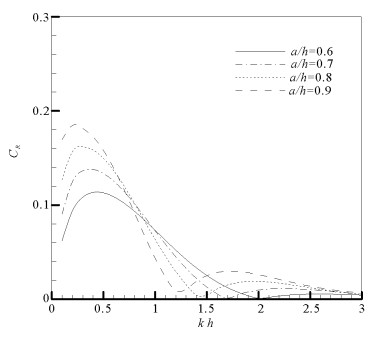
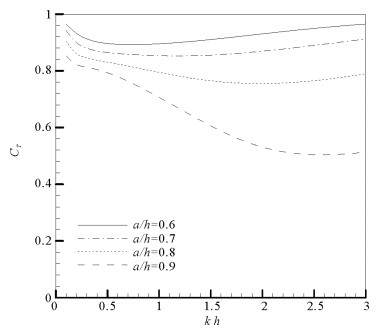
3.1 半径a的影响图 3和4分别给出了半圆型开孔潜堤的相对半径a/h对反射系数CR和透射系数CT的影响,计算中取开孔率ε=20%。从图 3可以看出:随着无因次波数kh的增大,潜堤的反射系数CR先增大后减小,在kh=0.5左右达到最大值;随着a/h的增大,CR的最大值不断增大。从图 4可以看出:随着波数的增大,潜堤透射系数CT先减小后增大;随着a/h的增大,透射系数CT显著减小,并且这一趋势在波数较大时更为明显。这说明在水深恒定时,增大潜堤半径可以显著减小波浪透射,提高潜堤的掩护效果。
|
图 3 潜堤相对半径a/h对CR的影响(ε=20%) Fig. 3 Effect of the relative radius a/h on CRof breakwater |
|
图 4 潜堤相对半径a/h对CT的影响(ε=20%) Fig. 4 Effect of the relative radius a/h on CT of breakwater |
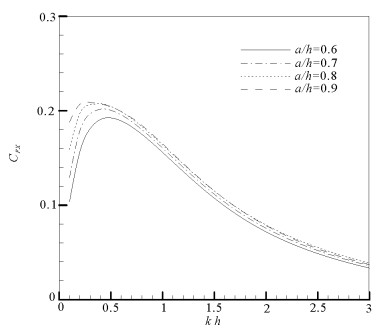
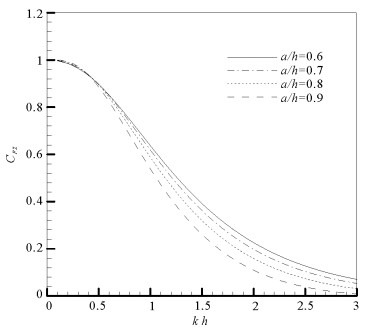
图 5和6给出半圆型开孔潜堤的相对半径a/h对结构所受波浪力的影响,计算条件与图 3和4相同。图中,CFx=Fx/ρgHa和CFz=Fz/ρgHa分别表示水平方向和垂向的无因次波浪力。由图 5可以看出:随着波数的增大,潜堤所受水平波浪力先增大后减小,在kh=0.7左右达到最大值;随着a/h的增大,潜堤所受水平波浪力的最大值小幅增加。由图 6可知:随着波数的增加,潜堤所受垂向波浪力显著减小;随着a/h的增大,潜堤所受垂向波浪力不断减小。对比图 5和6可以看出,对于较长周期波(波数较小),潜堤的垂向波浪力明显大于水平波浪力;随着波数的增大,二者在数值上的差距不断缩小。
|
图 5 潜堤相对半径a/h对CFx的影响(ε=20%) Fig. 5 Effect of the relative radius a/h on CFx of breakwater |
|
图 6 潜堤相对半径a/h对CFz的影响(ε=20%) Fig. 6 Effect of the relative radius a/h on CFz of breakwater |
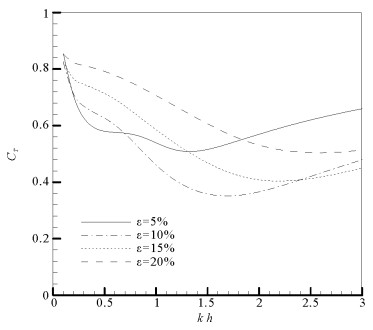
图 7和8分别表示半圆型潜堤开孔率ε对潜堤反射系数CR和透射系数CT的影响,计算条件为a=0.9h。从图 7可看出:随着ε的增大,潜堤的反射系数CR不断递减;当开孔率ε从5%增加到20%时,CR的最大值从0.5降低到0.2左右。这说明在潜堤表面开孔可以显著降低堤前反射波高。从图 8可以看到:随着ε的增大,潜堤的透射系数CT先减小后增大,存在一个透射系数最低的最优开孔率。这是因为:当开孔率很小时,总开孔面积很小,潜堤对波浪能量的耗散作用较弱;如果开孔率非常大,潜堤的半圆弧面对流场的影响非常小,能量耗散也非常小。在实际工程中,合理选择开孔率,可以有效提高潜堤的掩护效果。根据图 8的计算结果,当kh < 2时,推荐开孔率为10%~15%。
|
图 7 潜堤开孔率ε对CR的影响(a=0.9h) Fig. 7 Effect of porosity ε on CR of breakwater |
|
图 8 潜堤开孔率ε对CT的影响(a=0.9h) Fig. 8 Effect of porosity ε on CT of breakwater |
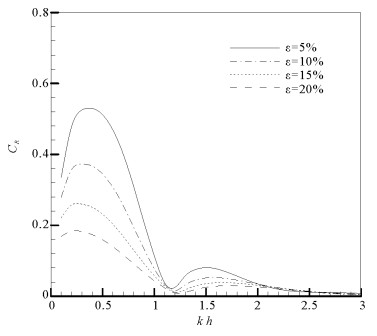
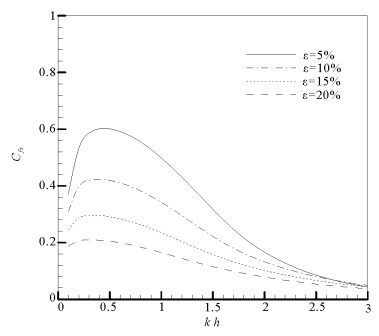
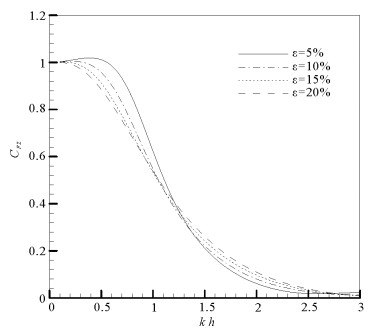
图 9和10给出半圆型潜堤开孔率ε对结构所受波浪力的影响,图中CFx和CFz的定义与图 5和6相同,计算条件与图 7和8相同。根据图 9,随着开孔率ε的增大,水平波浪力CFx显著减小,当开孔率ε从5%增加到20%时,CFx的最大值从0.6减小到0.2。这说明在半圆型潜堤表面开孔可以显著降低潜堤所受水平向波浪力,提高潜堤的稳定性。对比图 10和9可以看出:与水平波浪力不同,垂向波浪力CFz受开孔率变化的影响较小。
|
图 9 潜堤开孔率ε对CFx的影响(a=0.9h) Fig. 9 Effect of porosityεon CFx of breakwater |
|
图 10 潜堤开孔率ε对CFz的影响(a=0.9h) Fig. 10 Effect of porosity ε on CFz of breakwater |
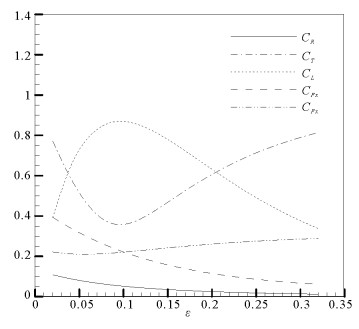
为进一步研究开孔率ε对半圆型开孔潜堤水动力特性的影响规律,图 11直接给出潜堤水动力参数随开孔率ε的变化曲线,图中计算条件为:kh=1.5,a/h=0.9。可以看到,当ε=10%左右,能量损耗系数CL达到最大值,透射系数CT达到最小值(掩护效果最好),这与图 8中的分析结果相符,也与Dhinakaran等[4]的试验研究结果基本一致。
|
图 11 潜堤开孔率ε对水动力参数的影响(kh=1.5,a/h=0.9) Fig. 11 Effect of porosity ε on the hydrodynamic coefficients of breakwater |
本文基于势流理论,利用多极子展开法和分离变量法,建立了波浪对半圆型开孔潜堤作用的解析解。解析解中引入了非线性压力损失边界条件,从而可以直接考虑波高变化对开孔板处能量损耗的影响。本文解析解为级数解,具有很好的收敛性。本文解析解的计算结果与分区边界元方法的计算结果一致。算例分析表明:增大半圆型开孔潜堤的半径会增大潜堤的反射系数,降低潜堤的透射系数,在工程设计中应根据波浪条件,合理选择较大的潜堤半径;增大半圆型开孔潜堤的开孔率可以显著降低潜堤的反射系数和水平波浪力,但是对潜堤垂向波浪力影响较小;为了达到良好的消浪、掩护效果,当kh < 2时,半圆型开孔潜堤的推荐开孔率为10%~15%。
| [1] |
Jarlan G E. A perforated vertical wall breakwater[J]. The Dock and Harbour Authority, 1961(486): 394-398.
(  0) 0) |
| [2] |
Tanimoto K, Takahashi S. Design and construction of caisson breakwaters-the Japanese experience[J]. Coastal Engineering, 1994, 22(1-2): 57-77. DOI:10.1016/0378-3839(94)90048-5
(  0) 0) |
| [3] |
谢世楞. 半圆形防波堤的设计和研究进展[J]. 中国工程科学, 2000, 2(11): 35-39. Xie Shileng. Progress in design and study of semi-circular breakwaters[J]. Engineering Science, 2000, 2(11): 35-39. (  0) 0) |
| [4] |
Dhinakaran G, Sundar V, Sundaravadivelu R, et al. Hydrodynamic characteristics of seaside perforated semicircular breakwaters due to random waves[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2008, 134(4): 237-251. DOI:10.1061/(ASCE)0733-950X(2008)134:4(237)
(  0) 0) |
| [5] |
Knoll A B. Laboratory Measurements of Wave Forcing and Reactions on a Model Submerged Mesh Breakwater[D]. Texas: Texas A & M University, 2014.
(  0) 0) |
| [6] |
Forbes L K, Schwartz L W. Free-surface flow over a semicircularobstruction[J]. Journal of Fluid Mechanics, 1982, 114: 299-314. DOI:10.1017/S0022112082000160
(  0) 0) |
| [7] |
Forbes L K. Critical free-surface flow over a semi-circularobstruction[J]. Journal of Engineering Mathematics, 1988, 22(1): 3-13.
(  0) 0) |
| [8] |
Kasem T H M A, Sasaki J. Numerical modeling and experimental visualization of wave propagation over semicircular obstacles[C].//The Twentieth International Offshore and Polar Engineering Conference. [s.l.]: International Society of Offshore and Polar Engineers, 2010.
(  0) 0) |
| [9] |
Yuan D, Tao J. Wave forces on submerged, alternately submerged, and emerged semicircular breakwaters[J]. Coastal Engineering, 2003, 48(2): 75-93.
(  0) 0) |
| [10] |
Liu Y, Li H J. Analysis of wave interaction with submerged perforated semi-circular breakwaters through multipole method[J]. Applied Ocean Research, 2012, 34: 164-172. DOI:10.1016/j.apor.2011.08.003
(  0) 0) |
| [11] |
Yu X. Diffraction of water waves by porousbreakwaters[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1995, 121(6): 275-282. DOI:10.1061/(ASCE)0733-950X(1995)121:6(275)
(  0) 0) |
| [12] |
Ursell F. Surface waves on deep water in the presence of a submerged circular cylinder. I[C]. //Mathematical Proceedings of the Cambridge Philosophical Society. Cambridge: Cambridge University Press, 1950, 46(1): 141-152.
(  0) 0) |
| [13] |
Thorne R C. Multipole expansions in the theory of surface waves[C]. //Mathematical Proceedings of the Cambridge Philosophical Society. Cambridge: Cambridge University Press, 1953, 49(4): 707-716
(  0) 0) |
| [14] |
Martin P A. Urse1l's multipoles and the Rayleigh hypothesis[C]. //Proc. 6th Intl. Woods Hde, MA, USA: Workshop on Water Waves and Floating Bodies, 1991: 163-167.
(  0) 0) |
| [15] |
Linton C M, McIver P. Handbook of Mathematical Techniques for Wave/Structureinteractions[M]. Boca Raton: CRC Press, 2001.
(  0) 0) |
| [16] |
Molin B. Hydrodynamic modeling of perforated structures[J]. Applied Ocean Research, 2011, 33(1): 1-11. DOI:10.1016/j.apor.2010.11.003
(  0) 0) |
| [17] |
Molin B, Remy F. Inertia effects in TLD sloshing with perforated screens[J]. Journal of Fluids and Structures, 2015, 59: 165-177. DOI:10.1016/j.jfluidstructs.2015.09.004
(  0) 0) |
| [18] |
Liu Y, Li H J. Iterative multi-domain BEM solution for water wave reflection by perforated caissonbreakwaters[J]. Engineering Analysis with Boundary Elements, 2017, 77: 70-80. DOI:10.1016/j.enganabound.2016.12.011
(  0) 0) |
| [19] |
Tuck E O. Matching problems involving flow through smallholes[J]. Advances in Applied Mechanics, 1975, 15: 89-158. DOI:10.1016/S0065-2156(08)70056-5
(  0) 0) |
| [20] |
Kakuno S, Liu P L F. Scattering of water waves by vertical cylinders[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1993, 119(3): 302-322. DOI:10.1061/(ASCE)0733-950X(1993)119:3(302)
(  0) 0) |
| [21] |
Suh K D, Ji C H, Kim B H. Closed-form solutions for wave reflection and transmission by vertical slotted barrier[J]. Coastal Engineering, 2011, 58(12): 1089-1096. DOI:10.1016/j.coastaleng.2011.06.001
(  0) 0) |
 2020, Vol. 50
2020, Vol. 50


