2. 青岛海洋科学与技术试点国家实验室 海洋矿产资源评价与探测技术功能实验室,山东 青岛 266237;
3. 山东省地震局青岛地震台,山东 青岛 266071;
4. 哈尔滨工程大学水声工程学院,黑龙江 哈尔滨 150050
时频分析是利用时频联合密度函数来描述信号在时域和频域的能量密度或强度,并对其进行分析和处理的方法,经过多年的理论扩充,已经成为主流的地震资料处理技术[1]。从最初的傅里叶变换发展了短时傅里叶变换[2],之后又有各种小波变换[3],紧接着结合了之前的方法发展了S变换[4],并在这些方法基础上提出广义变换[5-6]和同步挤压变换[7-8],在地震资料处理[9]和地震属性提取领域取得了巨大成功[10-11]。然而这些常用的时频分析方法均属于线性时频分布,都是信号与其他函数进行褶积等运算,存在信息泄露问题且精度低于双线性时频分布方法。常用的双线性时频分布方法有魏格纳(Wigner)分布[12],与上述的几种方法相比,该类方法对于时频分析精度很高,但是该类方法存在的问题也非常明显,在时频谱上会受到能量密度重叠或者交叉的影响,从而难以完成对信号的有效识别[13]。在魏格纳分布方法的基础上,发展了Cohen类时频分布,该类中各种不同的方法在时间和频率的联合密度函数中加入了不同的核函数,但是这些函数差异较小,并且只适用于某种信号,不能适用于所有类型的信号[14]。为了解决这些问题,许多学者进行了研究和改善,提出了垂直于直径方向的高斯核函数[15],该方法提高了双线性时频分布方法在不同类型信号种的适用性,但是对信号在时间方向上的特征识别存在一些困难。之后,Jones和Baraniuk在该类方法的基础上对短时间时频特征函数进行了优化[16],提出了自适应的方法,增强了核约束并很好地保留了边缘近似,解决了径向高斯核时频分布是时频分析种的困难,对不同类型的信号具有很好的适用性。有许多学者对该方法进行分析和改进[17],并成功应用于地震属性的提取等地震资料解释工作中。
现阶段常用的时频分析方法在信噪分离过程中,主要使用阈值去噪法以及划分定义域充零法这两种方式。去噪后往往会出现假频、重构误差等局部噪音,并且无法保留原始数据的带宽,滤波后信噪比虽然有所提升但是并不具备真正意义的保幅性[18]。
本文所提方法是基于双线性高精度时频分析方法自适应核时频分析的改进算法。该方法能很好地根据AOK划分的信噪定义域特征,设计出最佳算子,该算子与地震信号褶积,有效信号对它无贡献,而干扰噪声在与检噪算子褶积后呈现较大的振幅,从而有效地将干扰噪声从信号中识别出来,并将其从原始记录中剔除,然后在使用内插因子恢复其波形,多次迭代求得最佳效果。实际储层资料处理结果表明,本文所提方法避免了传统时频线性滤波方法的混播效应和能量再分配问题,不需要均匀空间采样,能应用于具高假频的局部噪声,同时能保留数据带宽,实现真正意义的保幅处理。对于叠后数据可以准确地刻画地震信号的局部层次,高精度地识别和定位储层油气藏,实现了同时提高地震资料的信噪比与分辨率。
1 方法原理 1.1 自适应核时频分析方法基于双线性时频分析方法的信号时频特征函数可以表示为:
| $ A(\theta, \tau)=\int\limits_{-\infty}^{\infty} s^*\left(t-\frac{\tau}{2}\right) s\left(t+\frac{\tau}{2}\right) \mathrm{e}^{-j \theta t} \mathrm{~d} t。$ | (1) |
式中: *表示函数的共轭; θ和τ是时频特征函数中的参数。对函数A(θ, τ)进行二维傅里叶变换,可以得到:
| $ P(t, \omega)=\frac{1}{4 \pi^2} \int\limits_{-\infty}^{\infty} \int_{-\infty}^{\infty} A(\theta, \tau) {\mathit{\Phi}}(\theta, \tau) e^{-j \theta t-j \tau \omega} \mathrm{d} \theta \mathrm{d} \tau 。$ | (2) |
式中: P(t, ω)是双线性时频分析方法表示的时频谱,对时频特征函数加权的函数Φ(θ, τ)就是核。该类方法的就是通过改变加权函数Φ(θ, τ)到达分析信号时频特征的作用,保护时频特征函数中的有效部分,从而消除对能量密度重叠或者交叉部分的影响。
自适应核时频分布(Adaptive optimal-kernel, AOK)方法在双线性时频分析方法的基础上建立一个短时窗的时频特征函数和在加权函数中加入时间参数[19]。在一个短时窗内得到与时间相关的时频特征函数A(t; θ, τ)和Φ(t; θ, τ)。短时窗时频特征函数可以表示为:
| $ \begin{gathered} A(t ; \theta, \tau)=\int\limits_{-T}^T s^*\left(u-\frac{\tau}{2}\right) W^*\left(u-t-\frac{\tau}{2}\right) \cdot \\ s\left(u+\frac{\tau}{2}\right) W\left(u-t+\frac{\tau}{2}\right) \mathrm{e}^{-j \theta u} \mathrm{~d} u 。\end{gathered} $ | (3) |
式中: T表示时窗长度; W为时窗函数; |u|≤T; t为某一时刻时间。自适应核时频分布的时频谱可以表示为
| $ \begin{gathered} P_{\mathrm{AOK}}(t, \omega)= \\ \frac{1}{4 \pi^2} \int\limits_{-\infty}^{\infty} \int_{-\infty}^{\infty} A(t ; \theta, \tau) \Phi_{\text {opt }}(t ; \theta, \tau) \mathrm{e}^{-j \theta t-j\tau\omega} \mathrm{d} \theta \mathrm{d} \tau。\end{gathered} $ | (4) |
其中Φopt(t; θ, τ)是该时窗内通过式(5)—(7)计算得到的最优核函数。式(6)和(7)是计算过程中的约束条件,求解最优核函数的过程在极坐标系中实现。
| $ {{\mathop{\rm Max}\nolimits} _\mathit{\Phi }}\int\limits_0^{2\pi } {\int_0^\infty | } A(t;r, \mathit{\Psi })\Phi (t;r, \mathit{\Psi }){|^2}r{\rm{d}}r{\rm{d}}\mathit{\Psi }。$ | (5) |
| $ \mathit{\Phi }(t;r, \mathit{\Psi }) = \exp \left( { - \frac{{{r^2}}}{{2{\sigma ^2}(\mathit{\Psi })}}} \right)。$ | (6) |
| $ \begin{array}{l} \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\int_0^\infty | } \mathit{\Phi }(t;r, \mathit{\Psi }){|^2}r{\rm{d}}r{\rm{d}}\mathit{\Psi } = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {{\sigma ^2}} (\mathit{\Psi }){\rm{d}}\mathit{\Psi } \le \\ {a}。\end{array} $ | (7) |
将核函数和时频特征函数变换到极坐标系中,其中
式(6)表示核函数的在任意垂直于直径的方向都是高斯函数。式(7)中,a表示核函数Φ(t; r, Ψ)的体积,1 < a < 5。
1.2 基于自适应核时频分析的最佳滤波极坐标系中的短时窗时频特征函数的离散形式可以表示为:
| $ \begin{array}{l} {A_{\rm{p}}}(n;b, q) = {\left. {A(n, r, \mathit{\Psi })} \right|_{r = b\Delta r, \mathit{\Psi } = q\Delta \mathit{\Psi }}} = \\ {\left. {A(n;\theta , \tau )} \right|_{\theta = b\Delta r\mathit{cos}q\Delta \mathit{\Psi }, \tau = b\Delta r\mathit{sin}\Delta \mathit{\Psi }}}。\end{array} $ | (8) |
其中Δr和ΔΨ表示是极坐标系中的变量变化大小。
极坐标系中的最优核函数的离散形式可以表示为:
| $ \varphi_{\mathrm{p}}(n ; b, q)=\exp \left(\frac{-b^2 \Delta_r{ }^2}{2 \sigma_q^2}\right) 。$ | (9) |
其中σq是扩展函数,控制核函数的变化范围,可以表示为:
| $ {\sigma _q} = \sigma \left( {q{\Delta _\mathit{\Psi }}} \right)。$ | (10) |
所以首先需要进行扩展函数σq的计算,可以通过式(11)和(12)计算得到最优扩展函数
| $ \tilde{\sigma}(i)=\sigma(i)+\mu(i) \nabla f(i)。$ | (11) |
| $ \sigma(i+1)=\tilde{\sigma}(i) \frac{\sqrt{4 \pi^2 a / \Delta_{{\mathit{\Psi}}}}}{\|\tilde{\sigma}(i)\|}。$ | (12) |
式中: μ表示计算步长,始终大于0,一般情况下可以取1~2。
现有的处理方法无法同时兼顾信噪比与分辨率的提升目标,往往是通过各种方式的滤波过程提升信噪比,然后通过反褶积的手段达到提升分辨率的目的。但是实际地震记录反褶积过程中往往很难满足地震子波和反射系数的要求,难以取得较好效果。
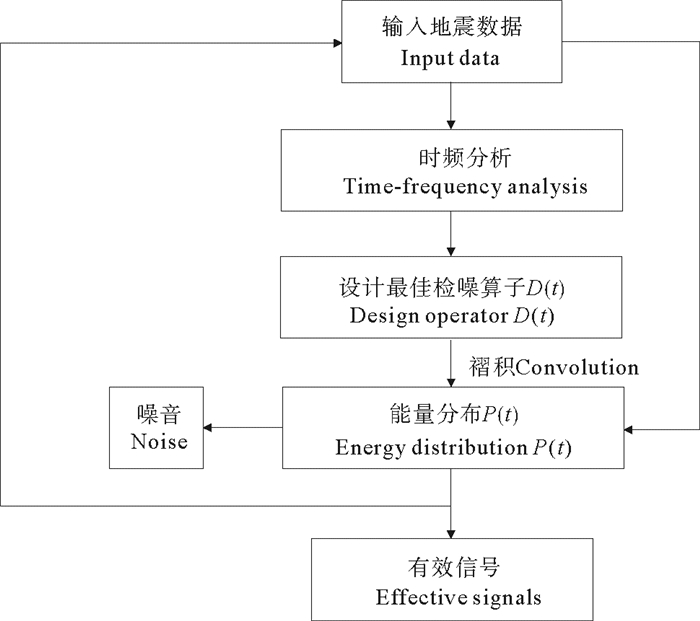
本文所提出的基于自适应核时频分析的最佳滤波方法的具体去噪流程(见图 1)如下:
|
图 1 基于自适应核时频分析的去噪流程 Fig. 1 The process denoising based on adaptive kernel time-frequency analysis |
(1) 利用自适应核对不同频带的时变地震信号进行时频分析,精确划分噪音与有效信号的分布范围;
(2) 根据信噪分布特征设计最佳检噪算子D(t)与内插算子I(t);
| $ D(t)=\frac{1}{f_{\mathrm{num}}}\left(\sum\limits_{f=f_{\min }}^{f_0} S(\tau, f)\right)。$ | (13) |
式中: S(τ, f)是地震记录时频谱,fnum是参与计算的频率点数。
(3) 在时空域中将原始信号与检噪算子褶积得到能量分布P(t);
(4) 取能量分布P(t)的绝对值并设振幅定门槛值,大于门槛值的能量判定为干扰;
(5) 将干扰与信号分离,并使用内插算子I(t)进行内插,拓宽有效信号的频带;
| $ \begin{aligned} I(t)= & {\left[\frac{\sin \pi \frac{t}{N \Delta}}{\pi \frac{t}{N \Delta}}\right] \Delta\left[\frac{\sin \pi\left(f_1+f_2\right) \Delta t}{\pi\left(f_1+f_2\right) \Delta t}\right] \cdot } \\ & \Delta\left[\frac{2 \sin \pi / 2\left(f_2-f_1\right) \Delta t}{\pi\left(f_2-f_1\right) \Delta t}\right]^2 。\end{aligned} $ | (14) |
式中: 采样间隔为Δ,N代表该点N个进行内插。
(6) 迭代上述过程直至获得最佳信号输出。
自适应核时频分析方法时频聚焦度比较高,但是需要频繁计算最优核函数,并且在计算最优核函数的过程中需要进行多次迭代,从而降低了计算效率。在进行时频谱分解时,在每个时间点都需要进行计算,非常影响时频分析的效率。因此为了能够更好地实现自适应最优核时频分析方法在实际地震资料分析中的应用,降低其运行时间是首要任务。
本文提出一种改进的自适应核时频分布方法,因为实际地震数据中,相邻道中的同相轴具有很强的相关性,因此采用中间地震道计算得到的时频特征函数和最优核函数代替其相邻地震道的方法,达到满足高效率自适应核时频方法的目的。
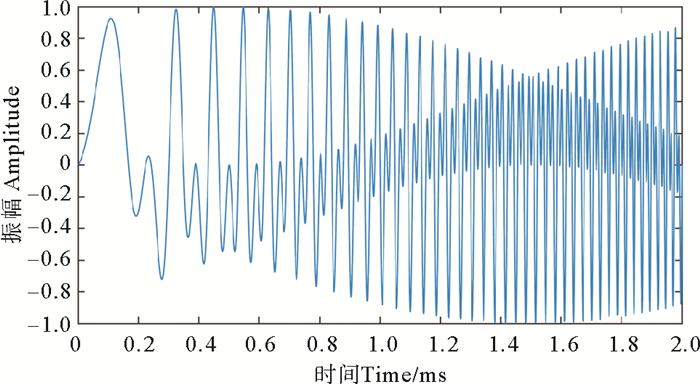
2 理论信号分析根据上述的理论知识,本文设计了一个线性调频信号,并分别使用魏格纳分布、小波变换、S变换、同步挤压变换和自适应核进行时频分析,对比分析五种时频分析方法的聚焦能力,并说明各种方法的特点。设计的信号是由频率变化为0.5~40 Hz和0.5~80 Hz信号叠加组成,采样频率为1 000 Hz,总记录长度为2 s,信号的频率随记录长度的增大变大,可以使用式(15)表示:
| $ f(t)=\sin (t \times(\pi+20 \pi t))+\sin (t \times(\pi+40 \pi t)) 。$ | (15) |
合成理论信号如图 2所示。对原合成信号分别使用魏格纳分布、高斯小波变换、S变换和自适应核进行时频分析,结果如图 3所示。如图 3(a)所示的时魏格纳分布时频谱,因为合成信号频率随着记录长度增大而变大,所以在时频谱上表现为两条清晰的能量线或者能量团,图 3(a)中可以清楚看到两条时频谱能量线,能量聚焦能力较强,但是明显受到严重能量密度重叠或者交叉的影响,在两条能量线中间存在着严重的干扰,对时频谱有效分析造成了困难。如图 3(b)所示的是高斯小波变换时频谱,在两条能量线中不存在严重的干扰,这也说明了线性时频分布不会受到能量密度重叠或交叉的影响,但是可以看到时频谱中的能量不均一,频率越大,能量越低,并且能量线也越粗,聚焦度较低,所以不能从时频谱中准确识别信号的时频特征。如图 3(c)所示的是S变换得到的时频谱,与小波变换相比,没有出现频率越大能量越低的问题,可以有效地从时频谱中识别信号的时频特征,但是同样存在频率越大能量线越粗的现象,S变换的聚焦能力也较差。如图 3(d)所示的是基于时频重分配思想及同步挤压变换的高精度时频分析方法同步挤压小波变换得到的时频谱,如图 3(e)所示的是自适应核时频分布得到的时频谱,可以明显看到消除了能量密度重叠或交叉造成的干扰,可以清晰看到两条能量线的存在,并且没有小波变换和S变换存在的频率变化能量线宽度同样变化的问题,自适应核具有很强的聚焦能力,可以从时频谱中对信号时频特征进行准确的识别。从合成理论信号中可以看出,由此可见,自适应核时频分布得到的时频谱具有高聚焦度,可以为非平稳信号时频分析提供有力帮助。
|
图 2 合成线性调频信号 Fig. 2 Synthesized signal |

|
( (a)魏格纳分布;(b)高斯小波变换;(c)S变换;(d)同步挤压小波变换;(e)自适应核。(a)Wigner Distribution Function; (b)Gaussian wavelet transform; (c)S transform; (d)Synchrosqueezing wavelet transform; (e)Adaptive kernel. ) 图 3 不同时频分析方法 Fig. 3 Different time frequency analysis method |
本文合成了两个模型数据来测试该方法的有效性。首先建立一个简单模型数据,如图 4(a)所示,并在模型数据上添加一定能量的随机噪音,如图 4(b)所示,图 4(c)是使用本文提出的方法去噪后的结果。该模型共有5个同相轴,有两组同相轴出现了交叉。该模型数据使用主频为25 Hz,采样频率为1 000 Hz的雷克子波。从图中可以看出,本文提出的方法可以有效地滤除随机噪音,在滤波结果剖面上恢复出原始同相轴的位置和能量,在差值剖面上没有有效同相轴的影子,初步证实该方法兼有去噪和保护有效信号的性能。

|
((a)合成地震数据;(b)含噪数据;(c)去噪数据。(a)Synthetic seismic data; (b)Seismic data with noise; (c)Seismic data denoised. ) 图 4 合成记录去噪结果的对比 Fig. 4 Denoised results of synthetic record |
然后建立另一个简单模型数据,如图 5(a)所示,图 5(b)是该方法提高分辨率的处理结果。该模型数据使用主频为25 Hz,采样频率为1 000 Hz的雷克子波。该模型共有7个同相轴,有两组同相轴因为地下反射层较薄,出现了重叠,分辨率较低,难以正确识别该地层。通过对比可以看出,使用该方法后同相轴变细,并且重叠的同相轴明显分开,地下纵向分辨率得到了显著提高,证实了该方法在提高分辨率和保护有效信号的有效性。

|
((a)合成地震数据;(b)提高分辨率的结果。(a)Synthetic seismic data; (b)Results using the proposed method. ) 图 5 合成地震记录提高分辨率的对比 Fig. 5 Improving resolution results of synthetic record |
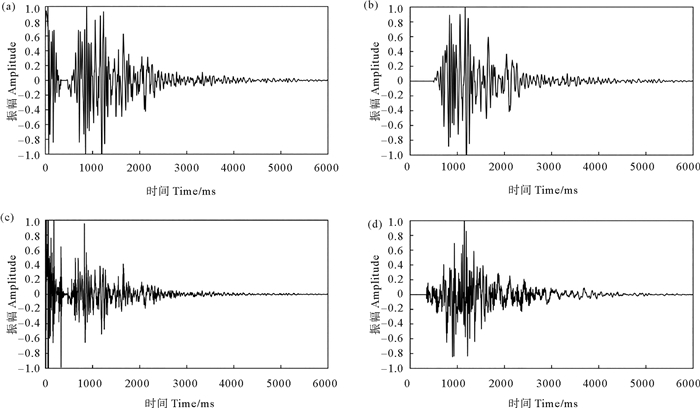
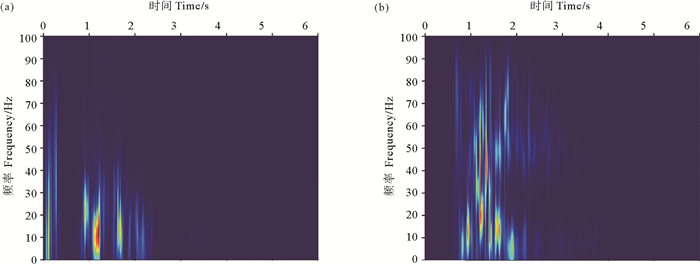
为了验证本文方法在实际地震资料中的应用效果,利用自适应核时频表示对某地区的地震资料进行处理,如图 6(a)所示的是该工区实际地震数据中的其中一道数据,分别使用FK滤波和脉冲反褶积对该数据进行处理,得到结果如图 6(b)和6(c)所示,使用本文提出的方法处理得到的数据如图 6(d)所示。通过对比可以看出,通过FK滤波可以提高数据的信噪比,但是分辨率明显降低,而通过脉冲反褶积方法可以提高分辨率,但是信噪比明显降低,特别是浅部的噪音产生了很大的影响。本文提出方法所对应的时频谱如图 7所示,不管是在浅层还是深部的噪音都得到了很好的压制,地震记录中的有效信号得到了突出,分辨率也得到了明显的提高。
|
((a)原始地震数据;(b)FK滤波;(c)脉冲反褶积;(d)本文方法处理后数据。(a)Original seismic data; (b)FK filter; (c)Spiking deconvolution; (d)Seismic data processed with the proposed method. ) 图 6 实际资料处理单道处理结果 Fig. 6 Results of single trace in real seismic data |
|
((a)原始地震数据;(b)处理后数据。(a)Original seismic data; (b)Seismic data processed. ) 图 7 实际资料处理单道处理结果时频谱 Fig. 7 Time-frequency spectrum of results of single trace in real seismic data |
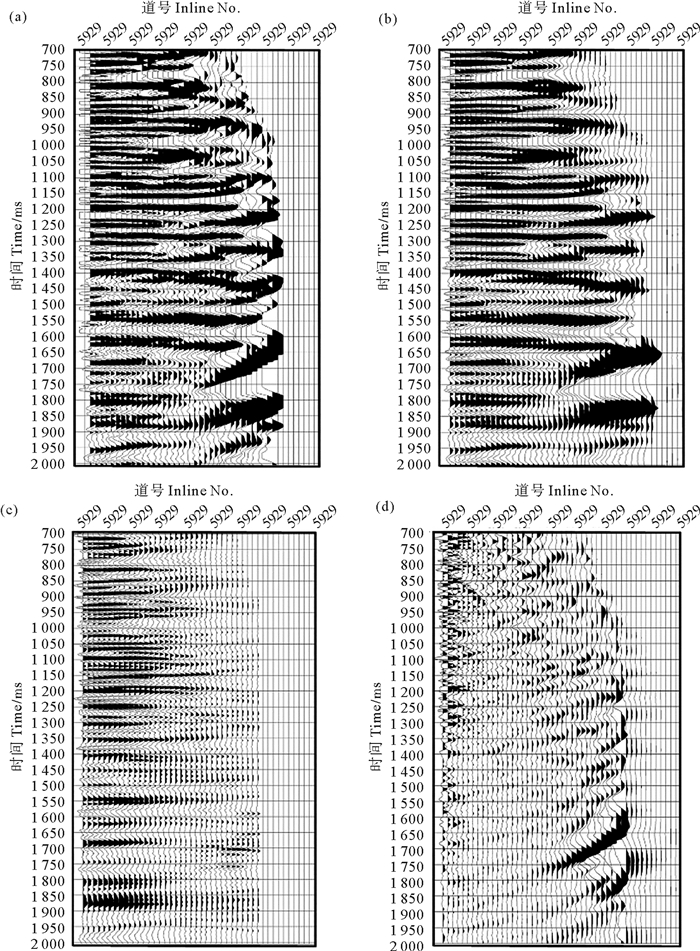
如图 8所示的是某三维工区的一CDP道集实际应用本文所提方法后各阶段的地震记录结果。图 8(a)所示为原始CDP道集,经自适应核最佳滤波进行噪音压制处理后的结果(见图 8(b))同相轴更加光滑,信噪比明显提高,原始道集的随机噪音与线性干扰得到了有效压制,并且也能很好地保证原有信号的振幅不被破坏,滤除的噪音如图 8(d)所示。图 8(c)展示了使用自适应核进行提高分辨率处理后的最终输出记录,可以看到通过内插算子对滤波后数据进行内插,有效信号频带得以展宽,远偏移距低频假轴被有效压制,反射同相轴连续性增强,从浅至深各层分辨率显著提升。
|
( (a)原始地震记录;(b)增强信噪比地震记录;(c)提高分辨率地震记录;(d)滤除的噪音。(a)Original seismic record; (b)The record after enhancing the SNR; (c)The record after enhancing the SNR and the resolution; (d)The separated noise by our proposed method. ) 图 8 CDP道集 Fig. 8 The comparison of CDP gathers |
如图 9所示的是经自适应核方法处理前后500~1 700 ms的叠后剖面。通过比较可以看出,经过自适应核方法处理后的剖面(见图 9(b))信噪比有了明显的提高,在保证同相轴振幅的前提下,大部分随机噪声被消除,同相轴更加连续。其次,经过自适应核方法处理,500~1 300 ms中浅层分辨率明显提高,下方深层区域噪音得到了有效压制,同相轴的连续性增强,可以更加清晰地表现出层位,为高精度的地震资料解释提高数据基础。

|
((a)原始地震记录;(b)自适应核处理结果。(a)Original seismic record; (b)The record processed by our proposed method. ) 图 9 叠后剖面 Fig. 9 The comparison of post-stack sections |
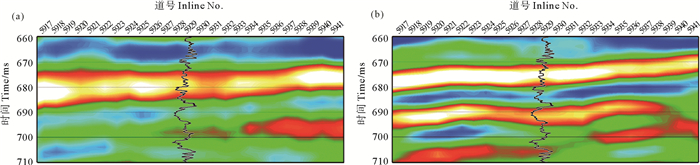
同时,还将经过90°相移和自适应核方法处理结果与实际测井曲线进行了对比,以更好地说明该方法的优越性。经过90°相移和自适应核方法处理地层正确归位,信噪比和分辨率得到了明显提高,处理结果如图 10所示,对图中黄色框内地震剖面结合实际测井曲线进行比较。通常情况下,测井曲线伽马低值对应砂岩储层。如图 11所示,处理后的地震剖面层间界限明显,具有比较高的聚焦度,并且在690 ms附近,在原始资料(见图 11(a))中未有能与伽马曲线低值匹配的波谷特征,能力值几乎被掩盖,而在处理后资料(如图 11(b)所示)中,在690 ms附近,存在与伽马曲线低值匹配明显的波谷特征,说明经过自适应核处理后的地震资料对地层岩性变化具有更高的匹配和识别精度。

|
((a)原始地震记录;(b)90度相移后地震记录;(c)自适应核后地震记录;(d)自适应核和90度相移后地震记录。(a) Original seismic record; (b)The seismic records after 90-degree phase shift; (c) The record processed by our proposed method; (d) The record processed by our proposed method after 90-degree phase shift. ) 图 10 叠后剖面与测井曲线的比较 Fig. 10 Comparison between post-stack sections and logging curve |
|
((a)原始地震记录;(b)处理后地震记录。(a) Original seismic record; (b) Seismic data with the proposed method. ) 图 11 伽马曲线 Fig. 11 Gamma curve |
本文提出的基于自适应核时频分析的最佳滤波方法是一种高精度地震资料处理技术,在时频谱上具有很强的聚焦能力和灵活性,相比于常规线性时频分布,具有更高的聚焦度和分辨率;相较于其他双线性时频分布,可以得到更加精确的时频谱。通过实际储层资料处理与测井曲线相结合证明该方法能有效滤除目标干扰,同时不损伤未受噪音干扰的有效信号。对噪声的振幅和相位变化不敏感,也不会产生假频等局部噪声,有效保留数据带宽,是一种稳健的地震资料处理方法。经该方法处理后,地震剖面上主要目的层段反射同相轴明显展现出来,信噪比与分辨率具有了较大提高,为后续层位识别和油气藏定位解释奠定了良好基础。
| [1] |
Liu N H, Gao J H, Zhang B, et al. Time-frequency analysis of seismic data using a three parameters S transform[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(1): 142-146. DOI:10.1109/LGRS.2017.2778045 (  0) 0) |
| [2] |
Kodera K, Villedary C D, Gendrin R. A new method for the numerical analysis of non-stationary signals[J]. Physics of the Earth & Planetary Interiors, 1976, 12(2-3): 142-150. (  0) 0) |
| [3] |
Morlet J, Arens G, Fourgeau E, et al. Wave propagation and sampling theory-Part Ⅰ: Complex signal and scattering in multilayered media[J]. Geophysics, 1982, 47(2): 203-221. DOI:10.1190/1.1441328 (  0) 0) |
| [4] |
Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: The S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 (  0) 0) |
| [5] |
Pinnegar C R, Mansinha L. The S-transform with windows of arbitrary and varying shape[J]. Geophysics, 2003, 68(1): 381-385. DOI:10.1190/1.1543223 (  0) 0) |
| [6] |
Radad M, Gholami A, Siahkoohi H R. S-transform with maximum energy concentration: Application to non-stationary seismic deconvolution[J]. Journal of Applied Geophysics, 2015, 118: 155-166. DOI:10.1016/j.jappgeo.2015.04.010 (  0) 0) |
| [7] |
Daubechies I, Lu J F, Wu H T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool[J]. Applied & Computational Harmonic Analysis, 2011, 30(2): 243-261. (  0) 0) |
| [8] |
黄忠来, 张建中. 同步挤压S变换[J]. 中国科学: 信息科学, 2016, 46(5): 643-650. Huang Z L, Zhang J Z. Synchrosqueezing S-transform[J]. Scientia Sinica Informationis, 2016, 46(5): 643-650. (  0) 0) |
| [9] |
张建中, 刘晗, 黄忠来, 等. 基于同步挤压变换的水合物储层地震信号时频分析[J]. 海洋地质前沿, 2015, 31(6): 23-29. Zhang J Z, Liu H, Huang Z L, et al. A synchrosqueezing transform based time-frequency analysis on seismic signals of hydrate reservoirs[J]. Marine Geology Frontiers, 2015, 31(6): 23-29. (  0) 0) |
| [10] |
高静怀, 陈文超, 李幼铭, 等. 广义S变换与薄互层地震响应分析[J]. 地球物理学报, 2003, 46(4): 526-532. Gao J H, Chen W C, Li Y M, et al. Generalized S transform and seismic response analysis of thin interbeds[J]. Chinese Journal of Geophysics, 2003, 46(4): 526-532. DOI:10.3321/j.issn:0001-5733.2003.04.015 (  0) 0) |
| [11] |
李斌. 同步挤压小波变换及其在薄互层中的应用[D]. 青岛: 中国石油大学(华东), 2021. Li B. Synchrosqueezing Wavelet Transform and Its Application on Thin Interben[D]. Qingdao: China University of Petroleum (East China), 2021. (  0) 0) |
| [12] |
Wigner E P. On the Quantum Correction for Thermodynamic Equilibrium[J]. Physical Review, 1931, 40(40): 749-759. (  0) 0) |
| [13] |
韩利. 高分辨率全谱分解方法研究[D]. 长春: 吉林大学, 2013. Han L. Research on the Methods of High-resolution Full Spectrum Decomposition[D]. Changchun: Jilin University, 2013. (  0) 0) |
| [14] |
Cohen L. Time frequency analysis: theory and application[J]. Englewood Cliffs: Prentice-Hall, 1995, 778: 299. (  0) 0) |
| [15] |
Baraniuk R G, Jones D L. Signal-dependent time-frequency analysis using a radially Gaussian kernel[J]. Signal Processing, 1993, 32(3): 263-284. DOI:10.1016/0165-1684(93)90001-Q (  0) 0) |
| [16] |
Jones D L, Baraniuk R G. An adaptive optimal-kernel time-frequency representation[J]. IEEE Transaction on Signal Processing, 1995, 43(10): 2361-2371. DOI:10.1109/78.469854 (  0) 0) |
| [17] |
岳龙, 刘怀山, 徐秀刚. 自适应核时频分析方法的改进及应用[J]. 物探化探计算技术, 2017, 39(1): 44-51. Yue L, Liu H S, Xu X G. Improvement of adaptive kernel time-frequency analysis and its application[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2017, 39(1): 44-51. (  0) 0) |
| [18] |
韩鹤威. 时频分析技术在薄层反演中的应用[D]. 北京: 中国地质大学, 2021. Han H W. Application of Time-Frequency Analysis Technology in Thin Layer Inversion[D]. Beijing, China University of Geosciences, 2021. (  0) 0) |
| [19] |
马成英. 时频属性提取方法及应用[D]. 青岛: 中国海洋大学, 2012. Ma C Y. Time-frequency Attributes Extraction Methods and Application[D]. Qingdao: Ocean University of China, 2012. (  0) 0) |
2. Laboratory for Marine Mineral Resources, Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao 266237, China;
3. Qingdao Earthquake Station, Shandong Earthquake Agency, Qingdao 266071, China;
4. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150050, China
 2023, Vol. 53
2023, Vol. 53


