2. 中国人民解放军 军事科学院国防工程研究院,北京 100036
世界经济在二十一世纪得到巨大飞跃,全球各个领域对于资源也出现了更高的需求。在市场需求和先进技术的联合推动下,中国深海装备和技术都取得了长足的发展。其中,深海载人/无人潜水器以及深海空间站都已被研制出,并在该研究方向取得许多成就,其提供的便捷功能也适用于不同领域的科学研究方面。通过无人系统能够对海底进行安全的研究和观察,并加以分析[1]。
作为自航式潜器的有益补充,本文提出一种新型的悬置海洋中部构筑物的技术设想。初步设定其主要功能是在固定地点为深海活动提供补给,为深潜器提供燃料和装备,为深海勘探、采集、观测和资源开发等活动提供非移动式的技术支持。
与深潜器和深海空间站相比,该构筑物长期悬浮在水下,用系泊缆将其固定在一定水深的位置,不具备自主航行能力。其成功的研发,能够快速提升中国对海洋资源开发的迫切需求。在深海矿物研究、油气田开发、深海生物学研究、构建完善海洋观察网络方面,都起到了巨大的作用。
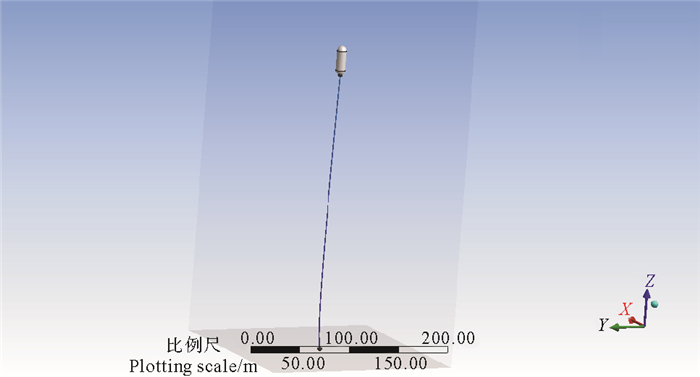
1 环境参数及设计条件本研究初步选取200 m水深为构筑物的悬浮水深,根据理论和软件模拟,当构筑物处于200 m水深时,波浪对其造成的影响可以忽略,故主要考虑洋流对构筑物可能造成的影响。构筑物示意图如图 1所示。
|
图 1 悬置海洋中部构筑物 Fig. 1 Suspended mid-ocean structures |
构筑物工作海域设定为中国近海,根据全球大洋变网格环流模式模拟的中国近海环流结果表明[3],南海等密面次表层环流盐度在25.0 kg·m-3时,与之对应的海水深度在150~220 m之间,最大流速在1~2 m·s-1之间。苏纪兰等[4]研究的中国近海的环流机制、李峣等[5]研究的中国东部近海环流特征等其他研究中国近海环流的研究成果均显示,中国近海200 m水深时最大流速不会超过2 m·s-1。因此按最不利荷载的角度出发,本文以2 m·s-1的流速为基础,研究不同形状构筑物的受力和位移。因200 m水深的铅直流速较小,一般为10-5 cm·s-1[3],因此只考虑水平流速。
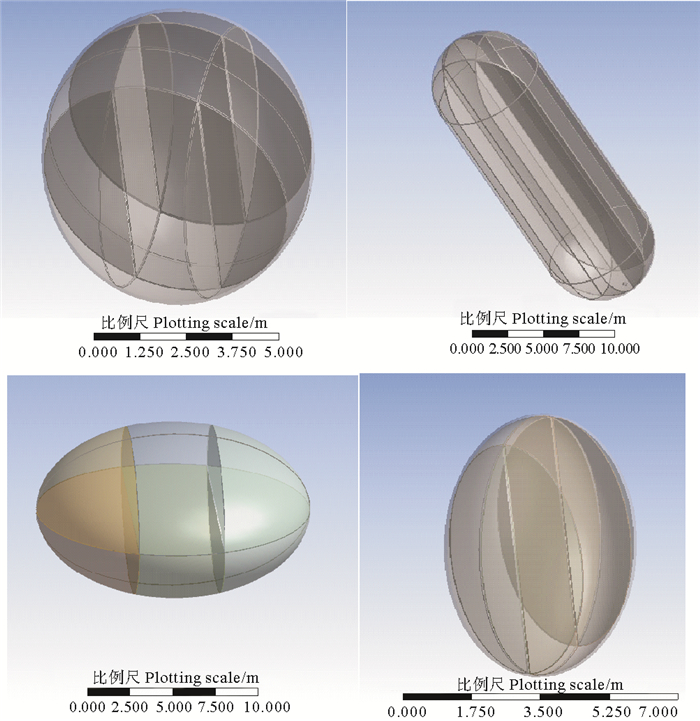
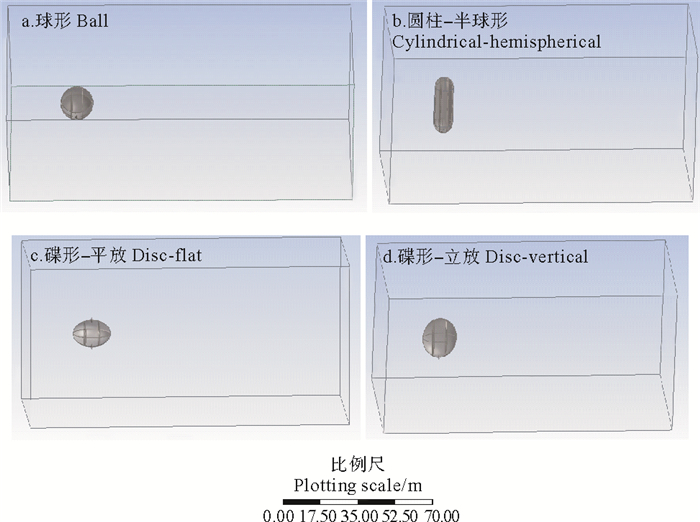
从流体受力和功能的角度出发,构筑物的形状初步选为球形、圆柱-半球形和碟形,如图 2所示。考虑结构尺寸的影响,体积选定为200和1 000 m3两个量级的尺寸,具体详见表 1。通过对比不同形状不同尺寸的构筑物分析结果,从而得出较为合理的结构形态和尺寸。
|
( (a.球形Ball; b.圆柱-半球形Cylindrical-hemispherical; c.碟形-平放Disc-flat; d.碟形-立放Disc-vertical) ) 图 2 悬置海洋中部构筑物形状 Fig. 2 Shape of suspended structures in the middle of the ocean |
由雷诺数与漩涡脱落的关系可知,当雷诺数大于3.5×106时,流场中会产生周期性的紊流漩涡[6]。而本文研究构筑物尺寸较大,雷诺数量级在108~1010远大于3.5×106,故在流速作用下产生涡激运动。
2 数值模拟计算方法基于上述环境参数及设计条件,构筑物主要受到海流和静水压力的共同作用,本文的有限元分析采用双向流固耦合的方法,在Workbench平台中,采用流体和瞬态结构双向组合的方法,中间数据交换平台采用系统耦合模块。
|
|
表 1 3种模型尺寸 Table 1 Dimensions of three types of models |
水流流体是属于不可压缩流体[6],在水流作用的影响下,悬置海洋中部构筑物形成了非定常有黏性不可压三维湍流问题的运动形式。
本次研究选择了雷诺平均N-S方程,同时选择K-Epision湍流模型进行模拟。针对畸变巨大的流动处理方面,通过RNG K-Epision模型能够令处理更加合理。在计算表达式的生成系数时引入了主流随时间变化的平均应变率[7]。这个过程获取的系数,和实际流动是相关联的,同时也能显示出空间坐标函数来。
基于雷诺平均的N-S方程为:
| $ \frac{\partial \rho}{\partial t}+\frac{\partial\left(\rho u_{j}\right)}{\partial x_{j}}=0 \text { 。} $ | (1) |
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{\partial {x_j}}} = \\ \rho {f_i} - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_i}}}\left[ {\left( {\mu + {\mu _i}} \right)\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}} - \frac{2}{3}\frac{{\partial {u_k}}}{{\partial {x_k}}}{\delta _{ij}}} \right)} \right]。\end{array} $ | (2) |
RNG K-Epision湍流模型的k和ε方程如下:
| $ \begin{gathered} \rho \frac{\partial k}{\partial t}+\rho \frac{\partial}{\partial x_{i}}\left(k u_{i}\right)= \\ \frac{\partial}{\partial x_{i}}\left(\alpha_{\mathrm{k}} \mu_{\mathrm{eff}} \frac{\partial k}{\partial x_{j}}\right)+G_{\mathrm{k}}+G_{\mathrm{b}}-\rho \varepsilon-Y_{\mathrm{M}} ; \end{gathered} $ | (3) |
| $ \begin{gathered} \rho \frac{\partial \varepsilon}{\partial t}+\rho \frac{\partial}{\partial x_{i}}\left(\varepsilon u_{i}\right)=\frac{\partial}{\partial x_{j}}\left(\alpha_{\varepsilon} \mu_{\mathrm{eff}} \frac{\partial \varepsilon}{\partial x_{j}}\right)+ \\ G_{1 \varepsilon} \frac{\varepsilon}{k}\left(G_{\mathrm{k}}+G_{3 \varepsilon} G_{\mathrm{b}}\right)-C_{2 \varepsilon} \rho \frac{\varepsilon^{2}}{k}-R_{。} \end{gathered} $ | (4) |
式中:ρ、p分别代表了流体密度,流体压强;x、u、f分别代表坐标分量、速度分量、惯性力分量;μ是分子黏性系数;μi是湍流黏性系数。
μeff为等效黏性系数:
| $ \mu_{\mathrm{eff}}=\mu+\mu_{i} \text {; } $ | (5) |
| $ G_{\mathrm{k}}=-\rho \overline{u_{i}^{\prime} u_{j}{ }^{\prime}} \frac{\partial u_{j}}{\partial x_{i}} \text { 。} $ | (6) |
式中Gk表示因为浮力而出现的湍流动能。如果流体不可压缩,则可忽略[8];YM表示可压缩紊流的膨胀条件,如果无法压缩,则可以将其忽略。
2.2 构筑物振动控制方程构筑物的结构动力学方程为:
| $ [\mathit{\boldsymbol{M}}]\{\ddot{\mathit{\boldsymbol{\delta}}}\}+[\mathit{\boldsymbol{C}}]\{\dot{\mathit{\boldsymbol{\delta}}}\}+[\mathit{\boldsymbol{K}}]\{\mathit{\boldsymbol{\delta}}\}=\{\mathit{\boldsymbol{F}}\}+\left\{\mathit{\boldsymbol{F}}_{\mathrm{P}}\right\} $ | (7) |
式中:[M]为结构的质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵;{F}、{FP}代表了动力学问题中的惯性矢量和构筑物受到的水流力;{δ}={u, v, w}T为节点移动向量,对于动态问题,u、v、w为时间的函数[9]。
2.3 双向流固耦合求解过程当一个物理场分析的输入过渡对其他分析结果产生依赖后,相关分析内容存在耦合性。构筑物上的压力取值范围,则是因为流体计算的结果说决定。而且,流体压力一旦发生了相关作用,构筑物发生位移、振动,也会对流体域产生影响,即双向耦合。本文选取3 cm厚的钢板作为构筑物表面壳体材料,并且内部设有高强度钢材支撑,由模拟结果可知构筑物自身的最大变形为0.7×10-2 m,对于选型研究主要考虑其位移变化,因此本文不再提及构筑物本身的变形影响。
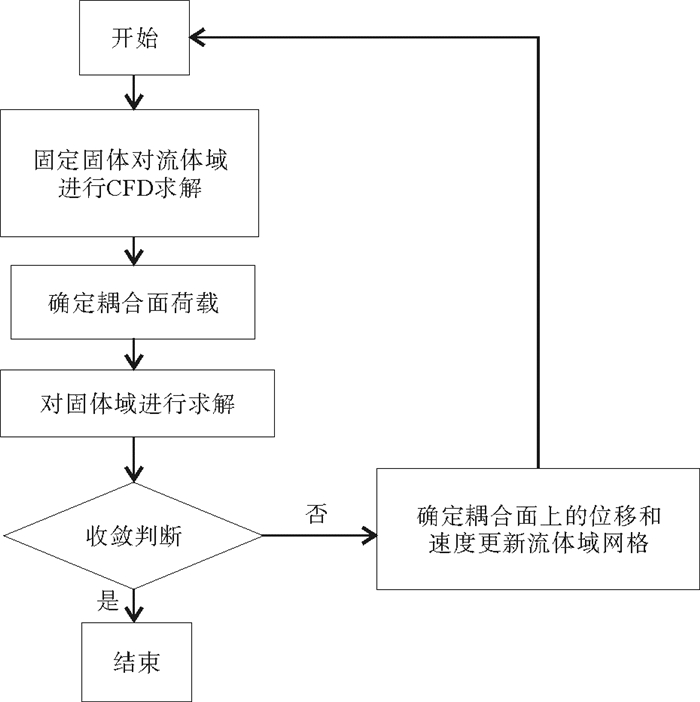
本文研究的构筑物是在流体的作用下发生运动的,因此第一步应先进行流体域计算。第一步,将2.1小节内的初始流场进行解算,完成解答后获取了构筑物刚体表面压力。第二步,要完成2.2小节内构筑物动力学方程的计算过程,求得构筑物表面的位移{δ}={u, v, w}T,也是下一步流场的初始条件。通过网格重构,将N-S方程再次进行计算,获取了更新的壁面压力数据。第三步,把该值再次加载进结构表面,以计算结构动力响应数据,进行反复迭代解算过程,最终令压力和位移满足收敛条件。图 3就是一套时间步的流程图。
|
图 3 求解流程 Fig. 3 Solving process |
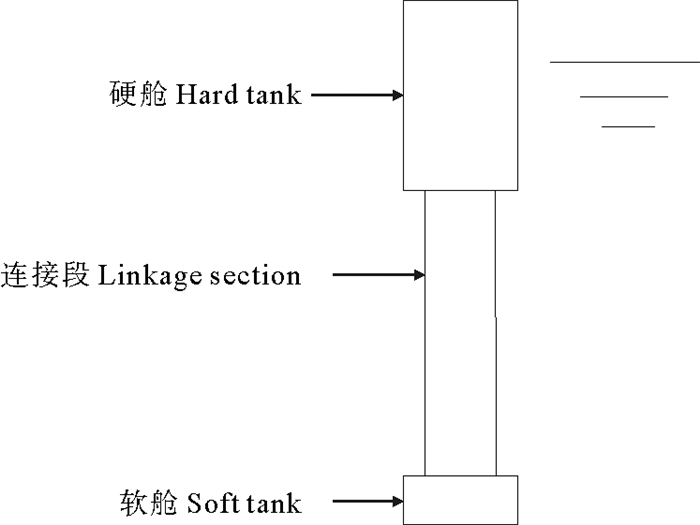
在分析构筑物之前,对文献[10]中大直径Spar平台的计算模型采用双向流固耦合方式进行了模拟,该模型体积较大,在流体作用下产生涡激运动,且固定方式同为系泊缆,因此对该平台进行分析可以验证所采用的网格、时间步、湍流模型和数值模拟方法是否能够准确模拟流场。具体简化模型及模拟结果如图 4、5所示。
|
图 4 Spar平台模型 Fig. 4 Model of Spar platform |
|
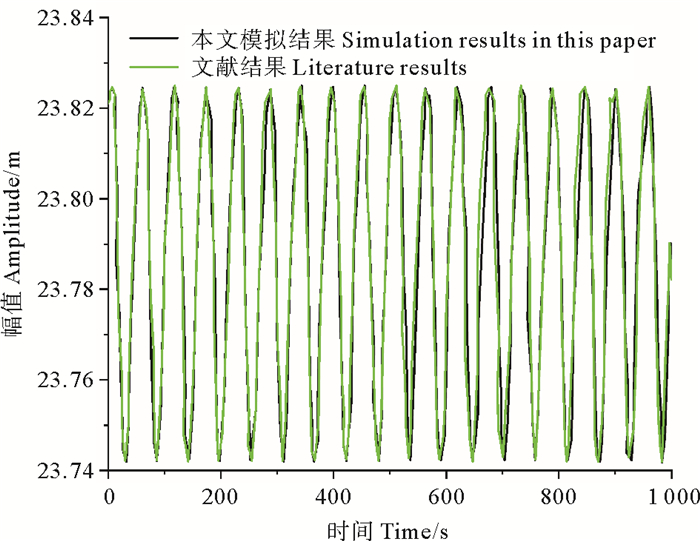
图 5 1 m·s-1时平台顺流向位移模拟结果对比 Fig. 5 Comparison of simulation results of platform downflow displacement at 1 m·s-1 |
本文模拟采用fluent计算流场,与文献[10]所用软件不同,但从模拟结果可以看出,本次模拟最终的验算结果同理论文献提供的结果近似,误差度在10%以内,说明两者的吻合度较高。
3 三维流固耦合模拟 3.1 分析模型建立Solid Works作为专业的3D造型应用,其设计的结构模型,能够无差别的导入ANSYS workbench平台之内,通过Enclosure命令建立长方体外流场计算域,并在构筑物下端预留固定支撑点。流场左侧为入口、右侧为出,除出口距构筑物表面距离为100 m外,其余各边界距构筑物表面皆为20 m。其中,碟形构筑物分2种姿态放置,一种是平放,一种是立放,其固定支撑点也随着姿态的不同设置在构筑物距离水面最远处,如图 6所示。
|
图 6 分析模型 Fig. 6 Analysis model |
ANSYS workbench自带的结构化网格划分可以作为本次研究中对流体域网格进行划分的方式,能够更好的重构动网格。靠近构筑物表面的网格最小尺寸为0.2 m,外部最大尺寸为2 m,网格自动变化率为1.2%(见图 7)。

|
图 7 流域网格划分 Fig. 7 Watershed grid division |
将入口边界条件调整至“速度入口”,其中的流速类目设定成2 m·s-1,出口为压力出口,压力为0,其余流体域表面设置为无滑移固壁。
3.4 动网格设置动网格设定可以通过fluent的Dynamic Mesh加以完成。通过smoothing以及remeshing两者同时使用,已完成对动网格的重构。本次命题中,可以将构筑物表面设定为流固耦合面,同时可以把构筑物表面调整成动网格区域,剩下的所有面,都能够调整成为固定面,这能够对构筑物是否存在变形等问题进行研究。
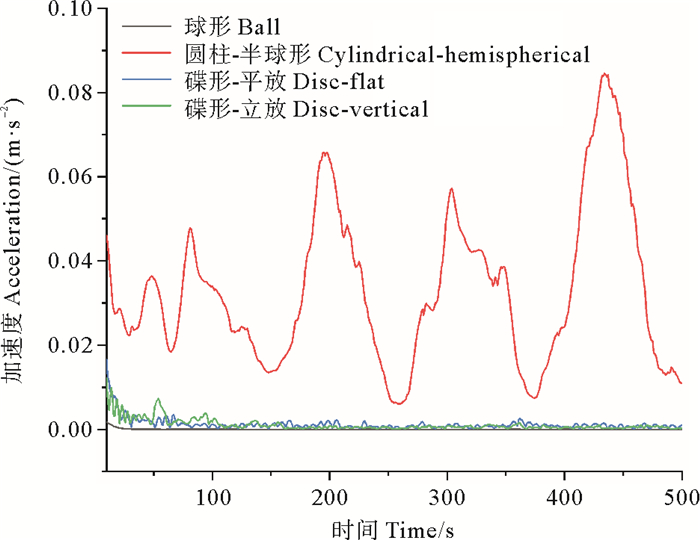
4 模拟结果分析 4.1 加速度结果分析 4.1.1 200 m3构筑物加速度结果分析200 m3 4种形状的构筑物加速度结果如图 8所示,可以明显看出圆柱-半球形构筑物的加速度变化幅度较大,最大值接近0.01重力加速度,而其余3种形状的位移加速度在初遇流体时较大,之后的初速度趋于稳定均小于0.005 m/s2,小于1‰重力加速度,根据表 2给出的船舶加速度对人体舒适度的影响可知,人体难以感觉到。
|
图 8 4种200 m3钢材构筑物加速度 Fig. 8 Acceleration of 4 types of 200 m3 steel structures |
|
|
表 2 船舶加速度对人体舒适度的影响 Table 2 Influence of ship acceleration on human comfort |
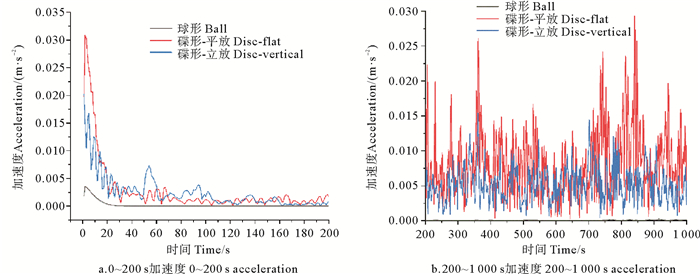
为进一步比较不同构筑物的加速度,如图 9所示为除圆柱-半球形以外另外3种构筑物的加速度对比。由前200 s的加速度可以看出球形构筑物的加速度最快趋向于稳定,在40 s时加速度已接近零,小于另外两种构筑物的加速度,随着海流作用时间的延长,加速度没有发生明显变化,始终接近零。碟形构筑物的加速度始终处于波动状态,没有达到稳定,碟形平放的加速度峰值大于立放,在初遇流体时平放的加速度峰值超过0.03 m/s2,在后续的时间里加速度峰值极少超过0.002 m/s2,多数时刻在0.002 m/s2以下。碟形立放的加速度在初遇流体的时刻达到了0.02 m/s2,之后加速度迅速下降,在60 s时降到0.005 m/s2,200 s之后加速度始终小于0.002 m/s2。
|
图 9 3种200 m3钢材构筑物加速度 Fig. 9 Acceleration of 3 types of 200 m3 steel structures |
综上,从加速度的对比结果可以看出:200 m3的钢材构筑物,除圆柱半球形构筑物外,其余3种加速度值在达到稳态后均小于5‰重力加速度,人体难以感觉,比较适合作为构筑物的形状。
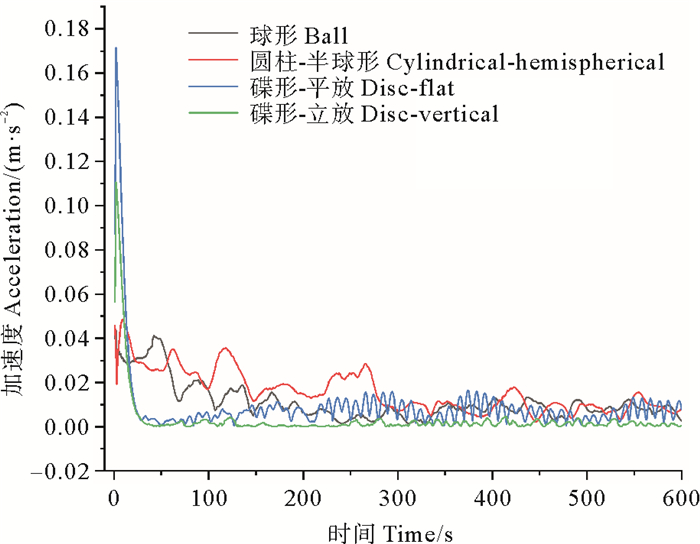
4.1.2 1 000 m3构筑物加速度结果分析如图 10所示为1 000 m3 4种钢材构筑物0~600 s加速度数据,可以看出在初遇流体时碟形构筑物位移较大,接近0.18 m/s2,超过1%重力加速度。但本章模拟初始流速为2 m/s,在实际工作中流速会有从0~2 m/s的渐变过程,因此,对于本章模拟结果重点分析构筑物达到稳态后的变化。
|
图 10 4种1 000 m3钢材构筑物加速度 Fig. 10 Acceleration of four types of steel structures of 1 000 m3 |
由图 10可以看出,在50 s后碟形立放加速度首先达到相对稳定状态,其波动幅度远小于其他3种形状的构筑物。圆柱半球形构筑物加速度数据依然较大,在300 s时其加速度值降到与球形和碟形构筑物平放相当的水平,加速度值下降速度明显小于碟形和球形构筑物,其加速度曲线在300~600 s的时间里出现多次波峰,加速度值大于球形和碟形构筑物。球形构筑物加速度曲线变化趋势与圆柱半球形构筑物类似,但加速度值小于圆柱半球形构筑物,与碟形构筑物平放数值相近。碟形平放加速度有明显的周期变化特征,但幅度较小,加速度值也小于圆柱半球形构筑物加速度。
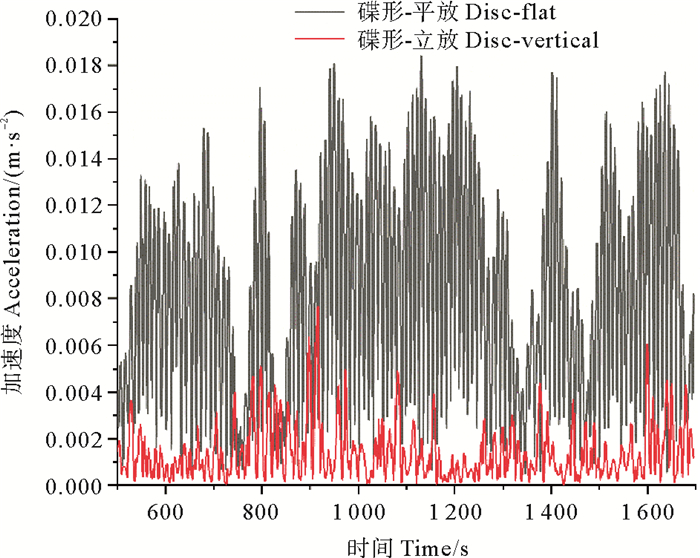
为得到碟形构筑物立放时的具体加速度,并将其与平放加速度比较,本文作者将2种姿态的构筑物模拟时间延长,如图 11所示为碟形构筑物500~1 600 s加速度数据。可以看出,碟形平放的加速度大于碟形立放的加速度,但都小于5‰重力加速度,碟形立放加速度最大值更是小于1‰重力加速度。
|
图 11 1 000 m3碟形钢材构筑物加速度 Fig. 11 Acceleration of 1 000 m3 disk-shaped steel structure |
综上,1 000 m3钢材4种形状构筑物中,圆柱半球形构筑物加速度值最大,相比之下,球形和碟形构筑物更适合作为构筑物的形状。
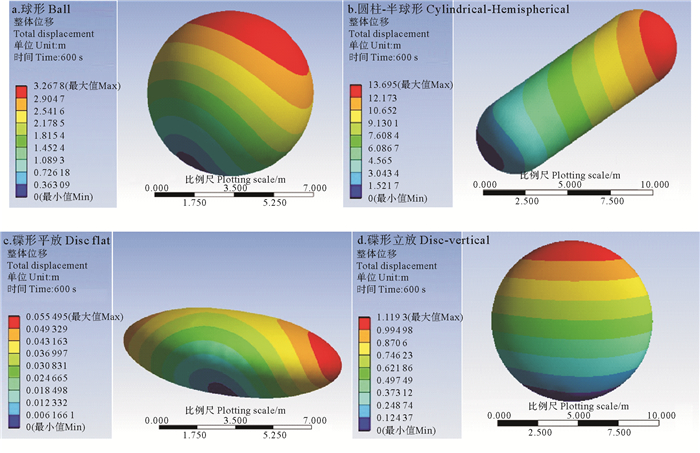
4.2 位移结果分析 4.2.1 200 m3构筑物位移结果分析构筑物的位移图以及位移时程曲线如图 12~14所示。所有位移图中水流方向均为从左到右,位移值为构筑物所走路径的长度。
|
图 12 200 m3构筑物位移图 Fig. 12 Displacement diagram of 200 m3 structure |
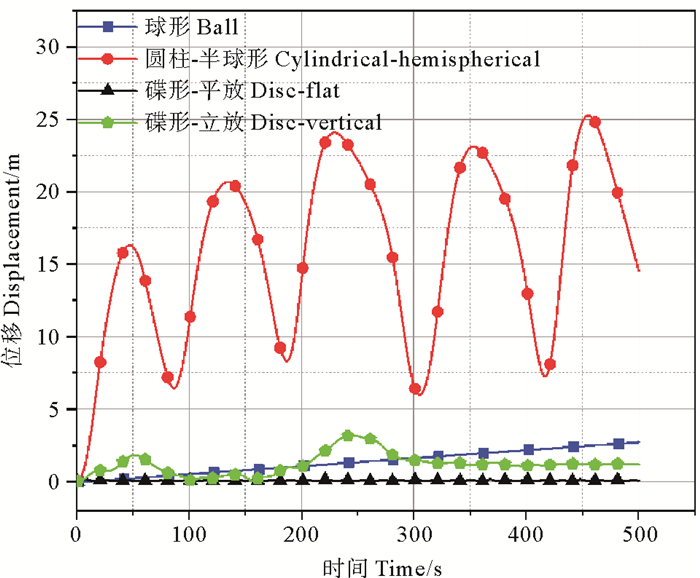
|
图 13 200 m3构筑物最大位移时程曲线 Fig. 13 Time history curve of maximum displacement of 200 m3 structure |
|
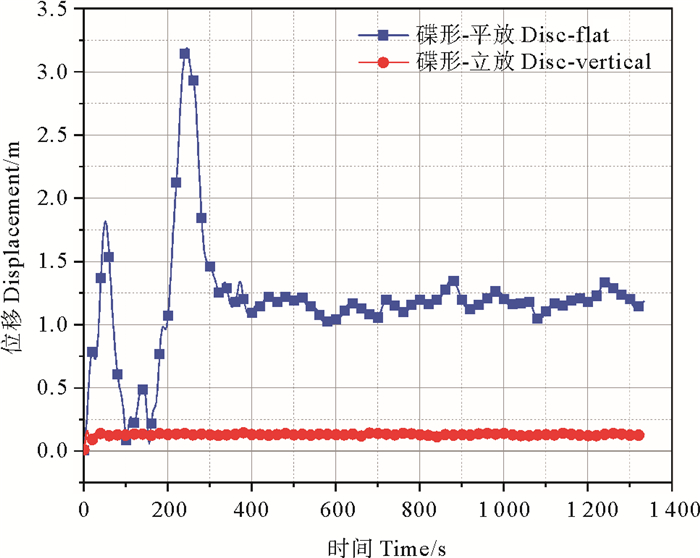
图 14 200 m3碟形构筑物最大位移时程曲线 Fig. 14 Time history curve of maximum displacement of 200 m3 disc-shaped structure |
由位移图可以看出,各种姿态的构筑物在水流作用下都发生了不同方式的运动。球形和圆柱半球形构筑物沿流速方向发生了偏移,碟形构筑物立放和平放时,都会围绕着支撑点发生了来回摆动。
由位移时程曲线可以看出,圆柱-半球形构筑物位移最剧烈,具有周期波动的特征,最大波动幅度已接近20 m,沿水流方向产生的最大顶端位移超过20 m,不适合作为构筑物的形状。球形构筑物以5.4×10-3 m·s-1的速度发生着偏移,随着时间的延长位移在增大,在500 s时已超过2 m,接近5 m,位移幅值较大。碟形构筑物平放位移最小,最大位移值不足0.2 m,且位移曲线最为平稳。碟形构筑物立放时过程中也有明显的波峰,但到达稳态后变化范围都在0.5 m以内,相对球形和圆柱-半球形构筑物受漩涡脱落影响较小。
因此,从位移角度出发,当构筑物体积是200 m3时,碟形-平放应是最合适的构筑物放置姿态,虽然碟形-平放也会在小范围内产生位移波动,但其波动范围最小,不足0.1 m,位移最为平稳,适合作为构筑物的姿态。
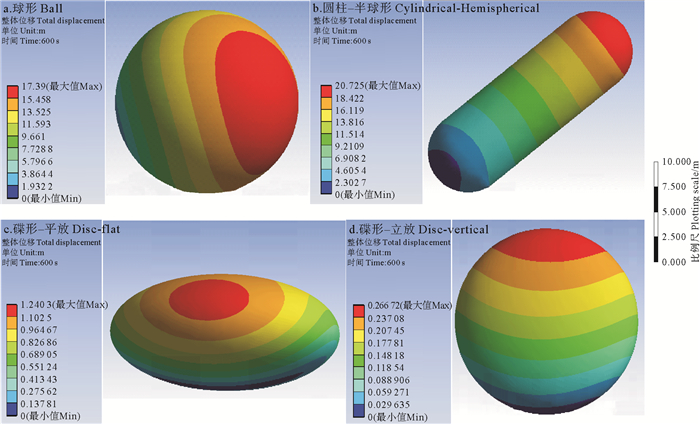
4.2.2 1 000 m3构筑物位移结果分析如图 15所示,当体积为1 000 m3时,球形和圆柱-半球形的构筑物在流速作用下围绕着支撑点发生大幅度的位移,最大位移出现在顶部。而碟形构筑物,无论平放还是立放,运动较缓,围绕着支撑点来回的摆动。
|
图 15 1 000 m3构筑物位移 Fig. 15 Displacement of 1 000 m3 structure |
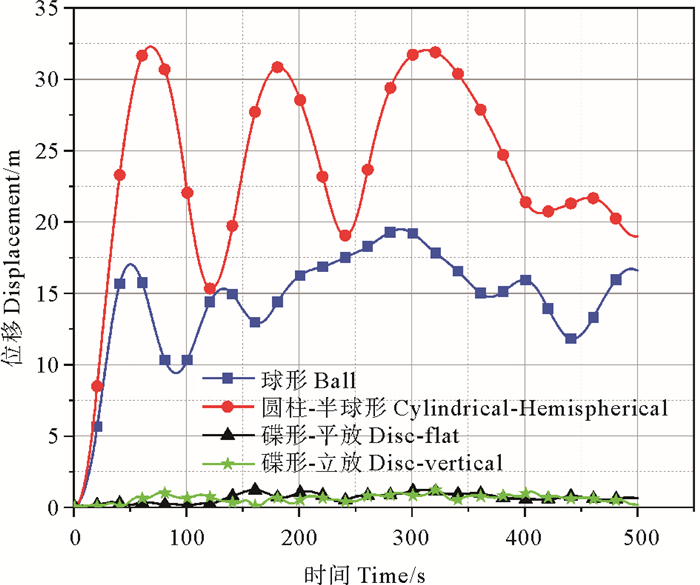
由图 16可以看出,4种构筑物位移差异明显,其中圆柱-半球形构筑物位移最大且最为剧烈,最大位移超过30 m;球形构筑物也产生了较大的位移,位移曲线波动较大,最大值接近20 m,受到漩涡的影响程度明显大于碟形。相比之下,碟形位移则较为平缓,2种姿态下位移幅值均在2 m以内,且波动方式即受漩涡影响程度类似。
|
图 16 1 000 m3构筑物最大位移时程曲线 Fig. 16 Time history curve of maximum displacement of 1 000 m3 structure |
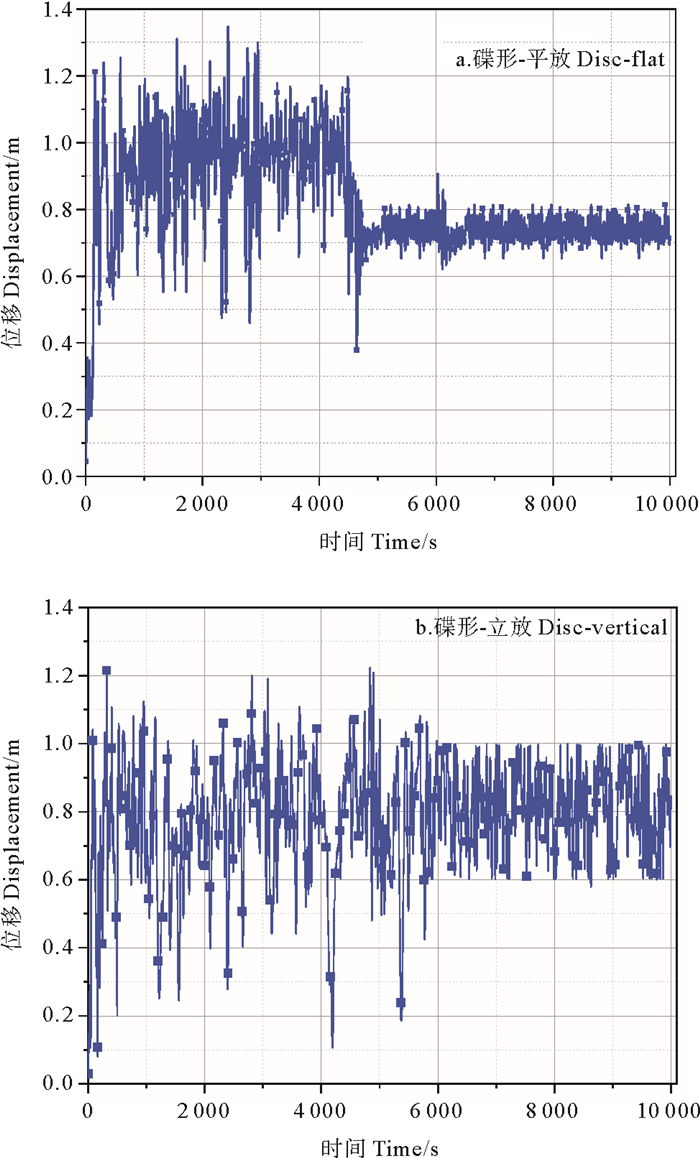
为进一步区分两者的区别,增加模拟时间,如图 17所示为最大位移时程曲线,可以看出两者最终都有一个相对稳定的状态。碟形-平放在6 500 s后接近稳定,位移幅值大部分在0.7~0.8 m之间,变化幅度在0.1 m范围内。碟形-立放在6 000 s后位移相对稳定,位移幅值在0.6~1.0 m范围内变化,变化幅度在0.4 m范围内,不如平放稳定。
|
图 17 1 000 m3碟形构筑物最大位移时程曲线 Fig. 17 Time history curve of maximum displacement of 1 000 m3 disc-shaped structure |
综上,碟形构筑物更容易满足构筑物在流体环境中对位移的要求,当体积达到1 000 m3时,在流速作用下前期2种姿态的位移基本相同,作用时间达到一定值后,碟形构筑物平放比立放更适合作为构筑物的放置姿态。
5 结论本文对3种形状不同体积的悬置海洋中部构筑物进行了有限元模拟。分析了200 m水深2 m·s-1海流作用下,不同体积的球形、圆柱-半球形、碟形-平放和立放的构筑物产生的加速度和位移变化,并根据结果对碟形构筑物做了进一步的模拟和受力分析,得到如下的结论:
(1) 当构筑物体积为200 m3时,在200 m水深的静水压力和2 m·s-1的流速作用下,圆柱-半球形构筑物加速度明显大于其余3种构筑物的加速度,且加速度值超过5‰重力加速度,部分时刻超过5%重力加速度,人体明显感到不适,不宜作为构筑物形状。其余3种构筑物在稳态时,加速度均小于5‰重力加速度,人体难以感知,比较适合作为构筑物的形状。
(2) 当构筑物体积为1 000 m3时,4种形状的加速度均小于5‰重力加速度,满足人体无感的标准,但圆柱-半球形构筑物加速度波动最大,且加速度值明显高于其他3种构筑物。故根据加速度数据可以得出球形和碟形更适合作为构筑物的形状。且当构筑物体积由200 m3增加到1 000 m3时,可以明显看出加速度值有明显的减小,即随着体积的增大构筑物受到流体作用的影响会降低。
(3) 当构筑物的体积为200 m3时,圆柱-半球形构筑物位移变化最复杂,变化幅度最大,有明显的周期,受漩涡脱落影响明显,位移最大值超过10 m。球形构筑物位移幅度次之,且随时间的延长位移持续增长,相对而言,碟形构筑物位移最小,两种姿态下的位移均在1 m以内,故碟形构筑物更适合作为构筑物的形状。
(4) 当构筑物的体积为1 000 m3时,相对于200 m3而言,圆柱-半球形构筑物位移变化幅值更大,受漩涡影响更剧烈,周期变化不如200 m3那么明显。球形构筑物位移也有明显增大,最大位移超过10 m,但碟形构筑物位移没有明显增大且位移曲线相对平稳,最大位移仍然在1 m以内,故在1 072 m3时,碟形依然是较为合适的形状。
综上,碟形在所研究的4种形状中更适合流体受力,加速度值较小,位移状态最稳定,适合作为构筑物的形状。其中在碟形构筑物中平放相对立放波动幅度更小,状态更稳定。随着体积的增大碟形构筑物加速度值减小,但最大位移的变化幅度会增大。同时,随着体积的增大不同形状的构筑物产生的涡激运动幅度也随之变化,针对流速对不同形状尺寸的构筑物造成的涡激运动影响可根据具体使用情况进行进一步参数化研究,以确定不同工况下合适的构筑物形状。
| [1] |
Zhang T W, Tang J L, Qin S J, et al. Review of navigation and positioning of deep-sea manned submersibles[J]. Journal of Navigation, 2019, 72(4): 1021-1034. DOI:10.1017/S0373463319000080 (  0) 0) |
| [2] |
Pere R, Marc C, David R, et al. Intervention AUVs: The next challenge[J]. Annual Reviews in Control, 2015, 40: 227-241. DOI:10.1016/j.arcontrol.2015.09.015 (  0) 0) |
| [3] |
魏泽勋. 中国近海环流及其季节变化的数值模拟[D]. 北京: 中国科学院研究生院(海洋研究所), 2004. Wei Z X. Numerical Simulation of China's Offshore Circulation and Its Seasonal Variation[D]. Beijing: Graduate University of Chinese Academy of Sciences (Institute of Oceanology), 2004. (  0) 0) |
| [4] |
苏纪兰. 中国近海的环流动力机制研究[J]. 海洋学报(中文版), 2001(4): 1-16. Su J L. Study on the dynamic mechanism of circulation in offshore China[J]. Haiyang Xuebao, 2001(4): 1-16. DOI:10.3321/j.issn:0253-4193.2001.04.001 (  0) 0) |
| [5] |
李峣. 中国东部近海夏季环流特征及其动力机制[D]. 北京: 中国科学院研究生院(海洋研究所), 2010. Li Y. A Review of the Global Circulation in Coastal China[D]. Beijing: Graduate University of Chinese Academy of Sciences (Institute of Oceanology), 2010. (  0) 0) |
| [6] |
娄敏. 海底管道悬跨段涡激振动动力特性及动力响应的数值模拟[D]. 青岛: 中国海洋大学, 2005. Lou M. Numerical Simulation of Dynamic Characteristics and Dynamic Response of Vortic-Induced Vibration in Suspended Span of Subsea Pipeline[D]. Qingdao: Ocean University of China, 2005. (  0) 0) |
| [7] |
Han Z, Reitz R D. Turbulence modeling of internal combustion engines using RNG κ-ε Models[J]. Combustion Science and Technology, 1995, 106(4-6): 267-295. DOI:10.1080/00102209508907782 (  0) 0) |
| [8] |
李永恒, 庞立军. 基于双向流固耦合的水轮机转轮动态特性研究[J]. 大电机技术, 2014(2): 53-57. LI Y H, Pang L J. Study on dynamic characteristics of turbine runner based on two-way fluid-structure coupling[J]. Large Electric Machine Technology, 2014(2): 53-57. DOI:10.3969/j.issn.1000-3983.2014.02.014 (  0) 0) |
| [9] |
王建超. 悬浮隧道锚索涡激振动分析[D]. 郑州: 郑州大学, 2019. Wang J C. Vortex Induced Vibration Analysis of Anchor Cable in Suspension Tunnel[D]. Zhengzhou: Zhengzhou University, 2019. (  0) 0) |
| [10] |
周阳, 黄维平. 大直径浮式结构涡激振动的数值模拟[J]. 中国海洋大学学报(自然科学版), 2014, 44(9): 98-103. Zhou Y, Huang W P. Numerical simulation of vortex induced vibration of large diameter floating structures[J]. Periodical of Ocean University of China, 2014, 44(9): 98-103. (  0) 0) |
| [11] |
孙震洲, 金伟良, 方滔, 等. 海上升压站在靠船工况下振动舒适性研究[J]. 海洋工程, 2019, 37(5): 148-155. Sun Z Z, Jin W L, Fang T, et al. Research on Vibration comfort of offshore booster station under shipside operating condition[J]. Ocean Engineering, 2019, 37(5): 148-155. (  0) 0) |
| [12] |
沈功田, 贺贵军, 张勇, 等. 载人设备人体加速度反应研究综述及应用展望[J]. 机械设计与研究, 2020, 36(6): 1-7. Shen G T, He G J, Zhang Y, et al. Review and application prospect of human acceleration response of manned equipment[J]. Mechanical Design and Research, 2020, 36(6): 1-7. (  0) 0) |
2. Institute of Defense Engineering, Academy of Military Sciences, Chinese People′s Liberation Army, Beijing 100036, China
 2022, Vol. 52
2022, Vol. 52

