2. 青岛市海洋可再生能源重点实验室,山东 青岛 266100
水平轴潮流能水轮机因其效率较高、转动平稳等优点而成为目前应用最广的潮流能转换机构形式[1],对其性能的准确预测是水轮机设计的必要条件,目前,使用CFD(Computational Fluid Dynamics)方法对水平轴潮流能水轮机进行性能预测已经成为一种趋势[2-4]。然而在对水轮机进行数值模拟及性能预测时,影响计算结果的因素中,湍流模型的选取至关重要。国内外学者在湍流模型选取方面进行了一系列研究,Michael Shives, Curran Crawford[5]在对潮流场驱动盘数值模拟中,比较了standard k-ε模型与SST k-ω的适用性,并通过试验数据说明SST k-ω在驱动盘模拟中更具有优势;Martin Miltner等[6]为选择合适湍流模型进行自由射流的模拟,对多种湍流模型(S-A、standard k-ε、RNG、Realizable k-ε、standard k-ω、SST k-ω、RSM)进行试验验证及比较;黄胜等[7]为了研究不同湍流模型在螺旋桨水动力性能预报中的适用性,运用计算流体力学软件对黏性流场中螺旋桨的敞水性能进行了计算研究;关鹏等[8]采用S-A、standard k-ε、RNG、SST k-ω四种湍流模型对某水平轴风力机叶片附近的三维湍流流场进行了数值模拟,比较了其适用性。在特定的湍流条件下,为选择合适的湍流模型对所设计水轮机的三维流场进行描述,本文拟采用不同的湍流模型(SST k-ω与Realizable k-ε)对水轮机进行数值模拟,得到不同工况下水轮机的功率系数、扭矩系数与轴向力系数以及近尾流场(1.5D位置)速度分布与湍流强度变化情况,并进行水槽试验验证,对比分析得到适合水轮机数值模拟的湍流模型。
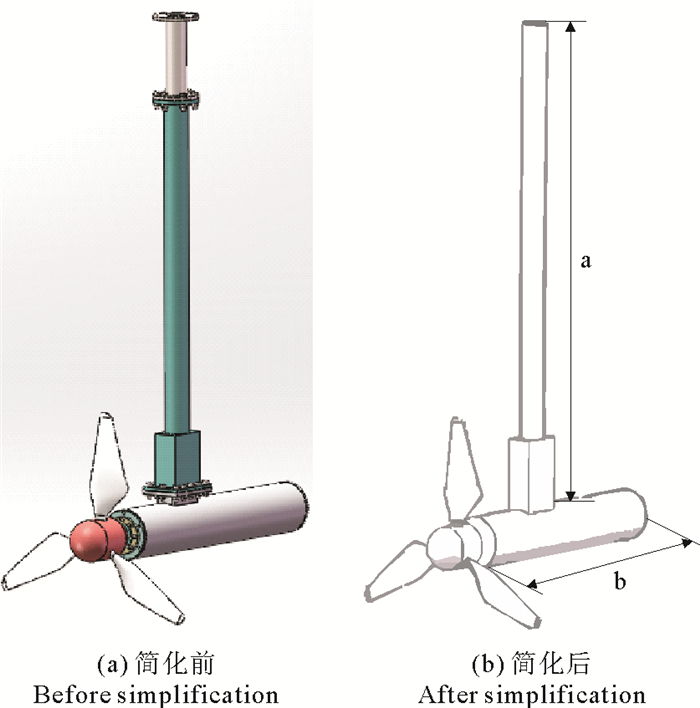
1 水轮机模型水轮机模型由转子、联轴器、扭矩传感器、增速器、发电机、数据采集系统等组成,叶片翼型、转子各部分尺寸以及装置整体尺寸如表 1所示。在数值模拟中为保证计算快速有效,将水轮机整体装置进行简化处理,水轮机简化前与简化后模型如图 1所示。
|
|
表 1 水轮机装置各部分尺寸 Table 1 Size of turbine′s parts |
|
图 1 水轮机模型 Fig. 1 Turbine model |
湍流模型的引入是为了解决流体运动方程不封闭问题。目前,针对不同描述内容存在多种湍流模型,考虑到实际流场环境以及流场与水轮机的相互影响,需要合理选择描述三维湍流流动模型,着重介绍两方程模型中Realizable k-ε与SST k-ω湍流模型。
(1) Realizable k-ε湍流模型
Standard k-ε对于时均应变率较大的情况容易出现负的正压力,Realizable k-ε采用新的湍流粘度公式,即公式中模型常数Cμ不是常数,而与应变率联系,有效的避免Standard k-ε的弊端。Realizable k-ε增加了对雷诺应力的约束,在雷诺应力的处理上保持与真实湍流一致。可以更精确地模拟平面和圆形射流的扩散速度,在旋转流计算、带方向压强梯度的边界层计算和分离流计算等问题中,计算结果更加符合真实情况[9],模型参数及系数[10]如下:
| $ \begin{align} &\ \ \frac{\partial }{\partial t}\left( \rho k \right)+\frac{\partial }{\partial {{x}_{i}}}(\rho k{{u}_{i}})=\frac{\partial }{\partial {{x}_{j}}}\left[\left( \mu +\frac{{{\mu }_{t}}}{{{\sigma }_{k}}} \right)\frac{\partial k}{\partial {{x}_{j}}} \right]+ \\ &{{G}_{k}}-\rho \varepsilon 。\\ \end{align} $ | (1) |
| $ \begin{align} &\ \ \ \ \frac{\partial }{\partial t}\left( \rho \varepsilon \right)+\frac{\partial }{\partial {{x}_{i}}}(\rho \varepsilon {{u}_{i}})=\frac{\partial }{\partial {{x}_{j}}}\left[\left( \mu +\frac{{{\mu }_{t}}}{{{\sigma }_{\varepsilon }}} \right)\frac{\partial \varepsilon }{\partial {{x}_{j}}} \right]+ \\ &\rho {{C}_{1}}E\varepsilon -{{C}_{2}}\rho \frac{{{\varepsilon }^{2}}}{k+\sqrt{\nu \varepsilon }}。\\ \end{align} $ | (2) |
其中:k为湍流动能;ε为湍动耗散率;σk,σε为湍动能k和湍动耗散率ε对应的Prandtl数,σk =1.0,σε=1.2;xi、xj为位置坐标分量;ui为速度坐标分量;Gk为平均速度梯度引起的湍流动能k的产生项;μ为流体动力粘性系数。湍流黏性系数μ=ρCμk2/σε,Cμ为模型常数,C2=1.9。
(2) SST k-ω湍流模型
Menter[11]综合近壁区standard k-ω模型的稳定性及边界层外部standard k-ε模型独立性的优点,提出了SST k-ω湍流模型φ3,可用standard k-ω模型φ1与standard k-ε模型φ2的加权相加来表示:
| $ {{\varphi }_{3}}={{\varphi }_{1}}{{f}_{1}}+{{\varphi }_{2}}(1-{{f}_{2}})。$ | (3) |
其中, f1为混合函数,并给出SST k-ω湍流模型方程[12]:
| $ \begin{align} &\ \ \ \ \ \ \frac{\partial \rho k}{\partial t}+\frac{\partial (\rho {{v}_{j}}k)}{\partial {{x}_{j}}}=={{P}_{k}}-{{\beta }^{*}}\rho \omega k+ \\ &\frac{\partial }{\partial {{x}_{j}}}\left[({{\mu }_{L}}+{{\sigma }_{k}}{{\mu }_{T}})\frac{\partial k}{\partial {{x}_{j}}} \right]。\\ \end{align} $ | (4) |
| $ \begin{align} &\ \ \ \ \ \frac{\partial \rho \omega }{\partial t}+\frac{\partial (\rho {{v}_{j}}\omega )}{\partial {{x}_{j}}}=\frac{\gamma }{{{v}_{T}}}P-\beta \rho {{\omega }^{2}}+ \\ &\frac{\partial }{{\partial {x_j}}}\left[({{\mu }_{L}}+{{\sigma }_{\omega }}{{\mu }_{T}})\frac{\partial \omega }{\partial {{x}_{j}}} \right]+2(1-{{f}_{1}})\frac{\rho {{\sigma }_{\omega 2}}}{\omega }\frac{\partial k}{\partial {{x}_{j}}}\frac{\partial \omega }{\partial {{x}_{j}}}。\\ \end{align} $ | (5) |
模型中常数β*=0.09,σω2=0.856,基于以上特点及处理,SST k-ω湍流模型能够广泛用于各种复杂流动。
3 初始条件采用Gambit作为前处理的工具。鉴于支撑装置的加入与叶片的复杂外形,采用非结构性网格。对网格进行分区划分,水轮机面采用三角形网格划分,流体域与旋转域采用四面体非结构性网格划分,由于网格尺度的不同,实现了旋转域的局部加密,加密程度约为10倍加密,在缩短运算时间的同时保证计算的准确性,网格加密情况如图 2所示。

|
图 2 旋转域网格加密 Fig. 2 Refinement of turbine model grid |
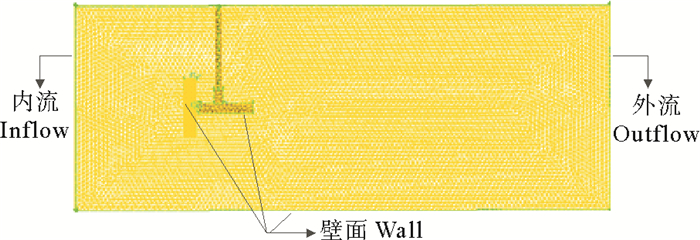
参考文献[12]及试验水槽的大小确定计算域的尺寸为10 D×2.5 D×5 D,将水轮机置于2.5 D深度,即高度的中心位置,并设定水轮机中心距入口处为3 D,距离出口处为7 D。具体的边界条件设定如图 3所示。
|
图 3 边界条件设定 Fig. 3 Boundary conditions |
借助计算流体力学软件ANSYS-fluent完成对于水轮机的数值模拟,采用标准壁面函数,分离隐式求解器进行模拟,动静转子间采用MRF(Multiple Reference Frame)耦合模型,入口条件采用湍流强度和水力半径进行确定,水力半径为0.3 m,湍流强度值根据实测数据确定。采用Realizable k-ε与SST k-ω两种湍流模型对水轮机进行数值模拟,除湍流模型的选取不同外,其他条件设置保持一致。
4 试验及数据采集水轮机所处的实际海洋地势环境并不是平坦的,通过设置障碍物近似表示由于地势不平产生的湍流情况。为了验证两种湍流模型在此湍流情况下的适用性,进行了模型水槽试验。模型试验在中国海洋大学物理海洋教育部重点实验室风浪流试验水槽中完成,对不同工况、不同桨距角下水轮机的运行状态以及尾流速度情况进行监测。以试验中获能较高的5°桨距角为例,流速设定为0.8 m/s。
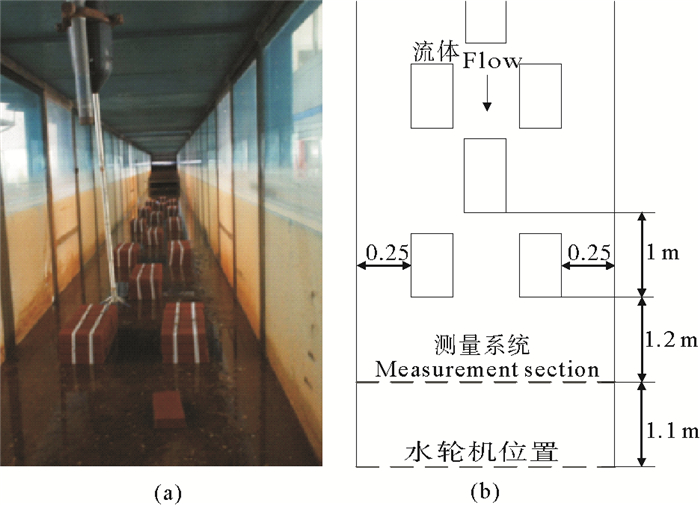
4.1 试验为了得到特定的湍流,进行相应的障碍物设置,如图 4(a)所示,障碍物由15组砖块组成,每组障碍物的尺寸为0.5 m×0.2 m×0.15 m,障碍物之间的距离以及距水槽边界的距离如图 4(b)所示。
|
图 4 流场障碍物布置 Fig. 4 Obstacle layout of flow field |
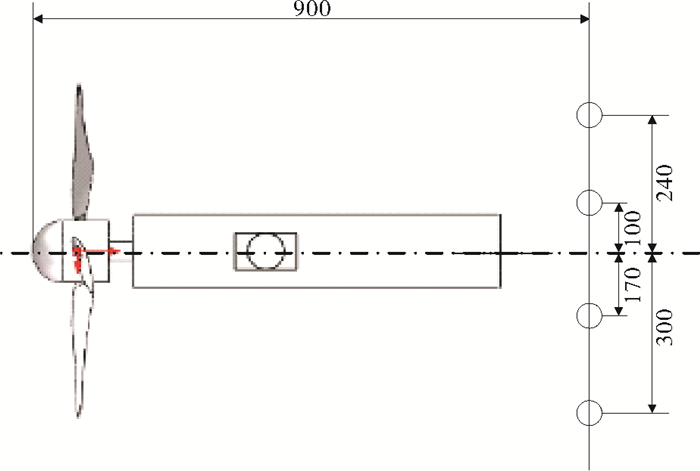
数据测量时,通过贴于吊装结构上的应变片对轴向力进行测量,置于水轮机内部的扭矩传感器对转速、扭矩进行测量,并通过Labview在计算机与扭矩功率仪上同时进行数据显示。在水轮机前方1.1 m处安放一台ADV(Acoustic Doppler Velocity)对障碍物产生的湍流进行测量,在水轮机后方1.5 D处安放4台ADV进行尾流流速及湍流强度测量,在过水轮机中心水平面内,根据流场的对称性[11],将4台ADV不对称布置,如图 5所示。
|
图 5 ADV布置图 Fig. 5 The arrangement diagram of ADV |
在试验过程中通过改变加载在水轮机上的负载改变转速,来流控制在0.8 m/s左右,得到不同的尖速比(1~9),并同步得到水轮机的功率系数、扭矩系数、轴向力系数;5台ADV在进行数据采集时存在相互干扰,并且受到结构震动的影响,产生波动较大的噪点,需要对数据进行处理使其更加准确,数据处理的原理公式[12]为:
| $ {{u}_{\text{min}}}=\bar{u}-\sqrt{2\text{ln}\left( N \right){{\sigma }_{u}}}, $ | (6) |
| $ {{u}_{\text{max}}}=\bar{u}+\sqrt{2\text{ln}\left( N \right){{\sigma }_{u}}}。$ | (7) |
式中:u为速度平均值;N为采集的点数;σu为速度标准差。
借助excel完成公式编辑,对噪点进行滤除,得到滤除后的速度数据,进行湍流强度的计算。湍流强度值由速度的3个分量确定,如下式:
| $ TI=\frac{\sqrt{\frac{1}{3}(\sigma _{u}^{2}+\sigma _{v}^{2}+\sigma _{w}^{2})}}{\sqrt{{{{\bar{U}}}^{2}}-{{{\bar{v}}}^{2}}+{{{\bar{w}}}^{2}}}}。$ | (8) |
试验中,ADV的采集频率为100 Hz,N取为9 000,时间约为90 s,经计算,在此时间段内,经过障碍物湍流强度平均约为8%,保证数值模拟与试验条件相契合,进行结果对比分析。
5 结果对比及分析残差曲线能够直观表示两种湍流模型的区别,在不同尖速比下,通过残差曲线的差异对两种湍流模型收敛速度和稳定性进行初步研究;另通过考察水轮机的性能参数验证不同湍流模型的适用范围,从而根据工况条件选择合适的湍流模型进行数值模拟;考虑到水轮机后1.5D处尾流速度及湍流强度对两种湍流模型的差异进行对比分析,得到适合此水轮机分析的湍流模型。
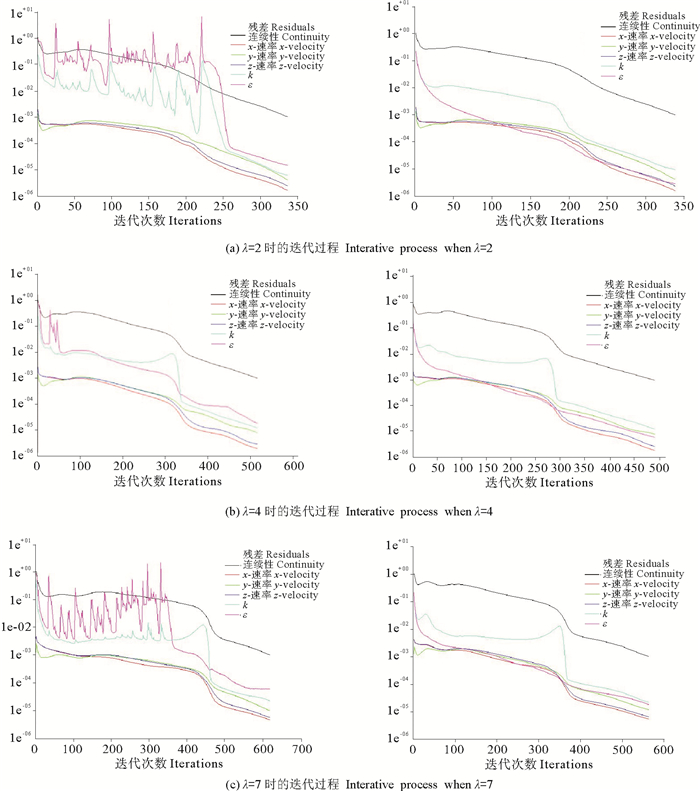
5.1 残差曲线对比选取尖速比为2、4、7时两种不同湍流模型下残差曲线进行对比,其他的尖速比存在一定的相似性,将不一一列举,两种湍流模型的收敛速度和稳定性均存在一定的差别,如图 6所示。
|
图 6 湍流模型(左为Realizable k-ε右为SST k-ω)残差曲线 Fig. 6 The residual curves of turbine model(left for Realizable k-ε; right for SST k-ω) |
从上图可以看出,就收敛稳定性而言,Realizable k-ε在尖速比较大或者较小时,会出现高位震荡,当尖速比为3~6时,表现较为平稳,SST k-ω在近壁面处理方面的优势使其迭代过程收敛较为平稳,稳定性较好。就迭代速度而言,对于不同尖速比下的迭代次数进行统计,Realizable k-ε湍流模型的平均迭代次数为668步,迭代时间为55 min;SST k-ω湍流模型的平均迭代次数为601步,迭代时间为40 min。
5.2 水轮机性能参数对比水轮机的水动力学性能可由功率系数CP,扭矩系数CT,轴向力系数CD三个性能参数表征,公式如下。不同工况下实测数据以及数值模拟结果如表 2和图 7所示。
| $ {{C}_{P}}=\frac{{{P}_{电}}}{0.5\rho {{V}^{3}}\pi {{R}^{2}}}, $ | (9) |
| $ {{C}_{T}}=\frac{T}{0.5\rho {{V}^{2}}\pi {{R}^{2}}}, $ | (10) |
| $ {{C}_{D}}=\frac{F}{0.5\rho {{V}^{2}}\pi {{R}^{2}}}, $ | (11) |
| $ \lambda =\frac{n\pi R}{30V}。$ | (12) |
|
|
表 2 不同湍流模型的计算结果 Table 2 The calculation results of different turbulence models |
|
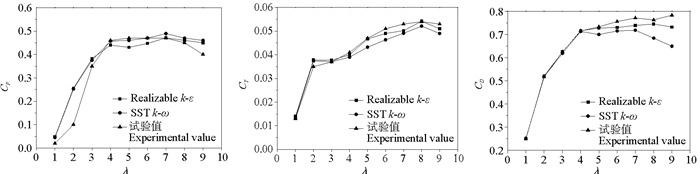
图 7 不同湍流模型性能曲线 Fig. 7 The performance curves of different turbulence models |
式中:P电为功率;T为水轮机转矩;F为轴向力;n为转速。
从试验值与仿真值可知,水轮机的功率系数最高达到0.47,具有良好的水动力学性能;两种湍流模型在一定的误差范围内都能对特定湍流情况下的湍流进行描述,就功率系数而言,在低尖速比(1~6)情况下,SST k-ω比Realizable k-ε接近试验值,而在较高尖速比(7~9)下,Realizable k-ε比SST k-ω更接近试验值;从扭矩系数和轴向力系数可知,Realizable k-ε的计算结果与试验值更加相似。随着转速增大,产生了较高湍流强度的湍流,湍流的脉动影响远远超过分子粘性的影响,这就是Realizable k-ε在高尖速比时接近试验值的原因。
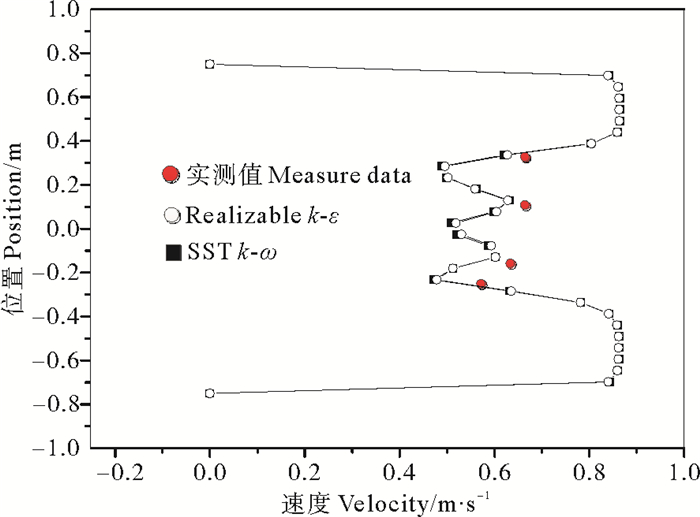
5.3 水轮机后1.5 D处速度及湍流强度对比尖速比为5.6时适合实际工况条件,故在尖速比为5.6时通过水轮机后1.5 D处速度与湍流强度分析及与实测值对比,对两种湍流模型进行更全面的对比分析。其中,水轮机后1.5 D处速度及湍流强度分布如图 8、9所示。
|
图 8 速度对比 Fig. 8 The contrast of velocity |
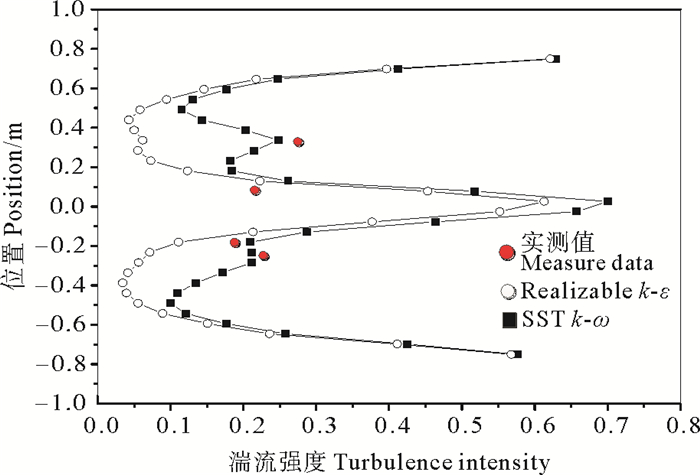
|
图 9 湍流强度对比 Fig. 9 The contrast of turbulence intensity |
由图可知,实测值与两湍流模型进行数值模拟得到的仿真值相近,说明数值模拟具有一定的准确性。采用Realizable k-ε和SST k-ω两种湍流模型进行数值模拟得到的速度分布具有一致性;因装置的影响,湍流强度在同一直线上的变化较大,SST k-ω湍流模型相比Realizable k-ε在数据处理上更接近实测值,得到的湍流强度值更接近实测值。
6 结论本文模拟了流速为0.8 m/s时不同湍流模型(Realizable k-ε与SST k-ω)下的水平轴潮流能水轮机水动力学性能、流场变化以及收敛速度与稳定性,并与试验数据进行对比,实测值与仿真值相契合,并得到以下结论:
(1) 比较两种湍流模型(Realizable k-ε与SST k-ω)的收敛速度及稳定性,湍流模型SST k-ω收敛速度快,稳定性较好,优于Realizable k-ε湍流模型。
(2) 通过对水轮机性能参数的对比可知,所设计的水轮机具有较好的水动力学性能,在低尖速比(1~6)时,SST k-ω比Realizable k-ε接近试验值,而在较高尖速比(7~9)下,采用Realizable k-ε湍流模型得到的计算结果比SST k-ω更接近试验值。
(3) 通过对水轮机后1.5D处流场速度及湍流强度的对比可知,采用两种湍流模型进行数值模拟速度分布相差不大,而采用SST k-ω湍流模型得到的湍流强度相比Realizable k-ε更接近实测值。在水轮机实际运行条件下,采用SST k-ω湍流模型更合理。
本文选取Realizable k-ε与SST k-ω两种湍流模型对水轮机所处的三维湍流情况进行描述,得到水轮机的参数及流场情况,并进行了模型水槽试验,但工程中,水轮机所处的海洋环境相比数值模拟与模型水槽试验环境更为复杂,并不能完全依靠单一的湍流模型进行描述,拟在以后的研究工作中,结合实海况测量数据,通过改变参数修正相应的湍流模型,对实际流场进行近似描述。
| [1] |
张亮, 李新仲, 耿敬, 等. 潮流能研究现状2013[J]. 新能源进展, 2013, 1(1): 53-68. ZHANG Liang, LI Xin-zhong, GENG Jing, et al. Tidal current energy update 2013[J]. Advances in New and Renewable Energy, 2013, 1(1): 53-68. (  0) 0) |
| [2] |
Nak Joong Lee, In Chul Kim, Chang Goo Kim, et al. Performance study on a counter-rotating tidal current turbine by CFD and model experimentation[J]. Renewable Energy, 2014, 79: 122-126.
(  0) 0) |
| [3] |
陈存福.潮流能水平轴水轮机叶片优化及水动力性能研究[D].青岛: 中国海洋大学, 2012. CHEN Cun-fu. Study on Blade Optimization and Hydrodynamic Performance of Horizontal Axis Marine Current Turbine[D]. QingDao: Ocean University of China, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10423-1012504874.htm (  0) 0) |
| [4] |
Nilay Sezer-Uzol, Long Lyle N. 3-D time-accurate CFD simulations of wind turbine rotor flow field[C]. //44th AIAA Areospace Science Meeting and Exihibit. Reno, Nevada: NASA Langley Research Center, 2006. https://arc.aiaa.org/doi/abs/10.2514/6.2006-394
(  0) 0) |
| [5] |
Michael Shives, Curran Crawford. Adapted two-equation turbulence closures for actuator disk RANS simulations of wind & tidal turbine wakes[J]. Renewable Energy, 2016, 92: 273-292. DOI:10.1016/j.renene.2016.02.026
(  0) 0) |
| [6] |
Martin Miltner, Christian Jordan, Michael Harasek. CFD simulation of straight and slightly swirling turbulent free jets using different RANS-turbulence models[J]. Applied Thermal Engineering, 2015, 89: 1117-1126. DOI:10.1016/j.applthermaleng.2015.05.048
(  0) 0) |
| [7] |
黄胜, 王超, 王诗洋.不同湍流模型在螺旋桨水动力性能计算中的应用与比较[J].哈尔滨工程大学学报, 2009, 30(5): 481-484. HUANG Sheng, WANG Chao. Application and comparison of different turbine turbulence models in the computation of a propeller's hydrodynamic performance[J]. Journal of Harbin Engineering University, 2009, 30(5): 481-484. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=HEBG200905003&dbname=CJFD&dbcode=CJFQ (  0) 0) |
| [8] |
关鹏, 丁汪, 翁培. 不同湍流模型对水平轴风力机三维粘性气流特性的影响[J]. 太阳能学报, 2010, 31(1): 86-90. GUAN Peng, DING Wang, WENG Pei. Separated flows around HAWT blade with different turbulent models[J]. Acta Energlae Solaris Sinica, 2010, 31(1): 86-90. (  0) 0) |
| [9] |
丁欣硕. FLUENT14.5流体仿真计算从入门到精通[M]. 北京: 清华大学出版社, 2014: 116-117. DING Xin-shuo. FLUENT14.5 Simulation from Entry to the Master[M]. Beijing: Tsinghua University Press, 2014: 116-117. (  0) 0) |
| [10] |
王福军. 计算流体力学分析-CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004: 125-126. WANG Fu-jun. Computational Fluid Dynamics-CFD Software theory and Application[M]. Beijing: Tsinghua University Press, 2004: 125-126. (  0) 0) |
| [11] |
Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA J, 1994, 32: 1598-1605. DOI:10.2514/3.12149
(  0) 0) |
| [12] |
Omer Musa, Zhou Changsheng, Chen Xiong. Prediction of swirling cold flow in a solid-fuel ramjet engine with a modified rotation/curvature correction SST turbulence model[J]. Applied Thermal Engineering, 2016, 105: 737-754. DOI:10.1016/j.applthermaleng.2016.03.091
(  0) 0) |
| [13] |
Chul-Hee Jo, Jun-Ho Lee, Yu-Ho Rho, et al. Performance analysis of a HAT tidal current turbine and wake flow characteristics[J]. Renewable Energy, 2012, 65: 175-182.
(  0) 0) |
2. Ocean Engineering Key Lab of Qingdao, Qingdao 266100, China
 2019, Vol. 49
2019, Vol. 49


