2. 国家海洋局第一海洋研究所, 山东 青岛 266061
海浪是发生在海面的一种风生重力波, 波长从几十厘米到几百米, 海浪作为物理海洋学的一个重要分支, 研究其生成、发展、消衰机制, 对于国防安全、航海航运、指导渔业生产都具有重要意义[1]。目前遥感手段探测海浪主要是通过合成孔径雷达(SAR), 然而SAR探测海浪存在以下缺陷:(1)方位向高波数截断(最小可探测波长是150~200 m)。(2)图像谱与海浪谱存在强非线性关系。(3)需要输入额外的数据(波浪场或者风场)作为第一猜测谱进行迭代计算。波谱仪作为一种专门探测海浪的遥感设备, 通过小入射角下发射短脉冲并测量海面的后向散射系数获得海面的相关信息。与传统SAR探测海浪相比, 波谱仪具有以下优势:由于采用真实孔径雷达, 其波数截断效应远小于SAR; 采用小角度入射, 电磁波与海面作用视为准镜面散射, 模型简单便于计算; 不需要额外的风场数据输入等。因此波谱仪探测海浪逐渐成为海浪探测的重要手段[2]。然而由于雷达传感器探测海浪时斑点噪声的存在, 机载波谱仪反演海浪谱精度降低, 这种现象在高海况下尤其显著, 因而开展斑点噪声去除方法研究对提高机载波谱仪海浪谱反演精度有着重要意义。
目前, 国内外有关学者对于波谱仪斑点噪声的研究仍处在发展阶段。1985年, Jackson[3]基于准镜面散射理论, 提出了在小入射角下探测海浪的方法并利用机载雷达ROWS(Radar Ocean Wave Spectrometer)对其相关理论进行了验证, 提出了利用雷达参数和地面几何参数计算斑点噪声谱的方法。Engen[4]在1985年使用交叉谱方法反演海浪谱, 提出通过计算交叉谱不仅可以消除海浪传播的180°模糊, 而且可以消除SAR斑点噪声。Hauser[5]基于交叉谱思想, 通过计算一定时间间隔内的相邻方位向调制函数的互相关谱去除斑点噪声。任林[6]基于垂直于海浪主波方向无海浪调制长波信息的理论, 提出了以垂直于海浪主波方向信号谱为噪声谱的计算方法。
本文通过对机载波谱仪探测海浪算法的研究, 实现了四种去除斑点噪声方法, 并针对高海况分别利用四种去噪算法去除斑点噪声, 并对去噪结果进行了定量分析与评价。
1 数据介绍 1.1 波谱仪数据本文所使用的波谱仪数据为机载波谱仪STORM(Système de Télédétection pour l’Observation Radar de la Mer)飞行数据。STORM是一种调频连续波雷达, 在小入射角下发射调频连续波并通过旋转天线进行360°扫描, 实现对每个方位向的海浪观测。STORM包括HH和VV两种极化方式, 每隔8 ms交替运行。其采用双天线, 一根用于信号发射, 另一根用于接收, 且都可以进行360°旋转, 从而实现逆时针和顺时针的交替扫描。
2002年10—12月在法国大西洋沿岸和英吉利海峡ENVISAT ASAR VALPARESO试验中进行了STORM飞行验证。在此次飞行验证中, STORM安装在Meteo-France的MERLIN-Ⅳ飞机上, 入射角为20°, 双波束的3 dB天线宽度在距离向为±15°, 方位向为±3.8°, 每分钟匀速旋转3圈。
1.2 浮标数据浮标数据采用了位于48°31′42″N, 5°49′03″W的“PHAROS”浮标, 该浮标数据时间间隔为1 h, 浮标主要提供风向、风速以及海浪谱等信息。
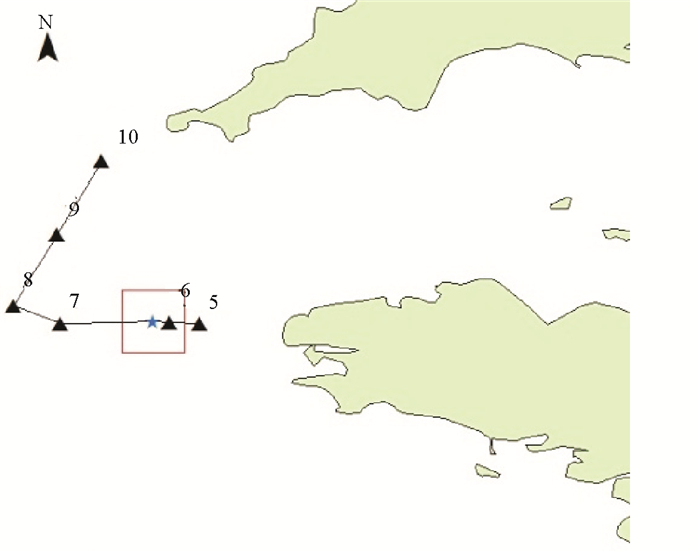
本文选择2002年11月4日试验中航次21的观测数据以及同步浮标数据, 该航次STORM飞行轨迹以及浮标位置见图 1。
|
图 1 STORM飞行轨迹以及同步浮标位置, 其中星号代表浮标位置, 方框代表匹配的空间窗口, 黑色实线代表飞行轨迹, 三角形代表数据点位置 Fig. 1 STORM flight and synchronization buoy location, star represent buoy location, boxes represent space window, black solid line represent the flight path, triangles represent dataset position |
斑点现象是指雷达发射相干电磁波到达地表单元, 由于地表随机散射单元散射信号与发射波发生干涉, 使得每一散射单元的回波为干涉信号的叠加, 表现为某一散射单元回波值随某一均值呈现起伏变化的现象。由于斑点现象导致散射单元回波值出现不同的噪声称为斑点噪声[7]。在机载波谱仪数据处理中, 斑点噪声对调制信号的影响为:
| $ P\left( {k, \phi } \right) \approx {S_R}\left( k \right){P_m}\left( {k, \phi } \right) + \left( {1 + {\eta ^2}} \right){S_N}(k)。$ | (1) |
其中:P为雷达实际接收信号的功率谱; SR表示雷达脉冲响应函数; Pm表示所需要的信号调制谱; SN(k)为斑点噪声谱; η2(φ)为RMS调制深度[8]。
在机载波谱仪数据处理过程中, 斑点噪声去除效果直接影响海浪谱反演精度。目前机载波谱仪斑点噪声去除方法主要有4种, 分别为数学法、阈值法、交叉谱法和小波分析法。
2.1 数学法通过雷达参数以及地面几何参数计算斑点噪声谱, 然后由回波信号谱减掉斑点噪声谱得到调制谱。Jackson给出了计算斑点噪声的计算方法[3],
| $ {S_{\text{R}}}(k) = {\text{exp}}\left( {\frac{{-{k^2}}}{{2{k_p}^2}}} \right), $ | (2) |
| $ {k_p} = 2\frac{{2\sqrt {{\text{ln}}2} }}{{\Delta x}}, $ | (3) |
| $ {S_N}\left( k \right) = \frac{1}{{N\sqrt {2{\text{π}}{k_p}} {\text{exp}}\left( {\frac{{-{k^2}}}{{2{k_p}^2}}} \right)}}。$ | (4) |
其中:Δx表示地距分辨率; k表示波数; N表示脉冲积分个数。
2.2 阈值法通常来讲, 海浪的能量主要沿主波方向传播, 因而当天线方向垂直于主波方向时, 此时调制谱中基本没有长波信息因而可以视作噪声谱, 在计算调制谱时, 将回波信号谱每个方位向谱值减掉该噪声谱值就可以得到调制谱[6]。
2.3 交叉谱法交叉谱反映的是两个不同的随机序列在频率域变化上的相互关系, 它等于两函数交叉相关的傅里叶变换。利用“交叉谱”的思想, 对一定时间间隔的回波信号进行相干处理, 计算二者的互功率谱直接得到调制信号谱, Hauser给出了机载波谱仪互功率谱计算方法[5],
| $ {P_m}\left( {k, \phi } \right) = Re\{ FT\left( {m\left( {x, \phi, t} \right)} \right)\cdot F{T^*}(m(x, \phi, t + \delta t))\} 。$ | (5) |
其中:Pm表示信号调制谱; m(x, φ, t)表示某一时刻某一方位向的调制函数; δt表示相邻方位向调制函数时间间隔; δt要求足够大使得一定时间间隔相邻两方位向斑点噪声不相关, 同样要求足够小使得二者不会超过一个分辨率单元。
2.4 小波分析法小波分析是目前主流的信号处理方法之一, 其良好的时频局部化和多分辨分析能力, 使得小波分析在数据处理过程中应用越来越广泛, 其中利用小波分解和重构技术, 可以很好的去除观测数据中的噪声, 本文通过对调制函数进行小波分解和重构, 再计算调制谱, 可以去除调制信号斑点噪声, 提高反演精度。
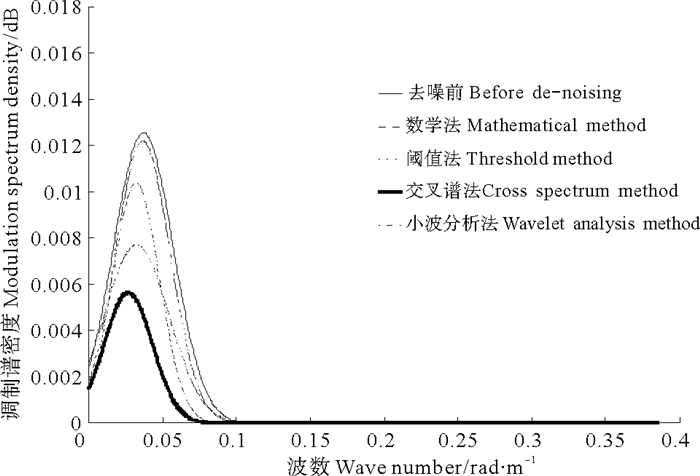
3 结果分析为验证STORM机载波谱仪反演海浪谱精度, 连续空间匹配窗口内数据点6位置附近连续8圈STORM飞行数据进行处理, 并分别利用上述4种方法对其进行去噪处理, 以其中一圈为例, 去噪前、后, STORM调制密度谱见图 2。
|
图 2 STORM调制密度谱 Fig. 2 STORM modulation density spectrum |
由图 2可见, 该方位向下能量主要集中0.01~0.1 rad/s波数范围内, 与波谱仪理论波数截断效应基本一致, 去噪前、后调制谱密度曲线整体趋势基本没有发生改变。去噪前, 调制谱值在0.03 rad/s波数位置达到峰值约为0.122 dB, 使用数学法去噪后, 调制谱值发生微小降低, 其中峰值降低至0.012 dB, 峰值波数位置基本没有发生改变, 仍位于0.03 rad/s附近。使用阈值法去噪后, 调制谱值发生较小降低, 其中峰值降低至0.01 dB, 峰值波数位置基本没有发生改变, 仍位于0.03 rad/s附近。使用交叉谱法去噪后, 调制谱值发生明显的降低, 其中峰值降低至0.006 dB, 峰值波数位置发生轻微左移, 但仍位于0.025 rad/s附近。使用小波分析法去噪后, 调制谱值发生明显的降低, 其中峰值降低至0.008 dB, 峰值波数位置也发生轻微左移, 但仍位于0.025 rad/s附近。
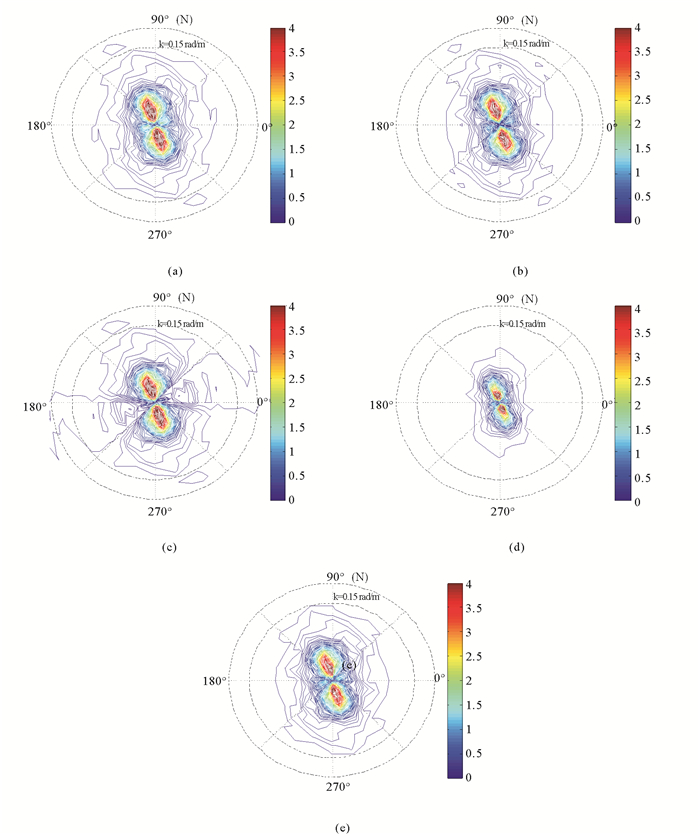
去噪前后, STORM反演所得海浪高度谱如图 3所示。
|
((a)表示去噪前,(b)表示利用数学法去噪后,(c)表示利用阈值法去噪后,(d)表示利用交叉谱法去噪后,(e)表示利用小波分析法去噪后。before de-noising(a),mathematical method(b),threshold method(c),cross spectrum method(d),wavelet analysis method(e).) 图 3 Storm反演所得海浪谱 Fig. 3 Storm inversed wave spectrum |
由图 3可见, 与(a)相比, (b)、(e)波高均发生减小, 海浪能量分布基本没有发生改变, 可见二者去噪效果相近, (c)主波方向波高基本没有发生改变, 垂直于主波方向波高发生减小, 海浪能量分布也发生了变化, 只保留了垂直于主波方向的能量, (d)去噪效果最明显, 不仅波高发生了明显减小, 而且海浪能量分布也发生了变化, 只保留了主要能量部分, 其他视为噪声被去除掉。
有效波高通常指三分之一大波平均波高, 由于其统计可变性最小, 因为可以作为海浪特征波高以表征海浪特性, 计算公式为:
| $ {F_{HND}}\left( k \right) = {\smallint _0}^{2\phi }F(k, {\text{π}})kd\phi, $ | (6) |
| $ {H_s} = 4\sqrt {{\smallint _k}{F_{HND}}\left( k \right)dk}。$ | (7) |
由以上海浪谱计算可得, 去噪前有效波高约为4.58 m, 使用上述4种方法去除斑点噪声后, 得到的有效波高分别约为4.24、4.05、3.96、4.18 m, 去噪前、后主波长与主波向基本没有发生变化, 分别约为210 m和135°。
利用“PHAROS”浮标数据与去噪前、后反演得到的海浪谱有效波高进行对比分析, 如表 1、2所示:
|
|
表 1 去噪前后有效波高值 Table 1 The significant wave height before and after de-noising |
|
|
表 2 去噪前后有效波高精度评价 Table 2 The significant wave height accuracy assessment before and after de-noising |
表示连续8圈测得的有效波高平均值, RMSE表示在连续8圈数据有效波高均方根误差, 绝对误差表示去噪后所得Hs与浮标所测得有效波高之差, 相对误差表示绝对误差与浮标所测得有效波高之比。
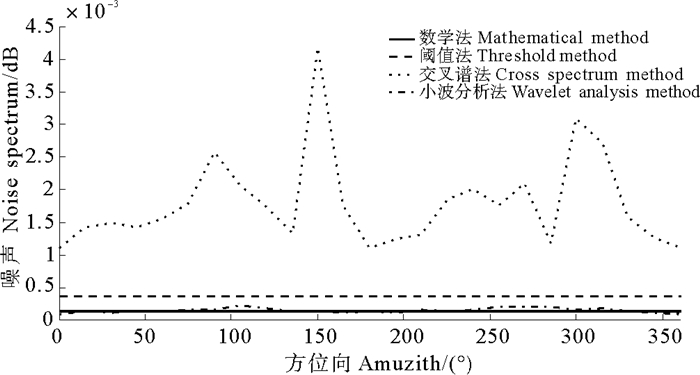
4种去噪方法得到的噪声谱如图 4所示:
|
图 4 斑点噪声方位向分布图 Fig. 4 speckle azimuth distribution |
(1) 由于现场浮标数据观测有限, 连续8圈飞行数据均采用“PHAROS”浮标进行验证。未去噪前反演的有效波高RMSE仅为0.075, 说明该8圈数据可以视为同一海况进行验证, 采用4种去噪方法反演的有效波高RMSE最小为交叉谱法, 约为0.008, 说明交叉谱法在去除斑点噪声过程中, 可以很好地降低不同圈数之间反演有效波高的差异, 提高反演精度。阈值法反演的有效波高RMSE最大, 约为0.127, 说明使用阈值法去除斑点噪声, 会使得不同圈数间反演得有效波高差异增大, 降低反演精度。
(2) 本文4种去噪方法均可以有效地去除斑点噪声, 其中使用交叉谱法去除斑点噪声效果最佳, 有效波高绝对误差为0.25 m, 相对误差为7%;其次为阈值法, 有效波高绝对误差为0.90 m, 相对误差为25.3%;最后为小波分析法和数学法, 有效波高绝对误差为1.04 m和1.1 m, 相对误差分别为29.2%和30.9%。
(3) STORM去噪前反演有效波高的绝对误差约为1.54 m, 相对误差约为43.3%, 与去噪效果最好的交叉谱方法反演结果相比, 有效波高绝对误差降低了1.29 m, 相对误差降低了36.3%, 与去噪效果最不理想的数学法反演结果相比较, 有效波高绝对误差降低了0.44 m, 相对误差降低了12.4%, 说明4种去噪方法可以很好地去除机载波谱仪斑点噪声, 提高海浪谱反演精度。
(4) 由交叉谱法计算得到的噪声谱在150°以及310°方位向有极大值0.004 dB, 其他方位向噪声谱值基本一致, 约为0.002 dB, 斑点噪声统计特性与反射面元密切相关, 可能由于海浪或者风的影响使得海浪表面斜率概率密度函数发生变化导致海浪传播方向噪声谱值变大, 本次试验由浮标测量得到风向约为275°, 反演得到海浪传播方向约为135°, 可近似认为噪声谱在主波方向和主波相反方向有极大值, 可见高海况下交叉谱法适用, 低海况下交叉谱法适用性将在以后的工作中进行验证。由阈值法计算得到的噪声谱, 由于取垂直于海浪传播方向调制谱值作为噪声谱, 其在方位向基本没有变化, 此方法适于单一涌浪传播海况, 对于复杂海况, 由于垂直于海浪主波方向可能存在海浪传播, 此法并不适用。由数学法和小波分许法计算得到的噪声谱, 二者谱值基本相同且不随方位向发生变化, 因而二者可能只适用于低海况下。
4 结语本文通过对STORM机载波谱仪数据去噪算法的研究, 实现了4种波谱仪斑点噪声去除方法, 并分别对4种去噪方法进行了对比验证与评价, 结果表明:4种去噪方法可以很好地去除机载波谱仪斑点噪声, 其中交叉谱方法去除斑点噪声效果最理想, 去噪后反演所得有效波高与浮标数据基本一致。另外, 由于本次试验数据量所限, 尚未对低海况以及其他复杂海况进行分析, 待CFOSAT发射后, 将分别针对其他海况展开更深入分析。
致谢 作者感谢法国国家太空研究中心(CNES)Dr.Hauser提供STORM数据集以及“PHAROS”浮标数据。
| [1] |
文圣常, 余宙文. 海浪理论和计算原理[M]. 北京: 科学技术出版社, 1985, 228-246.
(  0) 0) |
| [2] |
储小青. 海浪波谱仪海浪遥感方法及应用基础研究[D]. 青岛: 中国科学院海洋研究所, 2011.
(  0) 0) |
| [3] |
Jackson F C, Lyzenga D R. Microwave techniques for measuring directional wave spectra[M]. Surface Waves and Fluxes.Springer Netherlands, 1990, 221-264.
(  0) 0) |
| [4] |
Engen G, Johnsen H. SAR-ocean wave inversion using image cross spectra[J]. Geoscience and Remote Sensing, IEEE Transactions on, 1995, 33(4): 1047-1056. DOI:10.1109/36.406690
(  0) 0) |
| [5] |
Hauser D, Caudal G, Le Gac C, et al. KuROS: A new airborne Ku-band Doppler radar for observation of the ocean surface[C]. Geoscience and Remote Sensing Symposium (IGARSS), 2014 IEEE International. IEEE, 2014: 282-285.
(  0) 0) |
| [6] |
任林. 星载雷达微波遥感海浪方向谱仿真与反演研究[D]. 南京: 南京理工大学, 2011.
(  0) 0) |
| [7] |
韩春明, 郭华东. SAR图像斑点噪声抑制的本质[J]. 遥感学报, 2002, 6(6): 470-474. DOI:10.11834/jrs.20060612 (  0) 0) |
| [8] |
Hauser D, Caudal G, Rijckenberg G, et al. RESSAC:A new airborne FM/CW radar ocean wave spectrometer[J]. Geoscience and Remote Sensing, IEEE Transactions on, 1992, 30(5): 981-995. DOI:10.1109/36.175333
(  0) 0) |
| [9] |
Jackson F C, Walton W T, Hines D E, et al. Sea surface mean square slope from K u‐band backscatter data[J]. Journal of Geophysical Research:Oceans (1978-2012), 1992, 97(C7): 11411-11427. DOI:10.1029/92JC00766
(  0) 0) |
| [10] |
Hauser D, Soussi E, Thouvenot E, et al. SWIMSAT:A real-aperture radar to measure directional spectra of ocean waves from space-main characteristics and performance simulation[J]. Journal of Atmospheric and Oceanic Technology, 2001, 18(3): 421-437. DOI:10.1175/1520-0426(2001)018<0421:SARART>2.0.CO;2
(  0) 0) |
2. The First Institute of Oceanography, State Oceanic Administration, Qingdao 266061, China
 2018, Vol. 48
2018, Vol. 48


