2. 中国海洋大学山东省海洋环境地质工程重点实验室,山东 青岛 266100;
3. 中国海洋大学环境科学与工程学院,山东 青岛 266100
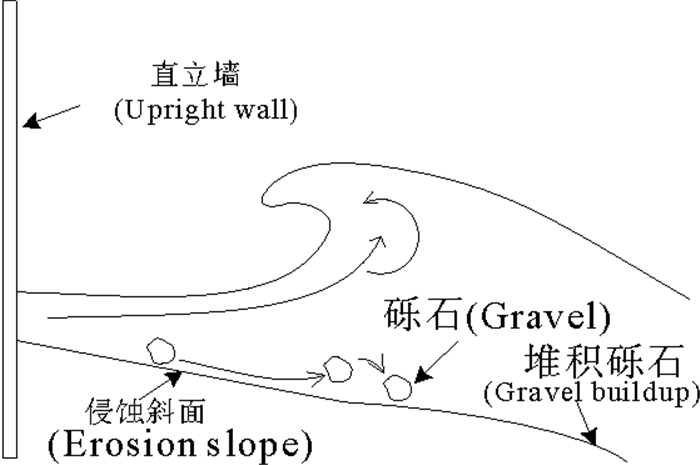
海岸堤坝用以港池或海岸的防护。在实际工程中,发现常见的抛石堤在长期的波浪作用下稳定性较差。以东营中心渔港为例,其航道南部采用的是纯抛石型防波堤,航道北部采用的是直立墙与抛石护坡组合堤(见图 1)。该海域多受北向来浪和东北向来浪的影响,北部的组合堤受到的波浪作用强于南部的纯抛石堤。但是,航道南部的纯抛石型防波堤破坏严重,栅栏板也发生错位,需要进行工程修复,而航道北部的组合堤却仍具有较好的结构完整性,甚至在经历了四十年一遇的海冰影响后还能安然无恙。可见直立墙与抛石护坡组合堤具有较高的稳定性。

|
(a.海冰作用后依然稳固的组合堤;b.被破坏的纯抛石防波堤图。a.Destroyed pure rubble-mound breakwater; b.Composite breakwater that remain solid aftersea ice effects.) 图 1 东营中心渔港防波堤位置(照片拍摄:何富荣) Fig. 1 Dongying central fishing harbor breakwater location(Photo taken by HE Furong) |
直立堤或抛石防波堤稳定性的研究成果有很多。赵子丹和薛晓春等通过室内水槽试验,分析了波浪作用下直立堤前的沙床冲刷规律[1-4],俞聿修等探究了斜向和多向不规则波作用于直墙堤上的波浪荷载的计算方法[5],日本的椹木亨提出波浪在抛石坡面上产生的共振现象是决定其稳定条件的重要因素并设计试验探究了其作用机理[6],李增志等通过物理模型试验和数值模拟的方法提出块体上的受力随着防波堤孔隙率以及块体平均半径的增加而减小[7],吴苏舒等则通过理论分析与试验对比确定了护底块石的稳定重量计算方法[8]。已有的研究成果主要是将直立墙与抛石护堤分开单独进行研究,并未考虑到两者结合后对于整体结构稳定性的影响。
利用水力冲沉预制桩的水力插板技术,可以高效率地形成根基稳定的直立墙[9-10],墙前增加抛石斜坡,有利于消浪和防止堤前冲刷,这样即可形成造价低廉的直立墙与抛石护坡组合堤。本文针对直立墙与抛石护坡组合堤形式,通过波浪水槽试验探究此组合堤前抛石斜坡稳定性问题,以期为实际工程设计提供依据。
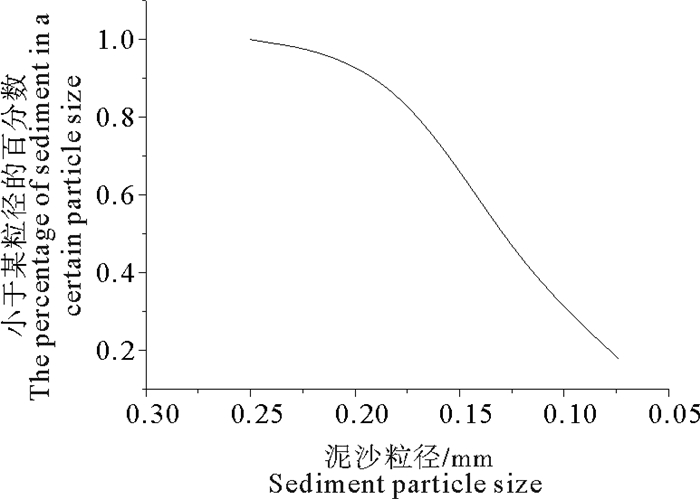
1 试验方法 1.1 材料与设备本文主要是开展波浪水槽试验探讨直立墙与抛石护坡组合堤稳定性的一般规律,在波浪条件和抛石材料的选择上以保证能够使斜坡表面抛石发生位移为主,不做考虑比尺问题的模型试验研究。通过预试验选取角砾作为抛石材料(见图 2),保证此粒径的砾石在实验室波浪条件下能够发生运动,砾石规格见表 1,砾石平均重量为8.28 g,中值粒径为2.7 cm。试验用基床沙取自青岛海滩,用标准孔目的孔筛进行筛分,获得粉细沙(<0.25 mm),级配曲线见图 3,中值粒径为0.12 mm。直立墙采用厚1 cm、宽50 cm、高135 cm的铁板。

|
图 2 试验用角砾图 Fig. 2 Test breccia |
|
|
表 1 砾石规格表 Table 1 Gravel specification table |
|
图 3 试验沙床沙级配曲线 Fig. 3 Grain-size distribution of sand used inthis experiment |
试验设备主要为波浪水槽。该水槽长14 m,宽0.5 m,高0.7 m,一端配有造波系统,可形成规则波,另一端配有消波系统。试验中使用了DEWE43V数据采集系统(误差小于0.1 mm)、波高仪(误差小于1 mm)、DV录像机等测量仪器。波浪作用后的剖面采用刻度尺进行测量(毫米级)。
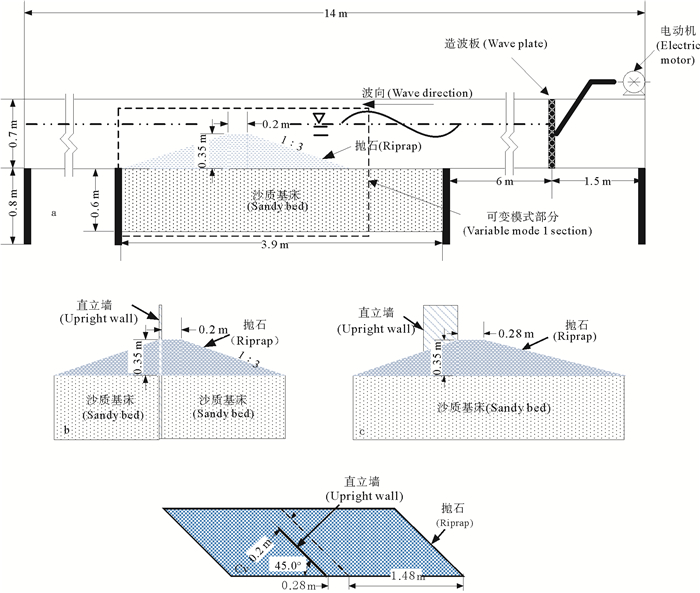
1.2 试验方案试验设计为三种模式,为纯抛石堤(模式1)、正向直立墙前抛石组合堤(模式2)和斜向直立墙前抛石组合堤(模式3),分别模拟纯抛石防波堤(见图 4a)、受正向来浪影响的组合堤(见图 4b)和受斜向来浪影响的组合堤(见图 4c),其中模式3抛石护坡的等高线平行于直立墙。抛石护坡设计为宽肩台式护坡,肩长20 cm,高35 cm,斜坡比为1: 3。试验水深设计为30、35、40 cm,在各水深条件下施加波况近似相同的大、小规则波进行试验。每组模型施加相同的工况,试验工况见表 2。试验结束的控制条件为抛石斜坡形态在波浪作用下不再发生变化。试验首先是铺设砂质基床,然后在基床上设置抛石堤或直立墙,加水至设计工况水深,在静置20 h以上后开始造波试验。
|
(a.纯抛石堤(模式1);b.正向直立墙前抛石组合堤(模式2);c.斜向直立墙前抛石组合堤(模式3)正视图;Cv.斜向直立墙前抛石组合堤(模式3)俯视图。a.Pure ripped-rock embankment; b.Combined dykes ofdirect upright wall and ripped-rock; c.The infront view of combined dykes of diagonal upright wall and ripped-rock; Cv.The.elevation view of combined dykes of diagonal upright wall and ripped-rock.) 图 4 试验堤设置形式图 Fig. 4 Schematic diagram of test bank model |
|
|
表 2 试验工况 Table 2 Experimental parameters |
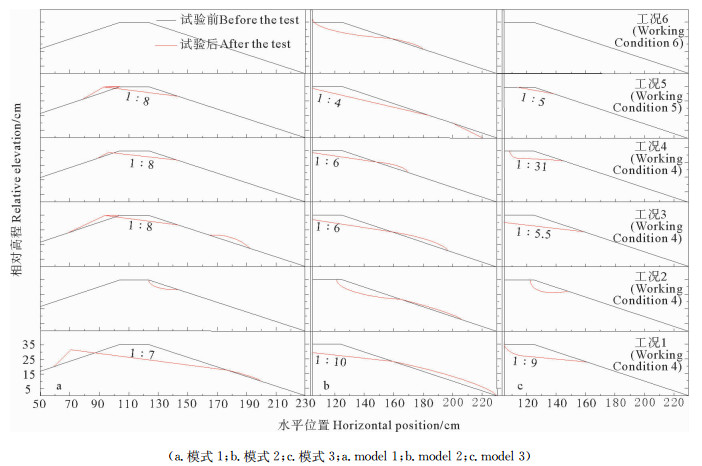
将纯抛石堤、正向直立墙前抛石组合堤和斜向直立墙前抛石组合堤在各工况下(见表 2)获得的最终稳定的抛石斜坡剖面,绘制成图(见图 5)。下文中所提到的斜坡比是指在波浪作用后形成的直斜面式侵蚀坑即图中堤前红色直线部分的斜坡比。
|
图 5 三种模式试验结果图 Fig. 5 Three models test results |
将纯抛石堤的试验结果绘制成图(见图 5a)。在不同的工况下,随着波浪的持续作用,砾石趋于紧密与稳定,直至最后达到静态稳定,即斜坡砾石不再发生运动。波浪作用后抛石斜坡大多被塑造成了一个具有1: 7至1: 8斜坡比的新斜坡。在形成新斜坡的试验中,破碎的波浪作用于护坡坡面,将坡顶砾石推至坡后堆积。工况3、4、5的三组试验中,坡顶的侵蚀深度均为7 cm左右,而在工况1的条件作用下,护坡的侵蚀深度为17 cm。另外,在工况2条件的试验中,波浪作用使得平顶前的砾石发生松动,但由于水深较低,波高较小,未能使得平顶上的砾石发生松动,因此未能塑造成新的斜坡,而是仅仅在平顶前形成了一个深度约为3 cm的侵蚀坑。工况6由于波浪未发生破碎,因此护坡剖面并未发生明显变化。
2.2 模式2在正向直立墙前抛石组合堤试验中(见图 5b),抛石护坡的稳定态表现为动态平衡,即斜坡砾石存在往复移动但斜坡形态不再发生改变。试验过程中,墙前的波浪出现较大扰动,砾石随着波浪运移至墙脚,被直立墙所阻挡,进而随墙前回流而滚落至侵蚀面以下位置。在模式2的6种试验工况下,相比于纯抛石堤试验,最后形成的稳态新斜坡坡度值域范围较大,并且侵蚀起点受破波位置影响明显。其中工况5的试验是模式2的第一组试验,试验中由于水深和波高较大,波浪扰动剧烈,发生了抛石护坡整体下沉的现象。在该次试验之后,护坡的砾石变得更加紧密,其下部沙质基床也变得更加密实,之后试验组次中再未出现护坡下沉现象。
2.3 模式3斜向直立墙前抛石组合堤试验中,认为波浪作用后的抛石护坡具有与直立墙平行的等高线,沿垂直等高线的方向测量护坡在波浪作用后的变化情况并绘制成图(见图 5c)。在工况6的波浪作用下墙前扰动较弱,抛石护坡未发生明显变化。在模式3试验过程中,墙前砾石在波浪作用下起动并跟随波浪爬上护坡在墙脚处碰撞直立墙发生斜向反射,沿直立墙延伸向运动,最终达到静态平衡。由于墙前波浪反射有一定角度,因此墙前扰动没有模式2试验中的扰动强烈,因此斜向直立墙前的护坡侵蚀程度较模式2弱。
3 分析与讨论本文通过对比波高、水深、波浪入射角度和有无直立墙对抛石护坡侵蚀情况的影响,分别给出在这四种影响因素起主导作用时的侵蚀模式下所产生的问题以及问题产生的原因,以此来提出每种模式下最好的设计方案。
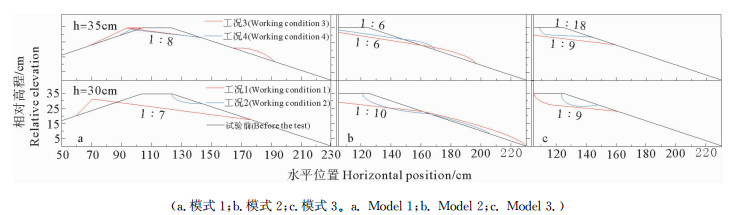
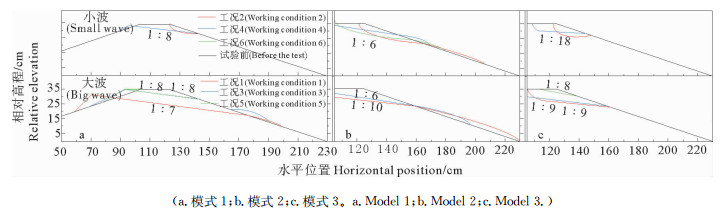
3.1 波高的影响将水深相同、周期相近、波高不同的三种模式下的试验结果绘制在一起(见图 6),比较波高对抛石斜坡形态的影响。波高的变化对侵蚀面起点位置有影响,试验结果给出抛石侵蚀面起点位置在大波作用下低于小波的,这是由于破波位置不同造成的,破波位置附近扰动最为强烈,大多数起动的砾石在这个位置起动,侵蚀面也在这个位置处开始形成。这符合大多数物体受波浪侵蚀的一般规律,对于抛石护坡,有几组例外,分别为模式1(见图 6a)35 cm水深的两组试验和模式2(见图 6b)30 cm水深的两组试验,前者在大波和小波分别作用下形成的侵蚀面起点位置几乎相同,这是因为在35 cm水深条件下,最先起动并发生运移的砾石是位于护坡平顶的砾石,波浪在越坡流动中,推动砾石,使得原斜坡被改造为与波浪动力相适应的具有一定角度的稳定斜坡,且稳定斜坡一旦形成,便不再轻易发生改变[11],因此在试验中形成的侵蚀面只发展到图中所示位置。
|
图 6 波高影响对比图 Fig. 6 Wave height impact comparison diagram |
堆积砾石的顶部起点位置是由来波和回波确定的,是一个固定位置,而在模式1工况3的试验中侵蚀面起点上移了,因此侵蚀面和堆积砾石没有相连。与之对比的模式2(见图 6b)和模式3(见图 6c)试验中,由于直立墙的影响使得墙前产生了较大扰动,使得不同波浪作用下侵蚀深度会产生变化,因此没有出现大波小波作用后侵蚀面相同的现象。在30 cm水深条件下的模式2试验中,出现了小波作用下产生的侵蚀面起点低于大波作用下产生的侵蚀面起点的情况,这是因为工况2条件下,波浪未能使平顶砾石起动,只塑造了一个平顶前的凹槽,砾石无法爬上坡度较大的凹槽,只能随着回流向坡下滚动,在滚落的砾石的摩擦和波浪回流的共同作用下,凹槽侵蚀面的下端点逐渐降低。
在以波高为主导影响因素的侵蚀模式下,波高影响的是砾石起动位置及起动砾石大小。波高对抛石斜坡侵蚀形态的影响大小与水深有关,水深和波高共同影响破波位置和波浪能作用到的最远位置,进而影响砾石起动位置即侵蚀面起点和终点位置。当砾石从顶部开始起动时,侵蚀面起点位置受破波位置即波浪大小影响较小。当砾石从斜坡腰部开始起动时,侵蚀面起点位置受破波位置即波高大小影响较大,且由于斜坡腰部的砾石起动较为困难,因此波高对起动砾石大小的影响也较大。可见,在工程中加大淹没抛石深度使砾石从护坡顶部开始起动可以减小波高对侵蚀作用的影响,同时也可以减轻侵蚀程度。
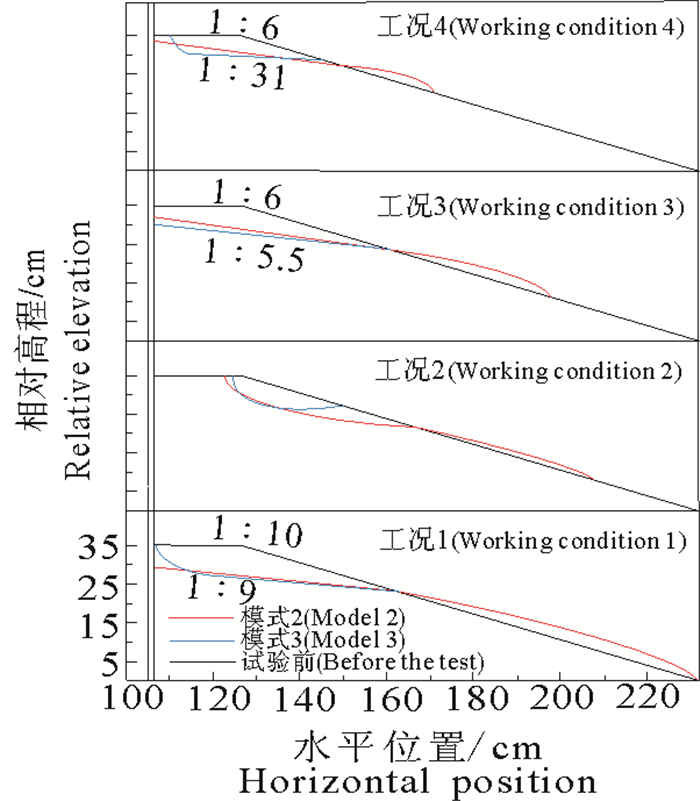
3.2 水深的影响将波高相同、周期相近、水深不同的三种模式下的试验结果绘制在一起(见图 7),比较水深对抛石斜坡形态的影响。D.斯蒂芬森研究指出,对于纯抛石防波堤,砾石可被波浪搬动而破坏的尺寸受控情况有两种:坡度较缓时(缓于1: 3),回落波控制;陡坡情况(陡于1: 1.5)则是上爬波控制[12]。本文试验采用的护坡坡度为1: 3,且由于直立墙的存在使得回流作用进一步增强,因此本文试验属于回落波控制,当回落波较强时,被搬运的砾石多,这也与试验中观察到的现象一致。
|
图 7 水深影响对比图 Fig. 7 Water depth impact comparisondiagram |
在模式2(见图 7b)和模式3(见图 7c)试验中发现,墙脚侵蚀面的形态是直斜面还是凹槽取决于来波能否使墙脚砾石起动以及回流能否使墙脚砾石发生运移,当两个条件都满足时侵蚀面的形态为直斜面,否则为凹槽。砾石起动受来波大小影响,运移受回流强弱影响,回流的强弱受水深影响。这是因为护坡中的砾石主要受到3个力:水流作用力、重力和砾石间嵌固力,水流作用力分为垂直于坡面方向的力和铅直方向的力,铅直方向的力即为浮力。波浪作用下,当水流作用力大于砾石间的嵌固力时,砾石便会发生松动,来波时的水流作用力主要体现在波浪破碎时对砾石的冲击力,回流产生的作用力主要体现在波浪回落时由于水质点运动产生的拖拽力。椹木亨通过对水质点运动加速度的记录发现,波浪无论上爬或回卷,水质点运动的最大加速度均在紧挨着静水位的下边出现峰值[6]。可见,当静水位线越接近抛石护坡、接触面积越大时,回流产生的作用力越大。因此在本文试验中,35 cm水深条件时护坡受到的回流作用力最大,40 cm水深时受到的回流作用力最小。在模式2试验中工况4和工况6的波浪均使得墙脚砾石松动,但因40 cm水深(工况6)时回流较弱,因此形成了凹槽式侵蚀面,35 cm水深(工况4)时回流较强,形成了直斜面式侵蚀面。同理,模式3大波作用下的三组试验中30 cm水深(工况1)时的波浪未作用到墙脚处,只有35 cm水深(工况3)时的波浪使得墙脚砾石起动并随回流发生运移,最终形成直斜面式的侵蚀面。
试验结果中,侵蚀面起点与水深具有相关性,水深越深,侵蚀面起点越高,这是破波位置的不同导致的,只有模式2中大波作用下的两组试验结果例外,两组试验形成的侵蚀面起点几乎一致。这是因为在大波作用下,来波受回波影响大,由于两组试验的波浪周期一样,所以回波均在图中侵蚀面起点处与来波相遇,并在该位置处产生了一个上升力(见图 8),使得回流携带的砾石在该位置处开始堆积。
|
图 8 模式2墙前波浪内质点运动示意图 Fig. 8 The motion diagram of the particles in front of the upright wall inmodel 2 |
在以水深为主导影响因素的侵蚀模式下,水深影响的是回流的强弱,进而影响侵蚀程度的强弱。产生这一影响的原因是水质点运动的最大加速度总是紧挨着静水位的下边出现峰值。针对这一特点,在组合堤抛石护坡的设计上建议采用三角形结构而不是平顶式结构以减轻回流作用对护坡的侵蚀程度。
3.3 波浪入射角度的影响对于波浪入射角度对抛石斜坡形态的影响,可以比较波浪正向入射与45°斜向入射的试验结果(见图 9)。波浪入射角度影响砾石的运移方向问题。正向入射波作用下部分砾石堆积在侵蚀面以下,斜向入射波作用下没有堆积产生。这是因为斜向波碰撞到直立墙后发生斜向反射,在垂直于直立墙方向上的扰动远不如模式2试验中的强烈,波浪沿墙体延伸向运动,因此回流较弱,此时砾石的起动和运移主要受来波影响,砾石在运动到墙脚后也沿着墙体延伸向运动。因此在侵蚀面以下没有形成堆积。在对比的四组试验结果中,除工况2外,其余三组试验的侵蚀程度相近。在工况2条件下模式2护坡的侵蚀情况比模式3的严重,这是因为两种模式均是在护坡平顶前部形成了一个凹槽侵蚀面,而正向波在直立墙前造成的扰动较斜向波强,在较强的回流作用下使得模式2中的侵蚀面逐渐扩大。同时,回流强度的不同也导致了在工况4和工况1条件下,正向波能使墙脚砾石起动并发生运移而斜向波不能。
|
图 9 波浪入射角度影响对比图 Fig. 9 Wave incidence angle impact comparisondiagram |
在以波浪入射角度为主导影响因素的侵蚀模式中,波浪入射角度影响墙前扰动的剧烈程度及砾石的运动方向。当波浪正向入射时,墙前扰动剧烈,波浪作用力强,当波浪入射角度为45°时墙前扰动弱,波浪作用力弱。Hsu[13]、Fenton[14]、Tsang[15]、李本霞[16]等通过试验和理论分析得出在波浪入射角度小于等于45°时波浪作用力随入射角度的增大而减小。可见,从减轻护坡侵蚀角度出发,防波堤朝向应与波浪入射方向有一定角度,且在小于45°的范围内越大越好。从砾石运动方向角度出发,防波堤朝向还应考虑所处水域经常出现的来浪方向、频率、强弱,找出一个能使砾石尽可能多的留在抛石护坡上以作备用砾石的朝向角度。
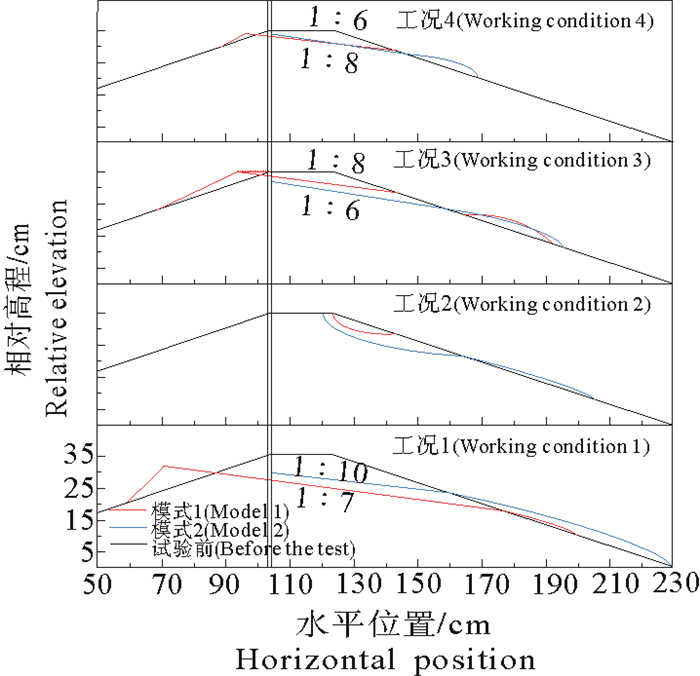
3.4 有无直立墙的影响对于直立墙的有无对抛石斜坡侵蚀形态的影响,可以通过比较模式1和模式2试验结果(见图 10)来获得。在侵蚀程度上,由于模式2试验中墙前扰动强烈,因此墙前护坡侵蚀程度更为严重,但是护坡砾石在波浪作用后会变得更加密实。在侵蚀面形态上,模式1和模式2试验结果均是形成一个具有相近斜坡比的侵蚀面,不同的是侵蚀面的斜坡比不同。工况3、4条件下模式2的侵蚀面较模式1的陡,这是因为侵蚀面的形成是一个坡度逐渐变缓的过程,模式2试验中可以认为侵蚀面最初期望变成一个更平缓的斜坡,但由于直立墙的阻碍,侵蚀面在变缓到一定程度后便无法继续变缓,同时因为来波与回波在某个特定位置处相遇,砾石也在该位置处开始堆积,即侵蚀面起点是一定的,而墙脚处的侵蚀深度无法继续加深,因此最终的侵蚀面较模式1的侵蚀面陡。同理,在工况1的试验中,侵蚀面起点一定,墙脚处侵蚀深度也无法太深,因此最终形成了一个较模式1波浪作用后形成的侵蚀面更浅更缓的侵蚀面。在工况2波浪作用下的两组试验中,模式2同样具有一个特定的来波与回波的相遇点即侵蚀面起点,而在相遇点之前属于扰动较为剧烈的区域,因此模式2形成了一个较模式1更深更大的侵蚀面。
|
图 10 直立墙影响对比图 Fig. 10 Uprightwall impact comparison diagram |
总体来说,模式1试验中的回波作用较模式2弱,且由于没有直立墙的阻挡,在波浪作用过程中顶部的砾石随波浪整体向堤后运移,其结果是整个结构发生破坏,无法继续完成工程任务。模式2中直立墙前护坡的侵蚀可以看作系统的内部调整,由于直立墙的存在,阻挡了砾石向墙后的运移,同时增强了墙前回波强度,结果是墙前护坡有侵蚀也有堆积,不会影响其继续完成工程任务。
从本文所做的工作来看,模式2回波强度的增强使得侵蚀面的起点不会因水深和波高的变化而改变过大,这就决定了侵蚀程度相差不会太大,即能较安全的应对各种波浪状况。模式2试验中侵蚀面最终是达到一个动态平衡,这意味着随着波浪的变化,其内部能够随时进行调整实现稳定从而达到一个能够长期稳定运作的状态,Summer通过室内试验发现抛石斜坡在不同波浪的持续作用下,侵蚀深度也会随之变化[17],这就证实了斜坡砾石是可以进行动态调整的。而模式1在波浪作用后可以说是达到了一个永久性破坏的程度,不具备动态调整能力,在长期的波浪作用下会使结构逐渐丧失其原有功能,最终彻底丧失使用价值。因此从长远效用来说,纯抛石堤中加入直立墙会使整个系统的使用寿命得到延长。
4 结论本文采用单一变量对比试验,从波高、水深、波浪入射角度、直立墙的有无四个影响因素探讨了对组合堤抛石稳定性的影响,得出主要结论如下:
(1) 波高因素会影响砾石的起动位置和起动砾石的大小。当水深较深、护坡坡顶处砾石最先起动时,侵蚀状况受波高影响较小。当水深较浅时,侵蚀状况受波高影响较大。
(2) 水深因素会影响砾石起动位置和回流作用的强弱。静水位线越接近抛石护坡、接触面积越大时,回流产生的作用力越大。增加水深、采用三角形护坡可以减轻回流作用的影响,减轻侵蚀程度。
(3) 波浪入射角度的改变影响墙前扰动的剧烈情况和墙前砾石的运移方向。墙前扰动的剧烈情况影响护坡侵蚀程度。砾石的运移情况决定了波浪作用后护坡上砾石的损失情况。正向波在墙前的扰动强于斜向波在墙前的扰动。正向波作用下会有砾石在坡面堆积,斜向波没有砾石堆积。
(4) 直立墙的存在阻挡了砾石向墙后运动并增强了墙前的回波作用。在正向波入射条件下墙前会达到一个动态平衡,护坡上堆积的砾石可以当作备用砾石在波浪持续作用下进行调整,延长使用寿命。
(5) 根据各因素的综合考量,直立墙与抛石护坡组合堤的使用寿命明显长于纯抛石防波堤。在组合堤的工程设计上,建议采用三角形护坡结构,坡顶低于静水位线一定深度,整体朝向的选取要综合考量所处水域常受来波方向、频率、强度等因素,找出一个受侵蚀程度最小、砾石损失量最小的朝向角度。
| [1] |
赵子丹, 薛小春. 直立堤前海床的局部冲刷[J]. 海洋学报, 1992, 20(5): 136-141. Zhao Z D, Xue X C. Scour in front of vertical breakwater by irregular waves[J]. Acta Oceanologica Sinica, 1992, 20(5): 136-141. (  0) 0) |
| [2] |
薛晓春, 赵子丹. 波浪作用下直立堤前床面边界层内传质速度[J]. 海洋学报, 1997, 19(1): 113-122. Xue X C, Zhao Z D. The velocity of mass transfer in the boundary layer of bed surface under wave action[J]. Acta Oceanologica Sinica, 1997, 19(1): 113-122. (  0) 0) |
| [3] |
高学平.波浪与海上建筑物及海床的相互作用[D].天津: 天津大学, 1992. Gao X P. The Interaction Between Waves and Marine Structures and Seabed[D].Tianjin: Tianjin university, 1992. (  0) 0) |
| [4] |
薛晓春.规则波、不规则波与直立式建筑物及沙质底床的相互作用[D].天津: 天津大学, 1995. Xue X C. The Interaction Between Regular Wave, Irregular Wave and Vertical Structure and Sandy Bottom Bed[D]. Tianjin: Tianjin university, 1995. (  0) 0) |
| [5] |
俞聿修, 李本霞, 张宁川, 等. 斜向和多向不规则波作用于直墙堤上的波浪荷载[J]. 水运工程, 2008(4): 1-4. Yu Y X, Li B X, Zhang N C, et al. Wave loads on vertical wall in oblique and multi-directional irregular wave[J]. Port & Waterway Engineering, 2008(4): 1-4. (  0) 0) |
| [6] |
椹木亨, 司月玲. 抛石防波堤坡面上共振现象引起的破坏机理[J]. 水道港口, 1984(4): 17-22. Shen M H, Si Y L. The mechanism of damage caused by resonance on the surface of riprap breakwater[J]. Journal of Waterway and Harbor, 1984(4): 17-22. (  0) 0) |
| [7] |
李增志, 别社安, 任增金. 抛石防波堤堤内波浪运动的数值模拟[J]. 工程力学, 2008(a01): 54-57. Li Z Z, Bie S A, Ren Z J. Numerical simulation of wave motion in riprap breakwater embankment[J]. Engineering Mechanics, 2008(a01): 54-57. (  0) 0) |
| [8] |
吴苏舒, 张玮. 海岸防护中护底块石稳定重量的确定[J]. 中国港湾建设, 2007(6): 13-16. Wu S S, Zhang W. Determination of the stable weight of the retaining rock in coastal protection[J]. China Harbour Engineering, 2007(6): 13-16. DOI:10.3969/j.issn.1003-3688.2007.06.005 (  0) 0) |
| [9] |
何富荣, 程义吉, 许国辉. 水力插板桩成套技术研究与应用[M]. 郑州: 黄河水利出版社, 2010. He F R, Cheng Y J, Xu G H. Technology Research and Application of Hydraulic Plugboard Pile[M]. Zhengzou: The Yellow River Water Conservancy Press, 2010. (  0) 0) |
| [10] |
刘爱霞, 何富荣. 水力插板在海港工程中的应用[J]. 海岸工程, 2010, 29(3): 74-78. Liu A X, He F R. The application of the hydraulic thrust sheet pile in harbour engineering[J]. Costal Engineering, 2010, 29(3): 74-78. DOI:10.3969/j.issn.1002-3682.2010.03.010 (  0) 0) |
| [11] |
余文畴.平顺抛石护岸若干问题水槽定性实验[C]. //长江中下游护岸工程经验选编.北京: 科学出版社. 1978: 18-22. Yu W C. A qualitative experiment of several flume in smooth riprap revetment[C].//Experience Selection in the Middle and Lower Reaches of the Yangtze river. Beijing: Science Press. 1978: 18-22. (  0) 0) |
| [12] |
D.Stephenson. Hydraulic Calculation of Rockfill Engineering[M]. Beijing: Ocean Press, 1984.
(  0) 0) |
| [13] |
Hsu J C.短峰波.海岸及海洋工程手册[M].李玉成, 陈士荫, 俞聿修等译.大连: 大连理工大学出版社, 1992: 69-129. Hsu J C.Short peak wave. Coastal and Marine Engineering Manual[M]. Dalian: Dalian University of Technology Press, 1992: 69-129. (  0) 0) |
| [14] |
Fenton J D. Wave forces on vertical walls[J]. Journal of Waterway Port Coastal and Ocean Engineering, 1985, 111(4): 693-718. DOI:10.1061/(ASCE)0733-950X(1985)111:4(693)
(  0) 0) |
| [15] |
Tzang S Y, Liaw S R. A Design Short-Crested Wave Force Model for Vertical Deep-Water Breakwaters[C].// Coastal Engineering (1996). ASCE, 2012.
(  0) 0) |
| [16] |
李本霞.斜向和多向不规则波对直立堤作用的研究[D].大连: 理工大学, 2003. Li B X. The Study of Oblique and Multidirectional Irregular Wave Action on Vertical Breakwater[D]. Dalian: Dalian university of technology, 2003. (  0) 0) |
| [17] |
Sumer B M, Fredsoe J. Experimental study of 2D scour and its protection at a rubble-mound breakwater[J]. Coastal Engineering, 2000, 40(1): 59-87.
(  0) 0) |
2. Shandong Provincial Key Laboratory of Marine Environment and Geological Engineering, Ocean University of China, Qingdao 266100, China;
3. College of Environmental Science and Engineering, Ocean University of China, Qingdao 266100, China
 2018, Vol. 48
2018, Vol. 48


