2. 中国海洋大学物理海洋教育部重点实验室, 山东 青岛 266100;
3. 国家海洋信息中心, 天津 300000
在各类海洋动力造成的灾害中,风暴潮灾害因其破坏力强、造成直接经济损失大而居于首位[1-3]。中国是全球遭受风暴潮灾害侵扰最为严重的国家之一[4-5],如0518号台风“达维”于2005年9月26日在海南省万宁市登陆,造成海南省630万人口受灾,直接经济损失高达116亿元[6];0814号台风“黑格比”在2008年9月广东省茂名市登陆,引发风暴潮最大增水达2.7 m,造成广东、广西和海南三省直接经济损失132亿元[7]。登陆中国的台风在全球气候变暖的背景下其强度呈现逐步增大的走势[8],再加上近年来海平面上升,沿海地区城市化水平不断提高,台风风暴潮造成的直接经济损失也呈现上升走势[9],对中国防灾减灾工作提出了新的要求。
由台风引发的风暴潮通常包含着复杂的物理过程,其风暴潮增水大小与台风的强度与尺度关系密切[10-13]。高娜等[14]对珠江口赤水湾近30年极端风暴潮增水数据进行分析,发现风暴潮增水强度与台风强度近似呈线性关系。Irish等[15]指出,台风强度与台风尺度的改变对于风暴潮增水有显著影响。Yin等[16]利用ADCIRC+SWAN耦合模式研究了海平面上升和台风强度对珠江口风暴潮和波浪的影响,研究发现,台风强度对风暴潮影响更大,海平面上升则对珠江口的海浪影响更大。Wu等[17]利用3D模型NearCoM-TVD在一个理想的大陆架-海滩-陆地系统进行数值模拟实验,结果发现,当台风最大风速半径与台风强度增大时,风暴潮增水与影响范围也会随之增大。
台风期间,风暴潮与巨浪过程常常相伴而生,二者之间的耦合强化效应近年来受到越来越多的关注,其耦合强化机理成为目前的科学研究前沿[18]。Guan等[19]在WAM模型的基础上,考虑了波流相互作用引起的辐射应力,模拟了法国南部Rhône河口地区不同风场情况下的风浪,发现即使在斜向离岸风的情况下,近岸区域也存在沿岸波。Jia等[20]以9414号台风“Doug”为例,利用POM+SWAN耦合模式,研究了波流相互作用对水位和有效波高的影响,结果表明,耦合模式在极值处的模拟结果更接近观测值。Feng等[21]建立了适用于中国浙闽海域的ADCIRC+SWAN波流耦合模型,以1319号台风“天兔”为例,研究了波流相互作用对风暴潮的影响,发现考虑波浪辐射应力时耦合模型能更好地模拟风暴潮过程。Yu等[22]利用ADCIRC+SWAN耦合模型,研究了0908号台风“莫拉克”期间台湾海峡的风暴潮过程,指出波浪通过辐射应力梯度影响水位高度,福州平潭区波浪增水达0.28 m,约占瞬时风暴潮的24.0%。因此,在台风风暴潮的数值模拟预报中,波浪耦合效应的影响是不可忽视的。
海南岛位于南海西北部,地处亚热带季风区, 是中国的“台风走廊”[23]。近年来随着海南省海洋经济快速发展,台风风暴潮、灾害性海浪等海洋动力灾害所造成的损失亦呈快速上升趋势。因此,研究风暴潮-灾害性海浪耦合作用机理,对台风风暴潮进行高质量、高效率的数值模拟预警预报,对于保障海南省沿海地区人民的正常生产生活与生命财产安全有重要意义。
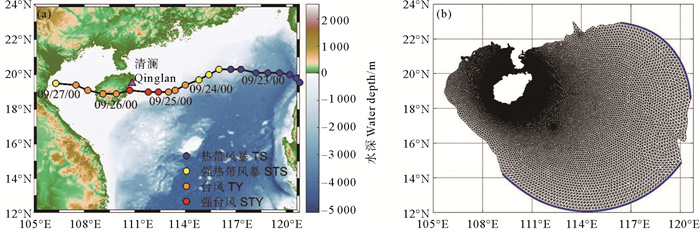
1 数值模型的建立和验证 1.1 台风数据超强台风“达维”是2005年西北太平洋第18号台风(被称为0518号台风),台风路径数据来源于西北太平洋热带气旋最佳路径数据集,时间分辨率为6 h。图 1(a)显示台风“达维”于北京时间2005年9月21日02时在菲律宾东北侧海面生成,整体向西北方向移动, 24日01时发展为强热带风暴,持续14 h,24日16时发展为台风,持续18 h,25日11时发展为强台风,26日4时于海南省万宁市沿海登陆,横穿海南岛,停留时间长达13 h,给全岛造成严重影响。超强台风“达维”引起的风暴潮给海南岛造成直接经济损失116.47亿元,受灾人口630.54万。
|
图 1 (a) 台风“达维”强度路径和海南岛周边水深地形图及(b)非结构化网格图 Fig. 1 (a) Intensity and track of typhoon 'Damrey' and elevation data around Hainan Island and (b) unstructured mesh |
本文采用ADCIRC+SWAN耦合模式, 选择笛卡尔坐标系,模式类型选择二维,底摩擦选择混合方式,考虑有限振幅,科氏力基于β面近似,潮汐仅考虑天文潮,NWS取305,模型风场输入间隔为1 h,模型水位计算步长1 s,模型结果1 h输出一次。
本文中数值模拟使用同一套网格,为了使大洋中的风暴潮以及波浪得到充分发展,减小开边界对模拟结果的影响,选取计算域中网格覆盖范围为105°E—121°E,12°N—24°N,可以有效模拟0518号台风期间海南岛地区的台风风暴潮等时间演变过程。计算网格从开边界处菲律宾群岛到海南岛逐渐加密,分辨率从菲律宾20 km逐渐过渡到蜈支洲岛附近的50 m(见图 1(b)),在实现了对于海南岛复杂岸线和地形的高精度的刻画的同时,又提升了计算效率,节省了计算资源。用于构建非结构网格的海岸线数据采用的是GSHHG数据集,水深数据是分辨率为50 m的电子海图数据和分辨率为1′的ETOPO1数据。
1.3 台风模型风场模拟结果的精确度对风暴潮的数值模拟起关键性作用。Jelesnianski模型风场可以很好的模拟南海风暴潮[24],因此本文选取该模型风场进行数值模拟。Jelesnianski模型风场的风速与气压公式如下:
| $ V=\left\{\begin{array}{l} \frac{r}{R_{\max }+r}\left(V_{\mathrm{ox}} i+V_{\mathrm{oy}} j\right)+V_{\max }\left(\frac{r}{R_{\max }}\right)^{\frac{3}{2}} \frac{1}{r}(A i+B j) \\ \quad\left(r \leqslant R_{\max }\right) \\ \frac{R_{\max }}{R_{\max }+r}\left(V_{\text {ox }} i+V_{\mathrm{oy}} j\right)+V_{\max }\left(\frac{R_{\max }}{r}\right)^{\frac{1}{2}} \frac{1}{r}(A i+B j) \\ \quad\left(r>R_{\max }\right) \end{array}\right., $ | (1) |
| $ \begin{equation} P_{\mathrm{a}}=\left\{\begin{array}{ll} P_{\mathrm{c}}+\frac{1}{4}\left(P_{\mathrm{n}}-P_{\mathrm{c}}\right)\left(\frac{r}{R_{\max }}\right)^3 & \left(r \leqslant R_{\max }\right) \\ P_{\mathrm{n}}-\frac{3}{4}\left(P_{\mathrm{n}}-P_{\mathrm{c}}\right)\left(\frac{R_{\max }}{r}\right) & \left(r>R_{\max }\right) \end{array}, \right. \end{equation} $ | (2) |
| $ \begin{equation} A=-\left[\left(x-x_{\mathrm{C}}\right) \sin \theta+\left(y-y_{\mathrm{C}}\right) \cos \theta\right], \end{equation} $ | (3) |
| $ \begin{equation} B=-\left[\left(x-x_{\mathrm{C}}\right) \cos \theta-\left(y-y_{\mathrm{C}}\right) \sin \theta\right], \end{equation} $ | (4) |
| $ \begin{equation} V_{\max }=3.029\left(P_{\mathrm{n}}-P_{\mathrm{c}}\right)^{0.644}, \end{equation} $ | (5) |
| $ \begin{equation} \begin{gathered} R_{\max }=28.52 \tan h[0.0873(\varphi-28)+ \\ \left.12.22 e^{\frac{\left(P_{\mathrm{n}}-P_{\mathrm{c}}\right)}{33.86}}+0.2 V_{\mathrm{mov}}+M\right]_{\circ} \end{gathered} \end{equation} $ | (6) |
式中:x, y代表研究区域中各计算点的位置;xc, yc代表台风坐标;r代表各计算点到台风中心的距离;V代表各计算点的风速;Vox和Voy代表台风移动速度在x和y方向投影;Vmax代表台风最大风速, 基于西北太平洋沿岸和岛屿观测站上近28年最大风速观测数据得到的经验公式计算所得[25];Rmax代表台风最大风速半径, 基于MEF经验公式计算得[26]; Pa代表各计算点的气压;Pc和Pn代表台风中心最低气压与无穷远处的大气压;φ代表台风中心的纬度;Vmov代表台风移动速度;θ代表入流角, 取20°;M代表起算径,取25 km。
Jelesnianski模型风场对台风中心风场结构的模拟有很高的精确度,但对于远离台风中心区域的模拟结果较差,因此本文使用背景风场与模型风场叠加后的合成风场。背景风场使用的是哥白尼气候变化服务中心研发的第五代再分析资料ERA5再分析风场数据集,合成风场使用的公式如下所示[27]:
| $ \begin{equation} V_{\text {ungride }}=(1-\alpha) V+\alpha V_{\mathrm{b}} \text {, } \end{equation} $ | (7) |
| $ \begin{equation} \alpha=c^4 /(1+c)^4, \end{equation} $ | (8) |
| $ \begin{equation} c=r / n R_{\max } 。\end{equation} $ | (9) |
式中:Vungride代表合成风场;α代表权重系数;Vb代表背景风场;V代表模型风场;n代表调节权重系数参数值,n=4时,合成风场能较真实的反应台风风场[28]。
1.4 模式验证准确模拟潮汐过程是准确模拟风暴潮增水过程的前提[29]。为检验耦合模型能否可靠的模拟沿岸水位变化,首先需要进行天文潮验证,此时模型不加入风场,仅依靠开边界天文潮驱动,单独运行ADCIRC模式,以保证模式在无风、无气压以及无波浪影响的条件下模拟天文潮。0518号台风的模拟时间为2005年9月20日8时至27日8时,验证站点选取为清澜港(位置见图 1(a))。本文利用线性相关系数(CC)、相对误差(RE)、均方根误差(NRMSE)作为评判模型优良性指标。
| $ \begin{equation} R E=\frac{\eta_{\max }^{\text {model }}-\eta_{\max }^{\text {obs }}}{\eta_{\max }^{\text {obs }}} \times 100 \% \end{equation} $ | (10) |
| $ N R M S E=\left[\frac{\frac{1}{N} \sum\limits_{n=1}^N\left(\eta_{n, j}^{\text {modle }}-\eta_{n, j}^{\text {obs }}\right)^2}{\sum\limits_{n=1}^N\left(\eta_{n, j}^{\text {obs }}\right)^2}\right]^{1 / 2} $ | (11) |
| $ \begin{equation} C C=\frac{\frac{1}{N} \sum\limits_{n=1}^N\left(\eta_{n, j}^{\text {modle }}-\bar{\eta}_{n, j}^{\text {obs }}\right)\left(\eta_{n, j}^{\text {obs }}-\bar{\eta}_{n, j}^{\text {obs }}\right)}{\sigma_{\text {modle }} \sigma_{\text {obs }}} \end{equation} $ | (12) |
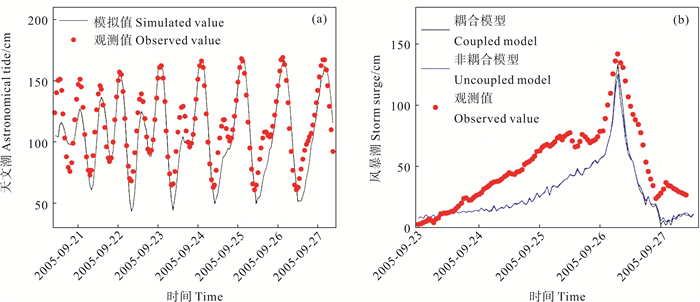
由图 2(a)可知,天文潮位模拟值与实测值整体趋势较为一致,在清澜港其相关系数、相对误差与均方根误差分别为0.889、-0.024和0.101,说明ADCIRC模式模拟的天文潮潮位具有较高的精确度,可以较好地再现天文潮时间演变过程,为ADCIRC+SWAN耦合模式精确的模拟风暴潮奠定了基础。
|
图 2 清澜港模式模拟(a)天文潮与观测值时间序列图及(b)风暴潮增水与观测值时间序列图 Fig. 2 Time series diagram of simulated (a) astronomical tide and (b) storm surge and observed values in Qinglan Port |
风暴潮增水是指站点的总水位减去天文潮增水,得到的差值即为风暴潮引起的增水。图 2(b)中红点为观测值,黑线为耦合模式模拟的风暴潮增水,蓝线为非耦合模式模拟的风暴潮增水,观测的最大风暴潮增水为142 cm,ADCIRC+SWAN耦合模式与单独运行ADCIRC模式数值模拟得到的最大风暴潮增水分别为134和125 cm, 相对误差分别为5.63%和11.97%,耦合模式数值模拟的结果相对误差更小,控制在10%以内,相位一致,更为接近观测数据。
结果表明:波浪引起的风暴潮增水效应是不可忽视的。与非耦合模式相比,耦合模式的数值模拟结果准确度更高。基于海南岛特殊地形的ADCIRC+SWAN耦合模式,可以有效对影响海南岛的台风风暴潮进行数值,为之后的敏感性实验等打下了坚实的基础。
2 风暴潮-海浪耦合相互作用研究台风浪与风暴潮并不是相互孤立存在的,二者之间存在着复杂的非线性相互作用[30-32]。风暴潮引起近海沿岸水位变化会改变波浪的底摩擦耗散,影响波浪破碎,同时风暴潮流也可能会导致波浪发生折射现象,对波浪造成影响[33]。波浪传播过程中伴随的辐射应力也会对风暴潮造成影响。
本章选择0518号台风为研究对象,设计三组数值实验,分别为考虑与不考虑水位、流场与波浪效应,对实验结果进行对比分析,探究水位和流场对有效波高的影响,波浪效应对风暴潮增水的影响。
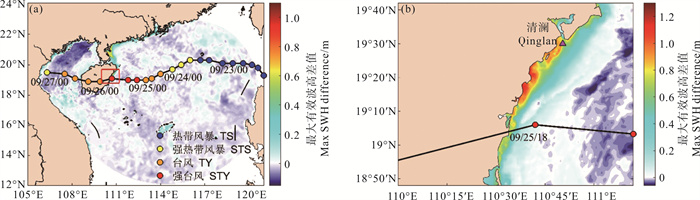
2.1 水位对台风浪的影响为了研究水位对有效波高的影响,本小节分别设计了考虑水位与不考虑水位两组实验。图 3显示的是将两组实验中有效波高最大值相减得到水位引起的有效波高变化,图 3(a)—3(b)分别显示有效波高差值在全场与清澜港附近沿海的分布。
|
图 3 水位作用产生的有效波高(a)全场及(b)清澜港附近空间分布图 Fig. 3 Distribution of the significant wave height(SWH) induced by water level (a) full court and (b) near Qinglan Port |
从图中可以明显观察到,图 3(a)中, 红色框以外区域水位引起的有效波高较小,水位引起的有效波高在有效波高研究中可忽略不计。图 3(b)中,近岸浅水区水位引起的有效波高较明显,有效波高差值在近岸主要表现为正值,即在近岸浅水区考虑水位作用的影响后使得有效波高增加。在图 3(b)中, 水位作用产生的有效波高最大值为1.1 m,该位置处考虑水位作用得到有效波高最大值为4.38 m, 水位作用产生的有效波高占总有效波高的25.1%,说明在近岸浅水区水位作用对台风浪具有显著影响。考虑为近岸区域水深较浅,波浪被天文潮涨落引发的水深变化调节,并且风暴潮增水引起水深增加,减少了波浪能量耗散,致使有效波高增大。
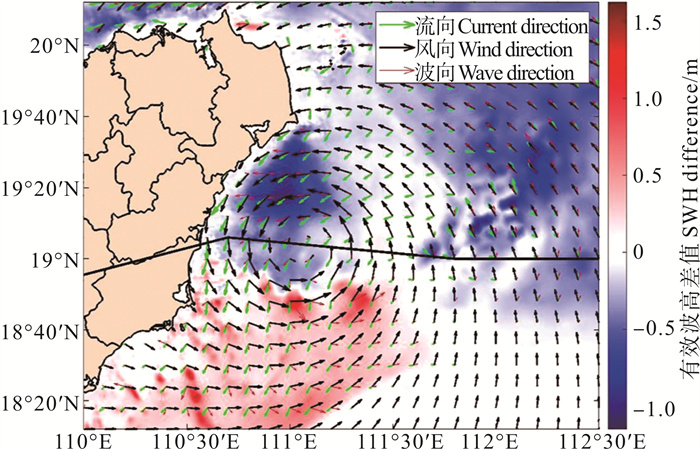
2.2 流场对台风浪的影响本小节通过考虑流场与不考虑流场两组实验产生的有效波高最大值作差,进一步分析流场对台风浪的影响。图 4显示的是流场作用产生的有效波高的空间分布,其中黑色、红色与绿色箭头分别表示风向、平均波向和流向。从图中观察到,台风中心及台风路径右侧主要分布的是负值区,此时流场作用使得总有效波高减小,有效波高差值最大值达到1.36 m;台风路径左侧呈现的主要是正值区,此时考虑流场作用使得有效波高增加。对于台风路径右侧有效波高差值为负时,风向、流向与平均波向之间夹角为锐角,即在向岸风的作用下,顺流增大了台风浪的相速度,抑制了风浪的成长,导致了有效波高的降低。对于台风路径左侧有效波高差值为正时,流向与平均波向之间夹角为钝角,波浪逆流传播,降低了台风浪的相速度,风能输入增加,从而导致了有效波高的增高。
|
图 4 流场作用产生的有效波高在海南岛附近的空间分布图 Fig. 4 Distribution of the significant wave height induced by current near Hainan Island |
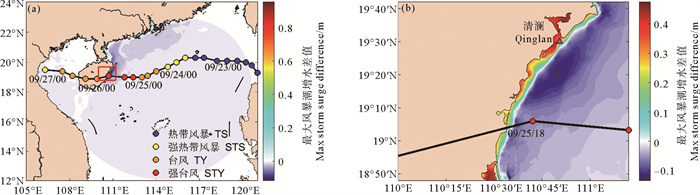
波浪效应是影响台风风暴潮增水的重要因素之一,为了研究波浪效应对风暴潮增水的影响,本小节分别设计了考虑波浪与不考虑波浪两组实验。图 5(a)—5(b)显示的是两组实验中风暴潮增水最大值之间的差值:波浪效应引起的风暴潮的空间分布。波浪增水的产生主要是由于波浪传播至近岸,受海底地貌与水深等影响发生波浪破碎现象。从图 5(a)中观察到,0518号台风“达维”过程中波浪效应主要呈现轻微波浪减水,部分近岸区域呈现波浪增水,波浪效应引起的风暴潮增水在清澜港附近最大值为0.42 m,约占风暴潮增水的14.2%,这说明波浪效应引起的风暴潮增水是不可忽略的。
|
图 5 波浪效应产生的风暴潮增减水在(a)全场及(b)清澜港附近空间分布图 Fig. 5 Distribution of the wave set-up/ set-down (a) the whole field and (b) near Qinglan Port |
本文设计了3组理想化的数值试验,以研究在不同台风参数(台风强度、台风尺度)下波浪增水变化。敏感性试验中台风强度(台风尺度)的变化是通过对照组中相对应的台风参数乘以系数,得出表 1中所列的台风登陆强度(最大风速半径)。
|
|
表 1 敏感性试验设置列表 Table 1 List of model designs |
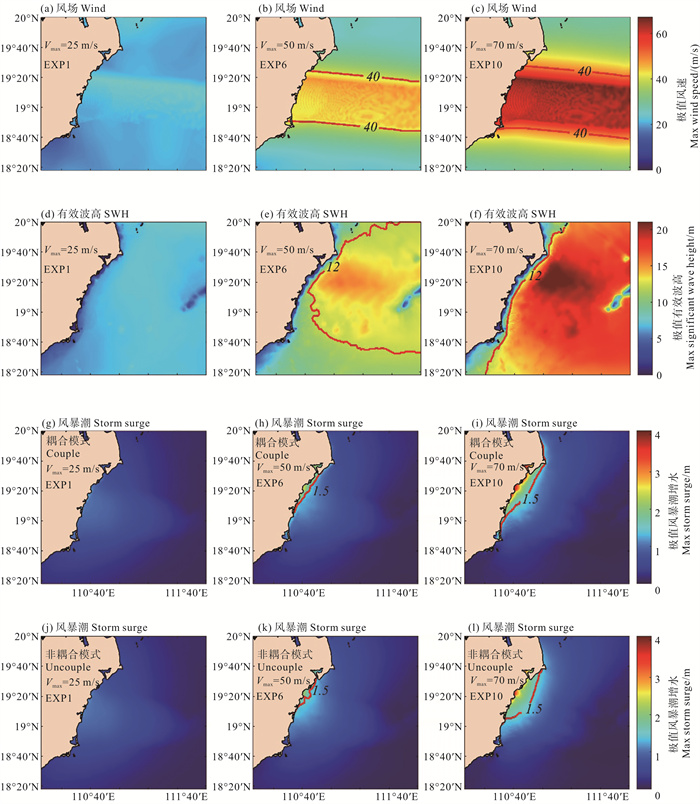
A组实验中模拟了不同台风强度下有效波高和风暴潮的变化过程,着重研究了浪流相互作用对风暴潮增水的影响。图 6为不同强度的台风下模式模拟的极值风场、有效波高和风暴潮的空间分布。
|
( (a)—(c)代表极值风速40 m/s包络图;(d)—(f)代表极值有效波高12 m包络图;(g)—(i)代表耦合模式下极值风暴潮1.5 m包络图;(j)—(l)代表非耦合模式下极值风暴潮1.5 m包络图。(a)—(c) represent the maximum of wind field with 40 m/s envelope line; (d)—(f) represent the maximum of SWH with 12 m envelope line; (g)—(i) represent the maximum of coupled storm surge with 1.5 m envelope line; (j)—(l) represent the maximum of uncoupled storm surge with 40 m/s envelope line. ) 图 6 不同台风强度下的各变量极大值分布图 Fig. 6 Maximum distribution of each variable under different typhoon intensities |
图 6(a)—6(c)中随台风强度的增强,大风速范围增大是符合常理的,并且台风路径沿线可能会增大发生风暴潮灾害的风险。
图 6(d)—6(f)代表的是在不同台风强度下的有效波高最大包络图。从图中可以看出,随台风强度的增加,台风引起的极值有效波高也随之增加。图 6(d)中有效波高最大值仅为8.04 m,图 6(e)—6(f)分别显著增加至15.97和21.93 m。在图 6(e)—6(f)中,有效波高超过12 m, 影响范围约从16 958 km2扩大为24 441 km2,增大了44.13%,对海岸线的影响范围也显著增大。
此外,随着台风风速的不断增加,台风在近岸沿海区域引起的风暴潮增水的范围也不断变大。图 6(g)—6(i)显示耦合模式不同,台风强度引起的最大风暴潮增水与非耦合模式(图 6(j)—6(l))模拟结果相比,前者模拟的风暴潮通常更大,考虑为波浪增水的影响。从EXP1到EXP10,风暴潮最大增水从1.22 m增加到4.13 m(考虑波浪增水),从1.14 m增加到3.78 m(不考虑波浪增水)。整体上波浪增水效应一般在0.08~0.35 m之间,占风暴潮增水高度的6.5%~8.5%。耦合模式下(见图 6(g)—6(i))风暴潮增水超过1.5 m,影响范围约从273 km2扩大为891 km2,增大了226%。与非耦合模式(见图 6(j)—6(l))相比,耦合模式下风暴潮增水超过1.5 m,影响范围通常更大。
通过对不同台风强度下不同深度节点(水深深度3~12 m,间隔3 m)处的有效波高、风暴潮增水和波浪辐射应力进行平均,发现风速越大的台风产生越大的有效波高、风暴潮增水和辐射应力。随着水深深度的增加,有效波高和辐射应力也随之增强,但风暴潮增水呈现相反的趋势。考虑到随着节点水深增加,波浪破碎效应与底摩擦效应减弱,波能耗散减弱,从而产生更大的有效波高。在水深节点较小时,由于波浪破碎,波浪辐射应力产生的波浪增水导致近岸的水位升高,从而产生更大的风暴潮增水。
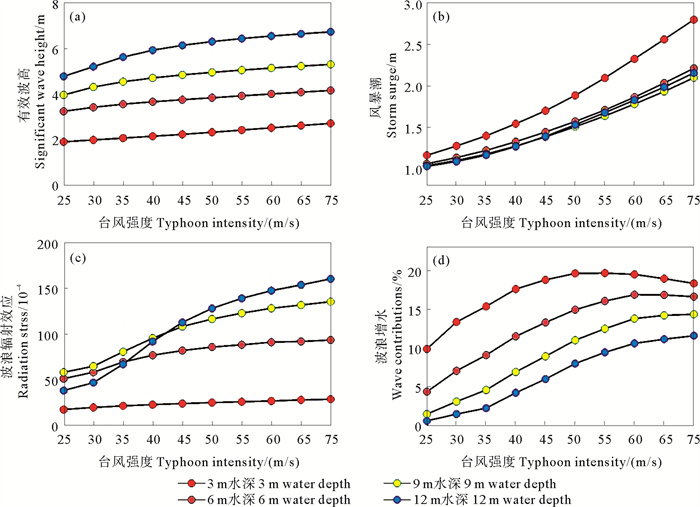
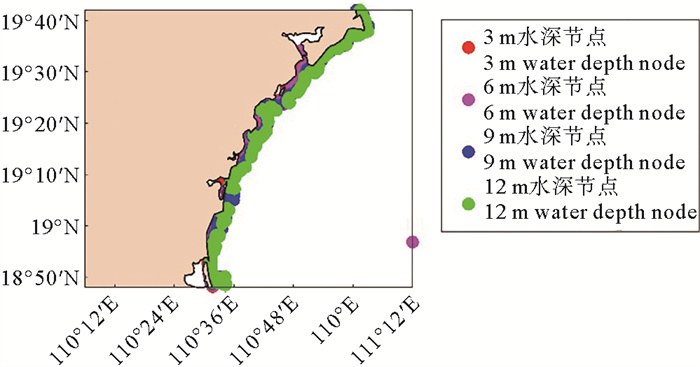
为了研究不同台风强度下波浪效应对风暴潮的影响,本文评估了ADCIRC+SWAN耦合模式模拟风暴潮和单独ADCIRC模式模拟风暴潮之间的差异,两者之间的差值即为波浪引起的风暴潮增水。图 7(d)显示波浪引起的风暴潮增水有着随台风强度的增加而增加的趋势,这种现象考虑为随着台风强度的增加,有效波高以及辐射应力也随之增加(见图 7(a)、(c)),从而导致耦合模式相比于非耦合模式产生更大的风暴潮增水。因此,风速越大的台风产生越大的有效波高和辐射应力,从而产生更大的波浪增水。波浪效应引起的风暴潮高度随台风强度的增加呈非线性增加,与以往的研究一致(见图 7(b))。考虑波浪增水对风暴潮的贡献百分比时,从图 7(d)中观察到:当台风强度达到并超过55 m/s时,波浪增水效应基本达到饱和。为保证实验的准确性,本文设置了4个水深节点(见图 8)。
|
图 7 不同深度节点下台风强度与(a)有效波高、(b)风暴潮增水、(c)波浪辐射应力及(d)波浪增水的关系 Fig. 7 The connection between typhoon intensities and (a) SWH, (b) coupled storm surges, (c) radiation stress and (d) wave contributions at different stations |
|
图 8 水深节点分布图 Fig. 8 The distribution of different depth nodes |
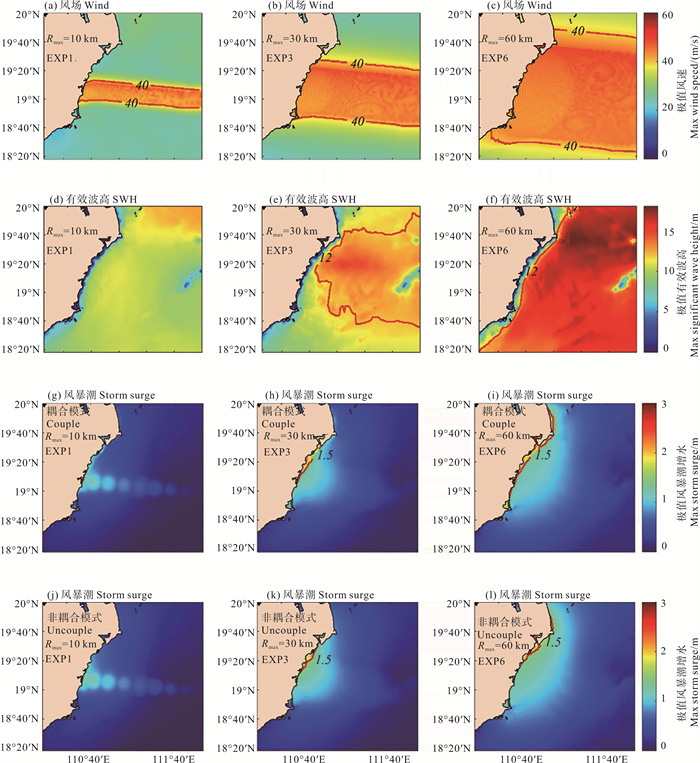
在风暴潮数值模拟中,台风尺度是一个不可忽视的因素。本文通过B组6个实验研究了不同台风尺度下风暴潮与有效波高的演变过程。图 9为不同尺度的台风下模式模拟的极值风场(见图 9(a)—9(c))、有效波高(见图 9(d)—9(f))和风暴潮(见图 9(g)—9(l))的空间分布。
|
( (a)—(c)代表极值风速40 m/s包络图;(d)—(f)代表极值有效波高12 m包络图;(g)—(i)代表耦合模式下极值风暴潮1.5 m包络图;(j)—(l)代表非耦合模式下极值风暴潮1.5 m包络图。(a)—(c) represent the maximum of wind field with 40 m/s envelope line; (d)—(f) represent the maximum of SWH with 12 m envelope line; (g)—(i) represent the maximum of coupled storm surge with 1.5 m envelope line; (j)—(l) represent the maximum of uncoupled storm surge with 40 m/s envelope line. ) 图 9 不同台风尺度下的各变量极大值分布图 Fig. 9 Maximum distribution of each variable under different typhoon size |
图 9(j)—9(l)代表的是在不同最大风速半径下的耦合与非耦合模式下模拟的最大风暴潮增水图。台风最大风速半径从10 km增加到60 km,耦合模式下最大风暴潮增水从1.55 m增加到2.87 m,非耦合模式下最大风暴潮增水从1.44 m增加到2.48 m。整体上波浪增水的贡献一般在0.11~0.39 m之间,占风暴潮增水高度的7.1%~13.4%。在Rmax=30 km条件下,非耦合模式下(见图 9(k))风暴潮增水超过1.5 m,影响范围约124 km2。耦合模式下(见图 9(h))风暴潮增水超过1.5 m,影响范围约212 km2。相比于非耦合模式,耦合模式影响范围增大了约71%。在Rmax=60 km条件下,非耦合模式下(见图 9(l))风暴潮增水超过1.5 m,影响范围约204 km2,耦合模式下(见图 9(i))风暴潮增水超过1.5 m,影响范围约330 km2。相比于非耦合模式,耦合模式影响范围增大了约60.8%。
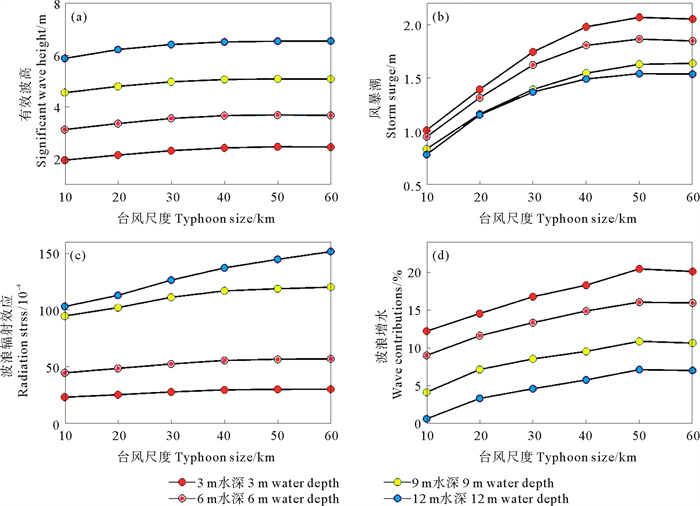
图 10显示了最大风暴潮、有效波高和波浪增水对最大风速半径变化的敏感性。不同深度节点的平均有效波高、风暴潮增水跟波浪辐射应力明显随着台风尺度的增加而增加,结果与上一节类似。随着台风尺度的增大,有效波高显著增大,从而产生更大的辐射应力,波浪效应增强,并且当台风尺度大于等于50 km时,波浪增水效应接近饱和。
|
图 10 不同深度节点下台风尺度与(a)有效波高、(b)风暴潮增水、(c)波浪辐射应力及(d)波浪增水的关系 Fig. 10 The connection between typhoon size and (a) significant wave height, (b) coupled storm surges, (c) radiation stress and (d) wave contributions at different stations |
本文基于Jelesnianski模型的合成台风风场,利用ADCIRC与SWAN耦合模型构建了一套适用于海南岛周边海域的台风风暴潮数值模型,以对海南省造成严重风暴潮灾害的0518号台风为基底台风,设计了一系列数值实验,结果表明:
(1) 在深水区,水位作用影响使台风浪的有效波高减小;在近岸浅水区,水位影响减少了波浪的能量耗散,使台风浪有效波高增大。
(2) 当平均波向与流向之间夹角为钝角时,流场作用表现为有效波高增大;当平均波向、流向与风向之间的夹角为锐角时,流场作用表现为有效波高减小。
(3) 波浪的耦合效应在近岸区域主要表现为风暴潮增水,贡献率约在14.2%,这在风暴潮的数值模拟中是不可忽视的。
(4) 随着台风特征参数Vmax与Rmax的增大,风暴潮与灾害性海浪的影响范围也随之增大。当台风强度从25 m/s增大到70 m/s时,耦合条件下风暴潮最大增水从1.22 m增加到4.13 m,非耦合模式下风暴潮最大增水从1.14 m增加到3.78 m,波浪耦合效应导致的风暴潮增水在0.08~0.35 m之间,占风暴潮增水高度的6.5%~8.5%。当台风强度达到55 m/s,波浪增水效应基本达到饱和。当台风最大风速半径从10 km增加到60 km时,耦合模式下风暴潮最大增水从1.55 m增加到2.87 m,非耦合模式下风暴潮最大增水从1.44 m增加到2.48 m,波浪耦合效应导致的风暴潮增水在0.11~0.39 m之间,占风暴潮增水高度的7.1%~13.4%。当台风尺度达到50 km,波浪增水效应基本达到饱和。
在全球气候变暖的大背景下,在中国南海登陆的台风其强度呈逐年增大的走势,在进行台风风暴潮的数值模拟时,充分考虑浪流耦合作用和台风特征参数(Vmax、Rmax), 对风暴潮进行更高质量的预警预报, 对于提高我国沿海城市防灾减灾能力, 保障人民正常的生产生活与生命财产安全有重要意义。
| [1] |
Yin B, Xu Z, Huang Y, et al. Simulating a typhoon storm surge in the East Sea of China using a coupled model[J]. Progress in Natural Science, 2009, 19(1): 65-71. DOI:10.1016/j.pnsc.2008.05.023 (  0) 0) |
| [2] |
Li R, Xie L, Liu B, et al. On the sensitivity of hurricane storm surge simulation to domain size[J]. Ocean Modelling, 2013, 67: 1-12. DOI:10.1016/j.ocemod.2013.03.005 (  0) 0) |
| [3] |
Feng J, von Storch H, Jiang W, et al. Assessing changes in extreme sea levels along the coast of C hina[J]. Journal of Geophysical Research: Oceans, 2015, 120(12): 8039-8051. DOI:10.1002/2015JC011336 (  0) 0) |
| [4] |
Shi X, Yu P, Guo Z, et al. Simulation of storm surge inundation under different typhoon intensity scenarios: Case study of Pingyang County, China[J]. Natural Hazards and Earth System Sciences, 2020, 20(10): 2777-2790. DOI:10.5194/nhess-20-2777-2020 (  0) 0) |
| [5] |
Yu H, Shen Y, Kelly R M, et al. Trends in social vulnerability to storm surges in Shenzhen, China[J]. Natural Hazards and Earth System Sciences, 2020, 20(9): 2447-2462. DOI:10.5194/nhess-20-2447-2020 (  0) 0) |
| [6] |
王青颜, 石海莹. 0518号台风"达维"风暴潮分析[J]. 海洋预报, 2007(1): 62-68. Wang Qingyan, Shi Haiying. Analyzing the storm surge of typhoon No. 0518 "DAMREY"[J]. Marine Forecasts, 2007(1): 62-68. (  0) 0) |
| [7] |
隋意, 石洪源, 钟超. 我国台风风暴潮灾害研究[J]. 海洋湖沼通报, 2020(3): 39-44. Sui Yi, Shi Hongyuan, Zhong Chao. Research on typhoon storm surge disaster in China[J]. Transactions of Oceanology and Limnology, 2020(3): 39-44. (  0) 0) |
| [8] |
Guan S, Li S, Hou Y, et al. Increasing threat of landfalling typhoons in the western North Pacific between 1974 and 2013[J]. International Journal of Applied Earth Observation and Geoinformation, 2018, 68: 279-286. DOI:10.1016/j.jag.2017.12.017 (  0) 0) |
| [9] |
Shen S, Feng X, Peng Z R. A framework to analyze vulnerability of critical infrastructure to climate change: The case of a coastal community in Florida[J]. Natural Hazards, 2016, 84: 589-609. DOI:10.1007/s11069-016-2442-6 (  0) 0) |
| [10] |
Zhao P, Jiang W. A numerical study of storm surges caused by cold-air outbreaks in the Bohai Sea[J]. Natural Hazards, 2011, 59: 1-15. DOI:10.1007/s11069-010-9690-7 (  0) 0) |
| [11] |
Liu J, Zhang H, Zhong R, et al. Impacts of wave feedbacks and planetary boundary layer parameterization schemes on air-sea coupled simulations: A case study for Typhoon Maria in 2018[J]. Atmospheric Research, 2022, 278: 106344. DOI:10.1016/j.atmosres.2022.106344 (  0) 0) |
| [12] |
Ma Y, Wu Y, Shao Z, et al. Impacts of sea level rise and typhoon intensity on storm surges and waves around the coastal area of Qingdao[J]. Ocean Engineering, 2022, 249: 110953. DOI:10.1016/j.oceaneng.2022.110953 (  0) 0) |
| [13] |
Wang J, Mo D, Hou Y, et al. The impact of typhoon intensity on wave height and storm surge in the Northern East China Sea: A comparative case study of typhoon Muifa and typhoon Lekima[J]. Journal of Marine Science and Engineering, 2022, 10(2): 192. DOI:10.3390/jmse10020192 (  0) 0) |
| [14] |
高娜, 赵明利. 风对珠江口风暴增水的影响分析[J]. 热带海洋学报, 2023, 42(1): 32-42. Gao Na, Zhao Mingli. Effect of typhoon on storm surge in the Pearl River Estuary[J]. Journal of Tropical Oceanography, 2023, 42(1): 32-42. (  0) 0) |
| [15] |
Irish J L, Resio D T, Ratcliff J J. The influence of storm size on hurricane surge[J]. Journal of Physical Oceanography, 2008, 38(9): 2003-2013. DOI:10.1175/2008JPO3727.1 (  0) 0) |
| [16] |
Yin K, Xu S, Huang W, et al. Effects of sea level rise and typhoon intensity on storm surge and waves in Pearl River Estuary[J]. Ocean Engineering, 2017, 136: 80-93. DOI:10.1016/j.oceaneng.2017.03.016 (  0) 0) |
| [17] |
Wu G, Shi F, Kirby J T, et al. Modeling wave effects on storm surge and coastal inundation[J]. Coastal Engineering, 2018, 140: 371-382. DOI:10.1016/j.coastaleng.2018.08.011 (  0) 0) |
| [18] |
侯一筠, 尹宝树, 管长龙. 我国海洋动力灾害研究进展与展望[J]. 海洋与湖沼, 2020, 51(4): 759-767. Hou Yijun, Yin Baoshu, Guan Changlong. Progress and prospect in research on marine dynamic disasters in China[J]. Oceanologia et Limnologia Sinica, 2020, 51(4): 759-767. (  0) 0) |
| [19] |
Guan C, Rey V, Forget P. Improvement of the WAM wave model and its application to the Rhône river mouth area[J]. Journal of Coastal Research, 1999, 966-973. (  0) 0) |
| [20] |
Jia Y, Yin B, Yang D. A numerical study of the influence of wave-current interaction on water elevation and significant wave height in the East China Sea[J]. Marine Sciences, 2009, 33(8): 82-86. (  0) 0) |
| [21] |
Feng X, Yin B, Yang D. Development of an unstructured-grid wave-current coupled model and its application[J]. Ocean Modelling, 2016, 104: 213-225. DOI:10.1016/j.ocemod.2016.06.007 (  0) 0) |
| [22] |
Yu H, Yu H, Wang L, et al. Tidal propagation and dissipation in the Taiwan Strait[J]. Continental Shelf Research, 2017, 136: 57-73. DOI:10.1016/j.csr.2016.12.006 (  0) 0) |
| [23] |
陈大可, 雷小途. 上层海洋对台风的响应和调制机理[J]. 地球科学进展, 2013, 28(10): 1077-1086. Chen Dake, Lei Xiaotu. Upper ocean response and feedback mechanisms to typhoon[J]. Advances in Earth Science, 2013, 28(10): 1077-1086. DOI:10.11867/j.issn.1001-8166.2013.10.1077 (  0) 0) |
| [24] |
Li A, Guan S, Mo D, et al. Modeling wave effects on storm surge from different typhoon intensities and sizes in the South China Sea[J]. Estuarine, Coastal and Shelf Science, 2020, 235: 106551. DOI:10.1016/j.ecss.2019.106551 (  0) 0) |
| [25] |
冯兴如, 杨德周, 尹宝树. 中国浙江和福建海域台风浪变化特征和趋势[J]. 海洋与湖沼, 2018, 49(2): 233-241. Feng Xingru, Yang Dezhou, Yin Baoshu. The change and trend of the typhoon waves in Zhejiang and Fujian coastal areas of China[J]. Oceanologia et Limnologia Sinica, 2018, 49(2): 233-241. (  0) 0) |
| [26] |
许灵静, 杨波, 江文胜. 台风对杭州湾水交换影响的定量研究[J]. 中国海洋大学学报(自然科学版), 2016, 46(6): 29-41. Xu Lingjing, Yang Bo, Jiang Wensheng. Quantitative study on water exchange affected by typhoons in the Hangzhou Bay[J]. Periodical of Ocean University of China, 2016, 46(6): 29-41. (  0) 0) |
| [27] |
Carr L E, Elsberry R L. Models of tropical cyclone wind distribution and beta-effect propagation for application to tropical cyclone track forecasting[J]. Monthly Weather Review, 1997, 125(12): 3190-3209. DOI:10.1175/1520-0493(1997)125<3190:MOTCWD>2.0.CO;2 (  0) 0) |
| [28] |
孙瑞, 侯一筠. 南海北部一次台风浪过程的数值模拟[J]. 海洋科学, 2013, 37: 76-83. Sun Rui, Hou Yijun. The simulation of a typhoon wave in the northern part of the South China Sea[J]. Marine Sciences, 2013, 37: 76-83. (  0) 0) |
| [29] |
Du M, Hou Y, Qi P, et al. The impact of different historical typhoon tracks on storm surge: A case study of Zhejiang, China[J]. Journal of Marine Systems, 2020, 206: 103318. (  0) 0) |
| [30] |
Feng X, Li M, Yin B, et al. Study of storm surge trends in typhoon-prone coastal areas based on observations and surge-wave coupled simulations[J]. International Journal of Applied Earth Observation and Geoinformation, 2018, 68: 272-278. (  0) 0) |
| [31] |
Wang K, Hou Y, Li S, et al. Numerical study of storm surge inundation in the southwestern Hangzhou bay region during Typhoon Chan-Hom in 2015[J]. Journal of Ocean University of China, 2020, 19: 263-271. (  0) 0) |
| [32] |
Li S, Jiang H, Hou Y, et al. Increasing historical tropical cyclone-induced extreme wave heights in the northern East China Sea during 1979 to 2018[J]. Remote Sensing, 2020, 12(15): 2464. (  0) 0) |
| [33] |
Feng X, Yin B, Yang D, et al. The effect of wave-induced radiation stress on storm surge during Typhoon Saomai (2006)[J]. Acta Oceanologica Sinica, 2011, 30(3): 20-26. (  0) 0) |
2. The Key Laboratory of Physical Oceanography, Ministry of Education, Ocean University of China, Qingdao 266100, China;
3. National Marine Data and Information Service, Tianjin 300000, China
 2024, Vol. 54
2024, Vol. 54


