2. 中国海洋大学山东省海洋工程重点实验室,山东 青岛 266100
海水入侵指滨海地区人为超量开采地下水,引起地下水位大幅度下降,海水与淡水之间的水动力平衡被破坏,导致咸淡水界面向陆地方向移动的现象[1]。海水入侵导致如水质恶化、土壤盐渍化等一系列生态、环境问题,是许多沿海国家和地区面临的主要环境地质灾害之一。
根据海水入侵的机理,要从根本上解决海水入侵问题,必须提高滨海地区的地下淡水水位,对此产生了各种防治海水入侵的措施:(1)改变现有的地下水开采模式;(2)人工回灌淡水;(3)抽水、注水或抽水-注水联合法;(4)修建地下截渗墙,地下截渗墙也称地下坝、截渗坝。地下截渗墙的渗透性比较低,修建时一般底部修至潜水含水层的隔水底板处,顶部修至含水层中间某一部位或地表,通过切断海水入侵通道来防止海水入侵。
目前,国内外已经存在很多修建地下截渗墙以防治海水入侵的示范工程。1988年,美国陆军工程师在密西西比河下游设计临时性的潜坝,以应对创纪录的枯水年所造成的盐水楔向上游入侵,保护了新奥尔良地区的淡水供应,节约投资5 000万美元[2]。1972年,日本在冲绳岛开始修建Komesu地下坝用于防治海水入侵,保护淡水资源,增加地下水储存能力。截止2004年,日本大约已修建15个地下坝,其中7个用于阻止海水入侵[3]。Ishida等[4]认为地下坝不仅可以阻止海水入侵,而且能够有效地储存孔隙水,有利于地下水的可持续利用,相比较地面坝又不受自然灾害影响,正因为这些优点,世界各地地下坝工程的规模在不断增长。在我国,山东滨海城市海水入侵问题较为严重,已建有不同规模的河口地下截渗墙工程6座,一定程度上缓解了海水入侵的问题,同时也形成了地下水库。如1995年,山东龙口黄水河地下截渗墙建成,起到了阻断海水入侵的作用,同时也改善了库区的生态环境[5];1998年大沽河下游胶州市麻湾附近修建了一道长4 km的地下截渗墙,防治海水倒灌,形成了一个容积近1亿立方米的永久地下水库[6]。
为了深入了解地下截渗墙防治海水入侵的效果,国内外专家对存在地下截渗墙的海水入侵问题也作了一些研究工作。Onder等[7]详细描述了地下坝的种类、设计和施工技术,并用两个示例研究分析了地下坝作为可持续发展的一种手段,在地下水管理方面的应用,然后利用MODFLOW程序进行模拟,评估地下坝的效果,分析其对地下水流场的影响。结果表明:地下坝可以增加含水层的有效存储量,也可以有效的控制地下水,有利于水资源的可持续利用。Roger等[8]通过实验研究了地下截渗墙安装前后咸水入侵的运移规律,并用SEAWAT模拟软件对实验结果进行了模拟验证,同时讨论了不同的截渗墙高度对咸水入侵的影响。贺国平等[9]利用FEFLOW软件建立模型,模拟了截渗墙建成后黄河侧渗量和地下水流场的变化,结果表明,随着截渗墙埋深的增加,黄河侧渗量呈减少的趋势;距离黄河大堤越近,流场受截渗墙的影响越大,距离越远,影响越不明显,距离黄河大堤10 km以外,流场不受截渗墙的影响。韩志勇等[10]利用V-MODFLOW软件模拟了存在截渗坝情况下大沽河地区残存咸水恢复的最优方案,通过3种不同咸水体恢复方案的模拟和分析对比,优化方案在咸水体的恢复效率、抽水量和治理末期的浓度分布等方面都明显优于抽水方案和抽-注联合方案。袁益让等[11]对三维海水入侵及防治工程系统提出渗流力学模型、迎风分数步差分格式,并对莱州湾地区防治海水入侵主要工程的后效、地下坝、防潮堤工程后效及工程调控应用模式进行了预测模拟计算和分析,数值模拟结果表明海水入侵区上、下游坝对海水入侵有着显著的影响,下游坝的深度和长度都直接反映减轻海水入侵的能力。这些研究大多数是对已建成的地下截渗墙进行数值模拟,分析其防治咸水入侵效果,未对地下截渗墙的高度及相对海水的位置做全面的探讨。
本文在前人物理模型试验的基础上,利用OpenGeoSys科学模拟软件,建立二维饱和多孔介质变密度地下水流的溶质运移模型,研究地下截渗墙对咸水入侵规律的影响,分析讨论咸淡水水位差、截渗墙高度以及截渗墙位置对海水入侵的防治效果。该研究揭示了地下截渗墙影响下的咸水入侵规律,而且对地下截渗墙的结构设计和规划布置、以及有效防治海水入侵提供了理论依据。
1 数值模型简介本文的数值模拟基于OpenGeoSys科学模拟软件,它是一个由C++实现、面向对象的建模源程序工具包,能够模拟多孔介质或裂隙介质中单个或者耦合的传热-流动-力学-化学过程(Thermo-Hydro-Mechanical-Chemical Processes)。事实表明,地下水密度的微小变化会对流速和流态产生显著的影响。因此在研究如地下咸水流运移问题时,需要考虑地下水的密度变化,基于对此问题的考虑,本文采用变密度的溶质运移模型。
在等温状态下,流体体积密度的线性方程可以用水头表示,
| $ \rho = {\rho _0}(1 + {\lambda _h}(h-{h_0}) + \lambda cC)。$ | (1) |
其中:h表示水头;h0为参考水头;ρ表示流体的密度;ρ0表示参考流体密度;λh表示流体在恒定溶质质量分数下与水头变化相关的压缩系数;λc表示流体在恒定水头下随着溶质质量浓度的变化引起的膨胀系数;C表示相对浓度。
变密度流动的控制方程包括连续性方程,水流运动方程及溶质运移方程。
(1) 流体的连续性方程
| $ \begin{array}{l} \varphi \frac{{\partial S}}{{\partial t}} + SS_0^h\frac{{\partial h}}{{\partial t}} + S\varphi {\lambda _C}\frac{{\partial C}}{{\partial t}} + \nabla \cdot \boldsymbol{\vec q }+ \\ {\lambda _C}\boldsymbol{\vec q} \cdot \nabla C = {Q_\rho }. \end{array} $ | (2) |
式中:φ表示孔隙率;S表示饱和度;t表示时间;Qρ表示含水层中流体源汇项;S0h表示多孔介质关于水头变化的贮水率;
(2) 水流运动方程
| $ \boldsymbol{\vec q}{\rm{ = }}\varphi \boldsymbol{\vec v} =-\frac{{\hat k{\rho _0}\boldsymbol{\vec g}}}{\mu }(\nabla h + \frac{{\rho-{\rho _0}}}{{{\rho _0}}}\boldsymbol{e})。$ | (3) |
式中:
(3) 溶质运移方程
具有源项的溶质运移可表示为以下对流-扩散方程
| $ \frac{{\partial (\varphi C)}}{{\partial t}} + \nabla \cdot (\varphi \vec vC)-\nabla \cdot (\varphi \hat D \cdot \nabla C) = {Q_C}。$ | (4) |
式中:QC表示溶质源项;
| $ \hat D = \gamma {D_m}\hat \delta + \alpha T\left| v \right|\hat \delta + ({\alpha _L}-{\alpha _L}\frac{{\overrightarrow {{v_i}} \overrightarrow {{v_j}} }}{{\left| v \right|}})。$ | (5) |
式中:γ为弯曲系数或迂曲度;Dm为分子扩散系数;
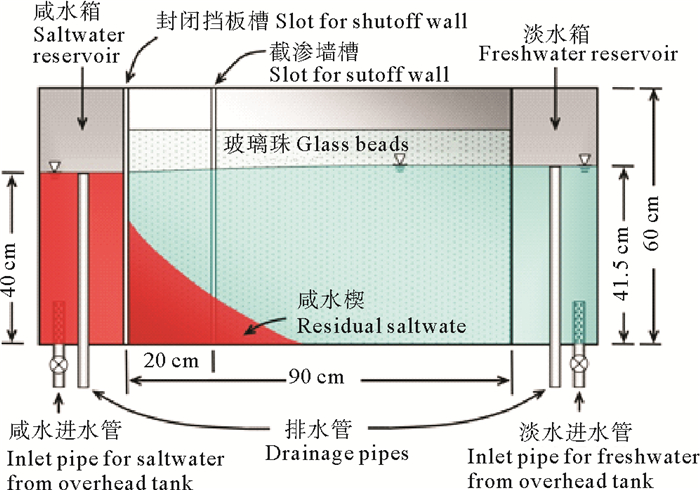
试验装置中,主水箱两侧为咸水箱和淡水箱,其中的主水箱长90 cm,高60 cm,宽8 cm,主水箱与两侧水箱由细网筛隔开。主水箱中装满直径为1.2 mm的玻璃珠,以模拟非承压含水层多孔介质。咸水箱中咸水的密度为1.025 g/mL,淡水的来源为自来水,为了区分咸水与淡水,咸水用染料染成红色。两侧水箱内的水头由可调节的排水管控制。试验装置中设有两个狭槽(见图 1),均由细筛网构成,分别用于插入封闭挡板和截渗墙。封闭挡板和截渗墙均由4 mm厚的丙烯酸板制作而成。主水箱上刻有正交网格,水箱的底部和两边贴有标尺,用以准确地测量并读取咸水楔的瞬时形态,记录的数据与用高分辨率数码相机拍摄的照片进行双重验证。
|
图 1 试验装置 Fig. 1 Schematic diagram of the experiment setup |
试验过程分为以下3个步骤:(1)试验准备阶段:该阶段初期,封闭挡板槽及截渗墙槽中均未插入挡板,两侧水箱都充满淡水,并分别调整排水管使两侧水箱内水头维持在一个恒定的高度,其中淡水侧为41.5 cm,咸水侧为40.0 cm,淡、咸水两侧的水力梯度将产生由淡水侧水箱向咸水侧水箱的流动,直至流动稳定,此时主水箱中水面线以下的多孔介质区域充满淡水。接着,快速插入封闭挡板,将咸水箱和主水箱隔离,通过调节排水管排出咸水箱中的淡水,然后通过进水管加入等水位的红色咸水,为模拟咸水入侵过程做准备。(2)抽出封闭挡板:快速抽出封闭挡板,此时咸水入侵过程开始,咸水楔的底端逐渐向淡水侧移动,测量不同时刻咸水楔的底部位置,并用数码摄影技术记录,直至咸水楔底部位置不再发生改变,并且咸水边界附近不再有淡水排出,此时咸水入侵达到稳定状态。(3)插入截渗墙后:快速准确地将20 cm截渗墙插入截渗墙槽中,同时尽量避免对已有流动条件的干扰。截渗墙安装后,记录不同时刻残留咸水楔底部的位置,当咸水楔底部位置不再发生改变或截渗墙右侧残留咸水被完全冲走时,该试验结束。
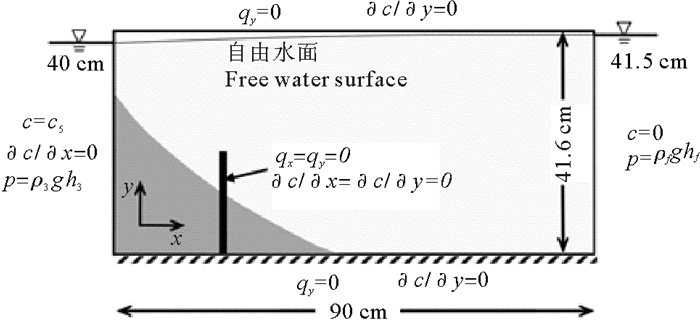
2.2 模型概化及网格划分本文将物理试验装置概化为90 cm×41.6 cm的二维计算域(图 2),咸、淡水侧的水头及压强边界条件恒定,底部为不透水层,顶部无补给。数值模拟所用参数值见表 1,咸水侧水位为40 cm,淡水侧水位值设为41.3 cm。
|
图 2 数值模拟的初始条件及边界条件 Fig. 2 Initial and boundary conditions for numerical simulations |
|
|
表 1 数值模拟参数 Table 1 Parameters for numerical simulations |
本文利用GINA_OGS软件采用有限元方法划分网格,该软件是有限元程序OpenGeoSys的交互式图形用户界面,模型采用三角形网格,本次共剖分个29 030单元,14 756个节点。
2.3 模型验证对应于试验步骤的(2)和(3),数值模拟分为2个阶段。第一阶段为安装截渗墙前,具体的初始条件和边界条件见图 2。由于咸水箱和主水箱之间的封闭挡板被快速抽出,咸水箱中的咸水向淡水一侧入侵,形成咸水楔,咸水楔逐渐向前推进,直至达到稳定状态。稳态时计算域内每个单元的压强水头及浓度值将作为下一阶段的初值条件。第二阶段从安装截渗墙开始,直至残留咸水完全消散或不再变化,残留咸水指截渗墙向陆一侧(右侧)的咸水楔部分。截渗墙的安装被假设为是瞬间完成,也就是说,第二阶段一开始,截渗墙就存在于系统中。
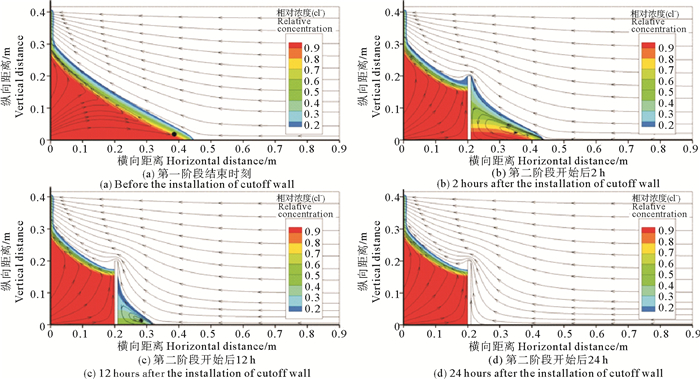
截渗墙高度hc =20 cm时不同时刻咸水楔形状的变化见图 3,图中带箭头的实线表示某一时刻的流线。Cl-相对浓度指Cl-浓度与咸水箱中咸水的Cl-浓度之比,图中楔形咸水楔取相对浓度0.1作为其靠近淡水一侧的边界。
|
图 3 自然条件下和有截渗墙存在情况下的咸水入侵数值模拟 Fig. 3 Simulations of saltwater intrusion before and after installation of cutoff wall |
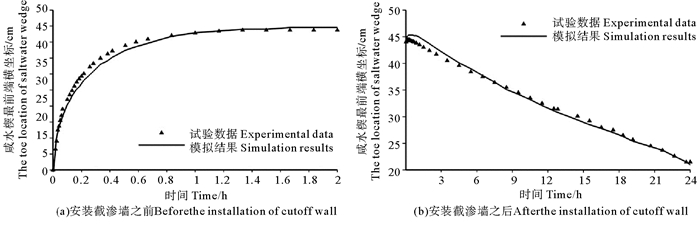
为了验证数值模型的有效性,将数值模拟结果与实验测得的不同时刻咸水锲最前端的位置进行了比较。第一阶段(见图 4a),咸水楔向右(淡水一侧)推进,2 h内达到稳态,模拟结果和试验数据基本吻合。第二阶段(见图 4b),安装截渗墙之后,残留咸水楔首先平坦化,咸水楔最前端略微前进,然后逐渐后退,最终从截渗墙向陆一侧完全被冲淡。由此可见,模拟结果再现了实验室物理模型实验的咸水入侵过程。表明所建数值模型能够准确地描述自然条件下和有截渗墙存在情况下的浓度场,并跟踪咸淡水分界面随着时间的运移情况,为后续截渗墙对海水入侵规律的深入研究奠定了基础。
|
图 4 试验数据与模拟结果的对比 Fig. 4 Comparisons between experimental data and simulation results |
为了更进一步分析研究地下截渗墙对海水入侵的影响,本文分别模拟了不同的咸、淡水侧水位差、截渗墙高度和截渗墙位置条件下截渗墙右侧残留咸水的消散过程。
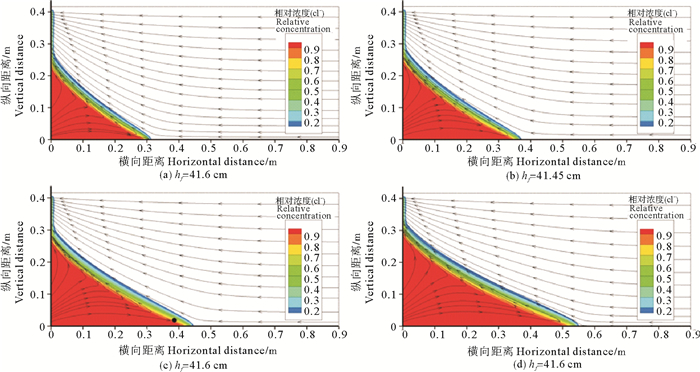
3.1 咸、淡水侧水位差的影响假设淡水侧水位hf大于咸水侧水位hs,将咸水侧水位固定为hs=40.0 cm,取淡水侧水位hf分别为41.6、41.45、41.3、41.15 cm,达到稳态时的相对浓度分布见图 5。图 6比较了不同咸、淡水侧水位差条件下,达到稳态时咸水楔最前端的位置x,横向距离30 cm处咸水楔厚度z。另外,在以上4种情况下,在横向距离20 cm处安装20 cm高截渗墙,比较残留咸水完全消散所用时间td。
|
图 5 不同咸、淡水侧水位差条件下达到稳态时的相对浓度分布 Fig. 5 Relative concentration distributions in the condition of different saltwater-freshwater level difference when reaching the steadystate |
|
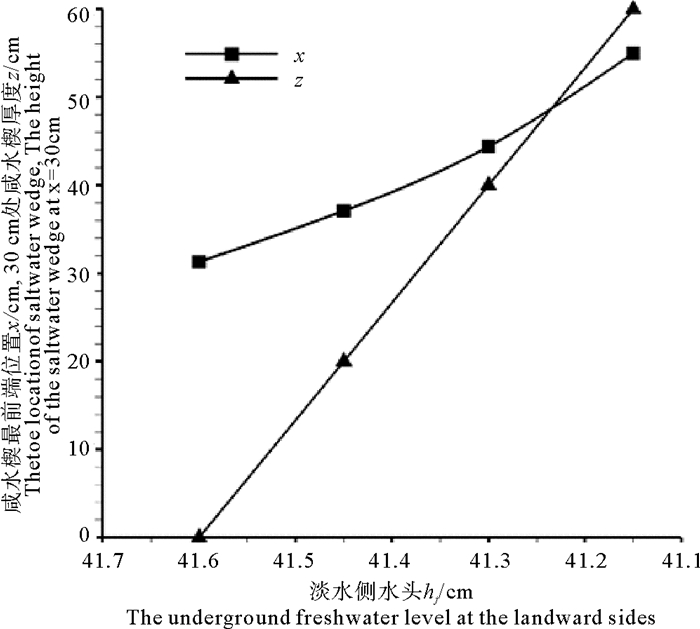
图 6 hs=40.0 cm时,x、z与hf的关系曲线 Fig. 6 Relations of x, z and hf when hs =40 cm |
从图 5和6可以看出,淡水侧水位hf越小,则达到稳态时,盐水入侵距离x越大。由图 1分析得出,咸水侧水头压力ps=ρsghs,淡水侧水头压力pf=ρfghf,经计算,ps < pf,当淡水侧水位越小时,水头压力差越小,咸水楔向前入侵的距离越大。
图 6中对应于不同的淡水侧水位41.6、41.45、41.3和41.15 cm,系统达到稳态时横向距离30 cm处咸水楔厚度z分别为2、6、10和14 cm。淡水侧水位hf每减少0.15 cm,横向距离30 cm处咸水楔厚度z就增加4 cm。说明随着hf降低,咸水楔形体增厚,上覆淡水层变薄。若在实际工况中横向距离30 cm处为抽水井,则该抽水井中就可能因为咸水入侵而抽出咸水,影响附近居民的农业灌溉甚至生活用水。
分别在横向距离20 cm处安装20 cm高截渗墙后,对应于不同的淡水侧水位41.6、41.45、41.3和41.15 cm,残留咸水完全消散所用时间td分别为12,17.5,24,34 h。这表明,淡水侧水位越小,安装截渗墙后,截渗墙右侧残留咸水体积越大,故消散所用时间越长。
3.2 截渗墙高度的影响将截渗墙的高度hc分别设定为25、20、15、10、9和5 cm,其他参数和模型验证时所用的一样,通过数值模拟结果比较墙右侧残留咸水能否完全消散,如果能,比较消散所用的时间td。
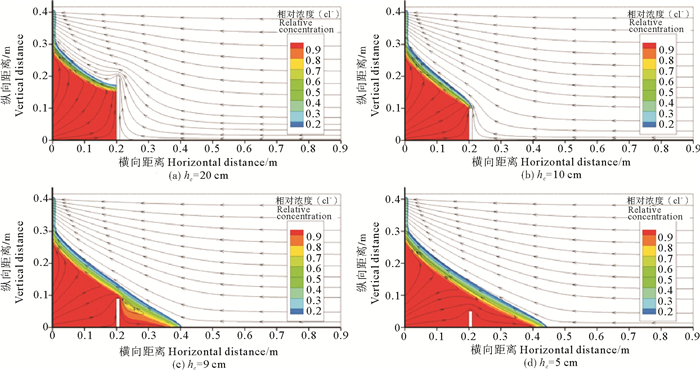
模拟发现,截渗墙的高度hc分别为25、20、15和10 cm时,残留咸水能够完全消散,而hc为9和5 cm时,残留咸水不能完全消散,其中截渗墙的高度分别为20、10、9、5 cm情况下的最终稳态见图 7(25、15与10 cm相似,故未列出)。
|
图 7 不同截渗墙高度条件下达到稳态时的的相对浓度分布 Fig. 7 Relative concentration distributions in the condition of different height for cutoff wall when reaching the steadystate |
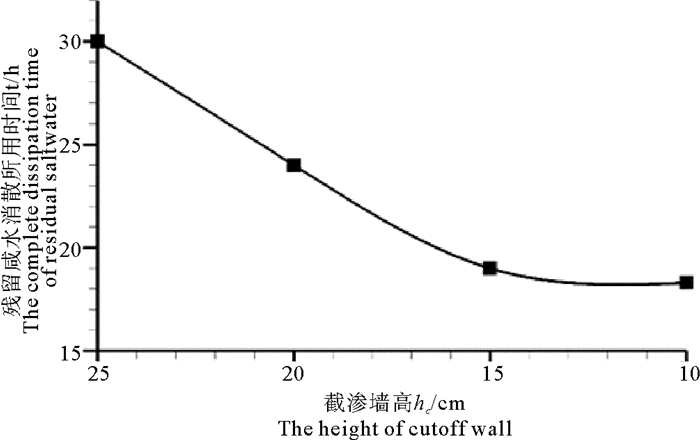
对于残留咸水能够完全消散的情况,图 8给出了hc~td近似关系图。可以看出,随着截渗墙高度hc的减少,截渗墙右侧残留咸水完全消散时间td逐渐减少,且10 cm截渗墙下消散速度最快,只有18.3 h,这表明相对较矮的截渗墙更有利于残留咸水被冲散;而截渗墙的高度为9和5 cm的情况下残留咸水则不能完全消散。
|
图 8 截渗墙高度与残留咸水完全消散所用的时间关系曲线 Fig. 8 Relationime of residual saltwater |
因此,要完全冲散残留咸水,截渗墙应有最小高度要求,否则,残留咸水将不能完全消散。图 7中的咸水、淡水交界处是混合区,混合区靠近淡水的部分不断地被淡水冲走,而新的咸水会不断地补充进来。截渗墙的高度hc分别为9和5 cm时,截渗墙墙顶均位于该混合区以下,但是10 cm截渗墙墙顶恰好位于混合区下,淡水补给恰好可以阻止新的咸水进入截渗墙右边区域,而9和5 cm的截渗墙,墙顶与混合区之间有足够的间隙使得咸水能够进入截渗墙右边区域,使得咸水楔不能完全消退到截渗墙向海一侧。同时可以看到,安装截渗墙之前,横向距离20 cm处的咸水楔厚度为15 cm,大于截渗墙的最小高度要求10 cm,所以实际情况下,地下截渗墙的高度大于此处咸水楔的厚度即可使截渗墙右侧的残留咸水完全消散。
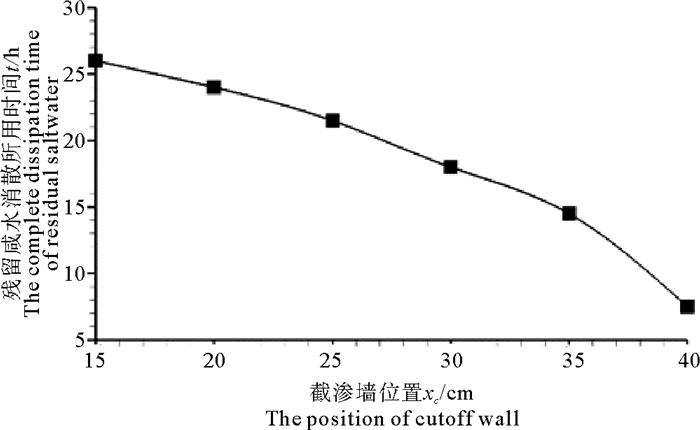
3.3 截渗墙位置的影响模拟的第一阶段保持初始条件、边界条件与章节3.2中的一样,达到稳态时如图 3(a),咸水楔最前端到达横向距离44.4 cm,第二阶段分别在横向距离为15、20、25、30、35、40 cm处安装20 cm高的截渗墙,由于横向距离15~40 cm处的咸水楔厚度小于截渗墙的高度20 cm,由上一节的分析可知,在这6种情况下,截渗墙右侧的残留咸水均能完全消散,图 9比较了残留咸水完全消散所用的时间tp。
|
图 9 截渗墙位置与残留咸水完全消散所用的时间关系曲线 Fig. 9 Relations between the position of cutoff wall and the complete dissipation time of residual saltwater |
由图 9可见,截渗墙离咸水侧距离越远,残留咸水排净所用时间越小。这是由于离咸水侧越远,截渗墙右侧咸水体的横向跨度越小,同时截渗墙处的咸水楔厚度减小,这样截渗墙右侧咸水体积大大减少,更容易被淡水冲散。
4 结论本文基于OpenGeoSys科学模拟软件,通过数值模拟,再现了室内物理模型实验的咸水入侵过程,模拟结果表明:所建模型能够准确描述自然条件下和有地下截渗墙存在情况下的浓度场并跟踪咸淡水分界面随着时间的运移情况。接着,本文模拟分析了不同的咸、淡水侧水位差、截渗墙高度和截渗墙位置条件下截渗墙右侧残留咸水的移动-消散过程,得出的主要结论如下:
(1) 不同的咸、淡水侧水位差条件下,保持咸水侧水位不变,淡水侧水位越小,咸水楔向前入侵的距离越大,导致横向距离同一位置咸水楔形体越厚,上覆淡水层越薄,这也正是咸水入侵情况下抽水井水质变咸的原因。安装截渗墙之后,淡水侧水位越小,截渗墙右侧残留咸水体消散所用的时间越长。结果表明,要从根本上解决咸水入侵问题,必须提高滨海地区向陆一侧的地下淡水水位,这在人们所采取的一些防治咸水入侵的方法中有所体现,如人工回灌淡水。
(2) 不同的截渗墙高度条件下,分析了截渗墙安装后残留咸水消散特性。淡水沿着混合区流向咸水侧,并越过截渗墙,逐渐稀释补充进混合区的咸水,最终完全冲散截渗墙右侧残留咸水。这表明地下截渗墙不仅能够有效阻咸海水入侵,而且可以在截渗墙向陆一侧形成淡水储存区,即地下水库。因此,要冲散残留咸水,截渗墙应有最小高度要求,且相对较矮的截渗墙更有利于冲散残留咸水。
(3) 不同的截渗墙位置条件下,截渗墙离咸水侧距离越远,残留咸水体积越小,全部消散所用的时间越少。实际情况下,可以结合具体的地质、水井分布情况以及当地土地的利用情况,在满足工业、农业、人民生活需求的情况下,尽可能地将截渗墙修建在离海岸较远的地方,以快速阻止咸水入侵。
| [1] |
郭占荣, 黄奕普. 海水入侵问题研究综述[J]. 水文, 2003, 23(3): 10-15. GUO Zhan-rong, HUANG Yi-pu. Comprehensive study on seawater intrusion[J]. Hydrology, 2003, 23(3): 10-15. (  0) 0) |
| [2] |
McAnally W H, Pritchard D W. Salinity control in Mississippi River under drought flows[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1997, 123(1): 34-40. DOI:10.1061/(ASCE)0733-950X(1997)123:1(34)
(  0) 0) |
| [3] |
Mundzer Hasan Basri. Two New Methods for Optimal Design of Subsurface Barrier to Control Seawater Intrusion[D]. Winnipeg, Manitoba: University of Manitoba, 2001.
(  0) 0) |
| [4] |
Ishida S, Tsuchihara T, Yoshimoto S, et al. Sustainable use of groundwater with underground dams[J]. Japan Agricultural Research Quarterly, 2011, 45(1): 51-61. DOI:10.6090/jarq.45.51
(  0) 0) |
| [5] |
林少伟, 徐梁, 赵鸿旭. 龙口市防治海水入侵措施与对策[J]. 山东水利, 2010, 8: 58-59. LIN Shao-wei, Xu Liang, Zhao Hong-xu. Counter measures for the prevention of seawater intrusion in Longkou City[J]. Shandong Water Resources, 2010, 8: 58-59. (  0) 0) |
| [6] |
郭鑫, 赵全升, 张建伟, 等. 大沽河下游地区地下水及地表植被对截渗墙的响应[J]. 干旱区资源与环境, 2014, 28(1): 142-147. GUO Xin, ZHAO Quansheng, ZHANG Jianwei, et al. Response of groundwater and vegetation to the cutoff wall in the lower reachesof Dagu River[J]. Journal of Arid Land Resources and Environment, 2014, 28(1): 142-147. (  0) 0) |
| [7] |
Onder H, Yilmaz M. Underground Dams-A tool of sustainable development and management of groundwater resources[J]. European Water, 2005, 11/12: 35-45.
(  0) 0) |
| [8] |
Roger L Jr, Kazuro M, Kei N. Laboratory-scale saltwater behavior due to subsurface cutoff wall[J]. Journal of Hydrology, 2009, 377: 227-236. DOI:10.1016/j.jhydrol.2009.08.019
(  0) 0) |
| [9] |
贺国平, 邵景力, 崔亚莉. 黄河下游截渗墙对地下水影响的数学模型与评价[J]. 人民黄河, 2003, 25(1): 22-23. He Guoping, Shao Jingli, Cui Yali. Mathematical model and evaluation of the influence of cutoff wall on groundwater in the lower reaches of the Yellow River[J]. Yellow River, 2003, 25(1): 22-23. (  0) 0) |
| [10] |
韩志勇. 大沽河下游地下咸水恢复方案的优化研究[D]. 青岛: 中国海洋大学, 2004. Han Zhiyong. Research of the Optimization on Restoration Schemesof Saline Groundwater at the Low Reach of DaguRiver[D]. Qingdao: Ocean University of China, 2004. (  0) 0) |
| [11] |
袁益让, 梁栋, 芮洪兴. 三维海水入侵及防治工程的渗流力学数值模拟及分析[J]. 中国科学, 2009, 39(2): 222-236. Yuan Yirang, Liang Dong, Rui Hongxing. Numerical simulation and analysis of 3D seepage mechanics in seawater intrusion prevention project[J]. Science in China, 2009, 39(2): 222-236. (  0) 0) |
2. The Key Laboratory of Ocean Engineering of Shandong Province, Ocean University of China, Qingdao 266100, China
 2018, Vol. 48
2018, Vol. 48

