船舶在遭遇恶劣海况时,为了避免遭受横风横浪的影响,通常会调整航向,选择纵浪或斜浪航行[1]。即使船舶在静水中有足够的稳性,在纵浪和斜浪航行时仍有发生大角度摇摆乃至倾覆的可能。特别是当船波遭遇频率与船舶横摇固有频率比为2时,很有可能发生参数横摇甚至倾覆。参数横摇发生的基本原理是船舶在航行过程中,由于波长近似等于船长,可认为波峰分别经过船首-船中-船尾整个过程是一个完整的参数激励周期。当波峰位于船首/尾(即波谷位于船中)时,船舶首尾处的水线面要比静水中的水线面大,即此时的船舶横摇复原力矩要比静水时的偏大;而当波峰位于船中时,船舶首尾处的水线面要比静水中的水线面小,即此时的船舶横摇复原力矩要比静水时的偏小。随着船-波相对位置的周期性变化,船舶横摇复原力矩也呈现出周期性变化,从而引发显著的参数横摇运动。因此,有必要研究纵浪和斜浪中航行船舶的稳性及运动状态,分析船舶倾覆的机理,为避免船舶倾覆提供操船决策。
早在1863年,Froude[2]就观察到在纵浪中航行的船舶受到波浪激励会发生大幅横摇的现象,只是当时的知识还无法解释该现象。随着非线性理论的发展以及计算机技术的飞速发展,各国学者针对船舶参数横摇运动进行了大量的研究并取得了一些新的成果。Matusiak[3]对参数共振的理论进行了研究。他提出了完整的六自由度数学模型。其研究表明:产生横摇参数共振的最主要的原因是傅汝德-克雷洛夫力和复原力矩的非线性特性。Silva等[4-5]提出了基于切片理论研究迎浪船舶动稳性的新方法,并将该方法拓展到船舶六自由度非线性运动模型,通过与试验结果对比,验证了该方法的可行性。Silva和Soares[6]采用横摇-纵摇-垂荡耦合的数学模型,进行了数值模拟和运动稳定性分析,并用模型试验对研究结果加以验证。研究发现:如果船舶遭受波浪的波长等于其船长、波浪的频率为横摇固有频率的两倍时,将有可能出现严重的横摇参数共振现象,其横摇角可达30°。Umeda[7]等考虑横摇恢复力矩的变化研究了规则和随机纵浪和斜浪中船舶的参数激励横摇运动,其横摇恢复力矩系数的变化根据倾覆实验求出。Vidic-Perunovic等[8]采用一阶可靠性方法计算船舶参数横摇运动超过限定角度的概率。鲁江、卜淑霞等[9]基于切片理论,提出了复原力的计算方法,计算过程中考虑了复原力中的辐射力和绕射力成分,并通过模型试验验证了数值计算方法的有效性。Dostal[10]针对随机海况,应用能量包线随机平均法,理论推导了船舶参数横摇响应的概率密度函数。彭东升等[11]针对C11集装箱船,计算了不同阻尼下船舶参数横摇响应。傅超等[12]对C11集装箱船进行了参数敏感性分析,提出通过改进船舶设计减少参数横摇发生的概率。Wei Chai[13]于2016年提出了一种能有效计算蒙特卡罗模拟的方法,并验证该方法适用于统计船舶在随机长峰波激励下的参数横摇响应极值。
本文在前人工作的基础上研究随机斜浪中船舶参-强激励横摇响应的概率密度函数。为实现解析求解,将数值模拟得到的复原力臂函数用近似的解析函数表示,将随机海浪谱处理为窄带随机过程以得到随机参数激励和随机强迫激励的谱密度函数,采用能量包线随机平均法计算系统响应的稳定概率密度函数。
1 船舶参数激励横摇运动方程考虑随机斜浪,假设船舶的垂荡及纵摇运动为小量,船舶横摇运动方程如下:
| $ \left( {I + A\left( {{\omega _n}} \right)} \right)\mathit{\ddot \Phi } + {b_1}\mathit{\dot \Phi } + {b_3}{{\mathit{\dot \Phi }}^3} + g\Delta GZ\left( {\mathit{\Phi },\eta ,\mathit{\Psi }} \right) = M。$ | (1) |
其中:Φ为横摇角;I为横摇惯性矩;A(ωn)为横摇附加惯性矩;b1与b3分别为线性阻尼系数与立方非线性阻尼系数;Δ为排水量;g为重力加速度;M为波浪强迫激励力矩;GZ(Φ, η, Ψ)为船舶复原力臂,由Φ、η和Ψ决定,其中η为长峰波的波动幅度,Ψ为船和波的相对位置,取值范围为[0,2π]。
船舶在长峰波中的复原力臂GZ(Φ, η, Ψ)可基于切片理论求解,一般采用数值的方法进行模拟[9]。
为了能够使用随机平均理论求解运动方程(1),将GZ(Φ, η, Ψ)展开为如下的关于横摇角Φ的多项式[14]:
| $ G{Z_a}\left( {\mathit{\Phi },\eta ,\mathit{\Psi }} \right) = {q_1}\mathit{\Phi } + {q_2}{\mathit{\Phi }^3} + {q_3}{\eta _c}\mathit{\Phi }。$ | (2) |
式中,ηc=ηcos(Ψ),是由随机波浪确定的随机过程,可通过窄带海浪谱展开得到;qi(i=1, 2, 3)为展开项的系数,使用最小二乘法确定,即使下式取得最小:
| $ E = \frac{1}{{4{\rm{ \mathsf{ π} }}{\mathit{\Phi }_0}{\eta _0}}}\int_0^{2{\rm{ \mathsf{ π} }}} {\int_0^{{\eta _0}} {\int_{ - {\mathit{\Phi }_0}}^{{\mathit{\Phi }_0}} {{{\left( {GZ - G{Z_a}} \right)}^2}} } } {\rm{d}}\mathit{\Phi }{\rm{d}}\eta {\rm{d}}\mathit{\Psi }。$ | (3) |
对于随机海浪,一般用谐波叠加法来模拟不规则长峰波波面函数。为采用随机平均法研究船舶随机参-强激励横摇运动,以下将随机波面升高处理为窄带随机过程Ze(x, t),其表达式如下[10]:
| $ {Z_e}\left( {x,t} \right) = {\eta _1}(t)\cos (2{\rm{ \mathsf{ π} }}x/L) - {\eta _2}(t)\sin (2{\rm{ \mathsf{ π} }}x/L)。$ | (4) |
其中,η1(t)和η2(t)均为高斯平稳随机过程,两者互不相关、统计独立[15-16],表达式如下:
| $ {\eta _1}(t) = \int_0^\infty {\frac{{2{\rm{ \mathsf{ π} }}\sin r}}{{{{\rm{ \mathsf{ π} }}^2} - {r^2}}}} \sin (\omega t + \zeta (\omega ))\sqrt {2S(\omega ){\rm{d}}\omega } ; $ | (5) |
| $ {\eta _2}(t) = \int_0^\infty {\frac{{2r\sin r}}{{{{\rm{ \mathsf{ π} }}^2} - {r^2}}}} \cos (\omega t + \zeta (\omega ))\sqrt {2S(\omega ){\rm{d}}\omega } 。$ | (6) |
式中:ω为海浪频率;S(ω)为海浪谱;ζ(ω)为随机相位角。r=(L/2)k,其中L为特征波长,k为波数。
η1(t)和η2(t)对应的谱密度函数分别为:
| $ {{\bar S}_1}(\omega ) = 2S(\omega ){\left( {\frac{{2{\rm{ \mathsf{ π} }}\sin r}}{{{{\rm{ \mathsf{ π} }}^2} - {r^2}}}} \right)^2}; $ | (7) |
| $ {{\bar S}_2}(\omega ) = 2S(\omega ){\left( {\frac{{2r\sin r}}{{{{\rm{ \mathsf{ π} }}^2} - {r^2}}}} \right)^2}。$ | (8) |
如果船舶以航向角β、航速U航行,则式(4)~(8)中的海浪频率ω和海浪谱S(ω)要用对应的遭遇频率ωe和遭遇谱S(ωe)来替换,其表达式为:
| $ {\omega _e} = \omega - kU\cos \beta ; $ | (9) |
| $ S\left( {{\omega _e}} \right) = S(\omega )\left| {\frac{1}{{\sqrt {1 - 4U{\omega _e}\cos \beta /g} }}} \right|。$ | (10) |
进一步将随机过程η2用受控自回归滑动平均模型(CARMA(2, 1))来模拟。对于CARMA(2, 1)过程,需要满足如下形式的微分方程:
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{d}}{u_1} = \left( {{u_2} - {c_2}{u_1}} \right){\rm{d}}t + {c_1}\bar \sigma {\rm{d}}W}\\ {{\rm{d}}{u_2} = - {c_3}{u_1}{\rm{d}}t} \end{array}} \right.。$ | (11) |
式中:u1、u2为状态变量;
| $ {H_2}(s) = \frac{{{c_1}s}}{{{s^2} + {c_2}s + {c_3}}}; $ | (12) |
| $ {S_2}(\omega ) = {H_2}(s){H_2}( - s)\frac{{{{\bar \sigma }^2}}}{{2{\rm{ \mathsf{ π} }}}}。$ | (13) |
其中,s=iω。采用最小二乘法,使式(13)与式(8)的误差最小,从而确定ci(i=1, 2, 3)。
3 船舶随机参-强激励横摇概率密度函数采用能量包线随机平均法研究船舶随机参-强激励横摇运动概率密度函数。将船舶运动过程处理为马尔可夫过程,将响应量分成快变量与慢变量,通过对快变量的平均得到慢变量的近似方程,从而使系统的自由度缩减。
将GZa(Φ, η, Ψ)代入船舶参数横摇运动方程(1),将随机波浪激励力矩近似处理为M≈Δgq0πsin(β)ηc(t)/L,令Φ=u、ηc=ξt,并对方程(1)做无因次处理,有:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot {\bar u} = \bar v}\\ {\dot {\bar v} = - \overline {{\alpha _1}} \bar u + \overline {{\alpha _3}} {{\bar u}^3} - \overline {{\beta _1}} \bar v - \overline {{\beta _3}} {{\bar v}^3} + (\overline {{\gamma _1}} + \bar u\overline {{\gamma _2}} ){\xi _t}} \end{array}} \right.。$ | (14) |
其中,
做如下的尺度变换:u=u、v=εv、
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}u}}{{{\rm{d}}t}} = v}\\ {\frac{{{\rm{d}}v}}{{{\rm{d}}t}} = - {\alpha _1}u + {\alpha _3}{u^3} - \varepsilon \left( {{\beta _1}v + {\beta _3}{v^3}} \right) + }\\ {\;\;\;\;\;\;\sqrt \varepsilon \left( {{\gamma _1} + u{\gamma _2}} \right){\xi _t}} \end{array}} \right.。$ | (15) |
将响应分量进一步写为快变量和慢变量,即系统由状态空间(u, v)变换为状态空间(u, H),其中H为系统总能量,其表达式为:
| $ H(u,v) = \frac{{{v^2}}}{2} - \frac{1}{4}{\alpha _3}{u^4} + \frac{1}{2}{\alpha _1}{u^2}。$ | (16) |
式中,每个能量值H(u, v)对应于特定的横摇运动。对于确定的α1、α3值,可得到对应于式(16)的能量等值线,用b(H)表示在特定能量值H下,系统所能达到的最大横摇角,以下用b(H)来度量船舶的横摇运动。
定义船舶横摇的稳性消失角如下:
| $ {B_1} = \left( {\sqrt {{\alpha _1}/{\alpha _3}} ,0} \right)。$ | (17) |
以该稳性消失角为临界横摇角,其所在的闭合曲线能量值为临界能量Hc,有Hc=α12/(4α3)。
使用如下的转换关系:
| $ {\left( {\frac{{{\rm{d}}u}}{{{\rm{d}}t}}} \right)^2} = 2H - 2\left( { - \frac{1}{4}{\alpha _3}{u^4} + \frac{1}{2}{\alpha _1}{u^2}} \right)。$ | (18) |
则运动方程(15)进一步写为:
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}u}}{{{\rm{d}}t}} = \sqrt {2H - {\alpha _1}{u^2} + \frac{1}{2}{\alpha _3}{u^4}} }\\ {\frac{{{\rm{d}}H}}{{{\rm{d}}t}} = \left[ { - {\beta _1}{{\left( {\frac{{{\rm{d}}u}}{{{\rm{d}}t}}} \right)}^2} - {\beta _3}{{\left( {\frac{{{\rm{d}}u}}{{{\rm{d}}t}}} \right)}^4}} \right]\varepsilon + \left( {\frac{{{\rm{d}}u}}{{{\rm{d}}t}}} \right)\left( {{\gamma _1} + u{\gamma _2}} \right)\sqrt \varepsilon {\xi _t}} \end{array}} \right.。$ | (19) |
引入中间变量Q(u, H)=v2,有:
| $ Q(u,H) = 2H - {\alpha _1}{u^2} + \frac{1}{2}{\alpha _3}{u^4}。$ | (20) |
则式(19)可进一步写为如下的随机微分方程式:
| $ \left\{ \begin{array}{l} {\rm{d}}u = \sqrt {Q(u,H)} {\rm{d}}t\\ {\rm{d}}H = Q(u,H){\left( { - {\beta _1} - {\beta _3}Q(u,H)} \right)_\varepsilon }{\rm{d}}t + \\ \;\;\;\;\;\;\sqrt {Q(u,H)} \left( {{\gamma _1} + u{\gamma _2}} \right)\sqrt \varepsilon {\xi _t}{\rm{d}}t。\end{array} \right. $ | (21) |
根据随机平均法,针对0≤H≤Hc,写出上式的漂移与扩散系数分别为[17]:
| $ \begin{array}{l} m\left( H \right) = \frac{1}{{T\left( H \right)}}\int_0^{T(H)} Q (u(t),H)\left[ { - {\beta _1} - {\beta _3}Q(u(t)),} \right.\\ H)]{\rm{d}}t + \frac{1}{{T(H)q}}\int_{ - \infty }^0 {{R_{\xi t\xi t}}} (\tau )。\\ \left\{ {\int_0^{4K(\bar k)} {\frac{{c{n_{t + \tau }} \cdot {\rm{d}}{n_{t + \tau }} \cdot \left[ {b(H){\gamma _2} \cdot s{n_t} + {\gamma _1}} \right]\left[ {b(H){\gamma _2} \cdot s{n_{t + \tau }} + {\gamma _1}} \right]}}{{c{n_t} \cdot d{n_t}}}} \cdot } \right.\\ {\rm{d}}(qt)\} {\rm{d}}\tau 。\end{array} $ | (22) |
| $ \begin{array}{l} {\sigma ^2}(H) = \frac{{b{{(H)}^2}q}}{{T(H)}}\int_{ - \infty }^\infty {{R_{{\xi _t}{\xi _t}}}} (\tau )\left\{ {\int_0^{4K(\bar k)} c {n_t} \cdot {\rm{d}}{n_t} \cdot } \right.\\ c{n_{t + \tau }} \cdot {\rm{d}}{n_{t + \tau }} \cdot \left[ {b(H){\gamma _2} \cdot s{n_t} + {\gamma _1}} \right]\left[ {b(H){\gamma _2} \cdot s{n_{t + \tau }} + } \right.\\ \left. {\left. {{\gamma _1}} \right]{\rm{d}}(qt)} \right\}{\rm{d}}\tau 。\end{array} $ | (23) |
其中,T(H)为时间区间,其表达式为:
| $ T(H) = 2\int_{ - b(H)}^{b(H)} {\frac{{{\rm{d}}u}}{{\sqrt {Q(u,H)} }}} = \frac{{4K(\bar k)}}{q}。$ | (24) |
上式中,K(k)为第一类完全椭圆积分, 且有:
| $ \bar k = \frac{{b{{(H)}^2}}}{2}\sqrt {\frac{{{\alpha _3}}}{H}} ; $ | (25) |
| $ q = \frac{{\sqrt {2H} }}{{b(H)}}; $ | (26) |
| $ b(H) = \sqrt { - \frac{{ - {\alpha _1} + \sqrt {\alpha _1^2 - 4{\alpha _3}H} }}{{{\alpha _3}}}} 。$ | (27) |
sn、cn、dn为雅克比椭圆函数,且有如下定义:
| $ s{n_t} = sn(qt,\bar k); $ | (28) |
| $ c{n_t} = cn(qt,\bar k); $ | (29) |
| $ {\rm{d}}{n_t} = {\rm{d}}n(qt,\bar k); $ | (30) |
| $ s{n_{t + \tau }} = sn(q(t + \tau ),\bar k); $ | (31) |
| $ c{n_{t + \tau }} = \mathit{cn}(q(t + \tau ),\bar k); $ | (32) |
| $ {\rm{d}}{n_{t + \tau }} = dn(q(t + \tau ),\bar k)。$ | (33) |
系统的能量H满足如下的伊藤随机微分方程:
| $ {\rm{d}}H = m(H){\rm{d}}t + \sigma (H){\rm{d}}{W_t}。$ | (34) |
对于上述伊藤随机微分方程,其响应为扩散过程,对应的转移概率密度p(H, t|H0, t0)满足如下的FPK方程:
| $ \frac{{\partial p}}{{\partial t}} = m(H)\frac{{\partial p}}{{\partial H}} + \frac{1}{2}{\sigma ^2}(H)\frac{{{\partial ^2}p}}{{\partial {H^2}}}。$ | (35) |
上式中,(H0, t0)表示初始状态。
式(35)可进一步写成如下的算子形式:
| $ \frac{{\partial p}}{{\partial t}} - {L^*}p = 0。$ | (36) |
其中,L*为椭圆算子的伴随算子,且有:
| $ {L^*}p = m(H)\frac{{\partial p}}{{\partial H}} + \frac{1}{2}{\sigma ^2}(H)\frac{{{\partial ^2}p}}{{\partial {H^2}}}。$ | (37) |
当随机激励输入系统的能量与系统阻尼耗散的能量达到统计平衡时,有∂p/∂t=0,对应的概率密度函数为平稳概率密度函数pst(H),其满足如下的平稳FPK方程:
| $ {L^*}{p_{st}}(H) = 0。$ | (38) |
引入尺度函数l(u)与速度函数υ(u):
| $ l(u) = \int_{u0}^u {{\varphi ^{ - 1}}} (U){\rm{d}}U; $ | (39) |
| $ v(u) = \int_{u0}^u {\frac{{\varphi (U)}}{{{\sigma ^2}(U)}}} {\rm{d}}U。$ | (40) |
其中,
| $ {L^*}{p_{st}} = \frac{1}{2}\frac{\partial }{{\partial v}}\left( {\frac{{\partial {p_{st}}}}{{\partial l}}} \right) = 0。$ | (41) |
求得式(41)的平稳概率密度函数为:
| $ {p_{st}}(H) = \frac{{\varphi (H)}}{{{\sigma ^2}(H)}}\left[ {{e_1}l(H) + {e_2}} \right]。$ | (42) |
其中,参数e1、e2由边界条件确定。
对于低强度噪声激励有e1=0[13],则式(42)
可进一步写为:
| $ {p_{st}}(H) = \frac{{{e_2}}}{{{\sigma ^2}(H)}}\exp \left( {2\int_0^H {\frac{{m(H)}}{{{\sigma ^2}(H)}}} } \right)。$ | (43) |
应用传递函数关系pst(b)=pst(H) ((d/dH)b)-1,得到基于变量b的平稳概率密度函数为:
| $ {p_{st}}(b) = {p_{st}}(H)\sqrt {\alpha _1^2 - 4{\alpha _3}H} \sqrt {\frac{{{\alpha _1} - \sqrt {\alpha _1^2 - 4{\alpha _3}H} }}{{{\alpha _3}}}} 。$ | (44) |
对平稳概率密度函数式(44)在某一角度范围[φ1, φ2]内积分,可进一步得到b(H)在该角度范围内的概率,从而对船舶的横摇稳定性进行判断。
4 计算结果与分析 4.1 船舶横摇响应本文针对C11集装箱船展开研究,该船主尺度如表 1所示。
采用文献[9]中所述的方法,在Φ∈[-0.6,0.6] rad、η∈[-10, 10] m、Ψ∈[0,2π] rad范围内数值模拟C11集装箱船的复原力臂GZ(Φ, η, Ψ),得到不同Φ、η和Ψ时的复原力臂。采用GZa(Φ, η, Ψ)近似GZ(Φ, η, Ψ),得到对应式(2)的各项拟合系数为q1=2.164 3、q2=-1.775 3、q3=-0.106 1。
本文研究采用ITTC海浪谱。对于特征波高3 m、特征波长262 m、航向角150°、航速1.43 m/s的情况,得到对应于式(14)的船舶横摇运动方程为:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot {\bar u} = \bar v}\\ {\dot {\bar v} = - 0.2373\bar u + 0.1947{{\bar u}^3} - 0.0269\bar v - }\\ {16.8258{{\bar v}^3} + (0.0013 + 0.0116\bar u){\xi _t}} \end{array}} \right.。$ | (45) |
取小参量取参量ε=0.1,得到对应于式(15)的无因次横摇运动方程为:
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}u}}{{{\rm{d}}{t_\varepsilon }}} = v}\\ {\frac{{{\rm{d}}v}}{{{\rm{d}}{t_\varepsilon }}} = - 23.73u + 19.47{u^3} - 0.1 \times (2.69v + }\\ {\left. {16.8258{v^3}} \right) + \sqrt {0.1} \times (0.4057 + 3.6777u){\xi _{{t_\varepsilon }}}} \end{array}} \right.。$ | (46) |
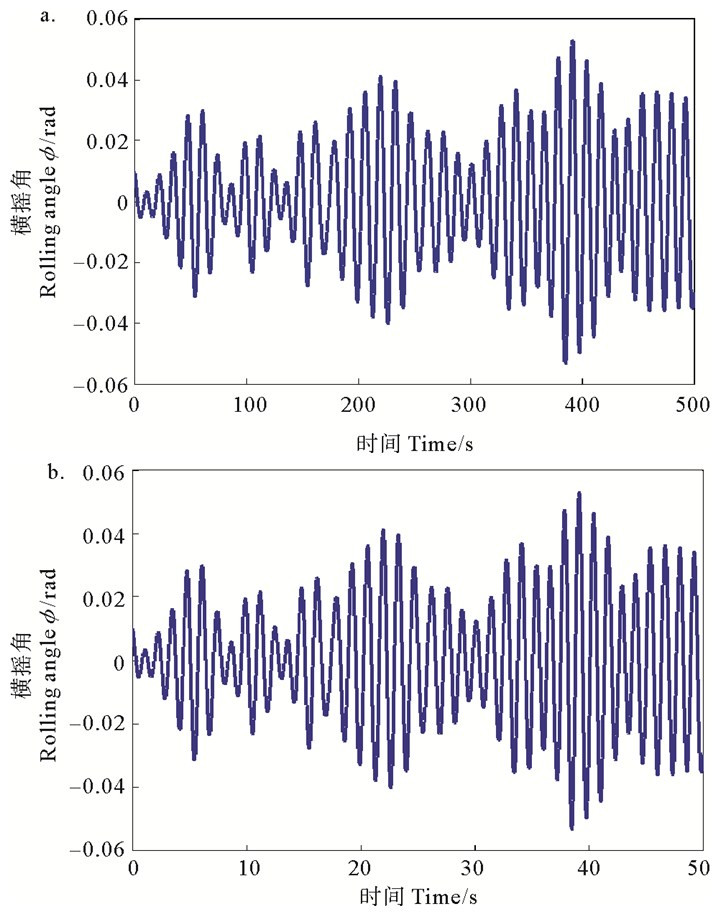
采用龙格库塔法数值求解式(45)和式(46),得到船舶横摇角响应时间历程,如图 1所示。
|
( a.时间尺度变换前 Before scale change;b.时间尺度变换后 After scale change. ) 图 1 船舶横摇响应历程 Fig. 1 Time history of the ship rolling response |
图 1表明,时间尺度变换前后,船舶横摇响应完全相同,验证了对船舶横摇方程进行尺度变换的正确性。
4.2 概率密度函数的蒙特卡洛验证蒙特卡洛方法通过数值方法在计算机上模拟实际的响应过程,然后进行统计。该方法在系统可靠度评估、风险评估及结构非线性随机动力响应分析方面具有广泛的应用[19]。以下采用蒙特卡洛方法验证本文理论计算概率密度函数的正确性。
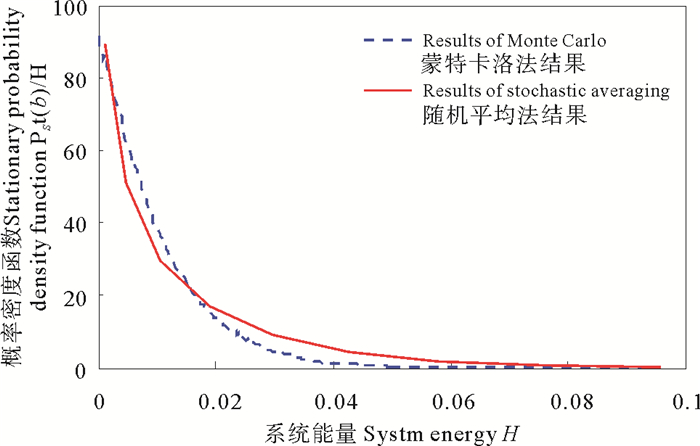
蒙特卡洛法计算参数如下:随机种子数n1=25、迭代步数n2=5 000 000、时间步长Δt=0.01 s,针对4.1中给出的海况,计算关于系统能量H的概率密度函数,并与采用随机平均法计算得到结果进行对比,如图 2所示。
|
图 2 概率密度函数验证 Fig. 2 Verification of PDF |
图 2表明,采用随机平均法计算的概率密度函数与用蒙特卡洛法得到的概率密度函数吻合较好,验证了本文理论推导及半解析计算方法的正确性。在第2节中,将随机海况的波面升高近似为CARMA(2,1)过程,从而得到海浪的自相关函数,该函数是能量包线随机平均法中漂移系数和扩散系数的组成部分。由于近似拟合存在一定的误差,因此在种子数足够多的情况下,随机平均法与蒙特卡洛法计算得到的概率密度函数仍会存在一定差别。
4.3 概率密度函数和概率考虑航速U=1.43 m/s、航向角β=45°、特征波高H=10 m,特征波长L分别为100、150、200、250、300 m,计算船舶机参-强激励横摇响应的概率密度函数和概率。
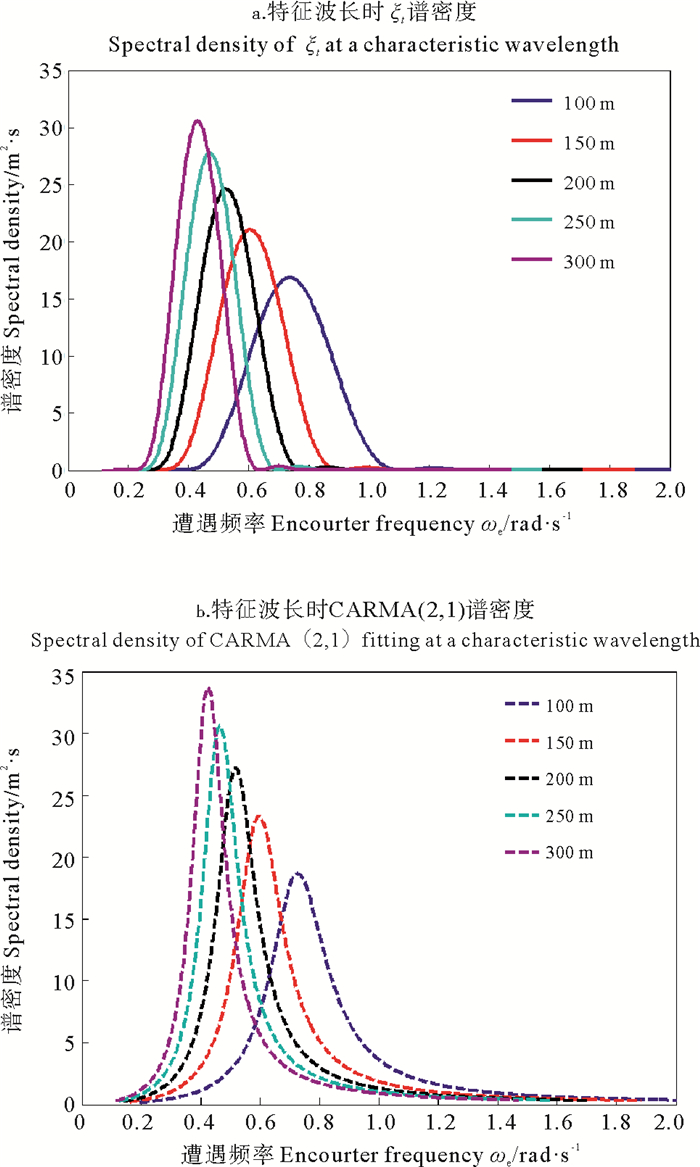
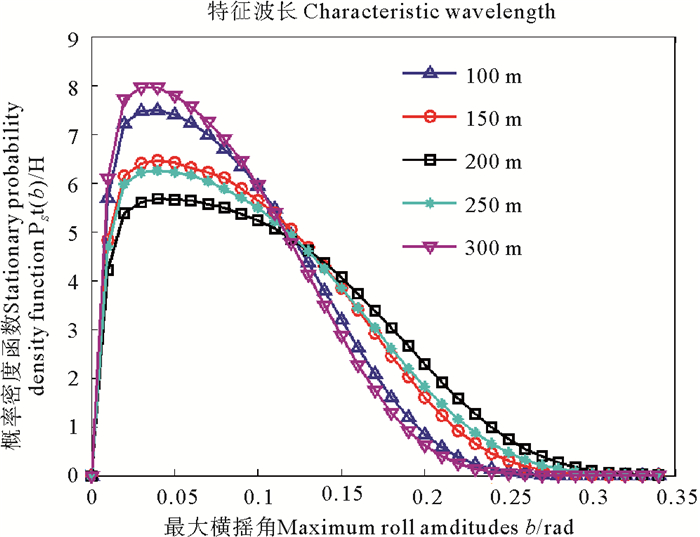
针对以上工况,由式(4)~(10),可得到遭遇频率下随机过程η2(t)的谱密度函数,如图 3(a)所示。根据式(11)~(13),应用CARMA(2, 1)过程拟合随机过程η2,得到拟合的谱密度函数,如图 3(b)所示。得到拟合系数ci(i=1, 2, 3)和γ1如表 2所示,计算得到不同工况关于b的概率密度函数,如图 4所示。
|
( a.由海浪普分解获得Obtained from the wave spectrum; b.由CARMA(2.1)过程拟合获得Obtained by CARMA(2.1) fitting. ) 图 3 ξt的谱密度 Fig. 3 Spectral density of ξt |
|
|
表 2 拟合参数 Table 2 The fitting parameters |
|
图 4 稳定概率密度函数 Fig. 4 Stable PDFs |
对图 4中概率密度函数进一步在[0,0.05]、[0.05,0.10]、[0.10,0.15]、[0.15,0.20]、[0.20,0.25]、[0.25,0.30]及[0.30,0.6] rad的区间内积分,得到b在各区间的概率,结果如表 3示。表 3表明,当遭遇波长(L/cosβ)远离船长时,b在小角度区间的概率较大;当遭遇波长接近船长时,b在大角度区间的概率增加,该结论与已有研究工作的结论相同[1]。以b在[0.25,0.30] rad区间的概率为例,L=200 m(遭遇波长为282.8 m)时为0.018 1,是L=150 m(遭遇波长为212.1 m)时的3.3倍,是L=100 m(遭遇波长为141.4 m)时的16.5倍。
|
|
表 3 b(H)在不同角度区间的概率 Table 3 The probability of b(H) within different angle intervals |
本文基于能量包线随机平均法,以C11船为例,半解析的研究了斜浪中船舶随机参-强激励横摇响应的概率密度函数及响应概率。结果表明,当遭遇频率远离船长时,b(H)在大角度区间的概率较小;当遭遇频率接近船长时,b(H)在大角度区间的概率增加。由b(H)可定量分析斜浪中船舶随机参-强激励横摇运动概率。
| [1] |
李红霞.纵浪和斜浪中船舶非线性运动特性研究[D].天津: 天津大学, 2008. Li H X. Study on Nonlinear Motion Characteristics of Ships in Longitudinal Waves and Oblique Waves[D]. Tianjin: Tianjin University, 2008. http://cdmd.cnki.com.cn/article/cdmd-10056-2009071019.htm (  0) 0) |
| [2] |
储纪龙.斜浪中船舶参强激励横摇运动研究[D].大连: 大连理工大学, 2013. Chu J L. Study on Forcedly-Parametrically Excited Rolling of a Ship in Oblique Seas[D]. Dalian: Dalian University of Technology, 2013. http://cpfd.cnki.com.cn/article/cpfdtotal-zgzc201308001064.htm (  0) 0) |
| [3] |
Matusiak J. Parametric resonance of the conical buoy in regular waves[C]. //Tasmania 7th International Conference on Stability of Ships and Ocean Vehicles, Athens: Natioral technical University of Athens, 2000.
(  0) 0) |
| [4] |
Silva S R E, Santos T A, Soares C G. Parametrically excited roll in regular and irregular head seas[J]. International Shipbuilding Progress, 2005, 52: 29-56.
(  0) 0) |
| [5] |
Silva S R E, Soares C G. Prediction of parametric rolling in waves with a time domain non-linear strip theory model[J]. Ocean Engineering, 2013, 72(4): 453-469.
(  0) 0) |
| [6] |
Soares C G, Silva S R E, Santos T A. Parametrically excited roll in regular and irregular head seas[J]. International Shipbuilding Progress, 2005, 52(1): 29-56.
(  0) 0) |
| [7] |
Akthiko M, Hirotada H, Naoya U. Capsizing sue to bow-diving in following waves[J]. Shipbuild Progress, 2004, 51: 121-133.
(  0) 0) |
| [8] |
Vidic P J. Influence of the GZ calculation method on parametric roll prediction[J]. Ocean Engineering, 2011, 38(2): 295-303.
(  0) 0) |
| [9] |
鲁江, 马坤, 黄武刚. 规则波中船舶复原力变化计算[J]. 武汉理工大学学报(交通科学与工程版), 2011, 35(5): 901-905. Lu J, Ma K, Huang W G. Calculation of restoring moment variation in regular wave[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2011, 35(5): 901-905. DOI:10.3963/j.issn.1006-2823.2011.05.008 (  0) 0) |
| [10] |
Dostal L, Namachchivaya N S. Non-standard stochastic averaging of large-amplitude ship rolling in random seas[J]. Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences, 2012, 468(2148): 4146-4173.
(  0) 0) |
| [11] |
彭东升, 田天齐, 向阳. 横摇阻尼对参数横摇计算精度影响研究[J]. 中国造船, 2015, 56(S1): 48-52. Peng D S, Tian T Q, Xiang Y. Research on the effect of rolling damping in parametric rolling[J]. Shipbuilding of China, 2015, 56(S1): 48-52. (  0) 0) |
| [12] |
傅超, 马山, 段文洋, 等. C11集装箱船参数横摇发生敏感性因素分析和改善措施研究[J]. 中国造船, 2015, 56(S1): 72-80. Fu C, Ma S, Duan W Y, et al. Sensitivity factors in parametric rolling of containership C11 and improvement measure[J]. Shipbuilding of China, 2015, 56(S1): 72-80. (  0) 0) |
| [13] |
Chai W, Naess A, Leira B J, et al. Efficient monte carlo simulation and grim effective wave model for predicting the extreme response of a vessel rolling in random head seas[J]. Ocean Engineering, 2016, 123: 191-203. DOI:10.1016/j.oceaneng.2016.07.025
(  0) 0) |
| [14] |
Dostal L, Kreuzer E. Probabilistic approach to large amplitude ship rolling in random seas[J]. ARCHIVE Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science 1989—1996 (203-210), 2011, 225(10): 2464-2476.
(  0) 0) |
| [15] |
王永安. 关于窄带随机过程的峰值分布和包络分布[J]. 食品与生物技术学报, 1993(1): 59-62. Wang Y A. On Distribution of peaks and envelope of narrow-band process[J]. Journal of Food Science and Biotechnology, 1993(1): 59-62. (  0) 0) |
| [16] |
彭兢, 金长江. 一种窄带平稳随机过程功率谱的简化拟合方法[J]. 航空学报, 2001, 22(3): 253-255. Peng J, Jin C J. Simplified method to fit the power spectrum of narrow-band stochastic process[J]. Acta Aeronautica et Astronautica Sinica, 2001, 22(3): 253-255. DOI:10.3321/j.issn:1000-6893.2001.03.006 (  0) 0) |
| [17] |
朱位秋. 非线性随机动力学与控制[M]. 北京: 科学出版社, 2003. Zhu W Q. Nonlinear Stochastic Dynamics and Control[M]. Beijing: Science Press, 2003. (  0) 0) |
| [18] |
张玉龙, 李红霞, 王文华, 等. 船舶横摇阻尼确定方法研究[J]. 中国造船, 2015, 56(S1): 155-160. Zhang Y L, Li H X, Wang W H, et al. Study on methods of determining roll damping[J]. Shipbuilding of China, 2015, 56(S1): 155-160. (  0) 0) |
| [19] |
赵桂峰, 李琳琳, 李大望. 基于稳态随机动力响应的蒙特卡洛模拟精度研究[J]. 河南科学, 2007, 25(4): 517-520. Zhao G F, Li L L, Li D W. Analysis for the precision of monte carlo simulation based on steady-state random dynamic responses[J]. Henan Science, 2007, 25(4): 517-520. DOI:10.3969/j.issn.1004-3918.2007.04.001 (  0) 0) |
 2019, Vol. 49
2019, Vol. 49

