2. 中国海洋大学 化学化工学院,山东 青岛 266100
多级闪蒸是海水淡化工业中最成熟,运行安全性最高,弹性大,适合于大型和超大型淡化装置的一项技术[1]。多级闪蒸过程中的循环盐水经过预热器加热,回收闪蒸淡水蒸汽的热量,温度升高,在流经换热器的过程中,某些组分的溶解度可能达到过饱和,导致结晶析出,在管道里形成析晶污垢[2-3],沉积于换热表面。污垢的存在不仅增大流体阻力,增加能量消耗[4],降低传热效率,严重时还会堵塞管路,使设备瘫痪。据分析海水析晶污垢的主要成分是CaSO4·2H2O[5],质量分数占到60.4%,其次为Mg(OH)2,质量分数占到39.6%。因此,探讨CaSO4·2H2O析晶污垢在换热管道里的形成过程很有必要。
Fahmi Brahim[6]在分析传质和表面反应的基础上,建立了污垢沉积率的数学模型,探讨了CaCO3在换热面上结垢过程的温度场和浓度场的分布规律,并依据温度场和浓度场计算CaCO3污垢的生成率、剥蚀率和污垢热阻等,但由于实际上污垢同时含有H2O和CaCO3,该研究没有考虑H2O分子对析晶污垢的影响。E.Nebot等[7]通过改进Konak模型,考察了流体流速对冷凝器中污垢沉积的影响,并指出增大流速有利于降低污垢热阻。程浩明等[8]应用FLUENT构建了Hasson[9]模型,从污垢沉积质量出发,计算出污垢热阻随时间的变化规律,并对比了光滑管和波纹管内CaCO3污垢沉积和剥蚀的规律,结果表明波纹管具有较好的抑垢特性。该研究将结垢模型从直管拓展到复杂管路,使模型的适用性得到加强,但Hasson模型涉及参数较多,形式复杂,求解困难,有待进一步改进。Feng Zhang等[10]使用MATLAB和多物理场耦合分析软件,将污垢形成过程以虚拟动态的形式直观地呈现出来。
目前,对CaSO4析晶污垢形成过程的模拟已有报道,但存在如下问题:一方面,大多研究是将主流体到热边界层的传质过程和垢层表面发生的反应结晶过程进行综合处理,很少有研究直接使用表面反应速率计算结晶率,且忽视了真实状况下CaSO4析晶污垢以CaSO4·2H2O的形式存在,即析晶污垢内CaSO4与H2O分子的摩尔数之比为1:2,未考虑H2O分子对结垢速率的影响。另一方面,忽视了结垢过程中流动区域、主体流速以及各组分浓度场的变化。随着垢层厚度不断增加,流体流动区域会随之发生改变,这将导致网格划分区域发生变化,在模拟计算中需要对主体流速进行修正,同时还应考虑析晶后各组分在流动场中浓度的变化。应该采用动网格进行模拟计算,但计算量大,且难以收敛。针对以上问题,本文拟通过在传质方程中添加组分源项对析晶结垢而导致的流体主体中各组分浓度的变化进行修正,建立化学反应模型。直接采用表面反应速率计算结晶率,进一步修正传统的Hasson模型,以减少计算量。同时在析晶污垢生成速率中添加H2O分子的质量,使模拟结果更接近实际生产的情况。以CaSO4的析晶结垢过程为例,运用提出的模型和求解方法探讨影响析晶污垢生成的流速、壁面温度因素,得到流速、温度对污垢生成过程的影响规律,为多级闪蒸海水淡化的设计及运行提供理论指导。
1 数学模型 1.1 物理模型本文探讨光滑直管的析晶结垢过程。由于直管内流体流动、传热、结垢等特性参数在径向上的变化规律是相同的,而流体仅沿轴向方向流动,故可将圆管内流体流动简化为二维模型(见图 1)。在二维空间内建立析晶结垢的数学模型并进行求解,获得的速度、温度和浓度分布结果,既能够满足计算精度要求,又能清晰地反应问题的本质。

|
图 1 物理平面模型 Fig. 1 Planar-physical model |
CaSO4析晶污垢的形成是一个典型的不可压缩、无内热源的二维对流换热问题。为了得到整个计算区域的速度场、温度场以及浓度场,需要将连续性方程、动量方程、能量方程以及传质方程联合求解,主要控制方程如下:
| $ 连续性方程:\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho V} \right) = 0。$ | (1) |
动量方程:
| $ \frac{{\partial \left( {\rho V} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho VV} \right) = - \nabla P + \nabla \cdot \left( \tau \right) + \rho g。$ | (2) |
能量方程:
| $ \begin{array}{l} \;\frac{{\partial \left( {\rho E} \right)}}{{\partial t}} + \nabla \cdot ((V(\rho E + p)) = \\ \nabla \cdot (k\nabla T - \sum {_{_j}} {h_j}{J_j} + \left( {\tau \cdot V} \right))。\end{array} $ | (3) |
溶液中发生的析晶反应:
| $ {\rm{C}}{{\rm{a}}^{2 + }} + {\rm{SO}}_4^{2 - } \to {\rm{CaS}}{{\rm{O}}_4} \downarrow 。$ | (4) |
溶液中每种组分的浓度随着析晶结垢过程的进行将发生变化,反应过程的速率可以用反应物Ca2+和SO42-减少的速率或生成物CaSO4增加的速率来表示,反应速率常数[11]可以通过阿伦尼乌斯定律计算得到:
| $ {k_r} = {k_{r0}}\exp ( - \frac{E}{{R{T_f}}})。$ | (5) |
其中:kr0=7.07 m4·kg-1·s-1;活化能E=37 143 J·mol-1;Tf为垢层表面温度,K。
因此传质方程可表示为:
| $ \frac{{\partial (\rho {Y_i})}}{{\partial t}} + \nabla \cdot (\rho V{Y_i}) = - \nabla \cdot {J_j} + {S_i}。$ | (6) |
其中Yi表示溶质的质量分数。
针对CaSO4组分,传质方程中的组分源项可表示为[12-13]:
| $ {S_i} = {k_r} \cdot {({c_f} - {c_s})^2}。$ | (7) |
其中:cf为CaSO4组分的浓度,kg·m-3;cs为CaSO4饱和浓度,kg·m-3,且cs是垢层表面温度Tf的函数,可以通过溶解度曲线的拟合公式[14]得到:
| $ {c_s} = 1.46 \cdot {10^{ - 4}}{T^2} - 0.12T + 26.60。$ | (8) |
由于垢层成分为CaSO4·2H2O,即生成一个CaSO4分子的同时需要消耗两个H2O分子,CaSO4分子和H2O分子的消耗速率之比为1:2。因此,修正H2O分子组分的源项为:
| $ {{\rm{S}}_{{{\rm{H}}_{\rm{2}}}}}_{\rm{O}}{\rm{ = 2}} \cdot \frac{{{{\rm{M}}_{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}}}{{{{\rm{M}}_{{\rm{CaS}}{{\rm{O}}_{\rm{4}}}}}}} \cdot {{\rm{S}}_{{\rm{CaS}}{{\rm{O}}_{\rm{4}}}}}。$ | (9) |
MH2O为H2O的摩尔分子质量,MCaSO4为CaSO4的摩尔分子质量。
1.3 结垢模型CaSO4·2H2O析晶污垢在换热面上的结垢过程主要包括:壁面结晶和颗粒剥蚀。其生成速率取决于表面结晶反应的速率,产生的析晶污垢量可由下式计算:
| $ \frac{{{\rm{d}}m}}{{{\rm{d}}t}} = {(1 + 2 \cdot \frac{{{{\rm{M}}_{{{\rm{H}}_{\rm{2}}}{\rm{O}}}}}}{{{{\rm{M}}_{{\rm{CaS}}{{\rm{O}}_{\rm{4}}}}}}} \cdot {k_r} \cdot ({c_F} - {c_S}))^2}。$ | (10) |
其中:m为单位面积污垢的生成量,单位为kg·m-2;cF为CaSO4组分在垢层表面处的浓度,单位为kg·m-3。kr与cs都是垢层表面温度Tf的函数,假设热流仅沿y轴方向一维传递,则垢层表面温度可表示为:
| $ {T_f} = {T_b} + \frac{{{T_w} - {T_b}}}{{1 + \alpha \cdot {R_f}}}, $ | (11) |
| $ \alpha = 0.023 \cdot \frac{\lambda }{d} \cdot {R_e}^{0.8} \cdot {R_r}^{0.4}。$ | (12) |
式中:Tb为流体主体温度,K;Tw为管壁温度,K;α为流体与垢层表面间的换热系数,W·m-2·K-1;Rf为污垢热阻,m2·K·W-1;λ为溶液导热系数;d为管道直径,m;Re为流体雷诺数;Rr为流体普朗特数。
污垢剥蚀率采用Brahim模型[15]求解:
| $ \begin{array}{l} \frac{{{\rm{d}}{m_r}}}{{{\rm{d}}t}} = \frac{K}{P} \cdot {\rho _f} \cdot \left( {1 + \beta \cdot \Delta T} \right) \cdot \\ \;\;{d_p} \cdot {({p^2} \cdot \eta \cdot g)^{1/3}} \cdot {x_f} \cdot {u^2}。\end{array} $ | (13) |
式(13)中:ρf为垢层密度,kg·m-3;β为线胀系数,K-1;dp为溶液中悬浮的CaSO4·2H2O晶体的平均粒径,m;η为流体的动力粘度,Pa·s;xf为垢层厚度,m;u为流体主体流速,m·s-1;P为晶间附着力,K表征垢层内缺陷点数目,根据文献[16]P/K采用下述公式:
| $ \frac{P}{K} = 83.2 \cdot {u^{0.54}}。$ | (14) |
污垢净生成速率为析晶污垢生成速率与剥蚀速率的差,可由下式计算:
| $ \frac{{{\rm{d}}{m_f}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}m}}{{{\rm{d}}t}} - \frac{{{\rm{d}}{m_r}}}{{{\rm{d}}t}}。$ | (15) |
单位面积上总污垢生成量mf为每个时间步内污垢净生成量的累积:
| $ {m_f} = {m_{f, t + \mathit{\Delta }t}} = {m_{f, t}} + \frac{{{\rm{d}}{m_f}}}{{{\rm{d}}t}}\cdot\Delta t。$ | (16) |
单位面积总的垢层厚度为xf, t+Δt每个时间步内污垢累积的厚度:
| $ {x_{f, t + \mathit{\Delta }t}} = {x_{f, t}} + \frac{{{m_f} \cdot \Delta t}}{{{\rho _f}}}。$ | (17) |
单位面积总污垢热阻Rf, t为总垢层厚度与垢层导热系数的比值:
| $ {R_{f, t}} = \frac{{{x_{f, t}}}}{{{\lambda _f}}}。$ | (18) |
λf为CaSO4·2H2O析晶污垢的导热系数,W·m-1·K-1。
1.4 流速的修正以及变量的初始化由1.3小节所给出的结垢模型可知,当CaSO4·2H2O析晶污垢在管道内生成时,管内垢层厚度随时间逐渐增加,流体的流道会减小,流速随之增加,即在轴向方向上,管内的流速是变化的。因此,计算过程中必须对流速进行修正。本文提出如下关联式进行流速的修正,以更接近管内的实际流动状况:
| $ u = {u_0} \cdot \frac{{{d^2}}}{{{{(d - 2{x_{f, t}})}^2}}}。$ | (19) |
计算时将3 600 s作为非稳态计算的时间步,即Δt取3 600,在t=0时刻,垢层表面温度取壁面温度,污垢剥蚀率、垢层厚度、污垢热阻均为零。
2 数值计算结果 2.1 模拟条件入流口的速度充分发展,平均速度为v,流体温度为主体温度。壁面无滑移且温度恒定。出流口的法向速度分布满足整体质量守恒。实际流速和垢层表面温度取修正过的值,污垢结晶率、剥蚀率和净生成率取处监测面上的平均值。在相同模型与边界条件下,对流域进行不同尺寸的网格划分,得到CaSO4组分的质量分布基本一致,证明模型结果与网格数无关,最终选网格尺寸为0.5 mm。
本文采用标准的湍流模型对CaSO4-H2O体系进行计算。由于流体浓度很低,所以流体物性近似取壁面温度条件下水的物性[11],分别讨论流速、壁面温度等因素对析晶污垢的影响。
2.2 流速对CaSO4·2H2O污垢生成速率的影响以CaSO4水溶液在换热器内的流动为例,流速的变化将影响CaSO4·2H2O在换热器管壁的生成率和剥蚀率。模拟条件为CaSO4的质量分数ω=0.000 1,流体温度Tb=300 K,壁面温度a320 K。分别取流速的值为:0.3,0.5,1.0,1.5,2.0 m/s,模拟结果如下:
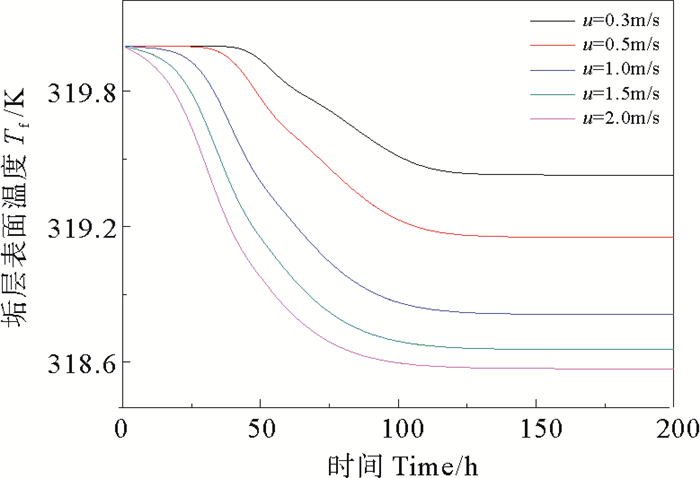
|
图 2 不同流速下CaSO4·2H2O析晶污垢的垢层表面温度 Fig. 2 Fouling layer surface temperature of CaSO4·2H2O crystallization at different velocity |
由图 2和图 4可得,流速越大垢层表面温度越低,垢层热阻越大;随着运行时间的延长,垢层表面温度逐渐降低,垢层热阻逐渐升高,在大约150 h以后,由于污垢净生成率降为零,污垢热阻不再增加,垢层表面温度趋于稳定。其原因是在流动开始时,壁面处于洁净状态,垢层表面温度等于壁面温度,流体主体与壁面的温差大,溶液的过饱和度增大,净生成率较大;随着时间的推移,污垢逐渐累积,污垢热阻增大,垢层表面温度逐渐降低,净生成率逐渐减小;时间进行越久,污垢结晶速率和剥蚀速率达到动态平衡,最终净生成速率趋于零,垢层厚度不再增大,污垢热阻(见图 4)趋于稳定。由图 3可知,流速增大有利于降低CaSO4·2H2O析晶污垢的净生成率。在流速较低的条件下,对流传热系数较小,传热热阻大,因此越靠近壁面处,温度越高,CaSO4·2H2O污垢的结晶速率越快。随着流速越大,污垢净生成率降低的幅度逐渐减小,当流速超过1.5 m/s后,增大流速对降低污垢净生成率的效果不再明显,而流速过高会导致较高的能耗,综合考虑,流速的适宜取值范围为1.0~1.5 m/s。
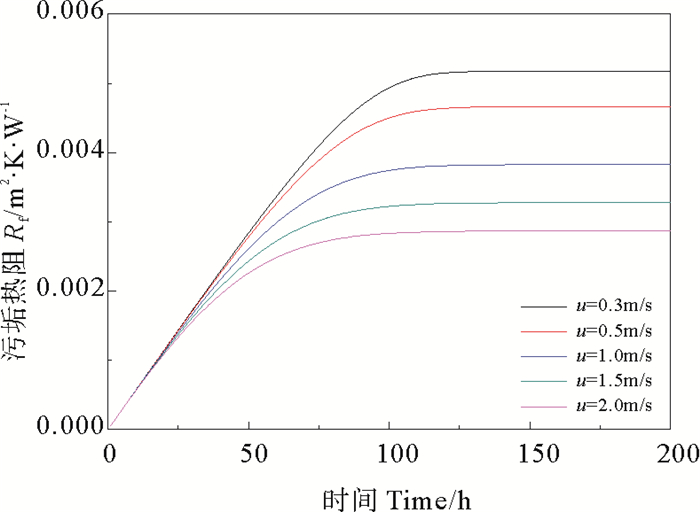
|
图 4 不同流速下CaSO4·2H2O析晶污垢的热阻 Fig. 4 Heat resistance of CaSO4·2H2O crystallization at different velocity |
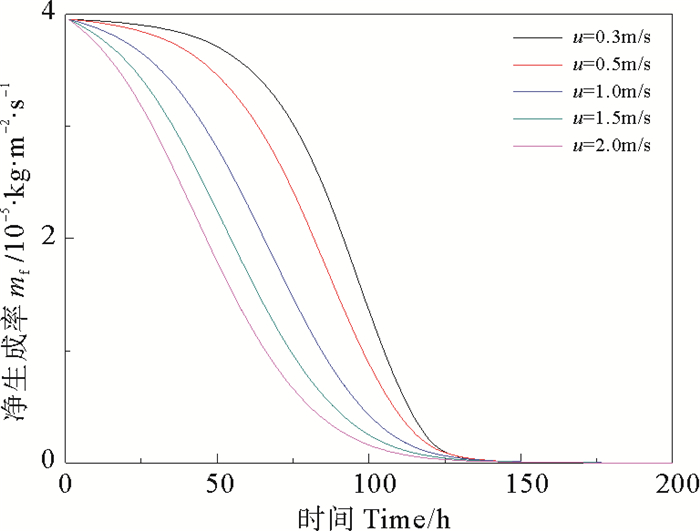
|
图 3 不同流速下CaSO4·2H2O析晶污垢的净生成率 Fig. 3 Net generation rate of CaSO4·2H2O crystallization at different velocity |
通过将本文模拟结果与Brahim等[6]的实验结果进行对比可知,在模型条件与实验条件相近的情况下,污垢热阻的计算数值与实验数值吻合较好且变化趋势相同,证明了本文建立的模型及模拟结果的可靠性。
2.3 换热管壁面温度对CaSO4·2H2O污垢生成速率的影响模拟条件为:CaSO4的质量分数ω=0.000 3,流体温度Tb=300 K,流速u=1.0 m/s。壁面温度TW分别取:310,320,330,340,350 K,模拟结果如下:
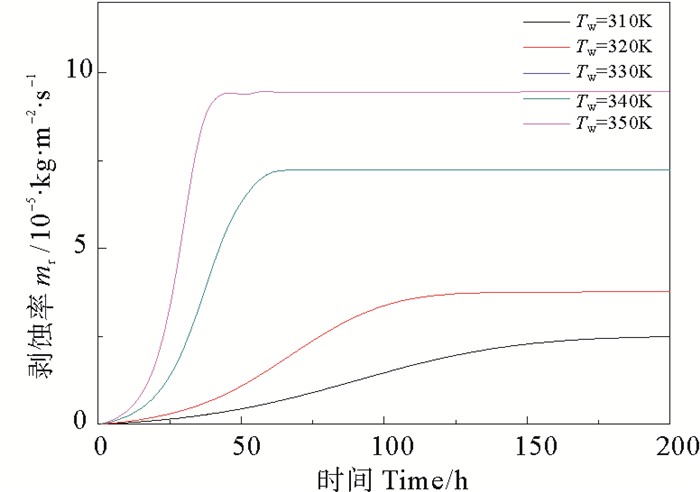
|
图 5 不同壁面温度下CaSO4·2H2O析晶污垢的剥蚀率 Fig. 5 Erosion rate of CaSO4·2H2O crystallization at different tube temperature |
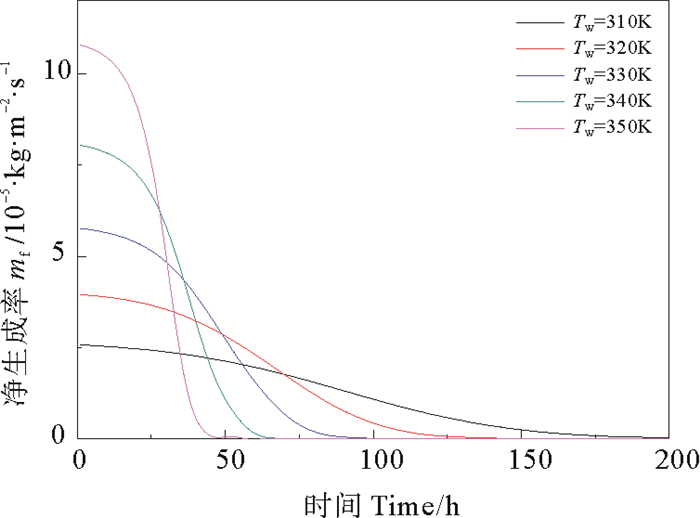
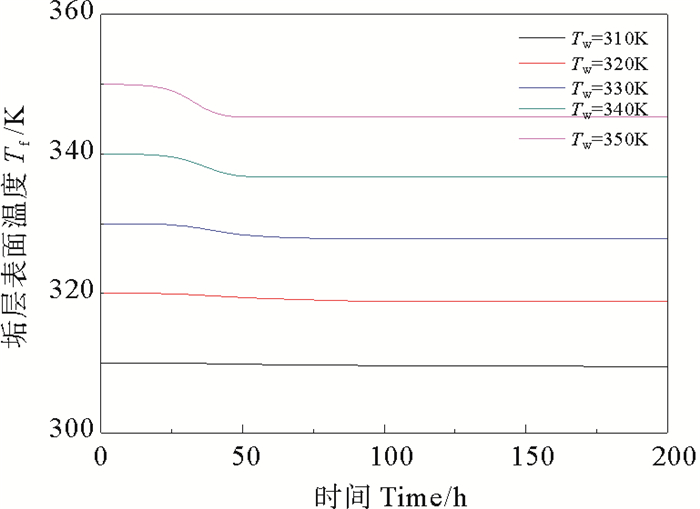
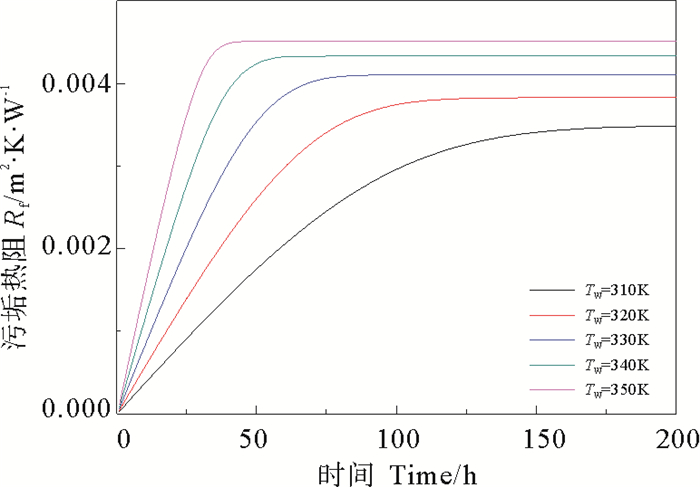
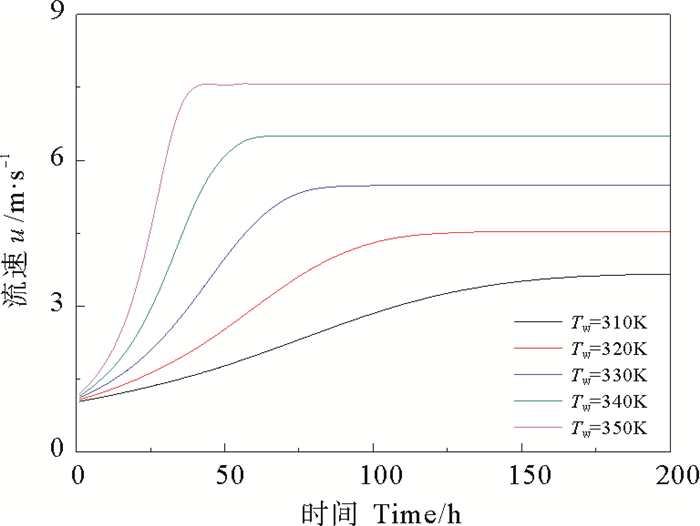
由图 6可看出,在污垢析出的过程中,温度越高,越有利于污垢的生成,且温度对于污垢析出的影响较流速而言更为显著(见图 7),随时间的推移,污垢净生成率逐渐减小。由图 8可知,壁面温度越高,污垢热阻增加的速率越快,污垢生成总量随时间逐渐增加,导致主体流速增大,流体对污垢的剥蚀速率增大,且壁面温度越高,剥蚀速率越大。由图 9可看出,对于不同温度,管道内主体流速都呈现逐渐增大最终趋于恒定的变化趋势,壁面温度越高,流速达到恒定时所用的时间越短,且流速越大。
|
图 6 不同壁面温度下CaSO4·2H2O析晶污垢的净生成率 Fig. 6 Net generation rate of CaSO4·2H2O crystallization at different tube temperature |
|
图 7 不同壁面温度下CaSO4·2H2O析晶污垢的垢层表面温度 Fig. 7 Fouling layer temperature of CaSO4·2H2O crystallization at different tube temperature |
|
图 8 不同壁面温度下CaSO4·2H2O析晶污垢的热阻 Fig. 8 Heat resistance of CaSO4·2H2O crystallization at different tube temperature |
|
图 9 不同壁面温度下管内的主体流速 Fig. 9 Bulk flow velocity at different tube temperature |
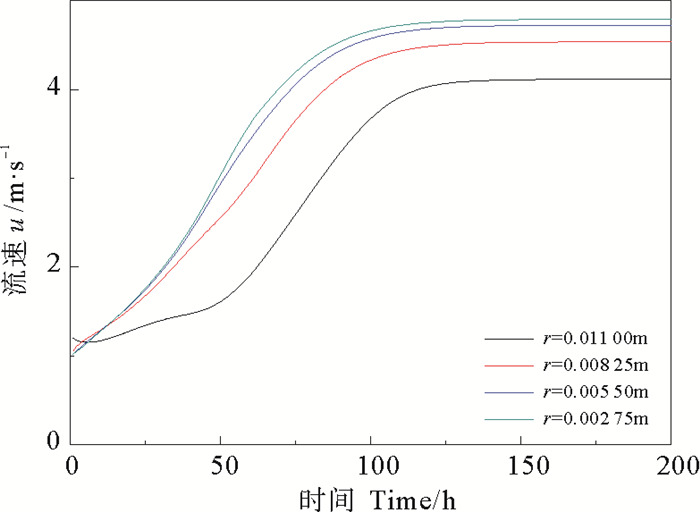
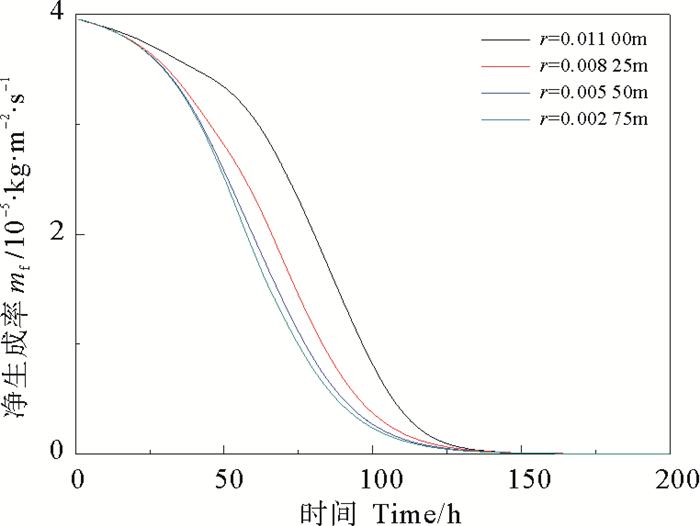
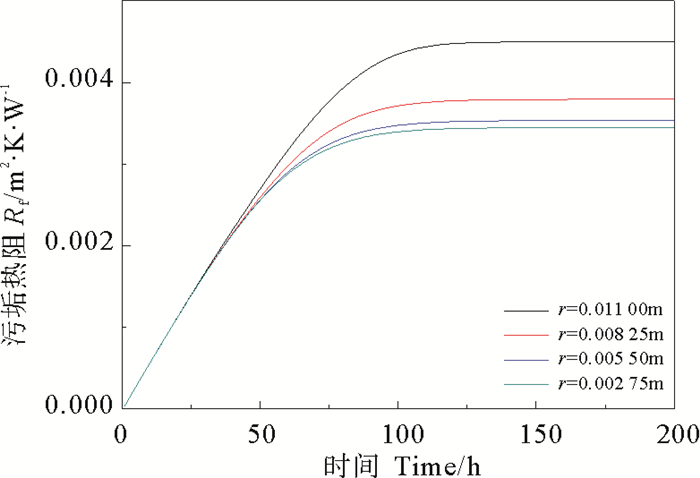
模拟条件为:流速u=1.0 m/s,CaSO4的质量分数ω=0.000 3,流体温度Tb=300 K, 壁面温度TW=320 K。在x=0.5 m处,取不同半径处的圆环面为假想壁面,得到不同假想壁面上污垢的净生成率和剥蚀率,结果如下图所示。
由图 10、11、12可知,越靠近管中心,即r越小,流速越大,析晶污垢净生成率越小,污垢热阻越小。该生成规律符合析晶污垢沉积扩散的方向,即析出晶体从流体中不断向壁面聚集,最终导致壁面垢层的生长,垢层热阻的增大。
|
图 10 管道不同内径处主体流速的变化 Fig. 10 Bulk flow velocity at different inner diameter |
|
图 11 管道不同内径处CaSO4·2H2O析晶污垢的净生成率 Fig. 11 Net generation rate of CaSO4·2H2O crystallization at different inner diameter |
|
图 12 管道不同内径处CaSO4·2H2O析晶污垢产生的热阻 Fig. 12 Heat resistance of CaSO4·2H2O crystallization at different inner diameter |
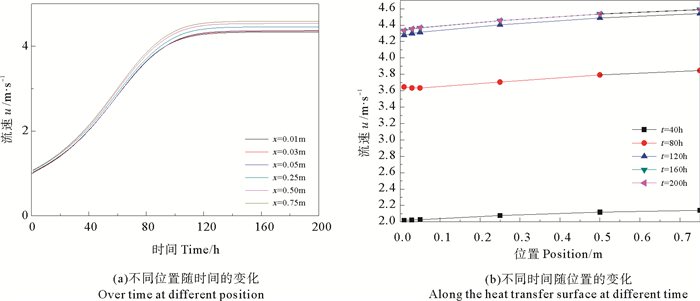
模拟条件为:流速u=1.0 m/s,CaSO4的质量分数ω=0.000 3,流体温度Tb=300 K, 壁面温度TW=320 K。在沿管道轴向的不同位置处,即x取不同值,得到不同位置上的流速、垢层厚度、污垢热阻和污垢净生成率,结果如下图所示。
由图 13(a)(b)看出,随着时间的延长,管道轴线方向不同位置处的流速都呈现出先增大后逐渐趋于平稳的变化趋势,且离入口处越远流速越大;在管道轴向的同一位置,随着时间的延长,流速也呈现出逐渐增大的趋势,且初始时间段内变化较大(t=40~120 h),而后逐渐趋于稳定(t=160~200 h)。
|
图 13 管道内的流速 Fig. 13 Velocity variation |
由图 14(a)看出,沿管道轴线方向的不同位置,垢层的厚度都呈现出先增大,而后趋于稳定的变化趋势;在管道的同一位置,随着时间的延长,垢层厚度有一个先快速增大,而后增加速率逐渐减小,以后,垢层厚度不再增加。垢层热阻的变化趋势与垢层厚度的变化趋势相同(见图 15),也呈现出先增大后趋于稳定的变化过程,在时以后,垢层热阻不再增加。
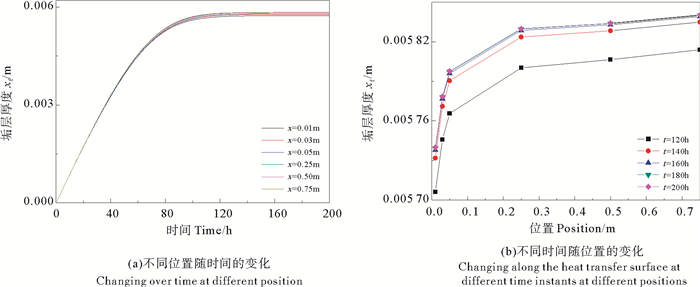
|
图 14 管道内的垢层厚度 Fig. 14 The thickness of fouling layer of CaSO4·2H2O crystallization |
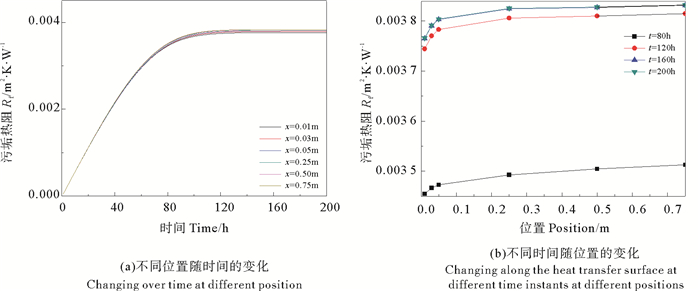
|
图 15 管道内的污垢热阻 Fig. 15 Heat resistance of CaSO4·2H2O crystallization |
由图 16可知,管道内不同位置的污垢净生成率在起始时刻最大,但随时间逐渐减小,150 h后,垢层不再生长,即沉积速率与剥蚀速率达到了平衡。管子入口处净生成速率最小,沿管长方向净生成速率逐渐增大并趋于稳定。
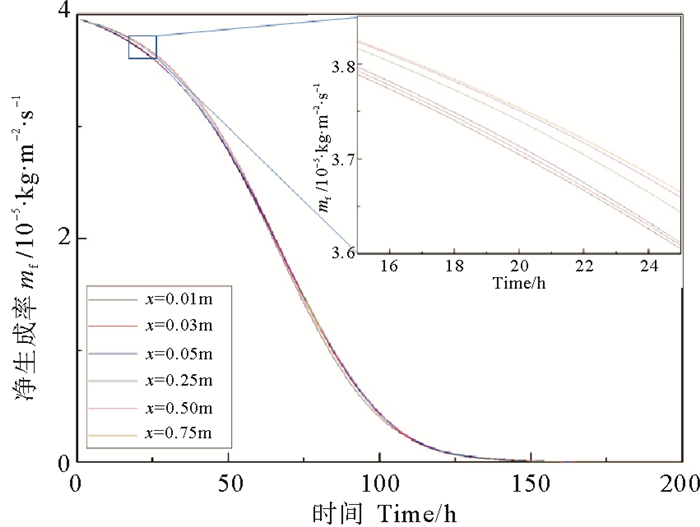
|
图 16 管道不同位置处CaSO4·2H2O析晶污垢的净生成率 Fig. 16 Net generation rate of CaSO4·2H2O crystallization at different position |
本文运用FLUENT软件对多级闪蒸海水淡化系统中析晶污垢形成过程进行了数值模拟。通过添加组分源项,修正流体中组分浓度的分布,采用修正后的流体主体浓度替代垢层表面处的浓度,对传统的Hasson模型进行改进;同时考虑H2O分子对析晶污垢生成速率的贡献,使模拟结果更符合实际情况。以CaSO4·2H2O污垢形成过程为例,分析了流速、壁面温度对污垢形成速率的影响以及管道径向和轴向方向的析晶规律,结果表明:管内流速越大,污垢的净生成率和热阻越小,但流速越高流体流动造成的能耗越大,综合考虑结垢和能耗因素,适宜的流速范围为1.0~1.5m/s;污垢生成速率随壁面温度的增大而显著增大;污垢净生成速率沿径向方向逐渐增大,而沿轴向方向,管子入口处污垢净生成率最小。
符合说明
cf 溶质的组份浓度(kg·m-3)
cF CaSO4组分在垢层表面上的浓度(kg·m-2)
cs 溶质的饱和浓度(kg·m-3)
d 管径(m)
dp 溶液中悬浮CaSO4·2H2O晶体的平均粒子直径(m)
E 活化能(J·mol-1)
K 垢层内缺陷点的数目
kr 反应速率常数(m4·kg-1·s-1)
kr0 指前因子(kg·m-2)
m 单位面积污垢的生成量(kg·m-2)
mr 单位面积污垢的剥蚀量(kg·m-2)
mf 单位面积污垢的净生成量(kg·m-2)
P 晶间附着力
Rr 流体普朗特常数
R 通用气体常数(J·mol-1·K-1)
Re 流体雷诺数
Rf 垢层热阻(m2·K·W-1)
Rf, t 污垢总热阻(m2·K·W-1)
Tb 流体主体温度(K)
Tf 垢层表面温度(K)
Tw 管壁温度(K)
u 流体主体流速(m·s-1)
xf 垢层厚度(m)
xf, t+Δt 垢层总厚度(m)
α 传热系数(W·m-2·K-1)
β 线性膨胀系数(K-1)
λ 溶液热导率(W·m-2·K-1)
λf CaSO4·2H2O结晶垢的热导率(W·m-2·K-1)
η 动力粘度(Pa·s)
ρf 垢层密度(kg·m-3)
Nomenclature
cf The component concentration(kg·m-3)
cF The concentration of CaSO4 component at fouling surface(kg·m-2)
cs The component saturation concentration (kg·m-3)
d The diameter of tube (m)
dp The average particle size of crystal CaSO4·2H2O suspended in solution (m)
E The activation energy(J·mol-1)
K The number of defect points inner fouling layer
kr The reaction rate constant (m4·kg-1·s-1)
kr0 The pre-exponential factor(m4·kg-1·s-1)
m The total generation quantity of crystallization fouling(kg·m-2)
mr The erosion rate of crystallization fouling(kg·m-2)
mf The net generation rate(kg·m-2)
P The adhesive force between crystals
Pr The Prandtl number of fluid
R The universal gas constant(J·mol-1·K-1)
Re The Reynolds number of fluid
Rf The fouling resistance (m2·K·W-1)
Rf, t The total fouling resistance(m2·K·W-1)
Tb The bulk temperature of fluid (K)
Tf The surface temperature of fouling layer (K)
Tw The tube wall temperature (K)
u The bulk velocity of fluid(m·s-1)
xf The thickness of fouling layer (m)
xf, t+Δt The total thickness of fouling layer (m)
α The coefficient of heat transfer (W·m-2·K-1)
β The coefficient of linear expansion (K-1)
λ The thermal conductivity of solution(W·m-2·K-1)
λf The heat conductivity of CaSO4·2H2O crystallization fouling (W·m-2·K-1)
η The dynamic viscosity of fluid(Pa·s)
ρf The density of fouling layer(kg·m-3)
| [1] |
Al-Hamahmy M, Fath H E S, Khanafer K. Techno-economical simulation and study of a novel MSF desalination process[J]. Desalination, 2016, 386: 1-12. DOI:10.1016/j.desal.2016.02.018
(  0) 0) |
| [2] |
Guan B, Yang L, Wu Z. Effect of Mg2+ ions on the nucleation kinetics of calcium sulfate in concentrated calcium shloride Solutions[J]. Industrial & Engineering Chemistry Research, 2010, 49(12): 5569-5574.
(  0) 0) |
| [3] |
Pääkkönen T M, Riihimäki M, Simonson C J, et al. Crystallization fouling of CaCO3 Analysis of experimental thermal resistance and its uncertainty[J]. International Journal of Heat and Mass Transfer, 2012, 55(23-24): 6927-6937. DOI:10.1016/j.ijheatmasstransfer.2012.07.006
(  0) 0) |
| [4] |
Melo L F, Bott T R. Biofouling in water systems[J]. Experimental Thermal & Fluid Science, 1997, 14(4): 375-381.
(  0) 0) |
| [5] |
杨大章, 柳建华, 鄂晓雪, 等. 海水冷却水结晶污垢分析及其生长模型[J]. 化工进展, 2015, 34(8): 3179-3182. YANG Dazhang, LIU Jianhua, E Xiaoxue, et al. Composition analysis and kinetic modeling of crystallization fouling in cooling seawater[J]. Chemical Industry and Engineering Progress, 2015, 34(8): 3179-3182. (  0) 0) |
| [6] |
Brahim F, Augustin W, Bohnet M. Numerical simulation of the fouling process[J]. International Journal of Thermal Sciences, 2003, 42(3): 323-334. DOI:10.1016/S1290-0729(02)00021-2
(  0) 0) |
| [7] |
Nebot E, Casanueva J F. Model for fouling deposition on power plant steam condensers cooled with seawater: Effect of water velocity and tube material[J]. International Journal of Heat & Mass Transfer, 2007, 50(17): 3351-3358.
(  0) 0) |
| [8] |
程浩明. CaCO3污垢生长过程的数值模拟[D]. 吉林: 东北电力大学, 2009. CHENG Haoming. Numerical Simulation of the CaCO3 Fouling Process[D]. Jilin: Northeast Dianli University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10188-2009098733.htm (  0) 0) |
| [9] |
Hasson D, Avriel M, Resnick W, et al. Mechanism of calcium carbonate scale deposition on heat-transfer surfaces[J]. Industrial & Engineering Chemistry Fundamentals, 1968, 7(1): 632-637.
(  0) 0) |
| [10] |
Zhang F, Xiao J, Chen X D. Towards predictive modeling of crystallization fouling: a pseudo-dynamic approach[J]. Food & Bioproducts Processing, 2014, 93: 188-196.
(  0) 0) |
| [11] |
孙卓辉. 换热面上结垢过程数值模拟[D]. 青岛: 中国石油大学(华东), 2008. SUN Zhuohui. Numerical Simulation of Fouling Process on Heat Transfer Surface[D]. Qingdao: China University of Petroleum(East China), 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1363166 (  0) 0) |
| [12] |
Mwaba M G, Golriz M R, Gu J. A semi-empirical correlation for crystallization fouling on heat exchange surfaces[J]. Applied Thermal Engineering, 2006, 26(4): 440-447. DOI:10.1016/j.applthermaleng.2005.05.021
(  0) 0) |
| [13] |
Bansal B, Chen X D, Müller-Steinhagen H. Analysis of 'classical' deposition rate law for crystallisation fouling[J]. Chemical Engineering & Processing Process Intensification, 2008, 47(8): 1201-1210.
(  0) 0) |
| [14] |
Hasson D, Avriel M, Resnick W, et al. Mechanism of calcium carbonate scale deposition on heat-transfer surfaces[J]. Industrial & Engineering Chemistry Fundamentals, 1968, 7(1): 632-637.
(  0) 0) |
| [15] |
Brahim F, Augustin W, Bohnet M. Numerical Simulation of the Fouling on Structured Heat Transfer Surfaces (Fouling)[C]. // Heat Exchanger Fouling and Cleaning: Fundamentals and Applications, New Mexico, USA: Engineering Conference International(ECI), 2004. http://www.researchgate.net/publication/254592539_Numerical_Simulation_of_the_Fouling_on_Structured_Heat_Transfer_Surfaces_Fouling
(  0) 0) |
| [16] |
Krause S. Fouling of heat transfer surfaces by crystallization and sedimentation[J]. International Chemical Engineering (A Quarterly Journal of Translations from Russia, Eastern Europe and Asia); (United States), 1993, 33:3(3): 355-401.
(  0) 0) |
2. Ocean University of China College of Chemistry and Chemical Engineering, Qingdao 266100, China
 2018, Vol. 48
2018, Vol. 48


