2. 中国海洋大学海洋环境与生态教育部重点实验室,山东 青岛 266100
风暴潮是指由于强烈的大气扰动(强风和气压骤变)导致的海面异常升高或降低的现象,是一种非常严重的自然灾害[1]。风暴潮位列中国海洋灾害的首位,在2020年影响中国沿海各省的主要海洋灾害中,直接经济损失的80%由风暴潮灾害造成[2-3]。山东省夏秋季的风暴潮灾害主要由台风诱发,且呈现出成灾比例高及成灾情况严重的特点,造成的人员伤亡和经济损失较大。气候变化会带来台风强度、发生频率以及海平面的变化,这些都会对风暴潮带来影响[4]。因此,分析气候变化背景下风暴潮危险性的变化,对沿海地区防灾减灾具有重大意义。
修建各种工程设施防御风暴潮是减小风暴潮灾害的重要手段,但这依赖于对风暴潮危险性的评估,往往用重现期即年极值增水的多年一遇来衡量,即假设某地的年极值增水符合某种概率分布,然后根据过去若干年的历史极值增水进行拟合,外推出更长时间的多年一遇极值增水。采用这种方法计算极值增水的一个限制是水位观测数据的不足,在现实中,一地拥有几十年的连续水位观测数据已属不易,但气象数据的连续性通常会好一些,为此人们采用数值模拟的方法用气象数据强迫出水位数据,构造出更长时间序列的极值增水。由于早期气象数据不全,受限于历史资料长度,一般也只能构造出60余年的数据,但根据刘永玲等[5]的研究,使用60 a的历史数据计算百年一遇极值增水不确定性已大于10%,显示了数据长度对结果的影响。为了解决历史样本不足的问题,有学者提出采用蒙特卡洛方法来扩充台风样本数量,以弥补历史观测数据的数量缺失问题[6-7]。刘永玲等[5]利用方伟华等[8]构造的500 a热带气旋随机事件集对福建连江的风暴潮增水多年一遇进行了研究。
然而风暴潮很重要的成灾路径是对陆地的淹没,也被称为漫滩,即在天文潮和风暴潮共同作用下,海水水位超过了沿岸陆地高程,从而海水涌上陆地,造成损失。漫滩是一个很局地的事件,影响范围不过10 km左右的岸线,需要高分辨率的计算,而且依赖于精确的近岸水深和海岸陆地高程,还牵扯到风暴潮和天文潮的配合等问题,使得漫滩计算比单纯计算风暴潮增水要复杂得多,因此只是停留在研究阶段,至今没有业务化漫滩预报,而且风暴潮漫滩面积多年一遇的研究也较少。
但是,风暴潮漫滩造成的损失巨大,气候变化对其带来的影响值得关注,并且当前人们对气候变化认识的需求已经从全球尺度聚焦到局地尺度,即开始关注气候变化对当地带来影响,这也使得气候变化对风暴潮漫滩的影响开始受到关注。
青岛是中国东部沿海重要城市,在建设具有国际竞争力和影响力的山东半岛城市群过程中发挥核心、引领作用①。历史上青岛不断受到台风风暴潮的侵袭[9],而位于青岛即墨区的蓝谷是青岛市致力打造的海洋科教产融合发展的现代化滨海新城区,是青岛发展的四大功能性战略节点之一②。蓝谷核心区包括即墨鳌山卫、温泉两街道陆域和海域全部,陆地地势低平,面向黄海,是易受风暴潮影响的区域。据文献记载,作为青岛百年间遭受的3次特大风暴潮灾之一,1992年的16号热带风暴引发特大风暴潮,最大险情区之一的即墨大桥盐场[10]就位于现在的蓝谷核心区附近;1997年即墨也曾遭受风暴潮袭击[11]。马艳等[12]也指出,即墨容易遭受西风槽和台风倒槽的共同作用,且作为迎风向和下风向地段受台风影响更大。
①《山东省国土空间规划(2021—2035年)》,2023年9月20日国务院批复。
②《青岛都市圈发展规划》,2023年10月6日山东省人民政府印发。
因此,蓝谷作为易受风暴潮影响又是未来发展重要区域,气候变化对该区域漫滩的多年一遇会带来什么影响是值得研究的。本文采用基于历史热带气旋样本信息及热带气旋气候学规律,依靠蒙特卡洛方法构造的500 a热带气旋随机事件集[8],研究全球气候变化下蓝谷区域风暴潮漫滩的变化。通过设置不同海平面增幅和台风风速增幅来展现未来气候情景,利用数值模拟得到台风风暴潮多年一遇最大漫滩淹没面积,并分析未来气候变化背景下的长期变化规律,结果可为其他海岸地区的风暴潮漫滩灾害危险性研究提供借鉴。
1 模型和数据 1.1 ADCIRC模型介绍本文使用海洋沿岸和河口水域环流模型(advanced circulation model for oceanic, coastal and estuarine waters,ADCIRC)来模拟风暴潮漫滩。该模型是由来自美国北卡罗来纳大学的Luettich教授和圣母大学的Westerink博士于1992年合作研发的,是基于有限元方法的较为成熟的海洋数值模式[13-14],常被用在风暴潮预报、多年一遇水位推算和海岸灾害评估中。
1.1.1 控制方程该模式的控制方程由深度积分得到的球面坐标二维方程,如式(1)、(2)和(3)所示,结合边界条件和初始条件可获取自由表面起伏和二维流速等三个变量(U,V,ζ)。
连续方程:
| $ \frac{\partial \zeta}{\partial t}+\frac{1}{R \cos \phi} \frac{\partial U H}{\partial \lambda}+\frac{1}{R} \frac{\partial V H}{\partial \phi}-\frac{V H \tan \phi}{R}=0 \text { 。} $ | (1) |
动量方程:
| $ \begin{aligned} & \frac{\partial U}{\partial t}+\frac{U}{R \cos \phi} \frac{\partial U}{\partial \lambda}+\frac{V}{R} \frac{\partial U}{\partial \phi}-\left(\frac{U \tan \phi}{R}+f\right) V= \\ & -\frac{1}{R \cos \phi} \frac{\partial\left[\frac{P_{\mathrm{s}}}{\rho_0}+g(\zeta-\eta)\right]}{\partial \lambda}+\frac{\tau_{\mathrm{s} \lambda}-\tau_{\mathrm{b} \lambda}}{\rho_0 H}+D_\lambda, \end{aligned} $ | (2) |
| $ \begin{gathered} \frac{\partial V}{\partial t}+\frac{U}{R \cos \phi} \frac{\partial V}{\partial \lambda}+\frac{V}{R} \frac{\partial V}{\partial \phi}+\left(\frac{U \tan \phi}{R}+f\right) U= \\ -\frac{1}{R} \frac{\partial\left[\frac{P_s}{\rho_0}+g(\zeta-\eta)\right]}{\partial \phi}+\frac{\tau_{\text{s} \phi}-\tau_{\text{b} \phi}}{\rho_0 H}+D_\phi 。\end{gathered} $ | (3) |
式中:H=ζ+h;f=2Ωsinϕ;ζ为从平均海平面起算的自由表面高度(m);t为时间(s);(λ,ϕ)为经度、纬度;(λ0,ϕ0)为网格计算区域中心点的经度、纬度;(U,V)为深度平均的x,y方向上的海水水平流速(m/s);h为水深,即平均海平面到海底的距离(m);H为瞬时海水水柱高度(m);R为地球半径(m),取值为6 378 135 m;g为重力加速度(m/s2);f为科氏参数(s-1);Ω为地球的自转角速度,取7.292 12×10-5rad/s;Ps为海表面大气压强(N/m2);ρ0为海水参考密度,取1 025 kg/m3;η为牛顿引潮势(m);Dλ,Dϕ为水平湍耗散项;τsλ,τsϕ分别为海表应力的经向分量,纬向分量;τbλ,τbϕ分别为海底摩擦力的经向,纬向分量。
1.1.2 模型风场本研究中台风风场的构造采取的是Jelesnianski的圆形台风模型[15],取决于风应力函数和压力函数,
当0≤r≤R时:
| $ \left\{\begin{array}{l} W_x=V_x \frac{r}{r+R}-W_{\mathrm{R}}\left(\frac{r}{R}\right)^{\frac{3}{2}}\left[\left(x-x_0\right) \sin \theta+\left(y-y_0\right) \cos \theta\right] \\ W_y=V_y \frac{r}{r+R}+W_{\mathrm{R}}\left(\frac{r}{R}\right)^{\frac{3}{2}}\left[\left(x-x_0\right) \cos \theta-\left(y-y_0\right) \sin \theta\right] \\ P_{\mathrm{a}}=P_0+\frac{1}{4}\left(P_{\infty}-P_0\right)\left(\frac{r}{R}\right)^3 \end{array}\right.。$ | (4) |
当r>R时,
| $ \left\{\begin{array}{l} W_x=V_x \frac{r}{r+R}-W_{\mathrm{R}}\left(\frac{r}{R}\right)^{\frac{1}{2}}\left[\left(x-x_0\right) \sin \theta+\left(y-y_0\right) \cos \theta\right] \\ W_y=V_y \frac{r}{r+R}+W_{\mathrm{R}}\left(\frac{r}{R}\right)^{\frac{1}{2}}\left[\left(x-x_0\right) \cos \theta-\left(y-y_0\right) \sin \theta\right] \\ P_{\mathrm{a}}=P_{\infty}-\frac{3}{4}\left(P_{\infty}-P_0\right)\left(\frac{R}{r}\right) \end{array}\right.。$ | (5) |
式中:r为计算点到台风中心的距离(m);R为最大风速半径(m);台风中心坐标和计算点坐标分别由(x0,y0)和(x,y)来表示;Wx,Wy为水平方向的风速(m/s);Vx,Vy分别为台风中心在x、y方向的移行速度(m/s);WR为最大风速(m/s), 通过经验公式获取;θ为流入角,当0≤r≤R时设为20°,r>R时设为15°;Pa为计算点气压(hPa);P0为台风中心气压(hPa);P∞为不受气旋影响处的环境气压(hPa)。
其中由于WR无法直接获取,我们通过Atkinson and Holliday[16]的经验公式计算:
| $ W_{\mathrm{R}}=3.447 \times\left(P_{\infty}-P_0\right)^{0.644} 。$ | (6) |
考虑到纬度ϕ对台风眼形态的影响,使用Shea and Gray[17]的经验公式对R进行修正:
| $ \begin{gathered} R=51.6 \exp \left(-0.0223 W_{\mathrm{R}}+0.0281|\phi|\right)+ \\ 50 \frac{(|\phi|-33)}{||\phi|-33|+10^{-3}} \exp (\tan h(|\phi|-33)-1)。\end{gathered} $ | (7) |
为研究蓝谷的风暴潮漫滩,本研究选取范围包括整个东中国海,研究区域地形见图 1。首先需要准备水深数据及蓝谷附近加密的水深及陆地高程数据,本文采取的水深数据为ETOPO1①数据,分辨率为1′。在蓝谷附近10 m等深线以内的海域,水深经海图数据(来自船讯网网站②)进行修正,分辨率可达到0.6′。本文中使用的高程数据来源于Derek Watkins基于SRTM数据集构建的数据③,其分辨率为30 m,因为本文主要考虑的是漫滩的情况,该数据下载后只保留最高80 m以下的高程,超过80 m的高程统一记为80 m。
① https://www.ncei.noaa.gov/access/metadata/landing-page/bin/iso?id=gov.noaa.ngdc.mgg.dem:316
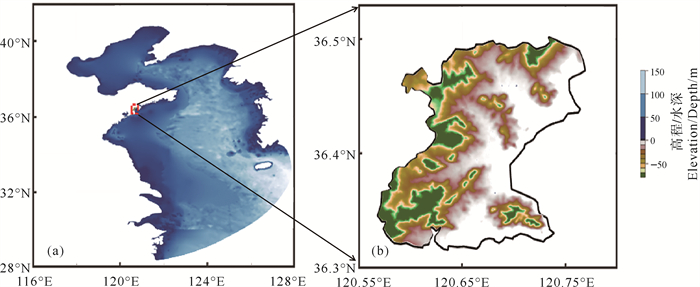
|
( 研究区域的水深分布图(图左)和蓝谷的陆地高程图(图右)。The water depth distribution of the area research area (left) and the land elevation of the blue valley (right). ) 图 1 水深及蓝谷附近高程图 Fig. 1 The water depth and elevation near the blue valley |
由于数据来源不同,需要将数据统一到一个坐标系中。在水平方向上,由于关系区域不大,数据所涉及的坐标差异很小,对于数值计算影响不大,不予变换。在垂直方向上,需要将3种数据统一换算到同一基准面上。ETOPO1数据的基准面是全球平均海平面,海图数据的基准面是理论深度基准面,SRTM的高程基准是EGM96大地水准面。但这3种基准面在不同地点的差异是不同的,不过由于数值计算本身的分辨率、精度等限制,只需要在相近区域有基本估计即可,本文将这3种数据都统一到黄海平均海平面(即1985国家高程基准)。
黄海平均海平面高于全球平均海平面29.8 cm[18],高于青岛潮高基准面239 cm[19],而青岛潮高基准面也可近似认为是理论深度基准面。有研究者得到85高程与WGS-84定义的似大地水准面两者的垂直偏差为35.7 cm[20-21],WGS-84中使用的似大地基准面可以理解为EGM96大地水准面的近似,在这里认为是等同的。因此在处理数据时,本文中的具体做法为先将水深数据变为负数,陆地高程变为正数,再将陆地高程数据减去35.7 cm、海图水深数据变幅负数后再减去239 cm,ETOPO1的水深数据也变为负数,再减去29.8 cm,最终将高程数据统一到黄海平均海平面,而计算得到的水位则需要加上203.3 cm才能回到以青岛潮高基准面起算的水位。
统一基准面后的水深及高程分布如图 1所示。从图中可发现研究区域地形呈西高东低分布,其海岸线较为曲折,呈现M型,东南角的山体增加了研究该地区的复杂程度,而沿海低洼部分除了面对台风来临时造成风暴潮增水和漫滩的灾害性影响外,还有风暴潮漫滩过程发生后由于地理位置的特殊性造成的海水滞留问题,对沿海的生产发展存在一定的隐患。
1.2.2 蓝谷热带气旋随机事件集青岛作为山东发展经济的重要城市,经常遭受台风风暴潮的侵袭。自1898—1994年,青岛沿岸受台风影响次数达120多次,每年平均1.3次[9],1958—2019年有4个登陆青岛的热带气旋造成的风暴潮增水超过100 cm[12]。
本文采用的热带气旋事件集是方伟华等[8]用蒙特卡洛方法构造的影响东中国海的500 a热带气旋随机事件集,该数据基于从历史气旋数据得到的分布规律,用随机方法生成了500年间影响东中国海的16 470场热带气旋。为研究蓝谷的区域性漫滩情况,以蓝谷为圆心,500 km为半径做圆,对数据集进行筛选,得到了影响蓝谷的538个热带气旋,平均每年1.1个,与林滋新等[9]得到的1.3次/a较为一致。大部分影响到青岛的热带气旋已降为热带风暴级别,挑选了200 a的热带气旋路径进行展示(见图 2)。
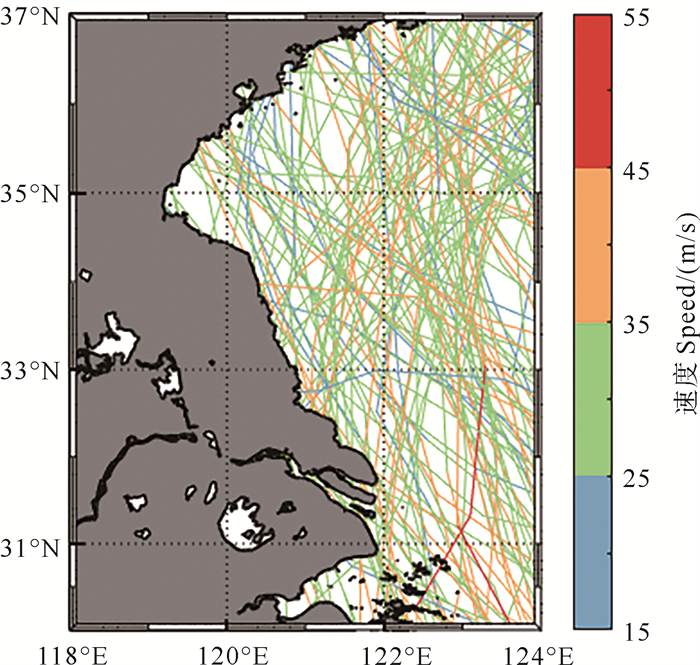
|
图 2 500 a热带气旋随机事件集中影响蓝谷的热带气旋路径图 Fig. 2 The typhoon cyclone paths of 500 years synthetic data mainly affected the blue valley |
为了进一步展示500 a热带气旋随机事件集的可靠性,本文收集了1958—2019年间经过东中国海的台风个例,也按上述原则挑选出了52场影响青岛的历史真实发生过的台风信息。按照中心气压、最大风速及距蓝谷的距离的不同将历史真实台风和500 a热带气旋随机事件集的数据进行分析,结果见图 3。
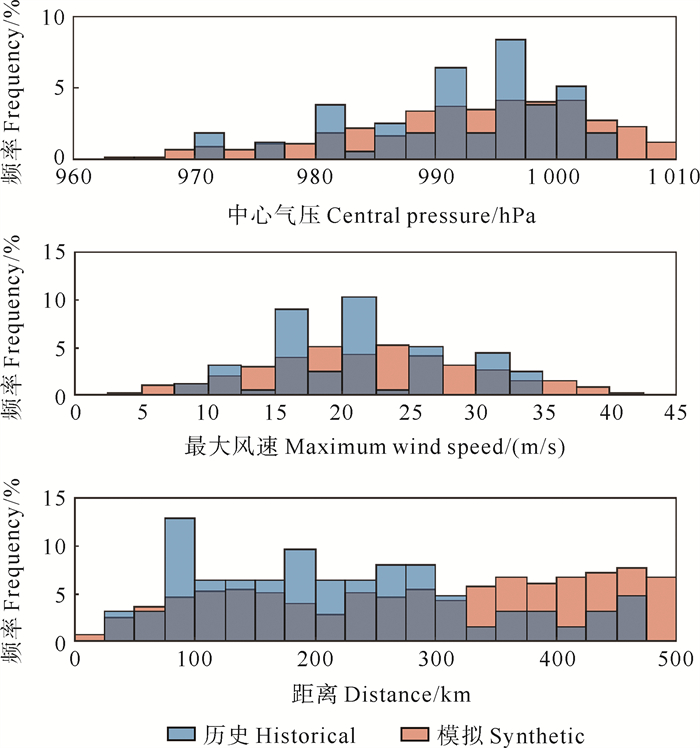
|
图 3 历史与模拟台风数据集台风统计特征对比 Fig. 3 Comparison between the histogram of the typhoon for historical tracks and synthetic tracks |
由图 3可知,500 a热带气旋随机事件集各变量的分布趋势和历史情况基本相一致,两种数据来源的台风中心气压都主要集中在990~1 005 hPa区间段,但500 a热带气旋随机事件集中出现了台风中心气压低于965 hPa的强台风。就中心最大风速来讲,出现最多的频次是在20 m/s左右,同样地,在500 a热带气旋随机事件集中,出现了最大风速高于40 m/s的情况。而从历史台风数据看,台风中心到蓝谷的距离在100~200 km之间的较多,在450 km以上有增多的趋势;从500 a热带气旋随机事件集来看,分布趋势更为明显,100~150 km是一个峰值,300 km及以上的台风占比逐渐增多。这些都说明500 a热带气旋随机事件集较好地抓住了历史台风的特点,并且由于其时间范围更长,因此出现的不同台风情况会更多,同时包含了更多极端的个例。
1.2.3 未来气候变化情景设置冯伟忠等[22]利用历史水位和风暴潮实际损失资料分析认为,将海平面上升简单叠加至重现期水位来研究气候变化影响是不科学的。Feng等[4]的研究也发现气候变化导致的台风风速变化,海平面上升对于青岛近海潮汐、风暴潮都会带来影响,最终总水位的变化由风速增大导致的增水加大,海平面上升本身以及海平面上升带来的潮差加大等3个主要因素来控制。因此本文用海平面上升和台风风速增强这两个因素来表征气候变化,并根据前人研究,设定不同情景来研究这两种因素单独或共同作用下,到本世纪末对蓝谷风暴潮漫滩多年一遇的影响。
根据IPCC AR5的结果,在低排放情景(RCP2.6)下21世纪末全球平均海平面将上升0.26~0.55 m[23]。有研究表明,青岛沿海海平面升高的平均速度为3.5 mm/a,且上升速度呈现逐年递增趋势[24]。目前距本世纪末约80 a,届时青岛海平面将上升30 cm,处于全球预估结果的范围之内,是一个较为合理的数值。另外设定一个更加保守的估计,即海平面上升12 cm作为另一个情景。对于台风的变化,Knutson等[25]根据实测资料和数值模拟结果预计其强度将会在2100年前增加2%~11%,而Lee等[26]也得到了类似的结果。Wang等[27]在研究未来风暴潮对青岛造成的影响时也考虑了海平面升高和台风强度增强的影响。本文通过调整全场风速来体现气候变化对台风带来的影响,设定为两种情景: 一种是台风风速增强3%的情景,另一种是增强10%的情景。这样就有了4种情景,另外设定海平面上升和风速增强联合的情景,所以一共是5种情景,设置方案见表 1。
|
|
表 1 气候变化情景设置方案 Table 1 Scenarios for climate change |
在确定验潮站(港口)的重现期总潮位时的规范应用是采取极值频率分析法。在研究台风风暴潮增水、最高水位的多年一遇问题时前人通过比较其他极值分布类型后,多采用耿贝尔分布来拟合单一变量的典型重现期计算[28-30],本文也采用耿贝尔曲线来研究增水、最高水位以及最大漫滩淹没面积的重现期。
具体的操作如下:对于n年实测年最高或最低潮位数据xi进行多年一遇预测时,按照耿贝尔分布进行估算,其累积分布函数公式见式(6):
| $ F(x)=e^{-e^{-\alpha(x-\beta)}}。$ | (6) |
式中α和β为参数。
假设年极值分布遵从耿贝尔分布,则可以从连续n年实测年极值序列{xi}中,统计出每个xi的累积分布近似值
有多种估算方法,本文采用经典矩法估算参数α和β,其相应估算值α和β的表达式见式(7):
| $ \left\{\begin{array}{l} \bar{\alpha}=\frac{\mathtt{π}}{\sqrt{6}} \cdot \frac{1}{\bar{\sigma}} \\ \bar{\beta}=\bar{\mu}-\frac{c}{\bar{\alpha}} \end{array}\right.。$ | (7) |
式中μ和σ分别是年极值序列{xi}的平均值和标准差,c=0.577 2为欧拉常数。这样就可以根据式(6)和式(7),得到计算多年一遇年极值的公式:
| $ x_{\mathrm{T}}=\frac{[-\ln (-\ln (1-1 / T))-c]}{\bar{\alpha}}+\bar{\mu} 。$ | (8) |
式中T为重现期。
1.4 模型设置及验证 1.4.1 计算范围ADCIRC模型的计算区域范围为117.3°E—127.8°E,28.2°N—40.8°N,网格总数277 032个,网格节点数70 854个。网格分布采取计算区域扩大,重点研究区域加密的方式设计,空间分辨率由外海的10 km逐渐加密至蓝谷区域的80 m分辨率(见图 4)。
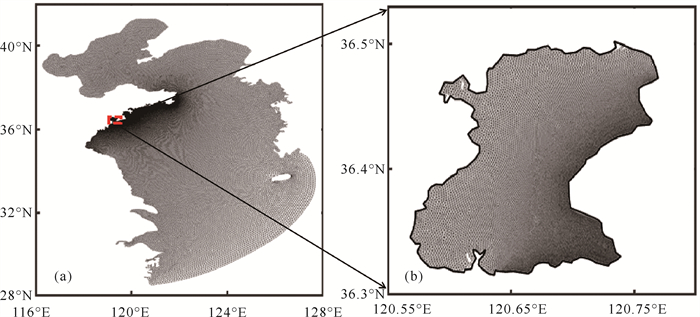
|
图 4 计算区域(左)及蓝谷局部区域(右)的网格图 Fig. 4 Grids of the calculate area (left)and Blue Valley area (right) |
模型采用冷启动,即初始水位场和流场均为0。陆地、岛屿边界处法向速度为0,外海开边界考虑8个主要分潮(M2、S2、K1、O1、N2、K2、P1、Q1)。ADCIRC时间步长设置为3 s,计算结果设置为每小时输出一次,个别组设置为每半小时输出一次。考虑干湿网格变化,当计算节点的水位低于事先设定的最小水深时,该节点被判定为干网格,不参与计算,反之则为湿网格。本文中根据模拟需要,将底摩擦项设置为基于二次底摩擦而来的可变底摩擦形式,将二次底摩擦系数Cfmin取值为0.001 3。
由于本文涉及到漫滩研究,天文潮和风暴潮发生时间的关系需要考虑,因为二者位相匹配的不同对于总水位及淹没来说影响较大。Feng等[4]研究了中国近海十余个站位风暴潮最大增水时刻与天文潮高潮时刻之间的关系,发现二者的位相差可以遍布整个周期,在不同的站点位相差在一个周期内的分布特征是不同的,但未得到机制上的认识。这应该是由风暴潮和天文潮的驱动力不同决定的。因此,可以理解为二者的关系具有随机性。在进行历史台风风暴潮模拟时,本文使用实际发生的时间来进行模拟,对于使用500 a热带气旋随机事件集进行多年一遇研究时,将热带气旋中心进入模拟区域时刻定为天文潮初始位相为0的时刻。由于500 a热带气旋随机事件集的热带气旋发生时间也是随机产生的,这就意味着天文潮和风暴潮发生时间没有特定关系。
最大漫滩淹没面积是本研究的一个重要统计量,在本文中定义为超出正常天文高潮淹没范围的那一部分淹没面积。由于海平面变化本身就会引起天文潮高潮时淹没范围的变化,因此,叠加上风暴潮的漫滩淹没要减去新的气候变化情景下的天文潮高潮淹没范围,这样其淹没区域也发生了变化,一般来说更加向内陆延伸。
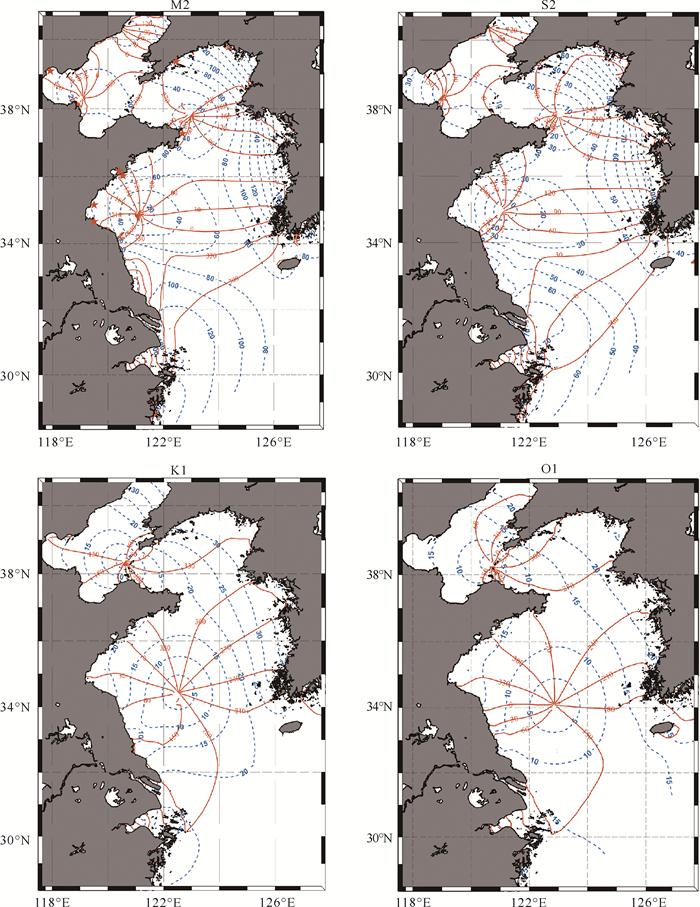
1.4.3 天文潮验证本文以2018年7月19日0时(UTC)为模型潮位验证启动时间,计算了30 d的黄东海潮位。通过对模型的水位结果进行调和分析,得到分潮M2、S2、K1、O1的同潮图(见图 5)。图 5中在渤海呈现的无潮点位置,以及在青岛附近的相位、振幅特征能够较好地和图集对应[32]。
|
( 图中红色实线表示等迟角线,蓝色虚线表示等振幅线。红色五角星代表验潮站,自北向南依次是:小长山站、塘沽站、成山头站、青岛站、小麦岛站、日照站、连云港站。The red solid line refers to co-phase lag line; The blue solid line refers to iso-amplitude line; The red five pointed-stars refer to the tide gauges. From north to south are: Xiaochangshan, Tanggu, Chengshantou, Qingdao, Xiaomaidao, Rizhao, Lianyungang gauge stations. ) 图 5 M2、S2、K1、O1同潮图 Fig. 5 M2、S2、K1、O1 cotidal chart |
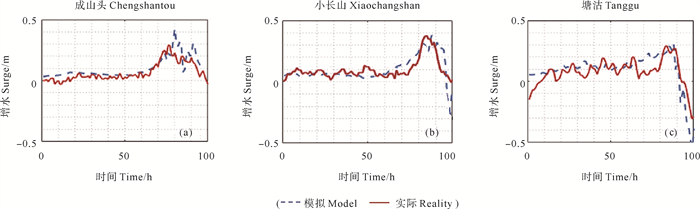
本文风暴潮增水验证数据取自2000年的两场台风过程,分别是2000年7月16日12:00 (UTC)开始模拟的0004号台风“启德(Kaitak)”和2000年8月27号12:00(UTC)开始模拟的0012号台风“派比安(Prapiroon)”,将距离研究区域较近的7个站位(见图 5)实测资料和模型计算结果进行对比验证。
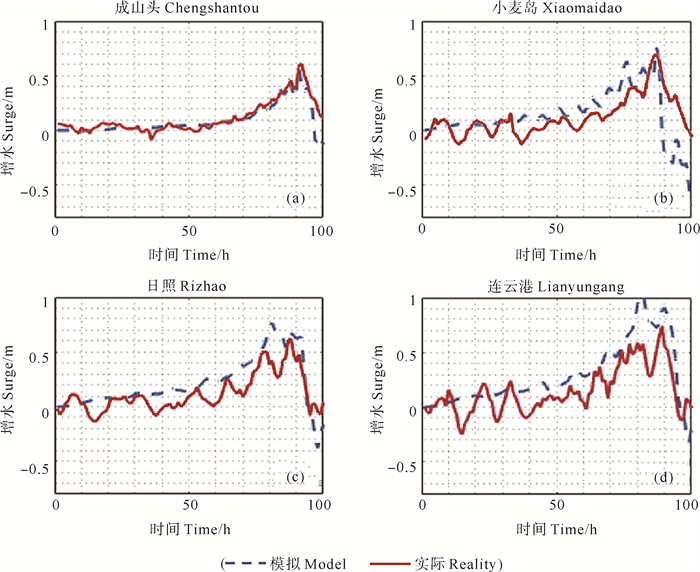
图 6和7分别显示的是0004号台风“启德(Kaitak)”期间各站位(包括成山头站、小长山站、塘沽站)和0012号台风“派比安(Prapiroon)”期间各站位(包括成山头站、小麦岛站、日照站、连云港站)模型和实测增水的比较。从两图中可以看出模型能够较好地刻画台风风暴潮的增水过程,选取站点的实测水位极值均小于模型验证结果。在图 6中,塘沽站的最大增水误差最小,成山头站的最大增水误差最大,相差13 cm。在图 7中可以发现,0012号台风模拟最大增水的变化趋势和出现时间与观测值吻合较好,小麦岛站模拟的最高水位峰值时刻与观测值几乎相等,成山头站、小麦岛站、日照站对于模拟最大增水与实际验潮站记录增水相对误差分别为7.5%、8.3%、22.5%,只有连云港站位的增水误差较大,模拟增水和实测值的绝对误差为25 cm(见表 2)。总体显示模型模拟与观测数据之间存在合理的一致性。
|
图 6 0004号台风“启德(Kaitak)”风暴潮过程增水验证 Fig. 6 Storm surge verification between 0004 typhoon Kaitak |
|
图 7 0012号台风“派比安(Prapiroon)”风暴潮过程增水验证 Fig. 7 Storm surge verification between 0012 typhoon Prapiroon |
|
|
表 2 误差对比 Table 2 Error comparison |
本文利用500 a热带气旋随机事件集计算了当前气候情景下不同重现期风暴潮最高水位和最大漫滩淹没面积的多年一遇值。漫滩淹没面积采用已知三点坐标叉积公式:已知假设三角形的三个顶点分别为A(x1,y1)、B(x2,y2)和C(x3,y3),则三角形的面积可以通过计算向量AB和向量AC的叉积的大小来获得,如式(9)所示:
| $ \begin{gathered} S_{\triangle \mathrm{ABC}}=A B \times A C= \\ \frac{1}{2}\left|\left(x_2-x_1\right)\left(y_3-y_1\right)-\left(x_3-x_1\right)\left(y_2-y_1\right)\right|。\end{gathered} $ | (9) |
式中|...|表示取绝对值。
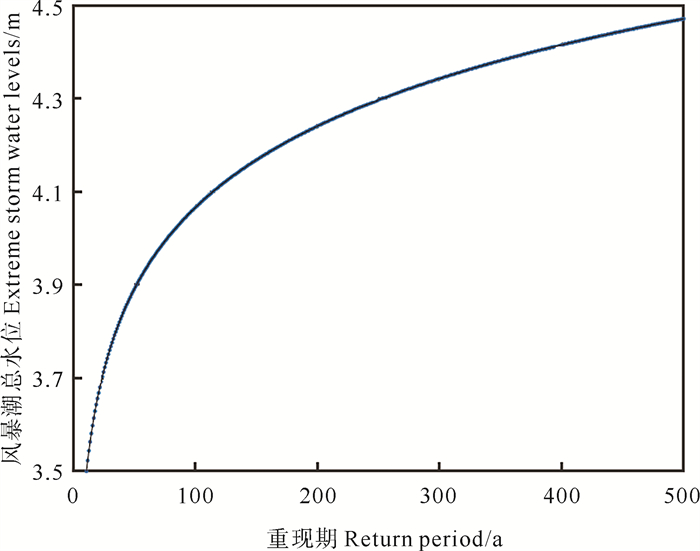
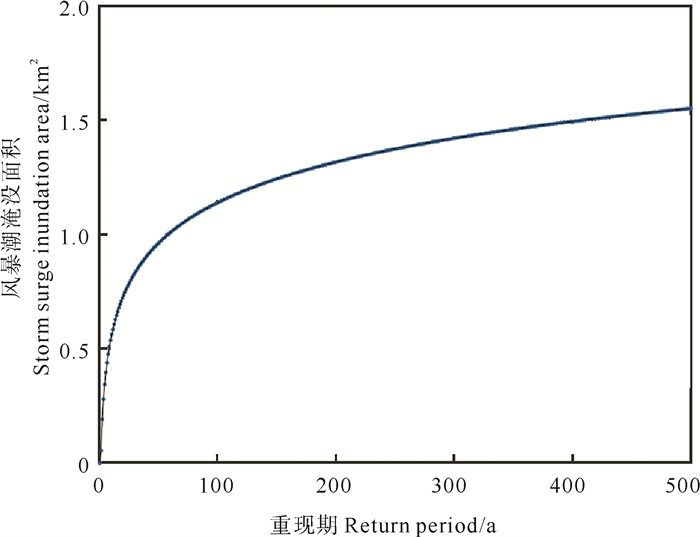
由图 8可知,500 a热带气旋随机事件集计算得到的百年一遇风暴潮最高水位为4.06 m,500年一遇的风暴潮最高水位为4.47 m,而从图 9可知,百年一遇的最大漫滩淹没面积为1.14 km2,500年一遇的最大漫滩淹没面积为1.55 km2。从图 8和9都可以看出,多年一遇的风暴潮最高水位和最大漫滩淹没面积随着重现期增长而增大,并且都显示了在前100 a变化较快,后面变化逐渐变小。
|
图 8 当前气候情景下蓝谷风暴潮最高水位随不同重现期的变化曲线 Fig. 8 Return level plot for extreme storm water levels for current scenario |
|
图 9 当前气候情景下蓝谷风暴潮最大漫滩淹没面积随不同重现期的变化曲线 Fig. 9 Return level plot for extreme storm surge inundation area for current scenario |
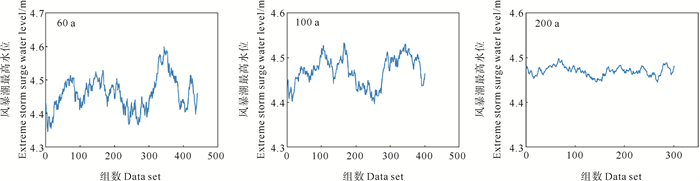
为了探究数据资料的长度对多年一遇结果的影响,本文将500 a热带气旋随机事件集数据分割成60、100和200 a的三组数据段,用各组数据分别计算了500年一遇的风暴潮最高水位值,结果见图 10。从图 10中发现,利用60 a长度的多组数据组计算得到的500年一遇风暴潮最高水位在4.34~4.60 m范围内波动,60、100和200 a数据资料长度得到的500年一遇风暴潮最高水位平均值分别为4.46、4.47和4.47 m,而标准差分别为0.049、0.032和0.010 m,说明随着数据组资料长度的增加,预测结果逐渐趋于稳定。这说明需要足够长的数据资料才能够得到较为稳定的多年一遇值,这和刘永玲等[5]在福建连江县利用不同长度数据资料评估风暴潮灾害时得到的结论是一致的。董胜等[33]对青岛大港站1948—1979年极值增水划分资料年限后,采用耿贝尔极值分布统计求得百年一遇的增水值在1.35~2.03 m范围内,50年一遇的增水值则在1.35~1.80 m范围内,利用不同的数据资料长度求得的差距可达0.28 m,这也说明了多年一遇极值分析结果对数据资料长度有很强的依赖性。
|
图 10 不同时长数据计算的500 a重现期风暴潮最高水位变化曲线对比图 Fig. 10 Comparison of the 500 a return level for extreme storm surge water levels between different length data set |
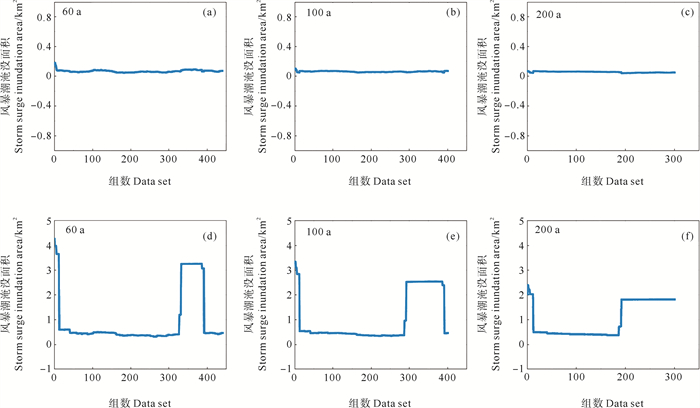
本文进一步做了数据长度对多年一遇最大淹没面积的影响。图 11(a)—(c)和(d)—(f)分别为利用不同时长数据资料得到的2年一遇、500年一遇最大漫滩淹没面积。从图中看出,2年一遇的最大漫滩淹没面积本身就比较小,60 a的资料长度相比于2 a也足够长了,因此其变化幅度也不大,基于多组60、100和200 a数据得到的2年一遇最大漫滩淹没面积平均值均为0.07 km2,而标准差分别为0.012、0.005和0.003 km2,再次说明了多年一遇的最大漫滩淹没面积结果依赖于数据资料长度。
|
( (a)—(c)2年重现期的结果;(d)—(f)500年重现期的结果。(a)—(c) 2 a return level; (d)—(f) 500 a return level. ) 图 11 不同时长数据得到的2 a和500 a重现期蓝谷风暴潮最大漫滩淹没面积变化曲线对比图 Fig. 11 Comparison of the 2 a return level and 500 a return level for extreme storm surge inundation area between length data set at blue valley |
然而,对于500年一遇的结果,情形有些不同。一个非常明显的现象是500年一遇的最大漫滩淹没面积在不同组间有急剧变化,其变化幅度远大于多年一遇最高水位的变化。分析其原因发现,影响漫滩淹没面积的因素多于影响最高水位的因素,其中很重要的一个因素是陆地地形、最高水位和淹没面积之间的关系只有在地形是线性变化的情形下才是线性的,比如遇到较陡的地形时,水位的增长未必引起多大的淹没面积的变化,反之,如果地形平坦,则淹没面积对于水位的变化就很敏感。另外,最大漫滩淹没面积反映的是淹没过程,相同强度不同路径的热带气旋可能带来不同的淹没。不过即使有上述因素,随着数据资料长度的增加,得到的最大漫滩淹没面积数值还是逐渐平稳的,如利用200 a的数据资料长度得到的500年一遇最大漫滩淹没面积变化在0.40~2.40 km2范围内,比起60 a的数据资料长度得到最高波动至4.30 km2更加稳定,也能够有效减少部分年份台风异常对长期预测结果带来的不稳定性与误差。
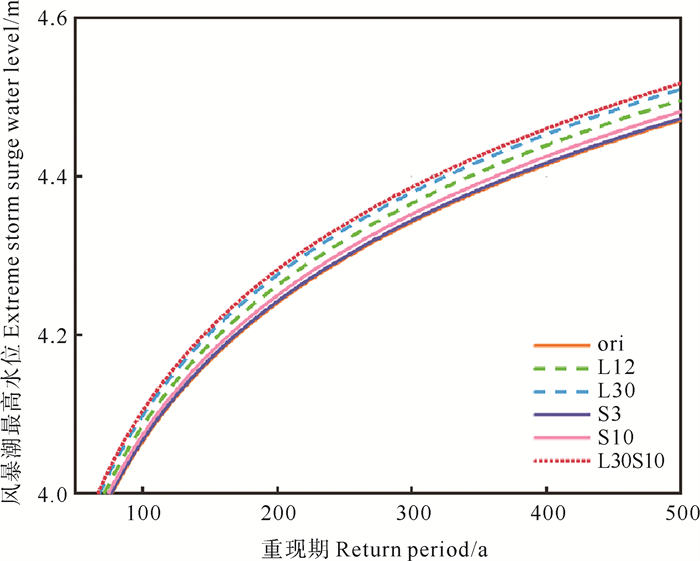
2.2 未来气候变化对多年一遇风暴潮最高水位和最大漫滩淹没面积的影响基于2.1节得到的认识,此后的多年一遇的计算均是利用500 a的年极值得到的。首先分析在气候变化情景下蓝谷多年一遇风暴潮最高水位的变化,结果见图 12。在图 12中未来气候变化情景下多年一遇风暴潮最高水位与当前气候情景结果相比,都有明显增大,主要体现在海平面上升带来的最高水位变化,但是这一差异随着重现期的增长而变大,说明这的确不是一个简单的线性叠加。如在海平面升高12、30 cm的情景下,百年一遇的风暴潮最高水位分别为4.08和4.09 m,相较于上一节气候条件未改变的情况下百年一遇风暴潮最高水位值分别增加了0.02和0.03 m,两种情景下预估的500年一遇风暴潮最高水位重现期分别为4.49和4.51 m,比不考虑气候变化的风暴潮最高水位分别将增加0.02、0.04 m。而且发现100和500年一遇风暴潮最高水位因海平面上升带来的额外变化,随着海平面升高而变大,也就是说,随着海平面升高,越严重的风暴潮受到的影响越大。
|
( 橙色实线、绿色虚线、蓝色虚线、紫色实线、粉色实线、红色点状线分别表示当前气候情景下、海平面升高12和30 cm情景下、台风风速增强3%和10%情景下、风速增强10%和海平面升高30 cm联合情景下的风暴潮最高水位多年一遇曲线。Orange solid line, green dash line, blue dash line, purple solid line, pink solid line, red dot line refer to extreme storm surge water level return level under current climate scenario, sea level rise 12 cm, sea level rise 30 cm, wind speed increase 3%, wind speed increase 10%, sea level rise 30 cm with wind speed increase 10%, respectively. ) 图 12 不同气候变化情景下蓝谷多年一遇风暴潮最高水位的变化 Fig. 12 Difference of different return period extreme storm surge water levels at blue valley under change climate scenarios |
从图 12还可以看出,在台风风速增强的情形下,多年一遇的风暴潮最高水位与当前气候情景时的结果相差不大。如在风速增强3%的情景下,500年一遇的水位为4.47 m,与当前气候情景是一致的。而台风风速增强10%的情景下,500年一遇的水位值为4.48 m,仅增加了0.01 m。对于重现期短的风暴潮最高水位,差异则更不明显。这说明按照预设的台风风速变化的情景,多年一遇的风暴潮最高水位变化不大。这一点在下一节进行讨论。
另外,本文考虑的联合情景海平面升高30 cm和风速增强10%的情景下,500年一遇的最高水位为4.43 m,该值按照海平面升高程度加剧和风速增强程度加剧的顺序,分别增加:0.46%、0.15%、0.97%、0.77%,即联合情景下多年一遇最高水位受海平面上升影响更大,且多年一遇最高水位的变化随事件极端程度的增加均会增加。
气候变化情景下蓝谷多年一遇风暴潮最大淹没面积的变化在图 13中显示。从图 13中看到在未来台风风速增强的情景下,多年一遇的风暴潮最大淹没面积都高于当前气候情景的值。当风速增强3%时,百年一遇的风暴潮最大淹没面积由1.14 km2上升到1.20 km2,增幅5%;而风速增强10%时,500年一遇的风暴潮最大淹没面积由1.55 km2上升到1.83 km2,增幅可达18%。说明风速变化对于最大淹没面积的影响是很大的。
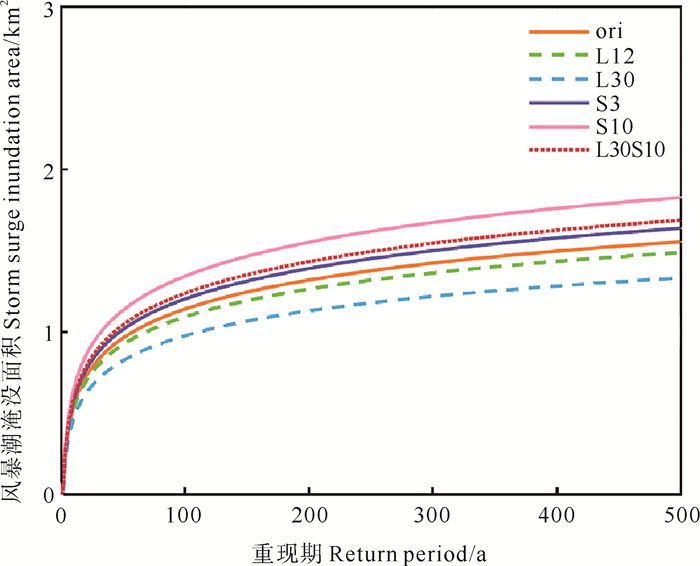
|
( 橙色实线、绿色虚线、蓝色虚线、紫色实线、粉色实线、红色点状线分别表示当前气候情景下、海平面升高12和30 cm情景下、台风风速增强3%和10%情景下、风速增强10%和海平面升高30 cm联合情景下的风暴潮淹没面积多年一遇曲线。Orange solid line, green dash line, blue dash line, purple solid line, pink solid line, red dot line refer to extreme storm surge inundation area return level under current climate scenario, sea level rise 12 cm, sea level rise 30 cm, wind speed increase 3%, wind speed increase 10%, sea level rise 30 cm with wind speed increase 10%, respectively. ) 图 13 不同气候变化情景下蓝谷多年一遇风暴潮淹没面积的变化 Fig. 13 Difference of different return period extreme storm surge inundation area at blue valley under change climate scenarios |
从图 13中可以看到,在海平面升高的情景下,风暴潮的多年一遇的风暴潮最大淹没面积反而呈现减小的趋势。当海平面升高12 cm时,风暴潮造成的500年一遇最大漫滩淹没面积为1.49 km2,比当前气候情景下预估的淹没面积减小了0.06 km2,百年一遇的淹没面积也缩小了0.04 km2,都减小了4%。
在海平面升高30 cm情景下计算的多年一遇淹没面积则更小,百年一遇的淹没面积为0.98 km2,500年一遇的淹没面积为1.33 km2,均减小了14%。不过当海平面升高30 cm并且台风风速增加10%时,百年一遇的值变为了1.24 km2,500年一遇的值变为了1.69 km2,较当前气候情景下均上升了9%。
因此,对于漫滩淹没面积来说,风速影响较大,海平面上升反倒出现了淹没减小的现象。下一节将对此进行讨论。
2.3 多年一遇风暴潮最高水位及最大漫滩淹没面积变化特征讨论在本研究中,多年一遇风暴潮最高水位变化主要受海平面上升的影响,这与Knutson等[25]综合评估结果是一致的,但是多年一遇风暴潮最高水位的变化仅靠海平面上升解释不了,这可以用海平面上升会给天文潮振幅也带来变化来解释。Feng等[34]研究青岛风暴潮受气候变化影响时已发现了这一现象, 也就是在海平面上升之外,还会额外产生最高水位的变化。
不过本文的研究结果发现,未来台风风速的变化对于最高水位影响不大,这一点与一般认知是不同的,也不同于Feng等[34]的结果,在那里风速增加会对风暴潮增水带来较大影响。分析其原因主要在于本文研究时考虑了漫滩过程,即海岸水位的升高会使得海水淹没陆地,海水不会在岸边持续堆积造成水位的进一步升高。在Feng等[34]的研究中,没有考虑漫滩,而是在海边设置了直立壁,这样风速增大时,更多的海水被带到了岸边,造成堆积,从而使得海水水位上升,得到了风速增强带来更多增水的结论。
在本文研究中,风速的增强虽然没有带来更大的增水,但是多年一遇风暴潮最大淹没面积却增大不少。在风速增加10%的情况下,百年一遇的风暴潮最大淹没面积增加了5%。这也说明水没有在岸边堆积,而是淹没了陆地。
上一节关于海平面上升对多年一遇风暴潮最大漫滩淹没面积的影响结果可能更加不易理解,这主要可以从两方面加以解释: 首先从最大漫滩淹没面积的定义来看,在2.1节,将淹没面积定义为将一场风暴潮过程中的最大水面面积减去只计算天文潮时的最大水面面积,原因是本文考虑的是风暴潮造成的淹没,要把正常的潮汐的淹水减掉,当海平面上升时,天文潮本身的淹水范围也扩大了,其差值即本文研究的风暴潮漫滩淹没面积未必一定会增大。
实际上,随着海平面的上升,天文潮本身涨落造成的淹没范围会向陆地推进,进入到一些原本并不会受影响的区域。值得注意的是,天文潮新影响区域的地形坡度与海平面升高前影响区域的地形坡度未必相同, 如果新影响区域的地形更为陡峭,这时发生风暴潮淹没面积反而会缩小,这就是本文遇到的情形,反之则可能造成更大的漫滩淹没面积。
从本文模拟结果中选取一场模拟台风期间天文潮最大淹水范围来进行分析。图 14是当前气候情景、海平面升高12和30 cm的情景下天文潮最大淹没范围,即图中沿着海岸的那一条带,表示的是相应情景下平均海平面以上的部分。从图中可以看出这一范围的确随着海平面的升高,向内陆推进了。
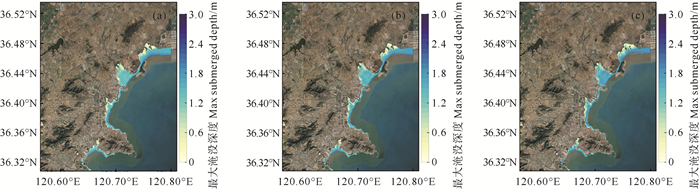
|
( (a)—(c)分别对应为当前气候背景、海平面升高12 cm以及30 cm情景的地形。(a)—(c) refer to topography under current climate scenario, sea level rise 12 cm and sea level rise 30 cm climate scenarios. ) 图 14 不同海平面情景下天文潮的最大淹没范围 Fig. 14 Maximum submerged area under different sea level rise scenarios |
当然,这是由于在这一区域目前未建立完整的堤坝来防御风暴潮,而且研究中假设天文潮影响之处为自然海滩,意味着随着海平面的升高,人是需要后退的,这样的话在某些地形情形下,未来的灾害可能会减少。但通常人们不会做这种选择,一般会建设堤坝来防御风暴潮。在模型中就会表达为直立壁,就像Feng等[34]中的一样,那样就造成了多年一遇风暴潮最高水位的增加。
3 结论本文围绕青岛蓝谷建立了风暴潮漫滩数值模型,从利用蒙特卡洛方法得到的500 a热带气旋随机事件集中挑选了影响青岛蓝谷的538场模拟台风风场,并设定了5种未来气候变化的情景,对蓝谷未来情景下多年一遇的风暴潮最高水位和最大漫滩淹没面积进行了数值研究,得出以下结论:
(1) 数据资料长度对多年一遇的计算结果有影响,数据资料长度越长得到的结果越稳定,用较短的数据资料去估算多年一遇会有较大的不确定性;
(2) 在考虑漫滩时,未来海平面上升是推高多年一遇风暴潮最高水位的主要因素,但不是线性叠加,天文潮振幅的变化也是一个因素,未来台风风速变化则影响不大;
(3) 多年一遇风暴潮最大漫滩淹没范围随台风风速增强而增大,体现了台风增强造成的灾害会加大;
(4) 海平面上升会使得天文潮的淹没范围向内陆推进,由于地形坡度的不同,在青岛蓝谷反倒使多年一遇风暴潮最大淹没范围减小。但是海平面上升本身会淹没陆地,因此总体上海平面上升造成的影响是负面的。
总之,未来气候变化会加重青岛蓝谷风暴潮灾害,需要积极应对。未来研究可以利用更加可靠的未来预估情景,降低预估结果的不确定性,另外可以将得到的成果应用到应对气候变化的策略研究中, 为地方政府决策提供支撑。
| [1] |
冯士筰. 风暴潮导论[M]. 北京: 科学出版社, 1982. Feng S Z. Introduction to Storm Surge[M]. Beijing: Science Press, 1982. (  0) 0) |
| [2] |
国家海洋局. 中国海洋灾害与减灾[J]. 中国减灾, 2020(4): 16-20. State Oceanic Administration People's Republic of China. China ocean disasters and disaster reduction[J]. Disaster Reduction in China, 2020(4): 16-20. (  0) 0) |
| [3] |
国家海洋局. 中国海洋灾害与减灾[J]. 中国减灾, 2021(10): 39-55. State Oceanic Administration People's Republic of China. China ocean disasters and disaster reduction[J]. Disaster Reduction in China, 2021(10): 39-55. (  0) 0) |
| [4] |
Feng J L, Jiang W S, Bian C W. Numerical prediction of storm surge in the Qingdao area under the impact of climate change[J]. Journal of Ocean University of China, 2014, 13(4): 539-551. DOI:10.1007/s11802-014-2222-4 (  0) 0) |
| [5] |
刘永玲, 冯建龙, 江文胜, 等. 热带气旋资料长度对风暴潮危险性评估结果的影响[J]. 海洋学报, 2016, 38(3): 60-70. Liu Y L, Feng J L, Jiang W S, et al. Effects of a tropical cyclone data sets length on the result of risk assessment of storm surge[J]. Haiyang Xuebao, 2016, 38(3): 60-70. DOI:10.3969/j.issn.0253-4193.2016.03.006 (  0) 0) |
| [6] |
梁海燕, 邹欣庆. 海口湾沿岸风暴潮风险评估[J]. 海洋学报(中文版), 2005(5): 22-29. Liang H Y, Zou X Q. Risk assessment on storm surge in the Haikou Bay[J]. Haiyang Xuebao, 2005(5): 22-29. (  0) 0) |
| [7] |
张月霞. 基于ADCIRC模式的台风风暴潮灾害风险评估方法研究与应用——以浙江台州为例[D]. 青岛: 中国海洋大学, 2014. Zhang Y X. Risk Assessment Method and Application of Typhoon Storm Surge Based on ADCIRC: A Case Study on Taizhou Abstract[D]. Qingdao: Ocean University of China, 2014. (  0) 0) |
| [8] |
方伟华, 石先武. 面向灾害风险评估的热带气旋路径及强度随机模拟综述[J]. 地球科学进展, 2012, 27(8): 866-875. Fang W H, Shi X W. Review on stochastic modeling of tropical cyclone track and intensity for disaster risk assessment[J]. Advances in Earth Science, 2012, 27(8): 866-875. (  0) 0) |
| [9] |
林滋新, 周庆满, 李培顺, 等. 青岛近海风暴潮灾害及其预报研究[J]. 海岸工程, 1996(3): 15-24. Lin Z X, Zhou Q M, Li P S, et al. The research of prediction of storm surge disaster in near shore of Qingdao[J]. Coastal Engineering, 1996(3): 15-24. (  0) 0) |
| [10] |
苗丰永. 抢险抗灾保盐场[M]. 北京: 中国轻工业年鉴, 1993. Miao F Y. Emergency Disaster-Resistant Salt Field[M]. Beijing: China Light Industry Yearbook, 1993. (  0) 0) |
| [11] |
丁希玲. 即墨年鉴1992—1998[M]. 北京: 新华出版社, 1999. Ding X L. Jimo Yearbook 1992—1998[M]. Beijing: Xinhua Press, 1999. (  0) 0) |
| [12] |
马艳, 郭丽娜, 郝燕. 1949-2020年影响青岛的热带气旋气候特征[J]. 海洋科学, 2022, 46(1): 44-55. Ma Y, Guo L N, Hao Y. Climate characteristics of tropical cyclones affecting Qingdao during 1949—2020[J]. Marine Sciences, 2022, 46(1): 44-55. (  0) 0) |
| [13] |
Luettich R, Westerink J J, Scheffner N W. ADCIRC: An Advanced Three-Dimensional Circulation Model for Shelves, Coasts and Estuaries. Report 1[R]. [s. l.]: Theory and Methodology of ADCIRC-2DDI and ADCIRC-3DL, 1992.
(  0) 0) |
| [14] |
Luettich R A, Westerink J J. Formulation and numerical implementation of the 2D/3D ADCIRC Finite Element Model Version 44. XX[R], [s. l.]: [s. n.], 2004, 74.
(  0) 0) |
| [15] |
Jelesnianski C P. A numerical computation of storm tides by a tropical storm impinging on a continental shelf[J]. Monthly Weather Review, 1965, 93(6): 343-358. DOI:10.1175/1520-0493(1993)093<0343:ANCOS>2.3.CO;2 (  0) 0) |
| [16] |
Atkinson G, Holliday C. Tropical cyclone minimum sea level pressure/maximum sustained wind relationship for the Western North Pacific[J]. Monthly Weather Review, 1977, 105(4): 421-427. DOI:10.1175/1520-0493(1977)105<0421:TCMSLP>2.0.CO;2 (  0) 0) |
| [17] |
Shea D J, Gray W M. The hurricane's inner core region. Ⅰ. symmetric and asymmetric structure[J]. Journal of the Atmospheric Sciences, 1973, 30: 1544-1564. DOI:10.1175/1520-0469(1973)030<1544:THICRI>2.0.CO;2 (  0) 0) |
| [18] |
赫林, 李建成, 褚永海. 1985国家高程基准与全球高程基准之间的垂直偏差[J]. 测绘学报, 2016, 45(7): 768-774. He L, Li J C, Chu Y H. The vertical shift between 1985 national height datum and global vertical datum[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(7): 768-774. (  0) 0) |
| [19] |
国家海洋信息中心编. 潮汐表第4册太平洋及其邻近海域[M]. 北京: 海洋出版社, 2018. National Marine Data and Information Service. Tide Tables Vol.4 Pacific Ocean and Its Adjacent Sea Area[M]. Beijing: China Ocean Press, 2018. (  0) 0) |
| [20] |
郭海荣, 焦文海, 杨元喜. 1985国家高程基准与全球似大地水准面之间的系统差及其分布规律[J]. 测绘学报, 2004, 33(2): 100-104. Guo H R, Jiao W H, Yang Y X, et al. The systematic difference and its distribution between the 1985 national height datum and the globalquasigeoid[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2): 100-104. DOI:10.3321/j.issn:1001-1595.2004.02.002 (  0) 0) |
| [21] |
许耿然, 朱紫阳, 周建营. 1985国家高程基准与全球似大地水准面在广东地区的垂直偏差[J]. 测绘通报, 2013(12): 15-17. Xu G R, Zhu Z Y, Zhou J Y, et al. The systematic difference between the 1985 national height datum and the global quasigeoid in Guangdong region[J]. Bulletin of Surveying and Mapping, 2013(12): 15-17. (  0) 0) |
| [22] |
冯伟忠, 张娟, 游大伟, 等. 被高估的"海平面上升对珠江口风暴潮灾害评估影响"的原因探析[J]. 热带地理, 2013, 33(5): 640-645. Feng W Z, Zhang J, You D W, et al. A Discussion on reasons for impact of over-estimated sea level rise on storm surge disaster forecasting of the Pearl River Estuary[J]. Tropical Geography, 2013, 33(5): 640-645. (  0) 0) |
| [23] |
IPCC Working Group Ⅰ. Climate Change 2013: the Fifth Assessment Report of the Intergovernmental Plan on Climate Change[R]. 2013. https://ar5-syr.ipcc.ch/index.php.
(  0) 0) |
| [24] |
廖琪, 于格, 江文胜, 等. 海岸带城市洪水淹没风险评价研究——以青岛市为例[J]. 海洋与湖沼, 2018, 49(2): 301-312. Liao Q, Yu G, Jiang W S, et al. Comprehensive evaluation of flooding risk in coastal ones: A case study of Qingdao City[J]. Occanologia et Limnologia Sinica, 2018, 49(2): 301-312. (  0) 0) |
| [25] |
Knutson T A, McBride J L, Chan J, et al. Tropical cyclones and climate change[J]. Nature Geoscience, 2010, 3(3): 157-163. DOI:10.1038/ngeo779 (  0) 0) |
| [26] |
Lee T C, Knutson T R, Nakaegawa T, et al. Third assessment on impacts of climate change on tropical cyclones in the typhoon committee region-Part Ⅰ: Observed changes, detection and attribution[J]. Tropical Cyclone Research and Review, 2020, 9(1): 75-86. (  0) 0) |
| [27] |
Wang Y P, Jiang W S, Liu X, et al. Estimation of future storm surge inundation and effects of the adaptation measures in Qingdao, China[J]. Marine Development, 2023, 1(1): 9. DOI:10.1007/s44312-023-00011-0 (  0) 0) |
| [28] |
尹逊福, 王以娇, 张廷廷. 极值分布的推算方法及其在黄河口海区的应用[J]. 黄渤海海洋, 1990, 8(1): 9-15. Yin X F, Wang Y J, Zhang T T. The methods for calculating the extreme distribution and their applications in the Yellow River Mouth area[J]. Advances in Marine Science, 1990, 8(1): 9-15. (  0) 0) |
| [29] |
王喜娜. 风暴潮灾害风险评估与事件预警研究[D]. 武汉: 武汉大学, 2016. Wang X N. Storm Surge Disaster Risk Assessment and Impact Forecasting Research[D]. Wuhan: Wuhan University, 2016. (  0) 0) |
| [30] |
庄圆. 中国沿海重现期水位算法研究及空间分布[D]. 舟山: 浙江海洋大学, 2020. Zhuang Y. Research on the Algorithm of Return Period Water Level and Its Spatial Distribution in the Coastal Area of China[D]. Zhoushan: Zhejiang Ocean University, 2020. (  0) 0) |
| [31] |
Liu Y X, Li S T, Wang Z F. Assessment of storm surge and flood inundation in Chittagong City of Bangladesh based on ADCIRC and GIS[J]. Journal of Ocean University of China, 2023, 22(6): 1473-1486. DOI:10.1007/s11802-023-5327-9 (  0) 0) |
| [32] |
海洋图集编委会. 渤海、黄海、东海海洋图集[M]. 北京: 海洋出版社, 1992. Board for Marine Atlas. Marine Atlas of Bohai Sea Yellow Sea East China Sea[M]. Beijing: China Ocean Press, 1992. (  0) 0) |
| [33] |
董胜, 李奉利, 孙瑞文. 风暴增水随机分析的过阈法及其统计计算模式[J]. 青岛海洋大学学报(自然科学版), 2000(3): 542-548. Dong S, Li F L, Sun R W, et al. On the peak over threshold method in the statistical analysis of storm surge elevation and its probability model[J]. Periodical of Ocean University of China, 2000(3): 542-548. (  0) 0) |
| [34] |
Feng J L, von Storch H, Jiang W S, et al. Assessing changes in extreme sea levels along the coast of China[J]. Journal of Geophysical Research: Oceans, 2015, 120(12): 8039-8051. (  0) 0) |
2. The Key Laboratory of Marine Environmental Science and Ecology, Ministry of Education, Ocean University of China, Qingdao 266100, China
 2025, Vol. 55
2025, Vol. 55


