2. 自然资源部国家海洋环境预报中心, 北京 100081
作为表面重力波,海浪是海洋上最常见的物理现象。海浪不仅对海气相互作用和气候变化有重要影响[1-2],也是海上航行、海上建筑物和港口设计等的重要参考依据[3-4]。在过去研究中,从区域到全球尺度,来自海洋浮标、卫星高度计、数值模拟的波浪数据已经被广泛用来分析海洋有效波高的时空特征[5-10]。
渤黄东海是西北太平洋的边缘海,水深大多在200 m以内(见图 1)。受东亚季风驱动,渤黄东海冬季盛行强偏北风,夏季以弱偏南风为主,该区域波浪的时空变化受风场和外海传播涌浪的显著影响[11]。目前研究渤黄东海波浪场的最常见方法就是数值模拟,虽然再分析数据集也提供了逐小时的波浪数据,但这些低空间分辨率的波浪参数难以满足对近岸水体的分析[12]。Zheng等[13]利用WAVEWATCH Ⅲ(WW3)波浪模型模拟了整个中国近海波浪场,揭示了1988—2011年期间有效波高和波浪能的长期趋势。Liang等[14]利用浅水波浪数值模型(simulating waves nearshore, SWAN)对1990—2011年的渤黄东海的波浪场进行了模拟,并分析了有效波高的季节变化。基于欧洲中期天气预报中心第五代数据集,Wang等[11]分析了1979—2014年期间东海有效波高和风场的多时间尺度变化。基于SWAN输出的长时间波浪数据,Zhai等[8]研究了黄海有效波高的年际变化强度以及驱动机制。Yang等[15]基于30年WW3模式输出,评估了中国近海有效波高和波浪能的气候态月变化。然而,前人关于渤黄东海有效波高变化的分析工作主要集中在某个海域或者若干个时间尺度,很少有研究对整个渤黄东海有效波高的多时间尺度变化进行全面分析。

|
(图中红色的线段表示各个海域的分界线。The red lines in the figure represent the boundaries of each sea area.) 图 1 渤黄东海水深分布 Fig. 1 Water depth in Bohai, Yellow and East China Seas |
此外,海浪数值模拟中一个非常重要的参数——拖曳系数(drag coefficient, Cd),其定义为:Cd=u*2/U102,其中:u*为摩擦速度;U10为海面10 m处的风速。Cd可以直接影响海-气界面的动量通量转化,是影响模式准确性的重要参数之一。因此,以浮标观测作为参考数据,选择最适用于渤黄东海的参数化方案,有望提高海浪数值模拟的准确性。本文的研究目标主要是以下两个方面:(1)基于WW3波浪模型的ST6源函数组合,并利用浮标观测数据作验证,确立最佳拖曳系数参数化公式;(2)以欧洲中期天气预报中心提供的风场资料为驱动,模拟2004—2022年期间渤黄东海有效波高时间序列,揭示有效波高时间序列的多尺度变化及其驱动机制,其中包括总体变化强度、季节变化、年际变化以及长期趋势。
1 数据和方法 1.1 数据驱动WW3模式的海面10 m风速数据来自欧洲中期天气预报中心的第五代再分析数据集(ERA5: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=form),时间分辨率为1 h,空间分辨率为0.25°×0.25°。本研究采用美国国家海洋和大气管理局(NOAA)提供的海洋尼诺指数(oceanic niño index, ONI)来量化ENSO信号,ONI的数值至少连续5个月超过+0.5 ℃或-0.5 ℃时,判定发生厄尔尼诺事件或拉尼娜事件(https://climatedataguide.ucar.edu/climate-data/ninosst-indices-nino-12-3-34-4-oni-and-tni/)。水深数据来自美国地球物理中心发布的全球数字高程模型(ETOPO2)(https://www.ngdc.noaa.gov/mgg/global/relief/ETOPO2/ETOPO2v2-2006/)。
验证模式使用的浮标观测数据包括每小时的风速、有效波高和有效周期。渤黄东海的浮标数量分别为2、6和4个,其中渤黄海的波浪浮标观测数据的时间段为2018年1月1日—2019年2月28日的若干个代表性事件过程,东海的波浪浮标观测数据的时间段为2019年1月1日—2020年12月31日的若干个代表性事件过程。
1.2 方法 1.2.1 模型简介和拖曳系数参数化方案在第三代海浪数值模式WAM[16]的基础上,NOAA/NCEP环境模拟中心海洋模拟小组开发了WAVEWATCH系列模型的第三个版本—WW3海浪数值模式[17]。WW3海浪数值模式是一个基于波作用量守恒,综合全面考虑了波浪浅水形变、海气温差、海流、地形等多种因素的相位平均波浪模型[18],修正了之前的版本误差,优化了物理和数值的处理方法、控制方程和程序结构等,极大地提高了模式模拟结果的准确性,已被广泛地应用于海洋能源、大浪的生成和传播、海洋气象、军事和海洋工程等领域[3, 19-21]。本文所采用的是Zieger等[22]在WW3模式中开发的ST6方案[18],细节可参见用户指南[23]。
基于WW3海浪数值模式(6.07版本)和ERA5风场资料,本文模拟了渤黄东海2004年1月1日—2022年12月31日期间的波浪场,模式输出时间分辨率为1 h,空间分辨率为0.05°×0.05°。
模式的初始场由JONSWAP-谱提供,最低频率为0.037 5 Hz,对谱频率做了35分离散化,各频段关系为fn+1=1.1×fn,波向共36个,分辨率为10°。
本文使用四种拖曳系数参数化方案来模拟渤黄东海的有效波高,并与浮标数据对比以选择最佳拖曳系数方案。拖曳系数参数化方案1为模式自带方案,由Hwang等[24]提出,只与海面10 m风速U10有关:
| $ {C_{\text{d}}} = \left\{ {\begin{array}{*{20}{l}} {\left( { - 0.016U_{10}^2 + 0.967{U_{10}} + 8.058} \right) \times {{10}^{ - 4}}} \\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{U_{10}} < 50.33{\text{m}}/{\text{s}}} \\ {{{\left( {u_*^c/{U_{10}}} \right)}^2}\quad {U_{10}}≥50.33{\text{m}}/{\text{s}}} \end{array}。} \right. $ | (1) |
式中uc*=0.026 m/s。
在大气中性稳定的条件下,拖曳系数与海面粗糙度(aerodynamic roughness length, z0)存在唯一对应关系:
| $ C_{\mathrm{d}}=\left[\frac{\mathrm{k}}{\ln \left(z/z_0\right)}\right]^2。$ | (2) |
式中:k=0.4为冯卡曼常数(von Kármán constant);z=10 m,为距离海面的海面高度。
拖曳系数参数化方案2、3和4为Edson等[25]提出的三个方案,分别与风速、波龄和波陡有关:
拖曳系数参数化方案2:
| $ z_0=0.11 \frac{v}{u_*}+\left(0.0017 U_{10}-0.005\right) \frac{u_*^2}{g} 。$ | (3) |
式中:v为空气运动学粘性系数(aerodynamic viscosity coefficient),取为v=1.48×10-5m2·s-1(在T=15 ℃);g为重力加速度,取为9.806 m/s2;u*为摩擦速度(friction velocity),与拖曳系数的关系为:
| $ u_*=U_{10} \sqrt{C_{\mathrm{d}}} 。$ | (4) |
拖曳系数参数化方案3:
| $ z_0=0.11 \frac{v}{u_*}+0.114\left(\frac{u_*}{c_{\mathrm{p}}}\right)^{0.622} \frac{u_*^2}{g} 。$ | (5) |
式中:u*/cp为波龄倒数;cp为谱峰速度(spectral peak velocity),可写为cp=gTp/2 π;Tp为谱峰周期(spectral peak period)。
拖曳系数参数化方案四:
| $ z_0=0.11 \frac{\nu}{u_*}+0.09 H_{\mathrm{s}}\left(\frac{u_*}{c_{\mathrm{p}}}\right)^2 \text { 。} $ | (6) |
式中Hs为有效波高(significant wave height)。
模拟区域设置为5.95°N—42.90°N,104.95°E—131.90°E,然后提取渤黄东海区域(23°N—42°N,117°E—131°E)来分析有效波高的时空变化。渤海和黄海的分界线辽东半岛南端老铁山角(121.2°E,38.8°N)与山东半岛北岸蓬莱角(120.9°E,37.8°N)的连线,黄海和东海的分界线——长江口北岸的启东角(121.9°E,31.7°N)与韩国济州岛西南角(126.2E°,33.2°N)的连线,在计算东海有效波高的区域平均时经度范围限制在127.5°E以内。由于东海的浅水区和深水区存在较大水动力环境差异,用100 m水深等值线作为东海沿海和东海外海的分界线。
由于本文主要聚焦有效波高在季节、年际以及长期尺度上的变化,我们将每个网格上的时间序列处理成月平均时间序列。
1.2.2 风场和模型精度的评估参数为了评估ERA5风速、模型输出有效波高和周期的精度,本研究所采用统计参数为:偏差(Bias)、均方根误差(root-mean-square error, RMSE)、相关系数(correlation coefficient, r),计算公式如下:
| $ \text { Bias }=\frac{1}{N} \sum\limits_{i=1}^N\left(Y_i-X_i\right) $ | (7) |
| $ R M S E=\sqrt{\frac{\sum\limits_{i=1}^N\left(Y_i-X_i\right)^2}{N}}, $ | (8) |
| $ r=\frac{\sum\limits_{i=1}^N\left(X_i-X_{\text {mean }}\right)\left(Y_i-Y_{\text {mean }}\right)}{\sqrt{\sum\limits_{i=1}^N\left(X_i-X_{\text {mean }}\right)^2 \sum\limits_{i=1}^N\left(Y_i-Y_{\text {mean }}\right)^2}} . $ | (9) |
式中:Xi为浮标观测值;Yi为模拟值;N为样本数量;Xmean和Ymean分别代表观测和模拟的平均值。
1.2.3 波高时间序列变化的量化指标标准差(standard deviation, Std)和变异系数(coefficient of variation, CV)通常被用来衡量数据的离散程度,本文利用标准差和变异系数量化有效波高(Hs)时间序列的变化强度:
| $ S t d=\sqrt{\frac{\sum\limits_{i=1}^N\left(X_i-X_{\text {mean }}\right)^2}{N-1}}, $ | (10) |
| $ C V=\left(S t d/X_{\text {mean }}\right) \times 100 \% \text { 。} $ | (11) |
式中:Xi为Hs月平均时间序列;Xmean为Hs月平均时间序列的平均值;N为Hs时间序列长度,其值为228。
有效波高和风速月平均时间序列在研究期间的长期趋势用以下步骤来计算:(1)从原始时间序列减去气候态月平均值得到月异常,其中某月份的气候态月平均值即为时间序列中该月的多年平均值[26],以1月为例,取2004—2022年1月的所有月平均数据相加再除以总年份(共计19 a),即得到1月的气候态月平均值;(2)通过最小二乘方法对月异常时间序列进行线性回归,斜率即为线性趋势,用F检验方法来验证线性趋势是否在95%置信水平上显著[26]。本文选择MATLAB“regress”函数用于执行F检验,该函数计算了F统计量并返回p值,如果p值小于所选择的显著性水平(本文取0.05),则认为线性回归模型是显著的。
有效波高(Hs)的季节变化占总方差比重的计算方法根据文献[27],每个网格点下的Hs月平均时间序列季节变化(seasonal variation, SV)的方差如下所示:
| $ S V=\frac{1}{n} \sum\nolimits_{i=1}^n\left(H_{\mathrm{s}_{-} \text {season_i }}-H_{\mathrm{s}_{-} \text {mean }}\right)^2, $ | (12) |
| $ H_{\mathrm{s}_{\text {_mean }}}=\frac{1}{n} \sum\nolimits_{i=1}^n H_{\mathrm{s}_{\text {seseson_i }}} 。$ | (13) |
式中:Hs_seseson_i表示Hs气候态月平均时间序列;Hs_mean代表Hs气候态月平均序列的平均值;n为Hs时间序列长度,其值为228。
每个网格点下的Hs月平均序列的总方差(total variance, TV)如下所示:
| $ T V=\frac{1}{n} \sum\nolimits_{i=1}^n\left(H_{s_{-} i}-H_{\mathrm{s}_{-} \operatorname{mean}}\right)^2, $ | (14) |
| $ H_{\mathrm{s}_{-}\operatorname{mean}}=\frac{1}{n} \sum\nolimits_{i=1}^n H_{\mathrm{s}_{-} i \circ} $ | (15) |
式中:Hs_i表示Hs月平均时间序列;Hs_mean代表Hs月平均时间序列的平均值。
因此,SV/TV×100%,即表示Hs季节变化强度解释的总方差比重。
2 结果与讨论 2.1 模型验证为了验证ERA5风场在渤黄东海的适用性,将ERA5风场数据与浮标观测风速进行对比。如图 2所示,ERA5风速与浮标观测风速一致性较好,共计129 488个样本点,相关系数高达0.90,均方根误差为1.47 m/s。ERA5风速系统偏差为-0.07 m/s,即存在系统的略微低估,大风情况下的风速低估更为明显,这意味着使用ERA5风场模拟台风等特殊海况可能存在较大误差。本文主要聚焦有效波高月平均时间序列的变化,而大风速低估效应对趋势分析影响较小,因此可以将ERA5风场作为模式的合理驱动。
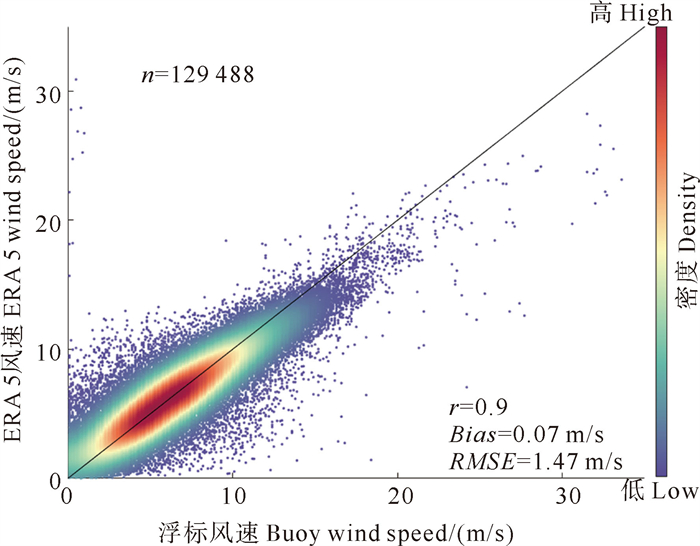
|
图 2 ERA5风速与浮标观测的散点对比图 Fig. 2 Scatter comparison between ERA5 wind speed and buoy observations |
4种拖曳系数参数化方案模拟有效波高的结果和浮标观测的散点对比如图 3所示,共计19 448个配对点。采用拖曳系数参数化方案一的模式输出有效波高的模拟值与浮标观测值非常接近,绝大部分点均位于1∶1线附近,相关系数高达0.96,均方根误差为0.34 m,偏差为-0.15 m。拖曳系数参数化方案1、2、4的模式模拟值与实测值的相关系数也为0.96,但系统低估为拖曳系数参数化方案1的1.8倍以上,均方根误差为拖曳系数参数化方案一的1.2倍以上。因此,本研究将采用拖曳系数参数化方案1来模拟渤黄东海2004—2022年期间的有效波高时空场。
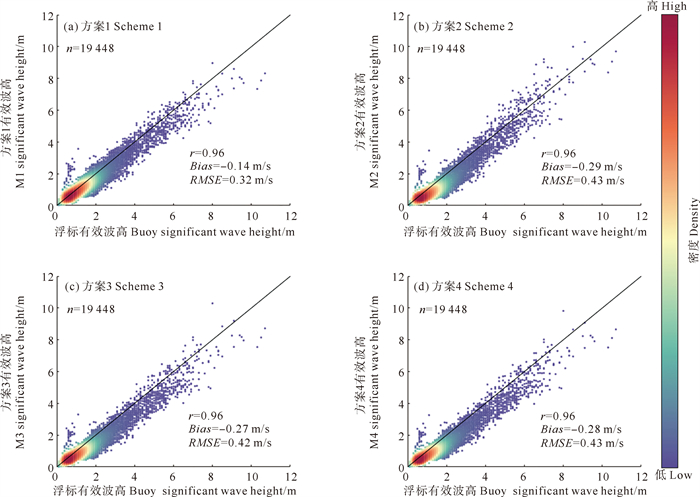
|
图 3 模式输出有效波高与浮标观测的散点对比图 Fig. 3 Scatter comparison between the model output significant wave height output and buoy observations |
在此基础上,本文将参数化方案1输出的一阶矩平均周期(T01)、二阶矩平均周期(T02)分别与浮标观测的有效周期(significant wave period, Ts)进行比较,从而更全面评估参数化方案1的波浪模拟精度。前人根据观测、实验等发现了浮标观测的Ts和模拟输出平均周期之间存在一定的系统偏差,通过线性矫正后的模式平均周期与观测Ts的一致性更好[28-29]。
因此,本文对参数化方案1输出的T01、T02分别进行类似的线性矫正:(1)基于过原点的线性拟合,计算T01、T02和Ts之间的经验关系分别为Ts=1.457 6×T01、Ts=1.640 7×T02; (2)基于以上经验关系,对T01、T02分别进行线性矫正,再与浮标观测的有效周期进行散点对比(见图 4),共计35 963个配对点。线性矫正后T01、T02的系统低估明显减小,且与浮标观测的Ts相关性较好,相关系数分别达0.69和0.64,均方根误差分别为1.4和1.5 s。总体上看,T01与浮标观测的Ts更为接近。
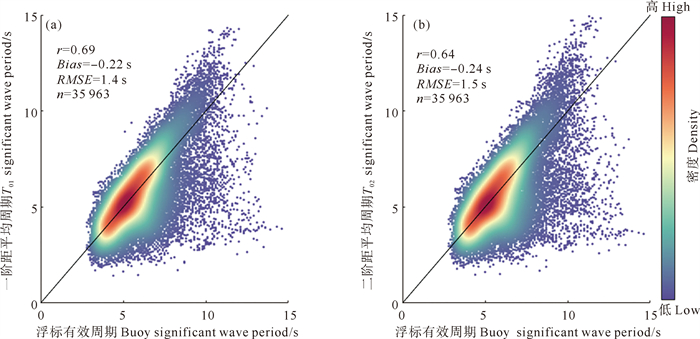
|
图 4 参数化方案1模式输出T01(a)、T02(b)与浮标观测有效周期的散点对比图 Fig. 4 Scatter comparison between the model output T01 (a), T02 (b) of parameterized scheme 1 and buoy observation Ts |
表 1为利用拖曳系数参数化方案1模拟的有效波高与12个浮标对比统计结果。12个浮标对比结果均呈现两者有效波高有良好的相关性,相关系数均在0.90以上,同时模式输出有效波高均存在略微系统性低估(Bias < 0)。黄海浮标3处于水深10 m以内的浅水区,低估最明显,相对偏差达-35.04%,相对均方根误差达48.59%,这意味着WW3模型输出有效波高在岸线附近的浅水区存在较大的不确定性,10 m水深以下的模拟结果需谨慎对待,原因可能来自于WW3模式在浅水区的自身局限性以及岸线附近输入风场的精度较低。除黄海浮标3外,相比于渤黄海区域,模式输出有效波高在东海的系统低估更为明显,相对偏差在-10%以下。东海浮标4处于水深近200 m的位置处,模式输出低估较严重,相对偏差达-17.53%,其原因可能是低估了外海传入的涌浪。尽管东海外海缺乏浮标数据验证模拟结果,但WW3模拟深水波的结果被广泛认为可信[7]。
|
|
表 1 有效波高逐浮标对比统计结果 Table 1 Statistical comparison results of significant wave height for each buoy |
对模式计算的2004—2022年期间的有效波高以及ERA5风速的时间序列进行多年平均,绘制有效波高、风速气候态年平均分布如图 5所示。总体来看,有效波高气候态年平均值在0.1~1.6 m之间,从北向南以及从浅水区到深水区逐渐递增,这些现象与前人的研究一致[7, 30-31]。低值(小于0.4 m)在沿岸区域清晰可见,而高值(大于1.4 m)出现在台湾海峡以及东海的外海区域。就海区而言,渤海的有效波高值主要集中在0.4~0.8 m之间,黄海的有效波高值主要集中在0.6~1.2 m之间,东海的有效波高值主要集中1~1.4 m之间。在渤黄海区域,水深与有效波高之间存在强正相关(r=0.84, p < 0.01)。在计算相关系数时,p值小于0.01代表相关系数在99%置信水平上显著。而在东海区域由于水深普遍较大,海浪受到海底的影响较小,有效波高与水深相关性较弱。除去东海外海,风速和有效波高的多年平均空间分布非常相似,两者存在强正相关(r=0.88, p < 0.01), 台湾海峡的强风速决定了该区域有效波高的高值。但对于东海外海,两者的空间分布存在一定差异,这表明在东海外海的波浪场,外海传入涌浪的贡献也不可忽略。
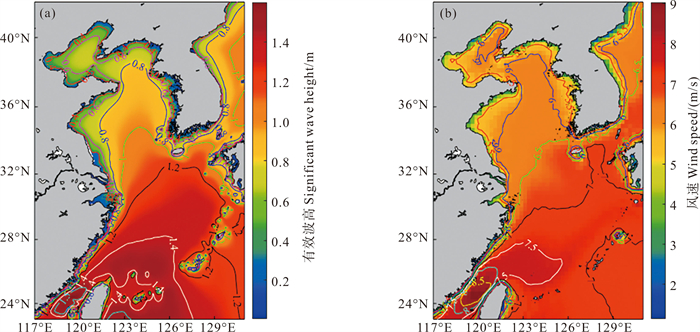
|
图 5 渤黄东海有效波高(a)、风速(b)气候态年平均 Fig. 5 Climatological annual mean significant wave height (a) and wind speed (b) over Bohai, Yellow and East China Seas |
通过计算标准差(见图 6(a))和变异系数(见图 6(b))来衡量有效波高月平均时间序列的总体变化强度,包括季节变化、年际变化及长期趋势等。对于渤黄东海的绝大多数海域,季节变化占总方差的比重达50%以上(见图 6(c)),即季节变化主导了有效波高的总体变化强度。在台湾海峡、渤海、北黄海、黄海东部以及日本海,季节变化占总体变率强度的占比达70%以上,而在黄海西部浅水区、对马海峡以及琉球群岛西南方向海域,季节变化占比相对较弱。标准差和变异系数最大的区域均位于台湾海峡,在该区域冬季风的强度远大于夏季风,这就导致了台湾海峡有效波高强烈的季节变化。如图 5(a)所示,标准差的空间分布呈现与多年平均图非常相似的特征,即从浅水区到深水区递增,且两者相关系数高达0.85(p < 0.01)。与标准差空间分布不同,变异系数呈现更加均匀的空间分布,在26°N以上,渤黄东海的有效波高变异系数多集中在10%~30%之间。
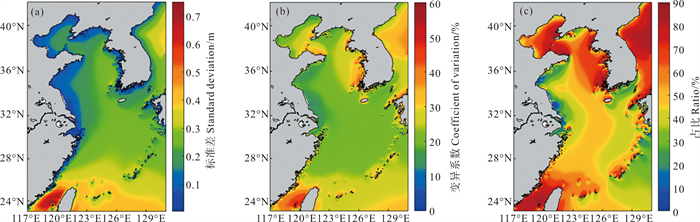
|
((a)标准差;(b)变异系数;(c)季节变化占总方差的比重。(a) Standard deviation; (b) Coefficient of variation; (c) Explained total variance by seasonal variation.) 图 6 有效波高月平均时间序列的总体变化强度 Fig. 6 Overall variation intensity of the monthly mean time series of significant wave height |
根据风速时间序列及有效波高时间序列,绘制2004—2022年期间风速以及有效波高气候态月平均分布,分别如图 7和8所示。渤黄东海处于典型的东亚季风区,冬季盛行强偏北风,渤海平均风速5~7 m/s,黄海平均风速6~8 m/s,东海平均风速8~10 m/s;夏季以弱偏南风为主,渤海平均风速4~5 m/s,黄海平均风速4~6 m/s,东海平均风速5~7 m/s。季风的变化主导该区域有效波高季节变化[11, 32]。
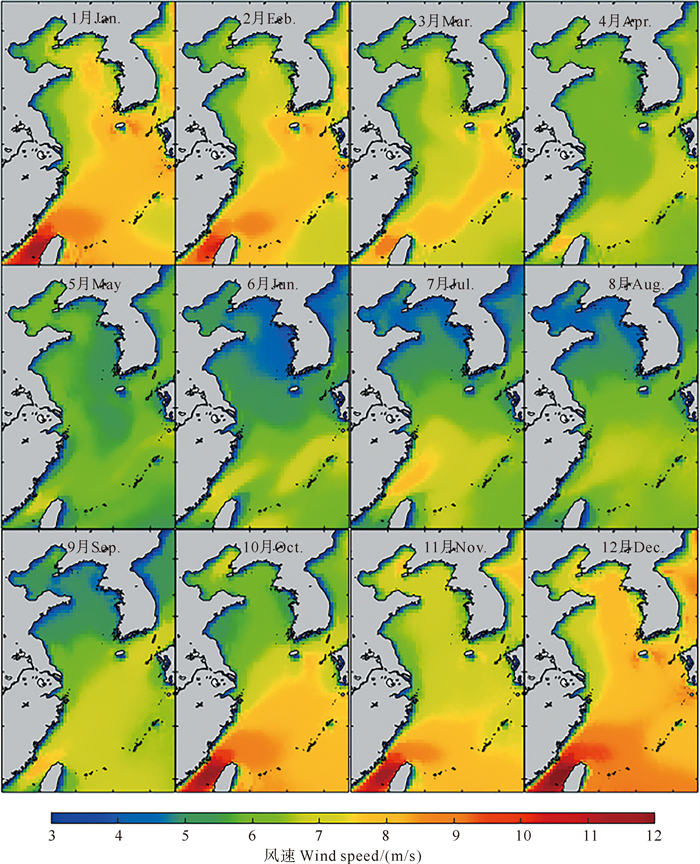
|
图 7 风速气候态月平均的空间分布 Fig. 7 Spatial distribution of climatological monthly mean wind speed |

|
图 8 有效波高气候态月平均分布 Fig. 8 Spatial distribution of climatological monthly mean significant wave height |
秋季开始,几乎整个渤黄东海有效波高值开始显著增大,随着强北风的盛行,冬季时有效波高达到最大值。时间上看,秋冬季节有效波高月平均值相对较大,春夏季节有效波高月平均值相对较小;空间上看,有效波高随着离岸距离的增大而增大,从北向南递增。
有效波高气候态月平均的最大值出现在冬季台湾海峡,达到2.5 m以上。ERA5风速气候态分布显示,在台湾海峡,冬季风速月平均值可达11 m/s以上,导致该区域有效波高值远大于其他海域。在春夏季,随着季风强度的减弱,大部分海域的海浪分布受到来自涌浪的较强影响[11, 30], 因此在春夏季节,波浪和风速空间分布之间的相关性相对变弱。
虽然前人的研究总体上已较好的阐释了渤黄东海有效波高季节变化趋势[7, 15, 30-32],但在逐网格尺度上有效波高气候态月平均序列达到最大值和最小值的月份还不确定。如图 9(a)所示,黄海和东海有效波高主要在12月达到最大值,而渤海有效波高主要在11月达到最大值。在渤海的三个海湾以及山东半岛,部分网格在春季出现最大值,浙闽沿岸及琉球群岛西南侧海域有效波高最大值主要出现在11月。有效波高的最小值出现的月份如图 9(b)所示,可以看出:除台湾海峡和长江口外,整个东海几乎都在5月出现最小值,南黄海在6月出现最小值,其他海域均在夏季或秋初出现最小值。
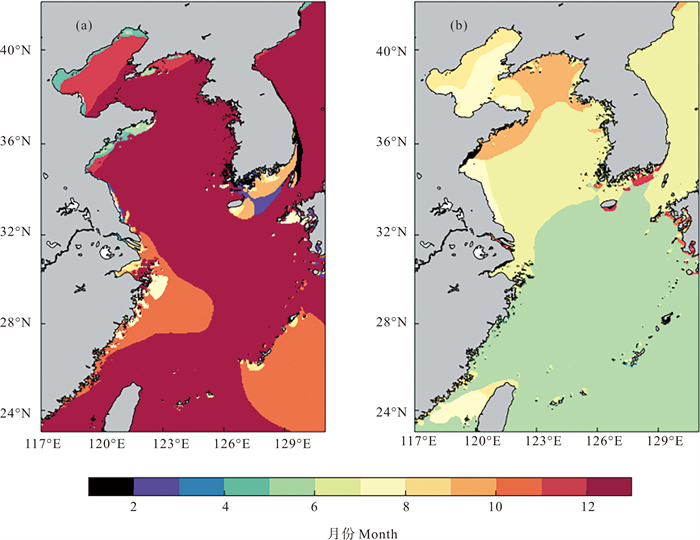
|
图 9 有效波高气候态月平均最大值月份(a)和最小值月份(b)分布 Fig. 9 Distribution of the maximum month (a) and minimum month (b) of the climatological monthly mean significant wave height |
通过有效波高年平均时间序列(去季节变化)的标准差和变异系数,可以衡量有效波高年际变化强度的空间分布[8, 33]。如图 10(a)所示,相比于季节变化强度,有效波高年际变化强度较弱,绝大多数区域的标准差值处在0.01~0.09 m之间。台湾海峡海域有效波高年际变率较明显,标准差达0.07 m以上。与总体变化标准差相同,有效波高年际变化标准差与有效波高多年平均的相关系数也达0.85(p < 0.01)。然而,衡量有效波高年际变化相对强度的变异系数图呈现较大的差异(见图 10(b)),黄海的年际变化相对强度明显强于渤海和东海,绝大多数区域的变异系数达4.5%以上,而渤海和东海主要海域的变异系数在4.5%以下。与月平均时间序列变化不同,标准差和变异系数均呈现有效波高年际变化强度最大的区域位于琉球群岛东南侧海域。
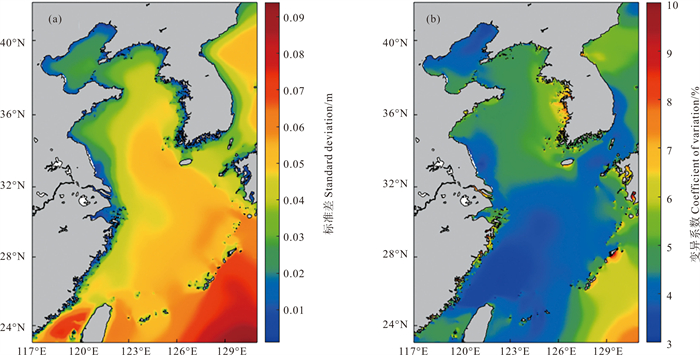
|
((a)标准差; (b)变异系数。(a) Standarddeviation; (b) Coefficientofvariation.) 图 10 有效波高年际变化强度空间分布 Fig. 10 Spatial distribution of interannual variation intensity of significant wave height |
2004—2022年期间,各海域有效波高和风速区域平均的时间序列年际变化如图 11所示,四个海区有效波高和风速年平均时间序列均未呈现统计学上显著的线性趋势。在年际尺度上,渤黄海有效波高年平均值均在2010年达到最大值,东海有效波高年平均则在2012年达到最大值;渤海、黄海、东海有效波高年平均最小值分别发生在2007、2015和2008年。在渤海、黄海以及东海沿海,有效波高时间序列变化与风速高度协同,相关系数分别高达0.96、0.98、0.92,这意味着这些海域的有效波高年际变化由风速年际变化所主导。在东海外海,有效波高年际变化与风速相关性明显减弱(r=0.69,p < 0.01), 原因可归结于来自外部波浪的协同影响相对较强。
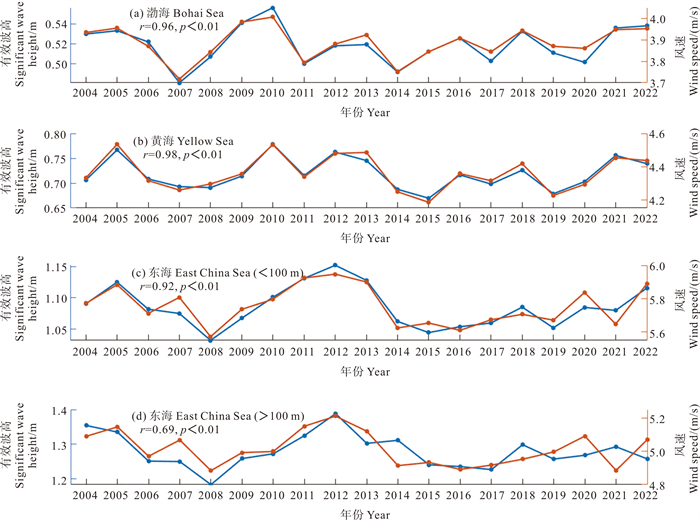
|
(图中蓝色和橙色的线段分别表示有效波高和风速。The blue and orange lines in the figure represent the significant wave height and wind speed, respectively.) 图 11 2004—2022年期间有效波高和风速年平均时间序列变化 Fig. 11 Annual mean time series changes of significant wave height and wind speed for the period of 2004—2022 |
已有研究证明,中国近海的风速和波高与ENSO主要呈现负相关,ENSO的具体影响存在一定的季节和区域差异[1, 11, 13, 34]。但在近二十年,ENSO在年际尺度上对整个渤黄东海风场和有效波高的定量影响还有待评估。
为量化ENSO在年际尺度上对风场和有效波高的影响,13个月的滑动平均应用于风速异常和有效波高异常,以移除剩余的季节内信号[8],最开始和最末6个月数据在计算相关系数之前被排除。在图 12中,我们逐网格计算了2004—2022年期间,ONI与风速异常和有效波高异常的相关系数,在相关系数的计算过程中仅纳入绝对值超过0.5 ℃的ONI序列。如图 12所示,东亚季风和有效波高的年际变化与ENSO有很好相关性,除了渤海和东海外海,ONI指数与风速异常和有效波高异常呈现显著的负相关,即季风强度在厄尔尼诺年相对较弱,有效波高异常低;季风强度在拉尼娜年相对较强,有效波高异常高。无论是风速异常还是有效波高异常,负相关最强的区域位于台湾海峡,最高相关系数分别达-0.72和-0.77。另外,黄海东部的大面积水域也发现较强的相关性。在渤海北部,ONI与风速异常和有效波高异常呈现弱正相关性,而在东海外海区域,ONI与风速异常和有效波高异常相关性均不显著, 这些区域差异的原因还有待后续研究。
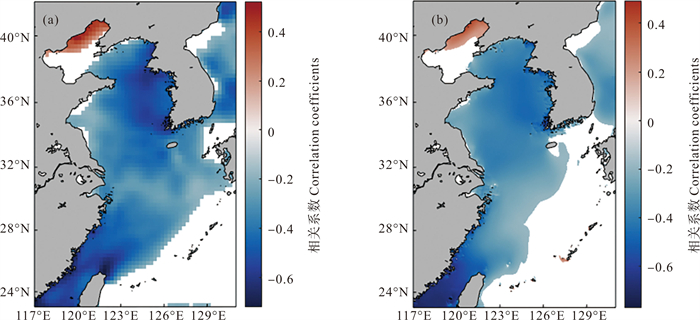
|
(颜色图仅显示相关系数在95%置信水平上显著的网格。Only the correlation coefficients, which are significant at the 95% confidence level, are shown in colour.) 图 12 ONI与风速异常(a)和有效波高异常(b)在年际尺度上相关系数的空间分布 Fig. 12 Spatial distribution of correlation coefficients between ONI and wind speed anomalies (a) and significant wave height anomalies (b) at the interannual timescale |
为了探究有效波高长期趋势在空间尺度上的差异,逐网格计算2004—2022年期间有效波高和风速时间序列的线性趋势。如图 13所示,除了台湾岛东侧,整个渤黄东海有效波高无显著变化趋势。相对于东海外海,沿海区域的有效波高长期趋势更弱。台湾岛东侧有效波高的长期趋势较整个渤黄东海非常显著,趋势范围约在-0.006 9~-0.002 3 m/a,区域平均的下降强度为0.006 2 m/a。基于多源卫星融合数据,Young等[6]报告在北太平洋的大多数地区,其中包括渤黄东海,1985—2008年期间有效波高月平均时间序列以微弱的线性负趋势为主,但无统计学上的显著趋势。在过去的近二十年时间,渤黄东海有效波高的长期趋势仍不显著。
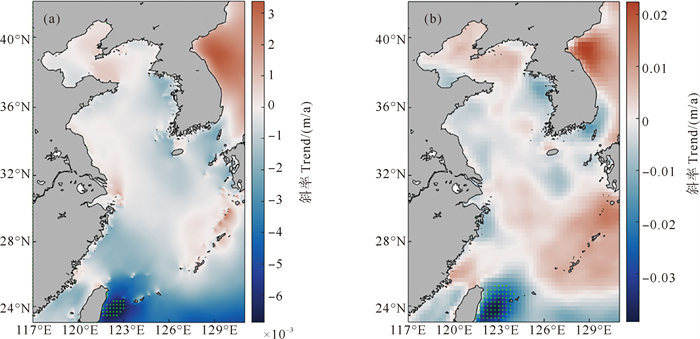
|
(绿点代表在95%置信水平上显著的趋势。The green dots represent trends that are significant at the 95% confidence level.) 图 13 2004—2022年期间有效波高(a)和风速(b)的长期趋势 Fig. 13 Long-term trends for significant wave height (a) and wind speed (b) during 2004—2022 |
对于风力产生的波浪,有效波高近似与风速成正比,风速的变化趋势直接影响有效波高的变化趋势[6, 11]。因此,尽管有效波高变化趋势还受到涌浪的影响,但总体上看渤黄东海区域有效波高长期趋势与风速的长期趋势吻合性较好。风速下降趋势最强的海域也位于台湾岛东侧,区域平均的下降强度达0.024 1 (m/s)/a。同时,该区域两者的显著趋势在网格尺度上吻合,因此,可以推断台湾岛东侧有效波高显著下降的趋势是由于风速降低导致的。
从图 14可以看到,有效波高的长期趋势存在明显的季节差异。春季,除渤海北部海域,整个渤黄东海的有效波高呈略微下降趋势,统计学上显著区域主要位于黄海东部、台湾岛北部和琉球群岛西北部,强度在0.01 m/a以下。夏季,渤黄海无明显变化趋势,有效波高显著下降的区域位于台湾海峡和台湾岛东侧,其中最强趋势位于台湾岛,强度范围约在0.01~0.02 m/a。秋季,在25.5°N以北的渤黄东海区域,有效波高呈现略微正趋势,但在统计学上无显著意义。冬季以32°N为分界线,北部正趋势和南部负趋势呈现异相的格局,而显著区域仅位于渤海湾和莱州湾。同时,本文对比有效波高和风速在四个季节的线性趋势,两者在网格尺度上吻合较好,但风速趋势的显著变化范围明显更大。风速变化趋势最强的区域位于夏季台湾岛东侧,最大强度接近0.1 (m/s)/a,因此,台湾岛东侧海域的有效波高下降趋势是由夏季风强度的下降所主导。
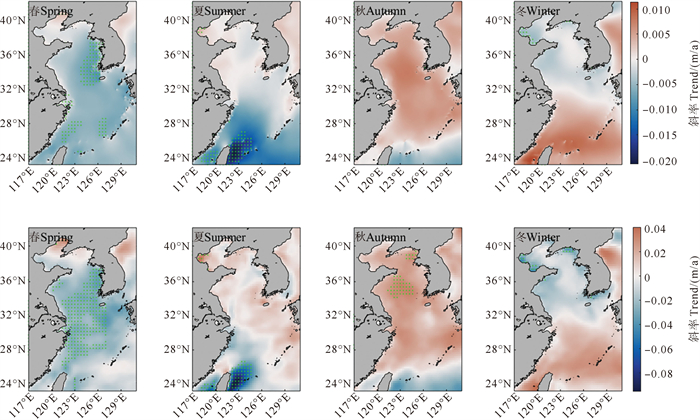
|
(绿点代表在95%置信水平上显著的趋势。The green dots represent trends that are significant at the 95% confidence level.) 图 14 2004—2022年期间有效波高(上)和风速(下)在四个季节的线性趋势 Fig. 14 Linear trends of significant wave height (top) and wind speed (bottom) in four seasons during 2004—2022 |
基于19 a(2004—2022年)风场资料和WW3模式输出结果,本文全面评估了2004—2022年期间渤黄东海有效波高多尺度时间变化及其相关驱动机制,总结如下:
(1) 基于Hwang等[24]提出的拖曳系数参数化方案,WW3模式输出有效波高(r=0.96, Bias=-0.15 m, RMSE=0.34 m)、一阶矩平均周期(r=0.69, Bias=-0.22 s, RMSE=1.4 s)、二阶矩平均周期(r=0.64, Bias=-0.24 s, RMSE=1.5 s)与浮标观测结果存在良好的一致性。相比其它拖曳系数参数化方案,本文所采用的拖曳系数参数化方案明显减小了模拟波高的系统低估。
(2) 有效波高气候态年平均分布呈现从北向南以及从浅水区到深水区递增趋势,在渤黄海区域,底部摩擦导致水深与有效波高之间存在强正相关(r=0.84)。
(3) 有效波高总体变化强度由季节变化所主导,而年际变化和长期趋势强度明显弱于季节变化强度,总体变化最强的区域出现在台湾海峡。巧合的是,有效波高月平均和年平均时间序列标准差与有效波高气候态年平均分布的相关系数均为0.85。
(4) 就季节变化而言,有效波高气候态月平均值在秋冬季节大,春夏季节小,最大值出现在12月台湾海峡,达到2.5 m以上。另外,有效波高气候态月平均在网格尺度上达到最大值和最小值的月份被阐明。
(5) 有效波高在年际时间尺度上的分析表明:黄海有效波高的年际变化相对强度明显强于渤海和东海,年际变化最强的区域位于琉球群岛西南侧海域;有效波高与风速的年际变化高度相关,且两者在黄海和东海区域与ONI指数呈显著负相关,负相关最强的区域位于台湾海峡。
(6) 从长期趋势看,对于渤黄东海,有效波高仅在台湾岛东侧出现显著变化趋势(-0.006 9~-0.002 3 m/a),原因在于该区域夏季风强度的明显减弱。
本文基于19 a(2004—2022年)风场资料和WW3模式输出的结果,围绕渤黄东海波高的多尺度时空变化展开较为全面的研究,但仍存在不足,未来将在以下两个方面开展进一步的研究工作:(1)本文未涉及有效波高在季节内时间尺度的研究,季节内尺度变化在波浪场也发挥重要作用,拟通过本文的模拟结果分析渤黄东海波高在季节内时间尺度的变化;(2)本文未涉及对极端海浪的研究, 未来将对渤黄东海的极端海浪的多尺度时空变化展开研究。
| [1] |
Mirzaei A, Tangang F, Juneng L, et al. Wave climate simulation for southern region of the South China Sea[J]. Ocean Dynamics, 2013, 63: 961-977. DOI:10.1007/s10236-013-0640-2 (  0) 0) |
| [2] |
He H, Xu Y. Wind-wave hindcast in the Yellow Sea and the Bohai Sea from the year 1988 to 2002[J]. Actaoceanologica Sinica, 2016, 35: 46-53. DOI:10.1007/s13131-015-0786-5 (  0) 0) |
| [3] |
郑崇伟, 李训强. 基于WAVEWATCH-Ⅲ模式的近22年中国海波浪能资源评估[J]. 中国海洋大学学报(自然科学版), 2011, 41(11): 5-12. Zheng C W, Li X Q. Wave energy resources assessment in the China Sea during the last 22 years by using WAVEWATCH-Ⅲ wave model[J]. Periodical of Ocean University of China, 2011, 41(11): 5-12. DOI:10.16441/j.cnki.hdxb.2011.11.002 (  0) 0) |
| [4] |
Yang S, Zhuang J, Xi L, et al. Long-term variation of the wave power density in the South China Sea over the past 28 years[J]. IEEE Access, 2020, 8: 128498-128508. DOI:10.1109/ACCESS.2020.2982853 (  0) 0) |
| [5] |
Carter D J T, Draper L. Has the north-east Atlantic become rougher?[J]. Nature, 1988, 332(6164): 494-494. (  0) 0) |
| [6] |
Young I R, Zieger S, Babanin A V. Global trends in wind speed and wave height[J]. Science, 2011, 332(6028): 451-455. DOI:10.1126/science.1197219 (  0) 0) |
| [7] |
Li J, Chen Y, Pan S, et al. Estimation of mean and extreme waves in the East China Seas[J]. Applied Ocean Research, 2016, 56: 35-47. DOI:10.1016/j.apor.2016.01.005 (  0) 0) |
| [8] |
Zhai F, Li P, Song D. Interannual wave height variability in the Yellow Sea[J]. Journal of Oceanography, 2019, 75: 235-256. DOI:10.1007/s10872-018-0496-7 (  0) 0) |
| [9] |
Dong S, Gong Y, Wang Z. Long-term variations of wind and wave conditions in the Taiwan Strait[J]. Regional Studies in Marine Science, 2020, 36: 101256. DOI:10.1016/j.rsma.2020.101256 (  0) 0) |
| [10] |
Zheng C, Li X, Azorin-Molina C, et al. Global trends in oceanic wind speed, wind-sea, swell, and mixed wave heights[J]. Applied Energy, 2022, 321: 119327. DOI:10.1016/j.apenergy.2022.119327 (  0) 0) |
| [11] |
Wang J, Dong C, He Y. Wave climatological analysis in the East China Sea[J]. Continental Shelf Research, 2016, 120: 26-40. DOI:10.1016/j.csr.2016.03.010 (  0) 0) |
| [12] |
Hersbach H, Bell B, Berrisford P, et al. The ERA5 global reanalysis[J]. Quarterly Journal of the Royal Meteorological Society, 2020, 146(730): 1999-2049. (  0) 0) |
| [13] |
Zheng C W, Li C Y. Variation of the wave energy and significant wave height in the China Sea and adjacent waters[J]. Renewable and Sustainable Energy Reviews, 2015, 43: 381-387. DOI:10.1016/j.rser.2014.11.001 (  0) 0) |
| [14] |
Liang B, Liu X, Li H, et al. Wave climate hindcasts for the Bohai sea, Yellow sea, and East China Sea[J]. Journal of Coastal Research, 2016, 32(1): 172-180. DOI:10.2112/JCOASTRES-D-14-00017.1 (  0) 0) |
| [15] |
Yang S, Fan L, Duan S, et al. Long-term assessment of wave energy in the China Sea using 30-year hindcast data[J]. Energy Exploration & Exploitation, 2020, 38(1): 37-56. DOI:10.1177/0144598719878777 (  0) 0) |
| [16] |
WAMDI Group. The WAM model-a third generation ocean wave prediction model[J]. Journal of Physical Ocean Ography, 1988, 18: 1775-1810. (  0) 0) |
| [17] |
Tolman H L. User Manual and System Documentation of WAVEWATCH Ⅲ Version 1.18[R]. Washington DC: National Oceanic and Atmospheric Administration, 1999: 110.
(  0) 0) |
| [18] |
Beyramzadeh M, Siadatmousavi S M, Derkani M H. Calibration and skill assessment of two input and dissipation parameterizations in WAVEWATCH-Ⅲ model forced with ERA5 winds with application to Persian Gulf and Gulf of Oman[J]. Ocean Engineering, 2021, 219: 108445. DOI:10.1016/j.oceaneng.2020.108445 (  0) 0) |
| [19] |
郑崇伟, 庄卉, 贾本凯, 等. 基于WW3模式的一次台风浪过程中掠海飞行器的击水概率分析[J]. 海洋学研究, 2013, 31(3): 36-40. Zheng C W, Zhuang H, Jia B K, et al. Analysis of ditching probabilitycaused bytyphoon wave using WAVEWATCH-Ⅲ wave model[J]. Journal of Marine Sciences, 2013, 31(3): 36-40. (  0) 0) |
| [20] |
郑崇伟, 林刚, 邵龙潭. 孟加拉湾一次热带气旋过程的海浪场模拟分析[J]. 海洋学研究, 2013, 31(4): 26-31. Zheng C W, Lin G, Shao L T. Analysis of wave field caused by tropical cyclone in the Bay of Bengal[J]. Journal of Marine Sciences, 2013, 31(4): 26-31. (  0) 0) |
| [21] |
郑崇伟, 游小宝, 陈晓斌, 等. 西北太平洋海域风浪、涌浪、混合浪波浪能资源特征[J]. 气象科学, 2014, 34(4): 408-413. Zheng C W, You X B, Chen X B, et al. Characteristics analysis on wave energy over Northwest Pacific ocean in the last 44 years[J]. Journal of the Meteorological Sciences, 2014, 34(4): 408-413. DOI:10.3969/2013jms.0062 (  0) 0) |
| [22] |
Zieger S, Babanin A V, Rogers W E, et al. Observation-based source terms in the third-generation wave model WAVEWATCH[J]. Ocean Modelling, 2015, 96: 2-25. DOI:10.1016/j.ocemod.2015.07.014 (  0) 0) |
| [23] |
Tolman H L, Abdolali A, Oceanic N, et al. User Manual and System Documentation of WAVEWATCH Ⅲ (R) Version 6.07[R]. [s. l. ]: Technical Note 333, NOAA/NWS/NCEP/MMAB333, 2019: 465.
(  0) 0) |
| [24] |
Hwang P A. A note on the ocean surface roughness spectrum[J]. Journal of Atmospheric and Oceanic Technology, 2011, 28(3): 436-443. DOI:10.1175/2010JTECHO812.1 (  0) 0) |
| [25] |
Edson J B, Jampana V, Weller R A, et al. On the exchange of momentum over the open ocean[J]. Journal of Physical Oceanography, 2013, 43(8): 1589-1610. DOI:10.1175/JPO-D-12-0173.1 (  0) 0) |
| [26] |
Guo J, Nie Y, Sun B, et al. Remote sensing of transparency in the China seas from the ESA-OC-CCI data[J]. Estuarine, Coastal and Shelf Science, 2022, 264: 107693. DOI:10.1016/j.ecss.2021.107693 (  0) 0) |
| [27] |
Lim H G, Dunne J P, Stock C A, et al. Attribution and predictability of climate-driven variability in global ocean color[J]. Journal of Geophysical Research: Oceans, 2022, 127(10): e2022JC019121. DOI:10.1029/2022JC019121 (  0) 0) |
| [28] |
Toba Y, Iida N, Kawamura H, et al. Wave dependence of sea-surface wind stress[J]. Journal of Physical Oceanography, 1990, 20(5): 705-721. (  0) 0) |
| [29] |
李瑞丽. 海浪周期关系的研究[J]. 海洋湖沼通报, 2007(2): 13-18. Li R L. On the relationships of various wind wave periods[J]. Transactions of Oceanology and Limnology, 2007(2): 13-18. DOI:10.3969/j.issn.1003-6482.2007.02.003 (  0) 0) |
| [30] |
Zheng C W, Zhou L, Jia B K, et al. Wave characteristic analysis and wave energy resource evaluation in the China Sea[J]. Journal of Renewable and Sustainable Energy, 2014, 6(4). DOI:10.1063/1.4885842 (  0) 0) |
| [31] |
Shi J, Zheng J, Zhang C, et al. A 39-year high resolution wave hindcast for the Chinese coast: Model validation and wave climate analysis[J]. Ocean Engineering, 2019, 183: 224-235. DOI:10.1016/j.oceaneng.2019.04.084 (  0) 0) |
| [32] |
谢冬梅, 陈永平, 张长宽. 东中国海波浪分布特征研究[J]. 水运工程, 2015(2): 189-196. Xie D M, Chen Y P, Zhang C K. On wave distribution of the East China Sea[J]. Port & Wateway Engineering, 2015(2): 189-196. DOI:10.16233/j.cnki.issn1002-4972.2015.02.036 (  0) 0) |
| [33] |
Guo J, Zhao Z, Cao R, et al. Regional to global assessments of ocean transparency dynamics from 1997 to 2019[J]. Progress in Oceanography, 2023, 219: 103165. DOI:10.1016/j.pocean.2023.103165 (  0) 0) |
| [34] |
Luang-on J, Ishizaka J, Buranapratheprat A, et al. Seasonal and interannual variations of MODIS Aqua chlorophyll-a (2003-2017) in the Upper Gulf of Thailand influenced by Asian monsoons[J]. Journal of Oceanography, 2022, 78(4): 209-228. DOI:10.1007/s10872-021-00625-2 (  0) 0) |
2. National Marine Environmental Forecasting Center, Ministry of Natural Resources, Beijing 100081, China
 2025, Vol. 55
2025, Vol. 55


