2. 青岛海洋气象研究院,山东 青岛 266034;
3. 中国海洋大学三亚海洋研究院,海南 三亚 572025;
4. 中国海洋大学深海圈层与地球系统前沿科学中心 物理海洋教育部重点实验室,山东 青岛 266100
近惯性内波是频率在科氏频率f附近的内波,以科氏力为该内波的恢复力,是全球海洋中最为常见的内波之一。在大洋中,近惯性内波占据了海洋内波谱一半以上的能量,贡献了海洋中绝大部分垂向剪切[1-2]。上层海洋近惯性内波的有效生成来源主要是海表面瞬变的风场,在中高纬度的海洋主要依靠大气风暴轴(Storm track)的能量输入,而在低纬度海区主要依靠热带气旋的能量输入。据观测和模式估计,大气强迫通过近惯性频带为全球上层海洋带来(0.3~1.5)×109 kW的能量输入[3-5],其中近30%的风生近惯性能量可以穿透混合层向海洋深层传播[6],最终在海洋内部耗散,是大气强迫驱动深层海洋混合的重要渠道之一。
近惯性内波向深层传播这一过程十分复杂,除了自身频散效应外,还受到其他海洋背景变率的显著调制。在传播过程中,波动场会被背景场的平流、折射和拉伸所调制[7-8]。非均匀背景流场在海洋中引起了背景涡度场的空间梯度,作用到近惯性内波上造成波动场空间上的位相差异,最终形成对波的折射,改变波的原有传播路径[9-10]。如,行星涡度f的向南衰减(β效应)可导致近惯性内波的南北传播差异,促使近惯性内波向低纬地区远距离传播;特别的,在海洋边界流、中尺度涡活跃的区域,相对涡度场ζ的变化所产生的涡度梯度比β效应强1~2个数量级,从而会更有效地影响近惯性内波的传播。
基于尺度分离方法,前人经理论推导发现,在相对涡度场ζ中传播的近惯性内波,其科氏频率f等效于feff(feff≈f+ζ/2,称有效科氏频率)。在此作用下,负相对涡度中(ζ < 0)生成的近惯性能量无法传播出该区域,因此在负涡度中聚集,而在正涡度区则正好相反,Kunze[9]形象地将近惯性内波无法传播出负涡度区域这一过程称为“波捕陷(Wave trap)”过程。波捕陷理论的普适性在于:海洋中充满多种正负涡度的偶极子系统,如经常成对出现的“冷暖涡对”,再如海洋锋面两侧由于流速水平剪切形成的正、负涡度,多个观测和数值模拟研究都验证了波捕陷的观点。Whitt和Thomas[11]通过射线追踪和数值模拟证明了近惯性内波会在异常低频区域被捕获。Jeon等[12],Rainville和Pinkel[13],Park等[14]利用观测和数值模拟发现,沿黑潮路径反气旋侧的负相对涡度可以捕获近惯性内波;而在气旋侧,则存在一个正的相对涡度屏障,阻碍近惯性内波的传播。
大尺度环流的平流作用可以使近惯性内波远离它们的源地。Jeon等[12]认为台风引起的近惯性内波可以逆β效应向极地传播是由于黑潮的平流作用。Park等[14]提出,黑潮延伸体以南近惯性内波较少的原因也与平流作用有关,认为是黑潮的平流作用将北面的近惯性内波向东输送,从而导致南面近惯性内波较少。Zhai等[15]的研究表明,大西洋的墨西哥湾流可以将近惯性内波向东远距离传播至离其源地很远的地方。Kung和Gan[16]基于三维海洋模型发现,南海一支射流的水平平流向远场输送了近惯性内波。
吕宋海峡位于台湾岛和吕宋岛之间,为双海脊结构,中间是吕宋海槽,东西两侧分别是吕宋岛弧(包括巴坦群岛和巴布延群岛)和恒春海脊。该区域蕴含高度活跃的复杂动力过程,包括大尺度环流、中尺度涡旋和内波等。而近惯性内波由于垂向群速度较小,易受其他动力过程影响而发生自身物理性质的变化,其传播路径在该海域尤为复杂。
人们对近惯性内波进行了大量的研究,对其生成过程已经有了比较清晰的认识,但是对于近惯性内波的传播过程仍理解尚浅,尤其是在吕宋海峡周围的特殊海域,前人研究鲜少提及黑潮及其形态变化对近惯性内波传播过程的影响。因此,我们在黑潮两侧部署潜标来研究近惯性内波的传播特征。
1 数据和方法 1.1 数据 1.1.1 潜标数据本文研究共使用了位于吕宋海峡附近黑潮两侧2个站位的潜标数据,潜标的在位时间为2010年8月—2011年4月,它们的位置如图 1所示。部署在南海一侧的潜标记为“S”,部署在西太平洋一侧的潜标记为“P”,相关信息见表 1。所有潜标上都配置有一个标注75kHz的多普勒声学流速剖面仪(Acoustic doppler current profilers,ADCP)用于测量海水流速,观测深度基本覆盖了上500 m。本文关注台风激发的近惯性内波与黑潮的相互作用,主要发生在上层海洋,因此使用了潜标上打ADCP的数据来开展研究。
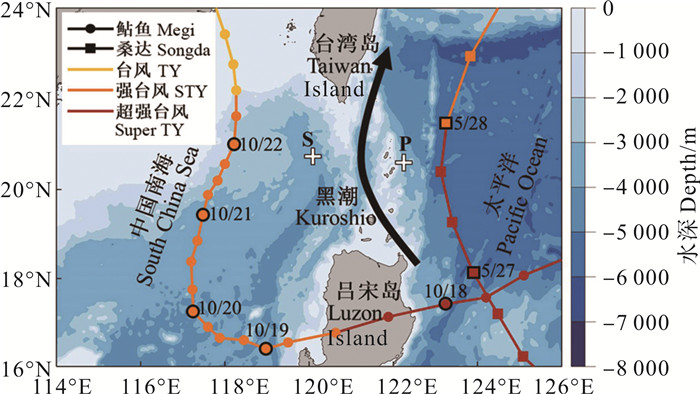
|
(圆点和方块表示台风每6 h时的位置,其颜色代表台风等级。Typhoons' 6 h positions are depicted with color points. Different colors of the curve and points stand for different intensities.) 图 1 台风“鲇鱼”和“桑达”的路径、黑潮的路径示意、潜标具体位置以及该海域海底地形 Fig. 1 Tracks of typhoon Megi and Songda, the schematic of Kuroshio, the mooring position and seafloor topography |
|
|
表 1 潜标的详细信息 Table 1 Detailedinformation about the moorings |
数据原始采样层之间为8 m,为便于计算,所有观测到的海水流速数据在垂向上均插值到5 m标准,同时,将流速数据进行1 h的时间平均并将数据插值到整点时刻上。在进行时间插值之前,若某一深度上流速数据在整个观测期间内的覆盖率不低于95%,则将该深度上的数据进行时间插值,并补齐缺测部分,否则该深度上的数据视为无效。本文使用了4阶Butterworth带通滤波器从流速数据中提取近惯性流速ui,使用的滤波频带为[0.85,1.15]f。
1.1.2 台风“鲇鱼”和“桑达”2010—2012年,有两个超强台风——“鲇鱼”(Megi)和“桑达”(Songda)经过了吕宋海峡附近海域。台风“鲇鱼”和“桑达”的路径如图 1所示,图中颜色代表等级,相关数据来自中国气象局热带气旋数据中心。使用的风场数据为NCEP/NCAR再分析数据集提供的海面10 m高度的风场数据,时间分辨率为1 h,空间分辨率为0.305 1°×0.304 2°(CFSR,包含2010年及以前数据)和0.201 3°×0.201 0°(CFSv2,包含2011年及以后数据)。为分析台风经过海洋时向海洋上混合层输入的动能,除了上述风场数据,还使用了CMEMS的混合层深度(Mixed layer depth,MLD)数据,时间分辨率为1 d,水平分辨率为0.833°×0.833°。
台风“鲇鱼”在2010年10月13日生成于11.8°N,141.4°E西北太平洋的海面上,并于10月18日升级为超级台风,最大持续风力达72 m·s-1。它在10月21日左右到达S潜标附近,之后向北移动并衰减。台风“桑达”于2011年5月20日生成在8.3°N,141.5°E附近的位置,并于5月26日加强为超强台风,中心最大风速为52 m·s-1。5月27日左右,“桑达”抵达潜标P位置附近之后向北移动并衰减(见图 2)。

|
((a)2010年10月21日20:00风场;(b)2011年5月27日20:00风场。黑色实线为台风路径,路径旁的日期为台风到达时间。(a)The wind speed on 20:00 21 October, 2010; (b) The wind speed on 20:00 27 May, 2011. The black curve denotes the track of typhoons Megi and Songda and the dates marked next to the tracks are at the time of their arrival.) 图 2 台风“鲇鱼”和“桑达”经过潜标阵列的风场结构 Fig. 2 Wind speed field when Typhoons Megi and Songda pass through the mooring arrays |
为了分析吕宋海峡黑潮形态特征,本文采用AVISO多卫星融合的海面绝对动力高度(Absolute dynamic topography, ADT)数据,水平分辨率为0.25°×0.25°,时间分辨率为1 d。此外,为了探索黑潮对近惯性内波的影响机制,研究采用了来自混合坐标海洋模式(Hybrid coordinate ocean model,HYCOM)的数据产品作为背景场,包括海水流速、温度、盐度和海表面高度(Sea surface hight, SSH)数据。时间分辨率为3 h和1 d,空间分辨率为1/12(°),垂直层数为32层。HYCOM模式嵌入了多种湍流混合模块以供选择,近年来广泛地用于大洋和区域海洋动力学研究。研究还使用了来自海军作战全球大气预测系统(NOGAPS)的数据,包括风应力、风速、热通量和降水数据。数据选取时间范围为台风“鲇鱼”和“桑达”经过潜标前、后各一个月时间。
1.2 方法 1.2.1 Slab模型台风经过海洋时会将大量的动能输入到海洋上混合层内,基于一个简单的平板假设,将混合层视为一个上下均一的平板,风输入的能量可以用Slab模型模拟[20]:
| $ \frac{\mathrm{d} u_i}{\mathrm{dt}}-f v_i=\frac{\tau_x}{H \rho}-r u_i, $ | (1) |
| $ \frac{\mathrm{d} v_i}{\mathrm{dt}}+f u_i=\frac{\tau_y}{H \rho}-r v_i $ | (2) |
式中:ui和vi分别为近惯性内波的纬向分量和经向分量;f为局地科氏频率;H为海洋混合层深度;ρ为海水密度;ρ=1 024 kg·m-3;r为阻尼系数r=0.15f, 表示速度衰减的e倍时间尺度;τx和τy是风应力的纬向分量和经向分量。它们通过以下方式计算:
| $ \left(\tau_x, \tau_y\right)=\rho_{\mathrm{a}} C_{\mathrm{d}} U_{10}\left(u_{10}, v_{10}\right) 。$ | (3) |
式中:ρa为空气密度,ρa=1.3 kg·m-3;u10和v10为10 m高度风速的纬向和经向分量,
风向混合层的近惯性输入做功Π可以通过如下公式计算:
| $ \mathit{\Pi}=\tau \cdot u_i $ | (4) |
式中:τ为风应力;ui为海表近惯性流速。正通量意味着能量从大气向海洋转移。
1.2.2 射线追踪模型为研究背景场的变化对吕宋海峡近惯性内波的影响,本文使用了射线追踪模型,模型的控制方程如下:
| $ \frac{\mathrm{d} \boldsymbol{r}}{\mathrm{~d} t}=\boldsymbol{C }{g}+\boldsymbol{V}, $ | (5) |
| $ \frac{\mathrm{d} \boldsymbol{k}}{\mathrm{~d} t}=-\boldsymbol{\nabla} \omega 。$ | (6) |
式中:r=r(x, y, z)是波射线位置;Cg为内波群速group velocity);V为背景流;k是三维空间波数(Wavenumber),k=(kx, ky, kz);
| $ \omega_0=f_{\mathrm{eff}}+\frac{N^2 k_{\mathrm{H}}^2}{2 f k_z^2}+\frac{1}{k_z}\left(\frac{\partial \boldsymbol{U}}{\partial z} k_y-\frac{\partial \boldsymbol{V}}{\partial z} k_x\right) 。$ | (7) |
其中:
| $ f_{\text {eff }} \approx f+\frac{1}{2} \zeta=f+\frac{1}{2}\left(\frac{\partial V}{\partial x}-\frac{\partial \boldsymbol{U}}{\partial y}\right) $ | (8) |
称为有效科氏频率(Effective Coriolis frequency);kH是水平波数,
观测发现,台风“鲇鱼”在观测海域的上层海洋引起了显著的近惯性响应,最大近惯性流速达0.4 m·s-1。图 3表明了观测期间的近惯性动能(Near-inertial kinetic energy,NIKE)和近惯性剪切(Near-inertial shear,NIS),其分别由式(9)和式(10)计算:
| $ N I K E=\frac{1}{2} \rho_0\left(u_i^2+v_i^2\right), $ | (9) |
| $ N I S=\sqrt{\left(\frac{\partial u_i}{\partial z}\right)^2+\left(\frac{\partial v_i}{\partial z}\right)^2} . $ | (10) |
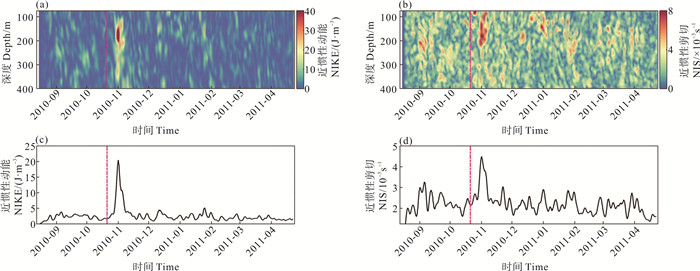
|
(垂向粉色虚线标记的是台风到达潜标P的时间。Vertical pink dashed lines denote the time Megi and Songda began to generate intense NIWs at mooring P.) 图 3 潜标P观测所得的(a)近惯性动能、(b)近惯性剪切、(c)近惯性动能深度平均、(d)近惯性剪切深度平均 Fig. 3 (a) NIKE at mooring P, (b) NIS at mooring P, (c) depth-averaged NIKE at mooring P and (d) depth-averaged NIS at mooring P |
式中:ρ0是海水密度(1 024 kg·m-3);ui和vi分别为近惯性内波的纬向分量和经向分量;z为深度。潜标P处近惯性内波生成的NIKE和NIS在2010年10月发生了显著的增强事件。该事件出现在台风“鲇鱼”通过后,到达时刻在图 3中使用红色虚线表注。台风“鲇鱼”通过期间,NIKE的最大值为75 J·m-3,出现在水深200 m左右,NIS最大值为0.010 s-1。
潜标S处近惯性内波生成的NIKE和NIS如图 4所示。显然,台风“鲇鱼”到达后,并没有出现和潜标P处对应的近惯性事件。台风“鲇鱼”通过后, 深度平均近惯性动能可以达到20 J·m-3,而潜标S处仅观测到小于5 J·m-3的峰值。
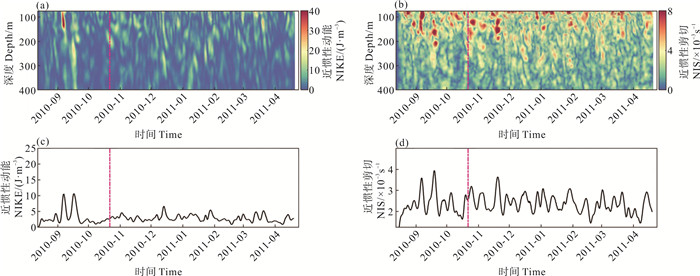
|
(垂向粉色虚线标记的是台风到达潜标S的时间。Vertical pink dashed lines denote the time Megi and Songda began to generate intense NIWs at mooring S.) 图 4 潜标S观测所得的(a)近惯性动能、(b)近惯性剪切、(c)近惯性动能深度平均、(d)近惯性剪切深度平均 Fig. 4 (a) NIKE at mooring S, (b) NIS at mooring S, (c) depth-averaged NIKE at mooring S and (d) depth-averaged NIS at mooring S |
在此基础上,为进一步探究近惯性响应的内波频率特征,本文对NIKE和NIS高值所在深度范围内的功率谱和剪切谱进行了计算(见图 5)。功率谱和剪切谱的主要谱峰主要出现在0.7、1和2 cpd左右,分别对应近惯性频带、全日潮频带和半日潮频带。这里,我们重点研究近惯性峰值出现的位置,关注近惯性内波的峰值相比科氏频率是否出现显著的偏移。分析结果显示,功率谱和剪切谱的NI谱峰均在潜标P处出现红移,频率约0.93f;在潜标S处出现蓝移,频率约1.14f。且潜标P处的近惯性峰强度大于潜标S处,功率谱近惯性峰值约为S处的2~3倍。
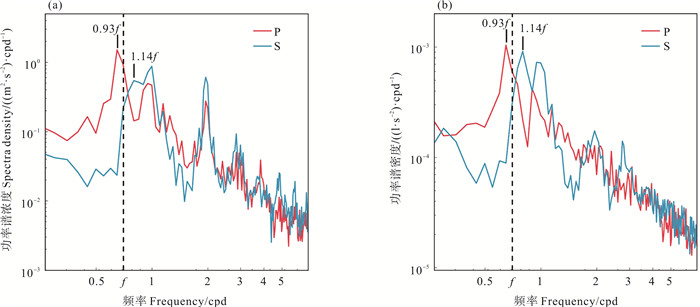
|
((a)功率谱; (b)剪切谱。垂直的黑色虚线表示局地科氏频率(f)。(a) Power spectra; (b) Shear spectra. Vertical black doted lines indicate the local inertial frequency (f).) 图 5 NIKE和NIS高值所在深度范围内的功率谱和剪切谱计算结果 Fig. 5 The average power spectra and shear spectra in the depth range of high values of NIKE and NIS |
为了分析台风期间整个研究海域NIKE的分布, 以探究海峡两侧上层海洋对台风的近惯性响应, 在此使用了时间分辨率为3 h的HYCOM再分析资料。本文提取了其中的近惯性流速, 并计算NIKE。图 6(a), 6(c)为台风"鲇鱼"期间, 该海域在50和200 m水深处平均NIKE的分布情况。50 m处的NIKE(见图 6(a))高值区基本沿台风"鲇鱼"路径分布, 且主要分布在吕宋海峡西侧。而200 m处的NIKE(见图 6(c))高值区主要分布在吕宋海峡以东的潜标P附近, 这与观测结果相一致。由此, 台风"鲇鱼"激发的NIKE在200 m处与50 m处并不匹配。为更好地探究这种不匹配现象的原因及其特殊性, 在此引入一个对照事件——2011年5月, 路径沿吕宋海峡方向行径的台风"桑达"事件。前后两个事件分别称为"事件A"和"事件B"。与事件A不同的是, 事件B中NIKE在50 m处和200 m处的分布大致相同(见图 6(b), (d)), 均主要分布在吕宋海峡以东台风路径经过区域。
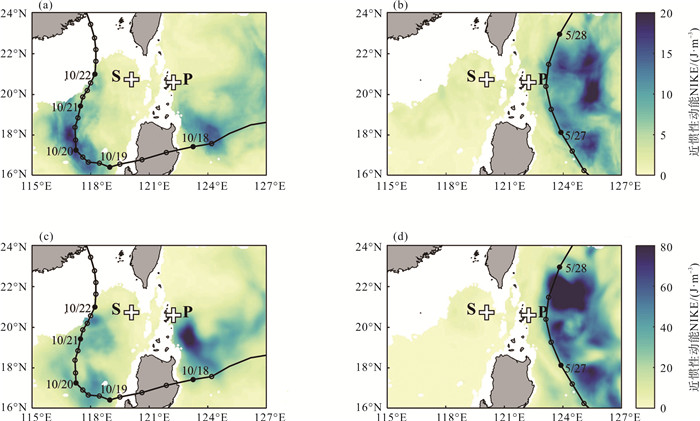
|
( 黑色曲线表示台风的路径,台风路径旁的日期是台风到达时间。Black curve denotes the track of typhoons. The dates marked next to the typhoon track are the time of their arrival. ) 图 6 台风“鲇鱼”期间(a)50 m和(c)200 m的近惯性动能及台风“桑达”期间(b)50 m和(d)200 m的近惯性动能 Fig. 6 NIKE at (a)50 m and (c)200 m during Typhoon Megi; NIKE at (b)50 m and (d)200 m during Typhoon Songda |
之前的分析表明,台风“鲇鱼”过后,潜标P处观测到两次近惯性事件,而潜标S处未观测到相关事件。特别的是,潜标S更靠近台风路径,其近惯性响应却比潜标P处的弱的多。为了探究这一差异产生的原因,本文首先对台风向海洋的风能输入进行了量化估算,探究是否是两个台风的初始能量输入存在差异。由图 4可以看到,S和P站位并未直接观测到台风输入能量到混合层这一过程,因此本文基于Slab假设,使用式(1)—(2)计算风能输入,计算中使用了CMEMS所提供的S和P处的混合层深度。
计算的结果显示,台风“鲇鱼”和“桑达”经过两个潜标位置附近后,风应力增大(见图 7(b)),风能输入增大(见图 7(c))。特别是在潜标P处,台风经过后的风应力和风能输入强度都弱于潜标S处。如图 7(d), (e)所示,通过Slab模式计算的混合层NIKE的时间积分可以看出,两次台风对混合层近惯性能量的贡献很大,大部分能量集中在台风路径右侧。事件A中,潜标P处NIKE积分值为8.3×103 J·m-3,潜标S处NIKE积分值为4.7×104 J·m-3;事件B中,潜标P处NIKE积分值为1.7×105 J·m-3,潜标S处NIKE积分值为3.1×104 J·m-3。事件A中潜标S处受风场影响最大,NIKE也最大。
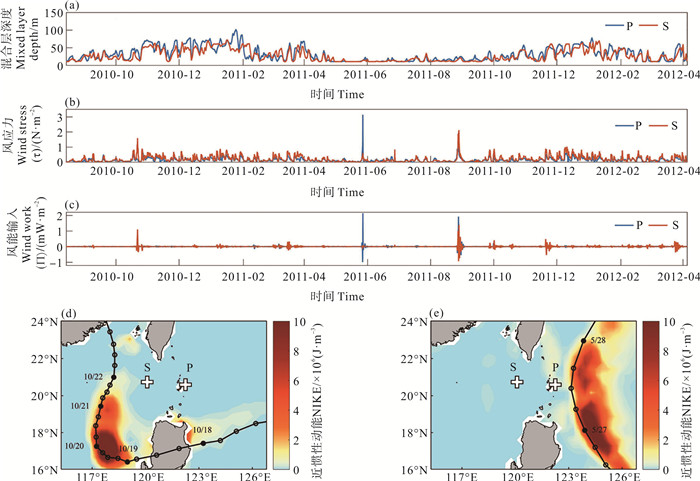
|
(黑色曲线表示台风的路径, 台风路径旁的日期是台风到达时间。Black curve denotes the track of typhoons. The dates marked next to the typhoon track are the time of their arrival.) 图 7 潜标P和S处的(a)混合层深度、(b)风应力和(c)风能输入及吕宋海峡及其附近海域在(d)事件A和(e)事件B中的混合层近惯性动能的时间积分 Fig. 7 (a) MLD, (b) wind stress τ, (c) wind work Π at mooring P and S; time-integrated NIKE in (d) event A and (e) event B |
混合层中风能输入强度的分布与上一节所述50 m处NIKE模式结果一致, 但与200 m处NIKE模式结果以及观测中的深层近惯性能量分布并不一致, 这表明近惯性能量分布可能受到了背景场的调制作用, 特别是黑潮的潜在作用, 其流速可达1 m·s-1, 且从S和P中间穿过。Park等[14]在中高纬度的研究发现, 黑潮可以通过其相对涡度调节近惯性内波的传播, 并通过平流作用将近惯性内波从源地输送至离源地很远的地方, 从而导致观测中的近惯性能量分布和混合层的近惯性能量分布不一致。因此我们将着重研究S和P处近惯性能量差异与黑潮之间的联系。
3 黑潮调制下近惯性内波的传播特征 3.1 黑潮形态为了探究黑潮对近惯性内波传播的影响,本文首先根据卫星高度计的观测提取了黑潮的形态。如图 8所示,黑色虚线表示125 cm的ADT等值线和87 cm的SSH等值线,等值线始自吕宋岛以东地区(17°N以北、123°E以西),用来大致表示黑潮路径[19]。在事件A中,黑潮蜿蜒北上,在台湾的南侧入侵南海形成一个小的流套(见图 8(a)、(c))。事件B中,黑潮向北流动,路径一直位于吕宋海峡的东侧,形态相对稳定(见图 8(b)、(d))。HYCOM的SSH与卫星高度计的ADT呈现出相似的形态,验证了HYCOM数据对于黑潮研究的可靠性。
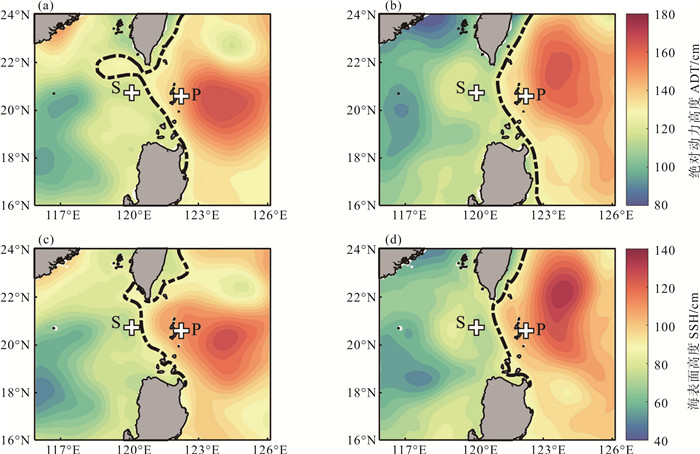
|
((a), (b)中125 cm处的绝对动力高度轮廓大致表示黑潮的路径; (c), (d)中87 cm处的海表面高度轮廓大致表示黑潮的路径, 如黑色粗虚线所示。The ADT contour at 125 cm roughly denotes the path of the Kuroshio in (a), (b) and the SSH contour at 87 cm roughly denotes the path of the Kuroshio in (c) (d), as shown as black thick dashed lines.) 图 8 (a) 事件A和(b)事件B中的绝对动力高度及(c)事件A和(d)事件B中的海表面高度 Fig. 8 ADT in (a) event A and (b) event B; SSH in (c) event A and (d) event B |
图 9展示了HYCOM再分析数据中选取S和P所在的平均纬度20.5°N各变量的纬向分布。等温线逐渐从南海向西太平洋倾斜, 坡度随着深度的增加而变陡(见图 9(a)、(b))。事件A的等温线倾斜程度略大。盐度垂向分布显示, 100~300 m层明显存在盐度高值区(见图 9(c), (d)), 这是西太平洋中常见的结构[25]。通过盐度最大值在34.8以上的高值区可以识别黑潮轴心(见图 9(c)、(d))。由此可以发现, 事件A中黑潮的入侵已经为南海带去了较高盐度的海水。在南海70 m深度附近存在着强的层结区域(见图 9(e)、(f)), 基于内波频散关系可以知道, 强的层结不利于内波的垂向传播。因此, 黑潮以东的近惯性内波比黑潮以西的近惯性内波进入海洋内部的速度更快, 这有助于黑潮以东区域近惯性能量高值区的形成。事件A中, 负相对涡度在潜标P处显著增强, 正相对涡度在潜标S处增强, 与前述近惯性内波的红蓝频移相一致(见图 5)。
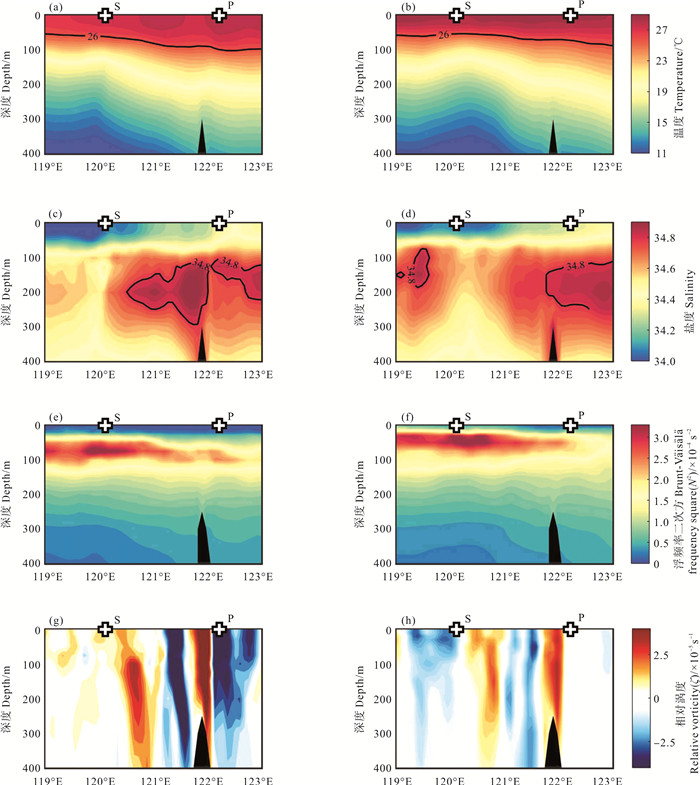
|
图 9 (a) 事件A和(b)事件B中的温度;(c)事件A和(d)事件B中的盐度;(e)事件A和(f)事件B中的浮频率二次方;(g)事件A和(h)事件B中的相对涡度 Fig. 9 Temperature in (a) event A and (b) event B; salinity in (c) event A and (d) event B; Brunt-Väisälä frequency square (N2) in (e) event A and (f) event B; relative vorticity (ζ) in (g) event A and (h) event B |
与黑潮的形态变化相对应, 这两个事件中该地区的流场差异也非常显著。在事件A中, 黑潮的流速较弱, 其轴线发生了形态变化, 产生弯曲, 并形成了一个向东的分支, 这里称为"射流分支"(见图 10(a))。潜标P位于射流分支南侧, 位于黑潮弯曲形成的反气旋结构内。而在事件B中, 黑潮以超过1 m·s-1的最大速度径直向北流动(见图 10(b)), 同时, 相对涡度场也随着流场的变化而发生了变化。事件A中, 黑潮的西侧呈现弱正涡度区, 而东侧则形成明显的负涡度区(见图 10(a))。由于射流分支的影响, 负涡度区几乎沿纬向分布。同时, 在射流分支的北面存在纬向正涡度屏障, 阻碍了近惯性内波向北传播。在事件B中, 黑潮西侧具有显著的正涡度, 可以阻碍近惯性内波在吕宋海峡中的传播(见图 10(b))。此时, 黑潮东侧为负涡度区, 利于近惯性内波聚集。
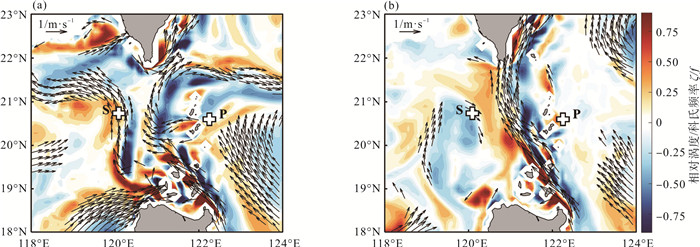
|
图 10 (a) 2010年10月21日和(b) 2011年5月27日50 m深度的流速(矢量箭头)和相对涡度/科氏频率(阴影) Fig. 10 Current velocity (vector arrows) and ζ/f (shading) at 50 m depth on (a) 21 October, 2010 and (b) 27 May, 2011, respectively |
上述分析表明,黑潮的形态和相关动力学性质在两个事件之间存在显著差异。事件A中的射流分支和强负相对涡度区都有利于近惯性内波在潜标P处聚集,因此,事件A中混合层近惯性能量分布与观测范围内近惯性能量分布的差异可以认为与黑潮的射流分支和相对涡度分布有关。
3.2 射线追踪试验为了进一步验证黑潮形态变化下背景流场和相对涡度分布对近惯性内波传播的作用,我们基于这两次事件发生时的三维海洋背景场开展了两次射线追踪试验,以此探究近惯性内波在其中传播的规律。值得说明的是,射线方程的求解在数学上本质为常微分方程求解的初值问题,给定波动的初始状态可推演出波动的传播规律。尽管我们使用HYCOM的数据提供了内波传播的三维背景场,但是内波的实际初始状态值(如初始波长、频率、位置和波向等)都是未知的。为了解决这个问题,前人利用一些理想条件对初始波动状态进行了假定,如James和Shay[24]假设了近惯性内波的水平尺度与其激发源台风相当,其垂向尺度与混合层厚度相当,从而给定了波动的初始尺度。本研究认为,特定的假设不具有普适性,基于某一条射线得到的传播规律往往不具有鲁棒性。在本研究中为了解决此问题,在两次试验都基于蒙特卡洛(Mont Carlo)方法在研究区域内设置了大量的射线初始点,这些点的初始波参数被设置为在一定范围内完全服从随机,我们关注这些随机射线在传播足够长的时间之后,是否显著受到黑潮的调制。
这些初始点的水平位置范围为118°E—124°E, 18°N—22°N,覆盖了吕宋海峡及其周围区域。由于射线的发射方向无法确定,所以它们的发射角在[0, 2π]的范围内随机取值。我们根据观测中的内波波数,设置了波的初始垂直波长随机范围[100, 500] m。根据台风水平尺度和内波的基本特征,近惯性内波的初始水平波数随机范围设置[50, 400] km, 即: 随机生成初始条件((rx)Rn∈118,124°E, (ry)Rn∈18,22°N, θRn∈0,2π, | kz | Rn∈2π/100,500m, | kh | Rn∈2π/[50, 400]km, n=10 000)。初始条件确定后,利用式(7)确定内波的初始欧拉频率,然后,利用四阶龙格-库塔方法求解微分方程(5)和(6)的数值解。时间步长设置为1 h,将方程循环迭代240次,以模拟近惯性内波约10 d的传播轨迹。在边界的位置规定为:任何运动至侧边界或底边界的射线被判定为消失。由于射线初始位置在空间上是随机且近乎均匀,因此其最终在空间上的密度具有物理意义。某处射线密度大,说明此处有较大概率是近惯性内波能量强的区域,反之则说明该处能量较弱。为了对应事件A和B,这两次射线试验分别称为试验A和试验B。
射线模拟的结果如图 11(a), 11(b)所示。在试验A中,潜标S附近的一些射线传播到南海,而另一些则沿着黑潮及其射流分支从南海传播到西太平洋。与此同时,黑潮上游的部分近惯性内波被射流分支阻挡,仅在台湾东部出现少量近惯性内波。试验B中,自西向东跨越海峡传播的射线数量减少,而在台湾东部出现了大量向北传播的射线。在垂直方向上,图 11(c), 11(d)显示,试验A中西太平洋出现了负涡度调制,射线更加密集,且主要集中在200 m以上。相比之下,试验B中黑潮西太平洋侧的射线密度低于试验A。
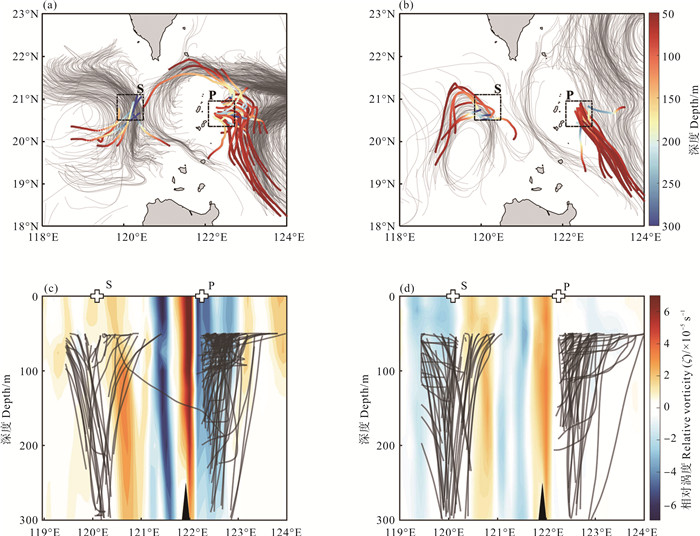
|
((a), (b)中灰色曲线表示水平长度大于300 km的射线。彩色散点射线是跑到框中水平长度大于100 km的射线, 但只显示其中的1/14, 它们的颜色代表深度。(c), (d)中背景彩色阴影与图 9(g), (h)相同。In (a), (b) the gray curve is for rays with a horizontal length greater than 300 km. The color scatter lines are the rays running in boxes with a horizontal length greater than 100 km, but only show 1/14 of them. Their color represents the depth. In (c), (d) the shadings are the same as Fig. 8(g), (h).) 图 11 (a) 事件A和(b)事件B的射线在水平方向的显示及(c)事件A和(d)事件B中跑进方框中的射线在垂直方向的显示 Fig. 11 The horizontal displays of the rays in (a) event A and (b) event B, the vertical displays of the rays running in boxes in (c) event A and (d) event B |
为了定量分析射线实验的结果, 我们在潜标周围选择了特定的0.6°×0.6°区域, 如图 11(a), (b)方框所示。并计算每次实验中进入方框的射线数, 以表示近惯性能量的强度。在试验A中, 进入P方框有376条射线, 是进入S方框(81条)的4.6倍。试验B中, P方框里有266条射线, 是S方框里(177条)的1.5倍。这表明, 试验A中潜标P处近惯性能量显著强于潜标S, 较好的复现了观测的结果。图 12描述了这些进入方框的射线的欧拉频率概率密度分布, 近似符合正态分布函数。P的数学期望为0.96f, S的数学期望为1.14f, 表明局地科氏频率发生了明显的频移, 且射线模拟的结果与观测中的功率谱分析结果呈现出一致性。黑潮形态变化引起的流场和相对涡度分布的差异可以调制近惯性内波的传播。因此, 观测到的近惯性能量与混合层近惯性能量分布之间的显著差异可归因于P处大量横向传播而来的近惯性内波的聚集。在这两种情况下, 黑潮重新分配了台风激发的近惯性能量。
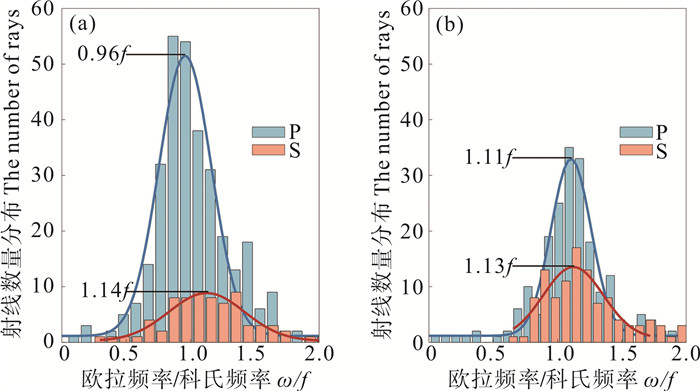
|
(曲线为正态分布函数拟合的结果。The curves are the result of fitting bars to normal distribution functions.) 图 12 (a) 事件A和(b)事件B期间在潜标P和潜标S附近聚集的射线频率分布 Fig. 12 The distribution of frequency of the rays gathering near the moorings P and S during (a) event A and (b) event B |
以上分析表明, 事件A中强近惯性能量主要集中在较远的潜标P处而不是台风路径旁的潜标S处这一现象可能是由黑潮导致的。黑潮形态变化引起的流场和相对涡度分布的变化可以调制近惯性内波的传播, 并让近惯性内波在西太平洋一侧聚集, 两个射线追踪实验已经证实了这一点。值得提出的是, 在吕宋海峡附近的地形较为复杂, 且初始的随机过程本身的误差很难估量, 因此我们设置了一组额外的对照试验, 将背景流场设置为0 m·s-1, N2恒定为3×10-5 s-1, 使射线仅仅在β平面传播。结果表明, 到达潜标P和潜标S附近的射线数几乎相等, 占初始总数为15.8%和16.4%。即射线在没有背景流场影响的情况下在S和P的位置几乎均匀分布, 验证了实验初始设置本身的随机性不影响结果。同时, 由于在这种情况下只有β效应会改变射线路径, 而结果是"几乎相等", 这也进一步支持了背景流场可以明显改变射线路径并造成射线在潜标P和潜标S之间偏置的结论。
5 结语本研究结合潜标数据、卫星高度计数据和HYCOM再分析资料,探讨了黑潮影响下的近惯性内波传播特征。两次台风引起的近惯性事件中,黑潮西太平洋侧潜标P处的近惯性能量较南海侧潜标S处的更强,特别是事件A。这与混合层的近惯性能量分布并不完全一致,黑潮被认为是造成这种现象的原因。当黑潮减弱时,可能由于在吕宋海峡缺少陆地支撑而形态变异,导致流轴弯曲并形成流向西太平洋的射流分支。这为近惯性内波从黑潮南海侧向西太平洋的传播提供了机会。同时,黑潮上游的部分近惯性内波被射流分支阻挡,仅在台湾东部出现少量近惯性内波。而当黑潮较强且径直向北流动时,黑潮南海侧的正涡度会阻碍近惯性内波向西太平洋传播。而射流分支的消失会导致近惯性内波随黑潮向北逃逸。这些都通过数据分析和射线追踪实验得到了验证。该研究结果表明, 像黑潮这样的背景海流及其形态变化在可用于全球海洋混合的近惯性能量再分配中扮演着重要的角色。
| [1] |
Ferrari R, Wunsch C. Ocean circulation kinetic energy: Reservoirs, sources, and sinks[J]. Annual Review of Fluid Mechanics, 2009, 41: 253-282. DOI:10.1146/annurev.fluid.40.111406.102139 (  0) 0) |
| [2] |
Alford M H, Mackinnon J A, Simmons H L, et al. Near-inertial internal gravity waves in the Ocean[J]. Annual Review of Marine Science, 2016, 8(1): 95-123. DOI:10.1146/annurev-marine-010814-015746 (  0) 0) |
| [3] |
Alford M H. Improved global maps and 54-year history of wind-work on ocean inertial motions[J]. Geophysical Research Letters, 2003, 30(8): 1424. (  0) 0) |
| [4] |
Furuichi N, Hibiya T, Niwa Y. Model-predicted distribution of wind-induced internal wave energy in the world's oceans[J]. Journal of Geophysical Research: Oceans, 2008, 113(C9): C09034. (  0) 0) |
| [5] |
Simmons H L, Alford M H. Simulating the long-range swell of internal waves generated by ocean storms[J]. Oceanography, 2012, 25(2): 30-41. DOI:10.5670/oceanog.2012.39 (  0) 0) |
| [6] |
Sun B, Wang S, Yuan M, et al. Energy flux into near-inertial internal waves below the surface boundary layer in the global ocean[J]. Journal of Physical Oceanography, 2021, 51(7): 2315-2328. (  0) 0) |
| [7] |
Young W, Jelloul M B. Propagation of near-inertial oscillations through a geostrophic flow[J]. Journal of Marine Research, 1997, 55(4): 735-766. DOI:10.1357/0022240973224283 (  0) 0) |
| [8] |
Asselin O, Young W R. Penetration of wind-generated near-inertial waves into a turbulent ocean[J]. Journal of Physical Oceanography, 2020, 50(6): 1699-1716. DOI:10.1175/JPO-D-19-0319.1 (  0) 0) |
| [9] |
Kunze E. Near-inertial wave propagation in geostrophic shear[J]. Journal of Physical Oceanography, 1985, 15(5): 544-565. DOI:10.1175/1520-0485(1985)015<0544:NIWPIG>2.0.CO;2 (  0) 0) |
| [10] |
Mooers C N. Several effects of a baroclinic current on the cross-stream propagation of inertial-internal waves[J]. Geophysical and Astrophysical Fluid Dynamics, 1975, 6(3): 245-275. DOI:10.1080/03091927509365797 (  0) 0) |
| [11] |
Whitt D B, Thomas L N. Near-inertial waves in strongly baroclinic currents[J]. Journal of Physical Oceanography, 2013, 43(4): 706-725. DOI:10.1175/JPO-D-12-0132.1 (  0) 0) |
| [12] |
Jeon C, Park J H, Nakamura H, et al. Poleward-propagating near-inertial waves enabled by the western boundary current[J]. Scientific Reports, 2019, 9(1): 1-7. DOI:10.1038/s41598-018-37186-2 (  0) 0) |
| [13] |
Rainville L, Pinkel R. Observations of energetic high-wavenumber internal waves in the Kuroshio[J]. Journal of Physical Oceanography, 2004, 34(7): 1495-1505. DOI:10.1175/1520-0485(2004)034<1495:OOEHIW>2.0.CO;2 (  0) 0) |
| [14] |
Park J H, Donohue K A, Randolph Watts D, et al. Distribution of deep near-inertial waves observed in the Kuroshio Extension[J]. Journal of Oceanography, 2010, 66: 709-717. DOI:10.1007/s10872-010-0058-0 (  0) 0) |
| [15] |
Zhai X, Greatbatch R J, Eden C, et al. On the loss of wind-induced near-inertial energy to turbulent mixing in the upper ocean[J]. Journal of Physical Oceanography, 2009, 39(11): 3040-3045. DOI:10.1175/2009JPO4259.1 (  0) 0) |
| [16] |
Kung H S, Gan J. Response of near-inertial energy to a supercritical tropical cyclone and jet in the South China Sea: Modelling study[J]. Ocean Science, 2020, 16(5): 1095-1110. DOI:10.5194/os-16-1095-2020 (  0) 0) |
| [17] |
Huang X, Wang Z, Zhang Z, et al. Role of mesoscale eddies in modulating the semidiurnal internal tide: Observation results in the northern South China Sea[J]. Journal of Physical Oceanography, 2018, 48(8): 1749-1770. DOI:10.1175/JPO-D-17-0209.1 (  0) 0) |
| [18] |
Xu X, Zhao W, Huang X, et al. Observed near-inertial waves trapped in a propagating anticyclonic eddy[J]. Journal of Physical Oceanography, 2022, 52(9): 2029-2047. DOI:10.1175/JPO-D-21-0231.1 (  0) 0) |
| [19] |
Zhang Z, Zhao W, Qiu B, et al. Anticyclonic eddy sheddings from Kuroshio loop and the accompanying cyclonic eddy in the northeastern South China Sea[J]. Journal of Physical Oceanography, 2017, 47(6): 1243-1259. DOI:10.1175/JPO-D-16-0185.1 (  0) 0) |
| [20] |
Pollard R T, Millard Jr R. Comparison Between Observed and Simulated Wind-Generated Inertial Oscillations[J]. Deep Sea Research and Oceanographic Abstracts, 1970, 17(4): 813-821. DOI:10.1016/0011-7471(70)90043-4 (  0) 0) |
| [21] |
Oey L Y, Ezer T, Wang D P, et al. Loop current warming by Hurricane Wilma[J]. Geophysical Research Letters, 2006, 33(8): 153-172. (  0) 0) |
| [22] |
Fernández-Castro B, Evans D G, Frajka-Williams E, et al. Breaking of Internal waves and turbulent dissipation in an anticyclonic mode water eddy[J]. Journal of Physical Oceanography, 2020, 50(7): 1893-1914. DOI:10.1175/JPO-D-19-0168.1 (  0) 0) |
| [23] |
Lelong M P, Cuypers Y, Bouruet-Aubertot P. Near-inertial energy propagation inside a Mediterranean anticyclonic eddy[J]. Journal of Physical Oceanography, 2020, 50(8): 2271-2288. DOI:10.1175/JPO-D-19-0211.1 (  0) 0) |
| [24] |
Jaimes B, Shay L K. Near-inertial wave wake of Hurricanes Katrina and Rita over mesoscale oceanic eddies[J]. Journal of Physical Oceanography, 2010, 40(6): 1320-1337. DOI:10.1175/2010JPO4309.1 (  0) 0) |
| [25] |
Mensah V, Jan S, Chiou M-D, et al. Evolution of the Kuroshio tropical water from the Luzon Strait to the east of Taiwan[J]. Deep Sea Research Part Ⅰ: Oceanographic Research Papers, 2014, 86: 68-81. DOI:10.1016/j.dsr.2014.01.005 (  0) 0) |
2. Qingdao Joint Institute of Marine Meteorology, Qingdao 266034, China;
3. Sanya Ocean Institute, Ocean University of China, Sanya 572025, China;
4. Frontiers Science Center for Deep Ocean Mutispheres and Earth System, Key Laboratory of Physical Oceanography, Ministry of Education, Ocean University of China, Qingdao 266100, China
 2025, Vol. 55
2025, Vol. 55


