2. 自然资源部第三海洋研究所海洋动力研究室,福建 厦门 361005
内孤立波是一种发生在分层流体系统中的重力波,广泛分布在世界各地的海洋和大型湖泊中[1-2]。内孤立波在传播过程中会引起水体的剪切运动,从而威胁海洋油气平台、潜艇等海洋设备的安全[3]。此外,内孤立波裹挟海底沉积物进行翻转混合,对海底生物圈和岩石圈有重要影响[4-7]。
近些年来,随着遥感技术的发展,人们开始利用合成孔径雷达(SAR)来研究内孤立波[8]。相较于实地观测,遥感观测具有探测周期短、空间覆盖范围广、时空分辨率相对较高等优势,可实现内孤立波高发区大面积、同步、直观、连续、密集的监测[9]。其原理是内孤立波在传播的过程中会引起海洋表面小尺度波浪的辐聚和辐散,从而影响雷达的后向散射截面,在卫星遥感图像上呈现出交替的亮暗条带,人们提取这种亮暗条带来获取内孤立波的波要素等信息[10-12]。因此,弄清内孤立波与受其调制的表面波特征的动力学关系显得极为重要。
在早期的研究中,内孤立波对表面波的影响通常被简化。例如,Lewis和Hughes等[13-14]认为,内孤立波和表面波的相互作用仅仅是内孤立波所引起背景流和表面波的相互作用过程。类似地,Alpers[15]提出了一种线性理论来解释由内孤立波相关的背景流变化引起的小尺度表面粗糙度变化,这一理论建立了图像强度与内孤立波诱发的流场之间的定量关系,从而反演内孤立波的波长、振幅等信息。Donato等[16]提出了一种非线性理论来模拟这一过程,使得理论应用的范围更加广泛。但在一些情况下,这些简化情况下的理论在计算时会出现奇点,因此,Craig等[17]认为,使用简化的波流作用理论无法对更复杂的表面特征的形成进行合理的解释与模拟。
虽然理论的研究面对诸多困境,但是得益于计算机技术的快速发展,人们开始使用数值模拟方法来研究海洋问题。对于内孤立波对表面波调制的问题,前人建立过很多数值模型。2012年,Craig等[17]出了基于弱非线性的KdV方程的两层海洋模型,并分析了内孤立波和表面波之间的共振作用。Jiang等[18]提出了一个Boussinesq模型,用于模拟内孤立波和表面波相互作用,并发现了内孤立波调制下表面波的不对称现象,这也是一个弱非线性模型,参考了KdV模型中所采用的计算方法。弱非线性模型适用于小振幅内孤立波,但随着内孤立波振幅的增加,将不再适用。Hao等[19]建立了一个两层的理论模型,通过表面波能量的变化,量化了粗糙区域和光滑区域的表面特征,这个模型避免了简化波-流理论中的奇点问题。在文献[19]的基础上,Yue等[20-21]设计了计算效率更高的数值模型,并使用谱分析方法将结果与现实环境中的观测结果进行比较。Wen等[22]使用多域边界元法模拟了传播方向相同的内孤立波和表面波的相互作用,根据表面波波长的变化,将受内孤立波影响的表面波分为辐聚、辐散和恢复三个区域,探究了不同振幅内孤立波对三个区域范围的影响情况。他们的研究侧重于方法技术的实践,但是对表面波波要素如何响应内孤立波的调制缺乏具体的探讨研究。
CFD软件Fluent拥有完善合理的仿真流程和成熟的求解方式,常被应用于流体计算领域,相较于其他数值模拟方法,Fluent的优势在于可以高效地获得高精度的数据来对流场进行精细化分析[23-24]。本文选择中国黄海海况数据[25],使用Fluent软件建立两层模型进行内孤立波对表面波调制作用的模拟,分别研究了在同反向传播情况下,内孤立波的表面特征生成过程和稳定阶段的内孤立波表面特征。将稳定阶段的表面特征分解为表面波波高特征和表面波波长特征,再通过改变内孤立波振幅和初始表面波波长,分析不同工况下,受内孤立波调制的表面波特征的变化情况。
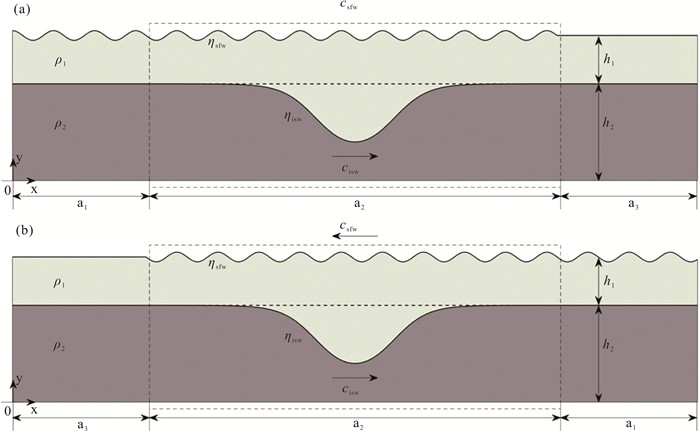
1 模式简介 1.1 模型设置根据He等[25]在2008年采集到的黄海的数据,以实际黄海近海的参数为依据,建立了一个具有双层流体系统的数值水槽来模拟内孤立波和表面波的相互作用。数值水槽模型示意图如图 1所示,其中图 1(a)为内孤立波与表面波共同向右而行的情况;图 1(b)为内孤立波向右传播,而表面波则向左传播的情况。除了表面波传播方向相反外,其他设置均一致。数值水槽模型总长L为400 m,总水深d为25 m,在水平方向上分为三个连通区域,a1区域为生成区域,用于产生表面波;a2区域为调制区域,是用于观察内孤立波和表面波相互作用的区域;a3区域为边缘区域,设置该区域足够长,使得表面波无法传播到该区域的边壁上,以此来杜绝反射波的产生,从而保证实验的准确性。上层水体厚度h1为5 m,密度ρ1为1 020 kg/m3,下层水体厚度h2为20 m,密度ρ2为1 022 kg/m3。表面波波速为csfw,波形为ηsfw,内孤立波波速为cisw,波形为ηisw。
|
图 1 模型设置示意图 Fig. 1 Scheme of the model setup |
实验通过改变内孤立波振幅和表面波波速以及表面波的传播方向来研究内孤立波对表面波的调制作用。实验工况设置如表 1,每组表面波波高均为0.05 m,A和B组为相同传播方向的工况,C和D组为相反传播方向的工况。计算时间步长为0.005和0.5 s输出一次数据,计算时间为40 s。
|
|
表 1 数值模拟工况设置 Table 1 Experimental parameters for the numerical simulations |
为了避免黏性耗散对表面波的影响,本实验使用了层流模型。经模拟分析,使用层流模型的情况下,表面波的衰减较小,可以忽略不计。本实验控制方程包括N-S(Navier-Stokes)方程和连续性方程。
N-S方程如下:
| $ \left\{\begin{array}{l} \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}=-\frac{1}{\rho} \frac{\partial P}{\partial x}+\nu\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}\right) \\ \frac{\partial v}{\partial t}+u \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y}=-\frac{1}{\rho} \frac{\partial P}{\partial x}-g+\nu\left(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}\right)^{\circ} \end{array}\right. $ | (1) |
式中:u和v分别为x和y方向上的速度分量;P为压力;ρ为流体密度;ν为流体动力黏度系数。
连续方程如下:
| $ \frac{\partial \rho}{\partial x}+\nabla \cdot(\rho V)=0 \text { 。} $ | (2) |
式中:ρ为密度;V为速度。
1.3 离散方法数值模拟采用二维2D求解器Solver进行瞬态求解。采用有限体积法来捕获不同相之间的自由表面[26]。在有限体积法中,引入了体积分数aq,aq代表所选相q占据网格的比值,如aq=1代表第q相物质完全占据该单元格,aq=0代表单元格内没有第q相物质,0 < aq < 1则代表单元格内有不止一种相,即交界面处。对于本研究,需要使用空气、上层水、下层水三种相,故aq满足连续方程[27]:
| $ \frac{\partial a_q}{\partial t}+\frac{\partial\left(u a_q\right)}{\partial x}+\frac{\partial\left(v a_q\right)}{\partial y}=0 \quad q=1, 2, 3 。$ | (3) |
压力耦合方程算法为SIMPLE,动量方程采用二阶迎风离散格式Second Order Upwind,体积分数求解采用几何重构方法Geo-reconstruct,时间项采用一阶隐式离散格式,其余参数采用默认设置[28]。
1.4 初始波形设置本文使用初始化流场法将表面规则波和内孤立波通过理论初始化到流场内再进行数值计算,相较于常用的边界造波法,初始化流场法可以节省计算时间,拥有更为灵活、更为直观等优点。此方法可以通过Fluent里的udf(user defined function)功能来实现。udf通过编写C语言程序来连接到Fluent动态函数库,对Fluent软件进行二次开发,从而满足用户的需求。
表面波使用二阶stokes波,其波面方程为[29]
| $ \begin{gathered} \eta_{\mathrm{ssw}}(x, t)=\frac{h_{\mathrm{sfw}}}{2} \cos (k x-\omega t)+ \\ \frac{h_{\mathrm{sfw}}}{8}\left(\frac{\pi h_{\mathrm{sfw}}}{\lambda_{\mathrm{ssw}}}\right) \frac{\cosh k d}{\sinh k d}(\cosh 2 k d+2) \cos 2(k x-\omega t) 。\end{gathered} $ | (4) |
x方向速度为
| $ \begin{gathered} u(x, y)=\frac{h_{\mathrm{sfw} } \omega}{2}\left[\frac{\tanh k(y+d)}{\sinh k d} \cos (k x-\omega t)+\right. \\ \left.\frac{3}{8} h_{\mathrm{sfw}} k^2 \frac{\cosh 2 k(y+d)}{\sinh ^4 k \mathrm{~d}} \cos 2(k x-\omega t)\right] . \end{gathered} $ | (5) |
| $ \begin{gathered} v(x, y)=\frac{h_{\mathrm{sfw} }\omega}{2}\left[\frac{\tanh k(y+d)}{\sinh k d} \sin (k x-\omega t)+\right. \\ \left.\frac{3}{8} h_{\mathrm{sfw}} k^2 \frac{\sinh 2 k(y+d)}{\sinh ^4 k \mathrm{~d}} \sin 2(k x-\omega t)\right] \end{gathered} $ | (6) |
式中:ω为波频率;k为波数;d为静水位。
内孤立波使用mKdV方程,其理论解为[30]
| $ \eta_{\mathrm{isw}}(x, t)=\frac{A_{\mathrm{isw}} \operatorname{sech}^2\left[\frac{\left(x-c_{\mathrm{mKd}} V t\right)}{\lambda_{\mathrm{mKd}} V}\right]}{1-\mu \tanh ^2\left[\frac{\left(x-c_{\mathrm{mKd}} V t\right)}{\lambda_{\mathrm{mKdV}}}\right]}, $ | (7) |
| $ \mu=\left\{\begin{array}{l} h_b / h_a, \bar{h}>0 \\ h_a / h_b, \bar{h} <0 \end{array}, \right. $ | (8) |
| $ \bar{h}=h_2-h_c, $ | (9) |
| $ h_c=\frac{d}{1+\sqrt{\rho_1 / \rho_2}}, $ | (10) |
| $ h_a=-\bar{h}-\left|\bar{h}+h_{\mathrm{isw}}\right|, h_b=-\bar{h}+\left|\bar{h}+h_{\mathrm{isw}}\right|, $ | (11) |
| $ \lambda_{\mathrm{mKdV}}=2\left(d-h_c\right) \sqrt{\frac{\left(d-h_c\right)^3+h_c{ }^3}{3 d h_a h_b}}, $ | (12) |
| $ c_{\mathrm{mKdV}}=c_{0 \mathrm{~m}}\left(1-\frac{1}{2}\left(\frac{\bar{h}+A_{\mathrm{isw}}}{d-h_c}\right)^2\right), $ | (13) |
| $ c_{0 \mathrm{~m}}=\left\{\frac{g d}{2}\left[1-\left(1-\frac{4\left(\rho_2-\rho_1\right) h_c\left(d-h_c\right)}{\rho_2 d^2}\right)^{1 / 2}\right]\right\}^{1 / 2} 。$ | (14) |
式中:hsfw为表面波波高;g为重力加速度。
2 结论与分析 2.1 内孤立波表面特征的演化为了研究内孤立波表面特征的形成过程,并选择合适的时间点来提取后续用作分析的瞬时剖面,故引入波陡比RS2/RS1。这里,R为平均表面粗糙度。将特定空间间隔x1到x2的平均表面粗糙度定义为
| $ R=\frac{1}{x_2-x_1} \int_{x_1}^{x_2} \frac{d \eta_{\mathrm{ssw}}(x)}{\mathrm{d} x} \mathrm{~d} x 。$ | (15) |
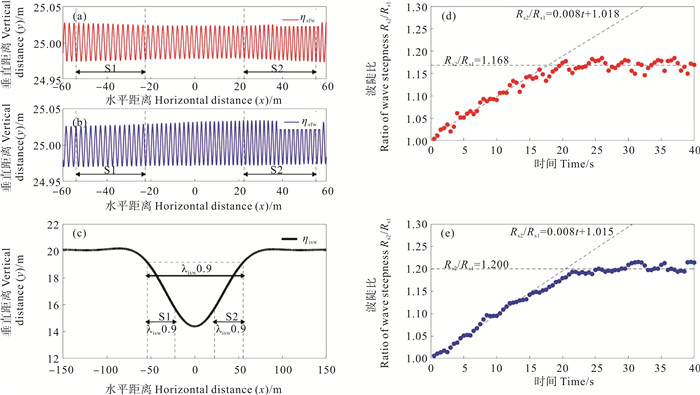
S1和S2为在“辐聚”和“辐散”区域中抽取的两小块采样区域。图 2(a)和2(b)分别为A6和C6工况下,内孤立波对表面波进行调制达到稳定时,受调制变形后的表面波的波形,他们为相同参数不同传播方向的结果。采样区S1和S2的位置如图 2所示,其定义方法见图 2(c)。图 2(c)为稳定时内孤立波的波形图,以跃层为基准线,在其下方1/10内孤立波振幅的深度处,取平行于x轴的一条线段定义为λisw0.9,其左右端点在内孤立波波形上,以λisw0.9的两端端点为基准点,分别向内孤立波对称轴方向取0.3λisw0.9,即为采样区S1和S2[22]。计算内孤立波对表面波调制过程中每个时刻的波陡比,得到A6和C6工况下,波陡比随时间的变化如图 2(d)和2(e)所示。内孤立波表面特征的形成包括生长阶段和稳定阶段,后续的分析应选取稳定阶段的数据来进行。当内孤立波刚刚生成时,表面波还未受到明显调制,因此S1和S2区域的平均表面粗糙度几乎相同。随着调制的发生,开始进入生长阶段(0~20 s)。在此阶段,内孤立波前侧上方的表面波变得更粗糙,而内孤立波后侧上方的表面波变得更平滑。S1和S2区域的平均表面粗糙度的不同变化导致了波陡比的增加,生长阶段波陡比的增加呈线性关系。20 s后,表面特征进入稳定阶段。对所有工况都计算波陡比随时间的变化。结果显示,无论什么传播方向,稳定阶段普遍在20 s之后,故对于所有工况都选择30 s时刻作为后续问题分析的瞬时剖面。
|
图 2 调制稳定时A6工况(a)、C6工况(b)表面波的波形,A6和C6工况下内孤立波的波形(c)、A6工况(d)、C6工况(e)波陡比随时间的变化 Fig. 2 Surface wave waveform of A6 condition (a), C6 condition (b) when the modulation is stable; waveform of internal solitary wave (c) under A6 and C6 conditions; A6 condition (d), C6 condition (e) wave steepness ratio change with time |
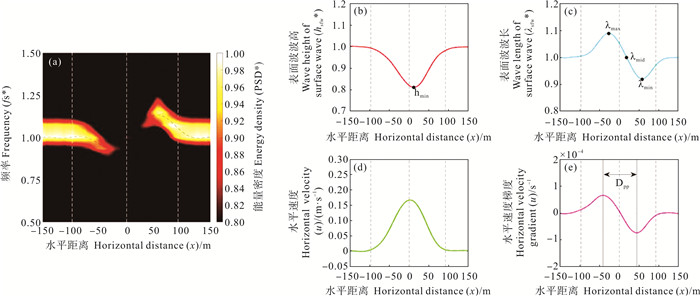
小波分析可以帮助人们从驳杂的海表信号中提取内孤立波的表面特征信号[31]。对图 2(a)中的表面波波形进行小波分析,得到图 3(a)为A6工况下稳定阶段表面波的空间能量谱。考虑到分析对象ηsfw是一个随x变化的空间信号,而不是一个随t变化的时间信号,我们引入了一个描述空间信号随x变化的量,称为空间频率fs。根据频率为周期的倒数,那么空间频率fs同样定义为波长的倒数。将空间频率fs和功率谱能量密度PSD进行归一化处理,得到fs*=fs/fs0和PSD*=PSD/PSD0,其中fs0和PSD0为该工况下未被调制的波形的空间频率和功率谱能量密度。用虚线绘制了不同位置的归一化峰值空间频率fsp,即波数在空间上的变化曲线。能量在空间上的变化具体表现为表面波波高在空间上的变化[22]。
|
图 3 调制稳定时A6工况下表面波的能量谱(a)、波高(b)、波长(c)随空间的变化,上层水体水平流速(d)、上层水体水平流速梯度(e)随空间的变化 Fig. 3 The surface wave energy spectrum (a), wave height (b) and wavelength (c) change with space under A6 condition when the modulation is stable; the variation of the upper water horizontal velocity (d) and the upper water horizontal velocity gradient (e) with space change |
为了更直观的研究表面波受内孤立波调制后形成的特征,将图 3(a)分解,分别得到图 3(b)和3(c)。3(b)为稳定时受内孤立波调制后的表面波的波高进行归一化后随x的变化图,图 3(c)为稳定时受内孤立波调制后的表面波的波长进行归一化后随x的变化图。根据Yue等[20]的方法,认为上层水体的平均水平流速梯度可以作为理论上判断辐聚区和辐散区的标准,故提取稳定时上层水体的平均水平流速随x的变化为图 3(d),对其作梯度,得到图 3(e)为该时刻上层水体的平均水平速度梯度随x的变化图。当水平速度梯度大于0时,认为区域水体辐散;当水平速度梯度小于0时,认为区域水体辐聚。以此为标准,图 3中每张子图背景都用虚线分割好了理论上的辐散和辐聚区域。将水平速度梯度峰谷间距记为Dpp。
将图 3(b)和3(d)对比,可以看出同方向的情况下,表面波受到内孤立波调制后,在内孤立波引起流速变化的区域表面波波高同样会发生变化,并且在水平平均流速达到最大值附近,表面波的波高减小到了最小值,这个结果与Hao等[19]在2020年的结果类似。取其最小值为hmin,将流场水平平均流速最大值处作为0点,故可以把hmin的横坐标看作空间场中表面波波高极值点与流场水平流速极值点的水平位置偏差,记为Xhmin。将图 3(c)和3(e)对比,可以看出同方向的情况下,内孤立波引起的上层水体水平流速梯度的结构分布调制影响了表面波波长的变化,两者的变化趋势几乎一致。在辐散区域,由于水体发散,拉伸表面波使得波长增长;在辐聚区域,由于水体聚拢,压缩表面波使得波长减小。值得注意的是,他们并非完全对应,表面波波长发生变化的区域相较于理论上的辐聚辐散区域存在明显的前移。故取波长受调制变化后的最大值和最小值为λmax和λmin,将表面波波长变长变短平衡位置处的点记为λmid,λmid的横坐标Xλmid可以看作表面波受调制后波长变化的平衡点相对于水平速度梯度空间变化平衡点的水平位置偏移。
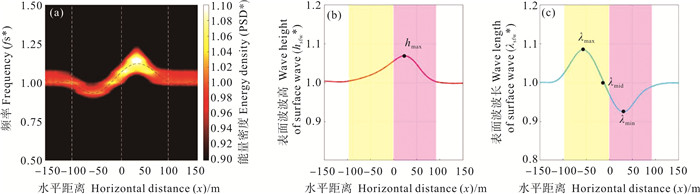
图 4(a)为C6组工况下稳定阶段表面波的空间能量谱。将其分解,分别得到图 4(b)和4(c)。将上层水体水平流速梯度所划分的辐聚和辐散区域设置为背景的粉色和黄色区域,两个区域交接处即为流场水平流速的最大值处。图 4(b)为受内孤立波调制后的表面波的波高进行归一化后随x的变化图,对比可以看出反方向的情况下,表面波受到内孤立波调制后,在内孤立波引起流速变化的区域表面波波高同样会发生变化,且在背景流的平均速度达到最大值附近,表面波的波高增大到最大值,这与传播方向相同的情况相反,这是由于内孤立波和表面波传播方向相反,内孤立波引起的流动挤压迎面而来的表面波导致的,而当表面波和内孤立波传播方向相同时,内孤立波引起的流动拉伸表面波故表面波波高会减小。取其最大值为hmax,把hmax的横坐标看作表面波波高空间变化的极值点与流场水平速度空间变化的极值点的相对位移,记为Xhmax。图 4(c)为受内孤立波调制后的表面波的波长进行归一化后随x的变化图。可以看出反方向的情况下,表面波受到内孤立波调制后,其波长的变化规律与上层水体水平速度梯度的结构分布几乎一致。与相同传播方向情况不同的是,传播方向相反时,表面波受调制后波长变化的平衡点相对于水平速度梯度空间变化平衡点的水平位置向后偏移。
|
图 4 调制稳定时C6工况下表面波的能量谱(a)、波高(b)、波长(c)随空间的变化 Fig. 4 The surface wave energy spectrum (a), wave height (b) and wavelength (c) change with space under C6 condition when the modulation is stable |
由此可知:无论表面波与内孤立波的传播方向同向或反向,表面波受内孤立波调制后,在内孤立波引起水平流速变化的区域,表面波特征会因此发生变化,具体表现在相同传播的情况下,表面波波高在最大流速附近变小;而在相反传播情况下,表面波波高在最大流速附近变大。另外,内孤立波引起的水平流速梯度的结构分布调制着表面波波长的变化。但是,这两种调制关系并不是完全匹配的,各自存在水平位置偏差。接下来的两节将分别改变内孤立波的振幅和初始表面波波长这两个因素来研究该偏差的变化规律,以及表面波受到内孤立波的调制后变化程度的变化规律。
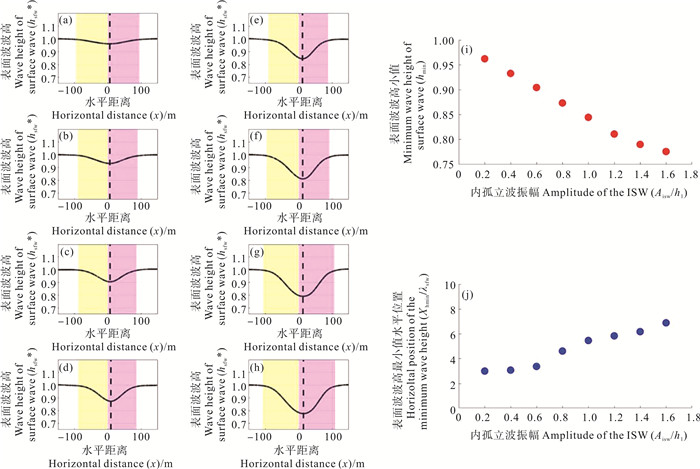
2.3 不同振幅的内孤立波对表面波波要素的调制 2.3.1 对表面波波高的影响为了研究相同传播方向的情况下不同内孤立波振幅对表面波波高的影响,选择A组工况进行分析。受到不同振幅的内孤立波调制的表面波波高归一化后随x变化的曲线如图 5(a)—5(h)所示。图 5(i)显示随着内孤立波振幅的增大,hmin逐渐变小,呈线性变化,说明相同的传播方向下,随着内孤立波振幅的增加,表面波波高受其调制后的变化程度加强。图 5(j)为Xhmin随内孤立波振幅的变化情况,也为线性变化。随着内孤立波振幅的增大,Xhmin逐渐变大,说明相同的传播方向下,内孤立波振幅的增加会强迫表面波的波高极值点的水平位置向内孤立波波前移动。这两个变化的趋势是可以预见的,在2.2节中,我们认为表面波的波高特征与流场水平流度相关,内孤立波振幅的增加使得上层流场流速增加,迫使表面波波高变化更为显著。
|
图 5 同向传播时受到不同振幅的内孤立波调制,表面波波高随空间的变化((a)—(h));hmin(i)、Xhmin(j)随内孤立波振幅的变化情况 Fig. 5 Changes of surface wave height with space ((a)—(h)) under internal solitary wave modulation with different amplitudes during simultaneous propagation; the variation of hmin (i) and Xhmin (j) with the amplitude of the internal solitary wave |
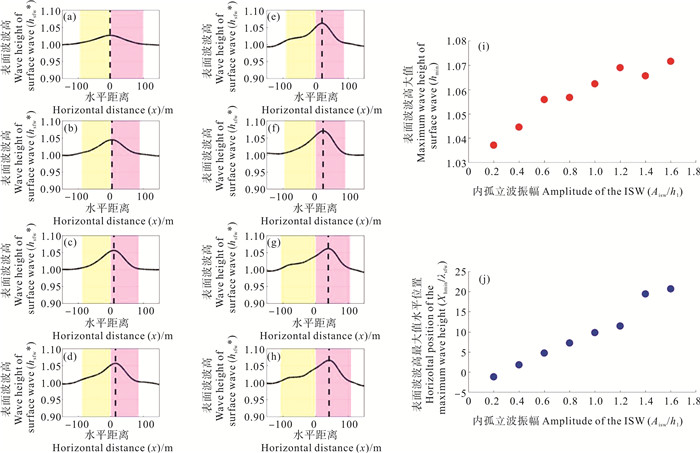
选择C组工况参数,在进行相反的传播方向下,不同内孤立波振幅对表面波波高的影响研究,受到不同振幅的内孤立波调制的表面波波高归一化后随x变化的曲线如图 6(a)到图 6(h)所示,hmax随内孤立波振幅的变化情况如图 6(i)所示,随着内孤立波振幅的增大,hmax逐渐变大,说明表面波波高受调制变化的更加强烈,这个结果与相同的传播情况一样,所以可以得到一个结论:无论表面波的传播方向如何改变,表面波波高受到内孤立波调制后的变化程度都会随着内孤立波振幅的增加而加强。与图 5(i)对比发现,相反传播促使表面波增大的程度要远小于相同传播情况下表面波减小的程度,这是因为波高的增加会导致波陡的增加,促使表面波不稳定,而波高的减少会导致波陡的减小,波形也更加容易维持[32]。如图 6(j)所示,随着内孤立波振幅的增大,Xhmax逐渐增大,这与相同传播方向的情况一致。以此得到结论:无论表面波的传播方向如何改变,内孤立波振幅的增加都会强迫表面波波高的极值点位置向内孤立波传播方向位移。
|
图 6 反向传播时受到不同振幅的内孤立波调制,表面波波高随空间的变化((a)—(h));hmax(i)、Xhmax(j)随内孤立波振幅的变化情况 Fig. 6 The surface wave height changes with space ((a)—(h)) when backpropagation is modulated by internal solitary waves with different amplitudes; the variation of hmax (i) and Xhmax (j) with the amplitude of the internal solitary wave |
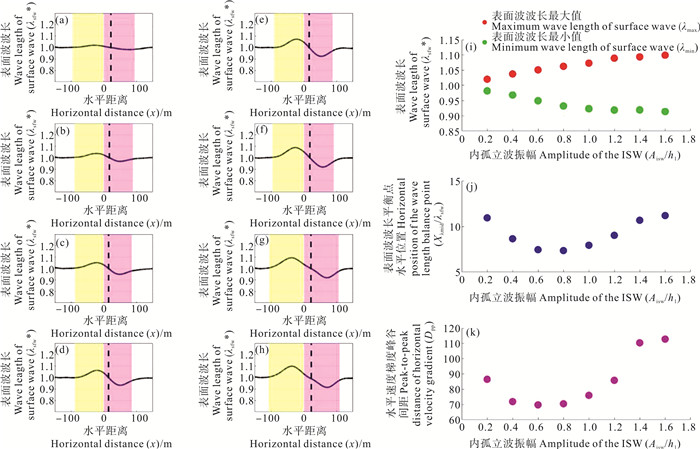
除却波高,波长也是组成表面波特征的重要指标之一。为了研究相同传播方向的情况下不同内孤立波振幅对表面波波长的影响,选择A组工况进行分析。如图 7(a)—7(h)所示,表面波的波长在辐散区域内受到流场的拉伸而变长,在辐聚区域内受到流场的压缩而变短。如图 7(i)所示,随着内孤立波振幅的增大,λmax和λmin都逐渐远离原始表面波波长(见图 7(i)),说明表面波波长受到内孤立波调制的影响逐渐显著。图 7(j)所示为Xλmid与内孤立波振幅的关系,在小振幅情况下,水平位置偏差随着内孤立波振幅的增加而减小;而在大振幅情况下,水平位置偏差随着内孤立波振幅的增加而增大,这种变化趋势与图 7(k)所示水平速度梯度峰谷间距Dpp随内孤立波振幅的变化规律有关,这进一步佐证了内孤立波引起的水平流速梯度场会使得表面波波长发生变化这一结论。
|
图 7 同向传播时受到不同振幅的内孤立波调制,表面波波长随空间的变化((a)—(h));λmax和λmin(i)、Xλmid(j)、Dpp(k)随内孤立波振幅的变化情况 Fig. 7 The surface wavelength changes with space ((a)—(h)) when the internal solitary wave is modulated with different amplitudes in the same direction propagation; λmax and λmin (i), Xλmid (j), Dpp (k) with the amplitude of the internal solitary wave |
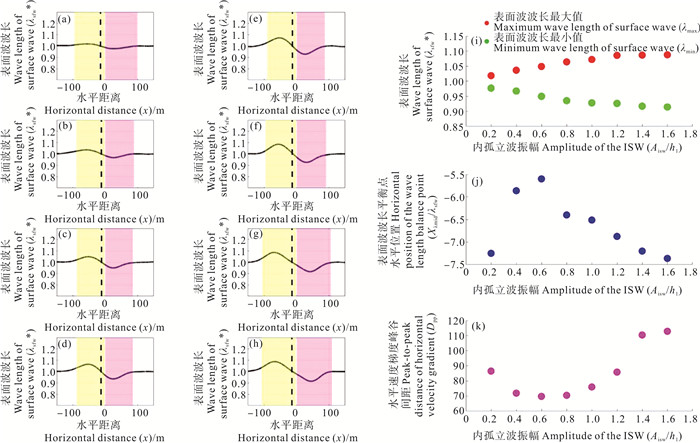
选择C组工况,研究内孤立波和表面波传播方向相反的情况下,不同内孤立波振幅对表面波波长的影响。如图 8(a)—8(h)所示,归一化后的表面波波长与同方向的情况类似,但是整体偏移的位置由内孤立波波前转移到了内孤立波波后。如图 8(i)所示,与相同方向的现象几乎一致。故得到结论:无论表面波的传播方向如何,随着内孤立波振幅的增加,表面波波长受到调制后的变化程度越显著,且表面波波长的变化程度与表面波的传播方向无关。图 8(j)所示为Xλmid与内孤立波振幅的关系。在小振幅的情况下,水平位置偏差随着内孤立波振幅的增加而增大;而在大振幅的情况下,水平位置偏差随着内孤立波振幅的增加而减小。与同方向的情况对比,可以发现,表面波波长受到内孤立波调制后,其波长变化平衡点的水平位置的偏差方向与表面波本身的传播方向一致,且偏差的程度与内孤立波引起的水平流速梯度的峰谷间距相关。
|
图 8 反向传播时受到不同振幅的内孤立波调制,表面波波长随空间的变化((a)—(h));λmax和λmin(i)、Xλmid(j)、Dpp(k)随内孤立波振幅的变化情况 Fig. 8 The surface wavelength changes with space((a)—(h)) when backpropagation is modulated by internal solitary waves with different amplitudes; λmax and λmin(i), Xλmid (j), Dpp (k) with the amplitude of the internal solitary wave |
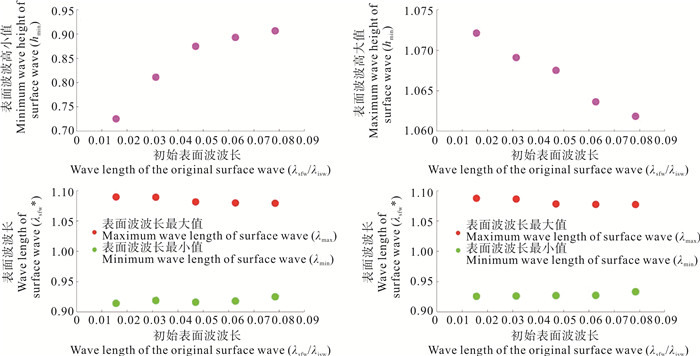
本节使用B和D组工况来研究初始表面波波长不同时, 受内孤立波调制的表面波特征的变化影响。图 9(a)和9(c)为表面波传播方向相同和相反的情况下,表面波波高的变化程度随不同初始表面波波长的变化情况。随着初始表面波波长的增加,hmin和hmax都逐渐接近原始表面波波高,使用内孤立波半波宽度λisw[33]对表面波波长进行无量纲化。结果表明,表面波波长和内孤立波波长尺度越接近,表面波波高受到内孤立波的调制影响越弱。在波长方面,传播方向相同和相反的情况下,表面波波长的变化程度随不同初始表面波波长的变化情况如图 9(b)—9(d)所示,它们的规律几乎一致,随着初始表面波波长的增加,表面波波长受到内孤立波的调制影响越弱。但是这种变化十分微小,远没有改变内孤立波振幅带来的影响大。说明表面波波长受内孤立波调制的强弱与初始表面波波长的关系较小。
|
图 9 同向传播hmin(a)、λmax和λmin(b)随初始表面波波长的变化情况;反向传播hmax随(c)、λmax和λmin(d)随初始表面波波长的变化情况 Fig. 9 Simultaneous propagation, hmin(a), λmax and λmin (b) change with the initial surface wavelength; back propagation, hmax with (c), hmax and λmin (d) with the initial surface wavelength |
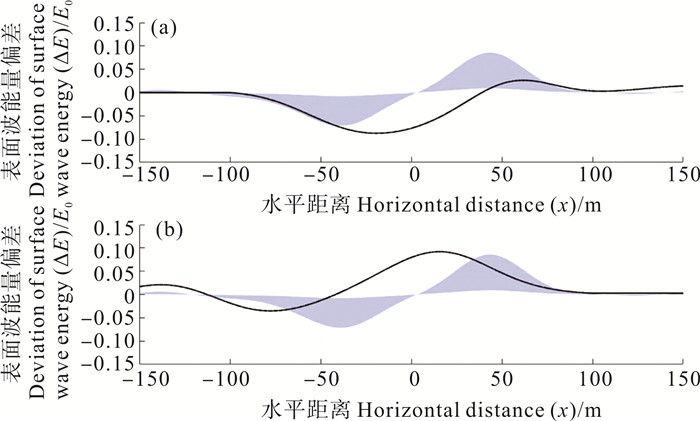
现有的SAR对于内波的成像过程主要可以分为三个阶段:首先是内孤立波在传播的过程中会影响流场,造成上层水体流速发生变化,在内孤立波的前端引起水体的辐聚,而在内孤立波的后端引起水体的辐散;接着流场的辐聚辐散对海表波浪造成调制,改变了海面的粗糙度;最后海面粗糙度的变化影响了雷达后向散射的强度,在SAR图像上显示出“亮暗相间的条带”[15]。本文的研究内容主要集中在第一和第二阶段,利用谱分析的方法计算表面波能量的偏差ΔE/E0在空间上的变化可以揭示出内孤立波引起的粗糙和光滑区域的特征分布。图 10(a)为B5工况下的结果(同向传播),图 10(b)为D5工况下的结果(反向传播)。背景紫色部分为应用了现有的SAR成像理论的结果,见公式(16),
| $ \frac{\Delta \sigma}{\sigma}=\frac{\Delta E}{E_0}=-(4+\gamma) \tau \frac{\mathrm{d} U}{\mathrm{~d} x} . $ | (16) |
|
图 10 表面波能量偏差在同向传播(a)、反向传播(b)的情况下随空间的变化 Fig. 10 Variation of surface wave energy deviation with space in the case of simultaneous propagation (a) and backpropagation (b) |
式中:Δσ/σ为归一化的雷达散射截面偏差;γ是布拉格波的群速度与相速度的比值(重力波的γ=为0.5);τ为内波引起调制的弛豫时间(τ=20~200)。可以看到他们并非完全吻合的。在水平位置上,他们之间存在偏差。本文的研究指出,当表面波和内孤立波同向传播时,后向散射截面发生变化的区域整体会向内孤立波波前偏移,且粗糙区域相对于光滑区域较小;反向传播时,向后偏移,且粗糙区域相对于光滑区域较大。这个结果与Hao等[19]使用数值模拟得到的结果非常类似。Kropfli等[34]通过对比遥感和实地观测的数据也发现了后向散射截面最大值的区域出现在内波的最前端,而水面最为平滑的区域则出现流场流速最大值处的结果。此外也有研究发现了“亮暗条带”不对称的现象[35],这些结果都证明了本实验结果的可靠性和可应用性。同时本研究也可以对这些观测结果产生的原因做出合理的解释。本研究的结果可以进一步与内波成像的模型相结合,有助于更好地解读内波成像的过程,以此来对现有的内波成像模型进行合理地校正。
3 总结与展望本文使用CFD软件fluent模拟了内孤立波对不同传播方向表面波的调制作用。首先分析了内孤立波表面特征的形成过程,将其分为生长阶段和稳定阶段,选择稳定时刻的瞬时剖面作为分析依据,然后使用小波分析分析表面波,将表面波特征分为波高特征和波长特征,波高特征和波长特征受不同因素的影响具体表现为:
(1) 内孤立波引起的表面流动会迫使受其调制的表面波波高发生变化:在同方向时,表面波波高由于拉伸在内孤立波引起的水平流速最大值附近逐渐变小达到最小值;而在反方向时,表面波波高由于挤压在内孤立波引起的水平流速最大值附近逐渐变大达到最大值。同时,同方向减小的程度远远大于反方向增大的程度,这是由于反方向情况下,波高的增加使得波陡增加,表面波更加难以维持导致的。除此之外,随着内孤立波振幅的增加,无论表面波的传播方向如何改变,表面波波高受到内孤立波调制后的变化程度都会随着内孤立波振幅的增加而加强,且都会强迫表面波的波高的极值点位置向内孤立波传播方向偏移。
(2) 内孤立波引起的水平流速梯度场会迫使受其调制的表面波波长发生变化,具体表现为表面波波长都会在辐散的区域内变长,在辐聚的区域内变短。当内孤立波振幅增加时,无论传播方向如何,表面波波长的变化程度都会更加强烈。而受到调制后波长变化平衡点的水平位置的偏差方向与表面波本身的传播方向一致。
(3) 初始表面波波长主要影响波高的变化程度。当初始表面波波长越接近内孤立波尺度时,表面波的波高受到内孤立波调制的变化程度逐渐减小;表面波的波长受内孤立波调制的强弱与初始表面波波长的关系较小。
本研究着重分析了内孤立波对表面波的调制作用,调整了不同工况,得到了内孤立波引起的上层水体流动和受调制的表面波具体的对应关系与变化规律,对于理解内孤立波对表面波的调制的水动力过程具有重要意义。后续可以调整模型海洋层结中的上下层水体密度差和厚度比等参数,这些参数都会导致内孤立波引起的上层水平流速发生变化,从中寻找合适的规律, 有助于更好地得到内孤立波对表面波的调制的机理过程。
| [1] |
Garrett C. Mixing with latitude[J]. Nature, 2003, 422(6931): 477-478. DOI:10.1038/422477a (  0) 0) |
| [2] |
Magalhaes Jorge M, Da Silva J C. Internal solitary waves in the Andaman Sea: New insights from SAR imagery[J]. Remote Sensing, 2018, 10(6): 861-877. DOI:10.3390/rs10060861 (  0) 0) |
| [3] |
Wang X, Zhou Ji-Fu. Numerical and experimental study on the scale effect of internal solitary wave loads on spar platforms[J]. International Journal of Naval Architecture and Ocean Engineering, 2020, 12: 569-577. DOI:10.1016/j.ijnaoe.2020.06.001 (  0) 0) |
| [4] |
Moore S E, Lien R C. Pilot whales follow internal solitary waves in the South China Sea[J]. Marine Mammal Science, 2007, 23(1): 193-196. DOI:10.1111/j.1748-7692.2006.00086.x (  0) 0) |
| [5] |
Wang Y H, Dai C F, Chen Y Y. Physical and ecological processes of internal waves on an isolated reef ecosystem in the South China Sea[J]. Geophysical Research Letters, 2007, 34(18): 312-321. (  0) 0) |
| [6] |
Sandstrom H, Oakey N. Dissipation in internal tides and solitary waves[J]. Journal of Physical Oceanography, 1995, 25(4): 604-614. DOI:10.1175/1520-0485(1995)025<0604:DIITAS>2.0.CO;2 (  0) 0) |
| [7] |
Ma X, Yan J, Hou Y, et al. Footprints of obliquely incident internal solitary waves and internal tides near the shelf break in the northern South China Sea[J]. Journal of Geophysical Research: Oceans, 2016, 121(12): 8706-8719. DOI:10.1002/2016JC012009 (  0) 0) |
| [8] |
Alford M H, Peacock T, Macinnon J A, et al. The formation and fate of internal waves in the South China Sea[J]. Nature, 2015, 521(7550): 65-69. DOI:10.1038/nature14399 (  0) 0) |
| [9] |
Fu Lee-Leung. Seasat Views Oceans and Sea Ice with Synthetic-Aperture Radar[M]. California: California Institute of Technology, Jet Propulsion Laboratory, 1982.
(  0) 0) |
| [10] |
Li X, Yang X, Zheng Q, et al. Deep-water bathymetric features imaged by spaceborne SAR in the Gulf Stream region[J]. Geophysical Research Letters, 2010, 37(19): 96-104. (  0) 0) |
| [11] |
Liu A K, Su Feng-Chun, Hsu Ming-Kuang, et al. Generation and evolution of mode-two internal waves in the South China Sea[J]. Continental Shelf Research, 2013, 59: 18-27. DOI:10.1016/j.csr.2013.02.009 (  0) 0) |
| [12] |
Helfrich K R, Melville W K. Long nonlinear internal waves[J]. Annual Review of Fluid Machanics, 2006, 38: 395-425. DOI:10.1146/annurev.fluid.38.050304.092129 (  0) 0) |
| [13] |
Lewis J E, Lake B M, Ko D R. On the interaction of internal waves and surface gravity waves[J]. Journal of Fluid Mechanics, 1974, 63(4): 773-800. DOI:10.1017/S0022112074002199 (  0) 0) |
| [14] |
Hughes B A. The effect of internal waves on surface wind waves 2. Theoretical analysis[J]. Journal of Geophysical Research: Oceans, 1978, 83(C1): 455-465. DOI:10.1029/JC083iC01p00455 (  0) 0) |
| [15] |
Alpers W. Theory of radar imaging of internal waves[J]. Nature, 1985, 314(6008): 245-247. DOI:10.1038/314245a0 (  0) 0) |
| [16] |
Donato A, Peregrine D, Stocker J. The focusing of surface waves by internal waves[J]. Journal of Fluid Mechanics, 1999, 384: 27-58. DOI:10.1017/S0022112098003917 (  0) 0) |
| [17] |
Craig W, Guyenne P, Sulem C. The surface signature of internal waves[J]. Journal of Fluid Mechanics, 2012, 710: 277-303. DOI:10.1017/jfm.2012.364 (  0) 0) |
| [18] |
Jiang S W, Kovacic G, Zhou D, et al. Modulation-resonance mechanism for surface waves in a two-layer fluid system[J]. Journal of Fluid Mechanics, 2019, 875: 807-841. DOI:10.1017/jfm.2019.501 (  0) 0) |
| [19] |
Hao X, Shen L. Direct simulation of surface roughness signature of internal wave with deterministic energy-conservative model[J]. Journal of Fluid Mechanics, 2020, 891: 807-841. (  0) 0) |
| [20] |
Yue L, Hao X, Shen L, et al. Directsimulation of the surface manifestation of internal gravity waves with a wave-current interaction model[J]. Journal of Physical Oceanography, 2023, 53(4): 981-993. DOI:10.1175/JPO-D-22-0097.1 (  0) 0) |
| [21] |
Lenain L, Pizzo N. Modulation of surface gravity waves by internal waves[J]. Journal of Physical Oceanography, 2021, 9: 51-61. (  0) 0) |
| [22] |
Wen Z, Zou L, Hu Y, et al. Numerical study on the surface signature of internal solitary waves[J]. Physics of Fluids, 2022, 34(7): 641-660. (  0) 0) |
| [23] |
Wood D, Grue J. Modelling of high amplitude internal waves integrating the primitive (Navier-Stokes) equations[J]. Applied Ocean Research, 2002, 24(6): 331-340. DOI:10.1016/S0141-1187(03)00016-6 (  0) 0) |
| [24] |
VanBergeijk V M, Warmink J J, Hulscher S J. Modelling the wave overtopping flow over the crest and the landward slope of grass-covered flood defences[J]. Journal of Marine Science and Engineering, 2020, 8(7): 489-501. DOI:10.3390/jmse8070489 (  0) 0) |
| [25] |
He Mingxia, Cai Haihua, Wang Bo. A new internal wave activity sea area discovered in the Yellow Sea near Qingdao[J]. Proceedings of Dragon, 2008(1): 2004-2007. (  0) 0) |
| [26] |
Hirt C W, NicholsI B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201-225. DOI:10.1016/0021-9991(81)90145-5 (  0) 0) |
| [27] |
Dong Chih-Ming, Huang Ching-Jer. Generation and propagation of water waves in a two-dimensional numerical viscous wave flume[J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 2004, 130(3): 143-153. DOI:10.1061/(ASCE)0733-950X(2004)130:3(143) (  0) 0) |
| [28] |
Schmitt F G. About Boussinesq's turbulent viscosity hypothesis: historical remarks and a direct evaluation of its validity[J]. Comptes Rendus Mécanique, 2007, 335(9-10): 617-627. (  0) 0) |
| [29] |
董志, 詹杰民. 基于VOF方法的数值波浪水槽以及造波、消波方法研究[J]. 水动力学研究与进展, 2009, 24(1): 15-21. Dong Z, Zhan J M. Comparison of existing methods for wave generating and absorbing in VOF based numerical tank[J]. Chinese Journal of Hydrodynamics, 2009, 24(1): 15-21. (  0) 0) |
| [30] |
Cui J, Dong S, Wang Z, et al. Experimental research on internal solitary waves interacting with moored floating structures[J]. Marine Structures, 2019, 67: 2641-2659. (  0) 0) |
| [31] |
Rodenas J A, Garello R. Wavelet analysis in SAR ocean image profiles for internal wave detection and wavelength estimation[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(4): 933-945. (  0) 0) |
| [32] |
Oh Sang-Ho, MizutanI Natsuki, Suh Kyung-Duck, et al. Experimental investigation of breaking criteria of deepwater wind waves under strong wind action[J]. Applied Ocean Research, 2005, 27(4-5): 235-250. (  0) 0) |
| [33] |
Sutherland B, Barrett K, Ivey G. Shoaling internal solitary waves[J]. Journal of Geophysical Research: Oceans, 2013, 118(9): 4111-4124. (  0) 0) |
| [34] |
Kropfli R, Ostrovski L, Stanton T, et al. Relationships between strong internal waves in the coastal zone and their radar and radiometric signatures[J]. Journal of Geophysical Research: Oceans, 1999, 104(C2): 3133-3148. (  0) 0) |
| [35] |
Xue J, Graber H C, Lund B, et al. Amplitudes estimation of large internal solitary waves in the Mid-Atlantic Bight using synthetic aperture radar and marine X-band radar images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 51(6): 3250-3258. (  0) 0) |
2. Ocean Dynamic Laboratory, Ministry of Natural Resources, the Third Institute of Oceanography, Xiamen 361005, China
 2025, Vol. 55
2025, Vol. 55


