2. 河北农业大学海洋学院,河北 秦皇岛 066000
自工业革命以来,大气中的二氧化碳(CO2)浓度从约6 204.8 mg/m3增加到了约9 273.6 mg/m3[1]。基于模型和数据的估计显示,化石燃料燃烧、水泥生产、土地的利用等人为活动是使大气中二氧化碳浓度增加的重要因素[2], 二氧化碳浓度的增加导致温室效应不断增强,造成全球气候变暖[3]。海洋作为大气CO2的一个主要汇,可吸收30%~40%人为排放的CO2,在调节大气CO2浓度,应对全球气候变化过程中发挥着至关重要的作用,因此,如何准确地确定海-气界面CO2通量,对全球碳循环及气候变迁有重大的意义[4-5]。
海-气界面CO2通量的计算通常采用下述块体公式:
| $ F=s k\left(p {{{\mathrm{CO}}}}_{2 {{{\mathrm{w}}}}}-p {{{\mathrm{CO}}}}_{2 {{{\mathrm{a}}}}}\right) 。$ | (1) |
式中:F为海-气界面CO2通量(正代表海洋为源,负则为汇);s为CO2在海水中的溶解度;k为CO2气体交换速率;pCO2w和pCO2a分别为海洋和大气的CO2分压。海水CO2的溶解度可以通过经验公式获得[6],海水分压的测量也有一套可行的方案,海-气界面CO2通量估算的最大不确定性在于CO2气体的交换速率k。
作为海-气界面的湍流交换过程,气体交换速率与海面附近湍流强度有关。由于海面附近的湍流受到海上风、海浪、海流和海面活性物质等复杂因素的影响,很难找到一个合适的参数来描述海面附近的湍流情况[7]。海上风是影响海面附近湍流强度一个主要因素,风速易于测量,利用起来较为方便,所以气体交换速率通常采用风速进行参数化。
另外,气体交换速率的大小还取决于海面附近湍流和分子扩散过程的相互作用,这种影响与海面附近的动量边界层与质量边界层厚度之比Sc=ν/D有关。式中:Sc为施密特数;ν为海水的运动粘性系数;D为气体扩散系数。Sc是确定气体交换速率的关键参数之一,与温度密切有关,对盐度只有较小的依赖性[8]。通常将气体交换速率归一化到水温20 ℃时CO2气体对应的施密特数,660和600分别对应于海水和淡水。研究表明,气体交换速率k与Sc-n成正比[10]。因此,气体交换速率通常表示为[8, 11]
| $ k={\mathrm{a}} U_{10}^{{\mathrm{b}}} Sc{^{-n}}。$ | (2) |
式中:U10为海表面10 m处的风速; a和b是由观测数据确定的常数。研究表明,当风速较大,海面为动力粗糙时,指数n=1/2;当风速较小,海面为动力学光滑时,n=2/3[16]。然而目前的大部分研究不考虑施密特指数n的变化,取n=1/2进行计算。
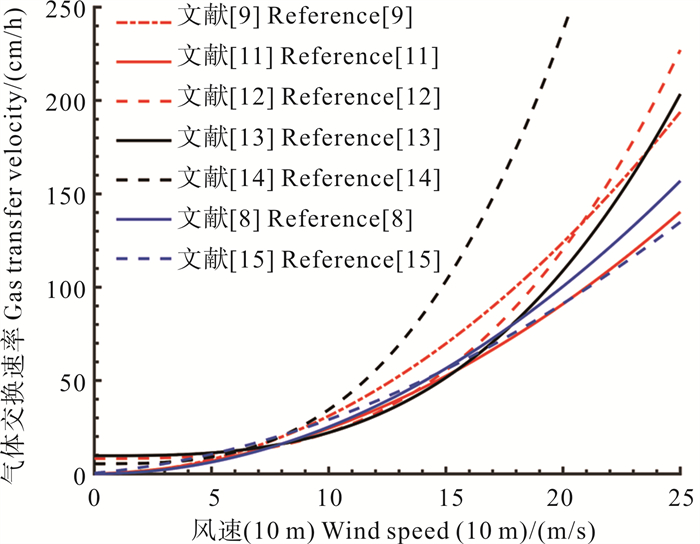
图 1为n=1/2时不同作者给出的以风速为参数的气体交换速率,其中的经验常数b从1次方到3次方的差异主要体现在中高风速区间。有研究认为气体交换速率的不确定性占全球海洋CO2通量估算不确定性的20%[8],因此准确地给出气体交换速率公式对全球海洋CO2通量估算具有重要意义。
|
( 气体交换速率是标准化为Sc=660后的结果。The gas transfer velocity is normalized to Sc=660. ) 图 1 不同作者提出的气体交换速率与风速的经验关系 Fig. 1 Empirical relationship between gas transfer velocity and wind speed proposed by different authors |
海浪作为全球海洋普遍存在的一种现象,其发展、传播和破碎等会直接影响海-气界面交换过程。同一风速可以对应不同的海浪状态,以风速为参数的气体交换速率的部分差异可归咎于忽略海浪效应的结果,因此越来越多的研究考虑海浪对气体交换速率的影响[7, 17-22]。
Jähne等[23]和Frew等[24]认为海浪引起的海面均方波陡可有效表征气体交换速率。Zappa等[25-26]对风浪槽中低风速下波浪破碎白冠进行观测,发现波浪破碎白冠覆盖率与气体交换速率直接相关。Zhao和Toba[27]发现,考虑波浪状态的风海雷诺数(RHa和RBa)在描述白冠覆盖率方面优于风速,其中RBa=u*2/ωpνa; RHa=u*Hs/νa,u*为空气摩擦速度; ωp为波浪的谱峰圆频率; νa为空气的运动粘性系数; Hs为波浪的有效波高。Zhao等[7]利用实测数据给出了气体交换速率与风海雷诺数的关系:
| $ k_{660}=0.13 R_{{\mathrm{Ba}}}^{0.63} 。$ | (3) |
在此基础上,Woolf[17]分别考虑波浪破碎和非破碎对气体交换的贡献,给出气体交换速率与风海雷诺数的关系:
| $ k_{600}=56.52 u_*+2 \times 10^{-5} R_{{\mathrm{Hw}}} 。$ | (4) |
这里的风海雷诺数RHw=u*Hs/νw;νw为水运动学粘性系数,可取为1.05×10-6 m2/s。Brumer等[20]根据涡相关法所得的气体交换速率数据和海浪模式给出的波浪数据,给出CO2气体的交换速率与风海雷诺数的关系为
| $ k_{660}=2.04 \times 10^{-4} R_{{\mathrm{Hw}}}^{0.88}。$ | (5) |
与风速相比,由于考虑了海浪的不同成长状态,风海雷诺数可以更有效地刻画气体交换速率的变化。
分别考虑湍流和气泡影响对气体交换速率的影响,Deike和Melville[21]给出气体交换速率为摩擦风速和波高的函数,再次强调了波浪效应对气体交换速率的影响:
| $ k_{660}=A_{{\mathrm{NB}}} u_*+\frac{A_{{\mathrm{B}}}}{\alpha}\left[u_*^{5 / 3}{\sqrt{g H_{{\mathrm{s}}}}}^{4 / 3}\right] 。$ | (6) |
式中: ANB=1.55×10-4;AB=(1±0.2)×10-5s2·m-2;α=0.08 205·s·(SST+273.15),α为Ostwald系数,0.082 05为气体常数,s为CO2在海水中的溶解度。公式右侧第一项和第二项分别为湍流对分子扩散和波浪破碎引起的气泡对气体交换速率的影响。
另一方面,在气体交换速率计算中,通常取施密特数Sc的指数n=1/2为常数,与海面状态无关,忽略指数n变化的影响。基于表面更新理论的小涡模型,气体交换速率与湍动能耗散率ε和νw的(ενw)1/4成正比,Esters等[16]给出了指数n的随风速的变化:
| $ n=-0.22 \log _{10}\left(u_*\right)+0.45 。$ | (7) |
在本文中,基于不同观测手段所得到的气体交换速率的实验室和外海数据,提出了一个以风海雷诺数和波龄为参量的双参数CO2气体交换速率公式,考虑指数n对海面状态的依赖性,计算了海-气界面的CO2气体交换速率和CO2通量,分析了指数n变化和海浪对海-气界面气体交换速率及CO2通量的影响。
1 所用数据说明关于气体交换速率参数化方案的讨论用到了外海和实验室的观测数据。Yang等[15]综合了由闭路CO2分析仪基于涡相关法测量得到的8个气体交换速率数据集,并给出了相应的波高和周期数据,在此基础上,我们又收集了大洋气体交换实验(GasEx-98, GasEx-01等)的涡相关方法测量数据[12, 28-30]、双气体示踪方法测量数据[31-35]、实验室测量数据[38]、漂流室技术测量数据[41-42]和控制通量技术测量[10, 43],其中涡相关法数据量为1 886个、双气体示踪方法数据量为42个、漂流式技术数据量为49个、控制通量技术数据量为42个、实验室数据量为43个,实验室数据将风速范围扩展到高风速86 m/s。
计算全球海-气界面气体交换速率和CO2通量时所用到的风速U10、有效波高Hs和波浪周期T数据来自欧洲中期天气预报中心(ECMWF; https://www.ecmwf.int/en/forecasts/dataset/ecmwf-reanalysis-v5)第五代ERA5再分析产品;海表面温度(SST)数据来自美国NOAA的国家环境信息中心(NCEI; https://www.ncei.noaa.gov/products/climate-data-records/sea-surface-temperature-optimum-interpolation)提供的每日最佳插值海表面温度(OISSTv2);海表面盐度(SSS)数据来自世界海洋地图集2023(WOA2023; https://www.ncei.noaa.gov/products/world-ocean-atlas),它是对世界海洋数据集(WOD)的剖面数据进行客观分析和质量控制后所得;二氧化碳分压差数据(ΔpCO2)来自Landschützer等[44]提供的基于海洋表层CO2观测数据(SOCAT; https://socat.info/index.php/data-access/)和两步神经网络插值法创建的数据集(SOM-FFN; https://www.ncei.noaa.gov/access/ocean-carbon-acidification-data-system/oceans/SPCO2_1982_present_ETH_SOM_FFN.html),该数据集的时间分辨率为月平均。
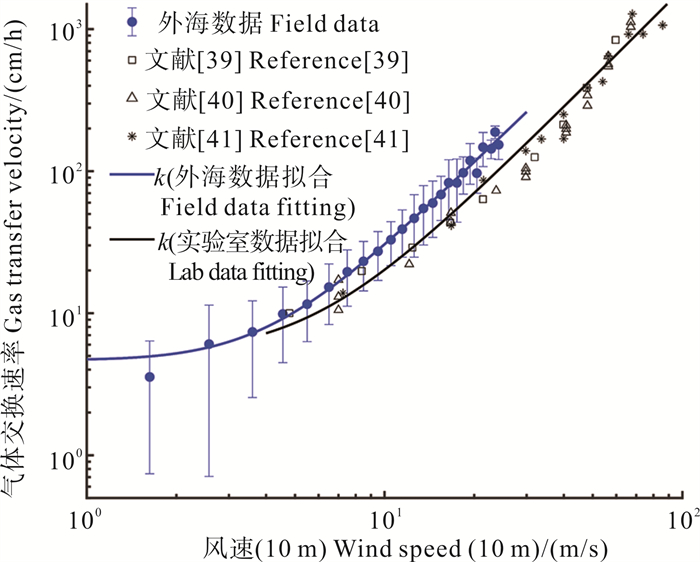
2 气体交换速率公式图 2为归一化的气体交换速率k660与风速的关系。为了简洁明了,便于与实验室数据进行比较,将外海数据按照1 m/s的风速间隔进行平均后画在图中。从图中可以看到,在相同风速下,实验室得到的气体交换速率系统性地小于外海结果,这显然与实验室的风浪相对外海非常年轻有关。在同样的风速下,外海的风浪波高远大于实验室风浪波高。
|
( 气体交换速率是标准化为Sc=660后的结果。The gas transfer velocity is normalized to Sc=660. ) 图 2 基于外海和实验室得到的气体交换速率观测数据与风速的关系 Fig. 2 Relationship between gas transfer velocity observations and wind speed based on offshore and laboratory-derived data |
显然,如果以风速为变量对气体交换速率进行拟合,很难将实验室和外海数据协调起来。因此,对外海和实验室数据分别进行拟合,得到的外海拟合结果为
| $ k_{660}=4.85-0.416 U_{10}+0.299 U_{10}^2 。$ | (8) |
对实验室数据拟合的结果为
| $ k_{660}=5.0+0.121 U_{10}^{2.1}。$ | (9) |
从前面的讨论可以看到,与风速相比,风海雷诺数RHw由于同时包括了风和浪的信息,可以更好地刻画气体交换速率。要计算实验室数据的风浪雷诺数RHw,需要相应的波高和周期信息,而实验室观测数据没有给出相应的波浪波高和周期的信息。实验室的风浪是标准的有限风区情形,根据实验室测量处的风区长度和风速,基于JONSWAP给出风浪成长关系[45]为
| $ \widetilde{E}=1.6 \times 10^{-7} \widetilde{x}, $ | (10) |
| $ \widetilde{f_{{\mathrm{p}}}}=3.5 \tilde{x}^{-0.33} 。$ | (11) |
式中:
Yang等[15]给出的数据集包含了风浪和涌浪情形。为了与实验室风浪情形的数据进行对比,我们仅保留了波龄β≤1.5的1 144个数据,并以RHw间隔100.2进行区间平均,得到的结果与实验室数据进行比较。
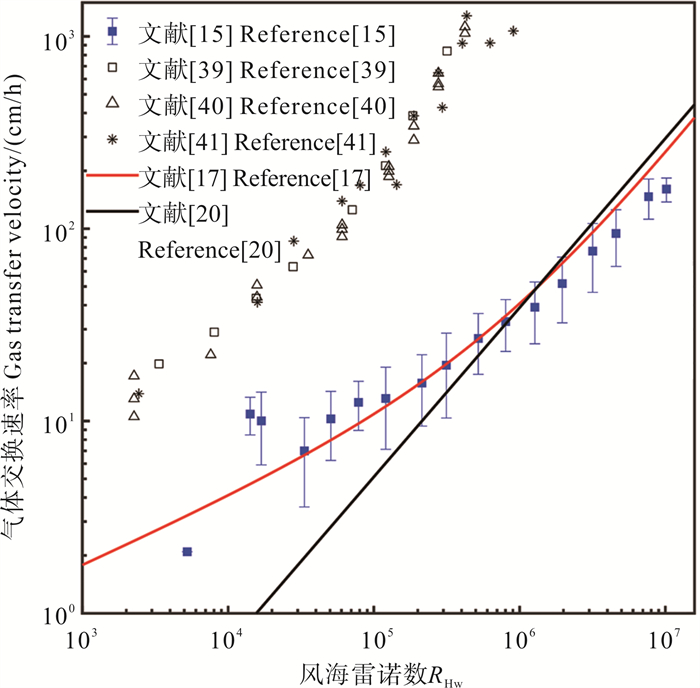
图 3给出了气体交换速率k660与风海雷诺数RHw之间的关系,同时显示了Woolf[17]和Brumer等[20]给出的参数化公式。图 3中一个显著的特征是实验室数据和外海数据严重偏离,这显然是相同风速下的实验室情形的波龄和波高均非常小,使得相应的RHw明显减小,导致在RHw相同时,实验室的k660偏大。但外海和实验室数据各自保持很好的收敛性。相对而言,Woolf[17]比Brumer等[20]的公式可以更好地刻画外海k660的变化,因为两者都是基于外海观测数据拟合得到的。
|
( 气体交换速率是标准化为Sc=660后的结果。The gas transfer velocity is normalized to Sc=660. ) 图 3 外海风浪情形和实验室的气体交换速率与风海雷诺数RHw的关系 Fig. 3 Gas transfer velocity versus wind-sea Reynolds number RHw for offshore wind-wave condition and laboratory |
为了调和实验室和外海数据,除RHw外,我们又引入波龄β作为变量进行拟合,得到双参数气体交换速率公式:
| $ k_{660}=2.13 \times 10^{-2} \beta^{-0.71} R_{{\mathrm{Hw}}}^{0.55} 。$ | (12) |
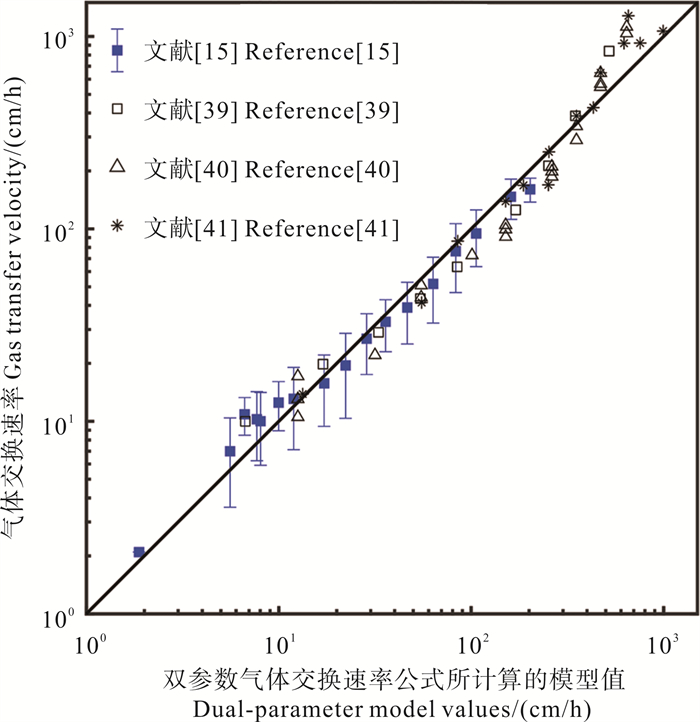
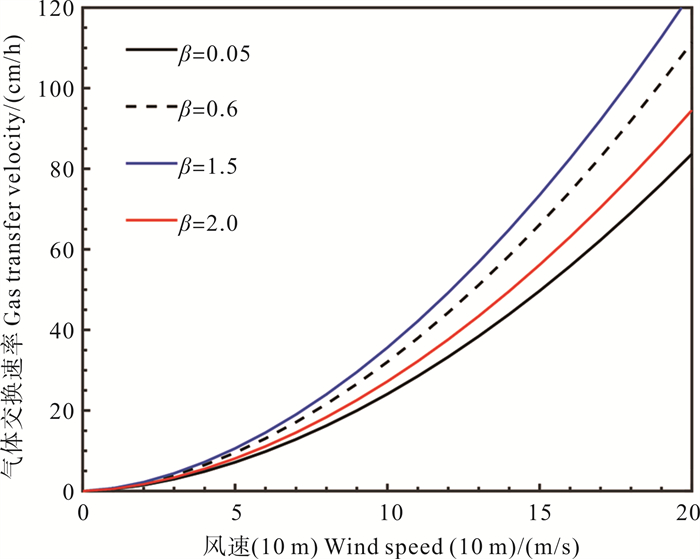
从图 4可以看到,双参数公式可以很好地协调实验室和外海数据,适用于风浪成长的不同状态。为了进一步展示双参数公式与波龄的关系,基于式(12),当β≤1.5时,根据风浪成长关系,令Hs=0.18β3/2U102/g,β>1.5时,令Hs=0.03U102,对应充分成长的波高,给出不同波龄时k660随风速的变化情况(见图 5)。
|
( 蓝色实点为外海数据的平均结果,黑色正方形、三角形和星号均为实验室数据,黑色实线为双参数公式的拟合结果。气体交换速率是标准化为Sc=660后的结果。The blue solid dots are averaged results from offshore data, and the black squares, triangles, and asterisks are laboratory data. The black solid line shows the fitting results of the dual-parameter equation. The gas transfer velocity is normalized to Sc=660. ) 图 4 外海风浪情形和实验室气体交换速率与波龄和风海雷诺数拟合 Fig. 4 Offshore wind-wave conditions and laboratory gas transfer velocity fitted to wave age and wind-sea Reynolds number |
|
( 气体交换速率是标准化为Sc=660后的结果。The gas transfer velocity is normalized to Sc=660. ) 图 5 理想情形下以波龄β和风海雷诺数RHw为变量的双参数气体交换速率与风速和波龄的关系 Fig. 5 Ideal two-parameter gas transfer velocity versus wind speed and wave age with wave age β and wind-sea Reynolds number RHw as variables |
从图 5可以看到,当波龄小于1.5的风浪情形,k660随波龄增大而增大,说明随着风浪成长,波浪破碎导致湍流增强,使气体交换速率增大,与之前的观测一致。而当波龄进一步增大时,波浪处于涌浪状态,海面趋于平静,会抑制波浪引起的湍流,使得气体交换速率降低,这也与之前的观测一致。显然,虽然双参数公式基于风浪情形的数据得到,当引入波龄后,也可以适用更为广泛的涌浪情形。
为了进一步验证这一观点,我们采用部分实际海上数据进行比较分析。在实际计算中,计算RHw时用到的摩擦速度u*采用Wu等[46]给出的拖曳系数公式进行计算:
| $ C_{{\mathrm{D}}}=u_*^2 / U_{10}^2=\left(0.8+0.065 U_{10}\right) \times 10^{-3} 。$ | (13) |
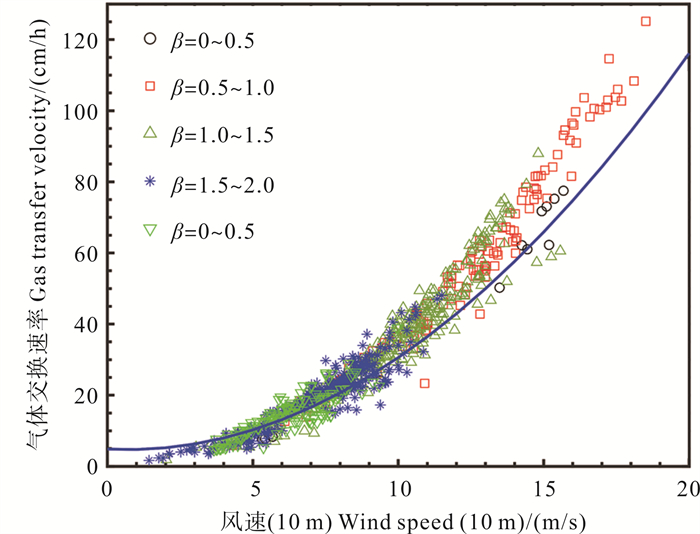
图 6为基于部分实际海上数据得到的双参数公式(12)计算的不同波龄时的气体交换速率,同时将以风速为参数的气体交换速率式(8)画在图中进行比较。从图中可以看到,当风速较大时,相应的波龄比较小,此时相同风速下,波龄越大,气体交换速率越大;而低风速通常对应于波龄较大的涌浪情形,随着波龄不同,气体交换速率在式(8)附近一定范围内变动,式(8)可视为其平均气体交换速率。
|
( 蓝实线为以风速为参数的气体交换速率式(8),不同的符号代表双参数公式所计算出的气体交换速率在不同波龄范围内的大小。图中的气体交换速率是标准化为Sc=660后的结果。The solid blue line in the figure shows the gas transfer velocity parameterized by wind speed Eq.(8). Different symbols represent the gas transfer velocity calculated by the dual-parameter equation corresponding to different wave age. The gas transfer velocity is normalized to Sc=660. ) 图 6 实际海上数据给出的双参数气体交换速率与风速和波龄的关系 Fig. 6 Two-parameter gas exchange rate versus wind speed and wave age given by offshore data |
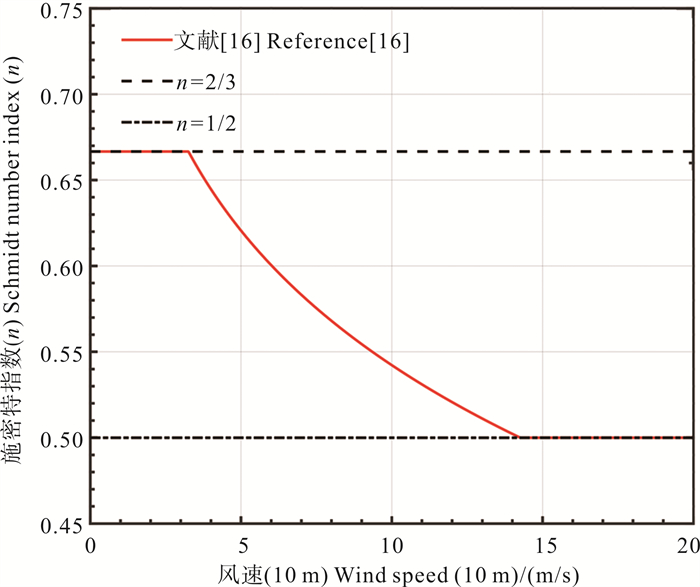
气体交换速率不仅依赖于风速和波浪状态,还与施密特数Sc的指数n的大小有关。传统上不考虑指数n的变化,在计算中取n=1/2,被认为对应于风速较大时海面粗糙情形。为了考察指数n变化的影响,我们采用Esters等[16]给出的公式,为了避免n过大或过小,在实际计算中,取指数n以如下方式随风速变化(见图 7):
| $ n=\left\{\begin{array}{l} 2 / 3 U_{10} \leqslant 3.1 {\mathrm{~m}} / {\mathrm{s}} \\ -0.22 \log _{10} u_*+0.453 .1<U_{10}<14.2 {\mathrm{~m}} / {\mathrm{s}} \\ 1 / 2 U_{10} \geqslant 14.2 {\mathrm{~m}} / {\mathrm{s}} \end{array}\right.。$ | (14) |
|
( 气体交换速率是标准化为Sc=660后的结果。The gas transfer velocity is normalized to Sc=660. ) 图 7 施密特数指数n随风速的变化 Fig. 7 Variation of Schmidt number index n with wind speed |
上式表明,当风速小于3.1 m/s时,海面为动力学光滑;当风速大于14.2时,会波浪破碎,海面为动力学粗糙;而当风速在3.1~14.2 m/s之间时,海面处于动力学光滑和粗糙之间的过渡阶段,这与实际观测大体一致。与传统上仅考虑n=1/2相比,考虑了n变化后,主要影响风速小于14.2 m/s的中低海况情形。
考虑施密特数指数n的变化,则式(8)和式(12)可以分别改写为
| $ k_{\text {Wind }}=\left(4.85-0.416 U_{10}+0.299 U_{10}^2\right)\left(\frac{S c}{660}\right)^{-n}, $ | (15) |
| $ k_{\text {Wave }}=2.13 \times 10^{-2} \beta^{-0.71} R_{\mathrm{Hw}}^{0.55}\left(\frac{S c}{660}\right)^{-n} 。$ | (16) |
在下面的讨论中,为了与传统上设定n=1/2的结果相对比,用kWind*和kWave*分别表示式(15)和(16)取n=1/2的情形,这4个公式相应的CO2通量分别用FWind、FWave、FWind*和FWave*表示。
3 世界大洋气体交换速率的估算利用1990年1月—2019年12月的海上10 m风速U10、有效波高Hs、波浪周期T、海表温度SST、二氧化碳分压差(ΔpCO2)和海表盐度数据,计算全球海-气界面的气体交换速率和CO2通量。这些数据都被线性插值成0.25°的空间分辨率,计算出每小时的气体交换速率再平均成每月的时间分辨率。
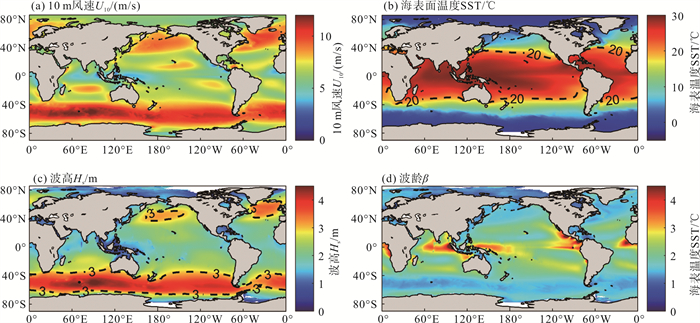
图 8给出了1990—2019年的海上10 m风速U10、海表温度SST、波高Hs和波龄β的平均空间分布。
|
图 8 1990—2019年不同物理量的气候态空间分布 Fig. 8 Spatial distribution of climate regimes for different physical variables from 1990 to 2019 |
1990—2019年的气候态平均风速的空间分布表明,在任何海域其风速的平均值均小于14.2 m/s,因此在计算气体交换速率时,都不同程度会受到施密特数Sc指数n变化的影响。由于Sc随温度升高而减小,SST越高,考虑了n变化的结果会使气体交换速率增大。在南北半球的西风带区域,波高较大,波龄较小,此时风浪占优;而在赤道海域,波高较小、波龄较大,对应着涌浪占优区域。
在计算海-气界面的气体交换速率时,海水中二氧化碳的施密特数Sc表示为SST的函数,计算公式为[8]
| $ \begin{gathered} S_c=2\;116.8-136.25 S S T+4.735\;3 S S T^2- \\ \quad 0.092\;307 S S T^3+0.000\;755\;5 S S T^4 。\end{gathered} $ | (17) |
式中SST的单位为℃。可见海水温度越高,Sc越小,气体交换速率越大。
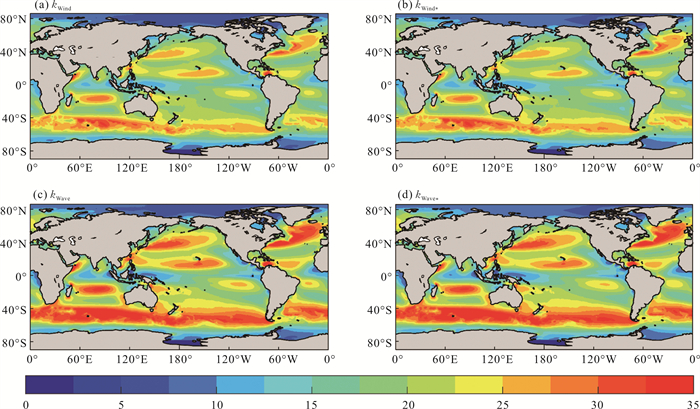
图 9为四种不同的气体交换速率参数化方案计算的1990—2019年的平均气体交换速率。考虑Sc指数n变化和波浪效应并不改变气体交换速率的空间结构,四者具有相似的空间分布,在南北半球的西风带海域、太平洋热带海域、大西洋热带海域和10°S—25°S的印度洋出现强度在35 cm/h左右的高值区,这与这些海域的信风或季风相关。北半球西风带的东部海区由于其夏季的气体交换速率较小,所以其气体交换速率的气候态平均值较西部海区要小。西北印度洋索马里洋流海区风速平均值并不大,但该海区受夏季季风的影响,会出现50 cm/h的气体交换速率,导致该海区的气候态平均值较大。太平洋的赤道东部和大西洋的赤道西部受信风影响,出现25 cm/h左右的高值区,除此之外的赤道海域以及高纬度海域的气体交换速率较小。
|
图 9 1990—2019年气体交换速率k(填色,单位:cm/h)的平均空间分布 Fig. 9 Mean spatial distribution of gas transfer velocity k (shaded, Unit: cm/h) from 1990 to 2019 |
从年平均值来看,kWind、kWind *、kWave和kWave *的年平均值分别为17.82、17.96、19.73和19.89 cm/h,可见,指数n变化使年平均值减小,而波浪效应使年平均值增大,指数n变化和波浪效应对气体交换速率具有抵消效应,从而使得kWind *和kWave的年平均值较为接近。换句话说,传统上的计算方法忽略了两种效应,并没有使估算值更加远离真实值,而是由于两种效应的抵消,使得传统的结果会接近真实值。
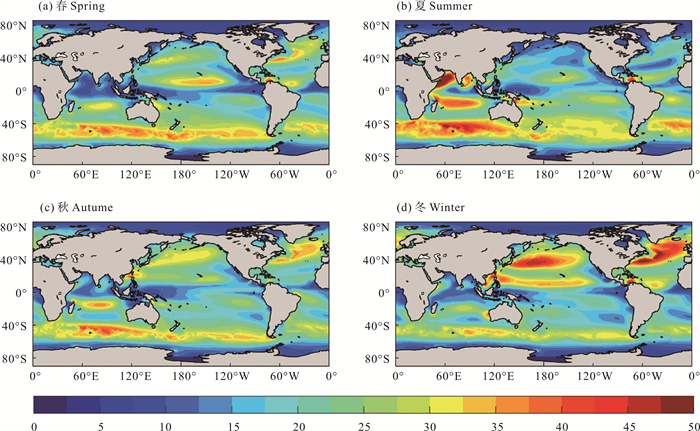
图 10为1990—2019年kWave的气候态季节平均气体交换速率。春季,最大值出现在太平洋热带海域、大西洋热带海域、10°S—25°S的印度洋以及南大洋,最大值为35 cm/h左右;夏季,索马里洋流海域出现明显的最大值,受季风的影响,此处的气体交换速率可达到50 cm/h左右,另外,南大洋也出现强度在45 cm/h左右的交换速率,北太平洋以及北大西洋的气体交换速率小于南太平洋及南大西洋;秋季的气体交换速率空间分布与春季相似,在太平洋热带海域和大西洋热带海域的气体交换速率有所减少;冬季,气体交换速率最大值出现在北半球的西风带,强度为50 cm/h左右,此时北大太平洋及北大西洋的气体交换速率大于南太平洋与南大西洋,与夏季相反。
|
图 10 1990—2019年气体交换速率kWave(填色,单位:cm/h)季节平均的空间分布 Fig. 10 Spatial distribution of seasonally averaged gas transfer velocity kWave (shaded, Unit: cm/h) from 1990 to 2019 |
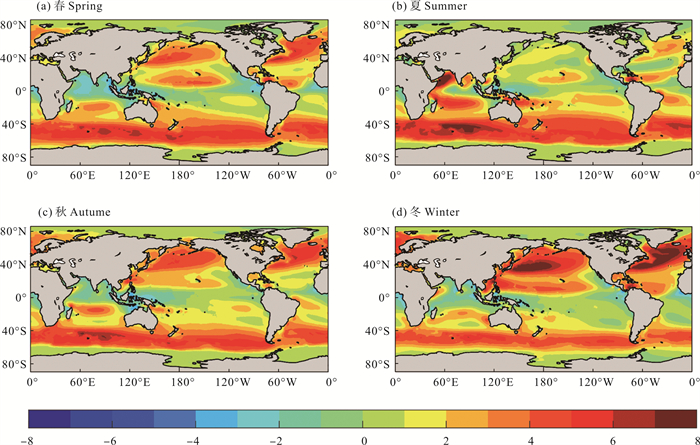
由波浪引起差异kWave -kWind的季节变化如图 11所示。整体而言,波浪效应使得全球海-气界面的气体交换速率增大,最大差异为12.65 cm/h,仅在部分赤道海域和高纬度海域气体交换速率减小,最大负差异为-5.66 cm/h。总体上,波浪效应引起的差异使得赤道海域(10°S—10°N)和南北半球西风带海域(40°N/S—60°N/S)的气体交换速率分别增大0.2%、18.7%和16.2%。波浪效应对赤道海域的影响主要体现春季和夏季,在春季的气体交换速率减小2.7%,夏季的气体交换速率增大3.7%;北半球西风带海域在冬季差异最大,气体交换速率增大19.5%;南半球西风带海域在夏季差异最大,气体交换速率增大19.5%。
|
图 11 1990—2019年气体交换速率kWave-kWind(填色,单位:cm/h)季节平均的空间分布 Fig. 11 Spatial distribution of seasonally averaged gas transfer velocity kWave-kWind (shaded, Unit: cm/h) from 1990 to 2019 |
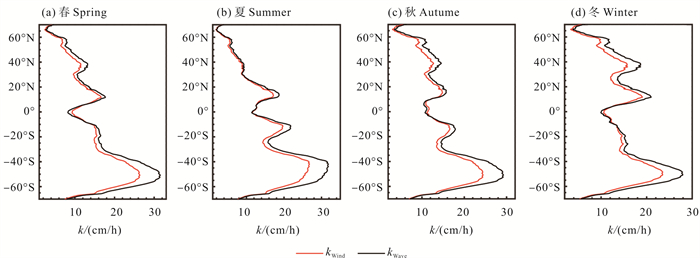
图 12为kWind和kWave季节纬向平均。气体交换速率在高纬度海域最低。春季、秋季和冬季在南北纬15°和45°左右出现四个峰值;夏季,北纬45°的峰值消失。气体交换速率的经向分布整体上呈现从较低的中心到两端先高后低的特征,主要与行星风带的分布有关,赤道海域气体交换速率较低;低纬度海域由信风控制,气体交换速率在四个季节都呈现出较高的值;中纬度海域受西风带的影响,该海域气体交换速率最大;中纬度海域气体交换受季节变化的影响,北半球冬季的气体交换速率较大,夏季较小。南半球夏季的气体交换速率较大,冬季较小。并且由于南半球的陆地面积相对较少,西风在全年都较强,所以南半球的气体交换速率常年都呈现出很高的值。
|
( 黑线和红线分别为kWave和kWind的结果。The black and red lines are the results of kWave and kWind, respectively. ) 图 12 1990—2019年气体交换速率kWave和kWind季节平均的纬向分布 Fig. 12 Latitudinal distribution of seasonally averaged gas transfer velocity kWave and kWind from 1990 to 2019 |
从图 12可以看到,夏季在赤道海域,kWave与kWind相当,其余季节kWave比kWind小,尤其以春季最为明显,说明该海域除夏季外的低风速和涌浪抑制了气体交换速率;在南北半球的西风带海域,kWave比kWind大,南半球四个季节的差异不明显,北半球以冬季最为明显。
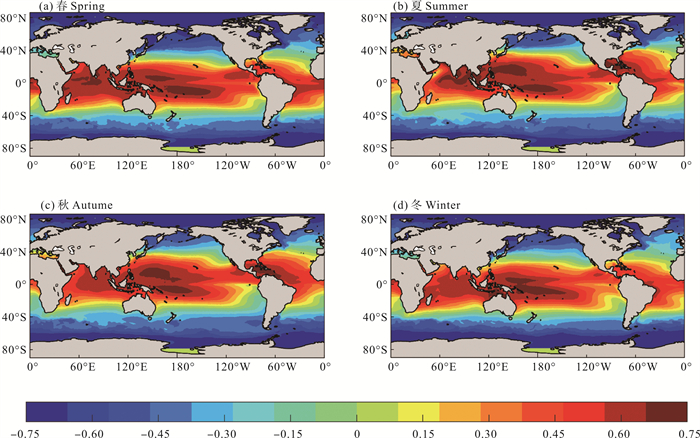
为了定量分析指数n变化对气体交换速率的影响,图 13给出了kWind -kWind *的季节平均分布。在低纬度和高纬度海域由施密特指数n引起的差异最大,中纬度海域差异较小。总体上,n的变化使低纬度海域(30°S—30°N)的气体交换速率增大2.3%,使高纬度海区(60°N/S—90°N/S)的气体交换速率减少6.1%。四个季节中,在热带海域会出现较大的正差异,约为0.98 cm/h;在高纬度海域会出现较大的负差异,约为-0.81 cm/h。春季,n的变化使低纬度海区(高纬度海区)的气体交换速率增大2.5%(减小6.2%);夏季,使低纬度海区(高纬度海区)的气体交换速率增大2.1%(减少6.6%);秋季,使低纬度海区(高纬度海区)的气体交换速率增大2.3%(减少5.8%);冬季,使低纬度海区(高纬度海区)的气体交换速率增大2.3%(减少6.2%)。低纬度海区在春季的差异最大,高纬度海区在夏季差异最大。
|
图 13 1990—2019年气体交换速率kWind -kWind * (填色,单位:cm/h)季节平均空间分布 Fig. 13 Spatial distribution of seasonally averaged gas transfer velocity kWind -kWind * (shaded, Unit: cm/h) from 1990 to 2019 |
从上面的讨论再次看到,波浪效应和指数n变化对气体交换速率的影响有相互抵消效应,即波浪效应(指数n变化)使赤道海域气体交换速率减小(增大),使西风带海域气体交换速率增大(减小)。
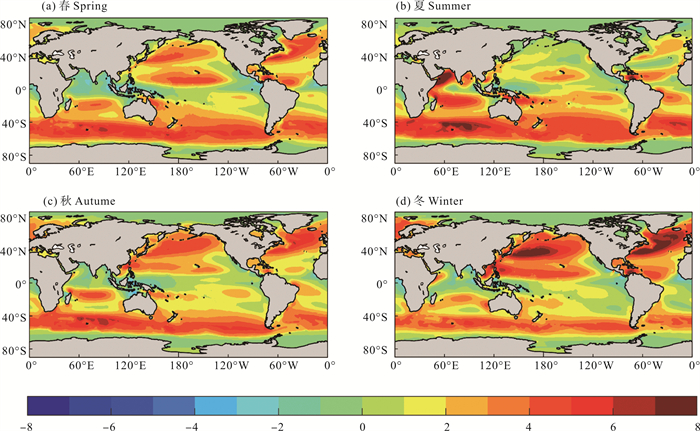
为了定量分析波浪效应和指数n变化对气体交换速率联合影响,图 14为kWave -kWind *的季节平均分布。
|
图 14 1990—2019年气体交换速率kWave-kWind *(填色,单位:cm/h)季节平均气空间分布 Fig. 14 Spatial distribution of seasonally averaged gas transfer velocity kWave -kWind * (shaded, Unit: cm/h) from 1990 to 2019 |
波浪效应和指数n变化联合引起的差异使得赤道海域(10°S—10°N)和南北半球西风带海域的气体交换速率分别增大3.7%、13.9%和13.6%。赤道海域在夏季差异最大,气体交换速率增大6.9%;北半球西风带海域在冬季差异最大,气体交换速率增大17.4%;南半球西风带海域在夏季差异最大,气体交换速率增大17.5%。在西风带海域,相较于波浪效应所带来的影响,由波浪效应和指数n变化联合引起的影响有所减小,这是两者相互抵消所带来的;在赤道海域,波浪效应和指数n变化联合引起的影响使得气体交换速率进一步增大。
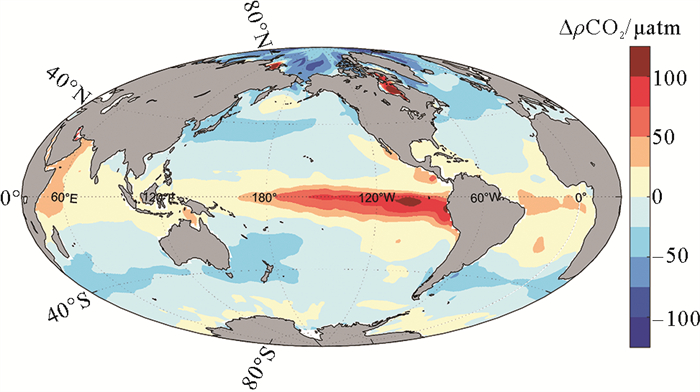
4 海-气界面CO2通量图 15为1990—2019年海-气界面ΔpCO2的气候态空间分布,低纬度海域为大气CO2的源区,尤其是赤道东太平洋以及西北印度洋,这些海域主要受到上升流的影响,上升流将富含碳的深层水带到表层,最终导致CO2排出海洋;中纬度海域主要为大气CO2的汇区;北半球高纬度海域为大气CO2的汇区,这可能是由于北冰洋海冰融化,促进了海水的通风过程[47];南半球高纬度海域为大气CO2的源,这主要与该海域的上升流有关。
|
( 图中数据基于Landschützer等[44]创建的海洋表层CO2数据。正值为源,海洋释放CO2,负值为汇,海洋吸收CO2。The data in the figure are based on ocean surface CO2 data created by Landschützer et al [44]. Positive values are sources, where the ocean releases CO2 and negative values are sinks, where the ocean absorbs CO2. ) 图 15 1990—2019年海-气界面CO2分压差的气候态空间分布 Fig. 15 Spatial distribution of climate regimes of CO2 partial pressure difference at the air-sea interface from 1990 to 2019 |
计算海-气界面CO2通量时,需要给出海水溶解度,海水溶解度由下式计算[48]:
| $ \begin{gathered} \ln (s)=A_1+A_2 \ln \frac{100}{S S T}+A_3 \ln \left(\frac{S S T}{100}\right)+ \\ S\left[B_1+B_2 \frac{S S T}{100}+B_3\left(\frac{S S T}{100}\right)^2\right]。\end{gathered} $ | (18) |
式中:SST的单位为K;S为海表面盐度;A1= -58.093 1;A2=90.506 9;A3=22.294 0;B1=0.027 766;B2=-0.025 888;B3=0.005 057 8。
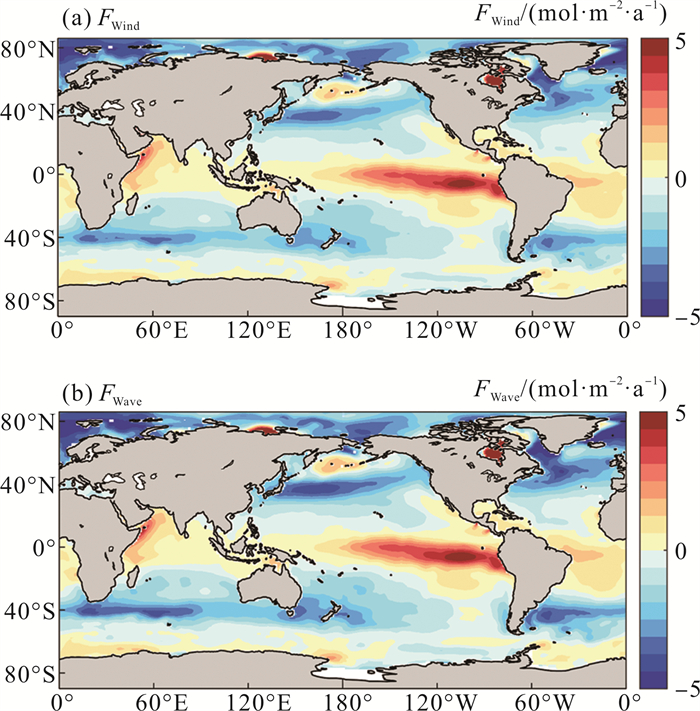
图 16为基于kWind和kWave计算得到的1990—2019年的年平均海-气CO2通量,相应的通量分别用FWind和FWave表示。空间上均在赤道东太平洋海域出现强度为5 mol·m-2·a-1左右的源区,在南北纬40°海域出现强度为-4 mol·m-2·a-1左右的汇区;北半球高纬度海域汇的强度最大,均为-5 mol·m-2·a-1左右。
|
( FWind是基于Landschützer等[44]的CO2分压数据集和kWind所计算出的通量结果,FWave是利用kWave所计算出的结果。FWind is the result of fluxes calculated based on the CO2 partial pressure dataset of Landschützer et al[44] and kWind, and FWave is the result calculated using kWave. ) 图 16 基于kWind和kWave计算的1990—2019年海-气界面CO2通量的年平均空间分布 Fig. 16 Annual mean spatial distribution of CO2 flux at the air-sea interface based on kWind and kWave calculations from 1990 to 2019 |
图 16(a)和16(b)的差异主要体现在赤道东太平洋、40°N/S海域和南极洲附近,图 16(b)中赤道东太平洋的源强度有所降低,而40°N/S海域的汇强度有所增强,这是由波浪效应所引起的差异。
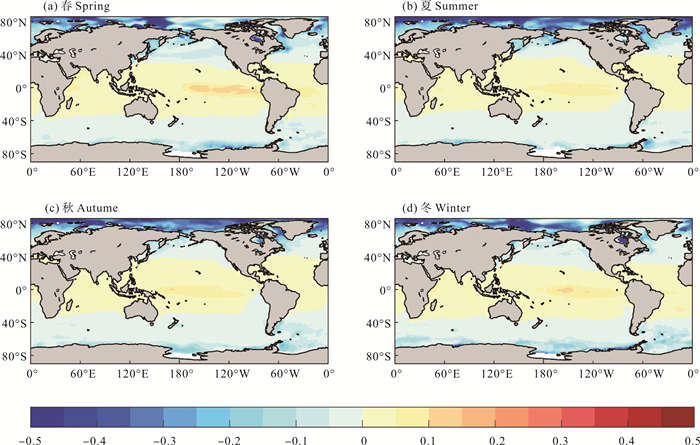
为了定量说明指数n变化对海-气界面CO2通量的影响,图 17给出了FWind与FWind *之间差值|FWind|- |FWind *|在2010年的季节平均分布。FWind *为基于气体交换速率kWind *计算的通量。这里取通量的绝对值是为了更容易看出二氧化碳源汇的变化情况。
|
图 17 2010年季节平均CO2通量|FWind|-|FWind *|(填色,单位:mol·m-2·a-1)的空间分布 Fig. 17 Spatial distribution of seasonally averaged CO2 flux |FWind|-|FWind *| (shaded, Unit: mol·m-2·a-1) in 2010 |
从图中可以看到,指数n的变化对低纬度太平洋(15°S—15°N;150°E—100°E) 以及南北半球的高纬度海区(60°N/S—90°N/S)产生的影响较大,使低纬度太平洋的通量值增大2.4%,使北半球高纬度海区的通量值减小8.2%,使南半球高纬度海区的通量值减小5.2%。在低纬度太平洋,受到影响最大的季节在春季,可使通量值增大3.1%;在北半球高纬度海区,受到影响最大的季节在夏季,可使通量值减小9.4%;在南半球高纬度海域,受影响最大的季节在冬季,可使通量值减小6.2%。
考虑指数n变化后,导致2010年源区的强度增强1.9%,排出气体增多,导致汇区的强度降低1.9%,吸收气体减少,总体上导致2010年海洋吸收CO2减少4.2%。
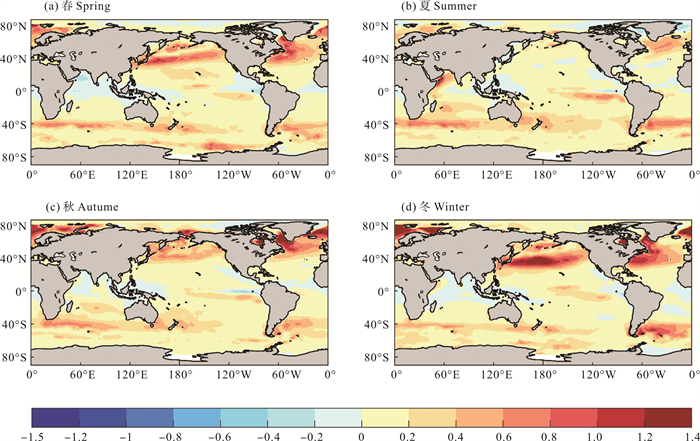
为了定量说明波浪效应对海-气界面CO2通量的影响,图 18给出了2010年|FWave |-|FWind |的季节平均分布。从图中可以看到,考虑波浪效应后,对通量的影响主要体现在赤道东太平洋(5°S—5°N,180°—100°E) 以及南北半球的西风带海域, 使赤道东太平洋和南北半球西风带海域的通量值分别增大4.8%、18.1%和16.7%。对于赤道东太平洋海域,在冬季受到的影响最大,考虑波浪效应后可使通量值增大6.5%;对于北半球的西风带,该海区在冬季受到的影响最大,考虑波浪效应后可使通量值增大19.6%;对于南半球的西风带海域,在夏季受到的影响最大,可使通量值增大19.1%。
|
图 18 2010年季节平均CO2通量差异|FWave|-|FWind|(填色,单位:mol·m-2·a-1)的空间分布 Fig. 18 Spatial distribution of seasonally averaged CO2 flux |FWave|-|FWind| (shaded, Unit: mol·m-2·a-1) in 2010 |
考虑了海浪效应后,气体交换速率不仅随着风速变化,同时也受到这些波浪参数的影响。在相同风速下,气体交换速率随着波浪的发展而增大。在西风带海域,波浪的发展较为充分,相较于风速的参数化方案,考虑波浪的发展会使得气体交换速率明显增大,同时该海域也是大气CO2的汇区,最终导致汇区的强度增强;考虑海浪参数后会使得气体交换速率在整体上小幅度增大,导致低纬度海域的源强度增强。波浪效应使得2010年海洋的源区和汇区强度分别增强4.8%和15.2%,最终导致2010年海洋吸收CO2增强21.8%。
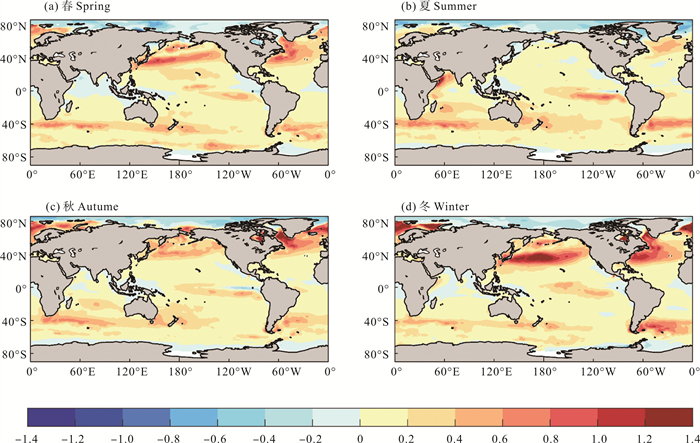
为了定量说明波浪效应和指数n变化对海-气界面CO2通量的联合影响,图 19给出了2010年|FWave |-|FWind * |的季节平均分布。从图中可以看到,两种效应对CO2通量的联合影响主要体现在西风带海域和赤道东太平洋海域。总体而言,联合影响使赤道东太平洋海域和南北半球的西风带海域的通量值分别增大7.4%、16.0%和13.9%。对于赤道东太平洋海域,在冬季受到的影响最大,使得通量值增大9.2%;在北半球的西风带海域,在冬季受到的影响最大,使得通量值增大17.0%;在南半球的西风带海域,在夏季受到的影响最大,使得通量值增大17.3%。
|
图 19 2010年季节平均CO2通量差异|FWave|-|FWind *|(填色,单位:mol·m-2·a-1)的空间分布 Fig. 19 Spatial distribution of seasonally averaged CO2 flux |FWave|-|FWind *| (shaded, Unit: mol·m-2·a-1) in 2010 |
在西风带海域,波浪效应和指数n变化对海-气界面CO2通量的联合效应减小了波浪效应对海-气界面CO2通量的影响,这是两种效应相互抵消后的结果。在赤道海域,两种效应联合增大了波浪效应对海-气界面CO2通量的影响。联合效应使得2010年海洋的源区和汇区强度分别增强6.8%和13.0%,最终导致2010年海洋吸收CO2增强16.7%。
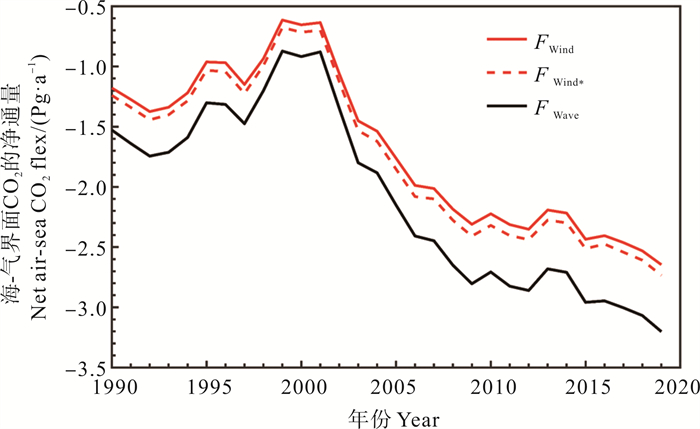
图 20为1990—2019年海-气界面净CO2通量年变化曲线。基于FWind、FWave、FWind *得到的年均净通量分别为-1.68、-2.09和-1.76 Pg/a,可见考虑波浪效应整体上使海洋吸收CO2增强。在1999年左右,海洋对CO2的吸收达到最小值,最小值分别为-0.61(FWind)和-0.87(FWave) Pg·a-1,考虑波浪效应后使最小值的通量值增大42.6%;2019年海洋对CO2的吸收达到最大,为-2.65(FWind)和-3.20(FWave) Pg·a-1,考虑波浪效应后使最大通量增大20.1%。图中特别给出了基于FWind *计算的结果,可见,同时忽略波浪效应和指数n变化时,并未使估算值更加远离真实值,而是在一定程度上使计算结果接近真实净通量值。
|
( 红色实线为公式(15)所得的通量结果,红色虚线为在公式(15)基础上不考虑施密特指数变化后的结果,黑色实线为公式(16)所得的通量结果。The red solid line is the flux result obtained from Eq.(15); The red dashed line is the result after disregarding the change in Schmidt index on the basis of Eq.(15); The black solid line is the flux result obtained from Eq.(16). ) 图 20 1990—2019年基于FWind和FWave、FWind *计算的海-气界面CO2净通量年变化 Fig. 20 Annual changes in net CO2 flux at the air-sea interface based on FWind、FWave and FWind * calculations from 1990 to 2019 |
本文基于前人的实验室和外海观测数据,提出了以波龄和风海雷诺数为变量的双参数气体交换速率公式。该公式可以很好地协调实验室和外海观测数据,同时可适用于风浪和涌浪情形,在此基础上,进一步考虑施密特数指数n变化对气体交换速率的影响。
研究表明,施密特指数n的变化使低纬度海域(30°S— 30°N)的气体交换速率增大2.3%,使高纬度海区(60°N/S—90°N/S)的气体交换速率减少6.1%;考虑波浪效应后,使得赤道海域(10°S—10°N)和南北半球的西风带海域(40°N/S—60N/S°)的气体交换速率分别增大0.2%、18.7%和16.2%;波浪效应和指数n变化联合引起的差异使得赤道海域(10°S—10°N)和南北半球西风带海域的气体交换速率分别增大3.7%、13.9%和13.6%。
考虑施密特指数n的变化后,使低纬度太平洋的通量值增大2.4%,南北半球高纬度海区的通量值分别减小5.2%和8.2%,导致2010年源区的强度增强1.9%,汇区的强度降低1.9%,总体上2010年海洋吸收CO2减少4.2%。考虑波浪效应后,使赤道东太平洋(5°S—5°N,180°—100°E)以及南北半球的西风带海域的通量值分别增大4.8%、18.1%和16.7%;波浪效应使得2010年海洋的源区和汇区的强度分别增强4.8%和15.2%,最终导致2010年海洋吸收CO2增强21.8%。两种效应对CO2通量的联合影响使赤道东太平洋海域和南北半球西风带海域的通量值分别增大7.4%、16.0%和13.9%;联合效应使得2010年海洋的源区和汇区的强度分别增强6.8%和13.0%,最终导致2010年海洋吸收CO2增强16.7%。
本文的研究成果对海-气界面气体交换速率的参数化和CO2通量的评估具有重要的参考意义。然而,由于实验室中的气体交换速率数据缺少部分海浪参数,会给参数化带来一定的不确定性。此外,高纬度海域海浪参数的缺失会对气体交换速率和CO2通量评估带来一定的误差。因此,需要在未来的研究中获取更多完善的数据, 减少这种不确定性及误差。
| [1] |
Friedlingstein P, O′Sullivanet M, Jones M, et al. Global Carbon budget 2022[J]. Earth System Science Data, 2022, 14: 4811-4900. DOI:10.5194/essd-14-4811-2022 (  0) 0) |
| [2] |
Khatiwala S, Tanhua T, Mikaloff S, et al. Global ocean storage of anthropogenic carbon[J]. Biogeosciences, 2013, 10(4): 2169-2191. DOI:10.5194/bg-10-2169-2013 (  0) 0) |
| [3] |
董原旭, 赵栋梁, 邹仲水. 海-气界面气体交换速率和全球海洋CO2通量的初步研究[J]. 中国海洋大学学报(自然科学版), 2017, 47(12): 1-8. Dong Y X, Zhao D L, Zhong Z S. A preliminary study on sea-air gas transfer velocity and global ocean CO2 flux[J]. Periodical of Ocean University of China, 2017, 47(12): 1-8. (  0) 0) |
| [4] |
宋朝阳, 赵栋梁, 张宇铭. 气体交换速率和时间平均尺度对海-气碳通量估计的影响[J]. 海洋学报, 2013, 35(4): 72-79. Song Z Y, Zhao D L, Zhang M Y. Influence of air-sea transfer velocity and average timescale on the estimation of air-sea CO2 flux[J]. Acta Oceanologica Sinica (in Chinese), 2013, 35(4): 72-79. DOI:10.3969/j.issn.0253-4193.2013.04.009 (  0) 0) |
| [5] |
姜亦飞, 吕洪刚, 季轩梁, 等. 气候变化背景下海-气CO2通量获取方法综述[J]. 海洋预报, 2015, 32(3): 84-91. Jiang Y F, Lv H G, Ji X L, et al. A review of the methods to obtain the air-sea CO2 flux under the background of climate change[J]. Marine Forecasts, 2015, 32(3): 84-91. (  0) 0) |
| [6] |
Weiss R F. Carbon dioxide in water and seawater: The solubility of a non-ideal gas[J]. Marine Chemistry, 1974, 2(3): 203-215. DOI:10.1016/0304-4203(74)90015-2 (  0) 0) |
| [7] |
Zhao D L, Toba Y, Siziki Y, et al. Effect of wind waves on air-sea gas change: Proposal of an overall CO2 transfer velocity formula as a function of breaking-wave parameter[J]. Tellus Series B-Chemical and Physical Meteorology, 2003, 55(2): 478-487. (  0) 0) |
| [8] |
Wanninkhof R. Relationship between wind speed and gas exchange over the ocean revisited[J]. Limnology and Oceanography: Methods, 2014, 12(6): 351-362. DOI:10.4319/lom.2014.12.351 (  0) 0) |
| [9] |
Wanninkhof R. Relationship between wind speed and gas exchange over the ocean[J]. Journal of Geophysical Research: Oceans, 1992, 97(C5): 7373-7382. DOI:10.1029/92JC00188 (  0) 0) |
| [10] |
Nagel L, Krall K E, Jähne B. Measurements of air-sea gas transfer velocities in the Baltic Sea[J]. Ocean Science, 2019, 15(2): 235-247. DOI:10.5194/os-15-235-2019 (  0) 0) |
| [11] |
Nightingale P D. In situ evaluation of air-sea gas exchange parameterizations using novel conservative and volatile tracers[J]. Global Biogeochemical Cycles, 2000, 14(1): 373-387. DOI:10.1029/1999GB900091 (  0) 0) |
| [12] |
McGillis W R, Edson J B, Zappa C J, et al. Air-sea CO2 exchange in the equatorial Pacific[J]. Journal of Geophysical Research, 2004, 109(C8). DOI:10.1029/2003JC002256 (  0) 0) |
| [13] |
David T, Cliff S L, Murray J S, et al. Reply to comment by X. Zhang on "Measurements of air-sea gas exchange at high wind speeds in the Southern Ocean: Implications for global parameterizations"[J]. Journal of Geophysical Research Letters, 2007, 34(23). DOI:10.1029/2007GL030943 (  0) 0) |
| [14] |
Edson J B, Fairall C W, Bariteau L, et al. Direct covariance measurement of CO2 gas transfer velocity during the 2008 Southern Ocean Gas Exchange Experiment: Wind speed dependency[J]. Journal of Geophysical Research: Oceans, 2011, 116(C4). DOI:10.1029/2011JC007022 (  0) 0) |
| [15] |
Yang M X, Bell T G, Bidlot J, et al. Global synthesis of air-sea CO2 transfer velocity estimates from ship-based eddy covariance measurements[J]. Frontiers in Marine Science, 2022, 9. DOI:10.3389/fmars.2022.826421 (  0) 0) |
| [16] |
Esters L, Landwehr S, Sutherland G, et al. Parameterizing air-sea gas transfer velocity with dissipation[J]. Journal of Geophysical Research Oceans, 2017, 122: 3041-3056. DOI:10.1002/2016JC012088 (  0) 0) |
| [17] |
Woolf D K. Parametrization of gas transfer velocities and sea-state-dependent wave breaking[J]. Tellus B: Chemical and Physical Meteorology, 2005, 57(2): 87-94. DOI:10.3402/tellusb.v57i2.16783 (  0) 0) |
| [18] |
Zhao D L, Xie L. A practical bi-parameter formula of gas transfer velocity depending on wave states[J]. Journal of Oceanography, 2010, 66: 663-671. DOI:10.1007/s10872-010-0054-4 (  0) 0) |
| [19] |
Li S Q, Zhao D L. Gas transfer velocity in the presence of wave breaking[J]. Tellus B: Chemical and Physical Meteorology, 2016, 68(1): 1-16. (  0) 0) |
| [20] |
Brumer S E, Zappa C J, Blomquist B W, et al. Wave-related reynolds number parameterizations of CO2 and DMS transfer velocities[J]. Geophysical Research Letters, 2017, 44: 9865-9875. DOI:10.1002/2017GL074979 (  0) 0) |
| [21] |
Deike L, Melville W K. Gas transfer by breaking waves[J]. Geophysical Research Letters, 2018, 45: 10482-10492. (  0) 0) |
| [22] |
Li S, Babanin A V, Qiao F L, et al. Laboratory experiments on CO2 gas exchange with wave breaking[J]. Journal of Physical Oceanography, 2021, 51(10): 3105-3116. (  0) 0) |
| [23] |
Jähne B, Münnich K O, Bösinger R, et al. On the parameters influencing air-water gas exchange[J]. Journal of Geophysical Research: Oceans, 1987, 92: 1937-1949. DOI:10.1029/JC092iC02p01937 (  0) 0) |
| [24] |
Frew N M, Bock E J, Schimpf U, et al. Air-sea gas transfer: Its dependence on wind stress, small-scale roughness, and surface films[J]. Journal of Geophysical Research, 2004. DOI:10.1029/2003JC002131 (  0) 0) |
| [25] |
Zappa C J, Asher W, Jessup A. Microscale wave breaking and air-water gas transfer[J]. Journal of Geophysical Research, 2001, 106: 9385-9391. DOI:10.1029/2000JC000262 (  0) 0) |
| [26] |
Zappa C J, Asher W E, Jessup A T, et al. Microbreaking and the enhancement of air-water transfer velocity[J]. Journal of Geophysical Research, 2004, 109(C8). DOI:10.1029/2003JC001897 (  0) 0) |
| [27] |
Zhao D L, Toba Y. Dependence ofwhitecap coverage on wind and wind-wave properties[J]. Journal of Oceanography, 2001, 57: 603-616. DOI:10.1023/A:1021215904955 (  0) 0) |
| [28] |
McGillis W R, Edson J B, Hare J E, et al. Direct covariance air-sea CO2 fluxes[J]. Journal of Geophysical Research, 2001, 106(C8): 729-745. (  0) 0) |
| [29] |
Edson J B, Fairall C W, Bariteau L, et al. Direct covariance measurement of CO2 gas transfer velocity during the 2008 Southern Ocean Gas Exchange Experiment: Wind speed dependency[J]. Journal of Geophysical Research: Oceans, 2011, 116(C4). DOI:10.1029/2011JC007022 (  0) 0) |
| [30] |
McNeil C, D′Asaro E. Parameterization of air-sea gas fluxes at extreme wind speeds[J]. Journal of Marine Systems, 2007, 66(1-4): 110-121. DOI:10.1016/j.jmarsys.2006.05.013 (  0) 0) |
| [31] |
Wanninkhof R, Asher W, Weppernig R, et al. Gas transfer experiment on Georges Bank using two volatile deliberate tracers[J]. Journal of Geophysical Research, 1993, 98(C11): 20237-20248. DOI:10.1029/93JC01844 (  0) 0) |
| [32] |
Ho D T, Law C S, Smith M J, et al. Measurements of air-sea gas exchange at high wind speeds in the Southern Ocean: Implications for global parameterizations[J]. Geophysical Research Letters, 2006, 33(16): 1-6. (  0) 0) |
| [33] |
Ho D T, Wanninkhof R. Air-sea gas exchange in the North Atlantic: 3He/SF6 experiment during GasEx-98[J]. Tellus B, 2016, 68(1): 1-10. (  0) 0) |
| [34] |
Wanninkhof R, Sullivan K F, Top Z. Air-sea gas transfer in the Southern Ocean[J]. Journal of Geophysical Research, 2004, 109(C8). DOI:10.1029/2003JC001767 (  0) 0) |
| [35] |
Iwano K, Takagaki N, Kurose R, et al. Mass transfer velocity across the breaking air-water interface at extremely high wind speeds[J]. Tellus B, 2013, 65(1): 1-8. (  0) 0) |
| [36] |
Krall K E, Jähne B. First laboratory study of air-sea gas exchange at hurricane wind speeds[J]. Ocean Science, 2014, 10(2): 257-265. DOI:10.5194/os-10-257-2014 (  0) 0) |
| [37] |
Krall K E, Smith A W, Takagaki N, et al. Air-sea gas exchange at wind speeds up to 85 m · s-1[J]. Ocean Science, 2019, 15(6): 1783-1799. DOI:10.5194/os-15-1783-2019 (  0) 0) |
| [38] |
Tokoro T, Kayanne H, Watanabe A, et al. High gas-transfer velocity in coastal regions with high energy-dissipation rates[J]. Journal of Geophysical Research, 2008, 113(C11). DOI:10.1029/2007JC004528 (  0) 0) |
| [39] |
Banko-Kubis H M, Wurl O, Mustaffa N L H, et al. Gas transfer velocities in Norwegian fjords and the adjacent North Atlantic waters[J]. Oceanologia, 2019, 61: 460-470. DOI:10.1016/j.oceano.2019.04.002 (  0) 0) |
| [40] |
Nagel L, Krall K E, Jähne B. Comparative heat and gas exchange measurements in the Heidelberg Aeolotron, a large annular wind-wave tank[J]. Ocean Science, 2015, 11(1): 111-120. DOI:10.5194/os-11-111-2015 (  0) 0) |
| [41] |
Landschützer P, Gruber N, Bakker D C E. Decadal variations and trends of the global ocean carbon sink[J]. Global Biogeochem Cycles, 2016, 30: 1396-1417. DOI:10.1002/2015GB005359 (  0) 0) |
| [42] |
Hasselmann K, Barnett T, Bouws E, et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP)[J]. Deut Hydrogr Z, 1973, 8: 1-95. (  0) 0) |
| [43] |
Wu J. Wind-stress coefficients over Sea surface near neutral conditions: A revisit[J]. Journal of Physical Oceanography, 1980, 10(5): 727-740. DOI:10.1175/1520-0485(1980)010<0727:WSCOSS>2.0.CO;2 (  0) 0) |
| [44] |
Yasunaka S, Murata A, Watanabe E, et al. Mapping of the air-sea CO2 flux in the Arctic Ocean and its adjacent seas: Basin-wide distribution and seasonal to interannual variability[J]. Polar Science, 2016, 10(3): 323-334. DOI:10.1016/j.polar.2016.03.006 (  0) 0) |
| [45] |
Gu Y Y, Katul G G, Cassar N. The intensifying role of high wind speeds on air-sea carbon dioxide exchange[J]. Geophysical Research Letters, 2021, 48(5). DOI:10.1029/2020GL090713 (  0) 0) |
2. College of Oceanography, Hebei Agricultural University, Qinhuangdao 066000, China
 2024, Vol. 54
2024, Vol. 54


