2. 中国海洋大学物理海洋教育部重点实验室, 山东 青岛 266100;
3. 南方科技大学海洋科学与工程系, 广东 深圳 518055;
4. 青岛海洋科学与技术试点国家实验室 海洋地质过程与环境功能实验室, 山东 青岛 266000
黄河是中国入海大河中含沙浓度最高的河流,多年平均结果显示黄河泥沙入海量高达109 t/年[1]。黄河泥沙在渤海和黄海的输运机制和源汇过程等问题一直受到科学家的关注,但是在黄河泥沙入海后的再分配问题上至今仍有很大争论。尤其是Milliman等[2]首先发现了山东半岛东南存在水下沉积体,在随后的研究中认为沉积体的物质来自黄河泥沙并把它称为山东水下三角洲[3-4]。Liu等[5]通过综合分析鲁北海域的2个钻孔和约1 700 km浅层地震测线解释了山东水下三角洲的成因。针对本区域这一输运体系,国内外学者通过钻孔沉积物分析、地球物理测线剖面解析、数值模拟等方法开展了大量研究[6-14]。然而本海域的现场原位观测比较缺乏,尤其是缺乏底边界层沉积动力观测数据,无法直接认识和确定沉积物在海底的起动、输运和沉积的动力过程和机制。
本文依托国家自然科学基金“黄河沉积物环山东半岛陆架的搬运和沉积过程及机制研究”,在黄河泥沙绕过山东半岛向水下三角洲输运的关键海域(山东半岛成山角海域)进行了一次持续156 h的原位座底连续观测,利用获取的观测资料研究了该海区潮流、波浪对底边界层水动力和沉积物输运过程的影响,并建立了该海区潮流和波浪对底剪切应力和悬浮物浓度(SSC)影响的参数化公式,可以用于定量研究黄河泥沙向山东半岛南端水下三角洲的输运过程。
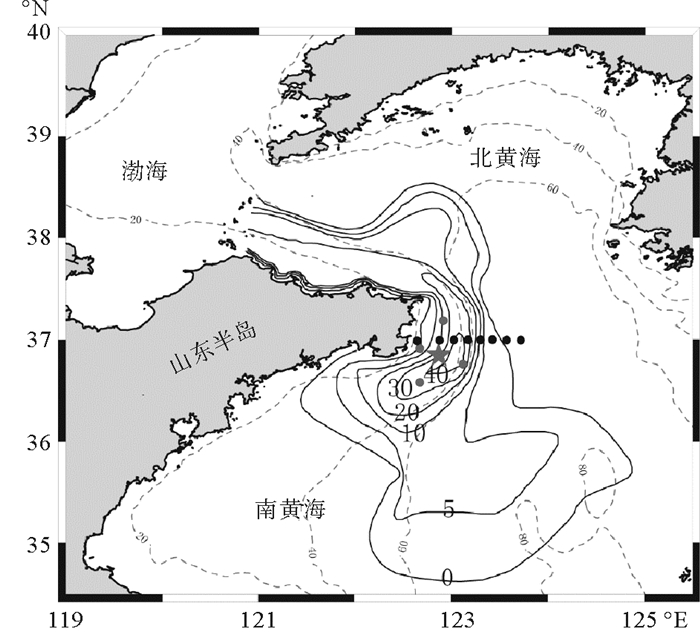
1 研究区域及方法观测站位(122°52.216′E,36°51.803′N)位于黄河沉积物向山东水下三角洲输运的关键通道—山东半岛成山角附近的黄海海域,观测站位的水深为27 m(见图 1)。该海域潮流类型为不规则半日潮,平均潮差较小,为0.75 m[15]。研究海域属于典型的季风气候,冬季盛行偏北风,平均风速6~7 m/s,夏季盛行南到东南风,平均风速为5~6 m/s[15]。研究站位所在海域底质类型为粘土质粉砂,其中粉砂含量可达40%~70%,其次为粘土,其含量为20%~50%[16]。
|
(五星标注的站位为本文研究站位。图中虚线为研究海区水深(单位:m),黑色实线为山东水下三角洲厚度分布[17]。The station labeled by the red star is used in this paper. The dotted line is the isobath of the study area (Unit: m), and the black solid line is the thickness distribution of the Shandong underwater delta.) 图 1 连续座底观测站位(红色五星和红点)和大面观测站位(黑点)分布图 Fig. 1 The distribution of mooring stations (red star and red dots) and transect stations (black dots) |
本文于2018年2月23日~3月2日在观测点放置座底三脚架平台,平台配备了一台高频点式流速仪(Nortek 6 MHz ADV)、一台浊度计(RBR-TU)和一台流速剖面仪(RDI WorkHorse 600 kHz ADCP),用以观测高频流速、浊度以及有效波高等,来换算底边界层湍混合强度、悬浮物浓度、水体流速和波浪状况。其中ADV以脉冲方式进行流速(u,v,w)采样,脉冲间隔为1 h,每次采样10 min,采样频率为32 Hz,采样体积位于距离海底71 cm处;RBR-TU每隔10 s记录一次浊度数据,采样点距离海底116 cm;ADCP设置为‘仰视’,本研究主要使用其波浪模块获取有效波高(Hs)和波周期(T)参数,采样时间间隔为20 min。除了本文研究所用的观测站,观测航次还在附近海域布放了其他四套海底边界层沉积物动力过程观测三脚架,并在37°N断面进行了SSC的大面观测(见图 1)。
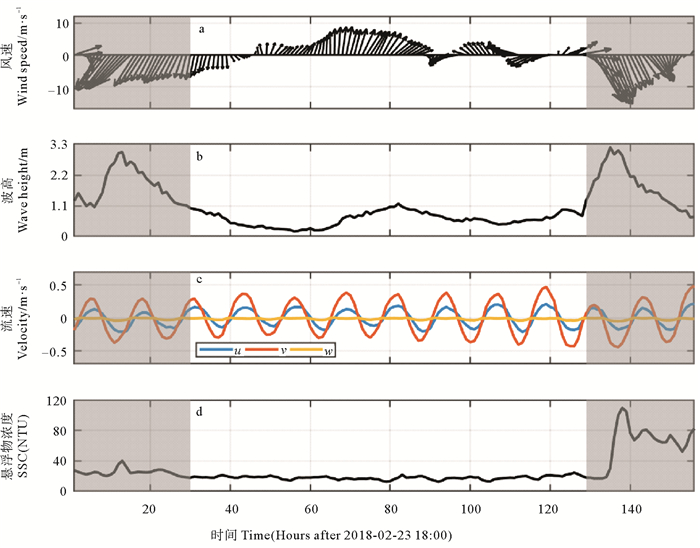
2 观测结果图 2所示为观测站位在观测期间的气象、水文和悬浮物分布情况。观测期间的风速资料来源于美国国家环境预报中心的气候预报系统NCEP CFSv2(NCEP Climate Forecast System version 2),据前人在东中国海的研究结果[18],NCEP风场数据与实测结果拟合度较高,相关系数达0.91。在观测初期(1~30 h)有一次较大的偏北风过程,最大风速可达13.33 m/s,随后风速变小,风向也变为南风,观测末期(129~156 h)又经历了一场较强的偏北风大风过程,风速最大达到16.42 m/s。图 2(b)中的有效波高结果来源于座底三脚架ADCP的测波模块。两次强风期间有效波高的最大值分别为3.02和3.19 m,而弱风期间有效波高的最大值仅为1.17 m。由于有效波高、悬浮物浓度等参数在两次强风期间明显升高,为方便讨论,我们以有效波高是否大于1 m为主要依据,将观测分为强风浪过程(见图 2阴影部分,除152~156 h外Hs>1 m)和弱风浪过程(见图 2非阴影部分,除80~83 h外Hs < 1 m)。观测站位的流速由ADV获取,将ADV在ENU坐标系下输出的高频流速做平均,得到u,v,w方向的10 min平均的流速时间序列(见图 2(c))。在观测期间,东西方向的最大流速约为0.21 m/s,南北方向的最大流速约为0.49 m/s。图 2(d)所示为观测站位的浊度时间序列,两次强风浪过程的浊度较弱风浪期间均有明显上升,且第二次强风浪过程的浊度峰值(109 NTU)远大于第一次强风浪过程的浊度峰值(40 NTU)。在强风浪过程临近结束时,第二次强风浪过程的浊度值也显著高于第一次强风浪过程。需要指出的是,前人在观测海区的研究表明,浊度跟悬浮物浓度基本是线性关系[19],为表述方便,本文直接将浊度计观测的浊度作为悬浮物浓度进行研究分析。此外,通过ADCP测量的水体剖面可以看出,底边界层的厚度约为4.1~4.6 m,ADV和RBR-TU的测量点位于海底边界层中的常应力层内,切应力不随深度变化。
|
(图中阴影区域为观测经历的两次强风浪过程。The shaded areas are observed during two strong wind waves.) 图 2 观测站位气象、水文和悬浮物浓度时间序列(a)风速与风向(b)有效波高(c)u,v,w方向平均流速(d)悬浮物浓度 Fig. 2 The time series of meteorological, hydrological and suspended sediment concentration (a) wind speed and direction (b) effective wave height (c) average velocity of u, v and w (d) suspended sediment concentration |
观测站位的底剪切应力(τ)由ADV高频流速数据计算得到,计算公式为:
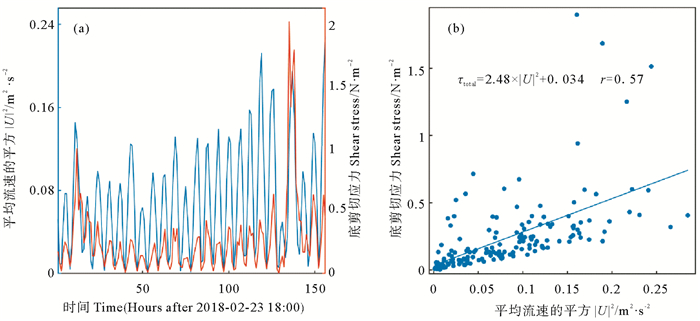
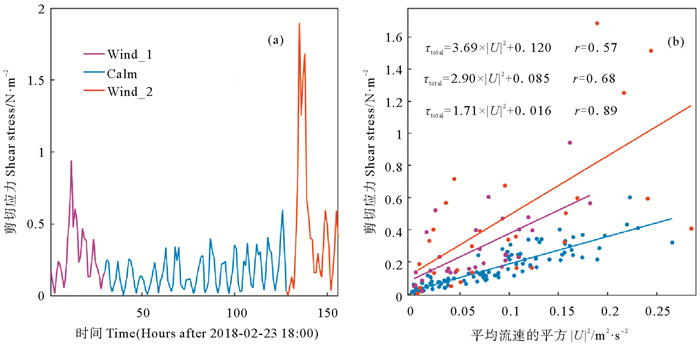
理论上,潮流流速大小(|U|)的平方跟潮致剪切应力成正比。如图 3(a)所示,观测期间的底剪切应力随流速大小变化而变化,但是在两次强风浪期间,底剪切应力会急剧升高。平均流速的平方与底剪切应力的线性拟合结果(见图 3(b))表明底剪切应力跟|U|2相关性较差(τtotal=2.48×|U|2+0.034,r=0.57)。这是由于在强风浪过程中,底剪切应力不再直接受控于潮流流速,浪致剪切应力可能起主导作用(见图 3(a))。为了区分潮流和风浪对底剪切应力的影响,我们按照图 2所示的三种风浪强度过程分别对|U|2和底剪切应力进行拟合(见图 4(a))。结果显示,在弱风浪期间,底剪切应力与潮流流速的相关系数较高(r=0.89),结合SPSS显著相关性检验结果(p=0.016),可认为底剪切应力受潮流流速控制,二者显著相关,其拟合关系式为:
|
图 3 (a) 观测期间平均流速的平方(|U|2)与底剪切应力(τtotal)的时间序列(b)观测期间平均流速的平方(|U|2)与底剪切应力(τtotal)的拟合关系 Fig. 3 (a)The time series of the square of mean velocity (|U|2) and bottom shear stress (τtotal) (b) The fitting relationship between the square of mean velocity (|U|2) and the bottom shear stress (τtotal) during the observational period |
|
(紫色、蓝色和橙色分别代表第一次强风浪、弱风浪和第二次强风浪过程。Purple, blue and orange represent the first strong wind wave weak wind wave and second strong wind wave processes, respectively.) 图 4 (a) 观测期间底剪切应力(τtotal)的时间序列和(b)观测期间平均流速的平方(|U|2)与底剪切应力(τtotal)的拟合关系 Fig. 4 (a) The time series of bottom shear stress (τtotal) during the observation and (b) the fitting relationship between the square of mean velocity (|U|2) and the bottom shear stress (τtotal) |
| $ {{\tau }_{\text{total }}}=1.71\times |U{{|}^{2}}+0.016。$ | (1) |
而在两次强风浪过程中,底剪切应力不仅受潮流流速大小的影响,更受波浪波轨速度的影响,因此|U|2与底剪切应力相关性较差(τtotal=2.90×|U|2+0.085,r=0.68;τtotal=3.69×|U|2+0.120,r=0.59)。
3.2 风浪对底剪切应力的作用强风浪期间的底剪切应力(τtotal)既包括波浪导致的浪致剪切应力(τwave)又包括潮流导致的潮致剪切应力(τtide)。如需量化风浪对底剪切应力的作用,需要先将潮致剪切应力从总剪切应力中剔除。在3.1节中,量化了潮流流速和底剪切应力的关系(公式(1))。因此只需要确定风浪期间潮流流速的大小,就可以根据上述关系式计算出强风浪期间潮致剪切应力的大小。需要注意的是,风浪和潮流的相互作用是非线性的,波流相互作用产生的底剪切应力的估算非常复杂。为便于研究,本文假定潮致剪切应力和浪致剪切应力是线性叠加的。基于上述假定可以计算出浪致剪切应力τwave=τtotal-τtide。
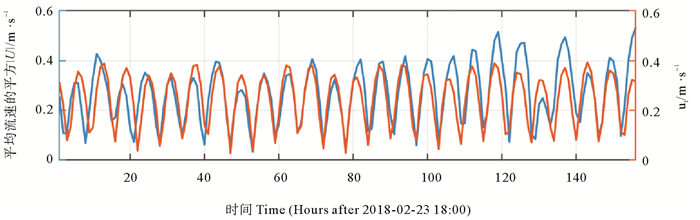
基于T_tide工具包[20],本文利用ADV观测的流速调和分析了观测期间观测站位各分潮的最大流速、最小流速以及潮流椭圆旋转方向等,然后模拟了观测期间的潮流流速时间序列(见图 5)。基于模拟的潮流流速结果和方程(1)计算了两次强风浪过程中潮致剪切应力,进而计算了强风浪期间的浪致剪切应力(见图 6(a),6(b))。结果表明,在第一次强风浪期间,波浪导致的剪切应力跟潮流导致的剪切应力量值相当。但是在第二次强风浪期间,最大浪致剪切应力远高于潮致剪切应力。值得注意的是,在某些时刻(如129~133 h),T_tide模拟的潮流流速大于观测的流速,高估了潮致剪切应力,导致浪致剪切应力在对应时刻为负值。产生误差的原因可能是潮流调和分析的时间不够长造成模拟的潮流流速偏大,也可能是波流相互作用减弱了潮流的能量。基于现有观测数据无法准确判断误差来源,有待进一步进行研究。风浪对底剪切应力的影响可通过两次大风期间波轨速度的平方(uwave2)与浪致剪切应力的相关关系量化。浅海的波轨速度是指在波浪的影响下,水质点做椭圆形运动时的速度。本文中观测站位的波轨速度是基于ADCP测波模块测得的有效波高、波周期和水深数据,利用Wiberg和Sherwood的方法[21]计算得到。图 6(c)所示为强风浪期间uwave2与浪致剪切应力的拟合关系:
|
图 5 观测期间ADV实测平均流速(蓝色)和T_tide调和分析模拟的潮流流速(橙色) Fig. 5 The measured average velocity (Blue) andthe tidal current velocity (Orange) simulated by T_tide harmonic analysis during the observational period |
|
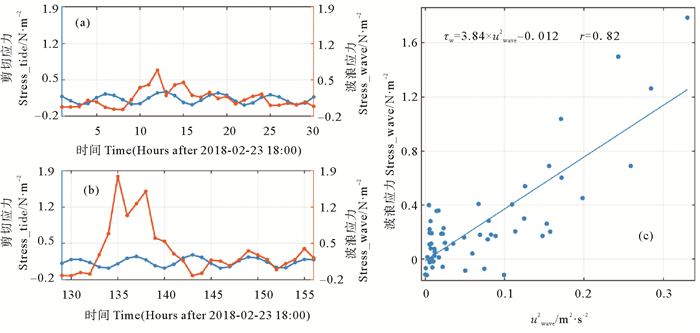
图 6 (a) 第一次强风浪过程潮致剪切应力(Stress_tide)和浪致剪切应力(Stress_wave)(b)第二次强风浪过程潮致剪切应力(Stress_tide)和浪致剪切应力(Stress_wave)(c)两次强风浪期间波轨速度的平方(uwave2)和浪致剪切应力(τw)的拟合关系 Fig. 6 The time series of tide-induced shear stress (Stress_tide) and wave-induced shear stress (Stress_tide) during (a) the first strong wind wave process and (b) the second strong wind wave process (c) The fitting relationship between the square of wave orbital velocity (uwave2) and wave-induced shear stress (τw) |
| $ {{\tau }_{\text{wave }}}=3.84\times u_{\text{wave }}^{2}-0.012。$ | (2) |
两者相关性较好(r=0.82),只是在波轨速度比较小的情况下,浪致剪切应力跟uwave2相关性较差。通过分析发现,在第二次强风浪过程临近结束时(146~156 h),尽管波轨速度急剧减小,但是风浪对水体湍混合的影响依然存在。虽然通过方程(1)的参数化公式剔除了潮致剪切应力的影响,但是波浪和潮流相互作用对剪切应力的影响也依然存在。因此在第二次强风浪过程临近结束这段时间的浪致剪切应力并没有随波轨速度减小而减小,而且与潮流流速具有很强的相关性(见图 6(b))。
3.3 弱风浪情况下潮流对SSC的影响在陆架浅海区,局地SSC的分布受到潮流和波浪等多种动力因素共同影响。在水平方向上,如果存在SSC水平梯度,则潮流的平流输运作用会引起局地SSC的变化;在垂直方向上,潮流和风浪导致的湍混合会造成局地悬浮物的垂向扩散,再加上悬浮物本身的沉降,都会引起局地SSC的垂向分布变化。Weeks等[22]和Krivtsov等[23]提出,在任意给定位置,SSC的变化是由平流输运和局地再悬浮共同决定的。Li等[24]对长江口的水文和泥沙观测进行定量化分析后指出,平流输运与局地再悬浮组分对研究区SSC变化的贡献量大小相当。本节通过原位观测的流速和悬浮物浓度数据量化平流输运作用和局地再悬浮作用对观测站位SSC的影响。
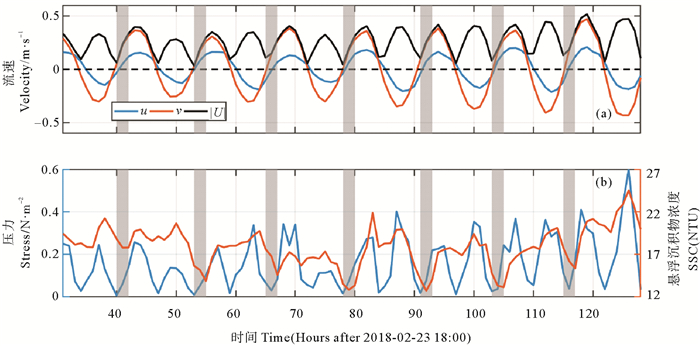
弱风浪过程中,悬浮物的局地再悬浮主要是由潮流流速决定的:潮流流速增大,底剪切应力增强,颗粒物再悬浮就增多,造成SSC升高;反之,潮流流速减小,底剪切应力变弱,颗粒物再悬浮就减少,造成SSC降低。然而,如图 7中阴影时刻所示,随着流速的增大,观测点的剪切应力逐渐增强,然而SSC却随流速增大而降低。SSC的变化具有显著的潮周期,但是又明显与潮流流速不相关。通过观测海区同步进行的其他站点的SSC分布发现,观测站位处存在较强的SSC水平梯度,西南方向的SSC高,东北方向的SSC低。因此,当潮流从西南方向流向东北方向时,就会携带高SSC水体经过观测站位,造成观测的SSC升高;反之,当潮流从东北方向流向西南方向时,就会携带低SSC水体经过观测站位,造成观测的SSC降低。因此,在研究站位,潮流从两方面影响SSC分布:潮流引起的底剪切应力变化对悬浮物的局地再悬浮和潮流的平流输运作用。
|
(阴影部分代表悬浮物浓度受平流输运作用控制。The suspended sediment concentration is controlled by advection in shadow area.) 图 7 (a) 弱风浪期间u方向平均流速(蓝色)、v方向平均流速(红色)和总平均流速(|U|,黑色)的时间序列(b)弱风浪期间潮流流速(ut)和悬浮沉积物浓度(SSC)的时间序列 Fig. 7 (a) The time series of averaged u (Blue), v (Red) and total (Black) velocities during weak wind waves (b) The time series of tidal current velocity (ut) and suspended sediment concentration (SSC) during weak wind waves |
为了量化潮流局地再悬浮和平流输运作用对SSC的影响,建立了一个参数化公式:
| $ \begin{matrix} SS{{C}_{\text{var}}}=SS{{C}_{0}}+u\times t\times dSS{{C}_{u}}+v\times t\times \\ dSS{{C}_{v}}+\left( {{u}^{2}}+{{v}^{2}} \right)\times dSS{{C}_{\text{resuspend}}} 。\\ \end{matrix} $ | (3) |
其中:SSCvar代表t时间段内SSC的变化量;SSC0为背景浓度;u,v为水平潮流流速;dSSCu、dSSCv为东西和南北方向的SSC梯度;dSSCresuspend为潮流再悬浮作用导致的SSC变化。利用弱风浪期间98h的观测数据可以确定参数化公式(3)中的SSC水平梯度(dSSCu、dSSCv)和SSC再悬浮量(dSSCresuspend)。
悬浮物的背景浓度在观测期间也有变化,以SSC最低点的连线作为SSC背景浓度值(见图 8中黄线)。此外,89~98 h内底剪切应力明显高于其他时刻(见图 4(a)),因此予以剔除。经过上述处理后,利用观测的88组流速和SSC浓度数据,通过最小二乘法求解公式(3)得到:dSSCu=12.2 NTU/m,dSSCv=-5.1×NTU/m,dSSCresuspend=16.7 NTU/m2·s-2。
|
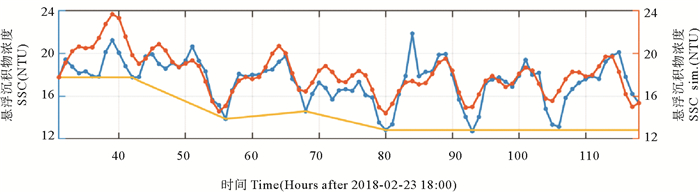
(黄线为公式(3)中所用的背景浓度值SSC0。The yellow line is the background concentration (SSC0) used in formula (3).) 图 8 弱风浪期间观测SSC(蓝色)与基于公式(3)预测的SSC(红色)的对比 Fig. 8 Comparisons between observed SSC (Blue) and predicted SSC (Red) based on formula (3) during weak wind waves |
图 8所示为观测的SSC浓度和基于参数化公式(3)计算的SSC浓度。从对比结果可以看出,模拟的SSC跟观测值符合较好,抓住了SSC变化的主要特征,说明弱风浪期间的SSC变化主要受控于潮流平流输运和再悬浮作用,公式(3)可以定量反映观测站位潮流的平流输运和再悬浮作用对SSC的影响。
3.4 风浪对SSC的影响强风浪期间,除了上述潮流的平流输运和再悬浮作用会对SSC产生影响以外,风浪导致的剪切应力增强也会导致SSC升高。为了量化强风浪期间风浪对SSC的影响,需要先将潮流对SSC的影响剔除。这里依然不考虑波流相互作用的影响,假定潮流和风浪对SSC的影响是线性的。利用T_tide调和分析的潮流流速和参数化公式(3)计算强风浪期间潮流对SSC的影响,然后用强风浪过程中实测的SSC减去潮致SSC和背景浓度即可得到浪致SSC(见图 9(a),9(b))。结果表明,在第一次强风浪过程中,潮流对SSC分布的影响要比波浪过程大,但是在第二次强风浪过程中,浪致剪切应力的急剧升高造成了大量沉积物再悬浮,浪致SSC也就远高于对应时刻的潮致SSC。
|
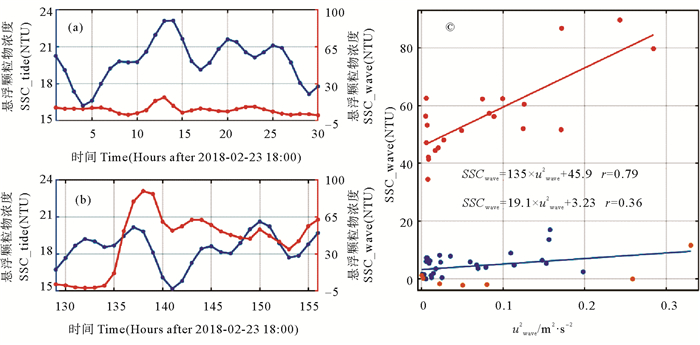
(蓝色点和黄色点代表波轨速度小于0.6 m/s,橙色点代表波轨速度大于0.6 m/s。Blue points and yellow points represent the wave orbital velocity is less than 0.6 m/s, orange points represent the wave orbital velocity is greater than 0.6 m/s.) 图 9 (a) 第一次强风浪过程中潮致悬浮物浓度(SSC_tide,含背景浓度)和浪致悬浮物浓度(SSC_wave)(b)第二次强风浪过程中潮致悬浮物浓度(SSC_tide,含背景浓度)和浪致悬浮物浓度(SSC_wave) (c)两次强风浪期间波轨速度的平方(uwave2)和浪致悬浮物浓度(SSC_wave)的拟合关系 Fig. 9 Blue points and yellow points represent the wave orbital velocity is less than 0.6 m/s, orange points represent the wave orbital velocity is greater than 0.6 m/s. |
为量化波轨速度与浪致SSC的关系,本文将波轨速度的平方(uwave2)与浪致SSC做线性拟合(见图 9(c))。拟合结果表明,波轨速度导致的SSC的变化明显分为两个阶段。通过跟波轨速度和浪致SSC的时间序列对比分析发现,在第一次强风浪过程中(见图 9(c)中蓝点)和第二次强风浪过程的前7 h(图 9(c)中黄点),波浪对SSC的影响较小,浪致SSC的参数化公式为:
| $ SS{{C}_{\text{wave}}}=19.1\times u_{\text{wave}}^{2}+3.23。$ | (4) |
而在第二次强风过程中(图 9(c)中橙点),波浪对SSC影响较大,浪致SSC的参数化公式为:
| $ SS{{C}_{\text{wave }}}=135\times u_{\text{wave }}^{2}+45.9。$ | (5) |
对比两次风浪过程可以发现,当波轨速度小于0.6 m/s时,波浪对SSC的影响较小(公式(4))。但是当波轨速度达到0.6 m/s时,波浪导致的剪切应力急剧升高,进而导致SSC显著增大(公式(5))。并且在强风浪过程后期,波轨速度降到0.6 m/s以下时,强风浪过程造成的高剪切应力和高SSC也不会马上消失,而是继续维持强风浪过程的影响。
4 结语本文基于山东半岛东侧进行的一次原位座底连续观测定量研究了潮流和风浪对底边界层底剪切应力和悬浮物浓度的影响。研究结果表明:在弱风浪条件下,潮流流速大小直接控制底边界层剪切应力(τtotal=1.71×|U|2+0.016);但是在强风浪海况下(有效波高大于1 m),底剪切应力受控于风浪的影响(τwave=3.84×uwave2-0.012)。潮流通过平流输运作用和局地再悬浮作用影响SSC分布(SSCvar=SSC0+u×t×dSSCu+v×t×dSSCv+(u2+v2)×dSSCresuspend),而波浪主要通过局地再悬浮影响SSC(SSCwave=28.4×uwave2+3.83uwave < 0.6m/s;SSCwave=136×uwave2+46.0, uwave>0.6m/s)。本研究获得的底边界层潮流和风浪对水动力和沉积物输运影响的参数化公式有助于我们定量地认识底边界层的沉积动力过程,为定量研究黄河泥沙向外海的输运过程以及山东水下三角洲的形成提供科学参考。
致谢: 部分海上观测工作搭载了“东方红2”号科考船执行的黄渤海共享航次。感谢中国海洋大学海洋地球科学学院王保铎老师和诸位同门在现场观测和室内实验中提供的支持与帮助。
| [1] |
Milliman J D, Meade R H. World-wide delivery of river sediment to the oceans[J]. The Journal of Geology, 1983, 91: 1-21. DOI:10.1086/628741
(  0) 0) |
| [2] |
Milliman J D, Qin Y S, Ren M E, et al. Man's influence on the erosion and transport of sediment by Asian rivers: The Yellow River (Huanghe) example[J]. Geology, 1987, 95: 751-762. DOI:10.1086/629175
(  0) 0) |
| [3] |
Milliman J D, Qin Y S, Park Y A. Sediments and sedimentary processes in the Yellow and East China Seas[J]. Sedimentary Facies in the Active Plate Margin, 1989, 233-249.
(  0) 0) |
| [4] |
Alexander C R, DeMaster D J, Nittrouer C. A. Sediment accumulation in a modern epicontinental-shelf setting: The Yellow Sea[J]. Marine Geology, 1991, 98: 51-72. DOI:10.1016/0025-3227(91)90035-3
(  0) 0) |
| [5] |
Liu J, Saito Y, Wang H. Sedimentary evolution of the Holocene subaqueous clinoform off the Shandong Peninsula in the Yellow Sea[J]. Marine Geology, 2007, 236: 165-187. DOI:10.1016/j.margeo.2006.10.031
(  0) 0) |
| [6] |
Zhang J, Huang W W, Shi M C. Huanghe and its estuary: sediment origin, transport and deposition[J]. Journal of Hydrology, 1990, 120: 203-223. DOI:10.1016/0022-1694(90)90150-V
(  0) 0) |
| [7] |
Martin J M, Zhang J, Shi M C, et al. Actual flux of the Huanghe (Yellow River) sediment to the western Pacific Ocean[J]. Netherlands Journal of Sea Research, 1993, 31(3): 243-254. DOI:10.1016/0077-7579(93)90025-N
(  0) 0) |
| [8] |
蒋东辉, 高抒. 渤海海峡潮流底应力与沉积物分布的关系[J]. 沉积学报, 2002, 20(4): 663-667. Jiang D H, Gao S. Relationship between the tidally-induced near-bed shear stress and the distribution of surficial sediments in the bohai strait[J]. Acta Sedimentologica Sinica, 2002, 20(4): 663-667. DOI:10.3969/j.issn.1000-0550.2002.04.021 (  0) 0) |
| [9] |
Jiang W S, Pohlmann T, Sun J. SPM transport in the Bohai Sea: Field experiments and numerical modelling[J]. Journal of Marine Systems, 2004, 44: 175-188. DOI:10.1016/j.jmarsys.2003.09.009
(  0) 0) |
| [10] |
Liu J, Milliman J, Gao S. The Shandong mud wedge and post-glacial sediment accumulation in the Yellow Sea[J]. Geo-Marine Letters, 2002, 21(4): 212-218.
(  0) 0) |
| [11] |
Liu J, Milliman J D, Gao S. Holocene development of the Yellow River's subaqueous delta, North Yellow Sea[J]. Marine Geology, 2004, 209(1-4): 45-67. DOI:10.1016/j.margeo.2004.06.009
(  0) 0) |
| [12] |
Lu J, Qiao F L, Wang X H, et al. A numerical study of transport dynamics and seasonal variability of the Yellow River sediment in the Bohai and Yellow seas[J]. Estuarine, Coastal and Shelf Science, 2011, 95(1): 39-51. DOI:10.1016/j.ecss.2011.08.001
(  0) 0) |
| [13] |
Bian C W, Jiang W S, Greatbatch R J. An exploratory model study of sediment transport sources and deposits in the Bohai Sea, Yellow Sea, and East China Sea[J]. Journal of Geophysical Research-Oceans, 2013, 118(11).
(  0) 0) |
| [14] |
程鹏, 高抒. 北黄海西部海底沉积物的粒度特征和净输运趋势[J]. 海洋与湖沼, 2000, 31(6): 604-615. Cheng P, Gao S. Net sediment transport patterns over the northwestern yellow sea, based upon grain size trend analysis[J]. Oceanologia et Limnologia Sinica, 2000, 31(6): 604-615. DOI:10.3321/j.issn:0029-814X.2000.06.004 (  0) 0) |
| [15] |
乔方利. 中国区域海洋学—物理海洋学[M]. 北京: 海洋出版社, 2012: 89. Qiao F L. Regional Oceanography of China Seas-Physical Oceanography[M]. Beijing: China Ocean Press, 2012: 89. (  0) 0) |
| [16] |
李家彪. 中国区域海洋学—海洋地质学[M]. 北京: 海洋出版社, 2012: 120. Li J B. Regional Oceanography of China Seas-Marine Geology[M]. Beijing: China Ocean Press, 2012: 120. (  0) 0) |
| [17] |
Yang Z S, Liu J P. A unique Yellow River-derived distal subaqueous delta in the Yellow Sea[J]. Marine Geology, 2007, 240: 169-176. DOI:10.1016/j.margeo.2007.02.008
(  0) 0) |
| [18] |
李明悝, 侯一筠. 利用QuikSCAT/NCEP混合风场及WAVEWATCH模拟东中国海风浪场[J]. 海洋科学, 2005(6): 9-12. Li Ming-Kui, Hou Yi-Jun. Simulating wind-wave field of the East China Seas wind QuikSCAT/NCEP blended wind and WAVEWATCH[J]. Marine Sciences, 2005(6): 9-12. DOI:10.3969/j.issn.1000-3096.2005.06.003 (  0) 0) |
| [19] |
鲍献文, 李真, 王勇智, 等. 冬、夏季北黄海悬浮物分布特征[J]. 泥沙研究, 2010(2): 48-56. Bao X W, Li Z, Wang Z Y, et al. Sediment distribution features in the North Yellow Sea during summer and winter[J]. Journal of Sediment Research, 2010(2): 48-56. (  0) 0) |
| [20] |
Pawlowicz R, Beardsley B, Lentz S. Classical tidal harmonic analysis including error estimates in MATLAB using T-TIDE[J]. Computers & Geosciences, 2002, 28(8): 929-937.
(  0) 0) |
| [21] |
Wiberg P L, Sherwood C R. Calculating wave-generated bottom orbital velocities from surface-wave parameters[J]. Computers & Geosciences, 2008, 34: 1243-1262.
(  0) 0) |
| [22] |
Weeks A R, Simpson J H, Bowers D. The relationship between suspended particulate matter and tidal processes in the Irish Sea[J]. Continental Shelf Research, 1993, 13: 1325-1334. DOI:10.1016/0278-4343(93)90086-D
(  0) 0) |
| [23] |
Krivtsov V, Gascoigne J, Jones S. Harmonic analysis of suspended particulate matter in the Menai Strait (UK)[J]. Ecological Modelling, 2008, 212: 53-67. DOI:10.1016/j.ecolmodel.2007.10.039
(  0) 0) |
| [24] |
Li Y, Jia J J, Zhu Q G, et al. Differentiating the effects of advection and resuspension on suspended sediment concentrations in a turbid estuary[J]. Marine Geology, 2018, 403: 179-190. DOI:10.1016/j.margeo.2018.06.001
(  0) 0) |
2. Physical Oceanography Laboratory, Ocean University of China, Qingdao 266100, China;
3. Department of Marine Ocean Science and Engineering, Southern University of Science and Technology, Shenzhen 518055, China;
4. Pilot National Laboratory of Marine Science and Technology (Qingdao) Laboratory for Marine Geology and Environment, Qingdao 266000, China
 2019, Vol. 49
2019, Vol. 49


