2. 青岛海洋科学与技术试点国家实验室 区域海洋动力学与数值模拟功能实验室,山东 青岛,266237
中尺度涡旋在世界各大洋中广泛存在,其移动对全球物质和能量的运输起到十分重要的作用,对海洋中的环境和气候变化具有深远影响[1-3]。近年来,随着卫星高度计和Argo浮标等海洋观测技术的发展,中尺度涡旋的识别和追踪方法不断完善[4],国内外学者对涡旋移动规律的研究越来越多。目前涡旋移动规律的研究方法主要分为两类:第一类是基于涡旋轨迹进行观察统计分析,如:Morrow等[5]系统地研究了印度洋东南部、大西洋东南部和太平洋东北部的涡旋轨迹,并发现暖涡倾向于向赤道方向偏转,而冷涡倾向于向极地方向偏转,Chelton等[6]发现涡旋主要向西移动,而在南极绕极流区域向东移动,但暖涡和冷涡的经向移动方向相反;第二类是运用人工智能方法对涡旋轨迹进行时空分析,如:Du等[7]运用基于密度的轨迹时空聚类方法,对南海涡旋轨迹进行时空聚类分析,得到了涡旋典型移动模式的空间分布和时间特征。Du等[7]的方法仅仅聚焦于时空距离,没有考虑涡旋运动的方向,从而聚类结果中包含一些短且方向相反的涡旋线段,聚类效果有待提高。因此,本文提出了一种基于方向的轨迹时空聚类算法,该方法综合考虑涡旋轨迹的方向变化差异和时空距离,进而得到更为准确和精细的涡旋迁移通道,有效地描述涡旋的移动特征。
南大洋(30°S以南)是指南极洲与太平洋、大西洋、印度洋的南部互相连通的海域[8]。南大洋最重要的海流系统是南极绕极流(Antarctic Circumpolar Current, ACC),它自西向东环绕南极洲流动,为各个大洋之间的物质和能量交换做出了重要贡献[9-10]。中尺度涡旋产生于斜压的不稳定,因此南大洋在ACC区域的涡旋动能较高[11-13]。与世界海洋的其他区域相比,中尺度涡旋在南大洋的动力和热力平衡中起着更为重要的作用[14]。目前对南大洋区域涡旋的前期研究主要是对涡旋进行统计分析,研究涡旋的形成机制和影响因素[15],然而涡旋的移动特征和规律才是南大洋涡旋研究的重点和难点。
本文基于1999—2018年共20年的涡旋识别和追踪数据集来提取南大洋区域的涡旋迁移通道。本文实验的主要流程是:首先,利用最小描述长度原则(Minimum Description Length,MDL)将涡旋轨迹划分为轨迹线段,综合考虑了线段的时空分布以及方向变化,根据基于方向的轨迹时空聚类算法,把具有相似时空特征和方向的涡旋轨迹线段聚为同一类别;其次,对得到的聚类结果进行定量化评价,根据评价标准提取涡旋迁移通道;最后,对涡旋迁移通道所包含的涡旋信息进行统计分析,获得涡旋在南大洋区域的移动特征以及相关的涡旋统计特征。
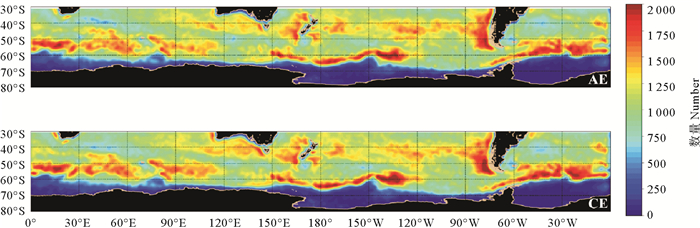
1 数据 1.1 涡旋识别和追踪数据本文采用的数据是由法国AVISO(Archiving Validation and Interpretation of Satellite Oceanographic)(http://www.aviso.oceanobs.com)数据中心提供的联合多颗测高卫星确定的网格化海平面异常数据(Sea Level Anomaly, SLA),其时间分辨率为1天,空间分辨率为(1/4)° ×(1/4)°。本文数据集的时间周期为20年(1999年1月—2018年12月)。涡旋识别数据是基于Liu等[16]提出的基于SLA等高线的涡旋识别算法获得,此算法是通过减少海平面异常等值线的搜索范围来简化涡旋识别过程。涡旋追踪算法是根据第一天确定的每个涡旋,搜索距离其质心(1/2)°半径范围内的第二天相同类型的涡旋,以找到最接近的涡流。若第二天没有与第一天对应的涡旋,则认为是新的涡旋,跟踪迭代该过程,即可得到涡旋追踪数据[17]。http://coadc.ouc.edu.cn/tfl/可获取涡旋识别和追踪数据集。根据(1)° ×(1)°的空间分辨率绘制网格,以涡旋质心所在的位置计算每个网格上的涡旋个数,南大洋区域的涡旋密度如图 1所示。从图中可以看出,南大洋区域暖涡和冷涡的分布基本一致。东南太平洋(50°S—70°S, 80°W—120°W)区域被Chelton称为“涡旋沙漠”,此处涡旋的活动频率较弱,在此区域几乎观察不到涡旋质心,其原因可能是存在无法被识别和追踪的涡旋,或生命周期小于16周的涡旋[18];涡旋高频率的活动区间大致分布在太平洋(40°S—50°S, 150°E—80°W)、(60°S—70°S, 150°E—120°W)、印度洋(50°S—60°S, 60°W—30°E)和大西洋(50°S—60°S, 150°E—120°W)区域以及大陆西边界区域。
|
图 1 南大洋区域涡旋质心数量统计图 Fig. 1 The census statistics for the centroid numbers of mesoscale eddies over the Southern Ocean |
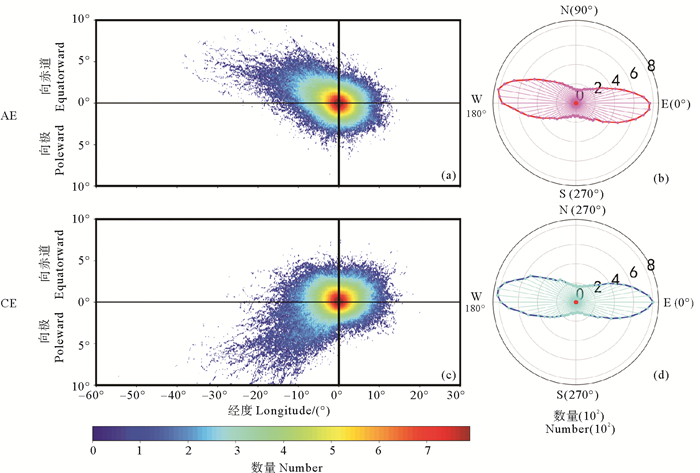
为了有效地描述涡旋运动的规律,本文通过筛选生命周期在30天以上的涡旋,对南大洋区域119, 744条暖涡(Anticyclonic Eddy, AE)和121, 930条冷涡(Cyclonic Eddy, CE)的涡旋轨迹分别进行实验。本文对涡旋轨迹所采用的归一化处理方法是将涡旋轨迹的起点设为原点,根据涡旋轨迹在每一天相对原点的位置信息,计算涡旋在每(1/10)° ×(1/10)°网格上的数量,并绘制密度分布图。图 2(a)和(c)分别显示了AE和CE归一化后的涡旋轨迹密度,当涡旋运动距离较大时(图中蓝色区域),AE的运动方向明显偏向赤道,而CE的运动方向则向极偏移[6]。同时,计算涡旋轨迹的方向角,这里的方向角定义为轨迹的起点与终点所形成的相对于正东方的逆时针角度。对AE和CE在每个角度上的轨迹数量进行统计,每5°的平均涡旋轨迹数量作为一组,轨迹数量分布如图 2(b)和(d)所示。图中灰色同心圆的半径代表在每个方向角上涡旋轨迹的数量,洋红(晶蓝)色细线的长度代表每一组的平均数量,并用红色(蓝色)粗线拟合出的椭圆来表示每个方向角上的数量分布。由图 2可知,方向角在0°~180°之间,涡旋的数量先随着角度的增大而减少,当方向角为90°时,涡旋的数量最小,然后涡旋的数量随着角度的增大而增多;当方向角在180°~360°之间时,涡旋的数量变化趋势与在0°~180°之间相似。由于研究区域包含ACC,约一半的涡旋轨迹是向东偏转,一半的涡旋轨迹是向西偏转,涡旋轨迹的南北运动方向偏移量基本一致。
|
图 2 AE(a), CE(c)涡旋轨迹归一化散点密度图及AE(b), CE(d)涡旋轨迹的运动方向统计图 Fig. 2 Normalized scatter density plot of eddy trajectories of AE(a), CE(c) and statistical plot of motion direction of eddy trajectories of AE(b), CE(d) |
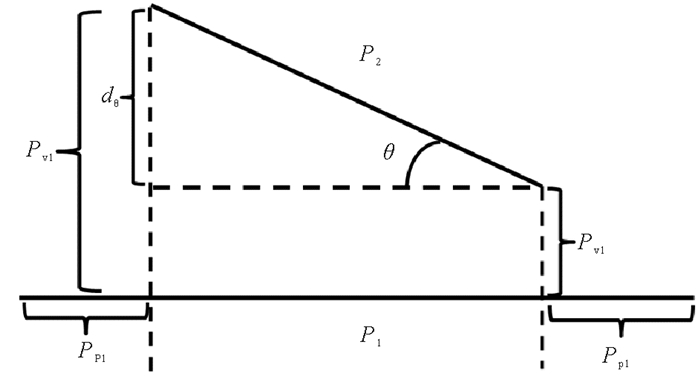
涡旋轨迹的时间分辨率是以天为单位,对涡旋轨迹分段的方法主要分为等时间分段、等距分段、起始点分段和提取轨迹特征点分段等。天尺度的涡旋轨迹与多间隔几天识别一次的涡旋轨迹相比,天尺度的涡旋轨迹是包括多间隔几天识别一次涡旋位置的信息,并且多间隔几天识别一次涡旋位置会忽略涡旋活动的细节,天尺度的涡旋轨迹充分考虑了涡旋的瞬时活动。由于涡旋运动的方向和速度存在差异,为了更好地描述涡旋移动特征,本文采用MDL原则提取涡旋轨迹特征点来进行分段,这一方法获得的轨迹线段既能减少数据冗余又能体现涡旋运动方向变化[19]。MDL可以看做是一种低通滤波,对于运动方向变化较大的涡旋,以及一些在原地打圈的涡旋使用高分辨率的数据(天尺度的涡旋轨迹)会保留涡旋轨迹一些重要的方向变化细节。MDL算法主要包括假设描述长度L1和再编码后数据的描述长度L2,其中,L1代表线段分割简洁程度,L2代表线段分割的精确程度。只有在L1和L2最小时,才能用最少的轨迹线段来代表原始轨迹的运动特征。本文定义两个线段P1和P2的三个距离参数:垂直距离dvPi, Pj、平行距离dpPi, Pj与角度距离dθPi, Pj。如图 3所示,P1和P2分别表示涡旋轨迹线段,θ表示P1和P2之间的夹角,dθ表示线段P1和P2之间的角度距离,Pv1和Pv2是用于线段P1和P2之间的垂直距离的计算,Pp1和Pp2是用于线段P1和P2之间的角度距离的计算。
| $ {d_v}\left( {{P_i}, {P_j}} \right) = \frac{{{P_{vi}}^2 + {P_{vj}}^2}}{{{P_{vi}} + {P_{vj}}}}, $ | (1) |
| $ {d_p}\left( {{P_i}, {P_j}} \right) = MIN\left( {{P_{pi}}, {P_{pj}}} \right), $ | (2) |
| $ {d_\theta }\left( {{P_i}, {P_j}} \right) = \left\| {{P_j}} \right\|\sin \theta 。$ | (3) |
|
图 3 线段距离函数的三个参数 Fig. 3 Three components of the distance function for line segments |
为了提取涡旋轨迹特征点,假设涡旋轨迹是由涡旋质心在每一天的位置点pn组成,涡旋轨迹可以用一组点p0, p1, p2, …, pn表示。Pn是由位置点pn-1和位置点pn组成的线段,涡旋轨迹可以由一组线段P1, P2, P3, …, Pn组成。假设经过MDL分段后生成的新特征点为p1t, p2t, p3t, …, ptn。
| $ L1 = \sum\limits_{t = 1}^{n - 1} {{{\log }_2}} len\left( {{p^{{t_i}}}, {p^{{t_{i + 1}}}}} \right), $ | (4) |
| $ \begin{array}{c} L2 = \sum\limits_{i = 1}^{tn - 1} {\sum\limits_{j = {t_i}}^{{t_{i + 1}} - 1} {\left\{ {{{\log }_2}\left[ {{d_v}\left( {{p^{{t_i}}}{p^{{t_{i + 1}}}}, {p^j}{p^{j + 1}}} \right)} \right] + } \right.} } \\ \left. {{{\log }_2}\left[ {{d_\theta }\left( {{p^{{t_i}}}{p^{{t_{i + 1}}}}, {p^j}{p^{j + 1}}} \right)} \right]} \right\}, \end{array} $ | (5) |
| $ L1 + L2 + {\rm{ cost }} > \sum\limits_{i = 1}^{tn - 1} {\sum\limits_{j = {t_i}}^{{t_{i + 1}} - 1} {{{\log }_2}} } len\left( {{p^j}, {p^{j + 1}}} \right)。$ | (6) |
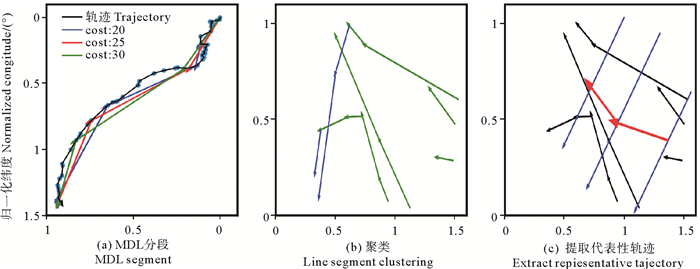
在公式(4)中len(pti, pti+1)是pti和pti+1两点之间的直线距离,在公式(5)中ptipti+1是pti和pti+1两点组成的线段。L2代表着原始轨迹与简化后轨迹的差异。简化后的轨迹包含原始轨迹的点信息,因此,本文不考虑平行距离,而是依据线段的角度距离和垂直距离之和来计算这些差异。对涡旋轨迹的点进行遍历,当满足公式(6)时,得到的点pti即为特征点。由于涡旋移动速度和方向不同,涡旋移动一天的距离会很短,甚至方向会发生明显的变化,MDL算法会提取出这类轨迹线段。这类轨迹线段会降低聚类的质量,因此,设置了一个参数cost来筛选这类轨迹线段,进而增加轨迹线段的长度。图 4(a)是对一条轨迹进行归一化后不同的cost值的分段效果,黑线为原始轨迹,蓝色点代表涡旋每一天的位置。当cost为20时,被划分后的线段(见图 4(a)中的蓝线)长度较短,而这些短的线段会导致聚类的效果变差;当cost为30时,被划分后的线段(见图 4(a)中的绿线)会忽略一些明显的转折点,进而聚类结果不能显示涡旋移动的部分细节;故本文设置cost为25,被划分后的线段(见图 4(a)中的红线),既简化了涡旋的移动路径,又保留了涡旋移动的细节变化。
|
图 4 基于方向的轨迹时空聚类算法示意图 Fig. 4 The schematic diagram of the trajectory clustering algorithm based on direction |
基于密度的聚类算法(Density-Based Spatial Clustering of Applications with Noise,DBSCAN)是在分类集合中将具有共同特性、数据量大的相似集合划分为同一类别,并且该算法还能够筛除数据集中的“噪音”,形成高密度连接的区域类别[20]。为了缩小同一类别所包含线段的方向差异,本文对DBSCAN算法进行优化,提出基于方向的轨迹时空聚类算法。图 4(b)中,蓝色线段和绿色线段分别表示不同的类别,可以看出方向变化较大的相邻两个线段被划分为不同的类别,而方向差距较小且在一定搜索范围的线段化为同一类。本文采用Lee等[19]提出的误差质量度量方法来选择参数[21],AE(CE)的邻域搜索范围为34(34),线段数量阈值为15(17)。该算法是在轨迹线段所组成的数据TRA中,对于每个未分类的线段P,分别计算该线段与数据集中其他所有线段的距离DT。
| $ \begin{gathered} D T\left(P_{i}, P_{j}\right)=W_{v} \times d_{v}\left(P_{i}, P_{j}\right)+ \\ W_{p} \times d_{p}\left(P_{i}, P_{j}\right)+W_{\theta} \times d_{\theta}\left(P_{i}, P_{j}\right) 。\end{gathered} $ | (7) |
式(7)中Wv, Wp, Wθ分别代表线段在垂直、平行和角度距离的权重。
本实验将这些权重均设置为1。若计算的两线段之间的角度θ < 90°且满足DT小于给定的邻域搜索范围,则将线段进行存储并计算线段的数量。若线段L在邻域范围内的线段数量N(L)大于线段数量阈值,则将线段L定义为核心线段,与线段L同类别的其他线段称为线段L的密度可达线段。若L的密度可达线段L1之前未分类,则对线段L1进行判断,若是核心线段则进行扩展,若不是核心线段则将线段L1划分为噪音,如此循环往复,直至线段集合中的所有的线段分类完成。最后,只保留每个类别所包含线段数量大于阈值的类别。聚类过程的伪代码为:
Algorithm: Trajectory direction clustering
Input: L={L1, L2, …, Ln};
Output: CLU={C1, C2, …, Cn};
Begin:
1.create a line segments subset L={L1, L2, …, Ln};
2.set cluster ID to be 0;
3.mark all line segment in L as unclassified;
4.for i from 1 to n {
5. if (Li is unclassified){
6. computer N(Li);
7. if (N(Li) > MinLns) {
8. insert N(Li)-Li into the queue C;
9. while (C) do {
10. let J be the first line segment in C;
11. computer N(J);
12. if (N(J) > MinLns) {
13. for j from 1 to N(J) {
14. if (Jj is unclassified or noise) {
15. assign cluster ID to Jj;}
16. else{
17. insert N(Jj)-Jj into the queue C;}}
18. remove J from the queue C;}
19. cluster ID+=1;}
20. else{
21. mark Li as noise;}
end
为了更好的描述聚类结果,本文用特征轨迹来表征聚类后每一类别的线段。图 4(c)中黑色线段为同一类别的轨迹线段,蓝色线段为扫描线,红色线段为特征轨迹。提取特征轨迹的方法为:首先,根据同一类别所有线段的矢量方向来计算平均方向,并将其作为该类别的主方向;用一条垂直于主方向的直线(见图 4(c)中蓝线)扫描每一条线段,每次经过一条线段的起点或终点时,都要判断此时与该直线相交的线段数量,若相交线段数量大于线段数量阈值,则计算在该直线上所有线段坐标的平均值,此平均值即为特征轨迹的坐标点;若特征轨迹相邻的两个坐标点之间的距离小于一定距离时,则舍弃第二个坐标点,最后得到特征轨迹(见图 4(c)中红线)的坐标信息。
为了定量描述涡旋轨迹聚类后特征轨迹的效果,本文设计了两种比例计算方式:
(1) 轨迹比例。“轨迹”的含义是一条涡旋从出生到死亡的运动路线,其比例的计算方式是参与聚类的轨迹数量与轨迹总数的比值。对于通道中所包含的轨迹线段,这条线段所属的涡旋轨迹若是这个通道的聚类集群则被标记为“真”,且一条轨迹可以在不同的通道聚类集群中标记为“真”。因此,所有通道的轨迹比例总和可能超过100%。
(2) 轨迹线段的比例。该方法是计算每一个通道中所包括的涡旋轨迹线段数量占所有轨迹线段数的比例。与轨迹比例不同,轨迹线段只能属于一个通道,因此,所有轨迹线段的比例之和小于或等于100%。
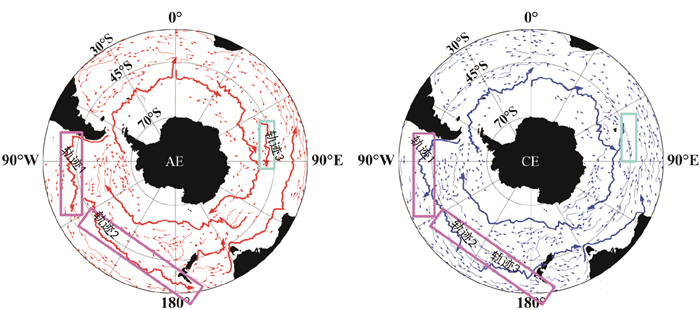
3 聚类结果及通道提取 3.1 南大洋涡旋聚类结果根据涡旋轨迹的聚类结果,AE有459条特征轨迹,CE有490条特征轨迹。涡旋特征轨迹的空间分布如图 5所示,AE(CE)的特征轨迹分别由图中红(蓝)色线表示,特征轨迹所包含轨迹线段数量前十的由红(蓝)色粗线表示。实验结果表明,特征轨迹主要表现为西向和东向运动,根据运动方向,将南大洋区域划分为北部(45°S以北)和南部(45°S以南)两个区域。
|
图 5 南大洋中尺度涡旋轨迹聚类结果 Fig. 5 Clustering results of mesoscale eddiestrajectories in the Southern Ocean |
在南大洋北部区域,特征轨迹的主要运动方向为西向,从大陆的西边界开始,特征轨迹沿着大陆的西海岸向西北方向延伸,在大洋的西边缘呈现明显的西南向偏转,直到大陆边缘结束。而在南部区域,特征轨迹的运动方向主要为东向,但也存在明显的非纬向性的运动,这与南极绕极流的运动方式基本一致;在大部分南极洲沿岸区域,特征轨迹沿着陆地西向运动。在90°W—180°的弧形区域内,在45°S以南(图中的两个洋红色框内)AE有两条主要的特征轨迹(轨迹1和轨迹2),而CE有三条主要的特征轨迹(轨迹1、轨迹2和轨迹3),这三条特征轨迹的长度明显比AE的短,这种情况下冷涡的特征轨迹发生了缩短与分裂;在0°—90°E的弧形区域内,在45°S附近(图中的晶蓝色框内),AE存在一条特征轨迹(轨迹3),而在冷涡中没有与此条特征轨迹位置方向相对应的特征轨迹,这种情况下冷涡的特征轨迹发生了消失。冷涡与暖涡的特征轨迹的运动模式基本一致,但冷涡的特征轨迹发生了缩短、分裂或消失等变化。根据实验结果可以得出规律,南大洋区域涡旋轨迹不能聚成一条完整的闭合环形通道,而是几条主要的涡旋迁移通道。
3.2 南大洋涡旋迁移通道提取涡旋迁移通道是指涡旋的移动模式,有效地体现涡旋移动的时空特征和移动规律。在通道内,涡旋的运动具有连续性和相似性等特征;涡旋轨迹数量所占比例越大,对应的特征轨迹所体现的涡旋总体移动规律就越具有代表性;涡旋轨迹线段数量所占比例越大,对应的特征轨迹不仅能体现涡旋总体移动规律,而且方向特征显著。因此,本文将涡旋轨迹线段数量占比前十的特征轨迹定义为涡旋迁移通道。AE和CE每一类涡旋通道的轨迹线段比例和轨迹的比例如表 1和表 2所示。
|
|
表 1 暖涡通道的线段比例和轨迹比例 Table 1 The proportion of line segments and trajectories of anticyclonic channels |
|
|
表 2 冷涡通道的线段比例和轨迹比例 Table 2 The proportion of line segments and trajectories of cyclonic channels |
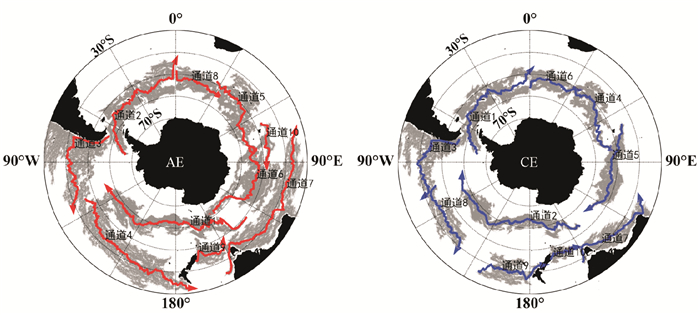
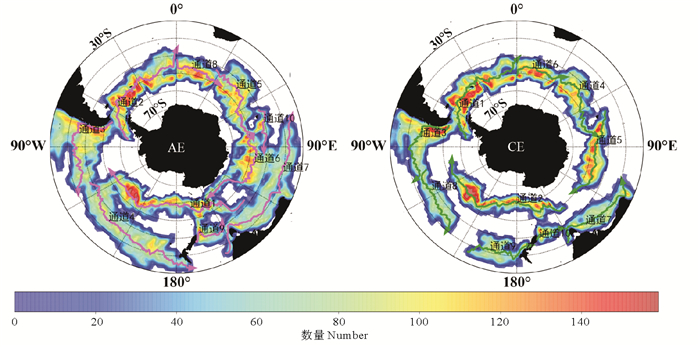
本文实验提取的南大洋区域涡旋通道的结果如图 6所示,图中红色实线代表AE的涡旋通道,蓝色实线代表CE的涡旋通道,灰色实线代表参与通道聚类的涡旋轨迹线段。涡旋通道轨迹线段的密度如图 7所示,可以看出涡旋迁移通道主要分布在轨迹线段密度较高(见图 7中橙红色区域)的区域,涡旋轨迹在ACC区域更加集中,而在其他区域相对稀疏。
|
图 6 基于轨迹聚类提取的涡旋迁移通道 Fig. 6 Eddy migration channels extraction based on trajectory clustering |
|
图 7 参与涡旋迁移通道的轨迹密度分布 Fig. 7 The trajectory density distribution of participating eddy migration channels |
对于AE,在南大洋的北部区域存在4条涡旋迁移通道,通道3、4、7和9为西向的迁移通道,涡旋迁移通道的纬度在40°S上下变化;在南部区域存在6条涡旋通道,通道1位于太平洋与南极洲的交界处,沿着60°S纬线东向移动,通道2和通道8位于大西洋与南极洲的交界处,沿着53°S纬线东向移动,在靠近0°经线时,通道2有明显的北向移动,而通道7在印度洋与南极洲的交界处向南移动。通道5、6、8和10都沿着53°S东向移动。
对于CE,冷涡在南大洋北部区域存在5条涡旋迁移通道,移动模式为西向的迁移通道有通道3、7、8、9和10,主要分布在40°S附近;南部区域存在5条涡旋通道,通道2位于太平洋与南极洲的交界处,沿着60°S纬线,自130°E向100°E西向移动,通道1和6位于大西洋与南极洲的交界处,通道1有向北移动的趋势,而通道6自低纬开始向北移动,在印度洋与南极洲的交界处,有通道4和5沿着53°S纬线东向移动。南极绕极流有着在大西洋扇形区与印度洋扇形区位置向赤道偏移,在太平洋扇形区向极地偏移的运动规律。在大西洋扇形区与印度洋扇形区所提取的涡旋通道的位置偏北,而在太平洋扇形区偏南的位置,涡旋通道的运动方式与南极绕极流的运动规律基本一致,这可能是南极绕极流牵带涡旋运动导致的。
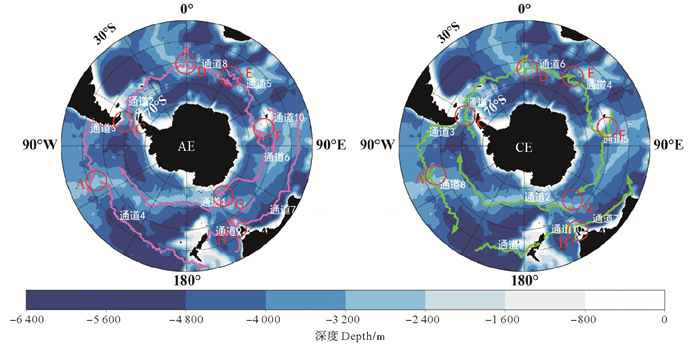
4 南大洋涡旋迁移通道分析 4.1 南大洋涡旋迁移通道与海底地形相关性在30°S—45°S区域,南大洋西向的涡旋迁移通道,其运动方向与南极绕极流的流动方向几乎一致;东向的涡旋迁移通道的运动方向与南赤道暖流的流动方向几乎一致。从图 5中看出,在南印度洋区域,涡旋特征轨迹分布相对均匀,但距离相对较大,很难通过聚类算法得到涡旋迁移通道。在大西洋和太平洋区域涡旋分布相对密集的区域,有西北向流动的涡旋通道。这些涡旋迁移通道之间存在断点(见图 8红色圆圈),如:在断点A处,太平洋海丘导致通道方向变化并产生新的涡旋通道;在断点B处,陆地阻碍了涡旋的运动并产生了多条涡旋通道。南大洋最显著的是东向的涡旋迁移通道,其运动方向与南极绕极流的流动方向几乎一致。这些涡旋迁移通道之间存在断点(见图 8红色圆圈),如:如C处的德雷克海峡、D处的中大西洋海岭、E处的西南印度洋海岭以及F处的凯尔盖朗群岛,涡旋迁移通道经过这些较浅的海域(此处海底地形均在-1 600 m以上)有显著的方向变化,并产生新的涡旋迁移通道。
|
图 8 南大洋海底地形图 Fig. 8 Topographic map of the Southern Ocean |
综上所述,大洋环流和地形会影响涡旋迁移通道的移动方向。涡旋迁移通道的移动方向与大洋环流的流向几乎一致。在海底平原或者大洋中脊这些地势较高的区域,涡旋迁移通道有北向偏转的趋势,并在地势最高处结束,新的涡旋迁移通道在此产生,并有南向运动的趋势;涡旋迁移通道经过德雷克海峡时,有明显的北向运动趋势,这可能与德雷克海峡东面的复杂地形的阻挡有关。
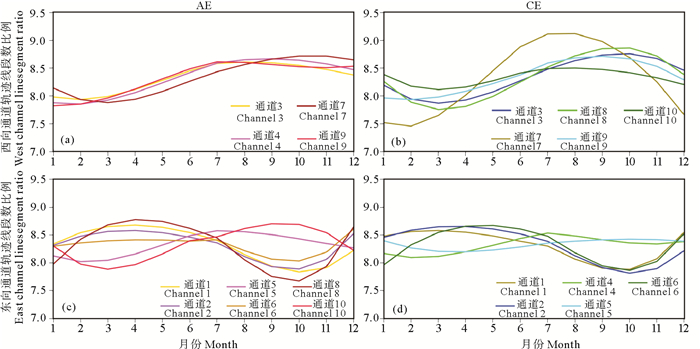
4.2 南大洋涡旋迁移通道统计分析受季节影响,涡旋表现出不同的移动规律。本文根据涡旋迁移通道的移动方向,对涡旋迁移通道所包含的涡旋轨迹线段进行分析。忽略涡旋的年份差异,根据上文中涡旋迁移通道,对每个通道所包含涡旋轨迹线段所在的月份进行统计,计算轨迹线段在每个月份所占的比例。如图 9(a)所示,AE西向迁移通道,一年四季都有涡旋沿着该通道移动,而且涡旋轨迹线段的数量在2—3月份之间开始有一个上升的趋势,在9月份有一个下降的趋势;如图 9(b)所示,CE西向迁移通道,涡旋轨迹线段的数量在3—4月份之间开始有一个上升的趋势,在9—10月份有一个下降的趋势,其中通道7受季节的影响,比其他西向迁移通道提前一个月出现峰值,这可能是由于通道7靠近陆地,温度随季节的变化相对较大。如图 9(c)所示,AE东向迁移通道,涡旋轨迹在4月开始有一个下降的趋势,在10月有一个上升的趋势;如图 9(d)所示,CE东向迁移通道,通道所包含的涡旋全年存在,涡旋轨迹数量在5月开始有一个下降的趋势,在9—10月有一个上升的趋势。AE的通道5和10以及CE的通道4和通道5,其涡旋轨迹线段数量比例的变化相对平稳,这可能是由于这几条迁移通道所包含的涡旋轨迹分布在中低纬度地区,且位于凯尔盖朗群岛附近。西向迁移通道呈现秋季涡旋轨迹数量相对较小,春季涡旋轨迹数量相对较多的特征;相反,东向迁移通道所包含的涡旋轨迹数量在秋季相对较多而在春季相对较少。
|
( (a), (b)分别是AE, CE西向迁移通道所包含涡旋的时间分布;(c), (d) 分别是AE, CE东向迁移通道所包含涡旋的时间分布。(a), (b) The time distribution of the eddies contained in the westward migration channels of AE and CE, respectively; (c), (d)The time distribution of the eddies contained in the eastward migration channels of AE and CE, respectively. ) 图 9 涡旋迁移通道所包含涡旋的时间分布模式对比 Fig. 9 Comparison of time distribution modes of the eddies in the eddy migration channels |
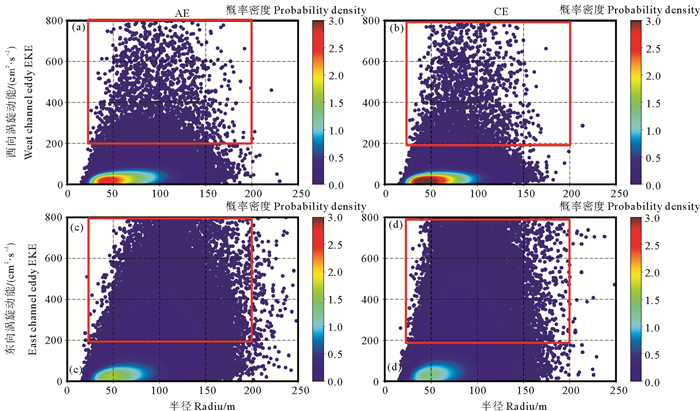
本文对参与涡旋迁移通道的涡旋轨迹线段进行统计,计算每条涡旋轨迹线段上的涡旋半径、涡旋动能的平均值,利用密度散点图来分析这些涡旋轨迹的半径与涡旋动能之间的关系。图 10中的点的横坐标代表涡旋轨迹的平均半径,纵坐标代表涡旋轨迹的平均涡旋动能,颜色表示核密度估计(KDE)计算的概率密度,即某点密度越大,具有此涡旋动能和半径的涡旋数量越多。西向迁移通道所包含的涡旋主要分布在图 10(a)、(b)中红色、橙色与黄绿色区域,可以看出其半径大多分布在30~100 km之间,涡旋动能分布在50~80 cm2·s-2;东向迁移通道所包含的涡旋主要分布在图 10(c)中橙色和黄绿色区域和图 10(d)中黄绿色区域,可以看出其半径主要分布在30~100 km,涡旋动能的50~100 cm2·s-2。由此可以看出,对于相同方向的涡旋通道所包含的涡旋,无论是AE还是CE,涡旋的半径与涡旋动能总体分布趋势基本一致。对于不同方向的迁移通道,当涡旋动能大于200 cm2·s-2,半径在50~100 km之间时,图 10(a)和(b)中有一些空白的区域,而图 10(c)和(d)中几乎被蓝色的覆盖。针对此现象,本文对迁移通道中涡旋动能大于200 cm2·s-2的涡旋数量占总涡旋的百分比进行统计,对于AE(CE),东向迁移通道中涡旋动能大于200 cm2·s-2的涡旋数量所占比为14.42%(18.94%),而西向迁移通道占比为3.01%(3.61%)。因此,相对于西向迁移通道,在东向迁移通道中,有大量的涡旋动能大于200 cm2·s-2的涡旋。南极绕极流锋面的斜压不稳定,导致涡旋动能较高。因此,东向迁移通道的涡旋运动特征更加明显,能够更好地体现出涡旋运动的规律性。
|
( (a), (b)分别是AE, CE西向迁移通道所包含涡旋的半径与涡旋动能的密度散点图;(c), (d) 分别是AE, CE东向迁移通道所包含涡旋的半径与涡旋动能的密度散点图。(a), (b) The density scatter plots of the eddy radius and EKE contained in the westward migration channels of AE and CE, respectively; (c), (d) The density scatter plots of the eddy radius and EKE contained in the eastward migration channels of AE and CE, respectively. ) 图 10 涡旋迁移通道所包含涡旋性质的密度散点图 Fig. 10 The density scatter plots of the eddy properties in the eddy migration channels |
本研究采用基于方向的轨迹时空聚类算法对南大洋区域20年的涡旋轨迹数据,提取了南大洋区域的涡旋迁移通道。在基于密度的轨迹聚类方法的基础上进行优化,综合考虑涡旋移动的时间、方向,实现了基于方向的轨迹时空聚类。实验结果表明:
(1) 南大洋涡旋迁移通道有两种不同的运动模式:北部区域的涡旋迁移通道为东向,南部区域的涡旋迁移通道为西向。
(2) 本文提取的涡旋迁移通道与南大洋的洋流的空间分布相吻合,这表明基于方向的轨迹时空聚类算法对于提取涡旋迁移通道以及研究涡旋运动特征颇为有效。
(3) AE和CE所提取的迁移通道在地理位置和方向上都极其相似,这可能是受到海底地形和洋流等因素的影响。
(4) 东向和西向迁移通道所包含的涡旋轨迹线段数量具有季节性,东向迁移通道包含的涡旋轨迹线段数量在春季达到峰值,而西向迁移通道在秋季达到峰值。
(5) 对于相同方向的涡旋通道,无论是暖涡还是冷涡,其涡旋动能与半径总体的分布趋势基本一致。相对于西向迁移通道,东向迁移通道中涡旋动能较大。
本文采用的方法在南大洋区域能够识别出相对准确的涡旋迁移通道,而对于局部区域回环移动的涡旋以及一些静止状态的涡旋,聚类方法仍需改进。当此方法应用于全球涡旋迁移通道提取时,由于涡旋在不同纬度上的涡旋半径、运动速度有显著的差异,对于聚类参数的选择更加困难。因此,本文中提到的聚类算法在用于区域聚类时,可以得到理想的结果,但针对全球涡旋迁移通道的提取,今后还需做更广泛深入的研究。
| [1] |
Zhang Z, Wei W, Qiu B. Oceanic mass transport by mesoscale eddies[J]. Science, 2014, 6194: 322-324. (  0) 0) |
| [2] |
Farneti R, Delworth T L, Rosati A J, et al. The role of mesoscale eddies in the rectification of the Southern Ocean response to climate change[J]. Journal of Physical Oceanography, 2010, 40(7): 1539-1557. DOI:10.1175/2010JPO4353.1 (  0) 0) |
| [3] |
Xu C, Shang X D, Huang R X. Horizontal eddy energy flux in the world oceans diagnosed from altimetry data[J]. Scientific Report, 2014, 5316: 1-7. (  0) 0) |
| [4] |
Castelao R M. Mesoscale eddies in the South Atlantic Bight and the Gulf Stream Recirculation region: Vertical structure[J]. Journal of Geophysical Research Oceans, 2014, 119(3): 2048-2065. (  0) 0) |
| [5] |
Morrow, Rosemary. Divergent pathways of cyclonic and anti-cyclonic ocean eddies[J]. Geophysical Research Letters, 2004, 31(24): 1-5. (  0) 0) |
| [6] |
Chelton D B, Schlax M G, Samelson R M. Global observations of nonlinear mesoscale eddies[J]. Progress in Oceanography, 2011, 91(2): 167-216. DOI:10.1016/j.pocean.2011.01.002 (  0) 0) |
| [7] |
Du Y, Wu D, Liang F, et al. Major migration corridors of mesoscale ocean eddies in the South China Sea from 1992 to 2012[J]. Journal of Marine Systems, 2016, 158: 173-181. DOI:10.1016/j.jmarsys.2016.01.013 (  0) 0) |
| [8] |
Duan Y, Liu H, Yu W, et al. Eddy properties in the Pacific sector of the Southern Ocean from satellite altimetry data[J]. Acta Oceanologica Sinica -English Edition, 2016, 35(11): 28-34. DOI:10.1007/s13131-016-0946-2 (  0) 0) |
| [9] |
Iudicone D, Madec G, lanke B, et al. The role of Southern Ocean surface forcings and mixing in the global conveyor[J]. Journal of Physical Oceanography, 2008, 38(7): 1377-1400. DOI:10.1175/2008JPO3519.1 (  0) 0) |
| [10] |
Rintoul S R. Antarctic Circumpolar Current[M]. Salt Lake City USA: Encyclopedia of Ocean Sciences, 2009.
(  0) 0) |
| [11] |
Olbers D, Borowski D, VLker C, et al. The dynamical balance, transport and circulation of the Antarctic Circumpolar Current[J]. Antarctic Science, 2004, 16(4): 439-470. DOI:10.1017/S0954102004002251 (  0) 0) |
| [12] |
Duan Y, Liu H, Yu W, et al. Eddy properties in the Pacific sector of the Southern Ocean from satellite altimetry data[J]. Acta Oceanologica Sinica-English Edition, 2016, 35(11): 28-34. DOI:10.1007/s13131-016-0946-2 (  0) 0) |
| [13] |
Meredith M P, Hogg A M. Circumpolar response of Southern Ocean eddy activity to a change in the southern annular mode[J]. Geophysical Research Letters, 2006, 33(16): 1-4. (  0) 0) |
| [14] |
Langlais C, Rintoul S, Schiller A. Variability and mesoscale activity of the Southern Ocean fronts: Identification of a circumpolar coordinate system[J]. Ocean Modelling, 2011, 39(1): 79-96. (  0) 0) |
| [15] |
Wolff J O, Maier-Reimer E, Olbers D J. Wind-driven flow over topography in a Zonal β-Plane channel: A quasi-geostrophic model of the Antarctic circumpolar current[J]. Journal of Physical Oceanography, 1959, 21(2): 236-264. DOI:10.1175/1520-0485(1991)0212.0.CO;2 (  0) 0) |
| [16] |
Chelton D B, Schlax M G, Witter D L, et al. Geosat altimeter observations of the surface circulation of the Southern Ocean[J]. Journal of Geophysical Research Oceans, 1990, 95(C10): 17877-17903. DOI:10.1029/JC095iC10p17877 (  0) 0) |
| [17] |
Liu Y, Chen G, Sun M, et al. A parallel SLA-based algorithm for global mesoscale eddy identification[J]. Journal of Atmospheric and Oceanic Technology, 2016, 33(12): 2743-2754. DOI:10.1175/JTECH-D-16-0033.1 (  0) 0) |
| [18] |
Miao S, Fenglin T, Yingjie L, et al. An improved automatic algorithm for global Eddy tracking using satellite altimeter data[J]. Remote Sensing, 2017, 9(3): 206-212. DOI:10.3390/rs9030206 (  0) 0) |
| [19] |
Chelton D B, Schlax M G, Samelson R M, et al. Global observations of large oceanic eddies[J]. Geophysical Research Letters, 2007, 34(15): 1-5. (  0) 0) |
| [20] |
Lee J G, Han J, Whang K Y. Trajectory Clustering: A Partition-And-Group Framework[C]. [s. l. ]: Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data ACM, 2007.
(  0) 0) |
| [21] |
Zorrilla M E, Diego García-Saizm, José L. Balcázar. Towards Parameter-free Data Mining: Mining Educational Data with Yacaree[C]. The Netherlands: Proceedings of the 4th International Conference on Educational Data Mining, Eindhoven, 2011.
(  0) 0) |
2. The Laboratory for Regional Oceanography and Numerical Modeling, Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao 266237, China
 2022, Vol. 52
2022, Vol. 52


