2. 青岛海洋科学与技术国家试点实验室,区域海洋动力学与数值模拟功能实验室,山东 青岛 266011
海冰是一种敏感的气候指标,限制海洋和大气之间的能量、动量和物质的交换。同时,海冰的存在影响海表反照率,减少地球表面吸收的太阳辐射量。海冰在形成过程中析出盐可以导致冰下海水密度增加,有助于垂直方向的海洋的温盐环流,而海冰融化会增加上层海洋的稳定性。此外,海冰直接影响高纬度地区船舶航行和近海作业。因此,在高纬或极地海域,准确确定海冰的范围,对航行安全十分重要[1]。同时,研究极地海冰的时空特性对于监测全球气候变化、天气预报、渔业捕捞和海洋运输具有重要意义[2]。
早期的海冰观测方式包括测量船、飞机探测等,这两种观测方式不仅效率低、成本高,而且对于位置偏远且环境恶劣的极地海冰,更是难以直接观测。随着遥感技术的发展,卫星遥感已经成为研究极地海冰的有效手段。用于海冰检测的遥感传感器主要包括可见、红外传感器和微波传感器。可见光与近红外波段传感器包括NOAA/AVHRR传感器、EOS/MODIS传感器、以及近年来发射的高分辨率可见和红外传感器等,它们所获取的各波段遥感资料被广泛应用于海冰范围及海冰密集度的监测研究[3]。但是可见和红外传感器在多云和极夜等条件下容易受到云或雾等天气的影响,造成遥感图像模糊影响观测结果。微波可以穿透云层,具备全天时、全天候的工作能力,因此微波传感器成为观测海冰的重要工具。目前有两种微波传感器用于海冰观测,被动微波传感器和主动微波传感器。被动微波传感器主要是指多波段微波辐射计如雨云系列卫星Nimbus-5搭载的电子扫描微波辐射计(Electronically Scanning Microwave Radiometer, ESMR),主要通过测量亮温获取海冰边缘等参数。搭载在Nimbus-7卫星的扫描多通道微波辐射仪(Scanning Multichannal Microwave Radiometer, SMMR),将SMMR海冰观测与飞机观测结果进行比较,SMMR对总冰密集度的估计精度为±3%,多年冰密集度的估计精度为+10%[4]。1987年开始的美国国防气象卫星计划(Defence Meteorological Satellite Program, DMSP)系列卫星先后搭载了专用微波成像仪和专用微波成像探测仪(Special Sensor Microwave/Imager and Special Sensor Microwave Imager/Sounder, SSM/I和SSMIS),成为海冰数据的主要来源[5]。2002年EOS-Aqua卫星搭载改进型多通道扫描辐射计(Advanced Microwave Scanning Radiometer-Earth Observing System, AMSR-E),比SSM/I具有更高的空间分辨率和更大的光谱范围,能够更好地评估不同类型海冰的空间分布[6]。
观测海冰的另一种微波传感器是主动微波传感器,主要包括合成孔径雷达(Synthetic Aperture Radar, SAR)和散射计等。1978年,海洋卫星Seasat-A成为第一颗提供高分辨率海冰SAR影像的卫星,SAR传感器以其高分辨率成像能力、不受多云天气影响,可以获取海冰边缘线和冰块缝隙等信息,在极地和高纬度海冰检测中发挥着重要作用。但SAR的覆盖范围小,资料成本高,其时空覆盖率难以满足极地海冰和中大尺度海洋现象的研究[7]。1990年代以来,微波散射计开始用于海冰探测,包括C波段的ERS-1、ERS-2、ASCAT以及Ku波段的NSCAT、QUIKSCAT、HY-2A/SCAT等。微波散射计是非成像传感器,其设计初衷是通过测量后向散射系数(σ0)反演风场,但是近年来在海冰方面的探测也逐渐成熟起来。
基于微波散射计进行冰水检测的算法主要分为两种:一种是RL-N算法(Remund/ Long-NSCAT Algorithm)[8], 一种是KNMI(Koninklijk Netherlands Meteorologisch Institute)海冰检测算法[9]。RL-N算法主要利用海冰和海水方位角与极化特性的差异,基于最大似然估计进行冰水区分,在此基础上利用图像处理技术降低误判[8]。KNMI算法是基于贝叶斯统计的海冰检测算法。针对笔状扫描散射计观测的[σVfore, σHfore, σVaft, σHaft]四个参数,基于海水和冰地球物理模式函数(Geophysical Mode Function,GMF),通过计算概率距离实现海冰和海水的检测。Siberian de Hana等建立了ERS海冰的GMF[10]。Verspeek等在此基础上,运用ERS-2散射计数据,提出了基于贝叶斯统计的KNMI海冰检测算法(后面称之为贝叶斯海冰检测算法)[11]。Rivas基于贝叶斯海冰检测算法利用ASCAT数据进行海冰检测研究,并将海冰范围检测结果与AMSR-E 15%海冰密集度以上的海冰范围相比,在冬季两者具有较好的一致性[12]。2009年KNMI将贝叶斯海冰检测算法应用于QUIKSCAT的Seawinds数据上,结果表明在海冰融化季(夏季)检测散冰的能力优于RL-N算法[9]。
2011年,中国成功发射第一颗海洋动力环境卫星——海洋二号A卫星,其上搭载散射计HY-2A/SCAT。虽然散射计数据已经应用到许多气象研究中,但在极地海冰检测方面的研究仍然较少。邹巨洪等基于HY-2A/SCAT数据,利用后向散射系数、极化比参数APR(APR=(σH0-σV0)/(σH0+σV0))进行了南极海冰检测算法研究,其结果与AMSR-2反演的海冰结果相比,在海冰发展趋势、季节变化、面积分布方面都具有很好的一致性[13]。同年,李明明在使用RL-N算法四维参数的基础上,对南北极HY-2A/SCAT数据进行了冰水线性判别分析(Fisher Linear Discriminant Analysis, FLDA),结果表明HY-2A/SCAT数据具有良好的海冰探测能力[2]。
目前来看,针对HY-2A/SCAT数据进行海冰检测算法还较少,缺少更加全面的比较。贝叶斯海冰检测算法虽然已经被很多散射计所应用,却还未用HY-2A/SCAT数据进行过实验;此外,李明明等[2]已经用FLDA算法对HY-2A/SCAT数据进行了海冰检测,模式识别中广泛应用的支持向量机和神经网络算法在很多方面都比FLDA表现出独特的优越性,因此将这两种算法加入HY-2A/SCAT数据的海冰检测研究具有重要意义。此外,参考文献[14]在参数选择方面的启发,本文在输入参数方面基于主成分分析(Principal Component Analysis, PCA)对特征参量进行选择,在此基础上利用BP神经网络检测算法来进行海冰检测。本文使用贝叶斯海冰检测算法、线性判别算法、支持向量机算法和基于PCA的BP神经网络算法对HY-2A/SCAT进行极地海冰检测,分析比较不同算法的结果,并在此基础上分析极地海冰的季节变化。
1 数据介绍 1.1 主要数据本文用于海冰检测的主要数据是HY-2A/SCAT L2A数据。HY-2A卫星于2011年8月16日成功发射,是中国第一个海洋动力环境卫星。HY-2A/SCAT是一个旋转笔形雷达,工作频率为13.256 GHz,采用1 m的碟形反射天线,包括内外2个波束,其中外部波束入射角48°、VV极化,内部波束入射角41°、HH极化,卫星轨道高度971 km,地面刈幅宽度约为1 350 km[16]。随着卫星的飞行,每个地面分辨单元被观测4次:内波束观测前后2次(σHfore, σHaft),外波束观测前后2次(σVfore, σVaft)[15],图 1为散射计观测几何示意图。
1.2 辅助数据本文所用辅助数据是搭载于DMSP的24通道无源微波辐射计SSMIS海冰密集度数据,用来与HY-2A/SCAT海冰检测结果进行对比分析。SSMIS频率范围为19~183 GHz,可获得每日海冰密集度,是目前公认的海冰数据集,该海冰密集度数据可以在美国数据冰雪中心获取[17]。
SSMIS极地网格海冰密集度数据的空间分辨率为25 km,数据来源:ftp://sidads.colorado.edu/pub/DATASETS/nsidc0051gsfc_NASAteam_seaice/。
1.3 数据时空范围本文使用HY-2A/SCAT全球数据对南北极地区的海冰进行探测。作为标准数据的SSMIS极地网格数据采用NASA和NSIDC提出的极地椭球投影方法(正轴等角割方位投影)[18],为了便于观察和比较,对HY-2A/SCAT南北极地区数据采用相同的方法进行投影,投影前后分辨率均为25 km。投影后北极和南极平面栅格大小分别为448×304和332×316。投影后北半球经纬度范围:30.98°N~90°N,180°W~180°E。投影后南半球经纬度范围:39.23°S~90°S,180°W~180°E。
本文所研究的时间范围:2013年9月—2014年8月。图 2为极地平面地图网格,其中lon表示经度(Longitude), lat表示纬度(Latitude)。

|
(方框内为研究区域。Rectangle region is the research area. ) 图 2 极地平面地图网格 Fig. 2 Polar spatial coverage maps |
贝叶斯海冰检测算法在海水和海冰地球物理模式函数(GMF)的基础上,通过统计到海水和海冰两个GMF对应的后向散射系数(σ0)分布的概率距离, 利用贝叶斯公式来实现海冰检测。后向散射系数的大小主要取决于海面粗糙度,在无冰的海面上海面粗糙度主要由风应力决定[10],因此海水GMF即海面风场的GMF。
根据贝叶斯公式,海冰的条件概率可以写成:
| $ \begin{array}{*{20}{c}} {p\left( {ice|{\sigma ^0}} \right) = }\\ {\frac{{p\left( {{\sigma ^0}|ice} \right){p_0}\left( {ice} \right)}}{{p\left( {{\sigma ^0}|ice} \right){p_0}\left( {ice} \right) + p\left( {{\sigma ^0}|wind} \right){p_0}\left( {wind} \right)}}}。\end{array} $ | (1) |
式中:p(ice|σ0)代表待识别单元分类为海冰的后验概率,p0(ice)与p0(wind)的初始值设定为0.5, 条件概率p(σ0|ice)与p(σ0|wind)可用下式表示:
| $ p\left( {{\sigma ^0}|\mathit{wind}} \right) = p\left( {ML{E_{\mathit{wind}}}} \right); $ | (2) |
| $ p\left( {{\sigma ^0}|\mathit{ice}} \right) = p\left( {ML{E_{\mathit{ice}}}} \right)。$ | (3) |
MLEwind和MLEice分别为特征值到海面风场GMF(相当于没有结冰的海面)和冰GMF对应的σ0分布函数的最大似然估计(Maximum Likelihood Estimators, MLE),表示特征值相对于两个模型σ0分布的最小平方距离。参考Seawinds海面风场反演时MLE的定义[9],MLEwind和MLEice分别可以表示为:
| $ ML{E_{\mathit{wind}}} = \frac{1}{{ < MLE > }}\sum\limits_{i = 1, \ldots , N} {\frac{{{{\left( {\sigma _{\mathit{obs}, i}^0 - \sigma _{\mathit{wind}, i}^0} \right)}^2}}}{{\mathit{var}\left[ {\sigma _{\mathit{wind}, i}^0} \right]}}} ; $ | (4) |
| $ ML{E_{ice}} = \sum\limits_{i = 1, \cdots , N} {\frac{{{{\left( {\sigma _{obs, i}^0 - \sigma _{ice, i}^0} \right)}^2}}}{{\mathit{var}\left[ {\sigma _{ice}^0} \right]}}}。$ | (5) |
式中:N表示观测个数(一般是4),σobs, i0表示后向散射系数观测值,σwind, i0表示在给定GMFwind下,根据不同的风速和风向得到的后向散射系数估计值。在实际计算过程中,垂直卫星飞行方向的不同分辨单元的MLE期望值会有所差异,< MLE>表示在某一个风矢量单元的平均MLE值。var[σwind, i0]是仪器噪声,也即Kp2(σwind, i0)2, Kp是仪器信号处理参数与信噪比的函数[19]。var[σice0]代表GMFice的方差。
MLEwind和MLEice函数的期望分布分别可以近似为具有N-2和N-1个独立自由度的卡方分布[20], 概率分布表示为:
| $ p\left( {ML{E_{wind}}} \right) = \frac{1}{2}\exp \left( { - ML{E_{\mathit{wind}}}/2} \right); $ | (6) |
| $ p\left( {ML{E_{ice}}} \right) = \sqrt {\frac{{ML{E_{ice}}}}{{2{\rm{ \mathit{ π} }}}}} \exp \left( { - ML{E_{ice}}/2} \right)。$ | (7) |
为了充分利用历史先验信息,每处理一轨数据都会更新p0(ice)与p0(wind)值,根据Seawinds进行贝叶斯海冰检测时的p0(ice)与p0(wind)的更新原则[9],对HY-2A/SCAT进行处理时也采用相同的阈值,即:
| $ {p_0}(ice) = \left\{ {\begin{array}{*{20}{l}} {0.50 \ {\rm{ if }} \ p\left( {ice|{\sigma ^0}} \right) > 0.30}\\ {0.15 \ {\rm{ if }} \ p\left( {ice|{\sigma ^0}} \right) < 0.30}。\end{array}} \right. $ | (8) |
最终,根据式(1)得到的p(ice|σ0)作为待识别单元判别为海冰的概率。本检测算法使用的散射计观测参数为[σVfore, σHfore, σVaft, σHaft]。
2.1.2 贝叶斯海冰检测算法参数获取 2.1.2.1 海面风场GMF与海冰GMF σ0分布函数参数本文使用的海面风场GMF为NSCAT-4 GMF,该GMF是在NSCAT双极化后向散射测量与ECMWF(European Centre For Medium Range Weather Forecasts)模式基础上建立的[20],将后向散射系数(σ0)表达为风速、风向、入射角以及极化方式的函数[21]。
海冰GMF的σ0分布函数需要通过统计不同极化后向散射系数的对应关系得到相关参数。海冰后向散射是相对各向同性的[10]。如图 3所示,垂直极化下前向与后向散射系数之差D(D=|σVfore-σVaft|)海冰和开阔海水有明显的差别,海冰的D值比开阔海水小很多。此外,冬季纯海冰对应的σ0(dB)在垂直和水平极化后向散射测量空间中整齐地沿着一条直线分布[9], 因此,海冰GMF σ0在垂直和水平极化后向散射测量空间中的分布拟合函数可以简单地表示为:
| $ {\sigma _{V, dB}} = A \times {\sigma _{H, dB}} + B。$ | (9) |

|
图 3 σVfore与σVaft之差的绝对值分布(单位:dB) Fig. 3 Absolute value of the difference between σVfore and σVaft (unit in dB) |
计算海冰GMF σ0分布函数的根本是确定线性方程的斜率A和截距B。海冰GMF σ0分布线性方程的斜率受混合冰水以及冰架等很多因素的影响,为了保证海冰GMF σ0分布线性方程的一致性,应选取最具代表性时间段的纯海冰拟合这条直线的斜率[9]。
图 4是不同海冰密集度下北极每日线性模式方程斜率。参考Seawinds海冰GMF σ0分布函数的参数计算过程,结合斜率曲线,选择1—3月份,60°N以上范围内的海冰的平均斜率为最终的海冰GMF σ0分布函数斜率。

|
(北极参考斜率用红色虚线标出。The reference Arctic winter slope is highlighted in red dashed line. ) 图 4 不同海冰密集度下北极每日海冰GMF σ0分布线性函数拟合斜率 Fig. 4 Arctic daily fitting slopes to sea ice GMF σ0distribution linear model of three different sea ice concentration |
最终确定的北极海冰GMFσ0分布函数的斜率为1.095 8,截距为-0.192 2。
得到海冰GMFσ0 分布拟合函数的斜率和截距后,可以最终确定NSCAT-4 GMF与海冰GMF在原始后向散射测量空间中的分布。图 5为两个模型在HH和VV两个极化后向散射测量空间中的σ0分布,虚线框选范围为海面风场GMF σ0分布,直线为HY-2A/SCAT冰GMF σ0分布的线性拟合。
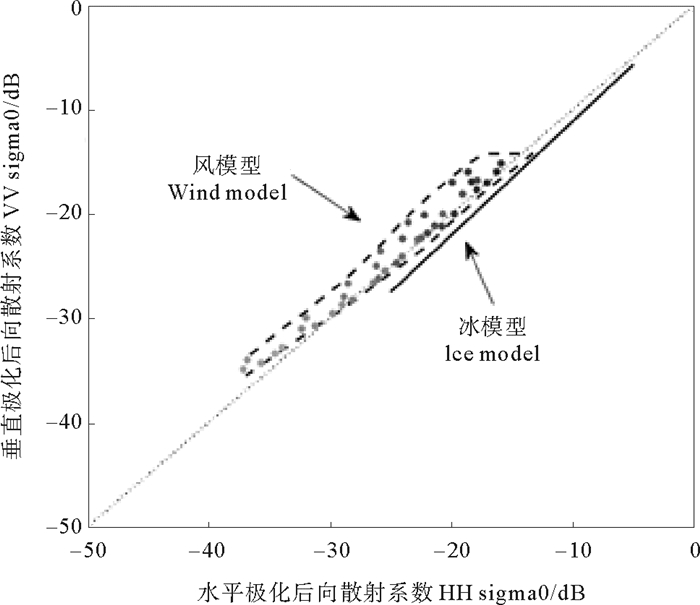
|
图 5 NSCAT-4GMF与HY-2A/SCAT海冰GMF在垂直和水平极化测量空间中的σ0 分布 Fig. 5 σ0 distribution of NSCAT-4 GMF and sea ice GMF in the space of HY-2A/SCAT HH and VV measurements |
var[σice0]是通过统计观测点的后向散射系数与海冰GMF σ0分布拟合函数的距离来获取的[9],误差方差表达为标准差的平方。图 6为观测点的后向散射系数与海冰GMF σ0分布拟合函数的距离示意图,也即标准差。
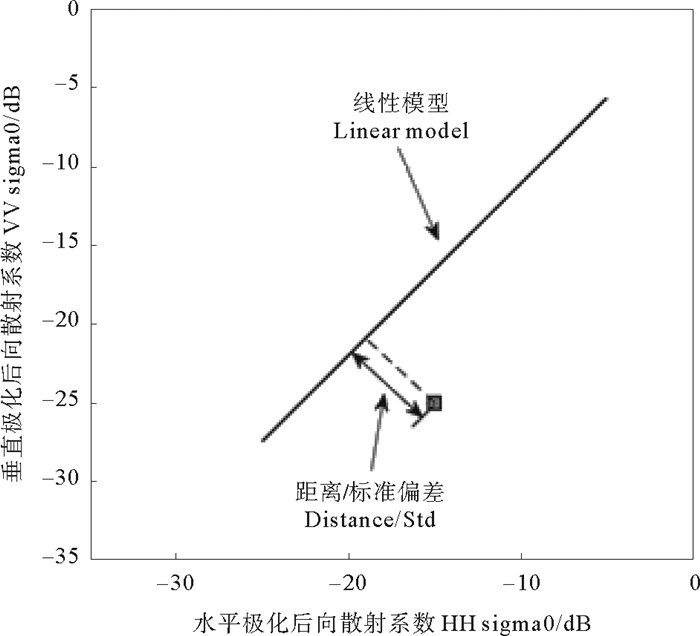
|
图 6 后向散射系数观测值到海冰GMF σ0分布线性函数的距离(标准差)示意图 Fig. 6 Distance(Std) of observed sea ice σ0 to sea ice GMF σ0distribution linear model |
如图 7为2014年HY-2A/SCAT海冰后向散射系数观测值与海冰GMF σ0分布拟合函数的距离的概率分布,高斯拟合以后得到北极地区标准差为0.4 dB,南极为0.5 dB,所以我们取0.5 dB作为std[σice0]的数值,但是混合冰水单元的存在会使var[σice0]比纯海冰单元要大,提高var[σice0],可以更好地检测低海冰密集度的海冰以及薄冰,所以实际应用中,设置容差系数α,并将α×std[σice0]的乘积作为最终的误差标准差。利用Seawinds散射计数据基于贝叶斯算法进行海冰检测结果表明,其最优海冰模型标准差为1.5 dB,即α=3,在这个容差系数下,误判点不会太多,但是又能较好的检测海冰生长季(秋冬季)的海冰[9]。

|
图 7 海冰后向散射到海冰GMFσ0分布线性函数的距离频率直方图分布 Fig. 7 Frequency histogram of sea ice backscatter distances to linear sea ice σ0 distribution model |
线性判别分析是常用的有监督分类算法。基于HY-2A/SCAT数据海冰与海水的检测,是在RL-N算法的基础上,通过对特征参数[σV48/σH41, σH41, ΔσH41, ΔσV48]实现线性判别分析的。具体步骤如下:
假设有n组样本数据,每一组样本数据可以表示为四维参数矢量xi,由于海冰检测只有冰和水两个类别,因此只需要把样本数据投影到一条直线上。对任意一组样本矢量, 它在直线w上的投影可以表示为wTxi, 设两个类别的中心点μ0, μ1,在直线w的投影分别为wTμ0和wTμ1。根据线性判别原理,需要让冰水两个类别中心的距离尽可能大,亦即最大化‖wTμ0-wTμ1‖2, 同时要求同一类别数据的投影点尽可能的接近,相当于要求协方差wT∑0w和wT∑1w尽可能小,即最小化wT∑0w+wT∑1w。综上所述,优化目标函数为:
| $ J\left( \mathit{\boldsymbol{w}} \right) = \frac{{{\mathit{\boldsymbol{w}}^{\rm{T}}}\left( {{\mu _0} - {\mu _1}} \right){{\left( {{\mu _0} - {\mu _1}} \right)}^{\rm{T}}}\mathit{\boldsymbol{w}}}}{{{\mathit{\boldsymbol{w}}^T}\left( {{\mathit{\Sigma }_0} + {\mathit{\Sigma }_1}} \right)\mathit{\boldsymbol{w}}}}。$ | (10) |
类间离散矩阵表示为
| $ {\mathit{\boldsymbol{S}}_B} = \left( {{\mu _0} - {\mu _1}} \right){\left( {{\mu _0} - {\mu _1}} \right)^{\rm{T}}}。$ | (11) |
类内离散矩阵表示为
| $ \begin{array}{l} {\mathit{\boldsymbol{S}}_W} = {\mathit{\Sigma }_0} + {\mathit{\Sigma }_1} = \\ \sum\limits_{x \in {X_0}} {\left( {x - {\mu _0}} \right)} {\left( {x - {\mu _0}} \right)^{\rm{T}}} + \sum\limits_{x \in {X_1}} {\left( {x - {\mu _1}} \right)} {\left( {x - {\mu _1}} \right)^{\rm{T}}}。\end{array} $ | (12) |
因此优化目标函数可以重写为
| $ J(\mathit{\boldsymbol{w}}) = \frac{{{\mathit{\boldsymbol{w}}^{\rm{T}}}{\mathit{\boldsymbol{S}}_B}\mathit{\boldsymbol{w}}}}{{{\mathit{\boldsymbol{w}}^{\rm{T}}}{\mathit{\boldsymbol{S}}_w}\mathit{\boldsymbol{w}}}}。$ | (13) |
采用拉格朗日乘子法解出上式的最佳投影方向
| $ {\mathit{\boldsymbol{w}}^*} = \mathit{\boldsymbol{S}}_w^{ - 1}\left( {{\mu _0} - {\mu _1}} \right)。$ | (14) |
则判别函数可以写为
| $ y = {\mathit{\boldsymbol{w}}^{*{\rm{T}}}}x。$ | (15) |
然后确定分类阈值w0, 本文采用下式来获得w0:
| $ {\mathit{\boldsymbol{w}}_0} = \frac{{{\mathit{\boldsymbol{w}}^{*{\rm{T}}}}{\mu _0} + {\mathit{\boldsymbol{w}}^{*{\rm{T}}}}{\mu _1}}}{2}。$ | (16) |
根据这个原则将所有样本数据投影至最优一维矢量空间后,比较投影后待识别单元的y值与阈值w0的大小, 判断该待识别单元属于海冰还是开阔海水。
2.3 支持向量机(SVM)海冰检测算法由于线性判别分析(FLDA)只能处理线性可分问题,但是数据样本通常并不一定线性可分。支持向量机(Support Vector Machine, SVM)算法通过引入核函数解决非线性可分问题。
与FLDA的降维不同,SVM是将[σV48/σH41, σH41, ΔσH41, ΔσV48]四维参数样本,通过核函数映射到高维空间,在高维空间上寻找一个最优超平面来实现海冰检测。假设有n组训练样本数据,每一组样本数据可以表示为四维参数矢量xi, 本研究中即HY-2A/SCAT观测到的[σV48/σH41, σH41, ΔσH41, ΔσV48]四维参数向量。用ϕ表示将样本映射到高维空间的一个非线性变换。假设在高维空间中是线性可分的,那么这个最优超平面为:
| $ {\mathit{\boldsymbol{w}}^{\rm{T}}} \times \mathit{\boldsymbol{\varphi }}\left( {{x_i}} \right) + \mathit{\boldsymbol{b}} = 0(i = 1, \cdots , n)。$ | (17) |
其中:w为权重向量;b为偏移向量。冰水两个类别之间的距离为2/||w||,那么分类问题就转换成了带有约束条件的最小值问题,即:
| $ \min {\left\| \mathit{\boldsymbol{w}} \right\|^2}/2; $ | (18) |
| $ {\rm{s}}.\;{\rm{t}}.\;\left( {\left( {{\mathit{\boldsymbol{w}}^{\rm{T}}} * \mathit{\boldsymbol{\varphi }}\left( {{x_i}} \right)} \right) + \mathit{\boldsymbol{b}}} \right) \ge 1\;(i = 1, \cdots , n)。$ | (19) |
式中:y是类别标签;yi是y的第i个分量。本文仅有海冰和海水两个类别,即y设置为+1和-1。这个公式可以使用拉格朗日乘数法来求解。即先对每条约束添加拉格朗日乘子βi≥0,则该问题的拉格朗日函数可写为:
| $ \begin{array}{l} L\left( {\mathit{\boldsymbol{w}}, \mathit{\boldsymbol{b}}, \mathit{\boldsymbol{\beta }}} \right) = \frac{1}{2}{\left\| \mathit{\boldsymbol{w}} \right\|^2} + \\ \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{\beta }}_i}} \left( {1 - {y_i}\left( {{\mathit{\boldsymbol{w}}^{\rm{T}}} \times \mathit{\boldsymbol{\varphi }}\left( {{x_i}} \right) + \mathit{\boldsymbol{b}}} \right)} \right)(i = 1, \cdots , n)。\end{array} $ | (20) |
用序列最小优化算法(SMO)可得w的最优解w*:
| $ {w^*} = \sum\limits_{i = 1}^n {\mathit{\boldsymbol{\beta }}_i^*} {y_i}\mathit{\boldsymbol{\varphi }}\left( {{x_i}} \right)(i = 1, \cdots , n)。$ | (21) |
得到w*后可代入式(17)得到的b最优解b*。则对于任意测试样本点m,其决策函数可以写为:
| $ \begin{array}{l} f(m) = \\ {\rm sign} \left( {\left( {\sum\limits_{i = 1}^n {\mathit{\boldsymbol{\beta }}_i^*} {y_i}{\mathit{\boldsymbol{\varphi }}^{\rm{T}}}\left( {{x_i}} \right)} \right)\mathit{\boldsymbol{\varphi }}(m) + {\mathit{\boldsymbol{b}}^*}} \right)\;(i = 1, \cdots , n)。\end{array} $ | (22) |
式中:m表示投影后测试样本点参数;φT(xi)φ(m)即为投影后测试样本点与训练样本的内积,由于直接计算这个内积比较困难,所以用核函数代替内积:
| $ \sum\limits_{i = 1}^n {\mathit{\boldsymbol{\beta }}_i^*} {y_i}\mathit{\boldsymbol{K}}\left( {{x_i}, m} \right) + {\mathit{\boldsymbol{b}}^*} = 0\;\;(i = 1, \cdots , n)。$ | (23) |
本文使用高斯核函数,可以表示为:
| $ {\rm{K}}\left( {{x_i}, m} \right) = \exp \left( {\frac{{ - {{\left\| {{x_i} - m} \right\|}^2}}}{{2{\sigma ^2}}}} \right)(i = 1, \cdots , n)。$ | (24) |
式中, σ是达到率,即函数值跌落到0的速度参数。
基于这个原则,本文利用[σV48/σH41, σH41, ΔσH41, ΔσV48]四维参数样本,对极地海冰进行检测,其中高斯核函数的σ设为1。
2.4 基于主成分分析的BP神经网络海冰检测算法主成分分析是通过正交变换将一组可能存在相关性的变量转换为线性不相关的变量。主成分分析可以减少特征数量,有助于降低数据变量的复杂性。BP(Back Propagation)神经网络是采用误差逆向传播算法训练的多层前馈神经网络[22],利用BP神经网络对目标进行分类,若输入太多的样本特征,则会降低网络的训练速度与效率,严重时会导致网络不收敛。所以结合PCA对原始数据进行主成分提取可以提高神经网络训练速度与效率。
本文根据HY-2A/SCAT观测和计算得到的可能用于海冰检测的参数组合:[σV48/σH41, ΔσH41, ΔσV48, σVfore, σHfore, σVaft, σHaft]作为PCA的样本输入进行主成分分析并保留前几个主成分,然后将带有类别标签的主成分输入到BP神经网络,调整神经网络节点个数、学习效率、迭代次数等进行网络训练。经过多次实验,最终确定当输入参数为3个主成分,BP神经网络为3层且隐藏节点数为12时,训练结果精确度较高。
3 结果分析为了对比不同算法检测海冰的能力,本文从冰水误判、海冰边界、海冰面积变化趋势三个方面对四种算法的海冰检测结果进行分析。
3.1 海冰检测结果误判率对比图 8为利用四种算法得到的2013年9月16日北极海冰范围检测结果,以及与同时期SSMIS 15%海冰密集度的海冰范围(见图 8(e))进行比较。从图中可以看出,FLDA和SVM算法得到的海冰检测结果在区域C处都存在大量海冰误判,贝叶斯算法与基于PCA的BP神经网络算法在这个位置的误判相对较少。四种方法的误判率(噪声点与全部测量点的比)进行统计见表 1。
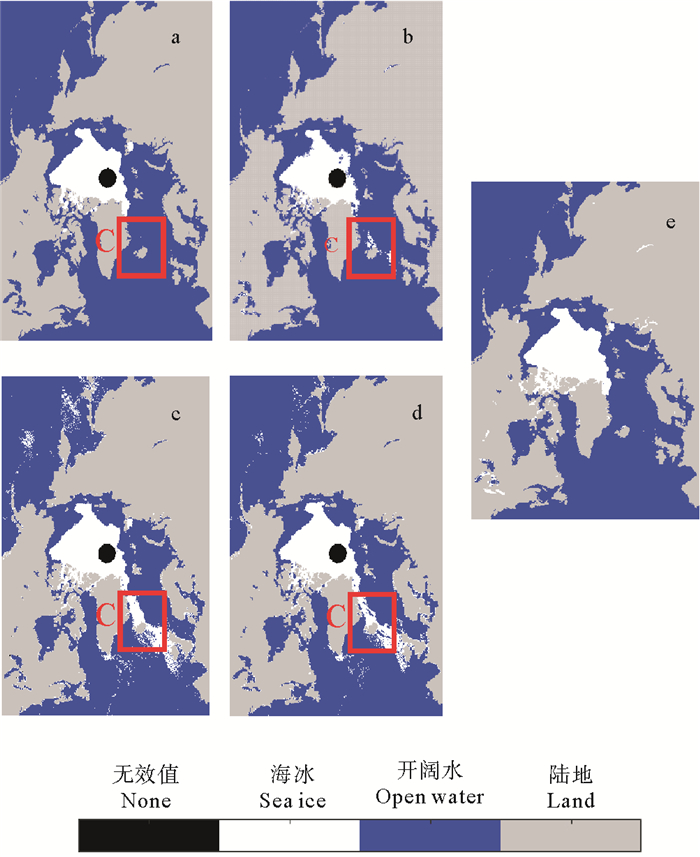
|
( a贝叶斯算法Bayesian;b基于PCA的BP神经网络算法BP neural network based on PCA;c线性判别算法FLDA;d支持向量机算法SVM;e SSMIS海冰范围SSMIS sea ice extent。区域C处表示四种算法的误判差异。Area C indicates misjudgment difference among four algorithms. ) 图 8 不同算法得到的2013年9月16日北极海冰范围和SSMIS结果 Fig. 8 Arctic extent on sept.16, 2013 based on Bayesian, NN, FLDA and SVM algorithms respectively with SSMIS result |
|
|
表 1 不同算法的误判率 Table 1 Misjudgment rate of different algorithms |
从表 1可知,贝叶斯算法的总误判率最小,其次是基于PCA的BP神经网络算法,SVM算法和FLDA算法的误判率较大。Rivas[20]利用贝叶斯算法对Seawinds数据进行冰水检测时,发现高风速会影响检测结果,因此利用数值预报NWP(Numerical Weather Prediction)风速进行校正;此外,应用RL-N算法海冰检测也发现,高风速影响检测效果,尤其是在格陵兰岛和威德尔海域[9]。其原因在于高风速的海面,海冰和开阔海水的后向散射系数非常相近,导致海冰和开阔海水的特征区分不明显。
为了验证区域C处产生误判的原因,对2013年9月16日区域C内后向散射系数分布(见图 9)和ECMWF风速(见图 10)进行分析。

|
图 9 北极地区σVfore(dB)分布(2013年9月16日) Fig. 9 Arctic foreword V-pol sigma0(dB) (Sept.16, 2013) |

|
图 10 北极地区ECMWF风速(m/s)(2013年9月16日) Fig. 10 Arctic ECMWF wind speed (m/s) (Sept.16, 2013) |
从图中可以看出,误判位置的后向散射系数比周围开阔海水区高的多,可以达到-10 dB,风速也都在15 m/s以上。因此,该位置产生的过多误判与风速有着很大联系。
贝叶斯方法由于结合了先验概率信息,其冰水检测不完全依赖当前观测的后向散射系数,结合海面风场和海冰GMF并加入了NWP风速,可以校正风速过高引起的误差,因此误判相对较低,优于FLDA和SVM算法;基于PCA的BP神经网络算法,在主成分分析时仅保留最主要的特征信息,并且BP神经网络通过反复的后向反馈,理论上可以实现任何非线性映射的功能,所以误判率也相对较低,但仔细分析冰水的边界,发现这种算法得到的海冰边界比较粗糙。
3.2 海冰边界对比SSMIS海冰密集度数据与HY-2A/SCAT海冰范围采用相同的极地投影方式,并且具有相同的分辨率,可以直接进行海冰边界的比较。将四种算法的海冰边界与SSMIS海冰边界进行对比后得到,四种算法的海冰边界均介于SSMIS 0%和30%海冰密集度海冰边界之间。
为了对HY-2A/SCAT南北极海冰边界进行具体分析,本文只列出了贝叶斯算法和SVM算法的海冰边界与SSMIS 0%、30%海冰密集度海冰范围边界的对比图(见图 11)。为了清楚地展示比较结果,海冰轮廓叠加在SSMIS 0%密集度图像上。

|
( a贝叶斯算法(南极) Bayesian(Antarctic); b贝叶斯算法(北极) Bayesian(Arctic); c支持向量机(南极) SVM(Antarctic); d支持向量机(北极) SVM(Arctic)。绿色线条表示SSMIS 0%密集度边界;黄色线条表示SSMIS 30%密集度边界;红色线条代表贝叶斯和SVM得到海冰边界。Green line indicates SSMIS 0% concentration edge; yellow line indicates SSMIS 30% concentration edge; red line indicates Bayesian and SVM edge. ) 图 11 基于贝叶斯和SVM算法得到的2013年9月20日极地海冰边界 Fig. 11 Polar sea ice edge based on Bayesian and SVM on Sept.20, 2013 |
从图 11可以看出,两种算法获得的海冰边界都在海冰密集度0%~30%之间,由此说明这两种算法都可以用于海冰边界的检测。
3.3 南北极海冰范围季节趋势分析考虑到PCA的BP神经网络算法运行效率,以及FLDA误判较多,本文选取贝叶斯算法和SVM算法海冰检测结果,对HY-2A/SCAT 2013年9月到2014年8月份极地海冰变化趋势进行分析(见图 12)。其中,对SVM算法结果进行了图像腐蚀膨胀技术处理,贝叶斯海冰检测算法中α取3,将SSMIS 0%、15%、30%密集度以上的海冰面积作为比较标准。

|
图 12 2013年9月1日~2014年8月31日基于HY-2A/SCAT的极地日海冰范围 Fig. 12 Dailysea ice extent of polar area based on HY-2A/SCAT(Sept.1, 2013~Aug.31, 2014) |
从整体来看,贝叶斯算法与SVM算法海冰面积变化趋势图都能很好的展现海冰面积的季节性变化。在海冰结冰期(冬季),与SSMIS 15%、30%密集度海冰面积相比,贝叶斯和SVM算法得到的海冰面积变化都
与其比较一致,且都介于SSMIS 0%、30%密集度海冰面积曲线之间;而在海冰融冰期(夏季),贝叶斯算法和SVM算法探测的海冰面积都要比SSMIS 30%海冰密集度以上的海冰面积大,且贝叶斯算法探测的海冰面积超过SSMIS 30%海冰密集度以上的海冰面积的程度更大,而SVM算法结果与SSMIS 15%海冰密集度以上的海冰面积比较一致, 该结果与之前研究[9, 23]基本相符。
4 结语本文针对HY-2A/SCAT可以进行海冰检测的有用参数,详细研究了贝叶斯、FLDA、SVM以及基于PCA的BP神经网络的海冰检测算法,分析HY-2A/SCAT在极地海冰检测中的应用效果,以及在冰水误判、海冰面积变化趋势等方面的表现。
从海冰检测结果来看,四种方法都能基于HY-2A/SCAT进行海冰检测。初步结果表明,高风速引起的误判对贝叶斯算法和基于PCA的BP神经网络算法影响较小, FLDA以及SVM算法受高风速影响较大。其中针对贝叶斯算法,本文基于HY-2A/SCAT数据获取了适合HY-2A/SCAT的海冰GMF σ0分布拟合参数及其方差,实现了HY-2A/SCAT贝叶斯海冰检测算法。
将贝叶斯和SVM算法得到的海冰边界与SSMIS 0%、30%海冰密集度的海冰边界相比,结果显示这两种算法的海冰边界都介于SSMIS 0%、30%海冰密集度的海冰边界之间。
对贝叶斯和SVM算法得到的海冰面积季节变化趋势与SSMIS 0%、15%、30%海冰密集度的海冰面积变化相比较,它们在结冰期(冬季)吻合度较高;而在融冰期(夏季),基于散射计的两种算法得到的海冰面积比SSMIS 30%海冰密集度以上的海冰面积要大,但SVM算法探测的海冰面积与SSMIS 15%海冰密集度以上的海冰面积比较一致。
综上所述,四种算法均适用于HY-2A/SCAT的海冰检测研究,证明了HY-2A/SCAT具有良好的海冰检测能力,不失为一种海冰探测的有效手段。在未来的工作中,将进一步探索HY-2A/SCAT在海冰分类方面的研究,了解不同算法的物理机制,以及寻找更多更适合的海冰检测特征,为极地海冰监测与全球变化研究服务。
| [1] |
Sandven S, Johannessen O M, Kloster K. Sea Ice Monitoring by Remote Sensing[M]. New Jersey: John Wiley & Sons, Ltd, 2006: 241-283.
(  0) 0) |
| [2] |
Li Mingming, Zhao C F, Zhao Alcide, et al. Polar sea ice monitoring using HY-2A scatterometer measurements[J]. Remote Sensing, 2016, 8(8): 688. DOI:10.3390/rs8080688
(  0) 0) |
| [3] |
谭继强, 詹庆明, 殷福忠, 等. 面向极地海冰变化监测的卫星遥感技术研究进展[J]. 测绘与空间地理信息, 2014(4): 23-31. Tan Jiqiang, Zhan Qingming, Yin Fuzhong, et al. On evolution of technologies in remote sensing for sea Ice change monitoring in polar regions[J]. Geomatics Spatial Information Technology, 2014(4): 23-31. DOI:10.3969/j.issn.1672-5867.2014.04.007 (  0) 0) |
| [4] |
Svendsen E, Kloster K, Farrelly B, et al. Norwegian remote sensing experiment: Evaluation of the Nimbus 7 scanning multichannel microwave radiometer for sea ice research[J]. Journal of Geophysical Research Oceans, 1983, 88(C5): 2781-2791. DOI:10.1029/JC088iC05p02781
(  0) 0) |
| [5] |
Bjørgo E, Johannessen O M, Miles M W. Analysis of merged SMMR-SSMI time series of Arctic and Antarctic sea ice parameters 1978-1995[J]. Geophysical Research Letters, 1997, 24(4): 413-416. DOI:10.1029/96GL04021
(  0) 0) |
| [6] |
Nishio F, Comiso J C. The Polar Sea Ice Cover from Aqua/AMSR-E[C]. Seoul: IEEE International Geoscience and Remote Sensing Symposium, 2005: 4933-4937.
(  0) 0) |
| [7] |
刘良明. 卫星海洋遥感导论[M]. 武汉: 武汉大学出版社, 2005: 280. Liu Liangming. An Introduction to Satellite Oceanic Remote Sensing[M]. Wuhan: Wuhan University Press, 2005: 280. (  0) 0) |
| [8] |
Remund Q P, Long D G. Sea Ice Mapping Algorithm for QUIKSCAT and Seawinds[C]. Seattle WA, USA: 1998 IEEE International Geoscience and Remote Sensing Symposium, 1998: 1686-1688.
(  0) 0) |
| [9] |
Belmonte Rivas M, Stoffelen A. Near Real-Time Sea Ice Discrimination Using Seawinds on Quikscat[R]. Netherlands: Royal Netherlands Meteorological Institute, 2009.
(  0) 0) |
| [10] |
de Haan S, Stoffelen A. Ice Discrimination Using ERS Scatterometer[R]. Netherlands: Royal Netherlands Meteorological Institute, 2001.
(  0) 0) |
| [11] |
Verspeek J. Sea Ice Classification Using Bayesian Statistics[R]. Netherlands: Royal Netherlands Meteorological Institute, 2006.
(  0) 0) |
| [12] |
Belmonte Rivas M, Verspeek J, Verhoef A. Bayesian sea ice detection with the advanced scatterometer ASCAT[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(7): 2649-2657. DOI:10.1109/TGRS.2011.2182356
(  0) 0) |
| [13] |
Zou J, Zeng T, Guo M. The study on an Antarctic sea ice identification algorithm of the HY-2A microwave scatterometer data[J]. Acta Oceanologica Sinica, 2016, 35(9): 74-79. DOI:10.1007/s13131-016-0927-5
(  0) 0) |
| [14] |
刘志怀, 秦芳, 刘娜. 基于主成分分析和BP神经网络的钢丝绳断丝定量检测方法[J]. 振动与冲击, 2018, 37(18): 276-281. Liu Zhihuai, Qin Fang, Liu Na. Quantitative testing method for broken wire in steel rope based on principal component analysis and BP artificial neural network model[J]. Journal of Vibration and Shock, 2018, 37(18): 276-281. (  0) 0) |
| [15] |
Wang X, Liu L, Shi H. In-orbit Calibration and Performance Evaluation of HY-2 Scatterometer[C]. Munich: 2012 IEEE International Geoscience and Remote Sensing Symposium, 2012: 4614-4616.
(  0) 0) |
| [16] |
林明森, 邹巨洪, 解学通. HY-2A微波散射计风场反演算法[J]. 中国工程科学, 2013, 15(7): 68-74. Lin Mingsen, Zou Juhong, Xie Xuetong. HY-2A microwave scatterometer wind retrieval algorithm[J]. Engineering Sciences, 2013, 15(7): 68-74. DOI:10.3969/j.issn.1009-1742.2013.07.010 (  0) 0) |
| [17] |
Kunkee D B, Poe G A, Boucher D J, et al. Design and evaluation of the first special sensor microwave imager/sounder[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(4): 863-883. DOI:10.1109/TGRS.2008.917980
(  0) 0) |
| [18] |
Frederick Pearson I. Map Projections Theory and Applications[M]. Florida: CRC, 1990.
(  0) 0) |
| [19] |
Dunbar R S, Lungu T, Weiss B, et al. QuikSCAT Science Data Product User Manual[R]. Pasadena: Jet Propulsion Laboratory, 2006.
(  0) 0) |
| [20] |
Belmonte Rivas M, Stoffelen A. New bayesian algorithm for sea ice detection with QuikSCAT[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 1894-1901. DOI:10.1109/TGRS.2010.2101608
(  0) 0) |
| [21] |
Wentz F J, Smith D K. A model function for the ocean-normalized radar cross section at 14 GHz derived from NSCAT observations[J]. Journal of Geophysical Research: Oceans, 1999, 104(C5): 11499-11514. DOI:10.1029/98JC02148
(  0) 0) |
| [22] |
闻新. 智能故障诊断技术:MATLAB应用[M]. 北京: 北京航空航天大学出版社, 2015. Wen Xin. Intelligent Fault Diagnosis Technology: Matlab Application[M]. Beijing: Beihang University Press, 2015. (  0) 0) |
| [23] |
Comiso J C, Zwally H J. Concentration gradients and gro wth/decay characteristics of the seasonal sea ice cover[J]. Journal of Geophysical Research Oceans, 1984, 89(C5): 8081-8103. DOI:10.1029/JC089iC05p08081
(  0) 0) |
2. Laboratory for Regional Oceanography & Numerical Modeling, Qingdao Pilot National Laboratory for Marine Science and Technology, Qingdao 266011, China
 2019, Vol. 49
2019, Vol. 49


