在渔船操作模拟器的研究方面，英国Transas的NTPRO 5000^[1]、俄罗斯Vector Marine Electronics公司的NFS-3000^[2]等产品都可以用于渔船船员培训，能够进行渔船拖网和围网作业仿真。利用渔船模拟器对相关人员进行培训，可以让船员在培训中熟练地操作各种船舶设备，提高应对危机和海上安全管理的经验能力。目前我国渔船模拟器领域尚处于起步阶段，还没有可用于培训的产品。

渔网作为渔业模块的重要组成部分，近年来其水动力特性的研究已取得很大进展。大多数学者采用集中质量法建立渔网的数学模型，来进行渔网的动态模拟。Takagi、Suzuki^[3-6]等针对特定的网片进行仿真分析，将网片的仿真与水槽实验进行比较，实现网片的三维显示；Chun-Woo Lee^[7-8]开发了渔网自动设计建模软件，该软件对拖网和围网都适用；在国内，李玉成^[9]研究了网箱在水流作用下网衣的变形和应力分布情况；孙霄峰^[10]并实现了单船中层拖网的实时仿真；黄小华^[11]研究了不同配重和流速下网的受力和变形；陈英龙^[12]考虑了拖网网板及升力帆布水动力的作用建立整个网具系统的仿真模型，通过海上试验验证了模型的准确性。渔网各质量点的运动方程相互联系，构成数目巨大的非线性微分方程组，这就给模型的数值解法提出了很高的要求，常用的求解方法主要有：四阶Runge-Kutta法、六级五阶Runge-Kutta法及Newmark-β法。Runge-Kutta是一种显式的数值解法, 其稳定求解的时间步长受到柔性体刚度的极大限制；而隐式的Newmark-β法其计算精度和模型解算时间有待于进一步提高。

钟万勰^[13]提出线性定常结构的精细时程积分方法，以其高精度、无条件稳定等优点得到广泛应用。而非线性问题研究的关键是如何求解非齐次项产生的Duhamel积分。谭述君^[14]在Duhamel项精细积分方法的基础上构造了单步法和多步法进行非线性微分方程的求解；高强^[15]则提出了一种针对大规模动力系统的改进的快速精细积分方法；邹洋^[16]通过精细积分方法对起重船吊物系统的三维非线性动力方程进行求解。

本文将采用集中质量法建立渔网网衣的数学模型，采用精细积分法进行模型的数值求解，并与模型试验数据进行对比，分别对水流作用下网衣所受的流体力、网衣形状和位移随时间的变化进行了动态模拟，验证了本文数值解法的可靠性。

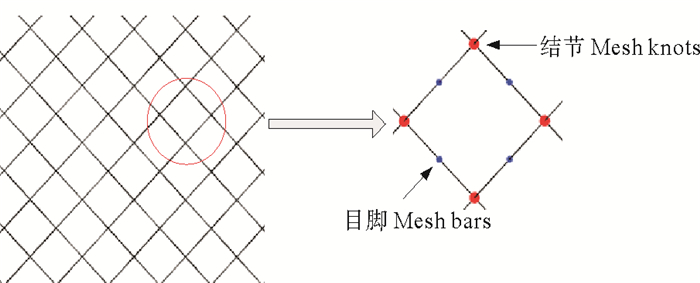
1 渔网网衣的数学模型

根据集中质量法将网衣离散为通过无质量弹簧相连的质量点集合。假设结节为球体，目脚为圆柱体，结节和目脚的质量分别集中于各自的形心，如图 1所示。球体的流体阻力在各个方向上均相同，而作用在圆柱体的流体阻力与来流方向有关，以下分别建立结节和目脚的数学模型。

1.1 结节的运动方程

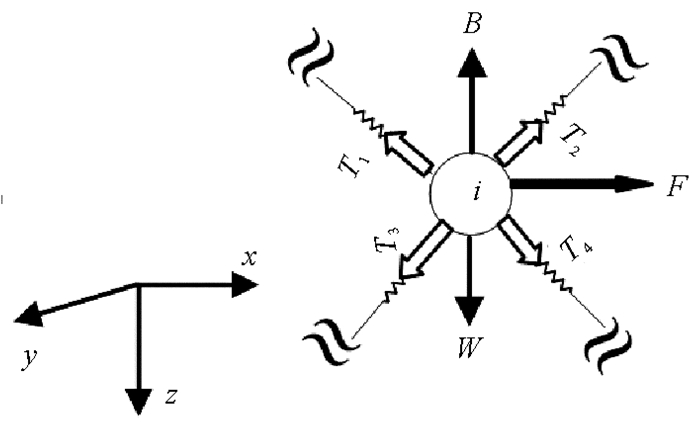
渔网网衣假设在均匀流作用下，由于球体的流体阻力系数在各方向上都相同，在空间坐标系下对第i个结节进行受力分析，如图 2所示。结节运动方程可表示如下：

$ \left( {{M_i} + \Delta {M_i}} \right)a = T + F + W + B。$

(1)

其中：a是结节i的加速度；T、F分别表示结节受到的弹力和流体阻力，其中弹力是结节i受到与其相连的所有质量点对其作用力的合力；W为结节的重力；B为结节所受的浮力；M_i和ΔM_i表示第i个结节的质量和附加质量。

结节i与目脚j相连，其受的弹性力的大小可表示如下：

$ \left\{ \begin{array}{l} \left| {{T_{ij}}} \right| = E{A_{ij}}\left( {{l_{ij}} - {l_{0ij}}} \right)/{l_{0ij}}\;\;\;\;\;{l_{ij}} > {l_{0ij}}\\ \left| {{T_{ij}}} \right| = 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{l_{ij}} \le {l_{0ij}} \end{array} \right.。$

(2)

其中：E, A_ij分别为质量点i, j之间目脚的弹性模量和横截面积；l_ij, l_0ij分别为质量点i, j之间的实际长度和未伸长时的长度。作用在结节i上的弹性力在空间坐标系三个坐标轴上的分量可表示如下：

$ \left\{ \begin{array}{l} {T_x} = \sum\limits_{j \in {\bf{N}}} {\left( {{x_j} - {x_i}} \right)\left| {{T_{ij}}} \right|/{l_{ij}}} \\ {T_y} = \sum\limits_{j \in {\bf{N}}} {\left( {{y_j} - {y_i}} \right)\left| {{T_{ij}}} \right|/{l_{ij}}} \\ {T_z} = \sum\limits_{j \in {\bf{N}}} {\left( {{z_j} - {z_i}} \right)\left| {{T_{ij}}} \right|/{l_{ij}}} \end{array} \right.。$

(3)

其中N表示同结节i相连的质量点的集合。

考虑结节在均匀流作用下，其流体阻力在空间坐标系三个坐标轴上的分量可表示如下：

$ \left\{ \begin{array}{l} {F_x} = \frac{1}{2}\rho {C_d}S\left| {{{\dot x}_i} - {v_{cx}}} \right|\left( {{{\dot x}_i} - {v_{cx}}} \right)\\ {F_y} = \frac{1}{2}\rho {C_d}S\left| {{{\dot y}_i} - {v_{cy}}} \right|\left( {{{\dot y}_i} - {v_{cy}}} \right)\\ {F_z} = \frac{1}{2}\rho {C_d}S\left| {{{\dot z}_i} - {v_{cz}}} \right|\left( {{{\dot z}_i} - {v_{cz}}} \right) \end{array} \right.。$

(4)

其中：ρ为流体密度；C_d为结节的阻力系数；S为结节的投影面积；v_cx, v_cy, v_cz分别为流速在空间坐标系三个坐标轴上的分量。

结节在水中的重力表示为：

$ W + B = \left( {{m_i} - \rho {V_i}} \right)g。$

(5)

其中：V_i是结节的体积；g为重力加速度。

把以上(2)~(5)式代入(1)式可得结节i在空间坐标系下的运动方程：

$ \left\{ \begin{array}{l} \left( {{M_i} + \Delta {M_i}} \right){{\ddot x}_i} = {T_x} + {F_x}\\ \left( {{M_i} + \Delta {M_i}} \right){{\ddot y}_i} = {T_y} + {F_y}\\ \left( {{M_i} + \Delta {M_i}} \right){{\ddot z}_i} = {T_z} + {F_z} + W + B \end{array} \right.。$

(6)

${\ddot x_i}{\rm{、}}{\ddot y_i}{\rm{和}}{\ddot z_i}$表示结节i在x, y, z轴的加速度。

1.2 目脚的运动方程

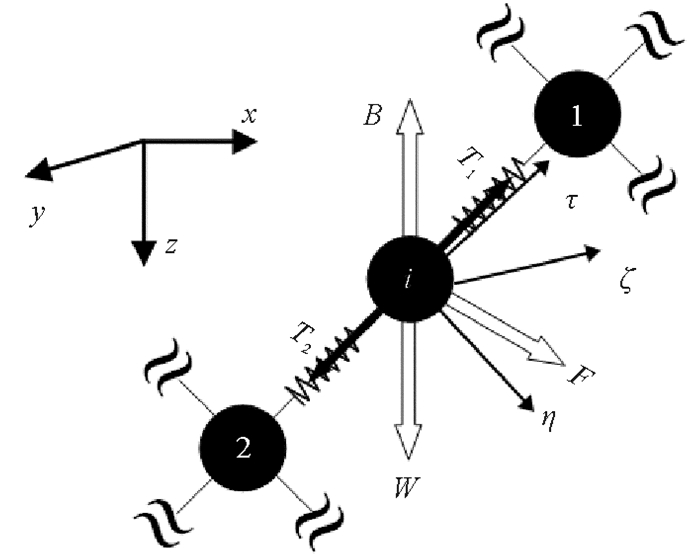
目脚的数学模型与结节相似，只是结节是在空间坐标系下进行受力分析，而目脚在局部坐标系下分析其受力(见图 3)。将目脚视作圆柱体，流体阻力系数与来流方向有关，目脚i的运动方程可表示如下：

$ \left\{ \begin{array}{l} \left( {{M_i} + \Delta {M_{i\tau }}} \right){{\ddot \tau }_i} = {T_\tau } + {F_\tau } + {W_\tau } + {B_\tau }\\ \left( {{M_i} + \Delta {M_{i\eta }}} \right){{\ddot \eta }_i} = {T_\eta } + {F_\eta } + {W_\eta } + {B_\eta }\\ \left( {{M_i} + \Delta {M_{i\xi }}} \right){{\ddot \xi }_i} = {T_\xi } + {F_\xi } + {W_\xi } + {B_\xi } \end{array} \right.。$

(7)

其中：${\ddot \tau _i}{\rm{、}}{\ddot \eta _i}{\rm{和}}{\ddot \xi _i}$表示目脚i在局部坐标系τ, η, ξ各轴的加速度；M_i为第i个目脚的质量；ΔM_iτ、ΔM_iη、ΔM_iξ为目脚在局部坐标轴方向的附加质量，ΔM_iτ=ρC_MτV_i, ΔM_iη=ρC_MηV_i, ΔM_iξ=ρC_MξV_i。目脚i所受弹力、重力和浮力的表示与结节相似。

目脚i所受的流体阻力表示为：

$ \left\{ \begin{array}{l} {F_\tau } = \frac{1}{2}\rho {C_{d\tau }}{S_\tau }\left| {{{\dot \tau }_i} - {v_{c\tau }}} \right|\left( {{{\dot \tau }_i} - {v_{c\tau }}} \right)\\ {F_\eta } = \frac{1}{2}\rho {C_{d\eta }}{S_\eta }\left| {{{\dot \eta }_i} - {v_{c\eta }}} \right|\left( {{{\dot \eta }_i} - {v_{c\eta }}} \right)\\ {F_\xi } = \frac{1}{2}\rho {C_{d\xi }}{S_\xi }\left| {{{\dot \xi }_i} - {v_{c\xi }}} \right|\left( {{{\dot \xi }_i} - {v_{c\xi }}} \right) \end{array} \right.。$

(8)

其中：S_τ, S_η, S_ξ分别为目脚在τ, η, ξ方向上的投影面积；v_cτ, v_cη, v_cξ分别为流速在τ, η, ξ方向上的速度分量；C_dτ, C_dη, C_dξ分别为目脚在τ, η, ξ方向上的阻力系数。

方程(4)和(8)中的阻力系数C_d在雷诺数小于200时会发生急剧的改变，因此应将C_d看作是雷诺数Re的函数^[5]。

对于结节：C_d=10^1.2Re^－0.6，

对于目脚：C_dτ=0.1，C_dη=C_dξ=10^0.7Re^－0.3。

由结节和目脚的运动方程(6)和(7)可知，每个节点的运动不仅是自身位移、速度和加速度的函数，由于弹性力作用，每个点的运动还受到与其相连节点运动的影响。这样所有点的方程组成了一个非线性方程组，通过数值分析方法得到每一解算时刻节点i的运动参数$\left( {{x_i}, {y_i}, {z_i}, {{\dot x}_i}, {{\dot y}_i}, {{\dot z}_i}, {{\ddot x}_i}, {{\ddot y}_i}, {{\ddot z}_i}} \right)$。

2 数值解法

精细积分法自钟万勰提出来后，在结构动力分析中获得了广泛应用。在此基础上进一步研究，使得非线性动力方程的高精度计算成为可能。结构系统非线性动力方程的一般形式为：

$ M\ddot x + C\dot x + Kx = f\left( t \right)。$

(9)

其中：M是质量矩阵；C是阻尼矩阵；K是刚度矩阵；f(t)代表激励；$\ddot x{\rm{、}}\dot x{\rm{、}}x$分别表示加速度、速度和位移。将(9)写成状态方程：

$ \dot v = Hv + F\left( t \right)。$

(10)

其中：

$v = \left\{ {\begin{array}{*{20}{c}} x\\ {\dot x} \end{array}} \right\}, H = \left[ {\begin{array}{*{20}{c}} 0&I\\ B&G \end{array}} \right], F\left( t \right) = \left[ {\begin{array}{*{20}{l}} 0\\ {{M^{ - 1}}f\left( t \right)} \end{array}} \right], $ B=－M^－1K，G=－M^－1C，I是单位矩阵。

方程(10)的解可写成如下形式：

$ v = {{\rm{e}}^{tH}}{v_0} + \int_0^t {{{\rm{e}}^{\left( {t - s} \right)}}F\left( s \right){\rm{d}}s} 。$

(11)

对式(11)进行数值离散，并假设时间步长Δt=t_k+1－t_k，则第k+1步时的响应公式可写成：

$ {v_{k + 1}} = {{\rm{e}}^{{t_{k + 1}}H}}{v_0} + \int_0^{{t_{k + 1}}} {{{\rm{e}}^{\left( {{t_{k + 1}} - s} \right)}}F\left( s \right){\rm{d}}s} 。$

(12)

为使(12)式能进行数值计算，选用计算格式较为简单同时精度又较高的辛普生积分法，也即：

$ \begin{array}{l} \int_{{t_k}}^{{t_{k + 1}}} {{{\rm{e}}^{\left( {{t_{k + 1}} - s} \right)H}}F\left( s \right){\rm{d}}s} = \frac{{\Delta t}}{6}\left( {TF\left( {{t_k}} \right) + } \right.\\ \left. {4{T_{\frac{1}{2}}}F\left( {{t_k} + \frac{1}{2}\Delta t} \right) + F\left( {{t_{k + 1}}} \right)} \right) + o\left( {\Delta {t^5}} \right)。\end{array} $

(13)

其中，${T_{\frac{1}{2}}} = \exp \left( {\frac{1}{2}\Delta tH} \right)$，所以(12)式可写成：

$ \begin{array}{l} {v_{k + 1}} = T{v_k} + \frac{{\Delta t}}{6}\left( {TF\left( {{t_k}} \right) + 4{T_{\frac{1}{2}}}F\left( {{t_k} + \frac{1}{2}\Delta t} \right) + } \right.\\ \left. {F\left( {{t_{k + 1}}} \right)} \right),k = 0,1,2, \cdots 。\end{array} $

(14)

式(14)即是计算系统响应的迭代公式，因为T，T_1/2都可以由数值方法精确算得，而F(t)又是已知载荷，因此通过这个迭代公式就能直接求出系统的响应。

由此，将结节和目脚的运动方程(6)式和(7)写式成矩阵形式：

$ M\ddot X = f\left( t \right)。$

(15)

上式两边都加上X，$X = {\left[ {x, y, z, \dot x, \dot y, \dot z} \right]^{\rm{T}}}$，可得：

$ M\ddot X + X = X + f\left( t \right)。$

(16)

其中$M = \left( {\begin{array}{*{20}{c}} {{m_i} + \Delta {m_i}}&0&0\\ 0&{{m_i} + \Delta {m_i}}&0\\ 0&0&{{m_i} + \Delta {m_i}} \end{array}} \right)$，$C = \left( {\begin{array}{*{20}{c}} 0&0&0\\ 0&0&0\\ 0&0&0 \end{array}} \right)$，$K = \left( {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right)$。

将X+f(t)看作外部激励，对结节运动方程来说：

$ \begin{array}{l} F\left( t \right) = \left[ \begin{array}{l} 0\\ {M^{ - 1}}f\left( t \right) \end{array} \right] = \\ \left[ \begin{array}{l} 0\\ 0\\ 0\\ \left( {x + {T_x} + {F_x}} \right)/\left( {{M_i} + \Delta {M_i}} \right)\\ \left( {y + {T_y} + {F_y}} \right)/\left( {{M_i} + \Delta {M_i}} \right)\\ \left( {z + {T_z} + {F_z} + W + B} \right)/\left( {{M_i} + \Delta {M_i}} \right) \end{array} \right]。\end{array} $

(17)

而对目脚运动方程，其解算在局部坐标系下，F(t)如下式：

$ \begin{array}{l} F\left( t \right) = \left[ \begin{array}{l} 0\\ {M^{ - 1}}f\left( t \right) \end{array} \right] = \\ \left[ \begin{array}{l} 0\\ 0\\ 0\\ \left( {x + {T_\tau } + {F_\tau } + {W_\tau } + {B_\tau }} \right)/\left( {M + \Delta {M_{i\tau }}} \right)\\ \left( {\eta + {T_\eta } + {F_\eta } + {W_\eta } + {B_\eta }} \right)/\left( {{M_i} + \Delta {M_{i\eta }}} \right)\\ \left( {\xi + {T_\xi } + {F_\xi } + {W_\xi } + {B_\xi }} \right)/\left( {{M_i} + \Delta {M_{i\xi }}} \right) \end{array} \right]。\end{array} $

(18)

(14)式右边各项是矩阵相乘，对于本文来讲，矩阵最高是6×6阶，而矩阵相乘的计算效率很大程度上的影响了整个程序的运行速度，所以对矩阵相乘算法进行一些改进是必要的。矩阵T，T_1/2的形式相同，其构造如下：

$ \left( {\begin{array}{*{20}{c}} {{a_{11}}}&0&0&{{b_{11}}}&0&0\\ 0&{{a_{22}}}&0&0&{{b_{22}}}&0\\ 0&0&{{a_{33}}}&0&0&{{b_{33}}}\\ {{c_{11}}}&0&0&{{d_{11}}}&0&0\\ 0&{{c_{22}}}&0&0&{{d_{22}}}&0\\ 0&0&{{c_{33}}}&0&0&{{d_{33}}} \end{array}} \right)。$

(19)

由此，将(14)式中的矩阵相乘写成矩阵各元素乘积的形式可得：

$ \left\{ \begin{array}{l} pos.x = {a_{11}}x + {b_{11}}{v_x} + \frac{{\Delta t}}{6}\left( {{b_{11}} + 4 \cdot {{b'}_{11}}} \right) \cdot {F_{tx}}\\ pos.y = {a_{22}}x + {b_{22}}{v_y} + \frac{{\Delta t}}{6}\left( {{b_{22}} + 4 \cdot {{b'}_{22}}} \right) \cdot {F_{ty}}\\ pos.z = {a_{33}}z + {b_{33}}{v_z} + \frac{{\Delta t}}{6}\left( {{b_{33}} + 4 \cdot {{b'}_{33}}} \right) \cdot {F_{tz}}\\ vel.x = {c_{11}}x + {d_{11}}{v_x} + \frac{{\Delta t}}{6}\left( {{d_{11}} + 4 \cdot {{d'}_{11}} + 1} \right) \cdot {F_{tx}}\\ vel.y = {c_{22}}y + {d_{22}}{v_y} + \frac{{\Delta t}}{6}\left( {{d_{22}} + 4 \cdot {{d'}_{22}} + 1} \right) \cdot {F_{ty}}\\ vel.z = {c_{33}}y + {d_{33}}{v_y} + \frac{{\Delta t}}{6}\left( {{d_{33}} + 4 \cdot {{d'}_{33}} + 1} \right) \cdot {F_{tz}} \end{array} \right., $

(20)

$ {V_k} = {\left[ {x,y,z,{v_x},{v_y},{v_z}} \right]^{\rm{T}}}, $

$ F\left( t \right) = {\left[ {0,0,0,{F_{tx}},{F_{ty}},{F_{tz}}} \right]^{\rm{T}}}。$

其中带“′”的元素表示T_1/2的相应元素。

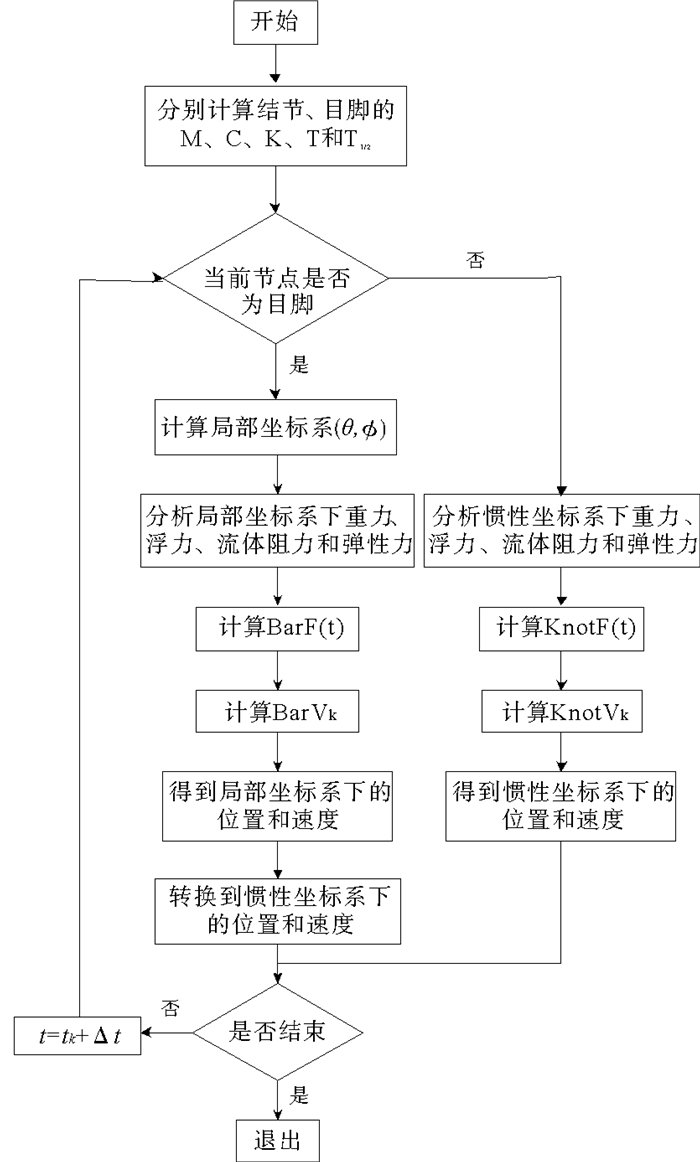
图 4是用精细积分法求解网衣数学模型的计算流程图，Bar和Knot分别表示目脚、结节。在实际程序中直接用(20)式求解结节和目脚的位置及速度，模型的解算时间比直接用(14)式矩阵相乘提高很大。

3 模型验证

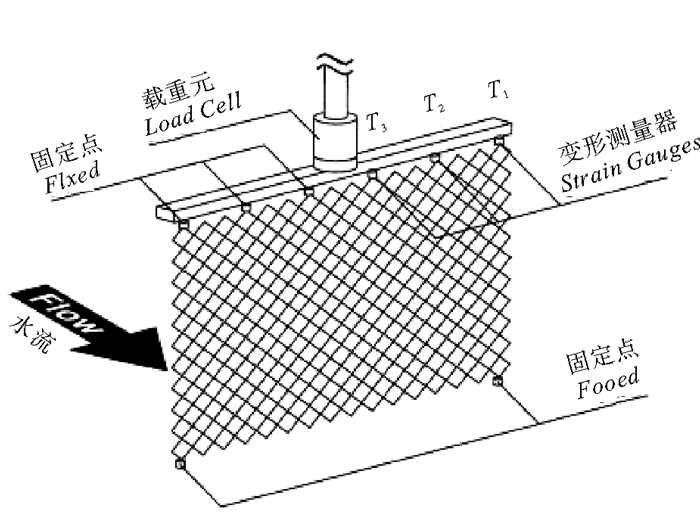
日本学者Takagi基于集中质量法建立了渔网网衣三维动态模拟^[4-6]，采用六级五阶Runge-Kutta法进行数值求解，并且通过水槽试验验证了数值计算的可靠性。其水槽试验方法如下：将网片垂直放置于水槽中，水深为1.0 m。网片上缘的6个结节等距固定在1.5 m长的钢杆上，其左下角和右下角用沉子固定于水池底部，以不同速度的水流(8，20，41 cm/s)沿垂直于网片的方向流向网片，如图 5所示。

本文选取其中一类网片B进行数值模拟，该网片目大50 mm，横向45目，纵向48目，其具体参数如表 1所示。图 6是Takagi在试验中，用数码相机拍摄到的网片在流速41.0 cm/s下达到稳定后图像。

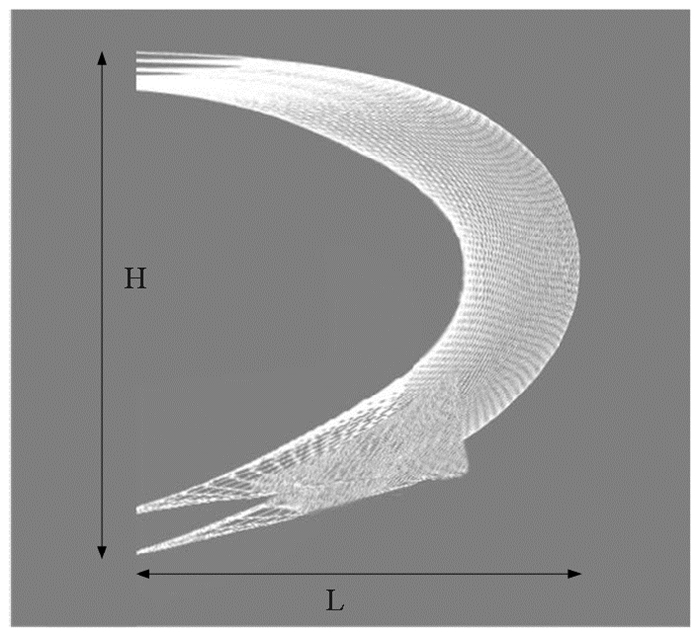
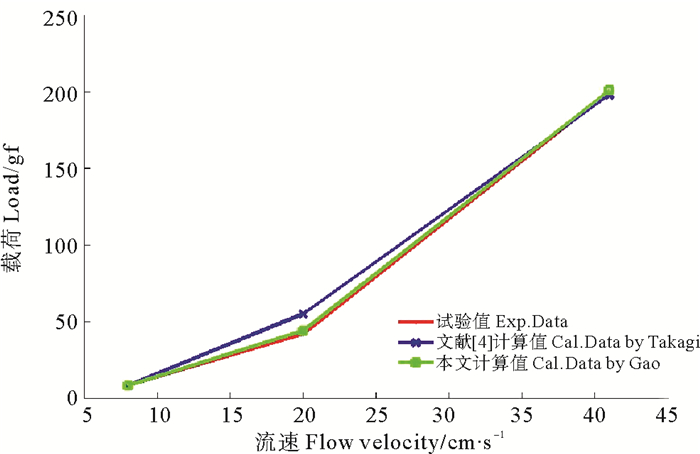
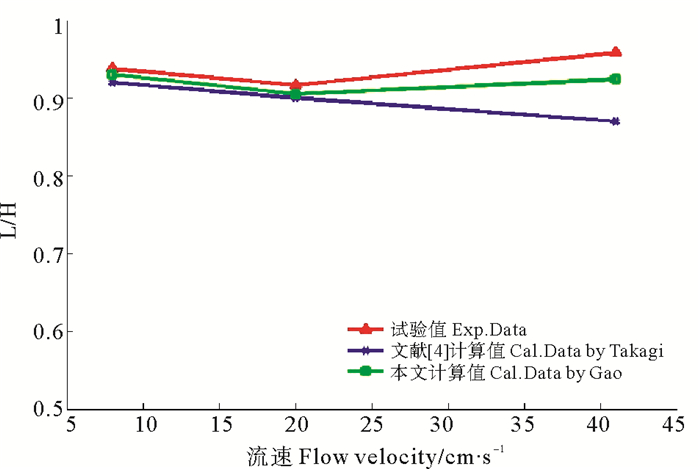
采用本文的精细积分方法进行网片数学模型的求解，在均匀流41.0 cm/s条件下网片稳定后得到图 7所示的仿真结果，图 8和9则是本文仿真结果与文献[4]计算值及其水槽试验值的比较，可以看出水平张力载荷和网片稳定后的L/H值，在不同水流作用下趋势是相同的，误差在可以接受范围内，仿真结果比较理想。

4 拖网仿真模拟

我国东海水产研究所在渔具模型静水槽内进行了中层拖网及底拖网共九项网具的模型试验，并给出了试验结果。本文选取其中一类型中层拖网ZT8909(52×26 m)进行了仿真研究，参数如表 2所示，将仿真结果同其水槽试验结果进行了比较。

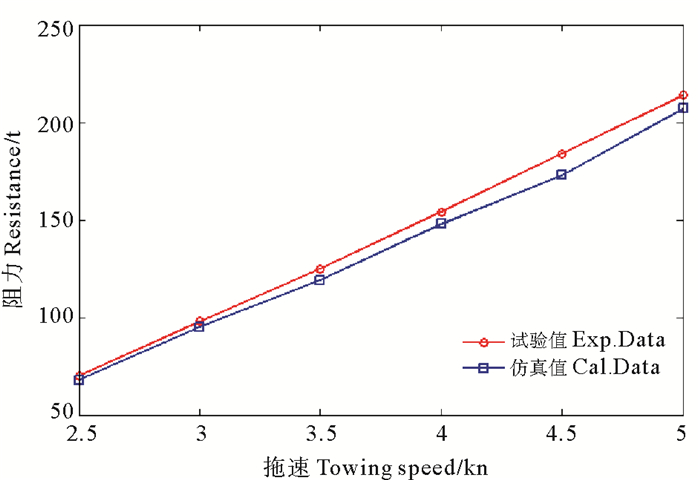
图 10是网具阻力随拖曳速度的变化曲线，阻力大小与拖曳速度基本呈线性增长，本文仿真值比实测值偏小，原因分析如下：本文计算时假设渔具不受洋流的影响，是在理想环境下计算的结果。

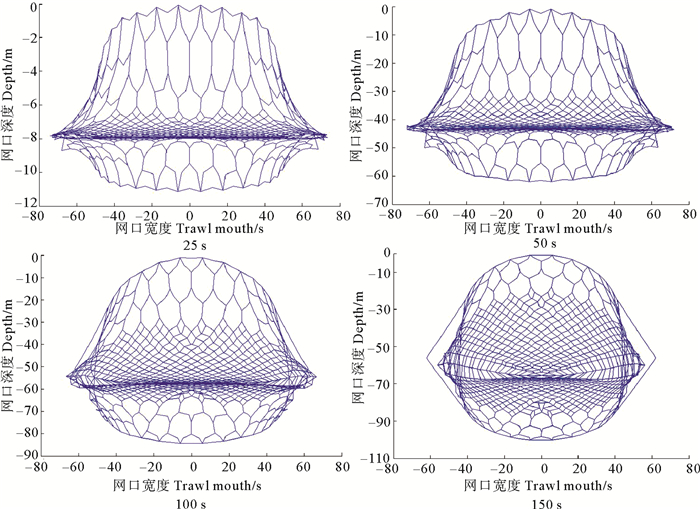
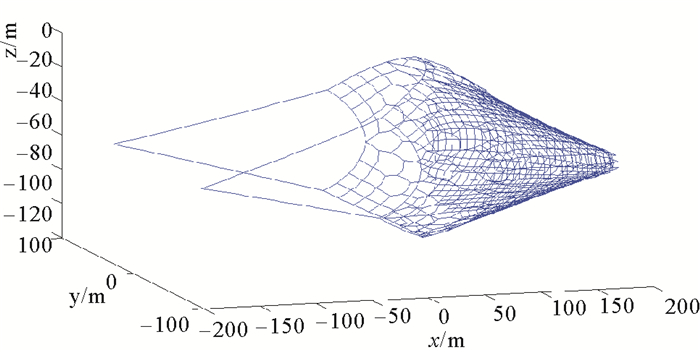
表 3中网口高度随拖速的变化可以看出本文精细积分法求解拖网运动方程的结果与试验值最大误差是6.6%，这说明本文数值方法的精确度较高。图 11是采用本文方法进行的拖网仿真，拖速为41.0 cm/s在不同时刻渔网网口的形状。图 12是采用本文方法实现的拖网三维仿真。

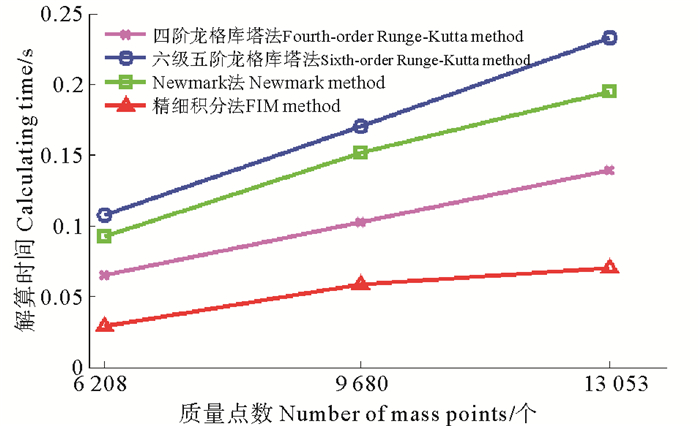
渔船模拟器中对渔网的仿真不仅需要其物理模型的准确性，更需要保证整个视景系统的实时性。前者也即仿真的效果和稳定性，后者则对应于仿真的速度，这两者之间的矛盾在计算机仿真中必须仔细衡量。图 13是采用不同数值解法进行网衣数学模型解算一次的耗时时间比，网衣质量点数是21 720时，六级五阶龙格库塔法解算时间为95 ms，Newmark法耗时68 ms，四阶龙格库塔法耗时56 ms，而精细积分法耗时30 ms；可以看出在这几种方法中，精细积分法的模型解算耗时是最少的。

5 结语

本文在渔网网衣建模理论和数值解法的研究基础上，基于集中质量法建立了渔网网衣的运动数学模型，采用精细积分的方法对数学模型进行求解，通过和相关文献中的水槽试验数据的对比证明该数值解法的准确性。整个系统的仿真速率也得到保证，从而为渔船模拟器中拖网模型建立和视景可视化研究打下了基础。