2. 中石化石油工程设计有限公司,山东 东营 257026
中国黄河三角洲等滩海地区蕴藏着丰富的石油资源,经常采用“海油陆采”的石油开发模式,即修建海上人工岛,在人工岛上设置采油平台,并通过进海路将人工岛与岸线相连。传统进海路采用堆砌式结构,透水性差,严重影响近岸环境。新型桩基支撑透空式进海路结构具有水体交换性能优良、对近岸环境影响小的优点,已经在胜利油田实际工程中应用,取得了很好的工程效果。但是,透空式进海路的波浪作用机理比较复杂,进海路上部结构的波浪荷载计算方法缺乏,给工程设计造成较大困难。
针对各类透空式建筑物上部结构的波浪荷载作用特性和计算方法,已经有许多学者开展了研究工作。合田良实[1]对栈桥面板所受波浪力进行了试验研究,认为栈桥面板受到的波浪压强均匀分布,作用长度为四分之一波长,并给出了浮托力的计算公式。谷本胜利等[2]认为水平板受到的波浪作用由静水压强和冲击压强组成,利用势流理论,在考虑水平板底面存在空气层的情况下,对水平板底部波浪力进行了理论分析和试验验证。过达和蔡保华[3]试验测量了透空式码头面板的波浪作用力,给出了破碎波与非破碎波作用下不同型式码头面板的浮托力计算公式。周益人等[4-5]开展了透空式水平板波浪浮托力的系列物理模型试验,发现透空式水平板总浮托力的最大值与冲击压强的最大值通常不同步出现,它们所对应的压强分布形式通常也不一致,并给出了水平板最大冲击压强和最大波浪浮托力的计算方法。任冰等[6]应用改进的SPH方法,研究了透空式结构底面受波浪冲击过程中的流场和压力场的变化特性。
以上研究工作主要考虑波浪对透空式薄板结构的浮托力作用,很少考虑结构承受的水平波浪力。透空式进海路桥面内部需埋设输油管线和电缆沟等,其上部桥面结构的厚度较大,在进行波浪力分析时,不能将其等同于水平薄板式结构,需要同时考虑浮托力和水平波浪力的作用。本文将通过物理模型试验,分析透空式进海路上部结构的浮托力和水平波浪力,研究结构的波浪力计算方法,为透空式进海路的工程设计提供指导。
1 物理模型试验 1.1 试验设备和方法物理模型试验在中国海洋大学山东省海洋工程重点实验室的波流水槽内进行,水槽长60 m、宽3 m、深1.5 m。水槽一端安装推板式造波机,另一端设置斜坡式多孔消波装置,可以有效降低水槽末端波浪反射的影响。
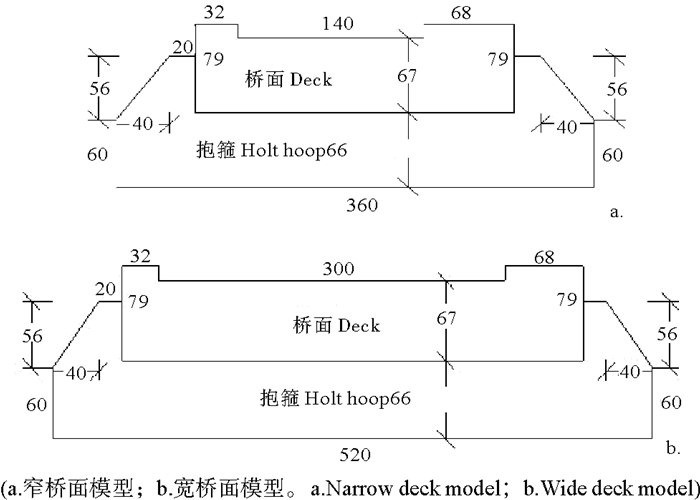
参照东营胜利油田某全直桩透空式进海路工程,按照1:25的比尺制作试验模型。试验模型主要由桩基础、抱箍(横梁)、桥面三部分组成,透空式进海路模型设置在距离造波机38 m远处,图 1给出进海路模型在水槽中的布置图。沿水槽宽度方向共布置七跨整桥面,每跨桥面长0.4 m(沿水槽宽度方向),高0.079 m,宽度为0.24和0.4 m两种。桥面固定在抱箍上,每个抱箍的宽度为7.2 cm,抱箍由外径为4.8 cm的空心钢管桩支撑,钢管桩焊接固定在水槽底部的预埋钢板上。对于0.24 m宽的窄桥面(单车道桥面),每个抱箍下面等间距设置三根管桩,对于0.4 m宽的宽桥面(双车道桥面),每个抱箍下面等间距设置四根管桩。桥面和抱箍均采用木板制作,结构的断面尺寸见图 2。

|
图 1 透空式进海路物理模型试验布置图 Fig. 1 Sketch of experimental test for pile-supported sea access road |
|
图 2 透空式进海路上部结构断面图(单位:mm) Fig. 2 Section of upper structure for pile-supported sea access road (unit:mm) |
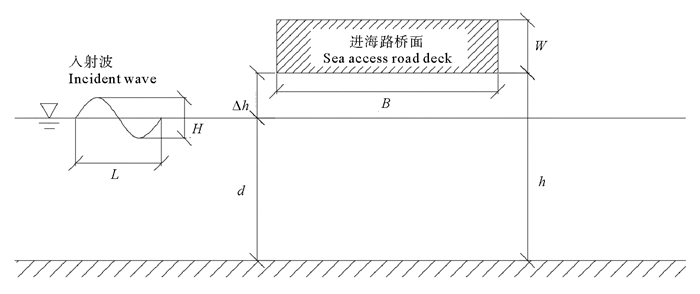
采用规则波进行透空式进海路波浪力试验,参照东营透空式进海路的工程设计波况,试验波浪周期T=1.6 s(原型波浪周期为8.0 s),试验波高取极限破碎波高,即水深的0.6倍。试验水深d取10种不同的值(d=0.23~0.40 m),进海路桥底面与海床之间的间距h取8种不同的值(h=0.26~0.42 m),桥底与静水面之间的净空高度Δh=h-d=-0.04~0.09 m,其中:当进海路桥底面在静水面以下时,桥面净空高度Δh为负值。表 1列出各物理模型试验参数的具体值,图 3则给出各试验参数的定义。需要说明的是,如果每排桩基础中的桩数目增加或桥面跨度减小,桩基础对波浪的反射作用会增加,进海路上部结构的波浪作用力有可能增加。对于该问题,有必要在今后开展进一步的研究工作。
|
|
表 1 透空式进海路物理模型试验参数 Table 1 Experimental Parameters for pile-supported sea access road |
|
图 3 透空式进海路模型参数定义图 Fig. 3 Parameter definition of pile-supported sea access road model |
试验中,在中间一跨桥面的迎浪面、底面及抱箍上安装点压力传感器,测量波浪作用下桥面上的动水压强分布。由于试验模型沿水槽中轴线对称布置,只在中间半跨桥面上布置了点压力传感器,认为未布置传感器的半跨桥面的压强分布与另一侧对称位置相同。点压力传感器的采样频率为50 Hz,每次试验重复2次,取平均值。
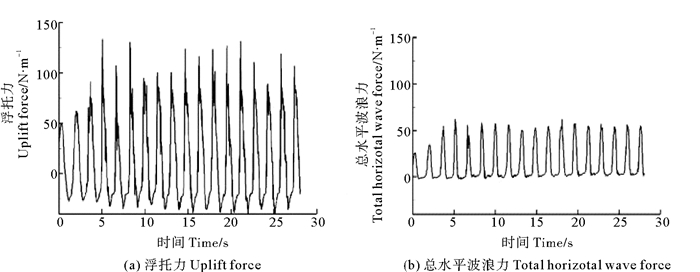
将各点压力传感器的动水压强测量值沿结构表面进行积分,得到透空式进海路单位长度上部结构的浮托力和总水平波浪力时间历程线。图 4给出典型工况下,透空式进海路单位长度上部结构浮托力Fu和总水平波浪力Fh时间历程线的试验结果。分析总波浪力的时间历程线,得到透空式进海路上部结构浮托力和总水平波浪力的峰值,通过分析总波浪力峰值的试验结果,给出透空式进海路上部结构的波浪力计算方法。
|
(d=0.40 m, h=0.38 m, H=0.24 m, B=0.4 m) 图 4 总波浪力时间历程线 Fig. 4 Time histories of total wave forces |
目前,有许多学者提出了不同的透空式结构浮托力计算方法,但是由于透空式结构浮托力的影响因素比较复杂,不同计算方法所考虑的具体结构型式和试验条件不同,因此不同方法的计算结果存在较大差异。
我国海港工程设计手册[7]给出码头上部结构底面平均波压力计算方法:
| $ \frac{p}{{\gamma H}}=\beta \left( {\frac{\eta }{H} - \frac{{\Delta h}}{H}} \right), $ | (1) |
| $ \eta =\frac{H}{2} + \frac{{k{H^2}}}{4}\frac{{{\rm{cosh}}kd\left( {{\rm{cosh}}2kd + 2} \right)}}{{4{{\left( {{\rm{sinh}}kd} \right)}^3}}}, $ | (2) |
式中:p为平均动水压强;γ为水的重度;β为压强反应系数,当上部结构的宽度B ≤ 10 m时,β=1.5,当上部结构的宽度较大时,取β=2.0;η为波峰面在静水面以上的高度;波数k=2π/L。将平均动水压强乘结构底面的受力面积,便可以得到码头面板承受的波浪浮托力。
过达和蔡保华[3]通过透空式码头面板的上托力试验,提出了波压强修正法,根据波浪理论及有关试验资料的分析,将面板上的波浪浮托力压强值表示为面板相对静空高度Δh/H的指数函数:
| $ \frac{p}{{\gamma H}}={\alpha _1}\left( {{\alpha _2}\frac{\eta }{H} - \frac{{\Delta h}}{H}} \right){\rm{exp}}\left[ {n\left( {\frac{{\Delta h}}{H} - a} \right)} \right], $ | (3) |
式中: α1为压强系数[3];α2为波面修正系数[3];a为最大压强值位置的超高系数,对非破碎波取a=0.2,对破碎波取a=0.3;n为指数曲线修正系数,当(Δh/H-a)> 0时,n=-3.5,当(Δh/H-a) < 0时,n=3.5,对于高桩码头面板,n=2.5。将浮托力压强与受力面积相乘,得到结构承受的浮托力。
周益人等[5]对透空式水平板进行了系列试验研究,给出单位长度透空式水平板上最大波浪浮托力Fu的计算公式:
| $ \frac{{{F_u}}}{{\gamma HB}}=K{\left( {1 - \frac{{\Delta h}}{\eta }} \right)^{0.8}}{\rm{exp}}\left[ { - 2.7K{{\left( {\frac{{\Delta h}}{H} - 0.35} \right)}^2}} \right], $ | (4) |
| $ K={K_0}{K_1}{\rm{exp}}\left[ { - 600{K_1}{{\left( {\frac{H}{L} - 0.055} \right)}^2}} \right], $ | (5) |
| $ {K_1}=0.9{\rm{tanh}}{\left( {\frac{B}{{2.5H}}} \right)^{1.5}}{\rm{tanh}}kd, $ | (6) |
其中:K为冲击角度影响系数;K0为相对板宽影响系数,当L/B>10时取1.7,当L/B≤10时取1.4;K1为板宽和水深影响系数,如果B/H < 1.68,取B/H=1.68。
我国海港水文规范[8]给出离岸式高桩码头单位长度面板承受最大浮托力Fu的计算方法:
| $ \frac{{{F_u}}}{{\gamma xH}}={\lambda _1}{\left( {1 - \frac{{\Delta h}}{{1.1\eta }}} \right)^{0.3}}{\rm{exp}}\left[ { - 0.8{{\left( {\frac{{\Delta h}}{{1.1\eta }} - 0.8} \right)}^2}} \right], $ | (7) |
| $ {\lambda _1}=0.75 + 0.25{\rm{tanh}}\left( {\frac{L}{{2B}} - 2} \right), $ | (8) |
| $ x=\frac{L}{\pi }{\rm{arccos}}\frac{{\Delta h}}{{1.1\eta }}, $ | (9) |
式中:λ1为面板宽度影响系数;x为面板底部的波浪作用宽度(沿波浪传播方向),当x>B时,取x=B。
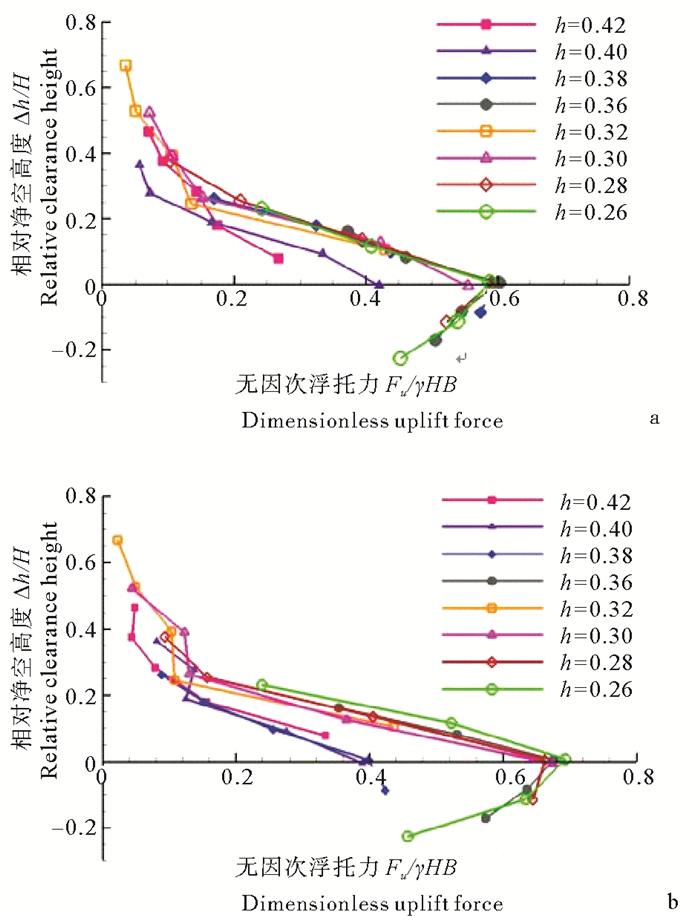
2.2 本文浮托力计算方法通过已有透空式结构的浮托力计算方法可以看出,相对净空高度Δh/H是浮托力的主要影响因素。图 5给出透空式进海路单位长度桥面上受到的无因次浮托力Fu/γHB与相对净空高度Δh/H之间的关系,可以看出:浮托力在Δh/H接近0时达到最大值,且随着Δh/H绝对值的增大而减小;窄桥面(B=0.24 m)和宽桥面(B=0.4 cm)的无因次浮托力变化规律基本一致,且在相同波况下无因次浮托力的值比较接近。
|
(a. 桥面宽度(B)=0.24 m;b. 桥面宽度(B)=0.4 m。a.Deck width(B)=0.24 m;b.Deck width(B)= 0.4 m.) 图 5 浮托力Fu与相对净空高度Δh/H之间的关系 Fig. 5 Relationship between the uplift force Fu and the relative clearance height Δh/H |
图 5中观察到的浮托力变化规律与过达和蔡保华[3]的研究结果比较一致,因此将过达和蔡保华[3]公式中的系数进行调整,得到透空式进海路上部结构的浮托力计算公式。将过达和蔡保华[3]公式进行改进的主要原因包括:(1)过达和蔡保华[3]公式中,压强系数和波面修正系数与透空式结构型式有关,本文透空式进海路结构与过达和蔡保华[3]所研究结构存在很大差异;(2)透空式进海路上部结构受到的最大浮托力出现在相对净空高度接近0的位置(见图 5),与过达和蔡保华[3]公式中超高系数取0.2不同。
参照公式(3),并通过分析本文试验数据,给出以下透空式进海路单位长度桥面上浮托力Fu的计算公式:
| $ \frac{{{F_u}}}{{\gamma HB}}={\mu _1}\left[ {1.2\left( {\frac{\eta }{H}} \right) - \frac{{\Delta h}}{H}} \right]{\rm{exp}}\left[ {{\mu _2}\left( {\frac{{\Delta h}}{H} - 0.05} \right)} \right]{\rm{。}} $ | (10) |
式中:η为波峰面在静水面以上的高度,其计算方法见公式(2);当Δh/H > 0时,μ1=0.65,μ2=-4;当Δh/H ≤ 0时,μ1=1 - Δh/H,μ2=4。图 6给出公式(10)的计算结果与试验结果的对比,可以看出:计算结果与试验结果符合较好,计算结果通常大于试验结果,对于工程设计而言偏于安全;窄桥面计算结果与试验结果的相关系数为0.955,宽桥面计算结果与试验结果的相关系数为0.925。
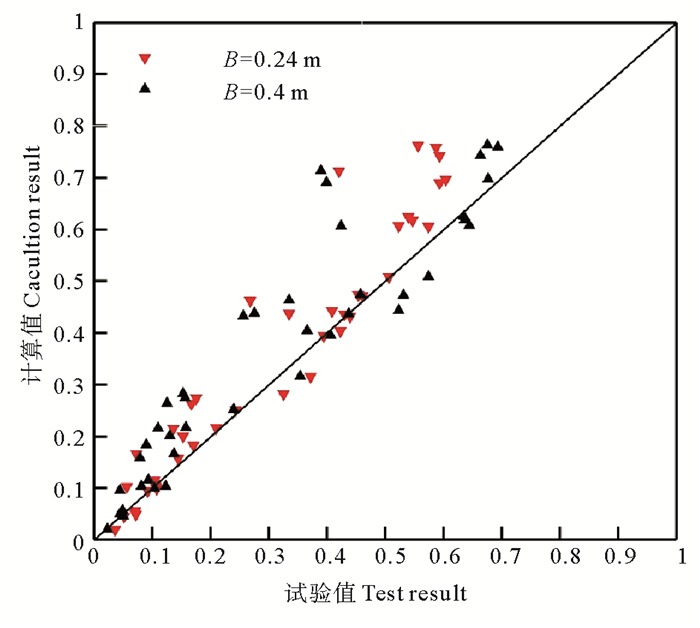
|
图 6 透空式进海路桥面无因次浮托力计算结果与试验结果对比 Fig. 6 Comparison between the calculated and experimental reuslts for the dimensionless uplift force on the deck of sea access road |
将本文提出的浮托力计算公式(10)与3.1节所述文献中的4种浮托力计算公式进行了对比,图 7给出典型的对比结果。从图 7可以看出:不同公式的计算结果差异很大,本文公式(10)的计算结果与透空式进海路上部结构浮托力的试验结果符合最好。本文公式的计算结果与周益人等[5]公式的计算结果比较接近,但是明显小于海港工程设计手册[7]、过达和蔡保华[3]以及海港水文规范[8]公式的计算结果,这说明:当透空式结构型式不同时,结构所承受的浮托力存在很大差异,在浮托力分析中要充分考虑结构型式的影响。
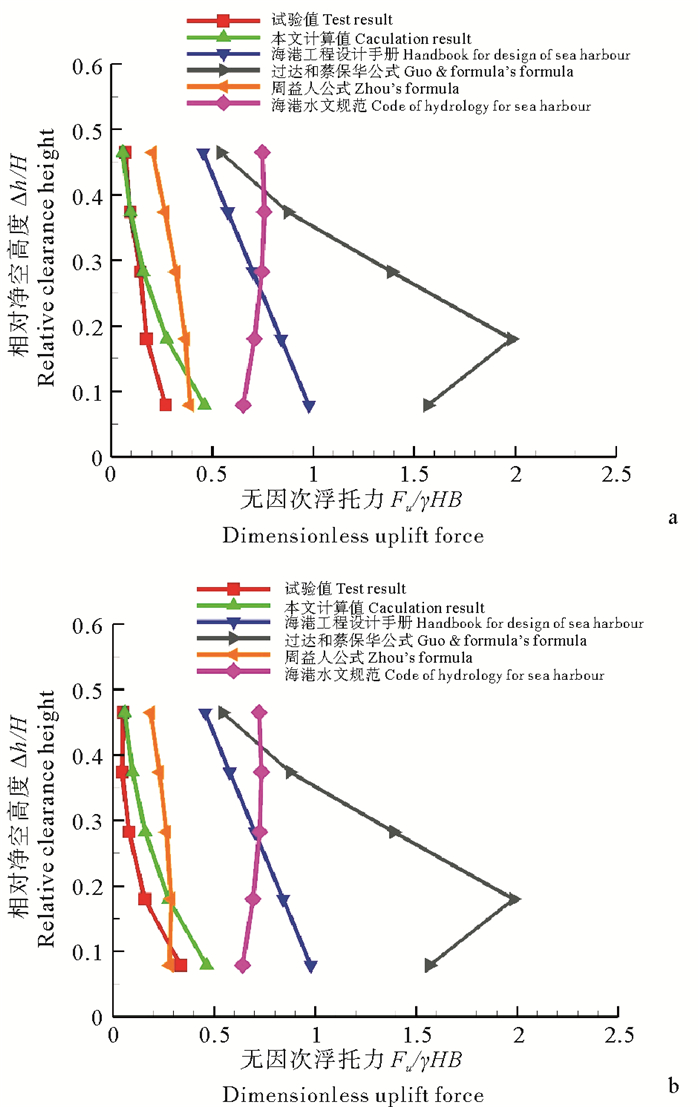
|
(a. 桥面宽度(B)= 0.24 m,桥面底高(h)= 0.42 m;b. 桥面宽度(B)= 0.4 m,桥面底高(h)= 0.42 m。a.Deck width(B)= 0.24 m,Bottom height of deck(h)= 0.42;b.Deck width(B)= 0.4 m,Bottom height of deck(h)= 0.42 m.) 图 7 不同方法浮托力计算结果对比 Fig. 7 Comparison of the caculation results by different methods for uplift forces |
在本文物理试验中,所有试验条件下波浪都会越过透空式进海路的上部桥面,即桥面的整个迎浪面都会承受水平波浪力的作用,因此在水平波浪力分析中,考虑单位长度桥面的整个迎浪面所受的波浪力。图 8给出无因次单位长度桥面的水平波浪力Fh/γHW与相对净空高度Δh/H之间的关系,图中横坐标为Δh/H,纵坐标为Fh/γHW的对数值,可以看出:-ln (Fh/γHW)近似为Δh/H的指数函数。
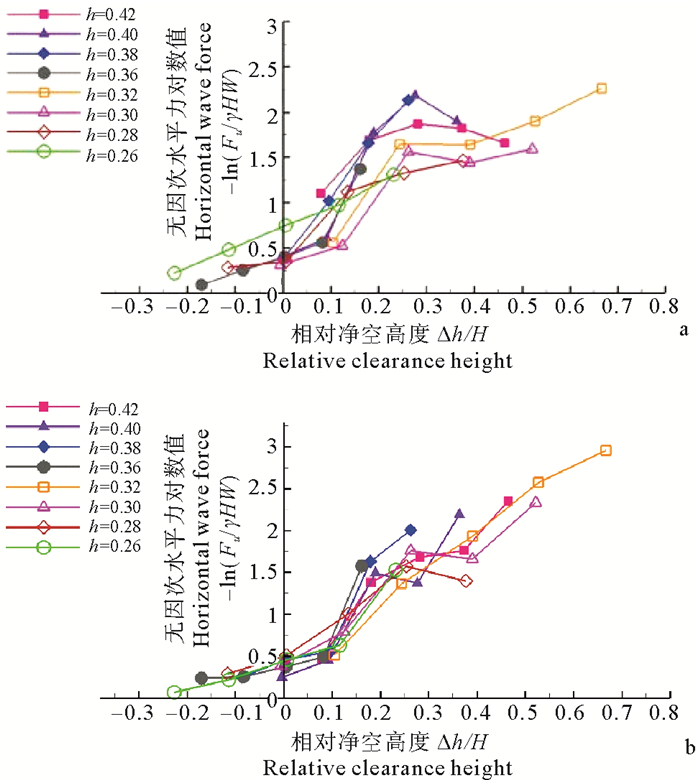
|
(a. 桥面宽度(B)=0.24 m;b. 桥面宽度(B)=0.4 m。a.Deck width(B)=0.24 m;b.Deck width(B)=0.4 m.) 图 8 水平波浪力Fh与相对净空高度Δh/H之间的关系 Fig. 8 Relationship betweenthe horizontal wave force Fh and the relative clearance height Δh/H |
依据图 8的分析结果,对试验数据进行多元线性回归分析,给出透空式进海路单位长度上部结构水平波浪力的计算公式:
| $ \frac{{{F_h}}}{{\gamma HW}}={\rm{exp}}\left( { - d{\eta ^1}} \right), $ | (11) |
| $ l=3.3{\left( {\frac{{\Delta h}}{H}} \right)^2} - 3.7\left( {\frac{{\Delta h}}{H}} \right) - 0.09{\rm{。}} $ | (12) |
图 9给出公式(11)的计算结果和试验结果的对比,可以看出:计算结果与试验结果比较接近,窄桥面计算结果与试验结果的相关系数为0.927,宽桥面计算结果与试验结果的相关系数为0.955。
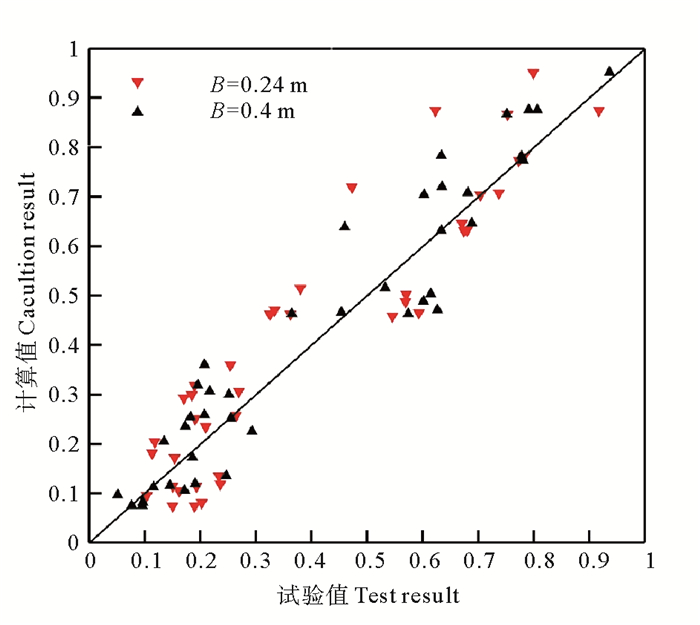
|
图 9 透空式进海路桥面无因次水平波浪力计算结果与试验结果对比 Fig. 9 Comparison of the calculated and experimental reuslts for the dimensionless horizontal wave forces on the deck of sea access road |
本文开展了系列物理模型试验,测量了透空式进海路上部结构的动水压强分布,分析了结构承受的浮托力和水平波浪力。研究发现:相对净空高度是透空式进海路上部桥面结构波浪力的主要影响因素,当相对净空高度接近0时,桥面浮托力达到最大值。以模型试验结果为基础,建立了透空式进海路上部桥面结构浮托力和水平波浪力的计算公式,并与文献中已有透空式结构浮托力的计算公式进行了对比分析。本文浮托力和水平波浪力公式的计算结果与试验结果符合较好,可用于透空式进海路结构的初步工程设计。
| [1] |
合田良实. 构造物に动く波力[C]. 东京: 1967年度水工学に关する夏期研修会议义集CB, 1967: 1-34. Goda Y. Wave forces on structures[C]. Tokyo: JSCE Hydraulic Eng Series, 1967: 1-34. (  0) 0) |
| [2] |
谷本勝利, 高橋重雄, 和泉田芳和. 水平版に働く揚圧力に関する研究[J]. 海岸工学講演会論文集, 1978, 25: 352-356. Tanimoto K, Takahashi S, Izumida Y. A calculation method of uplift force on a horizontal platform[J]. Report of Port and Harbour Research Institute, 1978, 25: 352-356. (  0) 0) |
| [3] |
过达, 蔡保华. 透空式建筑物面板波浪上托力计算[J]. 华东水利学院学报, 1980, 1: 14-33. Guo D, Cai B H. Caculation Methods of Uplift Forces of Waves on Open-piled Structures[J]. Journal of East China College of Hydraulic Engineering, 1980, 1: 14-33. (  0) 0) |
| [4] |
周益人, 陈国平, 黄海龙, 等. 透空式水平板波浪上托力冲击压强试验研究[J]. 海洋工程, 2004, 22(3): 30-40. Zhou Y R, Chen G P, Huang H L, et al. An experimental study on uplift impact pressure of waves on a horizontal plate of an open wharf[J]. The Ocean Engineering, 2004, 22(3): 30-40. (  0) 0) |
| [5] |
周益人, 陈国平, 黄海龙, 等. 透空式水平板波浪总上托力试验研究[J]. 海洋工程, 2004, 22(4): 43-50. Zhou Y R, Chen G P, Huang H L, et al. An experimental study on uplift forces of waves on horizontal plate of an open-wharf[J]. The Ocean Engineering, 2004, 22(3): 43-50. (  0) 0) |
| [6] |
任冰, 高睿, 金钊, 等. 波浪对透空式结构物冲击作用的光滑粒子流体动力学数值模拟[J]. 海洋学报, 2012, 34(1): 163-177. Ren B, Gao R, Jin Z, et al. The numerical simulation of wave slamming on an open piled structure using the SPH model[J]. Acta Oceanologica Sinica, 2012, 34(1): 163-177. (  0) 0) |
| [7] |
交通部第一航务工程勘察设计院. 海港工程设计手册(中)[M]. 北京: 人民交通出版社, 1994, 52. CCCC FDINE. Handbook for Design of Sea Harbour(Volume two)[M]. Beijing: China Communications Press, 1994, 52. (  0) 0) |
| [8] |
交通部第一航务工程勘察设计院. 海港水文规范[M]. 北京: 人民交通出版社, 2013, 90-91. CCCC FDINE. Code of Hydrology for Sea Harbour[M]. Beijing: China Communications Press, 2013, 90-91. (  0) 0) |
2. Sinopec Petroleum Engineering Design Co Ltd, Dongying 257026, China
 2018, Vol. 48
2018, Vol. 48

