细胞之间的交互过程通常是由蛋白质复合物而不是单个蛋白质来完成的[1-2]。蛋白质复合物是一组相互作用的蛋白质,它们形成一个单独的多分子机器[3],彼此之间合作来执行它们的生物学功能。可以说,蛋白质复合物是活细胞内生物过程的重要功能单位。研究蛋白质复合物,有助于人们更深入地研究生物体的生命特征、细胞系统的行为、疾病的发病机理等诸多生物医学课题。
通过实验手段从大量的蛋白质中寻找潜在的复合物,无疑是低效的。而随着高通量实验技术的发展,使得研究人员获得了大量的蛋白质相互作用数据,这就使得从蛋白质交互(PPI)网络中检测、探寻蛋白质复合物成为了可能。
PPI网络可以通过无向图来进行建模表示。在过去的十几年中,人们通过对图论、计算数学、统计学等学科中的方法加以研究,获得了许多从PPI网络中发现蛋白质复合物的方法,例如MCL[4]、MCODE[5]、RNSC[6]、CMC[7]、COACH[8]、ClusterONE[9]、ProRank+[10]、WPNCA[11]和RWRB[12]。这些方法的主要策略是从单个蛋白质出发,从PPI网络中提取高度链接的节点以形成簇,这些簇有可能成为蛋白质复合物的候选者。
但是,随着PPI网络中交互信息越来越多,传统的从单个蛋白质出发寻找连接度高的节点形成簇的方法越来越不适用。因为随着交互信息的增多,这种方法所形成簇的规模也越来越大,与已知的复合物匹配度也越来越低。为此需要寻找更合适的蛋白质复合物探测方法。
本文提出了一种基于图嵌入和布谷鸟搜索的二步蛋白质复合物预测方法(TSSComplex)。该方法将最优化问题中布谷鸟搜索方法的思想引入蛋白质复合物的搜寻中,代替传统的从单个蛋白质出发的搜索方法。利用相似度和亲和度来聚类蛋白质,从而获得候选簇。这样可以有效控制簇的规模,从而提高匹配率。另一方面,引入图嵌入技术,来获得PPI网络中节点的低维表示,并将两个节点表示向量之间的距离和传统的边权结合起来,形成了新的边权算法。之所以引入图嵌入方法,是因为它将每个节点的拓扑结构映射到低维向量表示中,可以很好地保留原始网络的邻近性[13-15]。图嵌入方法可以从原始网络中自动发现有用和潜在的特征,而非人工制作的网络特征。同时有研究表明,在节点分类[16]、链路预测[17]、节点聚类[18]等与网络相关的任务中,图嵌入方法都是非常有效的。在PPI网络应用方面,Liu Xiaoxia等就曾将图嵌入技术用于不同物种间的PPI网络整合,取得了较好的结果[19]。
1 方法基于图嵌入和布谷鸟搜索的二步蛋白质复合物预测方法主要分为三个步骤。第一步是利用图嵌入技术,用低维向量表示PPI网络中的蛋白质节点。然后,通过节点的低维向量表示和节点本身的网络结构给PPI网络中的边赋权。第二步是通过布谷鸟搜索,获取潜在的蛋白质复合物。第三步是针对布谷鸟搜索之后的剩余蛋白质节点,利用传统搜索方法,进行二次搜索。
1.1 图嵌入和蛋白质的低维向量表示图嵌入技术是一种对网络图中的节点在向量空间进行分布表示的一种技术。该技术最早来源于自然语言数据挖掘领域[20]。其最初希望通过将单词在向量空间中进行分布表示,以帮助学习算法对相似的单词进行分组,从而在自然语言处理任务中能够达到更好的性能。最早使用表示形式进行单词研究要追溯到1986年,源于Rumelhart、Hinton和Williams[21]。此后,该方法被不断地发展。最近,Mikolov等给出了一种Skip-gram模型,这是一种从大量非结构化文本数据中学习高质量的单词向量表示的有效方法[22]。随后,又有研究者将这种向量表示方法从线性结构的自然语言处理引入到各种网络结构中。Aditya Grover等在前人的研究成果上,提出了一种成熟完善的图嵌入算法—node2vec算法[15]。本文使用node2vec算法,将PPI网络中的蛋白质节点映射到低维向量空间上。
令G=(V, E)是一个给定的PPI网络,V是蛋白质节点集合,E是节点之间的边集合,每一条边表示一对蛋白质交互。目标是将每一个节点u∈V表示成一个低维空间Rd中的向量。即学习一个映射函数f: V→Rd,这里d≪|V|,d是一个参数,指定向量表示的维数。
1.1.1 优化函数我们希望下面的目标函数达到最大值,即在给定f的条件下,希望网络邻居NS(u)的对数似然概率达到最大:
| ${\max _f}\sum\limits_{u \in V} {\log } \Pr \left( {{N_S}(u)\mid f(u)} \right){\rm{。}}$ | (1) |
式中NS(u)⊂V是通过邻域采样策略S产生的节点u的网络邻居。
为了使这个最优化问题易于处理,两个标准假设是必须的[15]。
第一个假设是条件独立性。我们假设邻域中每个节点被观察的可能性是相互独立的,那么似然函数可以进行因式分解,从而给定源的特征表示:
| $\Pr \left( {{N_S}(u)\mid f(u)} \right) = \prod\limits_{{n_i} \in {\mathit{\boldsymbol{N}}_S}(u)} {\Pr } \left( {{n_i}\mid f(u)} \right){\rm{。}}$ | (2) |
第二个假设是特征空间的对称性。源节点和邻域节点在特征空间中具有对称效应。因此,我们将每个源-邻域节点对的条件似然建模为一个softmax单元,并通过其特征的点积进行参数化:
| $\Pr \left( {{n_i}\mid f(u)} \right) = \frac{{\exp \left( {f\left( {{n_i}} \right) \cdot f(u)} \right)}}{{\sum\nolimits_{v \in V} {\exp } (f(v) \cdot f(u))}}{\rm{。}}$ | (3) |
则公式(1)可改写为
| ${\max _f}\sum\limits_{u \in V} {\left[ { - \log {Z_u} + \sum\limits_{{n_i} \in {{\mathit{\boldsymbol{N}}}_S}(u)} f \left( {{n_i}} \right) \cdot f(u)} \right]} {\rm{。}}$ | (4) |
其中Zu=∑v∈Vexp(f(u)·f(v))。在大型网络中该目标函数的计算代价是昂贵的,因此可以采用负采样方法来逼近[19]。本文采用模拟退火算法来优化上述目标函数。
1.1.2 邻域采样策略对于线性自然语言文本,可使用句子中连续单词上的滑动窗口自然地定义单词序列概念[22]。然而PPI网络不同,它不是线性的,因此需要重新选择一种适合节点邻居的产生方式。常见的邻域采样策略有两种:广度优先采样(BFS)和深度优先采样(DFS)[15]。Aditya Grover等在node2vec算法中设计了一种灵活的邻域采样策略,能够平滑地在BFS和DFS之间进行插值[15]。因此,该方法可兼顾BFS和DFS的优点。
首先,对于给定的源节点u,我们仿真一条固定长度为l的随机游走。令ci表示随机游走链上的第i个节点,那么起点即c0=u。节点ci通过如下分布产生:
| $P\left( {{c_i} = x\mid {c_{i - 1}} = v} \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{{{\pi _{vx}}}}{Z}, }&{{\rm{ if }}(v, x) \in E}\\ {0, }&{{\rm{ otherwise }}} \end{array}} \right.{\rm{。}}$ | (5) |
式中:πvx是节点v和x之间非正则化的转移概率;Z是正则常数。
让随机游动产生偏差的最简单方法是基于静态边权值对下一个节点进行采样,即πvx=wvx。然而,这并不利于解释网络结构。为此,定义基于两个参数p和q的一个二阶随机游走。考虑一个随机游走穿过边(t, v)且现在停驻在点v。现在随机游走需要决定下一步的方向,因此需要评估由v引导的边(v, x)的转移概率πvx。我们令非正则化的转移概率为πvx=αpq(t, x)·wvx,这里
| ${\alpha _{pq}}(t, x) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{p}, }&{{\rm{ if }}\quad {d_{tx}} = 0}\\ {1, }&{{\rm{ if }}\quad {d_{tx}} = 1}\\ {\frac{1}{q}, }&{{\rm{ if }}\quad {d_{tx}} = 2} \end{array}} \right.{\rm{。}}$ | (6) |
且dtx记录了节点t和x之间的最短距离。注意到dtx一定是{0, 1, 2}之一,因此两个参数是必要的,并且足够指导随机游走。
通过将节点映射成低维向量的图嵌入技术,可以将相似的蛋白质节点嵌入到一起,因此能够捕获PPI网络的内部关系。
1.2 布谷鸟搜索布谷鸟搜索算法(Cuckoo search,CS)是Yang Xinshe等提出的一种最优化搜索算法[23]。自然界中,布谷鸟不会自己搭建巢穴,而是随机寻找鸟巢来孵化自己的蛋,布谷鸟的蛋与宿主巢穴中的鸟蛋越相似,就越不容易被宿主发现,从而也就越不容易被宿主抛弃。布谷鸟搜索算法正是模拟这一生物现象而提出的一种问题寻优算法。Gao Yin等又将CS算法的搜寻机理用在PPI网络复合物预测中,并在酵母PPI网络中对蛋白质复合物进行预测,取得了较好的结果[24]。本文也借鉴了Gao Yin等的想法。
首先对PPI网络中的边进行赋权。Wang等[25]和Peng等[11]引入了一种名为ECC(Edge clustering coefficient)的边聚类系数,来为网络中的边加权。
| ${\mathop{\rm ECC}\nolimits} (u, v) = \frac{{\left| {{Z_{uv}}} \right|}}{{\min \{ d(u) - 1, d(v) - 1\} }}, $ | (7) |
式中:Zuv是节点u和v的公共邻居集合;d(u)表示节点u的度。为了进一步刻画两个相邻节点u和v的共同领域之间的连通性,Ma Chengyu等引入了一种新的边聚类系数NECC(New edge clustering coefficient)[26]。该思想是用进一步分层的方式估计u和v的邻域连通性。NECC的定义如下:
| ${\mathop{\rm NECC}\nolimits} (u, v) = \frac{{{N_{uv}} + {\mathop{\rm ECC}\nolimits} (u, v)}}{{2\left| {{Z_{uv}}} \right| + 1}}, $ | (8) |
其中
| ${N_{uv}} = \sum\limits_{{v_i} \in {{\bf{Z}}_{wv}}} {\left( {{\mathop{\rm ECC}\nolimits} \left( {u, {v_i}} \right) + {\mathop{\rm ECC}\nolimits} \left( {{v_i}, v} \right)} \right)} {\rm{。}}$ | (9) |
显然,NECC更广泛地考虑了两个相邻节点的整个邻域的连通性,可以更好地确定某个蛋白质是否属于一个复合物。
再结合通过图嵌入技术将蛋白质节点映射成的低维向量,本文定义了属于自己的边加权方式,即两个相邻节点u和v之间的边权为
| ${W_{uv}} = {\mathop{\rm Dist}\nolimits} (u, v) \cdot {\mathop{\rm NECC}\nolimits} (u, v)$ | (10) |
式中Dist(u, v)是节点u和v之间通过表示向量计算的欧氏距离。这种赋权方式既考虑了PPI网络的拓扑结构,又考虑了节点的空间结构,从而能够更准确地衡量节点之间的相似度。
之后可以开始正式进行布谷鸟搜索。布谷鸟搜索算法主要分为四步。
第一步,确定聚类的中心点。我们根据式(1)计算节点的加权度:
| ${D_w}(u) = \sum\limits_{(u, v) \in E} {{W_{uv}}} , $ | (11) |
然后选择加权度大于阈值的节点作为聚类的中心点。不同于Gao Yin等以所有节点的平均加权度为阈值,本文采用所有非0加权度的中位数作为阈值,之所以采用这种阈值取法,是为了避免一些极端值(比如孤立点以及一些度特别大的点)对整体取值的影响。
第二步,获取初始簇。对于一个聚类中心u,判断每一个与其有交互的蛋白质节点v与该中心u的相似度(即边权),若相似度大于阈值,则将v归入到以u为中心的簇里。待所有与u有交互的节点都判断完成后,则形成一个以u为中心的初始簇。对每一个聚类中心,按此法形成若干个大小不同的初始簇。这里的阈值取法如下:将所有边权从小到大排列,去掉0值之后,取剩下数值的上四分位数作为阈值,之所以取上四分位数,是因为这时能够相对更好地控制一个复合物的规模。
第三步,簇的扩充。对于还未属于任一个簇的蛋白质节点,判断其与每一个簇的亲和度,并将其归入到亲和度大于阈值的簇中。蛋白质节点u和簇C之间的亲和度计算方法如下:
| ${\varphi _u} = \frac{{\sum\limits_{v \in C, (u, v) \in E} {{W_{uv}}} }}{{|C|}}, $ | (12) |
且亲和度的阈值一般取2。待所有节点判断完成,则获得了所有潜在的蛋白质复合物。
第四步,合并与剔除。我们用重叠得分OS(A, B)来度量两个蛋白质复合物之间的相似度。如果两个蛋白质复合物之间的重叠得分OS(Overlapping score)大于给定的阈值,则将两个复合物合并。两个复合物A和B的重叠得分计算方式如下:
| ${\rm{OS}}(A, B) = \frac{{{{\left| {{V_A} \cap {V_B}} \right|}^2}}}{{\left| {{V_A}} \right| \times \left| {{V_B}} \right|}}, $ | (13) |
式中VA表示A复合物中蛋白质集合。显著的,这种重叠得分已经被用在许多以往的研究中,来判断一个预测的复合物与一个已知的复合物是否匹配[5, 8, 11, 27-28]。代表性的,如果OS(A, B)≥0.2,则复合物A和B被视为匹配的。这个阈值同样适用于判断两个预测的蛋白质复合物需不需要合并。
为了保证候选复合物的高质量,我们采用加权边密度进行评估。边密度的概念最先由Coleman和More提出[29],Ma Chengyu等对其进行了拓展[26]。给定一个图G=(V, E, W), 加权边密度(Density,den)的定义如下:
| ${\mathop{\rm den}\nolimits} (G) = \frac{{2\sum\nolimits_{e \in E} W (e)}}{{|V| \times (|V| - 1)}}{\rm{。}}$ | (14) |
对于一个蛋白质复合物C,同样可以计算其加权边密度。我们剔除那些加权边密度小于阈值(这里一般取0.1,这是由于CORUM参考复合物集合中的复合物其加权边密度基本大于0.1)的或只包含一个蛋白质的复合物。保留下来的,即为通过布谷鸟搜索预测获得的预测蛋白质复合物。
当然在这一步中,涉及一些阈值的选取问题,不同的阈值设置肯定会对结果产生一定的影响,什么样的阈值设置是最好的,是我们还在继续研究的内容。
1.3 二次搜索布谷鸟搜索方法以加权度大于阈值的节点作为聚类中心,这样很容易略掉一些由加权度不大的蛋白质构成的复合物,尤其是一些小型复合物。因此,在布谷鸟搜索结束后,还需对未被纳入复合物当中的蛋白质进行二次搜索。我们参考NEOComplex算法[25],构造二次搜索方法。
将通过布谷鸟搜索获得的复合物中包含的蛋白质及其相关的交互边从PPI网络中删除,在剩下的子图网络G1中进行二次搜索。二次搜索过程如下:以G1中的一个蛋白质节点v1为种子节点,从G1的与v1有边相连的节点中选取边权最大的节点v2,加到v1的簇中;再从G1的与v2有边相连的节点中选取边权最大的节点v3,加到{v1, v2}的簇中,以此类推,直至簇的加权边密度小于阈值0.1为止。以G1的每一个节点作为种子节点,分别按照上述规则进行搜索,均可以获得一个潜在的蛋白质复合物。再将这些潜在的蛋白质复合物按照布谷鸟搜索中第四步的合并与剔除规则进行合并与剔除处理,保留下来的蛋白质复合物就是二次搜索获得的预测蛋白质复合物。
两次搜索获得的预测蛋白质共同构成了我们二步搜索算法探测得到的蛋白质复合物。
1.4 主要算法对于给定的蛋白质交互网络(PPI网络)G=(V, E),完整的复合物探测算法TSSComplex如下。
TSSComplex算法
步骤1. 准备工作
步骤1.1 根据G=(V, E),计算每条边的边聚类系数NECC。
步骤1.2 以NECC为初始边权,根据随机游走策略,确定每个顶点的邻居NS(u)。
步骤1.3 根据图嵌入技术,最优化目标函数,将每个蛋白质节点映射到低维向量空间。
步骤1.4 根据Wuv=Dist(u, v)·NECC(u, v)更新边权。
步骤2. 第一步搜索:布谷鸟搜索
步骤2.1 计算每个蛋白质节点的加权度。
步骤2.2 将加权度大于阈值的节点作为初始簇中心。
步骤2.3 对于每一个簇中心,判断与该簇中心相连接的节点与簇中心的相似度是否大于阈值,将大于阈值的节点归入该簇。
步骤2.4 对于剩余的节点,计算其与每一个簇的亲和度,并将其归入亲和度大于阈值的簇。
步骤2.5 合并重叠得分OS≥0.2的簇。
步骤2.6 删除边密度小于0.1或仅包含一个蛋白质的簇。
步骤3. 第二步搜索:二次搜索
将步骤2中获得的复合物中所包含的蛋白质及其相关的边从PPI网络中移除,剩下的节点与边构成子图G1=(V1, E1),在G1中进行二次搜索。
步骤3.1 以G1中任意一点v1为种子节点,在G1中寻找与v1相连且边权最大的节点v2加入该簇,再寻找与v2相连且边权最大的v3加入该簇,直至簇的边密度小于0.1。
步骤3.2 对G1中的每一个节点重复进行步骤3.1,共获得|V1|个簇。
步骤3.3 根据合并与剔除规则处理步骤3.2中获得的簇。
步骤4. 将步骤2和步骤3中保留下来的簇输出。其每一个簇即为一个通过TSSComplex算法获得的蛋白质复合物。
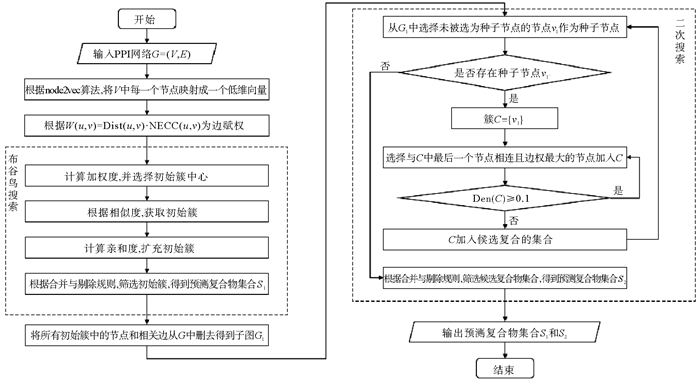
算法的简易流程见图 1。
|
图 1 TSSComplex算法的流程图 Fig. 1 Flow chart of TSSComplex algorithm |
我们将TSSComplex算法应用于人类的PPI网络,与其他几种蛋白质复合物探测方法作比较,同时结合数据集的特征,作综合分析,以评估算法的性能。
2.1 数据集人类PPI网络通过联合HPDR(Human Protein Refe-rence Database)[30]和BioGRID(version 3.5.173)[31]数据共同构建。最终获得的人类PPI网络中一共包含18 004个蛋白质节点和339 054条交互(边)。
为评估预测的蛋白质复合物,我们使用CORUM(Comprehensive Resource of Mammalian)作为蛋白质复合物参考集[32]。该集合具有较高的可靠性。它一共收录了2 916个蛋白质复合物,其中有2 643个复合物包含2个及以上的蛋白质。我们将这2 643个复合物作为参考集。这些复合物一共涉及3 627个蛋白质和93 884条交互。
2.2 性能标准为评估我们预测结果的质量,我们计算了两个在文献中广泛使用的统计指标:精确度和召回率。精确度是与至少一个已知复合物相匹配的预测复合物的数量与所有预测复合物的数量的比值:
| ${\rm{ Precision }} = \frac{{\left| {\left\{ {{c_i}:\exists g \in {\rm{RC}}, {\rm{OS}}\left( {{c_i}, g} \right)0.2} \right\}} \right|}}{{|{\rm{PC}}|}}{\rm{。}}$ | (15) |
式中:PC(Prediction complex)是预测的复合物集合;RC(Reference complex)是CORUM提供的参考复合物集合。召回率是已知复合物中符合至少一个预测复合物的比例:
| ${\rm{ Recall }} = \frac{{\left| {\left\{ {{c_i}:\exists g \in {\rm{PC}}, {\rm{OS}}\left( {{c_i}, g} \right) \geqslant 0.2} \right\}} \right|}}{{|{\rm{RC}}|}}{\rm{。}}$ | (16) |
F-measure是精确度和召回率的调和平均值,表示预测结果的总体表现,即
| $F{\rm{ - measure }} = 2 \times \frac{{{\rm{ Precision }} \times {\rm{ recall }}}}{{{\rm{ Precision }} + {\rm{ recall }}}}{\rm{。}}$ | (17) |
我们将TSSComplex算法的性能和8种蛋白质鉴定技术(MCL[4]、MCODE[5]、CMC[7]、COACH[8]、ClusterONE[9]、ProRank+[10]、PEWCC[32]和NEOComplex[26])做了比较(见表 1)。
|
|
表 1 9种方法的性能比较 Table 1 Performance comparison of nine methods |
表 1报告了包括TSSComplex在内的所有竞争方法的比较结果。如果仅从数值上看,TSSComplex算法并不是特别理想,但TSSComplex算法依然有其研究的价值,其理由主要有以下三个原因。
原因1:随着PPI网络中蛋白质交互信息的不断增多,其他方法将逐渐失效。
以其他8种算法中性能最好的NEOComplex算法为例,NEOComplex算法的PPI网络数据来自HPRD和BioGRID(version 3.2.109),共包含15 459个蛋白质和144 895条交互。而本文使用的来自HPRD和BioGRID(version 3.5.173),共包含了18 004个蛋白质和339 054条交互。可以发现,蛋白质数量增长了不到20%(仅增长了16.46%),但蛋白质之间的交互数量却增长了一倍多(增长了134%)。交互信息的大量增多,使得各种搜索方法产生的复合物容量越来越大。我们在本文的数据集上测试了NEOComplex算法,发现该算法获得的复合物容量基本在500以上,一个复合物里包含了500个以上的蛋白质。而根据匹配规则,两个复合物之间的重叠率要达到0.2才算匹配成功。以一个容量为500的复合物A计算,若一个复合物B能与其匹配成功,该复合物B的容量至少为100。而CORUM提供的人类2 643个蛋白质复合物中,仅有两个复合物的容量超过了100。也就是说,在交互信息增长了一倍多的条件下,NEOComplex算法的召回率已经近乎于0,不再是表 1中显示的0.47。同样,这时NEOComplex算法的精确率也会下降到近乎为0。因此,随着蛋白质间交互信息的不断增多,NEOComplex算法已经失去效应。
原因2:TSSComplex算法能够有效地控制复合物。
NEOComplex算法之所以会失效,就是因为它没有一个有效的手段来控制预测复合物的大小,而TSSComplex算法还可以继续使用,得益于它们所采用的布谷鸟搜索算法可以控制预测复合物的规模。布谷鸟搜索在获取聚类中心后,只有与中心点相连的节点,才有可能通过相似度的筛选,进入初始簇,因此这些点与中心点之间的最短路径长度均为1。而在第二步初始簇的扩充中,若一个点与初始簇内任何点均不相连,该点是不会被扩充进初始簇的。而一个点如果可能被扩充进初始簇,那么它必然至少与初始簇中的一个点相连,这时它与簇中心之间的最短路径长度的集合中最大值只能是2,而簇中最远的两个点之间最短路径长度的集合中最大值也仅可能为4,正是因为如此,布谷鸟搜索能够控制簇的规模。而NEOComplex算法,只要边密度不小于0.009,就一直可以有节点加入,加入的节点和初始种子节点之间的距离可以非常远,从而无法控制簇的规模。
原因3:TSSComplex算法可以有效缩小蛋白质复合物搜索的范围。
这里,我们为CORUM中的已知蛋白质复合物定义了最优重合率。一个复合物c∈RC,它的最优重合率(Optimal overlapping score,OOS)为
| ${\rm{OOS}}(c) = \frac{{{\max\limits_{{g_i} \in {\rm{PC}}}}\left| {c \cap {g_i}} \right|}}{{|c|}}{\rm{。}}$ | (18) |
这个最优重合率反映了该已知复合物中有多少蛋白质可以同时出现在某个预测复合物中。OOS越大,说明一个已知复合物越能完整的包含在一个预测复合物中。
对CORUM中的已知复合物进行分段统计,表 2报告了分段统计的结果。观察表 2中的数据可以发现,有55.42%的复合物,其所包含的蛋白质可以完全在某个预测的复合物中找到。有94.78%的复合物,其所包含的蛋白质有一半可以在某个预测的复合物中找到。这一结果远远优于召回率18.62%。这种现象在越小的复合物中越明显。之所以会出现这一情况,是由于随着蛋白质交互信息的增多,PPI网络中每个节点的度也在不断上升,蛋白质与蛋白质之间的联系更紧密,使得预测到的复合物规模偏大(从表 2中可以看出,包含蛋白质个数超过5的预测复合物的比率要远高于已知复合物中该类的比率),使得小型复合物很容易隐藏在一些大型簇中,从而无法被准确地找到。从另一个角度来说,召回率低意味着直接匹配到已知复合物的成功率低;但高最优重合率则意味着已知复合物基本是预测到的复合物的一部分,因此可以有效地为寻找已知复合物缩小范围,而且范围缩小的效率要比NEOComplex算法好。这样可以尝试通过一些方法,在这个缩小的范围内寻找更精确的蛋白质复合物。
|
|
表 2 参考复合物集合关于OSS的分段统计 Table 2 A piecewise statistic for reference complexes with OSS |
另一方面,TSSComplex算法所获得的预测复合物的个数与CORUM中所包含的已知复合物的个数比较接近,这使得可供进一步搜寻的复合物个数也比较少,而不是像CMC算法那样,即便具有很高的召回率,但在新数据集(即本文所使用的数据集)上却能获得近40万个预测复合物,这么庞大的潜在复合物数量,即使想做进一步筛选,其难度也非常大。
综上三个原因,虽然TSSComplex算法在性能指标上可能并不太理想,但其依然具有研究的价值。
3 结语本文提出了一种基于图嵌入技术和布谷鸟搜索的二步蛋白质复合物预测方法。传统搜索算法在蛋白质交互信息越来越多的情况下会逐渐失效,不同于传统算法,本算法在蛋白质交互信息增多的情况下,依然有一定的准确性。但同时也反映出,蛋白质复合物的探测技术未来不能仅依靠PPI网络,还要参考其他信息,例如蛋白质的生化性质信息。
本算法可为进一步精确探测复合物缩小搜索范围。这为蛋白质复合物搜索方法提供了一个新思路:先用搜索算法缩小复合物包含的蛋白质范围,再通过其他数据挖掘技术或实验技术,进一步精确探测复合物。我们现在正在试图构建一些算法,以实现在缩小了范围的蛋白质簇中能更精确地探测蛋白质复合物的目的。
| [1] |
Butland G, Li J, Yang W, et al. Interaction network containing conserved and essential protein complexes in Escherichia coli[J]. Nature, 2005, 433(7025): 531-537. DOI:10.1038/nature03239 (  0) 0) |
| [2] |
Rivas J D L, Fontanillo C. Protein-protein interactions essentials: Key concepts to building and analyzing interactome networks[J]. PLoS Computational Biology, 2010, 6(6): e1000807. DOI:10.1371/journal.pcbi.1000807 (  0) 0) |
| [3] |
Terentiev A A, Moldogazieva N T, Shaitan K V. Dynamic proteomics in modeling of the living cell[J]. Biochemistry, 2009, 74(13): 1586-1607. (  0) 0) |
| [4] |
Asur S, Ucar D, Parthasarathy S. An ensemble framework for clustering protein-protein interaction networks[J]. Bioinformatics, 2007, 23(13): 29-40. DOI:10.1093/bioinformatics/btm212 (  0) 0) |
| [5] |
Bader G D, Hogue C W. An automated method for finding molecular complexes in large protein interaction networks[J]. BMC Bioinformatics, 2003, 4(1): 2. DOI:10.1186/1471-2105-4-2 (  0) 0) |
| [6] |
King A D, Przulj N, Jurisica I. Protein complex prediction via cost-based clustering[J]. Bioinformatics, 2004, 20(17): 3013-3020. DOI:10.1093/bioinformatics/bth351 (  0) 0) |
| [7] |
Liu G, Wong L, Chua H N. Complex discovery from weighted PPI networks[J]. Bioinformatics, 2009, 25(15): 1891-1897. DOI:10.1093/bioinformatics/btp311 (  0) 0) |
| [8] |
Wu M, Li X, Kwoh C K, et al. A core-attachment based method to detect protein complexes in PPI networks[J]. BMC Bioinforma-tics, 2009, 10(1): 169. DOI:10.1186/1471-2105-10-169 (  0) 0) |
| [9] |
Nepusz T, Yu H, Paccanaro A. Detecting overlapping protein complexes in protein-protein interaction networks[J]. Nature Methods, 2012, 9(5): 471-472. DOI:10.1038/nmeth.1938 (  0) 0) |
| [10] |
Hanna E M, Zaki N. Detecting protein complexes in protein interaction networks using a ranking algorithm with a refined merging procedure[J]. BMC Bioinformatics, 2014, 15(1): 204. DOI:10.1186/1471-2105-15-204 (  0) 0) |
| [11] |
Peng W, Wang J X, Zhao B H, et al. Identification of protein complexes using weighted pagerank-nibble algorithm and core-attachment structure[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2015, 12(1): 179-192. DOI:10.1109/TCBB.2014.2343954 (  0) 0) |
| [12] |
Cai B, Wang H, Zheng H, et al. Identification of protein complexes from tandem affinity purification/mass spectrometry data via biased random walk[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2015, 12(2): 455-466. DOI:10.1109/TCBB.2014.2352616 (  0) 0) |
| [13] |
Wang H, Kakaradov B, Collins S R, et al. A complexbased reconstruction of the Saccharomyces cerevisiae interactome[J]. Molecular & Cellular Proteomics, 2009, 8(6): 1361-1381. (  0) 0) |
| [14] |
Tang J, Qu M, Wang M, et al. Line: Large-scale Information Network Embedding[C]. Florence, Italy: The 24th International Conference on World Wide Web, 2015: 1067-1077.
(  0) 0) |
| [15] |
Grover A, Leskovec J. Node2vec: Scalable Feature Learning for Networks[C]. San Francisco, USA: The 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016: 855-864.
(  0) 0) |
| [16] |
Tang J, Aggarwal C, Liu H. Node Classification in Signed Social Networks[C]. Miami, USA: The 2016 SIAM International Conference on Data Mining, 2016: 54-62.
(  0) 0) |
| [17] |
Cao B, Liu N N, Yang Q. Transfer Learning for Collective Link Prediction in Multiple Heterogenous Domains[C]. Haifa, Israel: The 27th International Conference on Machine Learning (ICML-10), 2010: 159-166.
(  0) 0) |
| [18] |
Luxburg von Ulrike. A tutorial on spectral clustering[J]. Statistics and Computing, 2007, 17(4): 395-416. DOI:10.1007/s11222-007-9033-z (  0) 0) |
| [19] |
Liu X, Yang Z, Sang S, et al. Detection of protein complexes from multiple protein interaction networks using graph embedding[J]. Artificial Intelligence in Medicine, 2019, 96: 107-115. DOI:10.1016/j.artmed.2019.04.001 (  0) 0) |
| [20] |
Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality[J]. Advances in Neural Information Processing Systems, 2013, 26: 3111-3119. (  0) 0) |
| [21] |
Rumelhart D E, Hinton G E, Williams R J. Learning representations by backpropagating errors[J]. Nature, 1986, 323(6088): 533-536. DOI:10.1038/323533a0 (  0) 0) |
| [22] |
Mikolov T, Chen K, Corrado G, et al. Efficient Estimation of Word Representations in Vector Space[C]. Scottsdale, USA: The International Conference on Learning Representations, 2013.
(  0) 0) |
| [23] |
Yang X S, Deb S. Cuckoo Search via Levy Flights[C]. Coimbatore, India: World Congress on Nature & Biologically Inspired Computing, 2009: 210-214.
(  0) 0) |
| [24] |
Gao Y, Lei X, Dai C. Cuckoo search algorithm inspired by artificial bee colony and its application[C]// Advances in Swarm Intelligence Lecture Notes in Computer Science. Bali: [s. n. ], 2016.
(  0) 0) |
| [25] |
Wang J, Min L, Wang H, et al. Identification of essential proteins based on edge clustering coefficient[J]. IEEE/ACM Transa-ctions on Computational Biology and Bioinformatics, 2012, 9(4): 1070-1080. DOI:10.1109/TCBB.2011.147 (  0) 0) |
| [26] |
Ma C Y, Chen Y P P, Berger B, et al. Identification of protein complexes by integrating multiple alignment of protein interaction networks[J]. Bioinformatics, 2017, 33(11): 1681-1688. (  0) 0) |
| [27] |
Jung S H, Hyun B, Jang W, et al. Protein complex prediction based on simultaneous protein interaction network[J]. Bioinformatics, 2010, 26(3): 385-391. DOI:10.1093/bioinformatics/btp668 (  0) 0) |
| [28] |
Wang J, Chen J, Li M, et al. Modifying the DPClus algorithm for identifying protein complexes based on new topology structures[J]. BMC Bioinformatics, 2008, 9: 398. DOI:10.1186/1471-2105-9-398 (  0) 0) |
| [29] |
Coleman T F, More J J. Estimation of sparse Jacobian matrices and graph coloring problems[J]. SIAM Journal on Numerical Analysis, 1983, 20: 187-209. DOI:10.1137/0720013 (  0) 0) |
| [30] |
Goel R, Kumar S, Mathivanan S, et al. Human protein reference database 2009 update[J]. Nucleic Acids Research, 2008, 37(suppl 1): 767-772. (  0) 0) |
| [31] |
Andrew C, Bobby-Joe B, Rose O, et al. The BioGRID interaction database: 2015 update[J]. Nucleic Acids Research, 2014, 43(D1): D470-D478. (  0) 0) |
| [32] |
Ruepp A, Waegele B, Lechner M, et al. CORUM: the comprehensive resource of mammalian protein complexes 2009[J]. Nucleic Acids Research, 2009, 38(suppl 1): 479-501. (  0) 0) |
| [33] |
Zaki N, Efimov D, Berengueres J. Protein complex detection using interaction reliability assessment and weighted clustering coefficient[J]. BMC Bioinformatics, 2013, 14(1): 163. DOI:10.1186/1471-2105-14-163 (  0) 0) |
| [34] |
Samanta M, Liang S. Redundancies in large-scale protein interaction networks[J]. Proceedings of the National Academy of Scie-nces of the United States of America, 2013, 100(22): 12579. (  0) 0) |
| [35] |
Wodak S J, Vlasblom J, Turinsky A, et al. Protein-protein intera-ction networks: the puzzling riches[J]. Current Opinion in Structural Biology, 2013, 23(6): 941. DOI:10.1016/j.sbi.2013.08.002 (  0) 0) |
| [36] |
Sabyasachi Patra, Anjali Mohapatra. Protein complex prediction in interaction network based on network motif[J]. Computational Biology and Chemistry, 2020, 89: 107399. DOI:10.1016/j.compbiolchem.2020.107399 (  0) 0) |
| [37] |
Rwa B, Cw C, Cla B. A novel graph clustering method with a greedy heuristic search algorithm for mining protein complexes from dynamic and static PPI networks[J]. Information Sciences, 2020, 522: 275-298. DOI:10.1016/j.ins.2020.02.063 (  0) 0) |
| [38] |
Zhang J, Zhong C, Huang Y, et al. A method for identifying protein complexes with the features of joint colocalization and joint co-expression in static PPI networks[J]. Computers in Biology and Medicine, 2019, 111: 103333. DOI:10.1016/j.compbiomed.2019.103333 (  0) 0) |
 2022, Vol. 52
2022, Vol. 52


