2. 中国海洋大学海洋生命学院,山东 青岛 266003;
3. 中国海洋大学水产学院,山东 青岛 266003
近海海域是一个集社会、经济、资源及环境于一体的综合系统,具有复杂性、开放性、动态性及稳定性等特点[1-2]。近海海域不仅受到陆地和海洋各种自然因素的作用,人类活动亦对其有较大影响[3-4]。中国作为一个海洋大国,拥有丰富海洋资源,但随着海洋资源利用规模的持续扩大和利用效率的不断提升,脆弱的海洋生态环境受到了不可逆转的诸多负面影响[5-6]。为促进海洋经济的永续发展,需促进海域承载力与经济效益之间协调发展[6]。
海域承载力是海洋永续发展的重要判断依据,在一定时期内,海域承载力强调海洋资源的永续利用和支持经济社会的发展能力,使得海洋能够支持社会、经济、资源和环境的协调发展[4, 7-8]。目前,众多学者开展了海域承载力的相关研究, 例如,钟舜彬和何均琳等[2]对中国东海近海海域承载力进行了评价,研究结果认为,在2006—2008年该海域承载力是处于适载状态,而2009年之后,该海域承载力则是呈现(严重)超载水平。叶文祯[9]分析了福建省县级海域承载力水平的空间差异,并据此提出了相关建议。高金田等[10]模拟了不同情景下北部湾(防城港、钦州、北海三市)海域承载力的动态变化,并据此提出了相关政策。狄乾斌等[5]以辽宁省为例,分析了海洋产业结构与海域承载力之间的关系。
系统动力学(System dynamics,SD)作为一门融合了信息论、系统论、控制论及决策论等学科综合知识的分析方法[11-13],不仅可对现行政策进行追踪和模拟,亦可对未来系统发展态势进行调控,进而为决策者提供理论参考依据[14]。系统动力学已被广泛应用于海域承载力、水资源承载力、土地承载力、城市规划、生物医药等方面的研究[15-20]。青岛作为中国重要的海滨城市,其区位优势明显[21],为保障青岛海洋经济的永续健康发展,本文基于多种数据来源,运用系统动力学模型对胶州湾海域承载力的发展状况进行模拟和预测,以期为其未来海洋经济发展提供科学依据和相应政策建议。
1 材料与方法 1.1 指标选取海洋是一个复杂系统,人类活动对其影响较大,因而海域承载力研究既要考虑沿海海域的地理特征,也要兼顾社会属性[22]。本文根据2015年国家海洋局发布的《海洋资源环境承载能力监测预警指标体系和技术方法指南》和2017年山东省质量技术监督局发布的地方标准《近岸海域海洋资源承载力评估技术规程》(DB37/T2910—2017),考虑胶州湾海域自然资源分布现状及特点,综合海域资源供给与需求因素,将海域承载力系统划分为社会、经济、资源及环境4个子系统。指标体系如表 1所示。
|
|
表 1 胶州湾海域承载力指标体系 Table 1 Index system of jiaozhou Bay sea area carrying capacity |
本文研究区域为胶州湾海域。胶州湾位于山东半岛南部,是一个典型的半封闭海湾,是中国近海生态系统的缩影,其沿岸一带滨海旅游、采捕和养殖活动发达,受人类活动和自然变化影响极为显著[23-24]。
本文选取2000—2020年作为胶州湾海域承载力的时间范围,相关数据来源于《青岛统计年鉴》、《青岛市海洋环境公报》、《青岛市环境状况公报》、《青岛市生态环境状况公报》、《山东渔业统计年鉴》、《中国海洋统计年鉴》及地方政府内部数据。
1.3 系统动力学模型 1.3.1 系统动力学建模步骤模型涵盖研究目的、边界确定、因果关系、流程图和结构方程、模型检验与情景设计及结果分析[8, 25]。
研究目的 应用系统动力学进行研究在于认识和预测承载力系统的未来状况,以进一步确定系统结构以及情景设计,为后续制定合理的政策提供参考依据。
边界确定 基于系统内部的因素,在建模时要确定边界,边界范围偏大或偏小都不能反映真实情况[26]。因此,需要合理判定模型的边界,保证系统不受外部因素的影响,这是建模过程中的核心要点。
因果关系 因果关系图可呈现出系统内部各变量间的因果关系,并用这种关系的反馈回路来进行描述。从系统中筛选除出合适的变量,综合衡量各变量间的内在联系,正号与负号则分别表示各变量间的正负关系。
建立模型 模型包括流程图与结构方程。流程图涵盖各子系统,要确定其变量的基本属性、合理区分速率、状态及辅助变量。结构方程体现各因素间的数量关系[27-28]。
模型检验与情景设计 在构建好整个系统的结构后,需对模型进行检测,通过计算相对误差,比较模型精度。检验完成之后,根据相关政策和发展规划要求,设置合理参数值,进行情景设计[10, 18]。
结果分析 对设计的情景进行模拟,然后对相关结果进行分析和讨论,最终找到适合系统发展的情景。
1.3.2 系统边界及基准年研究将系统边界确定为胶州湾海域及周边陆域。基于承载力边界的完整性,胶州湾海域承载力模型的时间边界为2000—2030年,其中2000—2020年为历史检验时间段,2021—2030年为模拟预测时间段,模拟步长为1年。基准年为2000年,模型的各项初始值采用基准年的各项指标值,以此来预测2021—2030年的各项指标值,从而反映胶州湾海域承载力的状况。
1.3.3 系统因果关系海洋资源承载力系统是一复杂系统,各组成部分之间存在着连锁关系,因果反馈关系图可全面展示系统内部各要素间所存在的关联性[8, 29]。通过分析系统中各因素之间的因果关系,用Vensim DSS 8.2.0软件绘制因果关系图,有利于更直观地了解模型中各因素之间的因果关系。本文中的因果关系图如图 1所示。
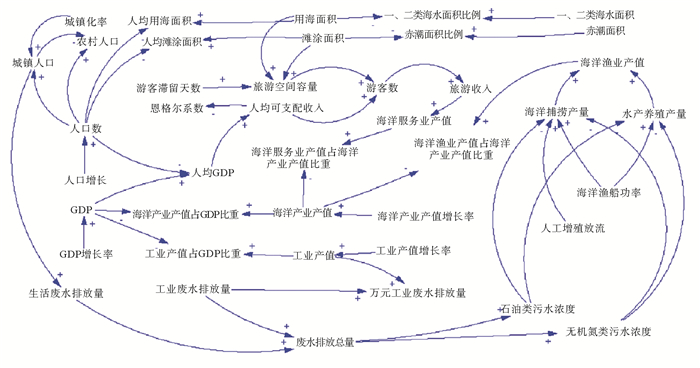
|
图 1 因果关系图 Fig. 1 Causality diagram |
通过分析各子系统各要素之间的正负反馈关系,以因果关系为依据,经过反复测试调整,用系统动力学建模软件Vensim DSS 8.2.0来构建胶州湾海域承载力社会-经济-资源-环境系统结构流程图(见图 2)。选取人口总数、GDP总额、海洋产业产值、工业产值作为水平变量,其它为辅助变量。
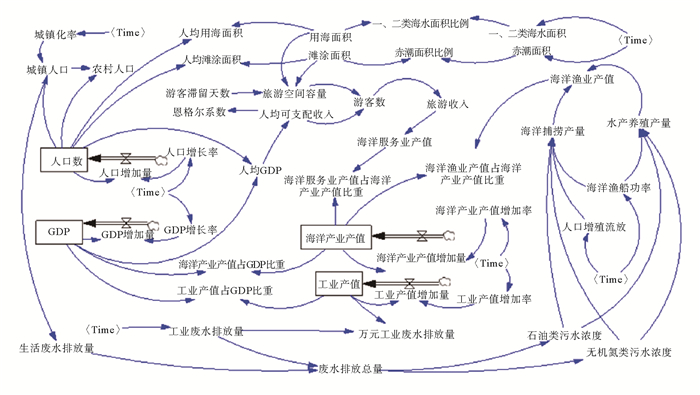
|
图 2 胶州湾海海域承载力系统结构流程图 Fig. 2 Structure flow chart of Marine carrying capacity system in Jiaozhou Bay |
社会系统 社会是以人为主体的大系统,人口总数、城镇人口以及农村人口是该系统的主要变量。其中,人口总数可直接反映青岛市沿海海域资源所能够承担的总人口数量,而城镇人口和农村人口数则进一步反映了能够承担的城镇人口数和农村人口数,因此可通过社会系统的这几个主要变量来反映青岛沿海海域的承载力状况。
经济系统 GDP总额、海洋产业产值和工业产值是该系统主要变量,其中,海洋渔业和海洋服务业产值都属于海洋产业产值,工业产值是胶州湾周边陆域进行工业生产所带来的经济产出。GDP总额可进一步通过海洋产业产值和工业产值反映海洋经济和工业生产带来的经济效益,进而反映出胶州湾海洋资源的承载力。
资源系统 滩涂面积、用海面积、一二类海水面积和赤潮面积是该系统主要变量,除此之外还包括人工增殖放流和海洋渔船功率,可以反映出青岛市沿海海域资源的供给能力。其中,滩涂和用海面积可以影响游客数,进一步影响海洋服务业的产值,人工增殖放流和海洋渔业船功率可通过海洋渔业产值最终影响海洋产业产值。可利用资源量的多少会进一步影响海洋经济的产值,最终反映出海洋资源的承载力。
环境系统 废水排放总量、工业废水排放量和生活废水排放量是该系统主要变量。废水的产生间接反映了人口和经济状况,同时也会进一步影响经济的发展,例如由此带来的石油类污水和无机氯类污水会进一步影响海洋渔业产量,并最终通过影响海洋渔业产值来反映沿海海域资源承载力状况。
1.3.5 系统主要方程及参数设定系统动力学模型由水平变量、速率变量、表函数及常量变量组成,在本文模型中设计的变量主要方程见表 2。
|
|
表 2 胶州湾海域承载力系统动力学模型主要变量及方程 Table 2 Main variables and equations of system dynamics model of marine carrying capacity in Jiaozhou Bay |
除上述水平和速率变量之外,模型的参数还包括常数、表函数和初始值,其中常数是模拟过程保持不变的参数,表函数是模拟过程随时间改变的参数,而初始值则在模拟初始阶段的参数值(见表 3)。由于2000—2020年为模型的历史检验期,因此,2000年的数据即为模型的参数初始值。
|
|
表 3 胶州湾海域承载力系统动力学模型常数和参数初始值 Table 3 System dynamics model constants and initial parameters of carrying capacity in Jiaozhou Bay |
将2000—2020年作为模型有效性检验时间段,将模拟值与实际值进行比较。这里,研究采用相对误差和平均绝对百分比误差(MAPE)进行分析。计算公式如下:
| $c=|a-b| / a \text { 。}$ | (1) |
式中:c为相对误差;a为统计数据(实际值);b为模拟数据(模拟值)。
| $M A P E=\frac{1}{n} \sum\limits_{i=1}^n \frac{\left|a_i-b_i\right|}{a_i} {\rm{。}}$ | (2) |
式中:MAPE为平均绝对百分比误差;a为历史统计数据;b为模型模拟数据。
考虑到影响海域承载力变化的因素较多,水平变量的误差存在波动是正常的,只要MAPE处于20%以下,构建的SD模型则可用来预测2021—2030年胶州湾海域承载力的状况。MAPE低于20%的模型适合于5年之内的中短期预测;若超过5年(长期预测),MAPE低于40%亦可接受[30-31]。
2 结果与分析 2.1 海域承载力SD模型模拟结果分析本文选取人口总数、GDP总额、海洋产业产值、工业产值四个变量检验误差,其误差检验结果见表 4。由表 4可以看出,人口总数的相对误差在2010—2020年(超过10%)相对2000—2009年(低于10%)较大,GDP总额也呈现类似的趋势,后面年份(2006—2020年)的相对误差大于前面年份(2000—2005年), 而海洋产业产值和工业产值的相对误差整体来说都较小(海洋产业产值个别年份除外,2014—2020年其相对误差处于14%~18%范围)。从平均相对误差来看,人口总数、GDP总额、海洋产业产值以及工业产值分别为9.15%、14.35%、3.9%和0.12%。上述数值表明,SD模型应用在青岛市沿海海域承载力研究上是可行的,本研究可将该模型用于未来年份的预测。
|
|
表 4 2000—2020年胶州湾海域承载力系统主要指标检验 Table 4 Main indicators of marine carrying capacity system from 2000 to 2020 in Jiaozhou Bay |
本文选取人口增长率、GDP增长率、海洋产业产值增长率和工业产值增长率作为模型的决策参数,设定现状延续和高质量发展两种情景来模拟2021—2030年胶州湾海域承载力状况。
现状延续是指保持现有的发展情况不变,参数的初始值以2000年为基础,对2021—2030年的海域承载力进行预测。高质量发展是以优化现有发展模式来提升沿海海域承载力为目标,调整参数的设定是尽可能满足2030年的理想状态值,并且研究结合地方规划目标和方案,最终设置了两种情景参数(见表 5)。
|
|
表 5 两种模拟情景参数设定 Table 5 Parameter setting of two simulated scenarios |
承载力预测结果表明(见图 3),当前发展方案中胶州湾海域承载力呈“先缓慢提升,后显著下降”态势,故这一方案不能确保胶州湾海域承载力可持续发展;高质量发展方案中胶州湾海域承载力则呈“先缓慢上升,后显著提升”态势,这主要得益于前期高质量发展重在于搭建产业发展的基础,后续发力日益显著。因此,实施高质量发展是实现胶州湾海域可持续发展的必由之路。
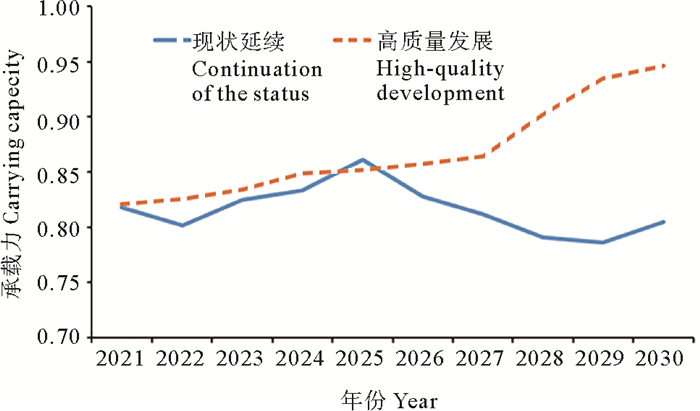
|
图 3 两种情景下的海域承载力预测结果 Fig. 3 Predictions of marine carrying capacity under two scenarios |
承载状态的划分标准[32]:当承载力(RC)≤0.80时,海域环境为强可载;当0.80<RC≤0.90时,海域环境为较强可载;当0.90<RC≤0.99时,近满载;当RC=1.00时,海域环境为满载。可知在维持现状发展这一情景下,胶州湾海域承载力总体处于强可载和较强可载状态,而在高质量发展这一情景下,其承载状态稳步提升,逐步从强可载、较强可载上升至近满载。
从模拟结果来看(见图 4),在两种情景下,人口总数、GDP总额以及海洋产业产值均呈现上升趋势。具体而言,在现状延续情景下,人口总数从2020年的891.53万人增长到2030年的1 026.81万人,GDP总额和海洋产业产值分别从期初的9 026.41和2 928.12亿元增长到期末的20 181.30和16 014.10亿元;在高质量发展情景下,上述指标至2030年时,其值分别为1 073.27万人、19 085.00和19 655.70亿元;人口总数指标是呈现线性上升趋势,后两个指标则是指数增长趋势。而工业产值则呈现相反的趋势,在现状延续情景和高质量发展情景下,其从期初的24 678.58亿元分别下降到期末的2 017.21和2 426.53亿元。
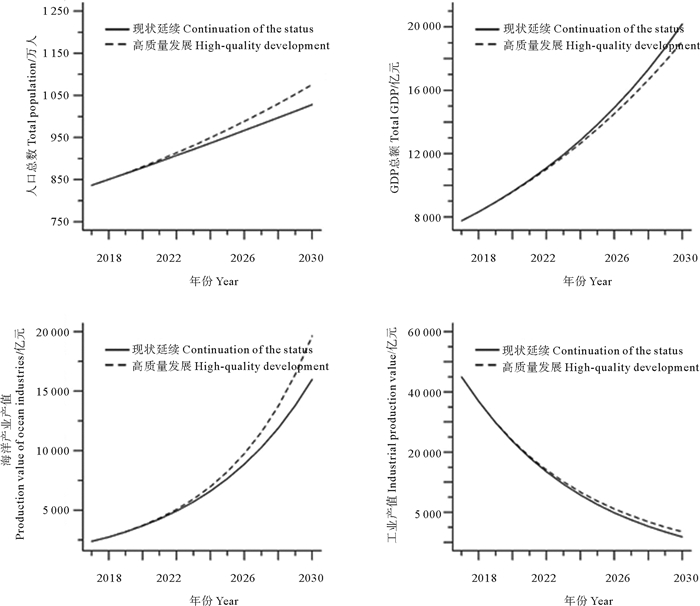
|
图 4 两种情景下主要指标仿真结果趋势 Fig. 4 Simulation results trend of main indicators under the two scenarios |
人口总数、海洋产业产值以及工业产值在现状延续情景下的增幅都低于高质量发展情景下,GDP则是高质量发展情景的增幅低于现状延续情景,这与期初设定的参数有关。随着中国经济高质量发展,各地GDP增幅会有一定程度下降。而在碳达峰、碳中和目标下,工业产值也会呈现逐年下降的趋势。由此可见,在高质量发展情景下,对一系列决策参数(包括人口增长率、GDP增长率、海洋产业产值增长率、工业产值增长率)的调整,将会更适合青岛市海洋经济的永续健康发展。
3 结论及建议青岛区位优势明显,海洋资源丰富,在山东半岛城市群中发挥着引领作用。近年来,政府加大对海洋产业的科技与资金投入,相关产业得到快速发展,海洋经济也稳步提升。同时,由于青岛市对城市基础以及交通设施(地铁、高铁及机场等)的不断优化,城市环境得到提升,吸引了许多外来人口,加上国家政策的支持,人口出生率增高,人口数量自然会逐年增高[33]。青岛市政府在《青岛市城市环境总体规划(2016—2030年)》中提出了坚持生态优先原则,着眼于“生态城市、美丽青岛”的战略目标[34]。此外,在国家碳达峰、碳中和目标下,青岛发展经济的同时更加注重对环境的保护,因此加强了对工业生产的管控,导致工业产值也受到了影响。研究有下述两点结论:
(1) 在研究年份各决策参数组合在设定的情景下动态趋势不同。2021—2030年,两种情景下的人口总数、GDP总额以及海洋产业产值均呈现上升趋势,而工业产值则呈现下降的趋势。其中人口总数、海洋产业产值以及工业产值在现状延续情景下的增幅都低于高质量发展情景下,而GDP则随着中国经济的发展,增长幅度会有所下降,因此在高质量发展情景下的增幅会低于现状延续情景。
(2) 高质量发展情景下的参数组合有利于改善海域承载力。在该情景下,通过对一系列决策参数(人口增长率、GDP增长率、海洋产业产值增长率、工业产值增长率)的调整,改善了胶州湾海域的资源环境状况,提高了人口数和经济总量,更利于青岛城市海洋经济的永续健康发展。
2021—2030年胶州湾海域承载力预测结果表明,在维持现状发展这一情景下其承载力总体处于强可载和较强可载状态,而在高质量发展这一情景下则从强可载、较强可载上升至近满载。因此,为避免胶州湾海域承载力出现过载现象,鉴于海洋是立体的、多层次的、复合式的利用模式,由此产生了海洋资源多重利用的产业,故构建海洋产业的一体化机制成为一种可能,而海洋产业彼此融合及其合理空间布局不仅有助于海洋生态资源环境的利用不超过其海域承载力,从而促进海域可持续发展利用,而且是海洋产业一体化这一机制能否成功构建及其实效强弱的一个关键环节。其中,通过市场化的手段这一无形之手可实现海洋产业结构和空间布局的一体化,而通过政府宏观调控这一有形之手建立健全行业组织或协会则可实现海洋产业结构优化和空间布局合理化的产业发展和协调机制。
研究结果表明,高质量发展情景下的参数组合有利于改善海域承载力。在该情景下,通过对一系列决策参数(人口增长率、GDP增长率、海洋产业产值增长率、工业产值增长率)的调整,青岛沿海海域的资源环境状况改善,人口数和经济总量均提高,这一变化更利于青岛城市海洋经济的可持续健康发展。在实际工作中,要实现上述决策参数同步优化推动,不可能仅仅依赖于单一管理部门,而且从产业自身角度而言,追求经济利益是其根本追求,故如何促使其在合理追求经济利益的同时,注重海洋生态资源环境的养护和产业生态化体系的创建,终究离不开跨部门行政管理力量的介入和引导。因此,建议建立不同层级协调组织机制以规划和引导高质量发展, 高效协商生态环境养护、资源共享、节能减排、基础设施配套等下一级组织难以完成的工作。
| [1] |
谭映宇, 海洋资源, 生态和环境承载力研究及其在渤海湾的应用[D]. 青岛: 中国海洋大学, 2010. Tan Y Y, Carrying Capacity of Marine Resources, Ecology and Environment, and Its Application in Bohai Bay Rim[D]. Qingdao: Ocean University of China, 2010. (  0) 0) |
| [2] |
钟舜彬, 何均琳. 东海近海海域承载力评价研究[J]. 厦门理工学院学报, 2016, 24(6): 39-45. Zhong S B, He J L. Evaluation of carrying capacity in the East China Sea[J]. Journal of Xiamen University of Technology, 2016, 24(6): 39-45. DOI:10.3969/j.issn.1673-4432.2016.06.008 (  0) 0) |
| [3] |
林秀春, 刘睿. 莆田市近海海域生态环境承载力评价[J]. 莆田学院学报, 2019, 26(2): 94-99. Lin X C, Liu R. Evaluation on environmental carrying capacity of offshore area of Putian[J]. Journal of Putian University, 2019, 26(2): 94-99. DOI:10.3969/j.issn.1672-4143.2019.02.022 (  0) 0) |
| [4] |
余璇, 胡求光. 中国海域承载力空间差异及其收敛性分析[J]. 海洋开发与管理, 2020, 37(7): 23-32. Yu X, Hu Q G. Analysis of spacial difference and its convergence of China's marine carrying capacity[J]. Ocean Development and Management, 2020, 37(7): 23-32. (  0) 0) |
| [5] |
狄乾斌, 王萌, 孟雪. 海洋产业结构与海域承载力的匹配关系探讨——以辽宁省为例[J]. 海洋开发与管理, 2016, 33(4): 14-18. Di Q B, Wang M, Meng X. On the matching relationship between marine industrial structure and sea area carrying capacity: Take Liaoning Province as an example[J]. Ocean Development and Management, 2016, 33(4): 14-18. DOI:10.3969/j.issn.1005-9857.2016.04.003 (  0) 0) |
| [6] |
狄乾斌, 吕东晖. 我国海域承载力与海洋经济效益测度及其响应关系探讨[J]. 生态经济, 2019, 35(12): 126-133+169. Di Q B, Liu D H. Research on measurements and response relationship between carrying capacity of marine region and marine economic benefits in China[J]. Ecological Economy, 2019, 35(12): 126-133+169. (  0) 0) |
| [7] |
Han Z L, Qian-Bin D I, Liu K. Research on the theories and assessment method of carrying capacity of marine region[J]. Areal Research and Development, 2006, 25(1): 1-5. DOI:10.3969/j.issn.1003-2363.2006.01.001 (  0) 0) |
| [8] |
胡典, 福州市资源环境承载力评价及系统动力学仿真研究[D]. 福州: 福建农林大学, 2020. Hu D, Evaluation of Resources and Rnvironment Carrying Capacity and System Dynamics Simulation in Fuzhou City[D]. Fuzhou: Fujian Agriculture and Forestry University, 2020. (  0) 0) |
| [9] |
叶文祯, 福建省县域单元海域承载力评价研究[D]. 福州: 福建师范大学, 2014. Ye W Z, Assessment on the Carrying Capacity of Fujian Province Offshore[D]. Fuzhou: Fujian Normal University, 2014. (  0) 0) |
| [10] |
高金田, 刘雪莹, 李京梅. 广西北部湾海洋环境承载力预测及政策设计[J]. 中国海洋经济, 2016(2): 182-197. Gao J T, Liu X Y, Li J M. Prediction and policy design of marine environmental carrying capacity in Beibu Gulf of Guangxi[J]. Marine Economy of China, 2016(2): 182-197. (  0) 0) |
| [11] |
Turcotte D L. Self-organized complexity in geomorphology: Observations and models[J]. Geomorphology, 2007, 91(3-4): 302-310. DOI:10.1016/j.geomorph.2007.04.016 (  0) 0) |
| [12] |
蒋甜, 陈端吕. 基于DEM的河网水系分形特征研究——以常德市桃源县为例[J]. 中国农学通报, 2013, 29(2): 166-171. Jiang T, Chen D L. Fractal geometry analysis of river system based on DEM: An example of Taoyuan County, Changde City[J]. Chinese Agricultural Science Bulletin, 2013, 29(2): 166-171. DOI:10.3969/j.issn.1000-6850.2013.02.029 (  0) 0) |
| [13] |
任娟, 杨武年, 许娟. 基于GIS与DEM的岷江上游流域水系分维值计算[J]. 地理空间信息, 2015, 13(1): 77-79. Ren J, Yang W N, Xu J. Fractal dimension calculation of drainage system in the upper reaches of Minjiang River Based on GIS and DEM[J]. Geospatial Information, 2015, 13(1): 77-79. (  0) 0) |
| [14] |
姜秋香, 董鹤, 付强, 等. 基于SD模型的城市水资源承载力动态仿真-以佳木斯市为例[J]. 南水北调与水利科技, 2015, 13(5): 827-831. Jiang Q X, Dong H, Fu Q, et al. Dynamic simulation of urban water resources carrying capacity based on system dynamic model a case study in Jiamusi City[J]. South-to-North Water Transfers and Water Science & Technology, 2015, 13(5): 827-831. (  0) 0) |
| [15] |
陈传美, 郑垂勇, 马彩霞. 郑州市土地承载力系统动力学研究[J]. 河海大学学报(自然科学版), 1999(1): 56-59. Chen C M, Zheng C M, Ma C X. System dynamics for Zhengzhou land resource bearing capacity[J]. Journal of Hohai University (Natural Sciences), 1999(1): 56-59. (  0) 0) |
| [16] |
冷红, 郭士元. 系统动力学方法在城市总体规划中的应用[J]. 哈尔滨建筑大学学报, 2001, 34(4): 100-104. Long H, Guo S Y. Application of system dynamics to city planning[J]. Journal of Harbin Jianzhu University of C. E. & Architecture, 2001, 34(4): 100-104. (  0) 0) |
| [17] |
陈威, 周铖. 基于系统动力学仿真模拟评价武汉市水资源承载力[J]. 中国工程科学, 2014, 16(3): 103-107. Chen W, Zhou C. Evaluation of water rsources carrying capacity in Wuhan based on system dynamics simulation[J]. Engineering Sciences of China, 2014, 16(3): 103-107. (  0) 0) |
| [18] |
王翠, 杨广, 何新林, 等. 基于系统动力学的水资源承载力研究[J]. 中国农村水利水电, 2016(9): 212-215+220. Wang C, Yang G, He X L, et al. Research on water resources carrying capacity based on system dynamics[J]. China Rural Water and Hydropower, 2016(9): 212-215+220. (  0) 0) |
| [19] |
王钦, 陈东明. 基于SD的新乡市生物医药产业竞争力仿真及评价[J]. 营销界, 2021(15): 5-6. Wang Q, Chen D M. Simulation and evaluation of Xinxiang biomedical industry competitiveness based on SD[J]. Market Survey, 2021(15): 5-6. (  0) 0) |
| [20] |
陈威, 周铖. 武汉市水资源承载力动态评价模型的构建及其应用[J]. 水电能源科学, 2014, 32(7): 48-51+43. Chen W, Zhou C. Construction and application of dynamic evaluation model of water resources carrying capacity in Wuhan City[J]. Water Resources and Power, 2014, 32(7): 48-51+43. (  0) 0) |
| [21] |
姜红, 刘俐娜. 新旧动能转换在海洋经济发展质量中的作用评析——以青岛市为例[J]. 海洋湖沼通报, 2021, 43(3): 159-166. Jiang H, Liu L N. Study on the conversion of new and old marine economic kinetic energy: Take Qingdao for example[J]. Transactions of Oceanology and Limnology, 2021, 43(3): 159-166. (  0) 0) |
| [22] |
靳超, 周劲风, 李耀初, 等. 基于系统动力学的海洋生态承载力研究——以惠州市为例[J]. 海洋环境科学, 2017, 36(4): 537-543. Jin C, Zhou J F, Li Y C, et al. Research on marine ecological carrying capacity based on system dynamics: A case study of Huizhou City[J]. Marine Environmental Science, 2017, 36(4): 537-543. (  0) 0) |
| [23] |
孙松, 张永山, 吴玉霖, 等. 胶州湾初级生产力周年变化[J]. 海洋与湖沼, 2005, 36(6): 481-486. Sun S, Zhang Y S, Wu Y L, et al. Annual variation of primary productivity in Jiaozhou Bay[J]. Oceanologia et Limnologia Sinica, 2005, 36(6): 481-486. (  0) 0) |
| [24] |
孙晓霞, 孙松, 张永山, 等. 胶州湾叶绿素a及初级生产力的长期变化[J]. 海洋与湖沼, 2011, 42(5): 654-661. Sun X X, Sun S, Zhang Y S, et al. Long-term changes of Chlorophyll-a concentration and primary productivity in the Jiaozhou Bay[J]. Oceanologia et Limnologia Sinica, 2011, 42(5): 654-661. (  0) 0) |
| [25] |
麦尔哈巴·麦提尼亚孜, 瓦哈甫·哈力克. 基于SD模型的吐鲁番地区地下水资源承载力理论研究[J]. 中国农村水利水电, 2015(8): 105-109. Matniyaz M, Halik W. Theoretical research on ground water resources carrying capacity based on SD model[J]. China Rural Water and Hydropower, 2015(8): 105-109. (  0) 0) |
| [26] |
莫际仙, 王亚静, 毕于运, 等. 基于SD模型的诸城市农业结构仿真优化研究[J]. 中国农业资源与区划, 2019, 40(11): 146-157. Mo J X, Wang Y J, Bi Y Y, et al. Simulation and optimization of agricultural structure in zhucheng based on system dynamics[J]. Journal of China Agricultural Resources and Regional Planning, 2019, 40(11): 146-157. (  0) 0) |
| [27] |
Hassanzadeh E, Zarghami M, Hassanzadeh Y. Determining the main factors in declining the Urmia Lake level by using system dynamics modeling[J]. Water Resources Management, 2012, 26(1): 129-145. (  0) 0) |
| [28] |
高雅. 基于系统动力学模型的闽三角城市群资源环境承载力研究[D]. 厦门: 厦门大学, 2018. Gao Y. Study on the Resource and Environment Carrying Capacity of Urban Agglomeration in the Fujian River Deltas Based on the System Dynamics Model[D]. Xiamen: Xiamen University, 2018. (  0) 0) |
| [29] |
马爱锄. 西北开发资源环境承载力研究[D]. 杨凌: 西北农林科技大学, 2003. Ma A C. Research of Carrying Capacity on Resource and Environment in the Campaigns of Development of Northwest China[D]. Yangling: Northwest Agriculture & Forestry University, 2003. (  0) 0) |
| [30] |
郭建龙, 陈艳, 吴利丰. 北京冬奥会期间的空气质量预测[J]. 数学的实践与认识, 2021, 51(17): 86-101. Guo J L, Chen Y, Wu L F. Air Quality forecast during Beijing Winter Olympics[J]. Mathematics in Practice and Theory, 2021, 51(17): 86-101. (  0) 0) |
| [31] |
吴永强, 李明凯, 唐中楠, 等. 基于动态灰色模型群的衡水市居民年用水量预测[J]. 环境工程技术学报, 2021(8): 1-13. Wu Y Q, Li M K, Tang Z N, et al. Projection of residential water consumption in Hengshui City based on dynamic gray model groups[J]. Journal of Environmental Engineering Technology, 2021(8): 1-13. (  0) 0) |
| [32] |
叶文祯. 福建省县域单元海域承载力评价研究[J]. 科技传播, 2014, 6(8): 90-91+67. Ye W Z. Assessment on the carrying capacity of Fujian Province off shore[J]. Public Communication of Science & Technology, 2014, 6(8): 90-91+67. (  0) 0) |
| [33] |
李兵, 李佳林, 孙兴. 基于多元回归分析的青岛市"十四五"人口预测[J]. 中华建设, 2020(12): 66-67. Li B, Li J L, Sun X. Population forecast of Qingdao during the 14th Five-year Plan based on multiple regression analysis[J]. The Construction of China, 2020(12): 66-67. (  0) 0) |
| [34] |
青岛市环保局. 青岛市环境保护局关于印发青岛市城市环境总体规划(2016—2030年)的通知[EB/OL]. http://www.qingdao.gov.cn/n172/n24624151/n24628355/n24628369/n24628383/180423171619664772.html, 2018-04-08. Qingdao Environmental Protection Bureau. Notice of Qingdao Environmental Protection Bureau on the issuance of Qingdao Urban Environment Master Plan (2016—2030)[EB/OL]. http://www.qingdao.gov.cn/n172/n24624151/n24628355/n24628369/n24628383/180423171619664772.html, 2018-04-08. (  0) 0) |
2. College of Marine Life Science, Ocean University of China, Qingdao 266003, China;
3. College of Fisheries, Ocean University of China, Qingdao 266003, China
 2023, Vol. 53
2023, Vol. 53


