近年来,随着工业化进程的不断加速,能源消耗越来越大。人类开采能源的脚步已经由陆地转到海洋,甚至是深海海域。经探查发现,海洋石油资源量与海洋天然气资源量分别占世界待发现资源量的47%与46%[1]。作为海洋资源的运输媒介,海底管道在油气资源开采过程中的重要性不言而喻。因此,海底管道的研究开发,对海洋资源的开采运输具有十分重要的意义。
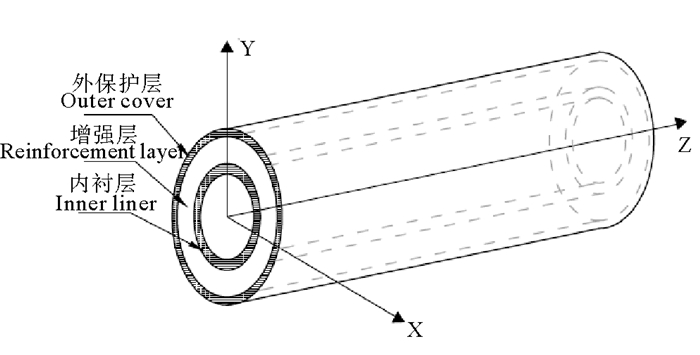
粘结型玻纤增强复合柔性管是一种新型热塑性复合增强管(RTP)[2],管体结构一般由三部分组成:内衬层、增强层与外保护层,如图 1所示。层与层之间通过挤压粘结,没有相互滑动,且各层都具有相应的承载保护功能。内衬层是与管道运输介质直接接触的部分,海水、石油等都有较强的腐蚀性,因此内衬层必须具有较强的防腐蚀性能、抗老化性能,同时还要能够防渗透防磨损。该层多由热塑性树脂基体或热固性基体加热定型而成,基体材料主要有环氧、聚乙烯、聚酰胺等。管道中间增强层是整个管道受力的主要承载构件,由纤维层按特定的角度在内衬层上缠绕铺设而成,且在缠绕过程中必须施加一定的预紧力,以保证每层纤维层紧密粘结在一起,最终形成中间增强层。每层纤维层由纤维与基体材料构成,常用纤维材料有玻璃纤维、碳纤维等,基体多采用高密度聚乙烯(HDPE)。管道的外保护层是与海底外部环境直接接触的部分,不仅需要一定的防腐蚀性、抗磨损性,还需要一定的刚度以保证管道内部结构的稳定。外保护层的材料一般与内衬层材料相同。
|
图 1 粘结型玻纤增强柔性管示意图 Fig. 1 Bonded glass-fiber RTP |
目前,国内外已有不少专家学者对复合管道的力学性能进行了理论研究分析。余彬彬[3]对纤维缠绕增强复合管的非线性屈曲理论进行了研究,基于非线性环理论,建立了管道在弯曲、弯曲和轴向拉力组合载荷作用下的屈曲理论模型,最后进行数值求解,并将计算结果与实验值对比,得到了较好的验证。张越等[4]采用弹性理论,考虑管道的内部工作压力及层间粘结压力,建立了复合管道的力学模型,推导出各层界面上法向应力的方程组。Chouchaoui等[5]将复合管道简化成各向异性板材组成的结构,同时对内压、外压、拉伸、扭转等载荷作用下的多层管道进行了应力求解。Xia[6]基于经典层合板理论,对不同载荷作用下的纤维缠绕管进行了理论求解分析,并对不同缠绕角度时的管道力学性能进行了对比,得出了力学性能较优的纤维缠绕角度。Xing等[7]对承受轴向拉力、内压、外压载荷共同作用下的纤维缠绕管进行了变形与应力研究分析,并将研究结果与有限元计算结果进行了对比,虽然结果验证具有较好的一致性,但是其研究忽略了切向应力、应变的影响。
由于纤维增强柔性管的造价昂贵,制造技术基本被国外一些公司垄断,所以对其实验研究公开资料较少。王诺思等[8]采用纤维增强管做了一系列力学实验,模拟了管道在弯曲、外压、内压等载荷作用下的屈曲失稳现象,为理论研究与数值模拟提供了实验依据。P.Mertiny[9]利用管道内部压力跟轴向力,进行了双轴向拉伸实验,研究了纤维多角度缠绕与单一角度缠绕对载荷承载能力的影响,结果发现多角度缠绕的纤维管具有较高的载荷承载能力。还有不少研究人员借助有限元分析软件对该类型管道进行了数值模拟研究。袁帅等[10]采用嵌入式建模方式,建立三维复合管道模型,对弯曲与外压组合荷载下的管道进行了数值模拟,并分别对不同加载路径进行了分析计算。孟祥剑等[11]基于不同的等效简化模型,对比研究了玻纤增强柔性管在轴向拉力、弯曲荷载以及内压荷载下的力学性能,并将计算结果与实验数据进行对比分析,完成等效模型的优选。Ashraf[12]采用数值模拟,对纤维复合管道在弯曲载荷下的力学性能进行了分析,得到与Rodriguez[13]类似的结论,在较大弯曲载荷下,复合材料容易发生基体材料失效。
本文主要针对粘结型玻纤增强复合柔性管(RTP),考虑结构内外层基体的影响,基于三维弹性力学理论与层合板理论,建立了RTP整体结构的数学理论模型,推导了管道各层径向位移的偏微分方程。随后考虑管道的边界条件与层间位移、应力关系,联合位移偏微分方程,求解得到管道各层的位移、应力等力学性能参数。并通过有限元数值模拟,计算了管道在内压载荷作用下位移、应力等参数,将计算结果与理论计算值进行对比,最终验证了理论模型的准确性。最后基于理论模型,在管道内衬层(外保护层)与增强层不同的相对厚度时,进一步研究了管体的变形、应力应变等响应参数。
1 理论模型研究 1.1 纤维层应力-应变关系与弹性系数本文研究对象为粘结型玻纤增强热塑性复合柔性管,主要特征是整体管道采用多层结构粘结组成,一般有内衬层(Inner liner)、增强层(TCP laminate)、外保护层(Outer cover),如图 1所示。内外层由各向同性材料高密度聚乙烯(HDPE)构成,其主要材料参数有弹性模量Em,泊松比μm和剪切弹性模量
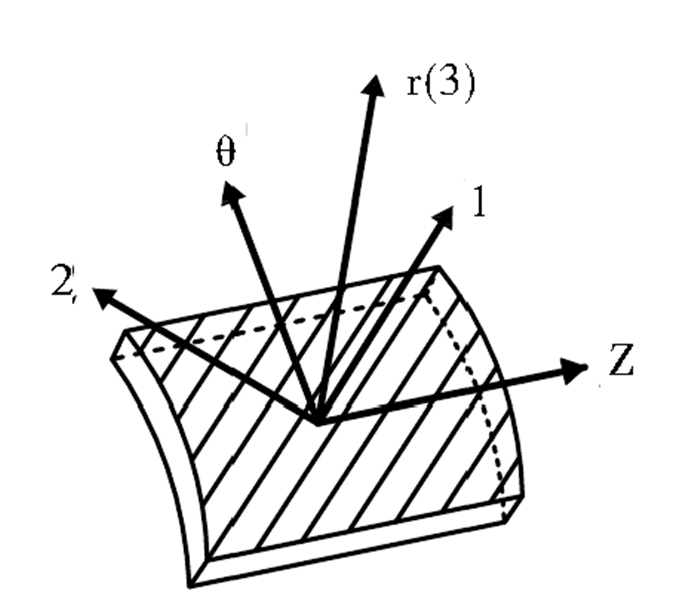
中间增强层是由多层玻璃纤维与HDPE混合的纤维层缠绕铺设而成,如图 2所示。增强层结构构成复杂,从宏观上看,增强层可以看成是均匀的各向异性材料。在此定义复合材料纤维层局部坐标系(1-2-3),1表示纤维的布置方向,2表示垂直于纤维的方向,3表示垂直于纤维铺层的方向。将纤维层视为横观各向同性材料,其应力-应变关系如公式(1)所示,[Sij]k表示局部坐标系下纤维层的柔度矩阵。
| $ {\left[ {\begin{array}{*{20}{l}} {{\varepsilon _1}}\\ {{\varepsilon _2}}\\ {{\varepsilon _3}}\\ {{\gamma _{23}}}\\ {{\gamma _{13}}}\\ {{\gamma _{12}}} \end{array}} \right]^k} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{S}}_{11}}}&{{\mathit{\boldsymbol{S}}_{12}}}&{{\mathit{\boldsymbol{S}}_{13}}}&0&0&0\\ {{\mathit{\boldsymbol{S}}_{12}}}&{{\mathit{\boldsymbol{S}}_{22}}}&{{\mathit{\boldsymbol{S}}_{23}}}&0&0&0\\ {{\mathit{\boldsymbol{S}}_{13}}}&{{\mathit{\boldsymbol{S}}_{23}}}&{{\mathit{\boldsymbol{S}}_{33}}}&0&0&0\\ 0&0&0&{{\mathit{\boldsymbol{S}}_{44}}}&0&0\\ 0&0&0&0&{{\mathit{\boldsymbol{S}}_{55}}}&0\\ 0&0&0&0&0&{{\mathit{\boldsymbol{S}}_{66}}} \end{array}} \right]^k} \times {\left[ {\begin{array}{*{20}{c}} {{\sigma _1}}\\ {{\sigma _2}}\\ {{\sigma _3}}\\ {{\tau _{23}}}\\ {{\tau _{13}}}\\ {{\tau _{12}}} \end{array}} \right]^k}。$ | (1) |
|
图 2 局部坐标系与整体坐标系之间的转换 Fig. 2 Transformation between local coordinate and global coordinate |
其中:
下式(2)将纤维层的柔度矩阵转换成刚度矩阵:
| $ [{\mathit{\boldsymbol{C}}_{ij}}] = {[{\mathit{\boldsymbol{S}}_{ij}}]^{ - 1}}。$ | (2) |
如图 2所示,在设计管道时,纤维层会按照一定的角度进行缠绕,因此在整体坐标系中,纤维层应力-应变关系也要按纤维缠绕角度进行相应的坐标转换。从而相应的刚度矩阵也要进行对应的坐标转换,如式(3)所示:
| $ [\overline {{\mathit{\boldsymbol{C}}_{ij}}} ] = {[{\mathit{\boldsymbol{T}}_\sigma }]^{ - 1}}[{\mathit{\boldsymbol{C}}_{ij}}][{\mathit{\boldsymbol{T}}_\varepsilon }]。$ | (3) |
式中[Tσ],[Tε]分别是单层材料应力与应变的坐标转换矩阵,具体表达如式(4a)、(4b)所示,其中,m=cosθ,n=sinθ, θ表示纤维缠绕方向与管道轴向之间的夹角,如图 2所示。
| $ [{\mathit{\boldsymbol{T}}_\sigma }] = \left[ {\begin{array}{*{20}{c}} {{m^2}}&{{n^2}}&0&0&0&{2mn}\\ {{n^2}}&{{m^2}}&0&0&0&{ - 2mn}\\ 0&0&0&0&0&0\\ 0&0&0&m&{ - n}&0\\ 0&0&0&n&m&0\\ { - mn}&{mn}&0&0&0&{{m^2} - {n^2}} \end{array}} \right]; $ | (4a) |
| $ [{\mathit{\boldsymbol{T}}_\varepsilon }] = \left[ {\begin{array}{*{20}{c}} {{m^2}}&{{n^2}}&0&0&0&{mn}\\ {{n^2}}&{{m^2}}&0&0&0&{ - mn}\\ 0&0&0&0&0&0\\ 0&0&0&m&{ - n}&0\\ 0&0&0&n&m&0\\ { - 2mn}&{2mn}&0&0&0&{{m^2} - {n^2}} \end{array}} \right]。$ | (4b) |
|
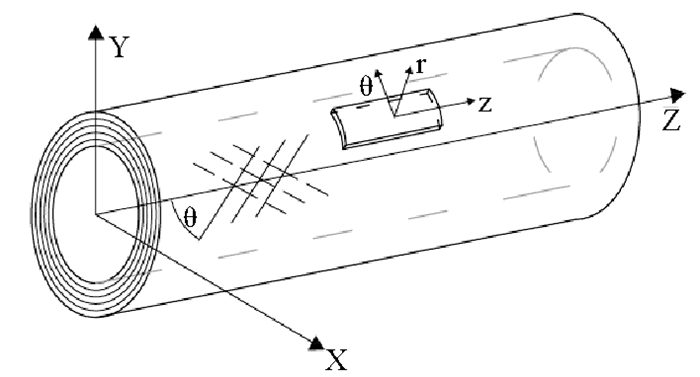
图 3 玻璃纤维复合材料增强层 Fig. 3 Reinforced layers in the RTP structure |
经过上面一系列的坐标转换,在整体坐标系中,不同纤维层(k)的应力-应变关系如公式(5)所示:
| $ {\left[ {\begin{array}{*{20}{c}} {{\sigma _z}}\\ {{\sigma _\theta }}\\ {{\sigma _r}}\\ {{\tau _{\theta r}}}\\ {{\tau _{zr}}}\\ {{\tau _{z\theta }}} \end{array}} \right]^k} = {\left[ {\begin{array}{*{20}{c}} {\overline {{C_{11}}} }&{\overline {{C_{12}}} }&{\overline {{C_{13}}} }&0&0&0\\ {\overline {{C_{12}}} }&{\overline {{C_{22}}} }&{\overline {{C_{23}}} }&0&0&0\\ {\overline {{C_{13}}} }&{\overline {{C_{23}}} }&{\overline {{C_{33}}} }&0&0&0\\ 0&0&0&{\overline {{C_{44}}} }&0&0\\ 0&0&0&0&{\overline {{C_{44}}} }&0\\ 0&0&0&0&0&{\overline {{C_{66}}} } \end{array}} \right]^k} \times {\left[ {\begin{array}{*{20}{c}} {{\sigma _z}}\\ {{\sigma _\theta }}\\ {{\sigma _r}}\\ {{\tau _{\theta r}}}\\ {{\tau _{zr}}}\\ {{\tau _{z\theta }}} \end{array}} \right]^k}。$ | (5) |
定义柔性管道的整体柱坐标系(z-θ-r),其中z表示管道的轴向方向,θ表示管道的环向方向,r表示管道的径向方向。假设整体管道由n层结构组成,第一层为管道内衬层,第n层为管道的外保护层,中间增强层由(n-2)层复合纤维层缠绕叠加而成。对每一层(k=1, 2, …, n)而言,结构的变形量与应变可以简化成如下的几何关系式:
| $ \begin{array}{*{20}{c}} {\varepsilon _r^{(k)} = \frac{{{\rm{d}}u_r^{(k)}}}{{{\rm{d}}r}},\varepsilon _\theta ^{(k)} = \frac{{u_r^{(k)}}}{r},\varepsilon _z^{(k)} = \frac{{{\rm{d}}u_z^{(k)}}}{{{\rm{d}}z}} = {\varepsilon _0},}\\ {\gamma _{zr}^{(k)} = 0,\gamma _{\theta r}^{(k)} = \frac{{{\rm{d}}u_\theta ^{(k)}}}{{{\rm{d}}r}} - \frac{{u_\theta ^{(k)}}}{r},\gamma _{z\theta }^{(k)} = \frac{{{\rm{d}}u_\theta ^{(k)}}}{{{\rm{d}}z}} = {\varepsilon _1}r}。\end{array} $ | (6) |
上式中将管道沿轴向方向(z)的位移看成常量,因此其向应变也为未知常数ε0。式中未知量ε为单位长度的管道沿环向方向的扭转角度。
忽略剪切应力τθr,τzr的影响,柱坐标系下结构的平衡微分方程可以简化为:
| $ \frac{{{\rm{d}}\sigma _r^{(k)}}}{{{\rm{d}}r}} + \frac{{\sigma _r^{(k)} - \sigma _\theta ^{(k)}}}{r} = 0。$ | (7) |
将应力-应变关系式(5)带入公式(7),同时考虑变形与应变关系式(6),从而得到关于结构径向变形的偏微分方程:
| $ \frac{{{{\rm{d}}^2}u_r^{(k)}}}{{{\rm{d}}{r^2}}} + \frac{1}{r}{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\rm{d}}u_r^{(k)}}}{{{\rm{d}}r}} - \frac{{u_r^{(k)}}}{{{r^2}}}{\beta ^2}(k) = \frac{{{\alpha ^{(k)}}{\varepsilon _0}}}{r} + \delta _{\varepsilon 1}^{(k)}。$ | (8) |
式中:
对各向同性的管道内外层而言,通过求解方程式(8),可以得到式(9a):
| $ u_r^{(k)} = {d^{(k)}}{r_k} + {e^{(k)}}r_k^{ - 1}(k = 1,n)。$ | (9a) |
对各向异性的中间各纤维层而言,求解方程式(8),可以得到式(9b):
| $ \begin{array}{l} \begin{array}{*{20}{c}} {u_r^{(k)} = {d^{(k)}}r_k^{\beta (k)} + {e^{(k)}}r_k^{ - \beta (k)} + \alpha _1^{(k)}{\varepsilon _0}{r_k} + }\\ {\alpha _2^{(k)}{\varepsilon _1}{r_k}(k = 2,3 \cdots n - 1),} \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ \alpha _1^{(k)} = \frac{{{\alpha ^{(k)}}}}{{1 - \beta {{(k)}^2}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha _2^{(k)} = \frac{{{\delta ^{(k)}}}}{{4 - \beta {{(k)}^2}}}。\end{array} $ | (9b) |
上述(9)式中的d(k),e(k)均为积分常数。
1.3 边界条件从上面的应力-应变关系,变形与应力关系等式中可以推导出复合管道径向位移。最终的径向位移由式中的未知量d(k),e(k),ε0,ε1,决定,因此如何求得这些未知量,成为下文需要解决的问题。
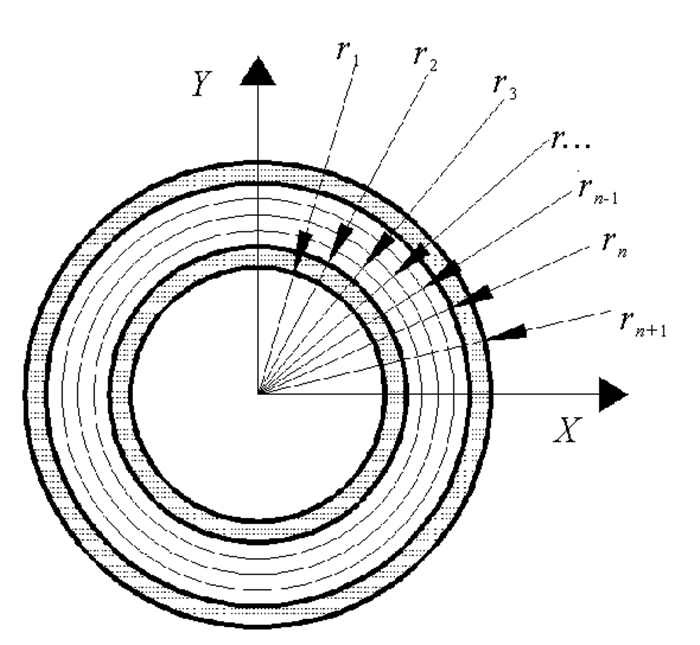
假设一个n层的管道,其横截面示意图如图 4所示。第层为内衬层,第层为外保护层,中间第二层到第(n-1)层为各纤维层组成的中间增强层。管道各层半径如下图所示,其中r1为管道内半径,rn+1为管道外半径。
|
图 4 管道横截面示意图 Fig. 4 Cross-section of RTP |
根据应力条件,假设管道最内层所受压力为p1,最外层所受压力为pn,因此管道内外层所受应力可以表示成公式(10):
| $ \sigma _r^{(1)}({r_1}) = - {p_1},\sigma _r^{(n)}({r_{n + 1}}) = - {p_n}。$ | (10) |
由于管道各层之间粘结在一起,层与层之间没有互相滑移,因此可以假设各层之间的径向应力与径向位移相等,关系式如式(11)所示:
| $ \begin{array}{*{20}{l}} {\sigma _r^{(k - 1)}({r_k}) = \sigma _r^{(k)}({r_k})}&{(k = 2 \cdots \cdots n),}\\ {u_r^{(k - 1)}({r_k}) = u_r^{(k)}({r_k})}&{(k = 2 \cdots \cdots n)}。\end{array} $ | (11) |
另外,根据管道两端固定的边界条件,有下述积分公式:
| $ 2\pi \sum\nolimits_{k = 1}^n {\int_{rk}^{rk + 1} {\sigma _z^{(k)}({r_k}){r_k}dr = \pi r_1^2{p_1} - \pi r_n^2{p_n} + {f_z}} } ; $ | (12a) |
| $ 2\pi \sum\nolimits_{k = 1}^n {\int_{rk}^{rk + 1} {\tau _{z\theta }^{(k)}({r_k})r_k^2{\rm{d}}r = M} } 。$ | (12b) |
式中:fz表示管道两端的端部轴向拉(压)力;M表示管道的扭转弯矩。
根据上述关系式,建立总层数为6层的粘结型玻纤增强复合柔性管的理论模型。将位移函数(9),联合边界条件(10—12),最终可以推导出式(13)。根据式(13),一共求得14个未知量d(k),e(k)(k=1……6)与ε0,ε1。再根据求得的未知量,带入到公式(9)、(6)、(5)可以分别计算出管道在不同载荷作用下的位移(u),应力(σ),应变(ε)等结构响应。
| $ \begin{array}{l} [{\mathit{\boldsymbol{f}}_{ij}}] = \left[ {\begin{array}{*{20}{c}} {{d^{(1)}}}\\ {{d^{(2)}}}\\ {{d^{(3)}}}\\ {{d^{(4)}}}\\ {{d^{(5)}}}\\ {{e^{(6)}}}\\ {{e^{(1)}}}\\ {{e^{(2)}}}\\ {{e^{(3)}}}\\ {{e^{(4)}}}\\ {{e^{(5)}}}\\ {{e^{(6)}}}\\ {{\varepsilon _0}}\\ {{\varepsilon _1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - {p_0}}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ { - {p_n}}\\ {\frac{{r_1^2{p_0}}}{2} - \frac{{r_n^2{p_n}}}{{{M^2}}} + \frac{{{f_z}}}{{2\pi }}} \end{array}} \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1 \cdots 14;j = 1 \cdots 14。\end{array} $ | (13) |
式中[fij]为一个14×14的系数矩阵。
2 管道分析计算为了计算方便,本文选取层数为6层的两端固定的粘结型复合柔性管道进行分析。如图 4所示,管道内半径50 mm,外半径58 mm,且内外层厚度都为3 mm。管道中间增强层有4层纤维层,每层厚度为0.5 mm。内外层HDPE的弹性模量Em=953 MPa,泊松比μm=0.42。中间每层纤维层的各向弹性模量为E1=141.6 GPa,E2=10.7 GPa,E3=E2;剪切模量G12=3.88 GPa,G13=G23=G12;各向泊松比为μ12=0.268,μ23=0.495,μ13=μ12。中间四层纤维层选取铺设角度由内往外分别为[+55°/-55°/+55°/-55°]。
同时采用有限元软件ABAQUS,对该类型管道进行了数值模拟分析,并将结果与理论计算值进行比较。有限元模型长度为500 mm,单元采用六面体C3D8R单元。为了提高计算结果的准确性,管道模型在轴向方向划分100个网格单元,环向划分为80个单元,径向每0.5 mm一个单元,整个有限元模型一共由128 000个单元组成。Composite layup模块用来对增强层部分进行详细的建模,包括每层厚度,铺设角度大小等的设置。铺层方向都是纤维带以管道轴向方向为基础,分别向两边偏转一定的角度,具体如图 2所示。管道两端采用刚性固定,与理论公式推导中假设的边界条件保持一致。图 5所示为结构模型在内压载荷作用下的应力云图与中间增强层的局部放大应力图。
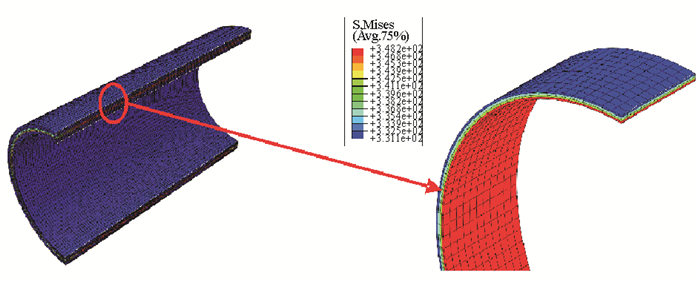
|
图 5 内压载荷作用下整体管道及增强层的应力云图 Fig. 5 Stress cloud diagram of RTP under inner pressure |
管道仅在内表面承受10 MPa的内压,不承受其它荷载。对该类型管道分别进行理论计算与数值模拟,对比分析其位移、应力响应,结果如图 6~7所示。图中的横坐标采用无量纲半径表示法,
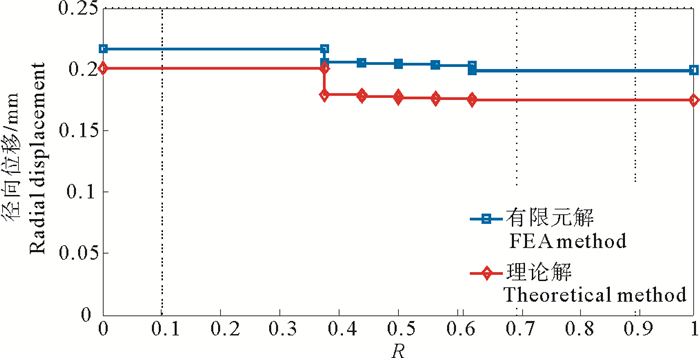
|
图 6 内压载荷作用下结构的位移变化比较 Fig. 6 Radial deformation of RTP under inner pressure |
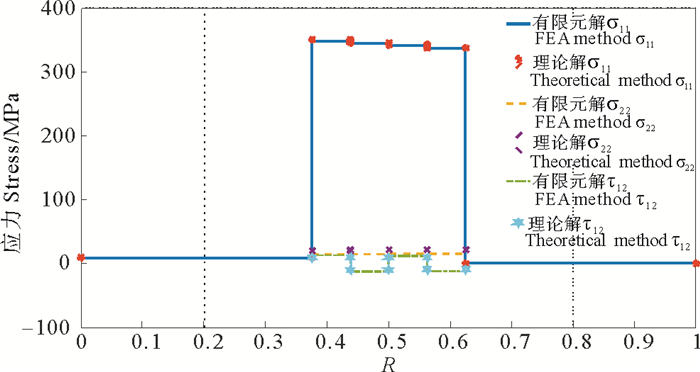
|
图 7 内压载荷作用下管道各层的应力对比 Fig. 7 Stresses of RTP under inner pressure |
中间增强层在数值模拟中得出的是沿着纤维方向的应力,而理论解给出的是管道整体坐标系(z-θ-r)下的应力。为方便进行对比分析,需将理论解的值进行坐标转换,表达成局部材料坐标系(1-2-3)下的应力。不同坐标系下的应力转换公式如(14)所示:
| $ {\left[ {\begin{array}{*{20}{c}} {{\sigma _1}}\\ {{\sigma _2}}\\ {{\sigma _3}}\\ {{\tau _{23}}}\\ {{\tau _{13}}}\\ {{\tau _{12}}} \end{array}} \right]^k} = {[{\mathit{\boldsymbol{T}}_\sigma }]^k} \times {\left[ {\begin{array}{*{20}{c}} {{\varepsilon _z}}\\ {{\varepsilon _\theta }}\\ {{\varepsilon _r}}\\ {{\gamma _{\theta r}}}\\ {{\gamma _{zr}}}\\ {{\gamma _{z\theta }}} \end{array}} \right]^k}。$ | (14) |
图 7展示了管道各层的应力变化趋势,包括内外层的应力、纤维层各个方向应力。图中在0 < R < 0.375或0.675 < R < 1时,为内衬层与外保护层的应力对比;在0.375 < R < 0.675区间内,为中间纤维层各个不同方向的应力对比。由于管道的中间增强层为主要载荷承载部分,因此从图中可以明显看出,管道内外层所受的应力远小于纤维层沿着纤维方向的应力。另外随着增强层沿着径向增厚,纤维方向所受的应力也逐渐减小,这种趋势与增强层结构位移的变化趋势相同。图中还可以看出,增强层沿着垂直于纤维方向的应力与剪切方向的应力都比较小。剪切方向的应力有明显的正负区别,这是因为在增强层中,第一纤维层跟第三纤维层是同样的铺设角度,第二层跟第四层是相反的铺设角,且铺层方向对称于管道轴向,所以使得管道的剪切应力有正负之分。总体上看,不论哪个方向的应力,有限元计算结果都与理论值有较好的吻合,因此可以验证理论模型的正确性。
2.2 内衬层(外保护层)与增强层相对厚度对管道力学性能的影响本文研究的粘结型柔性管道为三层结构,根据上面的研究结论可以得出,中间增强层是结构受力的主要承载部件,内外层所受应力相对于增强层甚至可以忽略不计。但是在管道设计研究中,内外层的厚度选择一直是个不确定的问题,其厚度的大小对管道力学性能的影响有多大我们不得而知。因此,基于本文的理论模型,选取了不同的内外层厚度,对管道在内压荷载作用下的力学性能进行了深入研究。
为了使计算结果的表达更清晰,这里定义无量纲参数厚度比
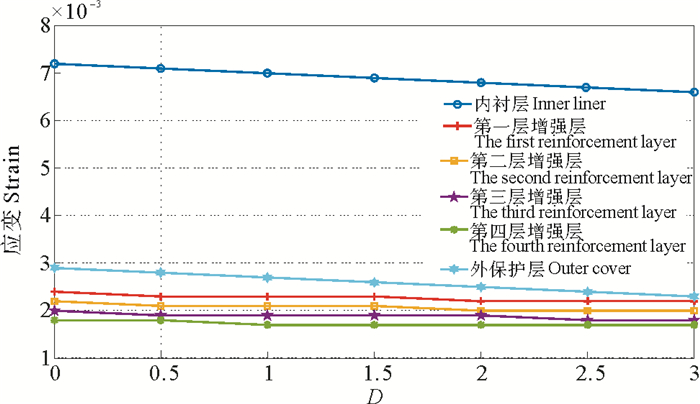
|
图 8 不同厚度比下管道每层的应变 Fig. 8 Strains of RTP with different thickness ratios |
从图 8中明显可以看出,管道内衬层的应变远大于其他各层的应变,这与上文中管道的位移、应力骤降的现象不谋而合。从图中还可以看出,随着厚度比的增加,管道内衬层与外保护层的应变下降较为明显,中间增强层的应变几乎没有变化。这是因为内外层为各向同性的基体材料,其弹性模量相对于增强层要小得多,因此在内压载荷作用下其应变的变化量较大。整体而言,内外层厚度的增加只对内外层本身的应变产生较大的影响,并不会对中间增强层的应变有多大的影响。
图 9~12分别显示了在不同厚度比下,纤维层不同方向应力的变化趋势,包括纤维方向的应力,垂直于纤维方向的应力,径向应力与剪切方向的应力。从图中可以看出,不同厚度比下,管道径向方向的应力与剪切方向的应力只有微小的变化,而在纤维方向与垂直于纤维方向的应力有明显的下降趋势。如图 9所示,在纤维方向的应力虽然下降较多,但是相对于没有内外层时候的应力大小而言,其整体下降幅度依旧很小。当厚度比从0变化到3,纤维方向的应力下降幅度不超过3%,因此内外层厚度对增强层纤维方向应力的影响基本可以忽略。图 10显示了增强层垂直于纤维方向的应力随厚度比变化的曲线。由于纤维层结构垂直于纤维方向的弹性模量较小,当厚度比从0到3时,该方向各层的应力均减少了12%左右。综上所述,管道的内外层厚度除了对垂直于纤维方向应力的影响较大,对其它方向应力的影响均较小。因此在设计粘结型玻纤增强柔性管的内外层厚度时,不要寄希望于增加内外层厚度给柔性管的力学性能带来较大的改善,而应重点考虑腐蚀、磨损等破坏对管道的影响,最终选择合适的内外层厚度。
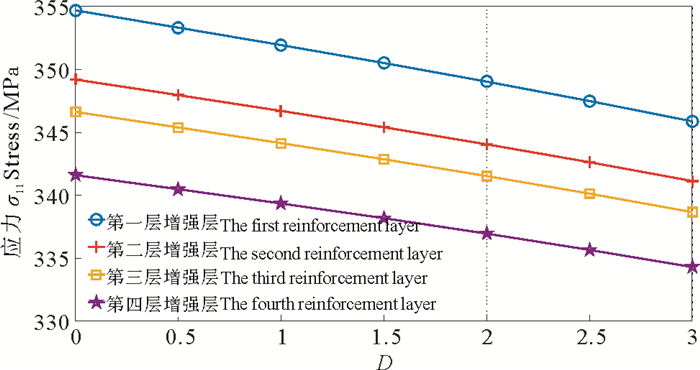
|
图 9 不同厚度比下纤维方向的应力 Fig. 9 σ11 of RTP with different thickness ratios |
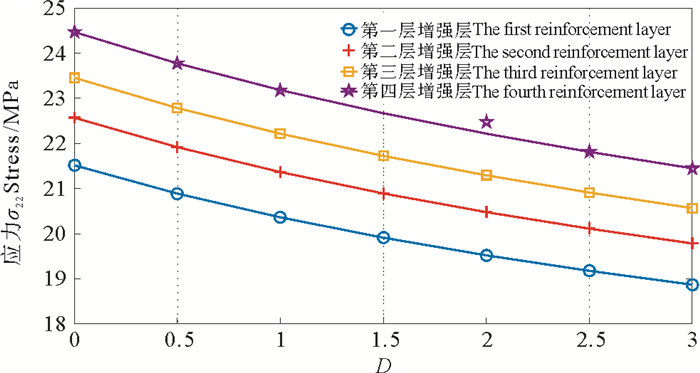
|
图 10 不同厚度比下垂直于纤维方向的应力 Fig. 10 σ22 of RTP with different thickness ratio |
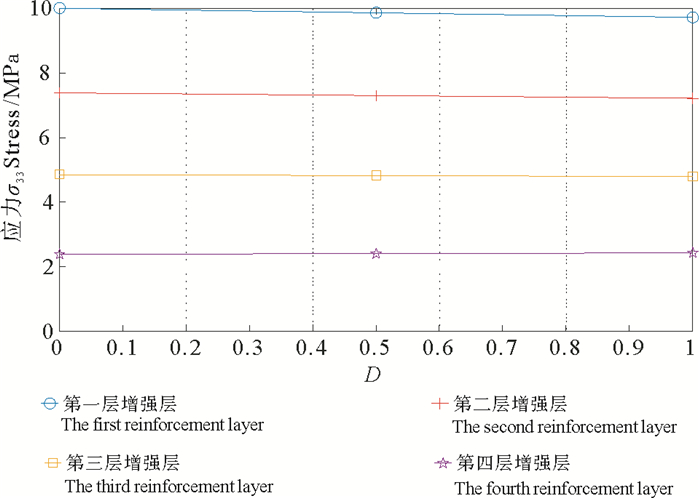
|
图 11 不同厚度比下径向方向的应力 Fig. 11 σ33 of RTP with different thickness ratios |
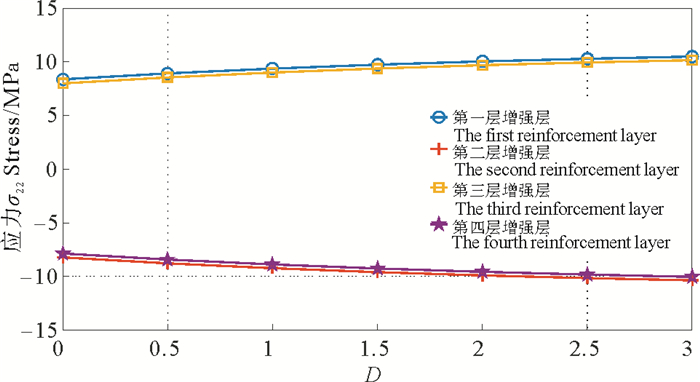
|
图 12 不同厚度比下剪切方向的应力 Fig. 12 τ12 of RTP with different thickness ratios |
本文主要采用三维弹性理论与复合材料层合板理论,基于一定的假设条件,考虑环向剪切应力的影响,结合管道的边界条件与各层之间变形、应力的相互关系,建立了海洋工程用粘结型玻纤增强复合柔性管的理论模型。在内压载荷作用下,对柔性管的理论力学模型进行了相关研究,分析了管体的变形与应力等响应。并利用有限元软件对该类型管道进行数值仿真计算,通过与理论计算值的对比,验证了理论模型的准确性。最后关于管道内衬层(外保护层)厚度与增强层厚度的相对比值对管体结构力学性能的影响做了进一步研究,可以得到以下一些结论:
(1) 柔性管在内压载荷作用下的径向位移从内向外逐渐减小,由于内衬层基体材料弹性模量较小,因此在内衬层到增强层过渡时,位移变化有较大的突降,所以在设计管道接头时,要充分考虑这方面的变化量,以免使得管道的密封性受损。
(2) 玻纤增强柔性管的主要承载部件是中间增强层,管道内外层不会承受较大的压力。增强层在纤维方向的应力远大于其他方向的应力,随着增强层从内向外扩展,纤维方向的应力也逐渐减小。
(3) 柔性管内外层的厚度对管道整体的力学性能不会有较大的影响,仅对垂直于纤维方向应力的影响较大。内衬层厚度0~6 mm,垂直于纤维方向的应力仅减小了10%左右。因此在设计管道内外层厚度时,应重点考虑腐蚀、磨损等破坏因素对管道的影响,从而选择合适的内外层厚度。
| [1] |
舟丹. 世界海洋油气资源分布[J]. 中外能源, 2017, 22(11): 55. Zhou Dan. Distribution of the world's offshore oil and gas resources[J]. Sino-Global Energy, 2017, 22(11): 55. (  0) 0) |
| [2] |
Det Norske Veritas. DNVGL-RP-119 Thermoplastic composite pipes[S]. Hovik, Norway: Det Norske Veritas Germanischer Lloyd, 2015.
(  0) 0) |
| [3] |
余彬彬.纤维缠绕增强复合管铺设中的非线性屈曲分析与研究[D].杭州: 浙江大学, 2013. Binbin Yu. Investigation on Nonlinear Buckling Mechanisms of Filament-Wound Fiber-Reinforced Composite Pipe During Installation[D]. Hangzhou: Zhejiang University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10335-1013147664.htm (  0) 0) |
| [4] |
张越, 樊新民, 孔德仁. 复合层合管力学模型的研究[J]. 南京理工大学学报, 1999(5): 446-449. Yue Zhang, Xinmin Fan, Deren Kong. Study on the mechanics model of multi-layered tube[J]. Journal of Nanjing University of Science and Technology, 1999(5): 446-449. DOI:10.3969/j.issn.1005-9830.1999.05.016 (  0) 0) |
| [5] |
Chouchaoui C S, Ochoa O O. Similitude study for a laminated cylindrical tube under tensile, torsion, bending, internal and external pressure. Part Ⅰ: Governing equations[J]. Composite Structures, 1999, 44(4): 221-229. DOI:10.1016/S0263-8223(98)00068-3
(  0) 0) |
| [6] |
Xia M, Takayanagi H, Kemmochi K. Analysis of multi-layered filament-wound composite pipes under internal pressure[J]. Composite Structures, 2001, 53(4): 483-491. DOI:10.1016/S0263-8223(01)00061-7
(  0) 0) |
| [7] |
Xing J, Geng P, Yang T. Stress and deformation of multiple winding angle hybrid filament-wound thick cylinder under axial loading and internal and external pressure[J]. Composite Structures, 2015, 131: 868-877. DOI:10.1016/j.compstruct.2015.05.036
(  0) 0) |
| [8] |
王诺思.纤维缠绕增强复合管外压及组合荷载下的屈曲性能研究[D].杭州: 浙江大学, 2013. Nuosi Wang. Investigation on Buckling and Collapse Mechanisms of Filament-Wound Fiber-Reinforced Composite Pipe Under External Pressure and Combined Load[D]. Hangzhou: Zhejiang University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10335-1013147643.htm (  0) 0) |
| [9] |
Kruijer M P, Warnet L L, Akkerman R. Analysis of the mechanical properties of a reinforced thermoplastic pipe (RTP)[J]. Composites Part A: Applied Science and Manufacturing, 2005, 36(2): 291-300. DOI:10.1016/S1359-835X(04)00168-X
(  0) 0) |
| [10] |
Bai Y, Yuan S, Tang J, et al. Behaviour of reinforced thermoplastic pipe under combined bending and external pressure[J]. Ships and Offshore Structures, 2015, 10(5): 575-586.
(  0) 0) |
| [11] |
孟祥剑, 王树青, 姚潞. 玻纤增强柔性管等效简化模型研究[J]. 海洋工程, 2017, 35(6): 71-83. Meng Xiangjian, Wang Shuqing, Yao Lu. Research on equivalent simplification model of glass fiber reinforced flexible pipes[J]. Ocean engineering, 2017, 35(6): 71-83. (  0) 0) |
| [12] |
Ashraf M A, Morozov E V, Shankar K. Flexure analysis of spoolable reinforced thermoplastic pipes for offshore oil and gas applications[J]. Journal of Reinforced Plastics and Composites, 2014, 33(6): 533-542. DOI:10.1177/0731684413491442
(  0) 0) |
| [13] |
Rodriguez D E, Ochoa O O. Flexural response of spoolable composite tubulars: An integrated experimental and computational assessment[J]. Composites Science and Technology, 2004, 64(13): 2075-2088.
(  0) 0) |
 2020, Vol. 50
2020, Vol. 50


