近年来极端波浪造成多起海洋事故,对海洋平台以及海洋船舶的安全构成极大威胁,而波浪聚焦是极端波浪的重要形成机理之一,因此对波浪聚焦的研究具有重要意义。波浪聚焦是指不同频率、不同方向的波浪在传播的过程中相互调制,使波能发生聚集,形成一个孤立的大波的过程。当波浪经过变水深区域时,如水底火山、海脊等,由于波浪折射作用波浪聚焦效果十分显著。早期对该问题主要通过射线理论进行研究[1],但由于射线理论忽略了波浪绕射与衍射作用,在焦散线附近无法精确求解。对此,Berkhoff[2]在1972年推导出二维缓坡方程,综合考虑了波浪折射和衍射现象,能显著模拟波浪聚焦效果,计算聚焦区域波高。基于上述基础,学者们针对不同地形的波浪聚焦问题开展了大量研究。
长波在海岛附近的聚焦问题,Yu和Zhang[3]、Zhang和Zhu[4]、傅丹娟等[5]针对不同的海岛简化模型,研究发现在一定的条件下,岛屿附近会发生波浪“俘获”现象,整个岛屿岸线都有较大波幅出现;Zhu和Harun[6]、Niu和Yu[7]研究了浅滩形状、浅滩尺寸以及浅滩淹没深度对浅滩附近波浪聚焦特性的影响;Longuet-Higgins[8]、Shaw和Neu[9]、熊梦婕等[10]对不同剖面海脊上俘获波的解析解进行了探讨;Berkhoff等[11]、Vincent和Briggs[12]等通过物理实验的方法对波浪通过浅滩后的波高变化进行了研究。但现阶段对于带凸起的不规则斜坡地形的波浪聚焦问题少有研究。Whalin[13]在1972年用物理实验的方法,在宽水槽中研究了凸起不规则斜坡地形上的波浪聚焦问题。但该实验是在水槽中开展,由于水槽两侧存在波浪反射现象,因此并不是单纯的波浪聚焦问题。本文在Whalin的实验基础上采用非静压模型对凸起不规则斜坡地形上的波浪聚焦特性进行了研究。
1 模型简介及验证本文选用由Zijlema等[14]建立的浅水非静压数值模型SWASH(Simulating Waves till SHore)对波浪聚焦问题进行研究。该模型同时适用于波浪和水流条件,主要用于模拟沿岸地区的波浪和水流运动,是一个用于模拟二维或三维条件下的非静压、自由表面的旋流和波流输运现象的数值工具。
1.1 控制方程及边界条件SWASH模型的控制方程采用的是常密度不可压缩流体三维雷诺平均下的Navier-Stokes方程,在笛卡尔直角坐标系(原点在静水面上,z轴向上为正)中的张量表达式为:
| $ \frac{{\partial {\mathit{\boldsymbol{U}}_j}}}{{\partial {x_j}}}=0, $ | (1) |
| $ \frac{{\partial {\mathit{\boldsymbol{U}}_i}{\mathit{\boldsymbol{U}}_j}}}{{\partial {x_j}}} = - g\frac{{\partial \zeta }}{{\partial {x_i}}} - \frac{1}{\rho }\frac{{\partial {\mathit{\boldsymbol{P}}_d}}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\frac{{\mathit{\boldsymbol{T}}_{ij}^\prime }}{\rho } - \overline {{u_i}{u_j}} } \right], i = 1, 2, $ | (2) |
| $ \frac{{\partial {\mathit{\boldsymbol{U}}_3}}}{{\partial t}} + \frac{{\partial {\mathit{\boldsymbol{U}}_3}{\mathit{\boldsymbol{U}}_j}}}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial {\mathit{\boldsymbol{P}}_d}}}{{\partial {x_3}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\frac{{\mathit{\boldsymbol{T}}_{3j}^v}}{\rho } - \overline {{u_3}{u_j}} } \right], $ | (3) |
| $ \mathit{\boldsymbol{T}}_{ij}^v = \mu \left( {\frac{{\partial {U_i}}}{{\partial {x_j}}} + \frac{{\partial {U_j}}}{{\partial {x_i}}}} \right)。$ | (4) |
式中:Ui表示速度矢量;ζ表示自由水面;Pd为动压力;Tijυ表示粘性应力张量;ρ表示流体密度;g为重力加速度;μ为运动粘性系数;
| $ {\mathit{\boldsymbol{P}}_t} = {\mathit{\boldsymbol{P}}_h} + {\mathit{\boldsymbol{P}}_d} = g(\zeta - z) + {\mathit{\boldsymbol{P}}_d}。$ | (5) |
方程在自由表面以及水底满足如下方程:
| $ \begin{array}{*{20}{c}} {{{\left. w \right|}_{z = \zeta }} = \frac{{\partial \zeta }}{{\partial t}} + u\frac{{\partial \zeta }}{{\partial x}} + v\frac{{\partial \zeta }}{{\partial y}}}\\ {{{\left. w \right|}_{z = - d}} = - u\frac{{\partial d}}{{\partial x}} - v\frac{{\partial d}}{{\partial y}}} \end{array}。$ | (6) |
计算过程忽略自由表面处风应力与张力,Pd|z=ζ=0,在底边界处忽略两个切向压力。
入流边界,由线性波浪理论得到波浪的法向速度分量,切向速度分量初始值为零。在出流边界采用海绵层吸收波浪能以模拟开边界,海绵层尺寸不计入计算域。在固边界处,采用自由滑移的边界条件。
1.2 数值求解SWASH模型采用交错网格有限差分法进行空间离散,三维计算中速度变量定义在网格侧面中心处,非静压定义在网格上表面中心处,自由表面的压力初始值为零,垂向分层一般选取1~3层。本文选用二阶显示有限差分法对水平动量方程做离散化处理,垂直动量方程选用Keller-box方法进行离散化处理,在求解压力速度耦合方程时采用分步法。垂向多层情况下的求解过程为由底边界条件通过Keller-box离散方程以及连续方程由下向上求解垂向速度分量,然后将由水平动量方程、垂向速度以及自由表面动压带入连续方程通过Bi-CGSTAB求解下一时刻动压,进而求得下一时刻各个速度分量,最后根据由自由表面方程求解下一时刻的自由表面水位值。更详细的模型介绍可参见Stelling等[14]的相关文献。
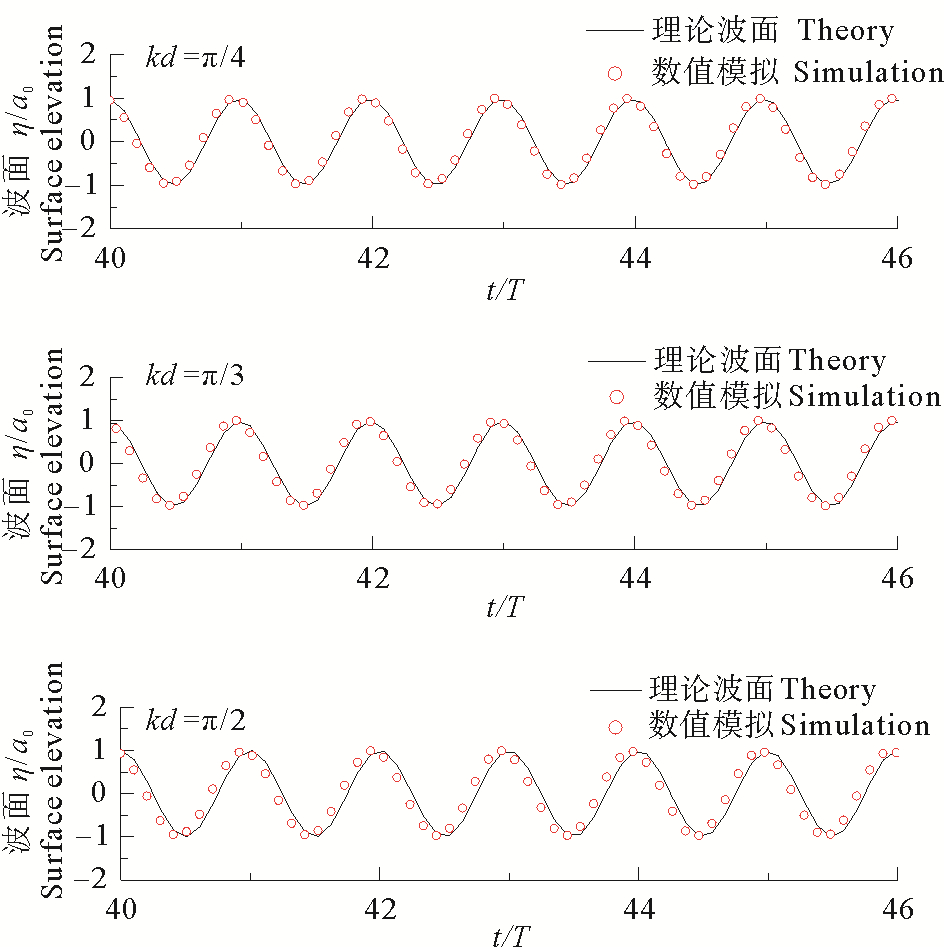
1.3 模型验证 1.3.1 色散性验证SWASH模型中色散精度由垂向分层控制,垂向分层越多,模型性能越好,但因此造成的计算量也会大幅增长。本文中垂向分层均采用均匀分层。本节通过模拟规则波在二维平底地形上的传播过程,验证SWASH模型的色散精度。数值模拟过程水深取0.5 m,波高0.006 m,选取3种不同工况,使kd =π/4、π/3、π/2。沿波浪传播方向网格步长取Δx=L0/50(L0为入射波波长),垂向均匀分为3层。采用速度入口边界,设定模拟过程中最大Courant数为0.5,水槽末端设置2倍波长的消浪区。距造波板10L0处三种不同工况下波浪模拟效果如图 1所示。图中纵坐标为无量纲化波面值,η为数值模拟波面,a0为初始波幅。由图 1可以看出,当ka在0.003π~0.006π之间,kd取值在π/2~π/4之间时,SWASH模型垂向均匀分三层时可有效地模拟浅水以及中等水深中的波浪色散,效果理想。
|
图 1 数值模拟波面与理论波面对比(x =10L0) Fig. 1 Computed surface elevations with 3 equidistant layers at x =10L0 |
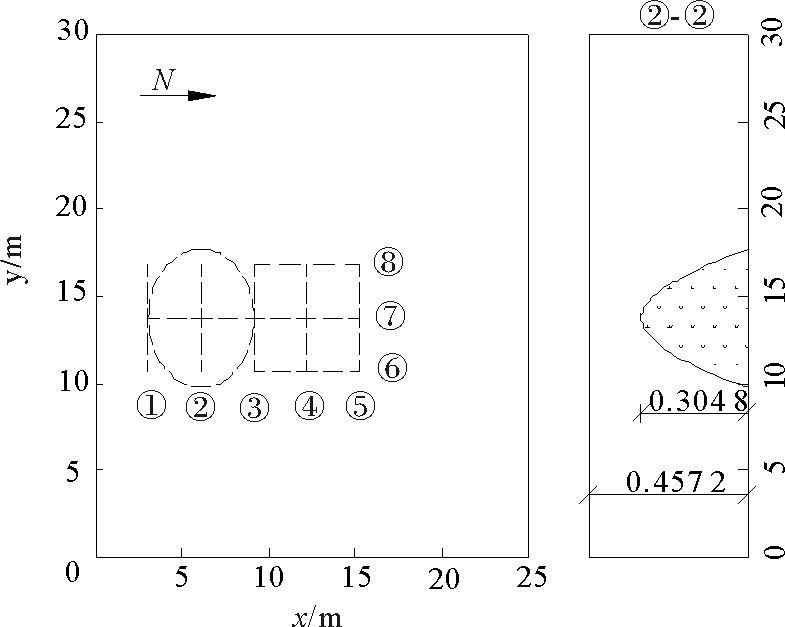
准确模拟波浪的传播除色散性以外另一个重要影响因素为非线性。本节采用SWASH模型模拟波浪在椭圆形浅滩地形上的传播过程,通过比较浅滩附近的波高变化验证SWASH模型的非线性模拟精度。实验地形采用Vincent和Briggs[12]的实验地形(见图 2),椭圆形浅滩中心坐标为x =6.10 m,y =13.72 m,地形及水深具体参数见Vincent和Briggs[12]。波浪由左侧正向入射,入射波周期T =1.3 s,波高H =5.5 cm,计算域取25 m×30 m,由于波浪主要传播方向为x方向,考虑到计算效率,计算网格沿x方向较密,y方向较稀疏,网格尺寸为0.05 m×0.1 m,计算区域末端设置5 m海绵层,用来吸收波浪能以模拟开边界。垂向均匀分三层,模拟时长78 s。
|
图 2 实验地形图 Fig. 2 Bathymetry corresponding to the experiment of Vincent and Briggs[12] |
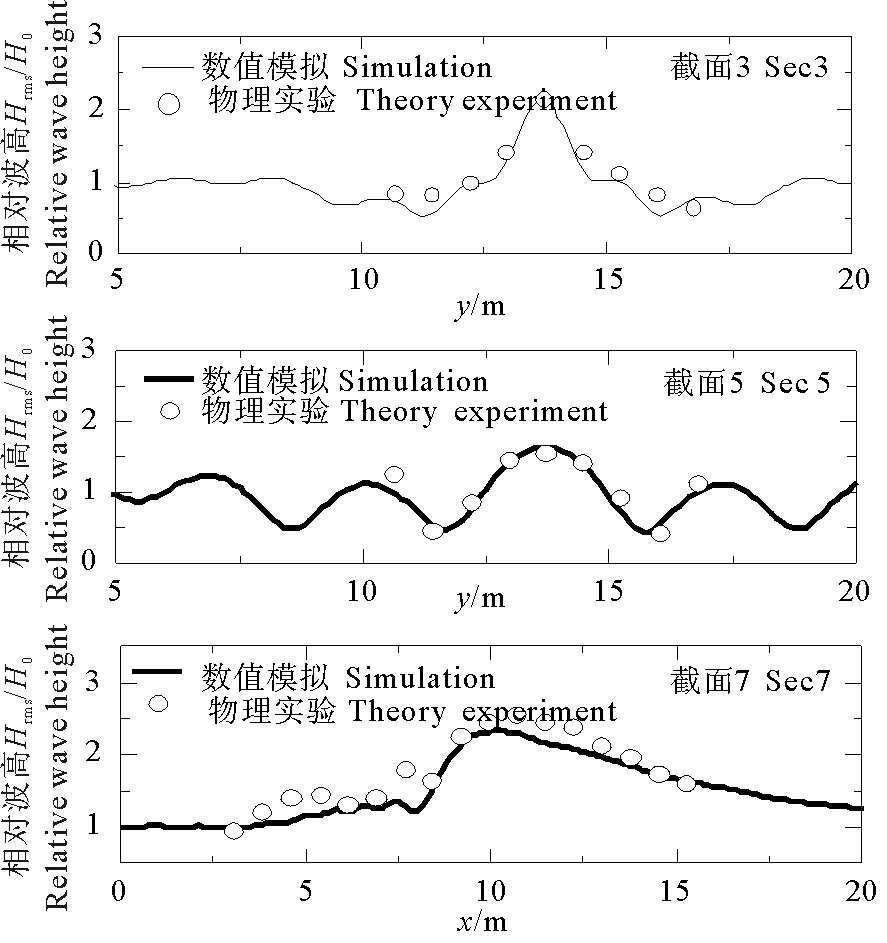
为验证SWASH模型模拟准确性,选取波高变化较明显的截面3、截面5和截面7上的波高分布与Vincent实验数据进行对比。通过上跨零点法统计数值模拟中截面处均方根波高值,与Vincent和Briggs[12]的实验结果对比如图 3所示,图中纵坐标为均方根波高与入射波高的比值,实线为SWASH模拟结果,空心圆圈为Vincent实验结果。由图可以看出数值模拟结果与实验结果吻合良好。
|
图 3 截面3、5、7上数模与Vincent实验相对波高对比 Fig. 3 Computed the relative waves height along sections 3、5、7 for the wave over elliptic shoal |
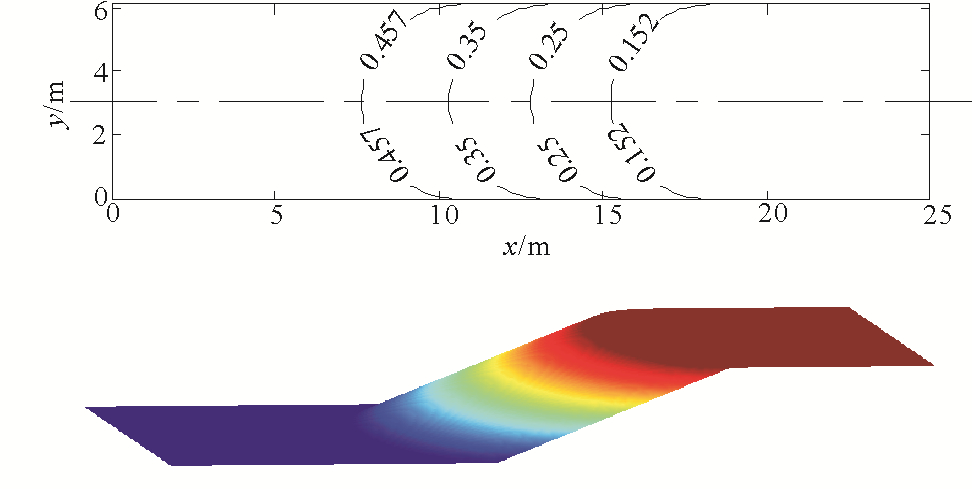
在上述验证基础之上,为进一步验证SWASH软件模拟波浪聚焦的准确性,模拟Whalin[13]实验过程。该实验是在25.603 m×6.1 m的水槽(见图 4)中放置了一个三维聚焦地形,浅滩变水深区域等深线相互平行,在几何上为直径等于水槽宽度的半圆。波浪由深水处正向入射,水槽深水侧水深为0.457 m,水槽末端浅水深为0.152 m。地形详细表达式见文献[13]。
数值模拟中计算域取30 m×6.1 m,考虑波浪传播方向以及计算效率,网格尺寸沿x方向较密,y方向较稀疏,为0.025 m×0.1 m,波浪从左侧正向入射,入射波为规则波周期T =2 s,波高H =2.12 cm,在计算域末端设置10 m海绵层以吸收波浪能量。时间步长取0.005 s,垂向均匀分3层。
通过谐波分析的方法分析水槽中轴线上的波浪组成,将数值模拟结果与Whalin实验结果进行对比(见图 5),其中横坐标为距造波板的距离,纵坐标为无量纲化谐波波幅,实线为SWASH模拟结果,实心点为Whalin实验结果。由图 5可以看出,数值结果与实验结果吻合良好,随着水深的减小,波浪在反射、折射以及浅水变形的作用下,基频能量增大,聚焦区域由于波浪非线性二倍频以及三倍频能量迅速增大,聚焦区域后由于波浪折射作用波浪传播方向发生改变,波浪迅速向水槽两侧传播并与两侧壁的反射波相互作用波高减小。
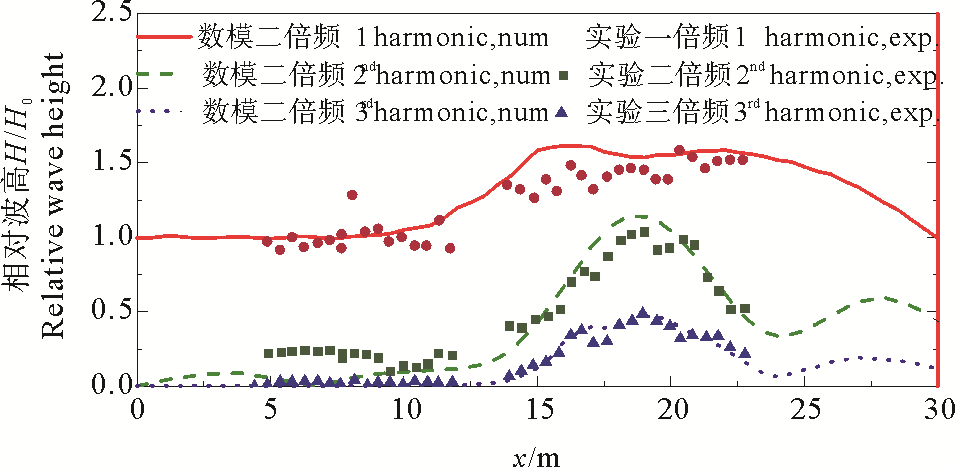
|
图 5 数模与物模谐波分布图对比 Fig. 5 The comparison of wave amplitudes of the first, second and third harmonics between numerical model value and experiment value |
波浪在斜坡地形上传播时,当地形等深线与波浪传播方向正交时,地形可简化为二维地形,但当斜坡起点不在同一条直线上波浪传播方向与等深线斜交时,该地形则无法简化成二维地形如Whalin实验地形。但由于Whalin实验中除波浪聚焦作用外还包含波浪反射的影响,为了研究单纯的波浪聚焦特性,本节对Whalin实验地形进行调整如图 6所示。在原实验地形的基础上,将地形向两侧拓宽,该地形两侧斜坡起点横坐标x0=10.68 m,中轴线附近斜坡起点在水平面上为半径等于3.05 m的半圆,借此消除波浪在水槽两侧的反射影响,波浪在该地形上的聚焦现象更接近实际地形上的波浪聚焦现象。
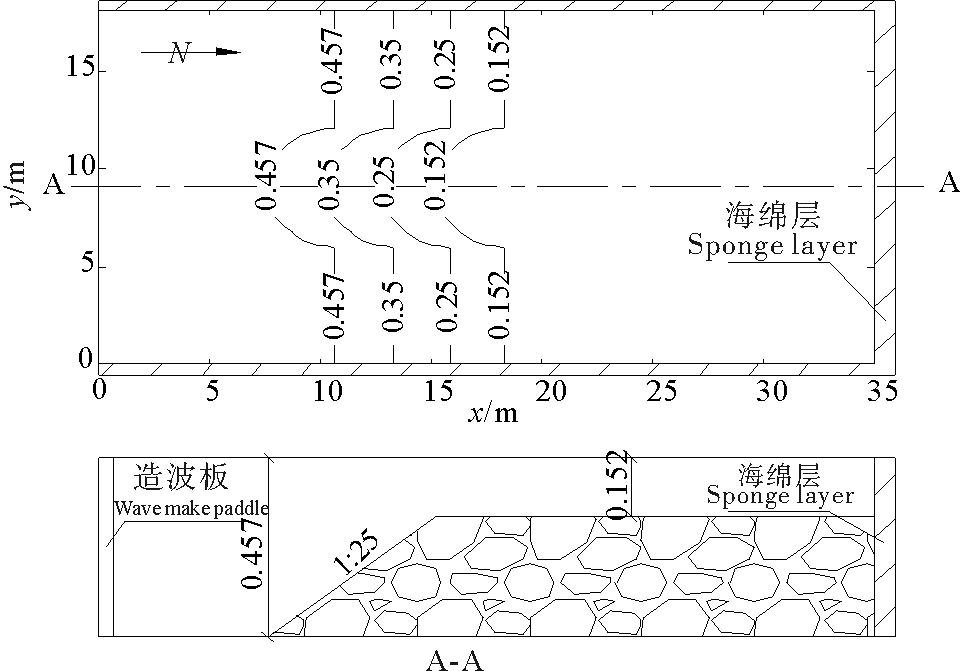
|
图 6 实验地形图 Fig. 6 Sketch of the model bathymetry |
数值模拟中的入射波波浪要素以及地形水深条件均与Whalin实验相同,波浪从左侧正向入射,波浪入射侧水深为0.457 m,浅滩顶水深为0.152 m,地形平行于x轴的截面均为1:25的斜坡。计算域取35 m×18 m,网格尺寸为0.025 m×0.1 m,为吸收波浪能量在计算域两侧各设5 m海绵层,波浪入射方向设置10 m海绵层。数值模拟过程中的时间步长取0.005 s,垂向均匀分3层。
通过上跨零点法统计波浪在三维聚焦地形中轴线上的均方根波高,将其与入射波高取比值得到相对波高。相对波高沿水槽方向分布如图 7中黑色实线所示,蓝色点划线为Whalin实验地形下中轴线上相对波高变化。由图可以看出,水槽两侧的波浪反射现象不仅导致计算域内波面分布现象不同,波高变化量也不同,反射波减小了聚焦区域内的相对波高。同时由于波浪聚焦过程中包含浅水变形的影响,因此将相同入射波浪在同等水深变化的二维地形上的波高变化用红色虚线表示。由图可以看出波浪在二维地形上传播时,由于浅水变形相对波高在浅滩顶出现最大值1.34H0(H0为入射波高),波浪在三维聚焦地形上传播时由于水深变化以及波浪折射作用波能聚集,最大波高出现在二维浅水变形中的最大波高之后,其值为2.81H0,而由于反射波作用的Whalin实验地形上相对波高变化介于两者之间。由结果可以看出,波浪在有凸起的斜坡浅滩上传播时,波高变化中只有一小部分由于浅水变形导致,而波高变化的最主要原因为波能聚集。也就是说有凸起的斜坡浅滩上波浪聚焦是波高变化的最主要原因。
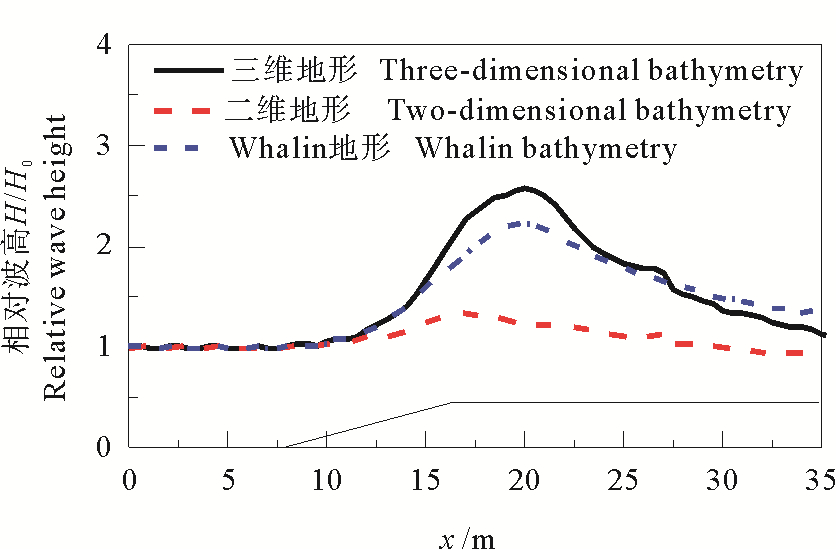
|
图 7 不同地形下相对波高对比 Fig. 7 Comparison of relative wave height between different bathymetry |
为进一步研究波浪聚焦特性,对二维地形以及三维聚焦地形中轴线上的波浪进行谐波分析如图 8所示,图中黑色实线为相对波高的沿程分布,彩色虚线为一倍频、二倍频、三倍频以及四倍频的沿程分布,黑色竖线表示最大相对波高所在位置。通过谐波分析的结果可以看出,波浪在二维地形上传播时,随着水深变化,基频、二倍频、三倍频以及四倍频能量依次开始增大,随着波浪传播非线性使谐波之间存在相互能量交换,基频能量减小,倍频能能量增加。二倍频、三倍频以及四倍频同时达到最大值,同时基频达到极小值,此后基频与倍频均在同一位置达到极值。最大相对波高位于基频最大值以及倍频最大值之间。波浪在三维聚焦地形上传播时,二倍频、三倍频以及四倍频同样在同一位置达到最大值,但基频最大值位于倍频最大值之后。与波浪在二维地形上传播时相同,非线性同样使谐波之间存在相互能量交换,但基频极值与倍频极值出现在不同位置。最大相对波高位于倍频最大值与基频最大值之间。通过比较可以看出波浪聚焦主要影响波浪的基频能量及其分布,倍频能量相比二维地形上大小变化明显,但极值位置变化不大。
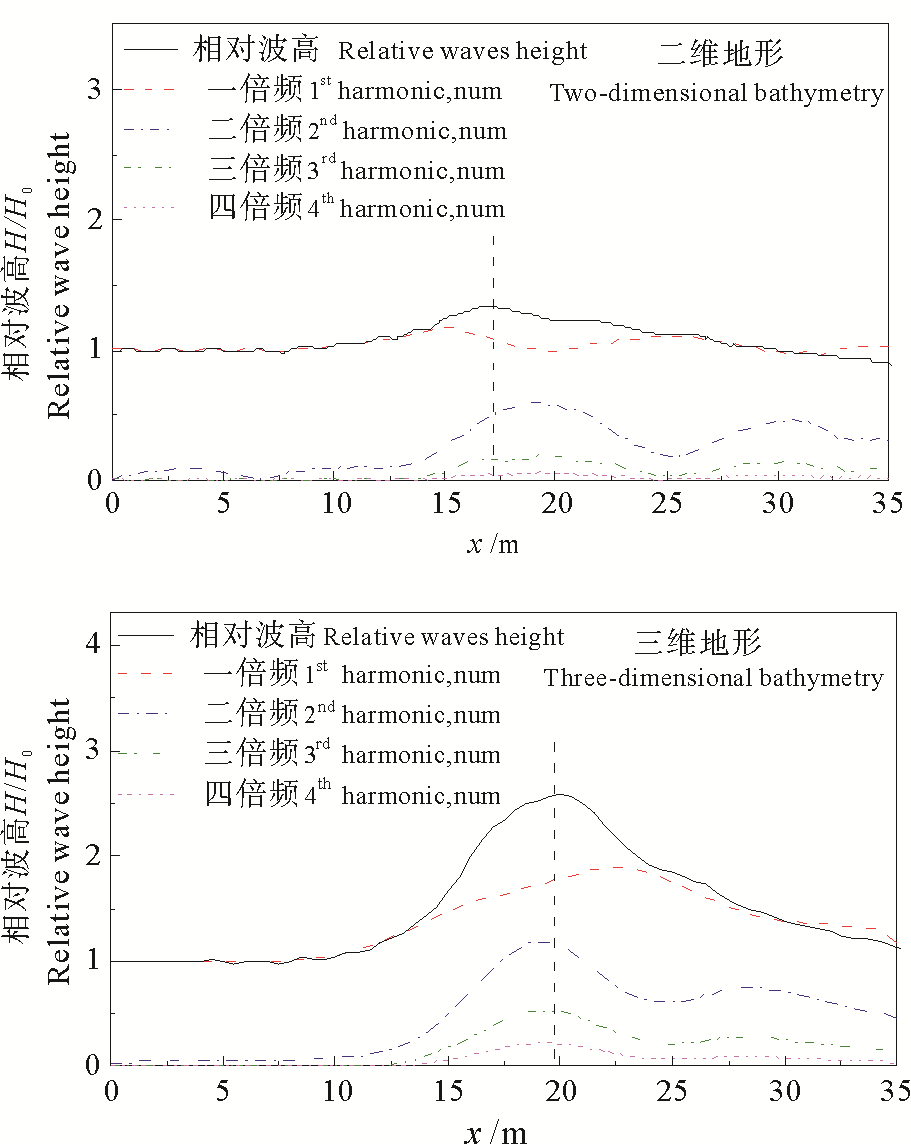
|
图 8 谐波分布图 Fig. 8 The wave amplitudes of the first, second and third harmonics for different bathymetry |
通过上节讨论可知,波浪在有凸起的斜坡浅滩上波浪聚焦现象十分显著。本节通过SWASH模型模拟同波陡不同波长的波浪在该三维聚焦地形上的传播,进一步研究初始无量纲参数kR对波浪聚焦位置的影响。本文中选取较小的入射波陡值保证计算域内出现的最大波浪未达到破碎指标,计算域内无波浪破碎。本节中共设置了7种同波陡不同波长的波况,波浪参数如表 1所示。实验参数设置与2.2节中三维聚焦地形相同。
|
|
表 1 波浪参数 Table 1 Parameters of waves |
数值模拟过程中,通过对波浪聚焦模拟过程的动画以及剖面波高进行观测,确保波浪聚焦达到的最大波高未发生破碎。对中轴线上最大波高位置处的波形进行监测,如图 9所示。图中分别为工况A01、A03、A06下中轴线上最大波高位置处的波浪形态,其中横坐标为无量纲时间,纵坐标为无量纲化波面,其中a0为入射波波幅,T为入射波浪周期。由图可以看出随着初始kR的减小,最大波高处波浪不对称性增大,非线性增强,聚焦区域距造波板越来越近。当初始kR =1.56π时,波浪在非线性作用下波浪形态由单峰变为双峰。
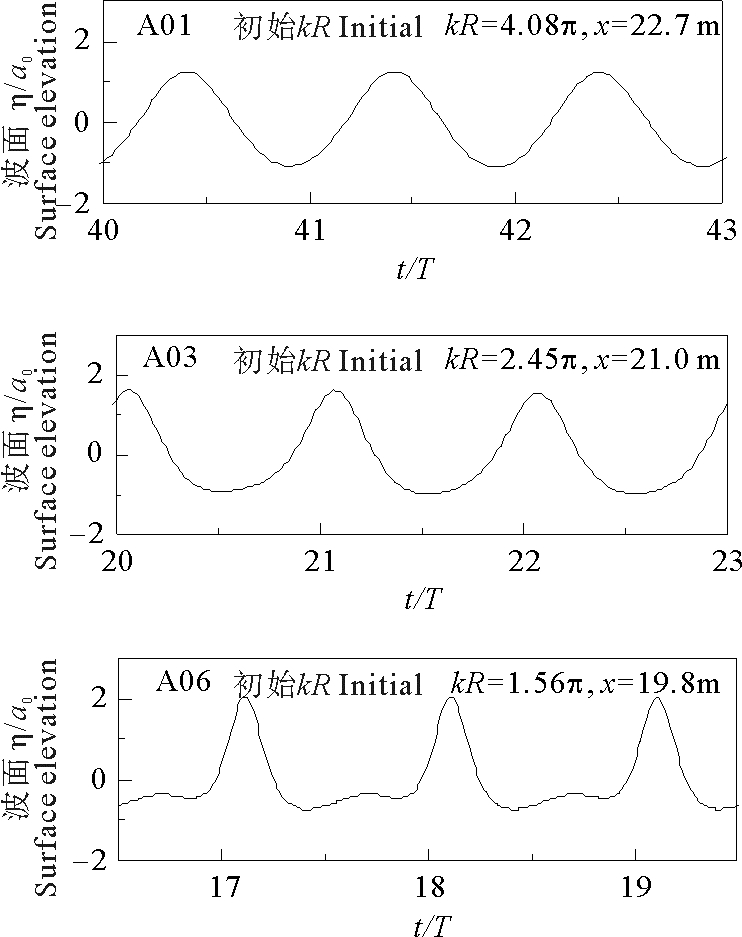
|
图 9 工况A01、A03、A06最大波高处波浪形态 Fig. 9 The surface elevations at the maximum wave height of case A01、A03、A06 |
通过上跨零点法统计不同波况下计算域内的均方根波高,与入射波高取比值得到相对波高。相对波高等值线在聚焦地形附近的分布情况如图 10所示。图中分别为波况A03和A06的相对波高等值线分布情况。对不同工况下最大相对波高距造波板的距离进行统计,最大相对波高位置与初始kR的关系如图 11所示,图中纵坐标表示最大相对波高距造波板的距离,横坐标为初始kR值。由图 10、11可以看出初始无量纲参数kR越大,聚焦区域越小,同时最大波高的位置距造波板越远,这是由于波浪在等深线为圆形的地形上传播时,入射角相同时初始kR越小,折射作用下波向线偏转速度越快[15],因此聚焦区域距聚焦地形越近。
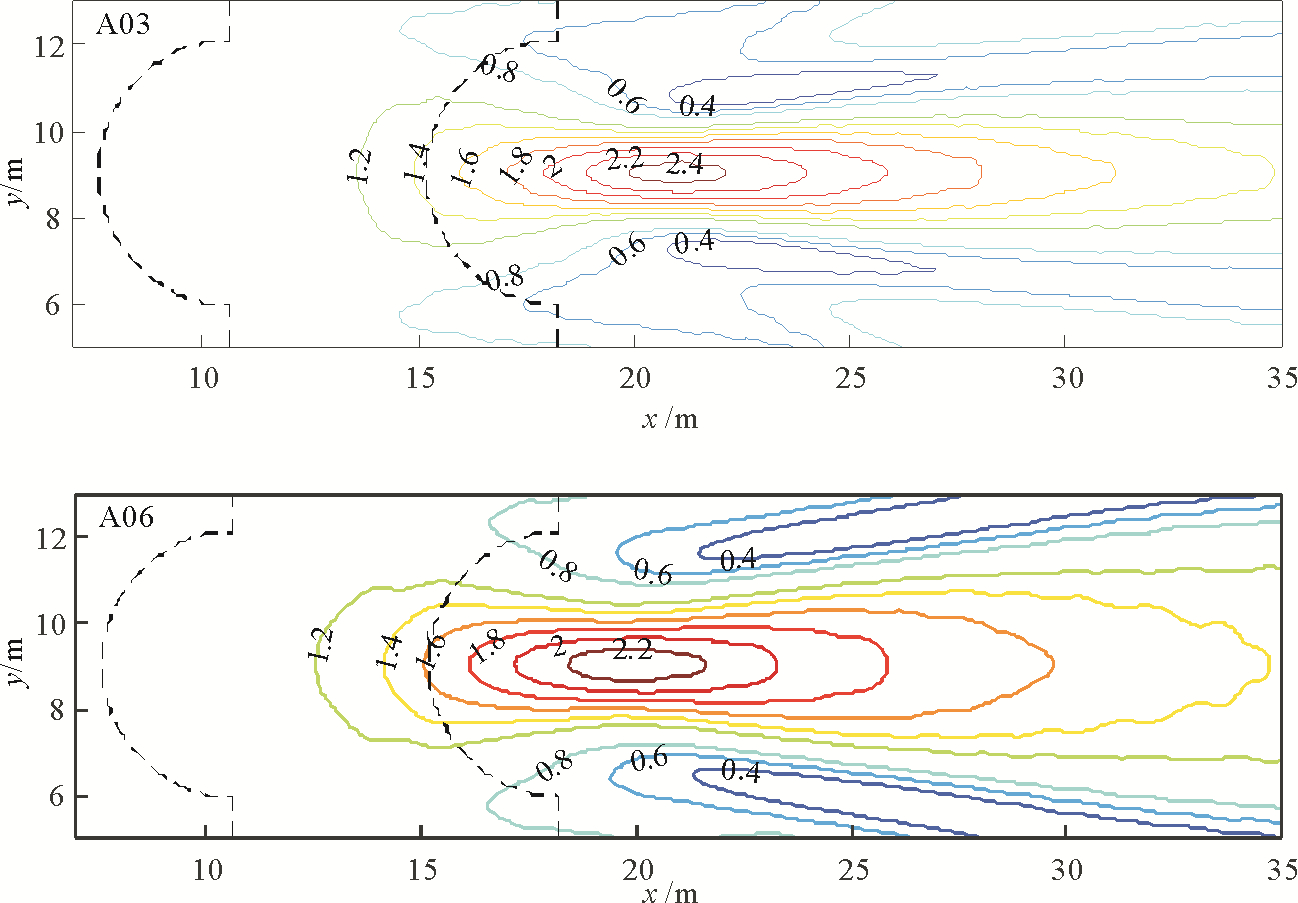
|
图 10 聚焦区域相对波高等值线分布图 Fig. 10 The contour plot of relative waves height in focusing region |
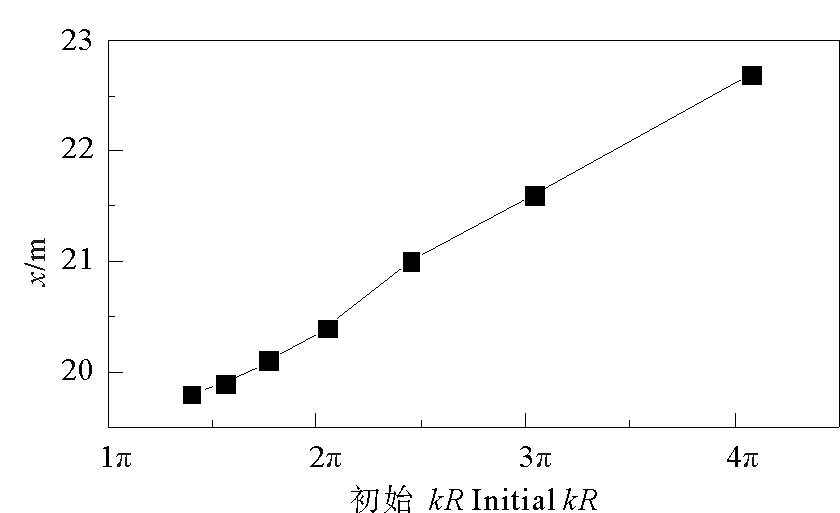
|
图 11 最大相对波高位置与初始波数的关系 Fig. 11 The relationship between the distance and the initial kR |
由前面的分析可知,初始kR越大聚焦区域越小,如果仅考虑聚焦区域的大小对相对波高的影响,则聚焦区域越小平均相对波高越大。但波浪能量在聚焦区域并非均匀分布因此不能仅仅通过聚焦区域的大小确定最大相对波高的大小,还需要考虑波浪能量在聚焦区域的分布以及不同波浪间的相互作用。通过图 9可以看出线性波浪随着非线性增加,波浪形态逐渐偏离正弦分布,波峰变尖波谷变平坦,但当非线性进一步增大,倍频能量增加时波浪将由单峰变为双峰甚至多峰,因此在最大波浪未达到破碎条件的情况下,最大相对波高的大小除需要考虑聚焦区域大小外,还要考虑波浪非线性的影响。图 12给出了不同工况下最大相对波高的值与初始kR的关系。由图可以看出当初始kR在1.4π~4.05π之间时,随着初始kR的减小,最大相对波高先增大后减小,在kR =2.45π时,最大相对波高达到极大值,可以达到2.48 H0(H0为入射波波高)。
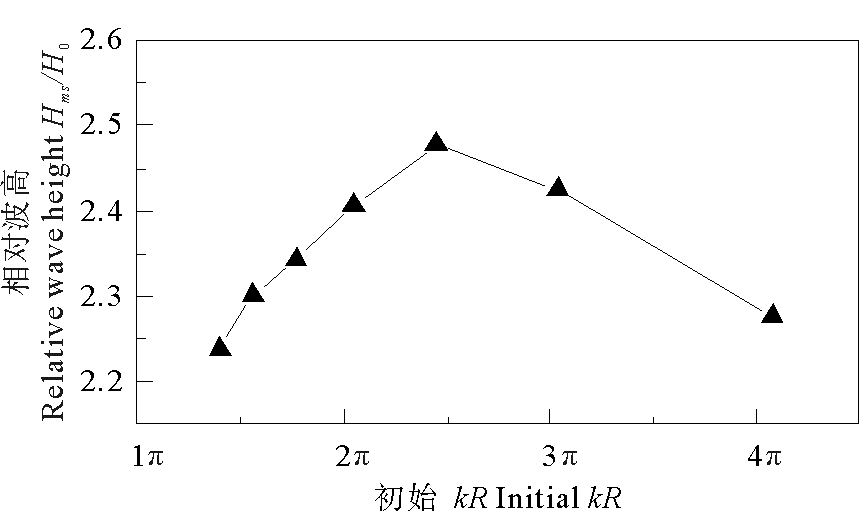
|
图 12 最大相对波高与初始波数的关系 Fig. 12 The relationship between the maximum relative wave height and the initial kR |
(1) 非静压模型SWASH软件通过将垂向压力分解为动压和静压以及区别于其他非静压软件的动压位置定义,采用三层垂向分层即可保证足够的色散精度以及非线性精度,准确高效的模拟波浪在浅水以及有限水深中的传播。
(2) 通过SWASH模型模拟波浪在三维聚焦地形上的传播,将数值模拟结果与物理实验结果进行对比,证明了SWASH模型在模拟地形导致的波浪折射、反射、衍射以及浅水变形等多重作用下的准确性。
(3) 采用SWASH模型模拟相同波浪在二维斜坡地形以及三维凸起斜坡浅滩地形上的传播,分析了相对波高的沿程分布以及谐波组成,对比发现,波浪非线性使谐波之间存在相互能量交换,波浪在二维地形上传播时,波浪传播过程中波能守恒,波浪在三维地形上传播时,波浪聚焦波浪能量增加,非线性增强,波浪聚焦引起的波高变化远大于二维浅水变形引起的波高变化。
(4) 通过SWASH模型模拟同波陡不同波长的波浪在相同三维地形上的传播,研究了最大波浪无破碎的情况下,聚焦区域的位置与初始无纲参数kR的关系,以及最大相对波高的影响因素。结果表明,在最大浪未发生破碎的情况下,等深线为圆形的聚焦地形下初始无纲参数kR对波浪聚焦有显著影响,初始kR值越大,波向线偏转速度小,最大波高位置距斜坡起点距离越大。波浪聚焦产生的最大波高值不仅与聚焦区域大小有关,还与波浪非线性的强弱有关,当kR在1.4π~4.05π之间时,随着无纲参数kR的减小,最大相对波高先增大后减小。kR =2.45π时,最大相对波高出现极大值,可以达到2.48 H0。
(5) 本文通过SWASH模型对规则波在半圆形凸起斜坡地形上的聚焦特性进行了研究,但未考虑最大波浪发生破碎对波浪聚焦特性的影响。未来还需对波浪破碎对波浪聚焦的影响进行系统研究。并且不规则波在凸起斜坡地形的聚焦特性,斜坡凸起的形状是否会对聚焦特性有所影响?波浪聚焦过程的能量时空变化是怎样,这些问题需要进一步深入分析与讨论。
| [1] |
Meyer R E. Theory of water-wave refraction[J]. Advances in Applied Mechanics, 1979, 19: 53-141. DOI:10.1016/S0065-2156(08)70309-0
(  0) 0) |
| [2] |
Berkhoff J C W. Computation of combined refraction—diffraction[J]. Coastal Engineering, 197: 796-814.
(  0) 0) |
| [3] |
Yu X, Zhang B. An extended analytic solution for combined refraction and diffraction of long waves over circular shoals[J]. Ocean Engineering, 2003, 30: 1253-1267. DOI:10.1016/S0029-8018(02)00104-X
(  0) 0) |
| [4] |
Zhang Y, Zhu S. New solutions for the propagation of long water waves over variable depth[J]. Journal of Fluid Mechanics, 1994, 278: 391-406. DOI:10.1017/S0022112094003769
(  0) 0) |
| [5] |
傅丹娟, 王岗, 郑金海, 等.水深为指数型圆岛周围波浪的俘获机制[C]. //左其华, 窦希萍.第十七届中国海洋(岸)工程学术讨论会论文集(上).北京: 海洋出版社, 2015: 507-513. Fu D J, Wang G, Zheng J H, et al. The capture mechanism of waves around an exponential circular island[C]. //Zuo Q H, Dou X P. Proceedings of the 17th China Conference Ocean Coastal Engineering. Beijing: Ocean Press, 2015: 507-513. (  0) 0) |
| [6] |
Zhu S P, Harun F N. An analytical solution for long wave refraction over a circular hump[J]. Journal of Applied Mathematics and Computing, 2009, 30: 315-333. DOI:10.1007/s12190-008-0175-8
(  0) 0) |
| [7] |
Niu X, Yu X. Analytic solution of long wave propagation over a submerged hump[J]. Coastal Engineering, 2011, 58(2): 143-150.
(  0) 0) |
| [8] |
Longuet-Higgins M S. On the trapping of waves along a discontinuity of depth in a rotating ocean[J]. Journal of Fluid Mechanics, 1968, 31(3): 417-434.
(  0) 0) |
| [9] |
Shaw R P, Neu W. Long-wave trapping by oceanic ridges[J]. Journal of Physical Oceanography, 1981, 11(10): 1334-1344. DOI:10.1175/1520-0485(1981)011<1334:LWTBOR>2.0.CO;2
(  0) 0) |
| [10] |
熊梦婕, 王岗, 郑金海.抛物型海脊上俘获波理论及其应用[C]. //左其华, 窦希萍.第十七届中国海洋(岸)工程学术讨论会论文集(上).北京: 海洋出版社, 2015: 544-551. Xiong M J, Wang G, Zheng J H. Theory and its application of wave capture on parabolic ridge[C]. //Zuo Q H, Dou X P. Proceedings of the 17th China Conference Ocean Coastal Engineering. Beijing: Ocean Press, 2015: 544-551. (  0) 0) |
| [11] |
Berkhoff J C W, Booy N, Radder A C. Verification of numerical wave propagation models for simple harmonic linear water waves[J]. Coastal Engineering, 1982, 6(3): 255-279. DOI:10.1016/0378-3839(82)90022-9
(  0) 0) |
| [12] |
Vincent C L, Briggs M J. Refraction—Diffraction of irregular waves over a mound[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1989, 115(2): 269-284. DOI:10.1061/(ASCE)0733-950X(1989)115:2(269)
(  0) 0) |
| [13] |
Whalin R W. Wave refraction theory in a convergence zone[J]. Coastal Engineering, 1972, 451-470.
(  0) 0) |
| [14] |
Zijlema M, Stelling G, Smit P. SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters[J]. Coastal Engineering, 2011, 58(10): 992-1012. DOI:10.1016/j.coastaleng.2011.05.015
(  0) 0) |
| [15] |
Mei C C, Stiassnie M, Yue D K P. Theory and Applications of Ocean Surface Waves[M]. Singapore: World Scientific Publishing Co pte ltd hackensack Nj, 2005: 82-90.
(  0) 0) |
 2020, Vol. 50
2020, Vol. 50