2. 青岛市海洋可再生能源重点实验室,山东 青岛 266100;
3. Prince of Songkla University, Hatyai, Songkhla 90112
潮流能清洁、无污染且储量丰富,其开发利用越来越受到国内外学者的重视,潮流能水平轴水轮机是应用最为广泛的一种潮流能捕获装置。叶片是潮流能水轮机直接承受水动力的部件,其结构、强度及稳定性对水轮机组的可靠性起着至关重要的作用。水轮机组在变幅载荷作用下容易导致叶片产生疲劳破坏,对水轮机组正常运行的可靠性和使用寿命产生重要影响。叶片疲劳损伤与应力应变有着密切关系,因此,本文开展了潮流能水平轴水轮机叶片应力疲劳特性分析的研究。
国外已有学者针对潮流能水轮机叶片的疲劳问题进行了研究。BOISSEAU等开展了不同类型玻璃纤维增强复合材料在海水及空气中的疲劳性能实验[1]。KENNEDY等基于流管模型和应变寿命模型分析作用在潮流能水轮机叶片上的水动力载荷并从材料角度对叶片的疲劳寿命进行了研究[2]。
国内针对叶片疲劳问题的研究主要集中在风力机领域。石可重等采用不同的加载方式探究环境温度、湿度等因素对风力机疲劳特性的影响[3]。李德源等对风力机叶片的疲劳性能及破坏准则等进行了探究,运用Miner线性累积损伤法则近似预估叶片寿命[4]。陈严等运用雨流计数法进行统计,通过FE-SFAFE分析风力机叶片疲劳寿命[5]。
本文在上述研究的基础上,针对潮流能水平轴水轮机叶片的应力疲劳特性进行时域分析,主要内容包括:基于叶素动量理论,计算作用在叶片上的载荷,并利用自编程序生成时序随机变幅载荷谱,应用有限元法分析叶片在变幅载荷下的应力及应变,并运用S-N全寿命分析方法对20 kW浮潜式潮流能水平轴水轮机叶片进行疲劳特性分析,以探究叶片的损伤机理及叶片的疲劳寿命。
1 叶片载荷计算对叶片进行疲劳特性分析首先要对作用在叶片上的载荷情况进行分析。针对潮流能水轮机叶片特殊的工作条件和工作介质,叶片所受的载荷可分为确定性载荷和随机载荷,为简化载荷计算,主要考虑确定性载荷。确定性载荷进一步地可分为瞬时性和周期性两类载荷。瞬时性载荷是指水轮机在固定状态产生的不等载荷,如在启动、刹车等情况下产生。周期性载荷,是可以预知和计算的载荷,所占比重较大。周期性载荷中,由于塔影或者偏航以及变桨引起的水动力载荷很小,在本文疲劳分析中暂不考虑其影响。因此,进行叶片疲劳分析时,主要考虑周期性载荷中的水动力载荷、重力载荷和惯性力载荷[4]。
1.1 水动力载荷计算潮流能水平轴水轮机水动力载荷计算的主要理论基础是叶素动量理论。叶素理论是将叶片沿径向分为若干要素,对每个叶素分别进行分析,然后将每个叶素上的力叠加,得到整个叶轮上的流体作用力[6]。叶片截面受力分析如图 1。

|
图 1 叶片截面受力分析 Fig. 1 Force analysis of the blade section |
通过库塔儒可夫斯基升力方程可以推导出叶素微元的升力L和阻力D分别为:
| $ {\rm{d}}L = \frac{1}{2}\rho c{V^2}{C_l}{\rm{d}}r, $ | (1) |
| $ {\rm{d}}D = \frac{1}{2}\rho c{V^2}{C_d}{\rm{d}}r。$ | (2) |
式中:ρ为水流密度,单位kg/m3;c为叶素弦长,单位m;V为水流相对于叶素合成速度,单位m/s;Cl为升力系数;Cd为阻力系数。
根据动量定理,叶轮受到的轴向力T和转矩M等于单位时间内通过叶轮的流体动量和角动量的变化量。对于叶轮上一个半径为r、宽度为dr的微元,其受到的轴向力dT和转矩dM可表示为:
| $ {\rm{d}}T = \frac{1}{2}\rho c{V^2}{C_y}{\rm{d}}r, $ | (3) |
| $ {\rm{d}}M = \frac{1}{2}\rho c{V^2}{C_x}r{\rm{d}}r。$ | (4) |
沿叶片展长方向,对叶片上的微元进行积分,可得作用在单个叶片上的轴向力和转矩分别为:
| $ T = \frac{1}{2}\rho c{V^2}{C_y}, $ | (5) |
| $ M = \frac{1}{2}\rho c{V^2}{C_x}r。$ | (6) |
切向力系数Cx与轴向力系数Cy表达如下:
| $ {C_x} = {C_l}\sin I - {C_d}\cos I, $ | (7) |
| $ {C_y} = {C_l}\cos I + {C_d}\sin I。$ | (8) |
式中,I为水流相对叶素的入流角,单位度。
1.2 重力载荷随着叶轮的转动,作用在叶片上重力的分力发生变化,给叶片带来变幅载荷。
重力可简化为:
| $ {F_g} = {m_B}g。$ | (9) |
式中:mB为叶片质量,单位kg;g为重力加速度。
1.3 惯性力载荷作用在叶片上的惯性力载荷即离心力引起的载荷,离心力主要由叶轮角速度、径向位置和叶片的单元质量决定。叶片根部的离心力为:
| $ {F_c} = {m_B}{\omega ^2}{r_G}。$ | (10) |
式中:rG为叶片质心到叶片转动中心的距离,单位m;ω为叶片旋转的角速度,单位rad/s。
叶片转到与地面垂直,叶尖朝下即离心力与重力方向一致时,叶片所受转动产生的离心力Fc和自身重力Fg的合力最大。
1.4 叶尖、叶根损失修正叶素理论是将绕水轮机的三维流动简化为互不干扰的二维流动,并未考虑到叶尖与叶根损失。PRANDTL等对叶尖处的流动进行了研究[7],引入叶尖损失修正系数Ftip;叶根部分,受轮毂阻水效果影响,半径方向的三维流动也比较明显,叶根部分的流动损失也不易忽略,因此引入叶根损失修正系数Fhub;叶尖与叶根损失系数表达式如下:
| $ {F_{tip}} = \frac{2}{\pi }{\cos ^{ - 1}}\left( {{{\rm{e}}^{ - {f_1}}}} \right), $ | (11) |
| $ {F_{hub}} = \frac{2}{\pi }{\cos ^{ - 1}}\left( {{{\rm{e}}^{ - {f_2}}}} \right)。$ | (12) |
式中:
叶尖、叶根损失总修正系数F为:
| $ F = {F_{tip}} \cdot {F_{hub}}。$ | (13) |
潮流能水轮机叶片的安全寿命设计要求叶片在一定的使用期限内不发生疲劳破坏,主要借助于疲劳损伤理论对叶片的疲劳寿命进行估算。其中,线性累积损伤理论认为在交变荷载作用下,结构或构件产生的疲劳损伤互不影响且相互叠加,当所有应力产生的损伤累积到一定程度时,结构或构件发生疲劳失效。
在不同的线性疲劳累积损伤理论中,Palmgren-Miner线性累积损伤理论应用最为广泛[8]。试件在给定应力的情况下进行反复作用,认为损伤与应力循环成线性累积的关系,各循环之间互不干涉,当损伤累积到一定程度时,就会产生破坏。
| $ D = \sum\nolimits_i^k {{D_i}} = \sum\nolimits_i^k {\frac{{{n_i}}}{{{N_i}}}} 。$ | (14) |
式中:D为循环载荷下的破坏程度,在[0, 1]内取值;ni为应力水平为σi时的工作循环数;Ni为σi时的材料破坏循环数。
2.2 疲劳分析方法疲劳分析根据结构的工作环境、载荷谱及材料的疲劳性能分为应力疲劳分析(S-N)和应变疲劳分析(E-N)。应力疲劳分析是针对循环应力水平低、使用寿命较长的高周疲劳的分析方法。应变疲劳分析是针对循环应力水平高、使用寿命短,屈服后应变变化大而应力变化小的低周疲劳的分析方法。
按破坏循环次数将疲劳分为低周疲劳和高周疲劳,低周疲劳一般低于104~105次循环,应力较低而应变较高;高周疲劳一般高于104~105次循环,应力较高而应变较低[9-10]。针对水轮机叶片的高周疲劳特性,本文采用S-N全寿命应力疲劳分析方法对水轮机叶片的疲劳可靠性进行分析。
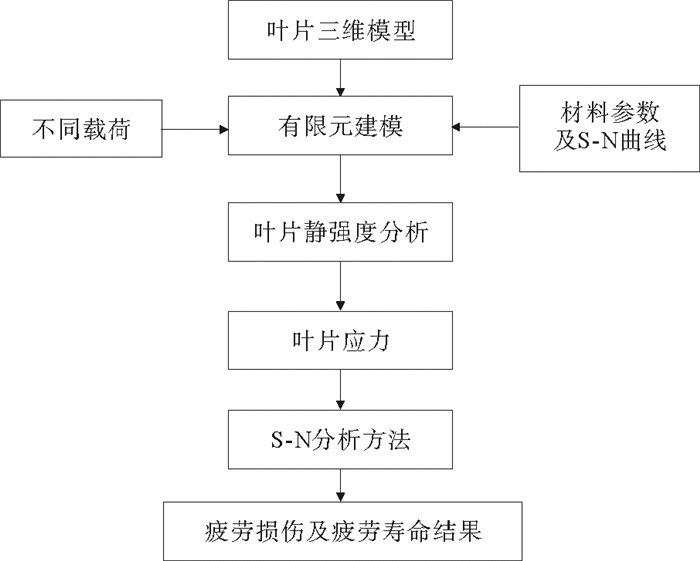
2.3 疲劳分析流程对潮流能水平轴水轮机叶片进行疲劳分析主要包含以下几个步骤:材料疲劳性能参数设定、疲劳分析和疲劳结果评估,水轮机疲劳寿命分析流程如图 2所示[11-12]。具体过程如下:
|
图 2 疲劳特性分析流程图 Fig. 2 Flow chart of fatigue analysis |
(1) 将叶片几何数据导入到三维建模软件中,构建叶片三维模型。
(2) 将叶片三维模型导入ANSYS Workbench软件中,建立有限元模型,在软件材料数据库中添加材料,设定材料物理参数以及材料的S-N疲劳特性曲线。
(3) 将惯性力和重力载荷加入模型,然后根据自编程序生成的水动力载荷,加入比例因子以产生工作应力时间历程,同时考虑叶片材料的力学性能参数,进行静力分析得到叶片的应力及应变[13]。
(4) 将叶片有限元结果导入到疲劳分析软件中,加载载荷谱及材料数据,进行疲劳特性分析。
(5) 疲劳损伤及寿命计算结果分析。
在不同的平均应力修正方法中,Soderberg直线模型在估算疲劳极限时比较保守,而Gerber模型偏于危险,Goodman直线模型介于两者之间。因此,本文应用Goodman平均应力修正理论来考虑平均应力对疲劳特性的影响。
3 实例分析20 kW浮潜式潮流能发电装置采用斜坡式浮箱载体,具有可靠性高、工作平稳、低流速下获能效率高等特点,现安放在青岛斋堂岛海域,20 kW潮流能水平轴水轮机如图 3所示。

|
图 3 20 kW潮流能水平轴水轮机 Fig. 3 20 kW power flow energy horizontal axis tidal turbine |
以20 kW潮流能水平轴水轮机为例进行分析,水轮机整体参数如表 1所示。
|
|
表 1 水轮机整体参数 Table 1 The overall parameters of the turbine |
英国南安普顿大学的学者通过分析不同系列翼型的升阻比特性,结果表明NACA63-8系列翼型的升阻比较高,水动力学性能较好[14]。因此本文以NACA63-816作为叶片的设计翼型。叶片截面数据如表 2所示,其中r表示叶片截面与旋转中心距离,θ表示扭角,c表示弦长。
|
|
表 2 叶片截面数据 Table 2 Parameters of blade section |
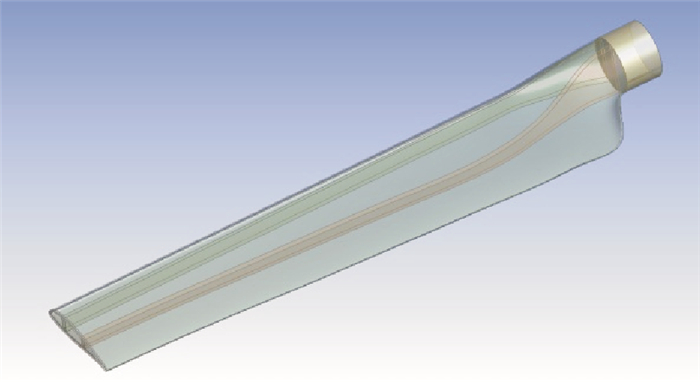
根据叶片的弦长与扭角沿叶片不同截面的分布数据,通过坐标变换矩阵将翼型二维数据转换成叶片各截面的三维空间坐标数据,在SolidWorks中建立叶片实体模型,对实体进行抽壳,添加腹板式支撑结构[15],叶片几何模型如图 4所示。
|
图 4 叶片几何模型 Fig. 4 Blade geometric model |
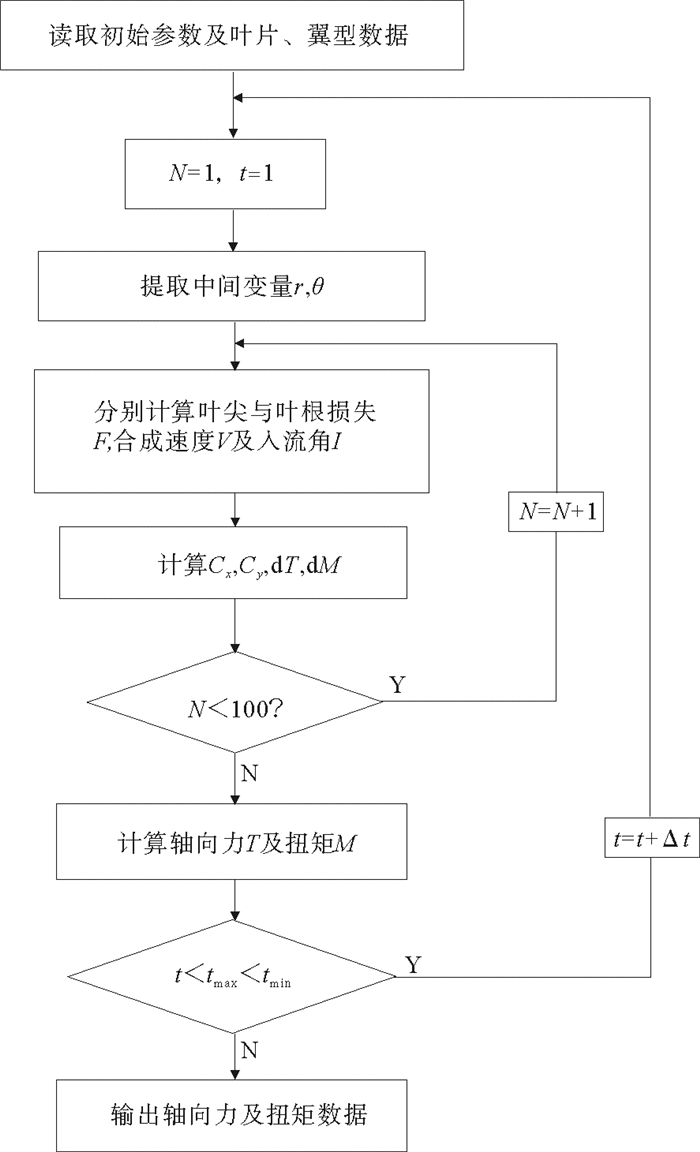
基于叶素动量理论,参考Wilson叶尖与叶根损失修正模型,根据不同的流速变化,编写相应的MATLAB计算程序,计算并输出叶片轴向力载荷与扭矩载荷的时间历程数据。通过模拟时序载荷,可以减少实测过程中的不便。程序以流速与时间为输入参数,读取叶片、翼型及水轮机参数,提取中间变量叶片截面与旋转中心距离r,叶片截面扭角θ等数据,计算并输出轴向力与扭矩载荷随时间变化的历程结果,MATLAB计算流程图如图 5所示。
|
图 5 MATLAB计算流程图 Fig. 5 MATLAB calculation flow chart |
不同流速下,水动力载荷随时间变化的MATLAB计算结果如图 6所示。在模拟载荷产生时,并未考虑突变载荷的影响。

|
图 6 不同流速下轴向力及扭矩数据 Fig. 6 Axial force and torque data at different velocity |
玻璃钢材料具有耐腐蚀性能好、缺口敏感性低、内阻尼大、抗震性能好的特点,是制作潮流能水轮机叶片的理想材料。因此,20 kW潮流能水轮机的叶片选择玻璃钢材料,参照风力机叶片的有关结构设计,设置蒙皮厚度为5 mm,内部支撑结构为15 mm。玻璃钢材料参数如表 3所示[16],材料的物理性质与参考文献保持一致。
|
|
表 3 玻璃钢材料参数[16] Table 3 Material parameters of FRP |
玻璃钢材料的疲劳曲线在S-lgN坐标上近似为直线[17],如式(15)所示。
| $ \alpha {\sigma _i} = \lg {N_i} = b。$ | (15) |
式中:常数α=1/B;常数b=σb/B,一般在10.0左右;σb为材料静强度,单位MPa;σi为试验应力水平,单位MPa;Ni为σi应力水平下的循环数。
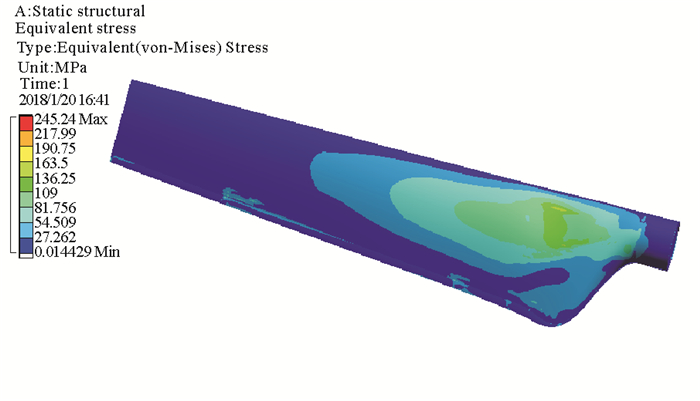
3.3 叶片静力学分析参照斋堂岛海域观测点实测流速数据,水轮机工作流速v =0.5~2.0 m/s。水轮机额定流速为1.5 m/s,额定转速为35rad·min-1。在ANSYS workbench中建立叶片有限元模型,采用自定义网格划分的方法划分叶片网格,共划分153 872个节点、27 730个单元。对叶片综合施加重力载荷、惯性力载荷及随时间变化的轴向力与扭矩载荷,在Workbench中进行静力学分析,计算得到叶片等效应力云图及等效应变云图分别如图 7和8所示。
|
图 7 叶片等效应力图 Fig. 7 Blade equivalent stress |
|
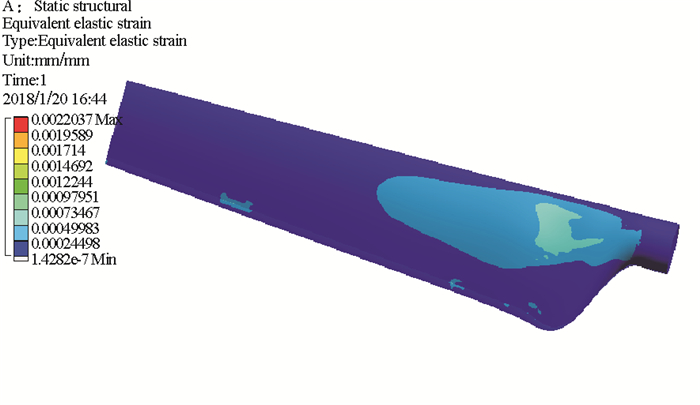
图 8 叶片等效应变图 Fig. 8 Blade equivalent strain |
由图 7和8可知,叶片应力最大可以达到245.24 MPa,应变最大为2.20×10-3mm,表明叶片在工作中产生的疲劳应力较大而应变较小。应力与应变较大的部位集中在靠近叶根的叶中处及叶片上下表面的连接部位。
3.4 疲劳分析将有限元分析结果模型导入到nCode Designlife中,对叶片施加轴向力及扭矩载荷,加载时间2 000 s,运用S-N全寿命方法分析叶片的应力疲劳特性,疲劳损伤与疲劳寿命分析结果分别如图 9和10所示。
|
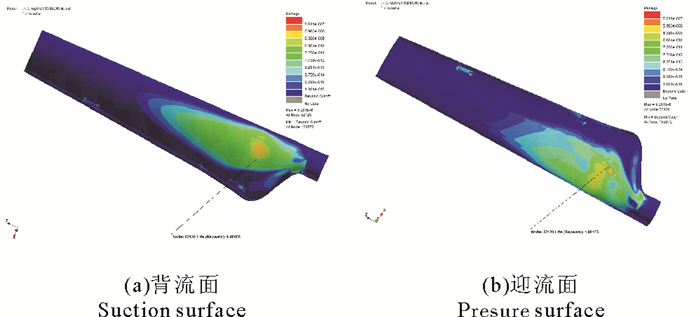
图 9 叶片疲劳损伤云图 Fig. 9 Blade fatigue damage cloud map |
|
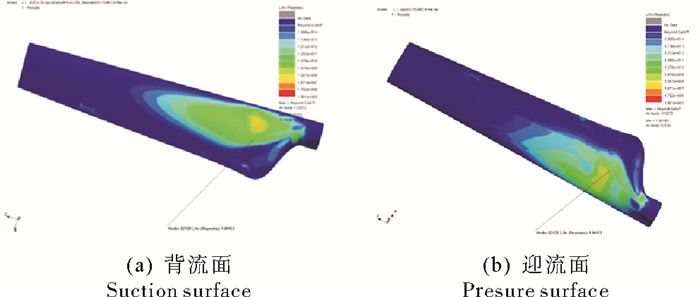
图 10 叶片寿命云图 Fig. 10 Blade fatigue life cloud map |
由图 9可知,靠近叶根的叶中部位且与内部腹板支撑连接处的叶片损伤较大,表明此处易产生疲劳破坏。叶片疲劳损伤较大的节点处同时是叶片等效应力较大的位置。应力寿命分析方法是在叶片应力分析的基础上进行疲劳特性分析,分析结果与叶片等效应力分析较为一致。由图 9及10可知,叶片最小寿命的应力节点为52 120,位于叶片迎流面靠近叶根的叶片中部。
此外,通过分析得出了叶片危险节点的损伤及寿命数据如表5所示。
由表 4可知,叶片除节点52 120外,其余节点的寿命都在106次循环以上。分析过程中,按静力加载的方法分析叶片的疲劳寿命,载荷加载时间为2 000 s,绝大多数部位的循环大于106次,满足叶片一般为20 a的年限使用要求。
|
|
表 4 叶片危险节点损伤及寿命 Table 4 Damage and life of blade dangerous node |
应用S-N全寿命分析方法,对判定叶片节点的应力疲劳特性简单有效,可准确得出叶片不同部位危险节点的疲劳损伤及疲劳寿命,在工程应用中具有指导意义。
4 结论基于MATLAB自编程序计算作用在水轮机叶片上随时间变化的变幅载荷,应用Workbench对叶片进行静应力分析,并将计算结果的有限元模型作为疲劳分析模型,分析叶片疲劳特性,结论如下:
(1) 以线性疲劳累积损伤理论为基础,应用S-N全寿命疲劳分析方法对叶片进行应力疲劳特性分析,分析结果表明叶片靠近叶根的叶片中部且与腹板支撑连接处易产生疲劳损伤,并得到叶片不同部位危险节点的疲劳损伤及疲劳寿命。
(2) 经计算分析后,结果表明20 kW潮流能水平轴水轮机叶片满足使用寿命要求。20 kW潮流能发电装置于2015年6月顺利安装在斋堂岛海域,已运行2 a多时间,叶片未出现异常情况。
为延长潮流能水轮机叶片的使用寿命,应尽量避免叶片产生应力集中的现象,可以优化叶片外形使叶片中部与叶片圆柱形叶根连接部位得到平滑的过渡,优化叶片内部结构以增强叶片中部的抗压、抗弯能力。此外,可进一步对叶片在潮流能水轮机启动、停机及正常运转过程中产生的瞬时突变载荷引起的疲劳损伤进行研究。目前正积极筹建潮流能水轮机叶片试验测试系统,以便进行更进一步的试验测试和验证。
| [1] |
Boisseau A, Davies P, Thiebaud F. Fatigue behaviour of glass fibre reinforced composites for ocean energy conversion systems[J]. Applied Composite Materials, 2013, 20(2): 145-155.
(  0) 0) |
| [2] |
Kennedy C R, Leen S B, Bradaigh C M ó. A preliminary design methodology for fatigue life prediction of polymer composites for tidal turbine blades[J]. Proceedings of the Institution of Mechanical Engineers Part L Journal of Materials Design & Applications, 2013, 226(3): 203-218.
(  0) 0) |
| [3] |
石可重, 赵晓路, 徐建中. 大型风电机组叶片疲劳试验研究[J]. 太阳能学报, 2011, 32(8): 1264-1268. Shi Kechong, Zhao Xiaolu, Xu Jianzhong. Research on fatigue test of large horizontal axis wind turbine blade[J]. Journal of Solar Energy, 2011, 32(8): 1264-1268. (  0) 0) |
| [4] |
李德源, 叶枝全, 陈严, 等. 风力机玻璃钢叶片疲劳寿命分析[J]. 太阳能学报, 2004, 25(5): 592-598. Li Deyuan, Ye Zhiquan, Chen Yan, et al. Fatigue life analysis of glass fiber reinforced plastic blades for wind turbines[J]. Journal of Solar Energy, 2004, 25(5): 592-598. DOI:10.3321/j.issn:0254-0096.2004.05.006 (  0) 0) |
| [5] |
陈严, 张林伟, 刘雄, 等. 水平轴风力机叶片疲劳载荷的计算分析[J]. 太阳能学报, 2013, 34(5): 902-908. Chen Yan, Zhang Linwei, Liu Xiong, et al. Fatigue load calculation and analysis of the blade of horizontal axis wind turbine[J]. Journal of Solar Energy, 2013, 34(5): 902-908. DOI:10.3969/j.issn.0254-0096.2013.05.029 (  0) 0) |
| [6] |
王俭超.水平轴潮流水轮机叶片设计和模型试验研究[D].青岛: 中国海洋大学, 2011. Wang Jianchao. The Blade Design and Experimental Study on Horizontal Axis Turbine Driven by Tidal Current Energy[D]. Qingdao: Ocean University of China, 2011. (  0) 0) |
| [7] |
PRANDTL L, TIETJENS O G. Applied Hydro and Aeromechanics[M]. Dover Publications, 1957.
(  0) 0) |
| [8] |
姚卫星. 结构疲劳寿命分析[M]. 北京: 国防工业出版社, 2003. Yao Weixing. Structural Fatigue Life Analysis[M]. Beijing: Defense Industry Press, 2003. (  0) 0) |
| [9] |
SCHIJVE J. Fatigue of Structures and Materials[M]. Berlin: Springer, 2009.
(  0) 0) |
| [10] |
曾春华, 邹十践. 疲劳分析方法及应用[M]. 北京: 国防工业出版社, 1991. Zeng Chunhua, Zou Shijian. Method and Application of Fatigue Analysis[M]. Beijing: Defense Industry Press, 1991. (  0) 0) |
| [11] |
张峥, 陈欣. 风力机疲劳问题分析[J]. 华北水利水电大学学报(自然科学版), 2008, 29(3): 41-43. Zhang Zheng, Chen Xin. Analysis of the fatigue of wind turbine[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power, 2008, 29(03): 41-43. DOI:10.3969/j.issn.1002-5634.2008.03.012 (  0) 0) |
| [12] |
BJORCK. A 2-D Airfoil Wind Tunnel Test at Stall[C]. Proceedings of IEA 7th symposium on Aerodynamics of Wind Turbines, Denmark, 1993.
(  0) 0) |
| [13] |
金卫东. 基于ANSYS Workbench协同平台的汽车膜片弹簧有限元分析[J]. 机械传动, 2012, 36(5): 71-73. Jin Weidong. Finite element analysis of diaphragm spring for automobile clutch based on ANSYS workbench[J]. Journal Mechanical Transmission, 2012, 36(5): 71-73. DOI:10.3969/j.issn.1004-2539.2012.05.021 (  0) 0) |
| [14] |
陈存福.潮流能水平轴水轮机叶片优化及水动力性能研究[D].青岛: 中国海洋大学, 2012. Chen Cunfu. Study on Blade Optimization and Hydrodynamic Performance of Horizontal Axis Marine Current Turbine[D]. Qingdao: Ocean University of China, 2012. (  0) 0) |
| [15] |
季采云, 朱龙彪, 朱志松, 等. 3MW海上风力机叶片的三维建模及模态分析[J]. 机械设计与制造, 2011(6): 192-194. Ji Caiyun, Zhu Longbiao, Zhu Zhisong, et al. Three-dimensional modeling and modal analysis for blades of 3MW offshore wind turbine[J]. Machinery Design & Manufacture, 2011(6): 192-194. DOI:10.3969/j.issn.1001-3997.2011.06.072 (  0) 0) |
| [16] |
Burton T, Sharpe D, Jenkins N, et al. Wind Energy Handbook[M]. Wiley: Wind Energy Handbook, 2011.
(  0) 0) |
| [17] |
陈余岳. 玻璃钢风力机叶片疲劳设计[J]. 风力发电, 1992(4): 17-21. Chen Yuyue. FRP fatigue design of FRP wind turbine[J]. Wind Power Generation, 1992(4): 17-21. (  0) 0) |
2. Ocean Engineering Key Laboratory of Qingdao, Qingdao 266100, China;
3. Prince of Songkla University, Hatyai 90112, Thailand
 2018, Vol. 48
2018, Vol. 48


