2) Department of Ocean Engineering, College of Engineering, Ocean University of China, Qingdao 266100, China;
3) Qingdao Municipal Key Laboratory of Ocean Renewable Energy, Ocean University of China, Qingdao 266100, China
Ocean renewable energy is considered a promising solution to environmental and resource issues related to energy generation. Wave energy is more adaptable in China due to its wide distribution comparing with other ocean renewable energy (Zhang et al., 2014; Shi et al., 2016). At the early stages of wave energy converter (WEC) development, fixed and nearshore structures were the majority of these devices. However, as deep-water exploitation has gradually become more popular, offshore floating WECs have become more popular (Falcão, 2010). Compared with ordinary WECs in shallow water, offshore floating ones are more flexible and free of water depth limitations; offshore WECs can extract more energy from the ocean (Falcão et al., 2010).
In general, offshore floating WECs can be divided into single or multi floater structures. A single heaving buoy, one of the simplest WEC devices, features a power take-off (PTO) system that is usually fixed to some stationary structure. However, the applications of such a device are usually restricted by the operating water depth. A two-body system absorbs energy by the reactive movement between floaters (Jaya Muliawan et al., 2013; Liang and Zuo, 2017). Under this principle, the limitation of water depth is overcome by a flexible mooring system, and steady efficiency can be obtained (Yu and Li, 2011). One of the earlier two-body WECs developed is the Bipartite Point Absorber, which consists of an outer floater as a reference and an inner floater as an oscillator (Ferdinande and Vantorre, 1986). Following this concept, Wavebob was adopted and carried out to sea trials (Weber et al., 2009). Other two-body system devices, such as AquaBuoy (Weinstein et al., 2004), SeaBeavI (Elwood et al., 2010b), and PowerBuoy (Edwards, 2011), have also been proposed.
As wave energy is a potential commercial-scale resource, many studies have focused on its practical utilization. Temeev et al. (2006) proposed WEC for hydrogen production. Zanuttigh and Angelelli (2013) proposed floating WECs as a new way to protect the coast line. Dai et al. (2017) conceived a novel WEC for monitoring the marine environment.
To explore the principle of two-body WEC systems, theoretical studies have been applied, many of which use the method of eigenfunction expansion to solve the related problems. Berggren and Johansson (1992) described the radiation problem of two bodies and the interaction effects between the plate and buoy on hydrodynamic coefficients. Eidsmoen (1995) utilized the IPS buoy system to find optimal hydrodynamic parameters. Falnes (1999) formed an equivalent system in two-body WECs to evident that it could obtain higher power than either consisting body. Wu et al. (2004) and Zheng et al. (2005) also investigated the mathematical descriptions of the two-body problem.
Despite the wealth of information provided by the afore-mentioned studies, however, theoretical analysis considers flow as non-viscous and irrotational, which is inconsistent with reality. Hence, numerical simulations have been considered to be an efficient and accurate means to reveal actual phenomena at sea. These simulations can be classified in many methods, including finite element, finite volume, finite difference, and boundary element. Yu and Li (2013) utilized a RANS approach to show nonlinear effects on hydrodynamic performance; these effects were found to significantly decrease the power output. Since mooring and PTO systems affect the hydrodynamic performance of WECs, studies related to these concepts have been published. Jaya Muliawan et al. (2013) and Muliawan et al. (2013), for example, determined the effect of mooring and PTO systems on energy capture. Amiri et al. (2016) investigated the effects of wave characteristics on energy conversion efficiency with consideration of both PTO and mooring configurations.
Experimental studies on two-body systems, as a direct and efficient means to observe actual phenomena, have drawn great attention. Elwood et al. (2010a) presented an innovative modeling technique that investigated the power performance of a two-body system by measuring wave forces. Li et al. (2012) revealed the hydrodynamic performance of a heaving buoy system with consideration of the viscous effect. Beatty et al. (2015) revealed the design implications of a PTO control scheme and relative motion constraints. Son et al. (2016) validated theoretical predictions and found the optimal shape leading to an increase in power absorption. Cho and Kim (2017) stated that large relative heave motion could be obtained near two resonant frequencies in the present two-buoy WEC model. To expand the utilization of two-body systems, Martin (2017) found the optimal mass ratio between the two bodies and the optimal shape of the submerged component. The control strategy of WECs has also been considered. Shek et al. (2008), Falcão et al. (2009), and Henriques et al. (2012) evaluated the performance of WECs under various control strategies, eventually concluding that the control strategy could be an effective method to increase energy absorption.
Most of the representative models applied in previous studies consist of a long tube-like or a submerged body. This paper focuses on a novel floating two-body WEC consisting of a platform that is treated as a carrier component and a heaving buoy that is considered the capture component. Both components are floating and have the same order of magnitude in the vertical direction scale. This two-body system is designed to supply energy to breeding net cages. The floating platform can also provide space for other facilities, such as monitoring equipment and bait storage. Thus, the platform is more complex than existing devices, which are purely power generating. Physical modeling is conducted to study the hydrodynamic performance of the novel WEC considering the effects of net cage, draft depth, and PTO.
This paper is organized as follows. The detailed design of the WEC and wave conditions are presented in Section 2, the setup of the experiment is described in Section 3, and the experimental data analysis and discussion are given in Section 4. Conclusions are drawn in Section 5.
2 Novel Floating Platform with WECThe characteristics of wide-banded wave spectrum are smaller average wave height and shorter wave period in China, which also leads to smaller floaters in a heaving buoy system (You et al., 2003; Shi et al., 2011). Considering the growing needs of deep-water development, aquaculture has extended from nearshore to offshore under the constraints of space and environment; in this situation, the power supply becomes a key problem. A floating WEC is chosen to provide an offshore aquaculture power supply, and the Ocean University of China proposes a novel floating platform assembled with a heaving buoy.
The net cage platform is intended for use in the cold water mass of the Yellow Sea, which is located northeast of China Sea. The statistical frequencies of monthly averaged significant wave heights and periods are shown in Table 1. The annual average significant wave height of the area is 1.3 m with 6.0 s in period. According to Table 1, the most frequently occurring wave heights are in the range of 1.0–1.6 m and the most frequently occurring periods are in the range of 5.8–6.0 s. A heaving buoy WEC is designed under these wave conditions.
|
|
Table 1 Scatter diagram of wave resource statistics |
The novel WEC system consists of a power platform with a heaving buoy set and a catenary-chain mooring system; it is used as the power supply for several breeding net cages, as shown in Fig.1. The platform is composed of energy capture, power generation, and support structures. The device harvests energy using the gyroscope buoy at the center of the platform under the guid ance of three rods. The support structure consists of a working deck, which provides space for the power generation system, a set of buoyancy pipes, and a wave damping plate. All of these components are interconnected by columns. Six hollow buoyancy pipes connected to form a hexagon provide the necessary buoyancy. The wave damping plate is set at the bottom of the device to steady the platform (Li et al., 2013; Beatty et al., 2015).

|
Fig. 1 Floating platform WEC system. |
A physical experiment was conducted in a wave tank in Shandong Provincial Key Laboratory of Ocean Engineering. The wave tank measured 60 m × 40 m × 1.5 m and included a piston wave maker that could generate waves with heights ranging from 0.05 m to 0.25 m and periods ranging from 0.5 s to 2.5 s in regular and irregular wave conditions. The wave tank absorbed energy via a porous medium at its end and flank.
The gravity similarity principle was applied at a scale of 1:16. The deployment of the test system is illustrated in Fig.2. The model was placed 28 m away from the wave maker and 13 m away from the flank. The still water depth h during the test was fixed to 1.2 m. The model was moored at the main buoyancy pipes to the bottom of the tank by three catenary anchor chains. A heaving buoy was installed at the center of the platform by three guide rods.
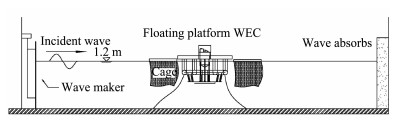
|
Fig. 2 Sketch of the deployment of the experimental model. |
The parameters of the model are shown in Table 2. The working deck forms a regular hexagon. Six columns connect the upper working deck and buoyancy pipes, beneath which are inclined struts connected to the wave damping plate, as shown in Fig.3(a). A heaving buoy shaped like a gyroscope is installed at the center of the deck. The diagram of the buoy, which has a mass of 0.97 kg and draft depth of 64.13 mm, is shown in Fig.3(b). The natural frequency of the buoy, which is calculated via the boundary element method, is 8.48 rad s-1. The model test did not consider friction damping between the buoy and the three guide rods because oil lubrication was applied to the system.
|
|
Table 2 Geometric and physical parameters of the scale model |
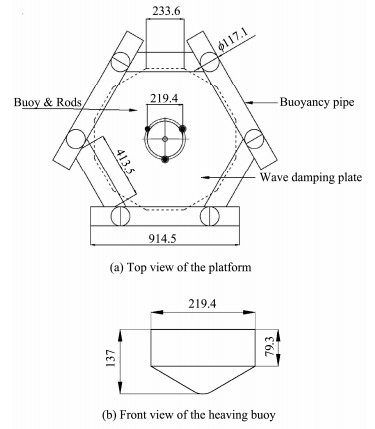
|
Fig. 3 Model diagrams of the support structures and buoy. |
A series of wave gauges and a laser range finder were used in the test to measure the water surface elevation and relative displacement of the heaving buoy. The sampling frequencies of the wave gauges and laser range finder were 50 and 15 Hz, respectively. The test employed both regular and irregular wave conditions. The regular wave test validated the design of the platform, while the irregular wave test determined the response performance of the proposed WEC in real-sea conditions. The test cases are shown in Table 3; here, H is the significant wave height, and T is the significant wave period in irregular wave conditions. The test covered the most frequent wave heights and periods observed in the Yellow Sea area. Tests for each case were repeated thrice to ensure reliability and repeatability, and the average value of these tests was reported as the result.
|
|
Table 3 Wave conditions in the test |
The nomenclature which would be used in Section 4 is explained. The relative displacement a, which is defined as the motion between the buoy and the platform, was measured by the laser range finder. The laser range finder was fixed on the platform, and the laser shot on the heaving buoy, by this way could a be got. The relative displacement versus the incident wave height, a/H, is used to describe the hydrodynamic performance of the system, as well as the ratio A/H, where A is the peak-valley value of a.
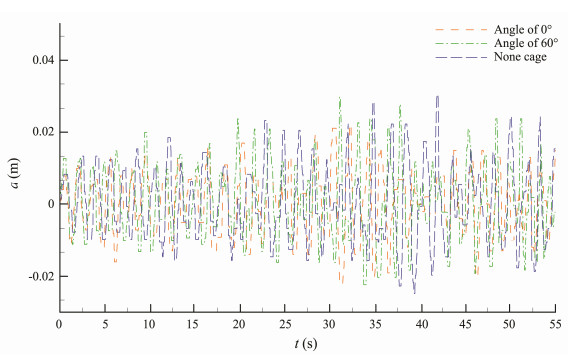
4.1 Effect of the Net Cage with Consideration of the Incident Wave AngleAlthough net cages are connected to the platform while working and can be expected to affect its hydrodynamic performance, a no-cage test was first conducted to enable comparison of the results. This test considered two incident wave angles, i.e., 0° and 60°, as shown in Fig.4. Under regular wave conditions, when the incident wave angle is 0°, the relative amplitude of the platform with net cages is smaller than that of the platform without cages; however, when the incident wave angle is 60°, the relative amplitude of the former is similar to or greater than that of the latter, as shown in Fig.5. These results may be explained by the fact that incident waves are diffracted and reflected when they pass through the front of the cage; as such, the buoy with net cages experiences smaller motion than the case without cages. However, when the cages are placed on both sides of the support structure, they give a tiny effect of the wave concentration; thus, the buoy with cages has a larger amplitude than that without cages. Fig.6 illustrates the relative amplitude under irregular wave conditions when the wave height is 81 mm and the wave period is 1.5 s. Results reveal that the angle of incident waves relative to the net cage is quite important; the relative amplitude obtained at 60° is consistently larger than that found at 0° when the net cages are mounted. The relative amplitude under irregular wave conditions is much poorer than that under regular wave conditions.
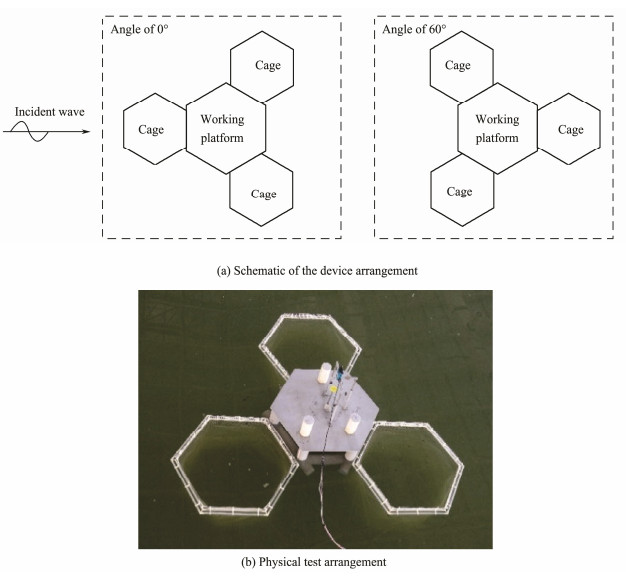
|
Fig. 4 Arrangement of the floating platform WEC and cages. |
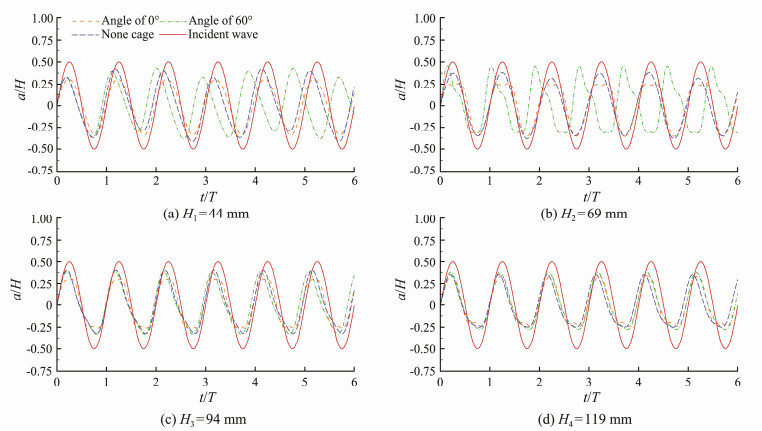
|
Fig. 5 Relative motion under regular wave conditions (T = 1.5 s). |
|
Fig. 6 Motion of the platform under irregular wave conditions. |
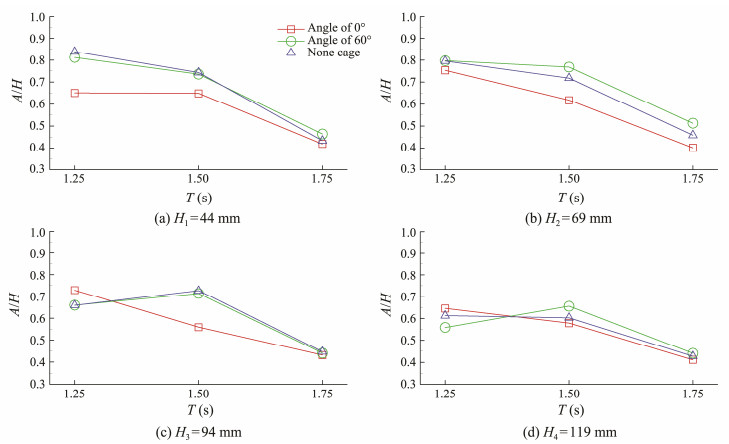
The range of A/H is 0.28–0.85 in the model test. In Fig.7, A/H at a certain wave height decreases with increasing wave period, which can be explained by the supposition that the longer the wave period, the more simultaneous between the buoy and the support structure. In Fig.8, the relative amplitude shows small fluctuations relative to the wave height, which means it is quite stable. The wave height exerts minimal effects on hydrodynamic performance. Hence, short periods are more suitable for the proposed floating platform WEC system than long periods.
|
Fig. 7 Relative amplitude under different wave periods. |

|
Fig. 8 Relative amplitude under different wave heights. |
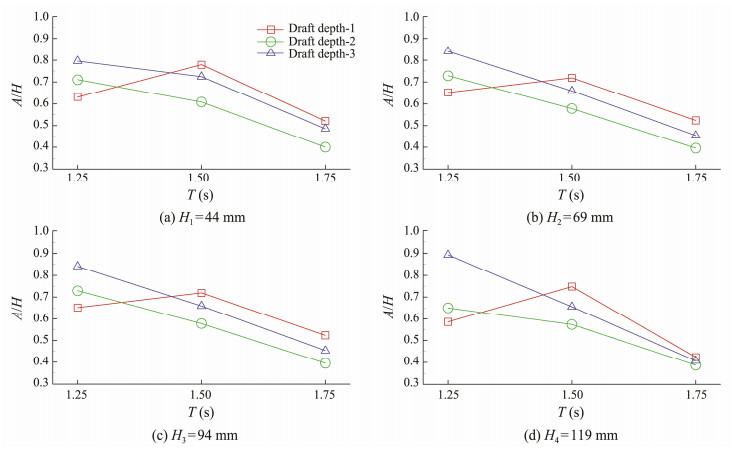
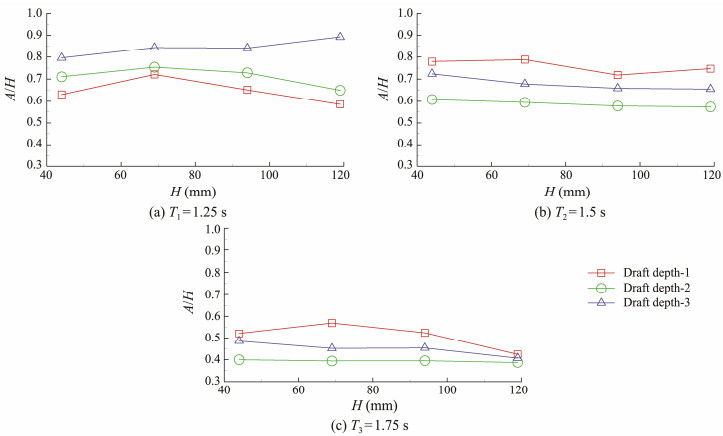
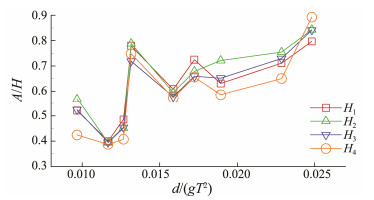
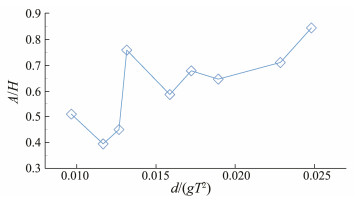
The draft depth of the platform (d), which is defined as the distance from the still water surface to the wave damping plate, is also an important factor affecting the hydrodynamic performance of the WEC. Three different d of 290, 350, and 380 mm, denoted as draft depth-1, 2, and 3, respectively, were tested, and the results obtained were compared. The incident wave periods are identical to those applied in earlier experiments. Figs. 9 and 10 compare the results under different wave periods and heights, respectively. As shown in Fig.9, the relative amplitude shows good performance under deep draft depths when the wave period is small. However, when the wave period T = 1.25 s, the curve of draft depth-1 differs from those of the other two draft depths. With increasing incident wave height, the response shows minor changes. To reveal the principle behind these results, the parameter d/gT2 is used to describe changes in relative amplitude as a function of draft depth and wave period. This parameter reflects the relationship between the draft depth and the incident wave period. Interestingly, regardless of the incident wave height, the curves of A/H versus d/gT2 are nearly the same, as shown in Fig.11. Fig.12 shows the average change trend of all incident wave conditions. It implies that when a capture structure is designed, the relationship between draft depth and incident wave period is determined. Thus, determining the best hydrodynamic response depends on the draft depth, can refer to the curve like Fig.12.
|
Fig. 9 Relative amplitude under different wave periods. |
|
Fig. 10 Relative amplitude under different wave heights. |
|
Fig. 11 Relationship between relative amplitude and d/gT2. |
|
Fig. 12 Average curve of all incident wave conditions. |
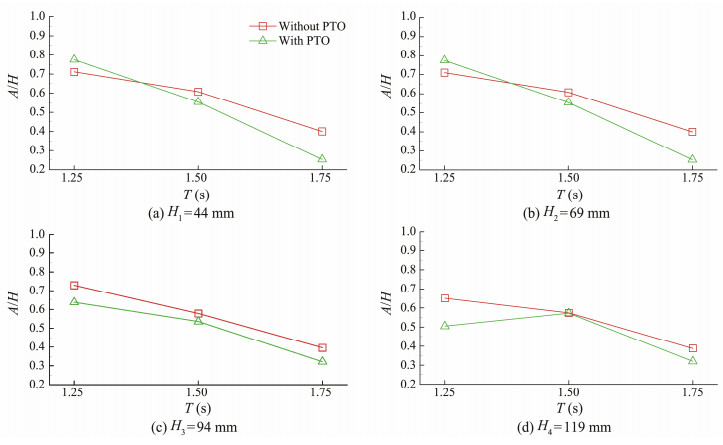
PTO damping exerts an extra force acting on the WEC. A constant optimal PTO was applied to the tests using controlled friction, which was validated before loading, modeling the feedback force from the PTO system, according to a previous study (Shi et al., 2018). Figs.13 and 14 compare the relative amplitudes of the corresponding wave periods and wave heights under two conditions; here, the red line represents the case without the PTO, while the green one represents the case with the optimal PTO. The relative amplitude is clearly smaller with the PTO than without it, and the WEC shows better performance in shorter wave periods. A slight difference in the results is observed under different wave heights. These findings indicate that the wave height has less effect on the hydrodynamic performance of the WEC than the wave period.
|
Fig. 13 Relative amplitude under different wave periods. |

|
Fig. 14 Relative amplitude under different wave heights. |
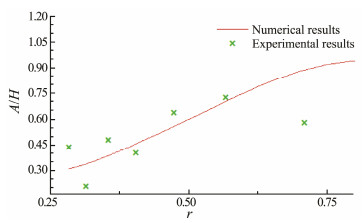
The RAO against r, which is defined as the ratio of incident wave frequency to the natural frequency of the floating platform WEC system under regular wave excitation, is shown in Fig.15. The calculated resonance period for the system is between 0.47 and 1.30 s. Seven different incident wave periods were applied from 0.99 to 2.47 s at the same wave height of 50 mm. The natural frequencies of the buoy, platform, and combined structure calculated by the boundary element method are 8.48, 1.34, and 8.97 rad s-1, respectively. The RAO values fluctuate with increasing incident wave period. The peak RAO is 0.72 and occurs at 5.09 rad s-1. The minimum RAO is 0.21 and occurs at 2.83 rad s-1. Some acceptable differences between the experimental and numerical results are observed. Thus, determining the resonance scope to balance the benefits of energy capture while preserving safety is important.
|
Fig. 15 Distributions of relative amplitude. |
A novel heaving buoy-based WEC applied to a floating net cage platform is proposed in this work, and an experimental study of this device was performed in a wave tank. Specifically, the hydrodynamic performance of the WEC was studied under regular and irregular wave conditions.
The experimental results show that the hydrodynamic performance of the device could be affected by incident wave angle, wave period, and draft depth. The relative response shows intense interactions at small wave periods, and the layout of the device and net cages is an important factor influencing performance. The draft depth could be determined according to wave period rather than wave height. The RAO of the device is also studied to determine the resonance period.
The experimental results provide a reference for the optimum design of WECs, including its mass and size and shape of the platform. In future work, the phase difference between the platform and buoy should be derived to accomplish maximal and safe energy capture.
AcknowledgementsThis work is financially supported by the Special Project for Marine Renewable Energy (No. GHME2016YY02), the National Key R & D Program of China (No. 2018YFB 1501900), the Shandong Provincial Natural Science Key Basic Program (No. ZR2017ZA0202), and the Qingdao Municipal Science & Technology Program (No. 15-8-3-7-jch).
Amiri, A., Panahi, R. and Radfar, S., 2016. Parametric study of two-body floating-point wave absorber. Journal of Marine Science and Application, 15(1): 41-49. (  0) 0) |
Beatty, S. J., Hall, M., Buckham, B. J., Wild, P. and Bocking, B., 2015. Experimental and numerical comparisons of self- reacting point absorber wave energy converters in regular waves. Ocean Engineering, 104: 370-386. DOI:10.1016/j.oceaneng.2015.05.027 (  0) 0) |
Berggren, L. and Johansson, M., 1992. Hydrodynamic coefficients of a wave energy device consisting of a buoy and a submerged plate. Applied Ocean Research, 14(1): 51-58. (  0) 0) |
Cho, I. H. and Kim, M. H., 2017. Hydrodynamic performance evaluation of a wave energy converter with two concentric vertical cylinders by analytic solutions and model tests. Ocean Engineering, 130: 498-509. DOI:10.1016/j.oceaneng.2016.11.069 (  0) 0) |
Dai, Y., Chen, Y. and Xie, L., 2017. A study on a novel two- body floating wave energy converter. Ocean Engineering, 130: 407-416. DOI:10.1016/j.oceaneng.2016.11.049 (  0) 0) |
Edwards, K., 2011. Ocean testing of a wave-capturing PowerBuoy. Marine Energy Technology Symposium. Ocean Waves Workshop, New Orleans, 1-30.
(  0) 0) |
Eidsmoen, H., 1995. Hydrodynamic parameters for a two-body axisymmetric system. Applied Ocean Research, 17(2): 103-115. (  0) 0) |
Elwood, D., Yim, S. C., Amon, E. A., von Jouanne, A. and Brekken, T. K. A., 2010a. Experimental force characterization and numerical modeling of a taut-moored dual-body wave energy conversion system. Journal of Offshore Mechanics and Arctic Engineering, 132(1): 011102. DOI:10.1115/1.3160535 (  0) 0) |
Elwood, D., Yim, S. C., Prudell, J., Stillinger, C., von Jouanne, A., Brekken, T., Brown, A. and Paasch, R., 2010b. Design, construction, and ocean testing of a taut-moored dual-body wave energy converter with a linear generator power take-off. Renewable Energy, 35(2): 348-354. (  0) 0) |
Falcão, A. F. D. O., 2010. Wave energy utilization: A review of the technologies. Renewable and Sustainable Energy Reviews, 14(3): 899-918. (  0) 0) |
Falcão, A. F. D. O., Justino, P. A. P., Henriques, J. C. C., and André, J. M. C., 2009. Reactive versus latching phase control of a two-body heaving wave energy converter. Tenth European Control Conference. Budapest, Hungary, 3731-3736.
(  0) 0) |
Falcão, A. F. D. O., Pereira, P. E. R., Henriques, J. C. C. and Gato, L. M. C., 2010. Hydrodynamic simulation of a floating wave energy converter by a u-tube rig for power take-off testing. Ocean Engineering, 37(14): 1253-1260. (  0) 0) |
Falnes, J., 1999. Wave-energy conversion through relative motion between two single-mode oscillating bodies. Journal of Offshore Mechanics and Arctic Engineering, 121(1): 32-38. DOI:10.1115/1.2829552 (  0) 0) |
Ferdinande, V., and Vantorre, M., 1986. The concept of a Bipartite Point Absorber. In: Hydrodynamics of Ocean Wave-Energy Utilization. Springer Berlin Heidelberg, 217-226.
(  0) 0) |
Henriques, J. C. C., Lopes, M. F. P., Gomes, R. P. F., Gato, L. M. C. and Falcão, A. F. O., 2012. On the annual wave energy absorption by two-body heaving WECs with latching control. Renewable Energy, 45(3): 31-40. (  0) 0) |
Jaya, Muliawan M., Gao, Z., Moan, T. and Babarit, A., 2013. Analysis of a two-body floating wave energy converter with particular focus on the effects of power take-off and mooring systems on energy capture. Journal of Offshore Mechanics and Arctic Engineering, 135(3): 031902. DOI:10.1115/1.4023796 (  0) 0) |
Li, B., Huang, Z., Low, Y. M. and Ou, J., 2013. Experimental and numerical study of the effects of heave plate on the motion of a new deep draft multi-spar platform. Journal of Marine Science and Technology (Japan), 18(2): 229-246. DOI:10.1007/s00773-012-0203-0 (  0) 0) |
Li, Y., Yu, Y.-H., Epler, J., and Previsic, M., 2012. Experimental Investigation of the power generation performance of floating-point absorber wave energy systems. 27th International Workshop on Water Waves and Floating Bodies. Copenhagen, Denmark, 1-6.
(  0) 0) |
Liang, C. and Zuo, L., 2017. On the dynamics and design of a two-body wave energy converter. Renewable Energy, 101: 265-274. DOI:10.1016/j.renene.2016.08.059 (  0) 0) |
Martin, D. M., 2017. Hydrodynamic design optimization and wave tank testing of self-reacting two-body wave energy converter. Master thesis. Virginia Polytechnic Institute and State University.
(  0) 0) |
Muliawan, M. J., Gao, Z. and Moan, T., 2013. Analysis of a two-body floating wave energy converter with particular focus on the effects of power take-off and mooring systems on energy capture. Journal of Offshore Mechanics and Arctic Engineering, 135(3): 317-328. (  0) 0) |
Shek, J. K. H., Macpherson, D. E., and Mueller, M. A., 2008. Phase and amplitude control of a linear generator for wave energy conversion. Conference on Power Electronics, Machines & Drives. IET. York, 66-70.
(  0) 0) |
Shi, H. D., Cao, F. F., Liu, Z. and Qu, N., 2016. Theoretical study on the power take-off estimation of heaving buoy wave energy converter. Renewable Energy, 86: 441-448. DOI:10.1016/j.renene.2015.08.027 (  0) 0) |
Shi, H. D., Zhao, C. Y., Liu, Z. and Cao, F. F., 2018. Study on hydraulic system efficiency of heaving-buoy wave energy converter. Journal of Ocean University of China, 17(5): 1044-1052. DOI:10.1007/s11802-018-3668-6 (  0) 0) |
Shi, W. Y., Wang, C. K. and Shen, J. F., 2011. Utilisation and prospect of ocean energy resource in China. Acta Energiae Solaris Sinica, 32(6): 913-923 (in Chinese with English abstract). (  0) 0) |
Son, D., Belissen, V. and Yeung, R. W., 2016. Performance validation and optimization of a dual coaxial-cylinder ocean- wave energy extractor. Renewable Energy, 92: 192-201. DOI:10.1016/j.renene.2016.01.032 (  0) 0) |
Temeev, A. A., Belokopytov, V. P. and Temeev, S. A., 2006. An integrated system of the floating wave energy converter and electrolytic hydrogen producer. Renewable Energy, 31: 225-239. DOI:10.1016/j.renene.2005.08.026 (  0) 0) |
Weber, J., Mouwen, F., Parish, A., and Robertson, D., 2009. Wavebob-Research and development network and tools in the context of systems engineering. The 8th European Wave and Tidal Energy Conference. Uppsala, Sweden, 416-420.
(  0) 0) |
Weinstein, A., Fredrikson, G., Parks, M. J., and Nielsen, K., 2004. AquaBuOY, the offshore wave energy converter numerical modelling and optimization. MTTS/IEEE Techno-Ocean'04 Conference. Kobe, Japan, 4: 1854-1859.
(  0) 0) |
Wu, B. J., Zheng, Y. H., You, Y. G., Sun, X. Y. and Chen, Y., 2004. On diffraction and radiation problem for a cylinder over a caisson in water of finite depth. International Journal of Engineering Science, 42: 1193-1213. DOI:10.1016/j.ijengsci.2003.12.006 (  0) 0) |
You, Y. G., Zheng, Y. H., and Ma, Y. J., 2003. Developments of wave energy utilization and technology in China. Proceedings of the 2003 CAE Engineer Technology Forum of Renewable Energy Developments. Beijing, 219-225 (in Chinese)
(  0) 0) |
Yu, Y. H., and Li, Y., 2011. A RANS simulation for the heave response of a two-body floating point wave absorber. International Offshore and Polar Engineering Conference. Hawaii, 1-7.
(  0) 0) |
Yu, Y. H. and Li, Y., 2013. Reynodls-averaged navier-stokes simulation of the heave performance of a two-body floating- point absorber wave energy system. Computers and Fluids, 73(6): 104-114. (  0) 0) |
Zanuttigh, B. and Angelelli, E., 2013. Experimental investigation of floating wave energy converters for coastal protection purpose. Coastal Engineering, 80(4): 148-159. (  0) 0) |
Zhang, Y. L., Lin, Z. and Liu, Q. L., 2014. Marine renewable energy in China: Current status and perspectives. Water Science and Engineering, 7(3): 288-305. (  0) 0) |
Zheng, Y. H., Shen, Y. M., You, Y. G., Wu, B. J. and Rong, L., 2005. Hydrodynamic properties of two vertical truncated cylinders in waves. Ocean Engineering, 32(3-4): 241-271. DOI:10.1016/j.oceaneng.2004.09.002 (  0) 0) |
 2019, Vol. 18
2019, Vol. 18


