1 Introduction

With the exploitation of marine oil and gas resources gradually extending to deep-water fields, top-tensioned risers (TTRs) are no longer suitable. Risers in the form of a catenary have been used widely for subsea engineering owing to the advantages of strong adaptability to vessel motion and no pretensioning. When the flow passes over the riser, an unsteady wake is generated in the form of shedding vortices. The vortices alternately fall off from both sides of the riser, producing a periodically varying lift force in the cross-flow (CF) and in-line (IL) directions (Liu et al., 2020). As the vortex-shedding frequency approaches the natural frequency of the structure, the lock-in phenomenon occurs; that is, the vortex-induced vibration (VIV) responses of the riser strengthen remarkably, thus triggering serious fatigue damage.

Numerous works concerning the VIV performance of risers have been published in the past two decades. However, most of them focus on the TTRs' behaviors (Chaplin et al., 2005; Guo and Lou, 2008; Song et al., 2011; Thorsen et al., 2015; Low and Srinil, 2016; Kang et al., 2018; Gao et al., 2019; Liang and Lou, 2020). With the rapid development of long flexible risers used in ocean engineering, studies on the VIVs of slender risers with large deformation have gradually become important. Halse et al. (1999) investigated the VIV performance of a real catenary-type riser (CTR) subjected to uniform flows experimentally, and the results showed that a single mode dominated the VIV responses. Morooka and Tsukada (2013) conducted VIV tests on a CTR and found substantial traveling wave behaviors of the structural vibration. Zhu et al. (2019) conducted similar experiments on a CTR. Wang et al.(2014, 2017, 2018) performed laboratory tests on a truncated model of a CTR under vessel motion and uniform flows. The fatigue damage induced by the VIV responses of the CTR model subjected to external uniform flow and vessel motion is in the same order of magnitude. However, experimental methods have some limitations, such as model scale limit, expensive cost, difficult flow profile generation, and others (Gao et al., 2019). Therefore, studying the VIV performance of large aspect-ratio CTR using the numerical simulation method is more effective.

Computational fluid dynamic (CFD) methods can analyze the VIV problems of marine risers from the perspective of the flow field (Herfjord et al., 1999; Lucor et al., 2005; Fu et al., 2018; Martins and Avila, 2019). CFD is computationally intensive and time-consuming in the VIV calculation of slender structures. In contrast to the CFD method, the Van der Pol wake oscillator in the semiempirical method has been gradually used for the VIV responses of risers (Bishop and Hassan, 1964; Facchinetti et al., 2004). Srinil et al. (2009) combined the reduced-order model with the wake oscillator to predict the VIV responses of the CTR, and the results demonstrated the feasibility of this model on the VIV responses of the curved riser. Meng and Zhu (2015) numerically studied the effect of internal flow and top tension on the VIV responses of a CTR subjected to uniform flows using a hydrodynamic model. Li et al. (2021) analyzed the incident angle of external flow on the VIV responses of the CTR based on vector form intrinsic finite element (VFIFE) theory coupled with the wake oscillator model. Because the IL-direction VIV amplitude is small, an order of magnitude lower than the CF-direction one, the VIV responses in the CF direction are investigated considerably and emphatically at present, and those in the IL direction are ignored. The dominant frequency in the IL direction is normally twice that in the CF direction, so Wan and Duan (2017) stated that the VIV-induced fatigue damage in both directions may be in the same order of magnitude. Kang and Jia (2013) found that the IL-vibration VIV frequencies displayed a 'multifrequency' phenomenon at different natural frequencies, which made the trajectory exhibit various forms of motion. Additionally, IL-direction VIVs trigger an oscillatory characteristic of the flow fields, which in turn affects the VIV responses in the CF direction. Therefore, the vibration provided by the IL direction of the riser cannot be ignored.

Solving the governing equations of nonlinear vibration of the structure is effective for the conventional finite element method. However, the conversion of local coordinates into global coordinates is inevitable, resulting in long computing time. In this paper, a new numerical scheme, the VFIFE method, is used to establish a CTR model, which can avoid the coordinate transformation. Moreover, the stiffness matrix is needless, and no iterative solution is required in the VFIFE method, leading to a simple calculation for a complex structure. The current research shows that the VFIFE method has great potential in the field of marine riser research (Wu et al., 2020; Xu et al., 2021; Yu et al., 2022).

In summary, the VIV response of CTRs in both directions considering the coupling effect has not been exhaustively studied, and it still needs to be explored comprehensively. Therefore, this paper establishes a VIV response prediction model of a CTR in both directions based on VFIFE theory coupled with wake oscillators. The explicit central differential algorithm is applied to solve the governing equation and update the time integration. The paper is divided into five sections. Model theory is briefly described in Section 2. The model is validated thoroughly in Section 3. The VIV response results are studied in Section 4. Conclusions are drawn in Section 5.

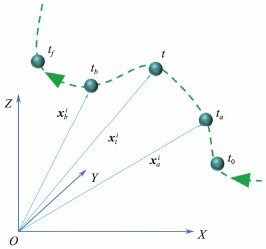
2 Model Description 2.1 Equation of Particle Motion

VFIFE theory is used to simulate the CTR, where the riser system is composed of an infinite number of particles, as shown in Fig.1. Adjacent particles are connected by beam elements. The beam element is massless. The particle motion is divided into several independent time nodes (t₀, t₁, t₂, ···, t_a, t_b, t_f), and the motion path of particle i at any time period (t_a ≤ t ≤ t_b) is considered its path unit, as shown in Fig.2.

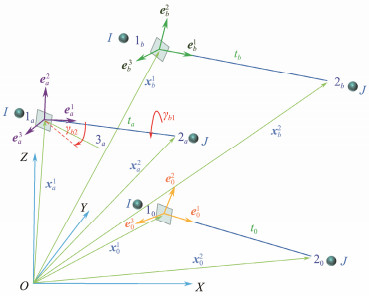
The axis of the riser is a time-varying curve under marine loadings, indicating that the axis direction of each beam element varies at different times. The particle position coordinates are calculated using a set of standard interpolation functions, and the principal coordinates of each beam element are constant. The principal coordinate system is established for pure deformation in Fig.3.

$ \boldsymbol{u}_b^1=\boldsymbol{x}_b^1-\boldsymbol{x}_a^1, \boldsymbol{u}_b^2=\boldsymbol{x}_b^2-\boldsymbol{x}_a^2, $

(1)

$ \boldsymbol{\beta}_b^1=\boldsymbol{\theta}_b^1-\boldsymbol{\theta}_a^1, \boldsymbol{\beta}_b^2=\boldsymbol{\theta}_b^2-\boldsymbol{\theta}_a^2, $

(2)

$ \boldsymbol{e}_a^1=\frac{x_a^2-x_a^1}{\left|x_a^2-x_a^1\right|}, \quad \boldsymbol{e}_a^2=\frac{\boldsymbol{e}_{13} \times \boldsymbol{e}_a^1}{\left|\boldsymbol{e}_{13} \times \boldsymbol{e}_a^1\right|}, \quad \boldsymbol{e}_{13}=\frac{x_a^3-x_a^1}{\left|x_a^3-x_a^1\right|}, \quad \boldsymbol{e}_a^3=\boldsymbol{e}_a^1 \times \boldsymbol{e}_a^2 . $

(3)

The rotation vector γ_b of the beam element in the time period t_b − t_a consists of two parts: γ_b1 is obtained by the beam element around its own axis. γ_b2 is determined by the rotation of the beam element from 1_a − 2_a to 1_b - 2_b at different moments. γ_b is expressed as γ_b = γ_b1 + γ_b2, γ_b1 = $ (\boldsymbol{\beta} _b^1 \cdot \boldsymbol{e}_a^1)\boldsymbol{e}_a^1 $, and γ_b2 = γ_bae_ba.

The external force on the riser is converted into an equivalent concentrated force on the particles. Correspondingly, the governing equations for the motion of the J particle are established as follows:

$ {m_J}\frac{{{{\text{d}}^2}}}{{{\text{d}}{t^2}}}\left[ {\begin{array}{*{20}{c}} {{x_J}} \\ {{y_J}} \\ {{z_J}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{P_{Jx}}} \\ {{P_{Jy}}} \\ {{P_{Jz}}} \end{array}} \right] + {\sum\limits_{j = {\text{1}}}^n {\left({\left[ {\begin{array}{*{20}{c}} {{p_{jx}}} \\ {{p_{jy}}} \\ {{p_{jz}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{f_{jx}}} \\ {{f_{jy}}} \\ {{f_{jz}}} \end{array}} \right]} \right)} _J}, $

(4)

$ {\left[ {\begin{array}{*{20}{c}} {{I_{xx}}}&{{I_{xy}}}&{{I_{xz}}} \\ {{I_{yx}}}&{{I_{yy}}}&{{I_{yz}}} \\ {{I_{zx}}}&{{I_{zy}}}&{{I_{zz}}} \end{array}} \right]_J}\frac{{{{\text{d}}^2}}}{{{\text{d}}{t^2}}}\left[ {\begin{array}{*{20}{c}} {{\theta _{Jx}}} \\ {{\theta _{Jy}}} \\ {{\theta _{Jz}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{Q_{Jx}}} \\ {{Q_{Jy}}} \\ {{Q_{Jz}}} \end{array}} \right] + {\sum\limits_{j = {\text{1}}}^n {\left({\left[ {\begin{array}{*{20}{c}} {{q_{jx}}} \\ {{q_{jy}}} \\ {{q_{jz}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{m_{jx}}} \\ {{m_{jy}}} \\ {{m_{jz}}} \end{array}} \right]} \right)} _J}, $

(5)

where X_J is the position vector of the particle J; θ_J is the angular vector of the spatial direction; P_J and pj are the concentrated external force and equivalent external force, respectively; Q_J and q_j are the concentrated external moment and equivalent external moment, respectively; f_j and m_j are the internal force and internal moment provided by beam element; m_J denotes the total mass of particle J, which is expressed as follows:

$ {m_J} = {\left({M + \sum\limits_{\alpha = {\text{1}}}^n {{m^\alpha }} } \right)_J} . $

(6)

The total mass of the riser is distributed equally among the particles:

$ {m^1} = {m^2} = {l_a}({m_s} + {m_f})/2, $

(7)

where m_s = ρ_s A, and m_f = C_a ρ_f D² π/4. The mass moment of inertia of the beam element relative to the main axis is expressed as follows:

$ {\hat I_{\text{2}}} = \left({\frac{{\text{1}}}{{\text{2}}}{\rho _a}{l_a}{A_a}} \right)r_{\text{2}}^{\text{2}}, {\hat I_{\text{3}}} = \left({\frac{{\text{1}}}{{\text{2}}}{\rho _a}{l_a}{A_a}} \right)r_{\text{3}}^{\text{2}}, $

(8)

where l_a is the length of the beam element; A_a is the cross-sectional area of the beam element; ρ_a is the physical density of the beam element; r₂ and r₃ are the gyration radii. The matrix of inertia for the section is ${\hat I_1} = {\hat I_2} + {\hat I_3}$. Then, the inertia moment in the principal coordinate is transformed into the domain coordinate matrix in the global coordinate by the transformation equation:

$ \boldsymbol{I}^j=\boldsymbol{\Omega}_u^{\mathrm{T}} \hat{\boldsymbol{I}}^j \boldsymbol{\Omega}_u, $

(9)

where Ω_a is the conversion matrix from the global coordinate to the principal coordinate. Finally, the total inertia matrix of the particle J in the global coordinate system is calculated using the following equation:

$ \boldsymbol{I}_J=\left(\boldsymbol{I}_m+\sum\limits_{\alpha=1}^n \boldsymbol{I}^\alpha\right)_J . $

(10)

2.2 Deformation Analysis

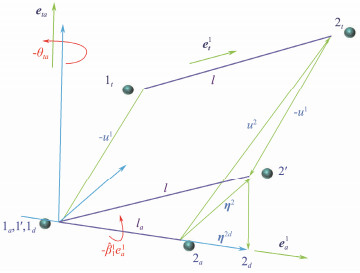
To address the pure deformation of the riser, the concept of virtual reverse motion is introduced in VFIFE theory. As shown in Fig.4, the beam element makes a virtual reverse motion, which includes translation and rotation. The displacement vectors of nodes 1 and 2 are shown in the following equation:

$ \left\{\begin{array}{l} \boldsymbol{\eta}^1=\boldsymbol{u}^1-\boldsymbol{u}^1=0 \\ \boldsymbol{\eta}^2=\boldsymbol{u}^2+\left(-\boldsymbol{u}^1\right) \end{array},\right. $

(11)

where u¹ and u² are the translation vectors of the beam element.

The rotations of the rigid body are classified as axial rotation and translational rotation. Node 1 is taken as the reference point of rotation, and the rotation vector component in $\boldsymbol{e}_a^1$ direction is as follows:

$ \hat{\beta}_1^1=\boldsymbol{\beta}_b^{\mathbf{l}} \cdot \boldsymbol{e}_a^1 . $

(12)

The other rotation component is the rotation of the beam element in time period t − t_a and is shown as follows:

$ \boldsymbol{\theta}_{t a}=\theta_{t a} \boldsymbol{e}_{t a}, $

(13)

where $ \theta_{t a}=\sin ^{-1}\left(\left|\boldsymbol{e}_a^1 \times \boldsymbol{e}_t^1\right|\right), \boldsymbol{e}_{t a}=\left(\boldsymbol{e}_a^1 \times \boldsymbol{e}_t^1\right) /\left|\boldsymbol{e}_a^1 \times \boldsymbol{e}_t^1\right| $.

The rotation vector γ_t can be expressed as follows:

$ \boldsymbol{\gamma}_t=\hat{\beta}_1^1 \boldsymbol{e}_a^1+\theta_{t a} \boldsymbol{e}_{t a}. $

(14)

In the principal coordinate system, it is expressed as follows:

$ \hat{\boldsymbol{\gamma}}_t=\mathbf{\Omega}_a \boldsymbol{\gamma}_t=\left[\begin{array}{lll} \hat{\beta}_1^1 & \hat{\theta}_{2 t} & \hat{\theta}_{3 t} \end{array}\right]^{\mathrm{T}}, \quad \boldsymbol{\Omega}_a=\left[\begin{array}{lll} \left(e_a^1\right)^{\mathrm{T}} & \left(e_a^2\right)^{\mathrm{T}} & \left(e_a^3\right)^{\mathrm{T}} \end{array}\right]^{\mathrm{T}} . $

(15)

As shown in Fig.4, the displacement of node 2 can be expressed as follows:

$ \boldsymbol{\eta}^{2 d}=\hat{\Delta}_e \boldsymbol{e}_a^1, $

(16)

where $ {\hat \Delta _e} = {\text{|}}{\boldsymbol{\eta} ^{2d}}{\text{|}} = {l_d} - {l_a} $, and l_d and l_a are the spatial spans of beam elements 1_d - 2_d and 1_a − 2_a.

The angular displacements of nodes 1 and 2 are known as follows:

$ \hat{\boldsymbol{\beta}}^j=\boldsymbol{\Omega}_u \boldsymbol{\beta}^j, j=1,2 . $

(17)

The amount of pure deformation occurring at unit nodes 1 and 2 in the principal coordinate system can be expressed as follows:

$ \hat{\boldsymbol{\varphi}}^j=\hat{\boldsymbol{\beta}}^j-\hat{\boldsymbol{\gamma}}_t=\left[\begin{array}{c} \hat{\boldsymbol{\varphi}}_1^j \\ \hat{\varphi}_2^j \\ \hat{\varphi}_3^j \end{array}\right]=\left[\begin{array}{l} \hat{\beta}_1^j+\left(-\hat{\beta}_1^1\right) \\ \hat{\beta}_2^j+\left(-\hat{\theta}_{2 t}\right) \\ \hat{\beta}_3^j+\left(-\hat{\theta}_{3 t}\right) \end{array}\right], j=1,2 . $

(18)

2.3 Van der Pol Wake Oscillator

In this study, the classical wake oscillator equation proposed by Facchinetti et al. (2004) is adopted:

$ \frac{{{{\text{d}}^2}{q_j}}}{{{\text{d}}{t^2}}} + 2{\varepsilon _x}{\omega _{fj}}\left({q_j^2 - 1} \right)\frac{{{\text{d}}{q_j}}}{{{\text{d}}t}} + 4\omega _{fj}^2{q_j} = {A_x}\frac{{{{\text{d}}^2}{x_j}}}{{{\text{d}}{t^2}}}, $

(19)

$ \frac{{{{\text{d}}^2}{p_j}}}{{{\text{d}}{t^2}}} + {\varepsilon _y}{\omega _{fj}}\left({p_j^2 - 1} \right)\frac{{{\text{d}}{p_j}}}{{{\text{d}}t}} + \omega _{fj}^2{p_j} = {A_y}\frac{{{{\text{d}}^2}{y_j}}}{{{\text{d}}{t^2}}}, $

(20)

where ε_x, ε_y, A_x and A_y are the parameters estimated according to the experiment. As reported in a study by Srinil and Zanganeh (2014), for flexible cylinders/pipes oscillating in the CF and IL directions, the values of A_y /ε_y or A_x /ε_x can be of the order of magnitude of 40 - 1920. In this work, the values of the four key parameters are set as ε_x = 0.05, ε_y = 0.04, A_x = 96, and A_y = 12.

q_j and p_j are the wake oscillator variables in both directions. ω_fj is the vortex shedding frequency. In the analysis of VIV in the direction of CF and IL, the vortex shedding frequency ω_fj fully considers the relative velocity between the IL direction motion and the flow fields

$ \omega_{f j}=\frac{2 \pi S_t\left|U_c-\dot{x}\right|}{D}, $

instead of just considering the velocity of the fluid particles, and S_t is the Strouhal number.

Because the vibration frequency in the IL direction is twice that in the CF direction, the vibration frequency in the IL direction in Eq. (19) is 2ω_fj, whereas the vibration frequency in the CF direction in Eq. (20) is ω_fj.

The fluid force on space particle j is calculated by the following equation:

$ {F_{Dj}} = \frac{1}{2}({C_{Dm}} + {C_D})\rho D{U_{jn}}^2, $

(21)

$ {F_{Lj}} = \frac{1}{2}{C_L}\rho D{U_{jn}}^2, $

(22)

where C_Dm is the mean drag coefficient, C_D is the fluctuating drag coefficient. and C_L is the lift coefficient. C_D = $ {C_{D0}}\frac{{{q_j}}}{2} $, C_D0 is the drag amplitude. $ {C_L} = {C_{L0}}\frac{{{p_j}}}{2} $, C_L0 is the lift amplitude.

2.4 Numerical Solution

Considering the iterative complexity and convergence difficulties of nonlinear problems, the explicit central difference method is adopted to solve the governing equations of the VIV responses of the CTR. The central differential solutions for position coordinates, the directional angle of particles, and the wake oscillator are as follows:

$ \left[ {\begin{array}{*{20}{c}} {x_J^{n + 1}} \\ {y_J^{n + 1}} \\ {z_J^{n + 1}} \end{array}} \right] = 2{C_1}\left[ {\begin{array}{*{20}{c}} {x_J^n} \\ {y_J^n} \\ {z_J^n} \end{array}} \right] - {C_2}\left[ {\begin{array}{*{20}{c}} {x_J^{n - 1}} \\ {y_J^{n - 1}} \\ {z_J^{n - 1}} \end{array}} \right] + {C_1}{h^2}\left({\left[ {\begin{array}{*{20}{c}} {F_{Jx}^{{\text{ext}}}} \\ {F_{Jy}^{{\text{ext}}}} \\ {F_{Jz}^{{\text{ext}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {F_{Jx}^{{\text{int}}}} \\ {F_{Jy}^{{\text{int}}}} \\ {F_{Jz}^{{\text{int}}}} \end{array}} \right]} \right) / {m_J}, $

(23)

$ \left[ {\begin{array}{*{20}{c}} {\theta _{Jx}^{n + 1}} \\ {\theta _{Jy}^{n + 1}} \\ {\theta _{Jz}^{n + 1}} \end{array}} \right] = 2{C_1}\left[ {\begin{array}{*{20}{c}} {\theta _{Jx}^n} \\ {\theta _{Jy}^n} \\ {\theta _{Jz}^n} \end{array}} \right] - {C_2}\left[ {\begin{array}{*{20}{c}} {\theta _{Jx}^{n - 1}} \\ {\theta _{Jy}^{n - 1}} \\ {\theta _{Jz}^{n - 1}} \end{array}} \right] + {C_1}{h^2}\left({\left[ {\begin{array}{*{20}{c}} {M_{Jx}^{{\text{ext}}}} \\ {M_{Jy}^{{\text{ext}}}} \\ {M_{Jz}^{{\text{ext}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {M_{Jx}^{{\text{int}}}} \\ {M_{Jy}^{{\text{int}}}} \\ {M_{Jz}^{{\text{int}}}} \end{array}} \right]} \right) / \left[ {\begin{array}{*{20}{c}} {{I_{Jx}}} \\ {{I_{Jy}}} \\ {{I_{Jz}}} \end{array}} \right], $

(24)

$ q_j^{n + 1} = \frac{{\frac{{{A_x}{h^2}(F_J^{{\text{ext}}} + F_J^{{\text{int}}})}}{{D{m_J}}} + q_j^n(2 - 4\omega _{fj}^2h) - q_j^{n - 1}(1 - {\varepsilon _x}{\omega _{fj}}h({{(q_j^n)}^2} - 1))}}{{1 + {\varepsilon _x}{\omega _{fjn}}h({{(q_j^n)}^2} - 1)}}, $

(25)

$ p_j^{n + 1} = \frac{{\frac{{{A_y}{h^2}(F_J^{{\text{ext}}} + F_J^{{\text{int}}})}}{{D{m_J}}} + p_j^n(2 - \omega _{fj}^2) - p_j^{n - 1}(1 - 0.5{\varepsilon _y}{\omega _{fj}}h({{(q_j^n)}^2} - 1))}}{{1 + 0.5{\varepsilon _y}{\omega _{fj}}h({{(p_j^n)}^2} - 1)}}, $

(26)

where h is the time step. C₁ and C₂ are the damped compound terms expressed as C₁ = 1/(1 + ξh/2) and C₂ = C₁/(1 − ξh/2), respectively. ξ is the damping coefficient of the structure. $ F_J^{{\text{ext}}} $ and $ M_J^{{\text{ext}}} $ are the external forces and external moments of particle J, respectively. $ F_J^{{int} } $ and $ M_J^{{int} } $ are the integrals of the internal forces and internal moments of particle J, respectively.

3 Model Validation

Before the examination of the structural VIV responses, the accuracy and applicability of the proposed numerical scheme should be strictly verified. In this paper, VIV tests on a small-scale model of a flexible riser conducted by Zhu et al. (2016) and a numerical simulation result of VIV responses of a cylinder based on the CFD method by Yamamoto et al. (2004) are selected as references. The key parameters are set according to the literature.

Fig.5 presents the VIV displacement distributions along the span using the proposed theory compared with the experimental results given by Zhu et al. (2016). The VIV responses calculated by the wake oscillator model agree with the reference results, particularly in Fig.5. A small difference can be clearly observed, namely, the VIV displacement at z/L = 0.3 obtained by the wake oscillator model is lower than that from the reference, and the relative error between the calculated results using the proposed model and the experimental results of Zhu et al. (2016) is lower than 15%, which could be due to the different damping coefficients. In addition, the result is attributed to the possibly uncaptured nonlinear physics (such as splashing-over). However, the correlation between the predicted and published results is reasonable, which also indicates the accuracy and applicability of the proposed numerical scheme in calculating the VIV responses of a CTR.

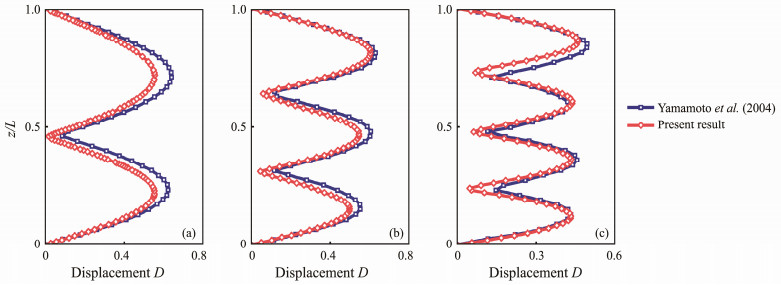
To verify further the accuracy of the proposed model in calculating the coupled VIV responses of marine risers in both directions, the calculated result based on the wake model is compared with those presented in Yamamoto et al. (2004) using the CFD methods, as shown in Fig.6. The displacement distributions of the cylinder in the CF direction calculated based on the two methods are consistent; despite a few differences, the relative error between the proposed model and Yamamoto et al. (2004) is lower than 8%. Furthermore, the reason for the difference could be the different damping coefficients. Overall, the proposed model is applicative in predicting the coupled VIV responses.

4 VIV Response Analysis of the CTR

The coupled VIV responses of a CTR in the CF and IL directions, including displacement distribution, dominant frequency, standing wave behavior, traveling wave behavior, motion trajectory, and energy transfer, are investigated systematically under the effects of uniform flows with different flow velocities of with U = 0.25, 0.35, 0.45, and 0.55 m s⁻¹. The research in this section aims to provide scientific support for the design, operation, and maintenance of catenary-type flexible risers. The main parameters of the CTR model are listed in Table 1.

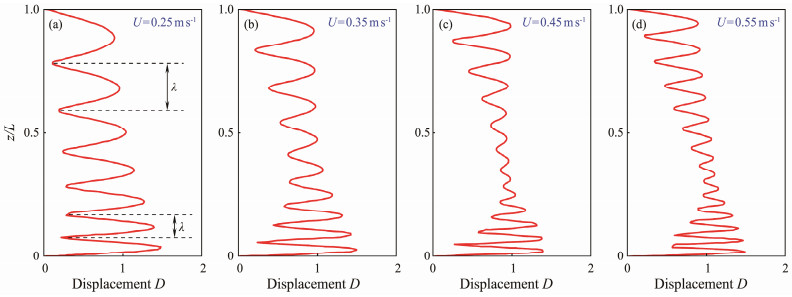
Fig.7 presents the VIV displacement distributions of the CTR in the CF direction under uniform flows with U = 0.25, 0.35, 0.45, and 0.55 m s⁻¹. Prominent multimode characteristics occur in the VIV responses of the riser under the excitation of uniform flows, and with the increase of the external velocity, higher-order modes continuously participate in the CF-direction VIV response of the structure. The dimensionless wavelength λ decreases gradually from the top end to the bottom end along the span of the riser, which is different from the dimensionless wavelength of TTRs subjected to uniform flows (Gao et al., 2019). The increased flow velocity has a slight effect on this unique characteristic, indicating that structural nonlinearity triggers the nonuniform distribution of the dimensionless wavelength. Moreover, the maximum amplitude only varies slightly with increasing velocity, and the position corresponding to the maximum is still at the bottom part of the riser. The VIV amplitudes remain high, which is because the normal component of the external flow is larger. The higher tension at the top part of the riser also poses a limitation on the development of VIV performance, indicating the tension has important effects on the VIV amplitudes of the CTR. Additionally, the fluctuation characteristic of the VIV displacement distributions is remarkably reduced in the range of z/L = 0.50 - 0.75.

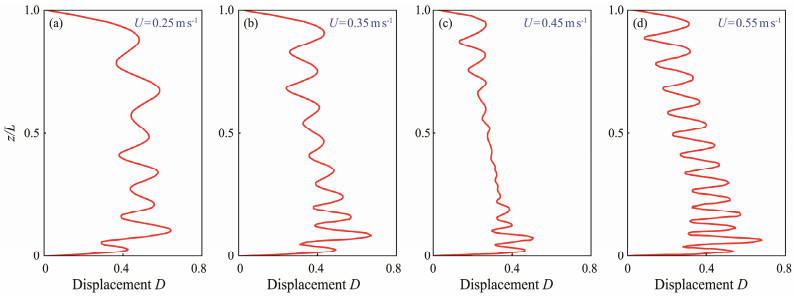
Fig.8 presents the VIV displacement distributions of the CTR in the IL direction under uniform flows with U = 0.25, 0.35, 0.45, and 0.55 m s⁻¹. The VIV performance in the IL direction exhibits properties similar to those in the CF direction. For example, multimode responses participate in the structural vibration, the maximum amplitudes occur near the bottom region of the CTR, higher-order modes are involved in the VIV behaviors, and the dimensionless wavelength λ varies along the span of the CTR. In addition, the IL-direction amplitude is dramatically lower than the CF-direction one, which is similar to the VIV responses of top-tensioned risers. Higher-order modes usually appear in the IL-direction VIV responses of the top-tensioned riser than the CF-direction ones. However, the same phenomenon is hardly seen in the VIV performance of the CTR. This outcome is closely related to the coupled velocity and the structural characteristic, of course. Fig.8(c) presents that the displacement fluctuation in the lower parts of the riser nearly disappears, which may be due to the high-order modal conversion at a flow velocity of 0.45 m s⁻¹, and the vibration response is unstable.

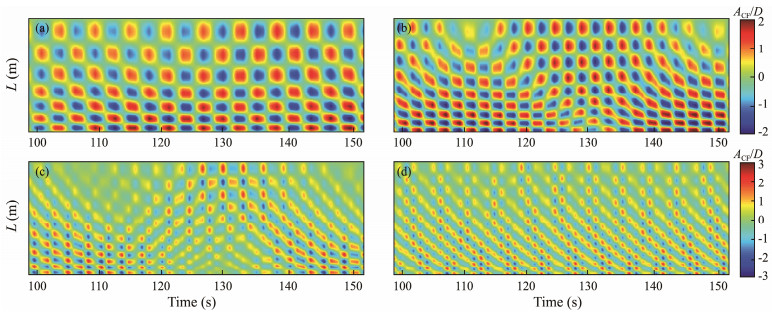
Fig.9 presents the spatiotemporal distributions of VIV displacements of the CTR in the CF direction under uniform flows with U = 0.25, 0.35, 0.45, and 0.55 m s⁻¹. The standing wave behavior dominates the structural vibration at U = 0.25 and 0.35 m s⁻¹, particularly in the upper part of the riser, but slight traveling wave characteristics are observed in the bottom region of the riser. This result indicates that the VIV response in the bottom parts is more sensitive to the external velocity, possibly because the bottom tension of the riser is much smaller than that of the top despite the lower normal component of external flow velocity. As the flow velocity grows continuously, traveling wave behaviors become increasingly evident, and the structural vibration exhibits a mixture of traveling wave and standing wave performance. The standing wave still dominates the VIV response of the CTR in the top region, which is due to the restriction of the top hinge and its high tension.

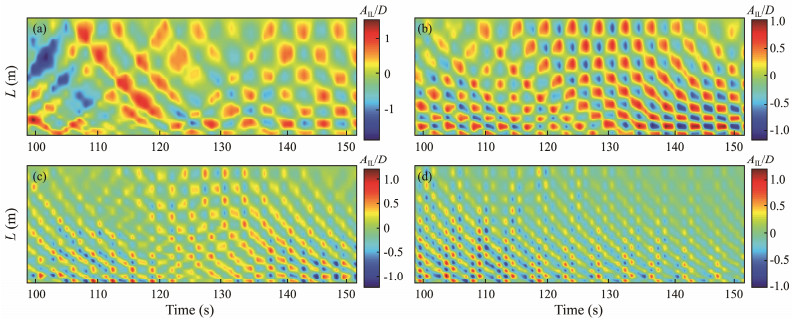
Fig.10 presents spatiotemporal distributions of VIV displacements of the CTR in the IL direction under uniform flows with U = 0.25, 0.35, 0.45, and 0.55 m s⁻¹. Traveling wave characteristics are clear in the structural VIV responses. However, the standing wave property does not disappear, indicating that the structural vibration in the IL direction also behaves the mixed characteristic of traveling wave and standing wave. The traveling wave of the VIV performance fades in the period of 120 - 135 s, while the standing wave behavior is substantial. This result could be due to the vibration instability.

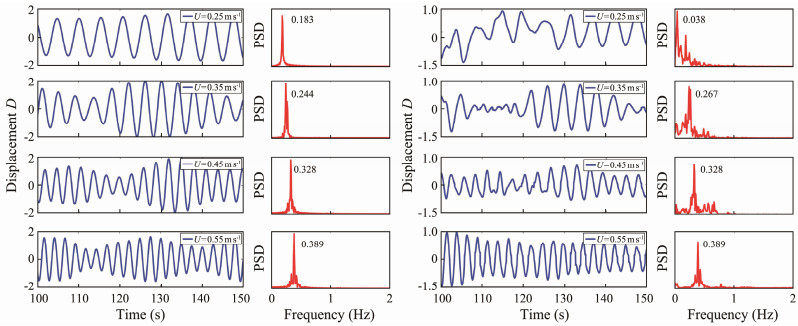
Fig.11 presents the time series of VIV displacement and frequency spectrum at z/L = 0.5 under different flow velocities with U = 0.25, 0.35, 0.45, and 0.55 m s⁻¹. The dominant frequencies in the CF and IL directions at z/L = 0.5 increase with the increase of the external flow velocities, and a slightly lower frequency component and a slightly higher frequency component are vaguely captured in the CF direction. This result indicates that the CF-direction VIV responses are unstable. However, the IL-direction VIV responses demonstrate a trend opposite to that of the CF-direction ones. For example, the VIV performance in the IL direction transforms from instability to stability, and sub-frequency components gradually disappear. A possible reason is that at high flow velocity, the relative velocity induced by structural vibration has a slight influence on the external velocity. The dominant frequency in the IL direction is nearly the same as that in the CF direction, while a substantial dual-frequency relationship between the dominant frequencies of top-tensioned risers in the IL and CF directions can be clearly captured. The main reason for this difference is also the asymmetry of vibration modes induced by the geometric nonlinearity of the structure.

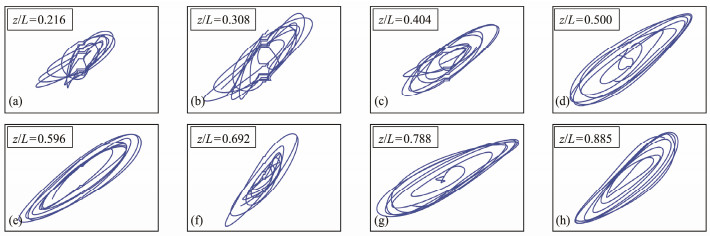
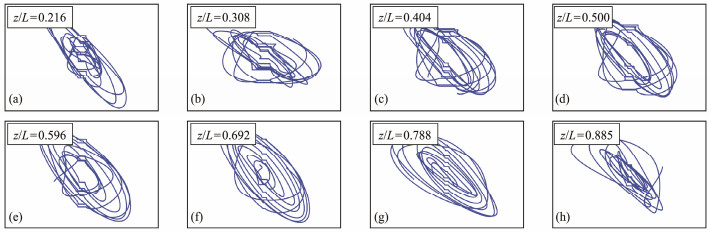
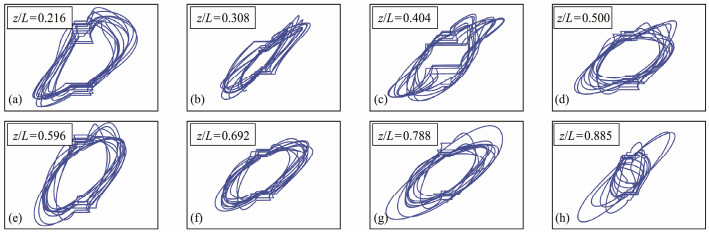
Figs. 12 - 15 present the oscillation orbits of the VIV responses of the CTR under uniform flows of U = 0.25, 0.35, 0.45, and 0.55 m s⁻¹ at different positions. All the VIV trajectories exhibit a common elliptical orbit, which is due to the nearly equal relationship between the IL- and CF-direction dominant frequencies. However, some of the chaotic tracks can be observed, where figure-eight shapes are faintly visible, especially at the external flow velocity of 0.25 m s⁻¹. This outcome is because the VIV frequency spectrum in the IL direction may have a relatively high-frequency component at some locations, but it is not strictly twice the CF-direction dominant frequency. With the increase of the flow velocity, the oscillation orbits of the CTR are stable, and the different inclination direction of the elliptical orbit is due to the dissimilar phase between the CF- and IL-direction VIV responses.

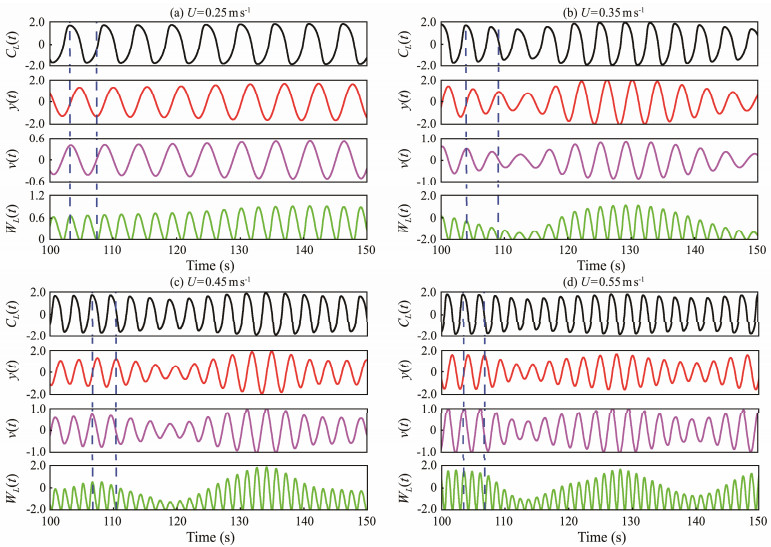
Fig.16 presents the instantaneous lift force coefficient, structural displacement, structural velocity, and transferred energy at z/L = 0.5 with four different flow velocities. The first three concepts are easy to understand, and the flow-solid energy transfer is introduced by the equation proposed by Newman and Karniadakis (1997):

$ {W_L}(z, t) = {C_L}(z, t) \cdot v(z, t) = 0.5 \cdot {C_{L0}} \cdot p(z, t) \cdot \partial y(z, t)/\partial t . $

(27)

Fig.16 shows that when the lift force coefficient is zero, the structural displacement reaches its maximum value, and the lift force coefficient has its minimum value with nearly no structural displacement. The peaks of the energy transfer are about 1.6, 2.0, 3.5, and 3.5, indicating that the transferred energy increases with the increase of the flow velocity. When the energy value is positive, the flow fluids transfer energy to the riser structure, leading to vibration intensification; otherwise, the riser transfers energy to the flow field, resulting in decreased VIV responses. According to the equation, when the lift force coefficient is positive and structural velocity is negative, the transferred energy is negative. However, the negative energy region is not noticeable under the excitation of the uniform flow. This finding is because the phase of the displacement is always lagging the velocity by π/2, causing the lift force coefficient to be nearly in phase with the structural velocity, which is similar to the results of the vertical riser (Gao et al., 2019).

5 Conclusions

The VIV responses of a CTR subjected to uniform flows by using the VFIFE scheme with wake oscillator equations are investigated thoroughly. The VIV response characteristics, including displacement, frequency, standing wave, traveling wave, and energy transfers from fluid flows to the riser, are determined and systematically discussed. The following conclusions are drawn:

1) The multimode characteristics are very substantial under the effect of uniform flows, and higher-order modes continuously participate in the CF-direction VIV response of the structure by increasing the flow velocity. The VIV displacements at the top and bottom parts of the riser are apparent but only vary slightly with the flow velocity. The maximum RMS displacements in the CF and IL directions are 1.45 D and 0.624 D, respectively.

2) As the external flow velocity increases, the VIV responses of the CTR change from a predominantly standing wave behavior to a mixed mode of the standing wave and traveling wave behaviors. With the increase of flow velocities, the vibration modes also gradually increase, and the corresponding modes are 7, 9, 12, and 14. Compared with the CF-direction VIV responses, the traveling wave phenomenon in the IL direction is more noticeable. However, the VIV performance at the top region of the riser is still dominated by the standing wave characteristic due to the influence of the high tension and joint restriction.

3) The double relationship of the dominant frequency in the CF and IL directions is hardly captured due to the structural nonlinearity characteristic, which leads to the shape of an inclined elliptical orbit for the vibration trajectory. The CF-direction VIV responses are unstable, the IL-direction VIV responses transform from instability to stability, and sub-frequency components gradually disappear. A figure-8 shape appears vaguely at several locations due to the higher frequency components in the IL direction.

4) Under the flow velocities of 0.25, 0.35, 0.45, and 0.55 m s⁻¹, the peaks of energy are about 1.6, 2, 3.5, and 3.5, respectively, indicating that the transferred energy increases with the increase of the flow velocity. Because the phase of the displacement is always lagging the velocity by π/2, the transferred energy calculated by Eq. (23) is positive. This outcome indicates that the energy always flows from the flow fields into the structure. With the increase of the external velocity, the energy transfer gradually becomes unstable.

Acknowledgements

This research was supported by the National Key R & D Program of China (No. 2022YFB2602800), the National Science Foundation of China (No. 51979257), the Basic Funding of the Central Public Research Institutes (Nos. TKS20210101, TKS20220103, TKS20230102), the Fundamental Research Funds for the Central Universities (No. 202413018), the postdoctoral project of Shandong (No. SDCX-ZG-202400218), and the postdoctoral project of Qingdao (No. QDBSH20240101013).