2) College of Oceanic and Atmospheric Sciences, Ocean University of China, Qingdao 266100, China;
3) Southern Marine Science and Engineering Guangdong Laboratory, Zhuhai 519082, China;
4) Rykell Scientific Editorial, Placentia, CA 92871, USA
Ocean energy is promoted by governments as a form of renewable energy that will aid in the mitigation of climate change and contribute to energy security in the relevant countries. Many coastal countries are developing specific strategies and plans for extracting ocean energy and committing national funding toward ocean energy research and deployment (The Executive Committee of OES, 2019). As one form of renewable energy, tidal current energy extraction is a feasible energy source with the advantages of High Technical Readiness Level of Level 7–8 (Mofor et al., 2014), no land occupation, predictable, and relatively low environmental impact compared to tidal range energy extraction (Brooks, 2006). Moreover, because the sites with much tidal energy potential are usually near large coastal cities with great electricity demand, transmission loss is reduced.
The Zhoushan Archipelago, located in the eastern Chinese province of Zhejiang, contains hundreds of channels that are potential sites for tidal energy extraction. A fundamental method for tidal energy assessment is the measurement of tidal current data. A comprehensive study assessed over 130 water channels at the national level in 1989 based on the tidal data from a marine atlas; the results of the study showed that the power density of tidal energy in most of their water channels is 15–30 kW m−2, with particularly high power densities in Jintang Channel, Guishan Channel, and Xihou Channel in the Zhoushan Archipelago (Wang and Lu, 2009). Wang et al. (2010) discussed the characteristics of tidal current energy based on measured tidal current at 5 sites in the Gaoting Channel and 8 sites in the Guanmen Channel; he also used the Technical Available Resource method of Farm and Flux to reveal that the utilizable tidal power is 4.67–5.31 MW in the Gaoting Channel and 7.92–9.37 MW in the Guanmen Channel. However, these results may overestimate the energy potential because it is hard to correlate the level in the whole channel with the exited power density at a specific point.
With the development of numerical simulation, ocean modeling based on the Navier-Stokes equations has been increasingly applied to the assessment of tidal energy in recent years as it can provide substantially more 'field' tidal current data to describe the elaborate and accurate spatial and temporal distribution of tidal energy. The tidal current energy levels of eight channels in this archipelago with maximum currents greater than 2.5 m s−1 were analyzed based on an ocean model. This study also showed that the total tidal current energy of the important watercourse can be 1400 MW (Hou et al., 2014). A more comprehensive assessment of tidal energy over this region was subsequently carried out using ocean modeling; the assessment showed that the theoretical annual average potential of tidal energy resources in Zhoushan Archipelago of 58 main channels is approximately 3950 MW, which is almost equal to the capacity of two Three Gorges Power Stations (Luo et al., 2017). A study of Deng and coworkers (Deng et al., 2020) provided insight into the environmental impacts of a large-scale tidal array via a numerical investigation in Zhoushan waters, with focus on the changes in current velocity, tidal elevation, and sediment transport. The hydrodynamic responses, especially after deployment of the tidal turbine array, are still not fully understood and may give rise to significant effects on the marine environment. For example, the tidal energy utilization may affect numerous environmental variables, such as the tidal regime, hydrodynamics, suspended and sediment transport, and water quality (Couch and Bryden, 2004; Blunden and Bahaj, 2007; Ramos et al., 2013; Nash et al., 2014; Bai et al., 2016; Chen and Liu, 2017; Lin et al., 2017).
Among the potential sites for the execution of tidal current energy extraction, the one that lies between Putuoshan Island and Huludao Island (hereby named the PuHu Channel) is one of the most plausible sites. Large-scale operation of dozens of tidal turbines array can become a long-term, sustainable renewable energy source for Zhou-shan City. Zhang et al. (2020a) carried out numerical experiments on tidal energy extraction in the PuHu Channel using the two-dimensional OpenTidalFarm model and investigated the optimal array layout for energy extraction; the hydrodynamic impact of large-scale (i.e., 115 turbines) tidal energy extraction in this channel was examined by Zhang et al. (2020b) via the 3-D hydrodynamic model with turbine representation based on the blade element method.
In this paper, an assessment of the tidal current energy levels over the Zhoushan Archipelago, with focus on the PuHu Channel, is presented in detail based on FVCOM (The Unstructured Grid Finite Volume Community Ocean Model, Chen et al., 2003, 2006). In contrast to previous studies, a resource assessment of the tidal stream energy in the PuHu Channel is carried out first to determine the suitable capacity of the tidal array. Next, the representation of the tidal turbine is integrated into this ocean model via momentum sink terms. The impacts of the tidal arrays on the hydrodynamic conditions are then investigated with the wake characteristics of the tidal current turbines and the wake recovery in the downstream of devices; the results of the investigation could be taken as a scientific reference for the future design of a tidal power demonstration project.
2 Methods 2.1 Governing EquationsFVCOM is an ocean modeling software that can simulate the water surface elevation, velocity, temperature, salinity, sediment transport, and water quality constituents. With unstructured triangular cells in the horizontal plane and a sigma-stretched coordinate system in the vertical direction, this model could represent optimally the complex horizontal geometry and the bottom topography of estuaries. The unstructured-grid and finite-volume approaches employed in the model provide geometric flexibility and computational efficiency that are well suited for simulation of tidal energy extraction, which requires higher grid resolution in the region of a tidal turbine array, nestled within the larger model domain. Finer grid resolution is mandatory for the tidal turbine array surroundings to account for shifts in flow fields, the dissipation of kinetic energy, and downstream wake signatures.
FVCOM is governed by a set of primitive equations representing momentum, continuity, temperature, salinity, and density. The Navier-Stokes (N-S) equations solved by the numerical model in the original Cartesian coordinate form are depicted as (x- and y- directions displayed):
| $\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0, $ | (1) |
| $\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}} - fv = - \frac{1}{\rho }\frac{{\partial P}}{{\partial x}} + \frac{\partial }{{\partial z}}({K_m}\frac{{\partial u}}{{\partial z}}) + {F_u} + {M_x}, $ | (2) |
| $\frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} + w\frac{{\partial v}}{{\partial z}} + fu = - \frac{1}{\rho }\frac{{\partial P}}{{\partial y}} + \frac{\partial }{{\partial z}}({K_m}\frac{{\partial v}}{{\partial z}}) + {F_v} + {M_y}, $ | (3) |
| $\frac{{\partial w}}{{\partial t}} + u\frac{{\partial w}}{{\partial x}} + v\frac{{\partial w}}{{\partial y}} + w\frac{{\partial w}}{{\partial z}} = - \frac{1}{{{\rho _0}}}\frac{{\partial q}}{{\partial z}} + u\frac{\partial }{{\partial z}}({K_m}\frac{{\partial w}}{{\partial z}}), $ | (4) |
where t is the time; x, y, and z are the east, north, and vertical axes in the Cartesian coordinate system, respectively; u, v, and w are the three velocity components in the x, y, and z directions, respectively; ρ0 is the water density; P is the pressure arising from the sea surface and the water; q is the non-hydrostatic pressure; f is the Coriolis parameter; and K m is the vertical eddy viscosity coefficient. F u and F v represent the horizontal momentum terms. M x and M v represent the additional horizontal momentum terms from tidal turbines specified in the later section. The total water column depth is D = H + z, where H is the bottom depth (relative to z = 0), and z is the height of the free surface (relative to z = 0).
The σ-coordinate transformation is used in the vertical direction to obtain a smooth representation of the bottom topography irregularities and is defined as:
| $\sigma = \frac{{z - \zeta }}{{H + \zeta }} = \frac{{z - \zeta }}{D}, $ | (5) |
where the value of sigma ranges monotonically from σ = −1 (bottom) to σ = 0 (surface). Interestingly, ocean models differ from atmospheric models in that the σ-coordinates are normalized, varying from σ = 1 (surface) to σ = 0 (top of atmosphere),
The surface and bottom boundary conditions for u, v, and w are:
| $\left\{ {\begin{array}{*{20}{l}} {{K_m}(\frac{{\partial u}}{{\partial z}}, \frac{{\partial v}}{{\partial z}}) = \frac{1}{{{\rho _0}}}({\tau _{sx}}, {\tau _{sy}})} \\ {w = \frac{{\partial \zeta }}{{\partial t}} + u\frac{{\partial \zeta }}{{\partial x}} + v\frac{{\partial \zeta }}{{\partial y}} + \frac{{E - P}}{\rho }} \end{array}} \right., {\rm{ at }} \; z = \zeta (x, y, t), $ | (6) |
| $\left\{ {\begin{array}{*{20}{l}} {{K_m}(\frac{{\partial u}}{{\partial z}}, \frac{{\partial v}}{{\partial z}}) = \frac{1}{{{\rho _0}}}({\tau _{bx}}, {\tau _{by}})} \\ {w = - u\frac{{\partial H}}{{\partial t}} - v\frac{{\partial H}}{{\partial x}} + \frac{{{Q_b}}}{\Omega }} \end{array}} \right., {\rm{ at }} \; z = - H(x, y), $ | (7) |
where (τ sx, τ sy) and (τ bx, τ by) =
| $ {C_d} = \max ({k^2}/\ln {(\frac{{{z_{ab}}}}{{{z_0}}})^2}{\rm{ }} \; 0.0025) $ | (8) |
where k = 0.4 is the von Karman constant, and z0 is the bottom roughness parameter. FVCOM features a wide choice of ocean turbulence closure models for the parameterization of the vertical eddy viscosity and the vertical thermal diffusion coefficient; furthermore, an updated version of the MY-2.5 model used in this model has been testified successfully in many cases.
2.2 Parameterization of Tidal Current TurbinesOne important aspect of the study is the modeling of the hydrodynamic changes from a turbine array acting on the water column. In fact, the extraction process is extremely complex because the fluid that has passed the turbines becomes rotational and attached to the boundary layer at high Reynolds number flow, and the structure of the wake immediately behind the body depends strongly on the body's geometry. To simplify the process of macro effect on the hydrodynamic environment, the following three approaches are applied widely: the bottom friction approach, the momentum sink approach, and the blade element actuator disk approach (Chen et al., 2014). Among these approaches, the momentum sink approach is the most popular method; this method represents the loss of momentum due to tidal energy extraction by adding a term to the momentum equations (Ahmadian and Falconer, 2012; Chen et al., 2013; Chen et al., 2014; Sanchez et al., 2014; Wu et al., 2017).
The horizontal-axis tidal turbine is placed into an element of the grid, i.e., flow point, and the blades cover several vertical layers; the thickness of the turbine blade is assumed to be very small. Momentum is exchanged across the flow-facing rotor surface area, and a portion is lost from the flow via power generation (Chen et al., 2015). The effects of the turbine are represented by the momentum sink term
| ${M_x} = - \frac{1}{2}A\left({{C_T} + {C_D}} \right)\mathop u\limits^ \to \sqrt {{u^2} + {v^2}}, $ | (9) |
| ${M_y} = - \frac{1}{2}A\left({{C_T} + {C_D}} \right)\mathop v\limits^ \to \sqrt {{u^2} + {v^2}}, $ | (10) |
where (M x, M y) is the momentum sink rate in x- and y- directions; A is the total flow-facing surface area swept by turbine blades; C T is the thrust coefficient due to momentum removal; C D is the blade element drag coefficient;
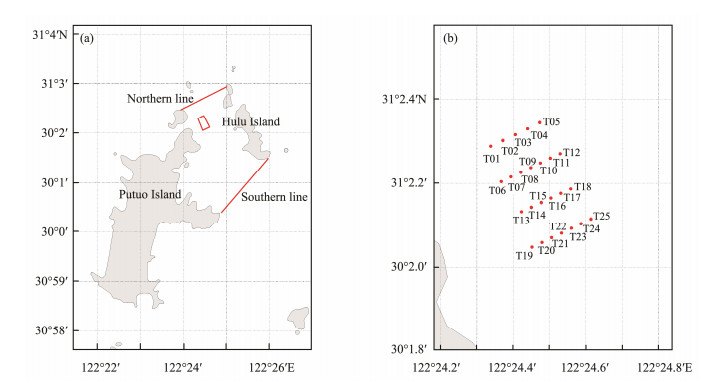
The PuHu Channel is located 6 km (latitude-wise) to the east of Zhoushan Island and is approximately 3.0 km by 2.0 km, with an orientation of northwest–southeast (Fig.1). A small isle splits the north exit into two pathways; the eastern and western pathways are 1.2 km and approximately 1.0 km in length, respectfully. The depth of the PuHu Channel is between 20 m and 60 m, the bathymetric gradient along coastlines is steep, and the central area of the bathymetry is relatively flat. The flooding and ebbing directions are northwestward and southeastward along the coast, respectively.

|
Fig. 1 Location of the PuHu Channel (red box) which is between Huludao Island and Putuoshan Island in the Zhoushan Archipelago, with the locations of the tidal current observation stations, C1 and C2, and the tidal elevation gage, T1 (red dots). |
This study used an unstructured-grid coastal ocean model with a resolution refinement for the PuHu Channel region. The model covers the entire Hangzhou Bay, the grid size of which is from approximately 2.5 km along the open boundary to 10 m around the potential site for tidal turbines array at the north of the channel in order to describe it elaborately (Fig.2). Ten vertical layers of uniform thickness were specified in the water column using the sigma-stretched coordinate system. The Smagorinsky scheme for horizontal mixing and the MY-2.5 turbulent closure scheme for vertical mixing were used in this model. The bottom friction is described by the quadratic law with the drag coefficient determined by the logarithmic bottom layer as a function of the bottom roughness. A bottom friction coefficient of 0.0025 and a bottom roughness of 0.001 m were used in the model. The model run time step was 0.2 s. Open boundary conditions for the model were specified at the east side of Hangzhou Bay using 9 harmonic tidal constituents (i.e., S2, M2, N2, K2, K1, P1, O1, Q1, and M4) provided by the global tidal model TPXO7.2. The dominant tidal constituents are the principal semidiurnal tide M2 and the principal diurnal tide K1. The Qian-tang River inflows were assumed to be 697 m3 s−1, and other geophysical factors (such as wind field, evaporation, atmospheric precipitation, and bottom freshwater) were neglected.

|
Fig. 2 Model mesh of the Zhoushan Archipelago (a) and the PuHu Channel (b). |
The model was validated by observation data at one tide gauging station and two tidal current stations shown in Fig.2. The simulation period, which lasted for 31 days starting from 1st to 31st August, 2014, includes two springneap cycles. Fig.3 and Fig.4 show the comparison between model result and measure data on surface elevation and depth-averaged current speed, respectively. It can be seen that the water level from the model predictions follows the observed data closely, except for a couple of centimeters of underestimation on a few occasions at high tides. The current speed predictions are in reasonable agreement with the measured data, with a RMSE of 15 cm s−1 at the T1 station and 17 cm s−1 at the T2 station, except that the magnitude of the current speed at the midflooding moment was slightly underrated. This discrepancy could be related to the complex bathymetry and meteorological force that might not be represented accurately in the model.

|
Fig. 3 Validation of surface elevation at the tidal elevation gauging station, T1 (refer to Fig.1 for mapped tidal gage station location, RMSE = 12 cm). |

|
Fig. 4 Comparison of the measured (black stars) and the simulated (red lines) tidal current speed and direction at two tidal current observation stations T1 (a) and T2 (b) (refer to Fig.1 for mapped tidal current observation station locations). |
Because of the good model validation results described above, the model was used to calculate the unaltered tidal flow velocities over the channel. Fig.5 depicts the flow velocities at mid-flood and mid-ebb on a spring tide of 23rd August, 2013, which indicates there are 3 sites with stronger flow at the north, middle, and south of the channel. The maximum speeds in the three areas is 2.1 m s−1, 2.3 m s−1, and 1.8 m s−1 during the flooding period, and they are 2.1 m s−1, 1.9 m s−1, and 1.7 m s−1 during the ebb period. The main velocity direction along the coastlines of islands is northwest-southeast. It can also be observed that the velocity decreases from the middle of the channel to the coastline.
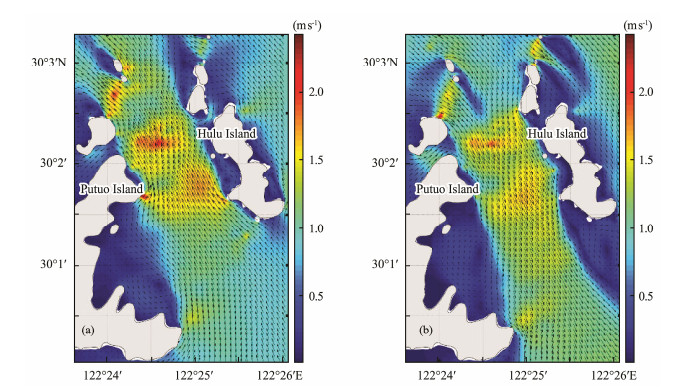
|
Fig. 5 Distribution of tidal current at mid-flood (a) and mid-ebb (b) in the PuHu Channel, presented in velocity vectors (black arrows) and speed magnitude (background colors). |
It is obvious that tidal asymmetry exists in the channel, with the flood tide being stronger than the ebb tide. In this case, this asymmetry can be caused by the different layout of the estuary at different tidal levels or by the distortion of the tidal wave as it propagates over the coastal shelf, as suggested by Ramos et al. (2013).
The tidal current power density calculated from the vertically averaged currents has a similar pattern with tidal current because of the cubic relationship (Fig.6). The maximum power densities at 3 potential sites (Fig.7a) mentioned above are approximately 3.4 kW m−2, 3.6 kW m−2, and 3.1 kW m−2 at mid-flood tide and 2.5 kW m−2, 2.2 kW m−2, and 1.8 kW m−2 at mid-ebb tide.
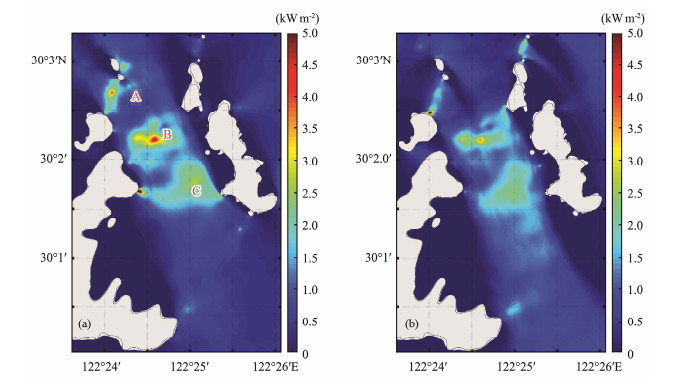
|
Fig. 6 Distribution of tidal current energy power density at mid-flood (a) and mid-ebb (b) in the PuHu Channel. |
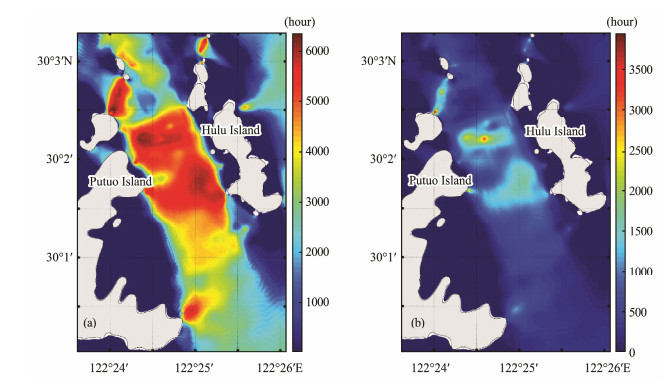
|
Fig. 7 Distribution of H g (a) and H r (b) of tidal energy in the PuHu Channel. |
There are two key parameters, 'Annual generation hours' (H g) and 'Annual generation hours at rated power' (H r), adopted by the Chinese wind power industry that describe the power generation duration of wind turbines (National Development and Reform Commission, 2004). Similarly, H g and H r can also be introduced for tidal energy sources to describe power generation (Eqs. (11) – (12)). The former H g defines the working time of a tidal turbine in one year, and H r denotes the power generation hours with the rated power in one year, i.e., the total annual energy production divided by the rated power. Fig.7 describes the distribution of H g and H r over the PuHu Channel, both of which have a rather similar trend. There are also 3 peaks in the middle of the channel. The highest H g reaches 5500 h, whereas the highest H r is only approximately 2000 h. Considering 1800 h (H r) as the economic value for tidal energy utilization, the area where H r is greater than 1800 h is approximately 2.1 km2 in the channel.
| ${H_g} = \int\limits_{t|v \geqslant {v_c}} {{\rm{d}}t}, $ | (11) |
| ${H_r} = \int\limits_{t|v \geqslant {v_c}}^{t|v \leqslant v{}_r} {\frac{{{v^3}(t)}}{{{v_r}^3}}{\rm{d}}t} + \int\limits_{t|v \geqslant {v_r}}^{} {{\rm{d}}t}, $ | (12) |
where H g is the annual generation hours; t is the time; v is the current speed; v c is teh cut-in current speed; v r is the current speed for the turbine at rated power; H r is the annual generation hours at the rated power.
4.3 Extractable Power OutputEstimation of the energy potential for a specific area is critical to the development of tidal energy sources. An easy method for assessing the potential used broadly named FLUX was used to calculate a certain percentage of the kinetic energy flux through the undisturbed channel, as it only requires measurements of tidal currents and a cross-sectional area that is expressed with Eq. (13) – (14) (Legrand, 2009).
The annual average available power Pavail is the product of the power flux passing through the site and the significant impact factor (SIF). Previous work by Black and Veatch in conjunction with Robert Gordon University (Bryden et al., 2007) suggested that the SIF will be dependent on the type of site. The SIF represents the percentage of the total resource at a site that can be extracted without significant economic or environmental effects. Extraction percentage is set to 15% in this paper according to the suggestions of EPRI (Hagerman et al., 2006).
| ${P_{{\rm{avail}}}} = {P_{{\rm{FLUX}}}} \cdot SIF .$ | (13) |
The power flux (PFLUX) passing through a certain section of a channel can be calculated using:
| $P_{{\rm{FLUX}}}^{} = 0.5\rho \overline {{v^3}} S, $ | (14) |
where ρ is the water density; v is the current speed; S is the area of delegate section ranging from 0.5 km2 to 0.6 km2.
The annual available power gradually increases from the north exit to the south exit of the channel because of the different areas of a typical section and the different distributions of current speed. The maximum Pavail is 3.23 MW at the north exit, whereas the minimum value is 1.98 MW (Fig.8); the average value of 2.60 MW along the channel can be considered as the available potential of this channel. Note that the results cannot be used to calculate the power capacity and turbine number of a tidal farm, as it is annually averaged.
|
Fig. 8 Location of the tidal array chosen for the tidal energy extraction points. Note the staggered turbine configuration aligned in the tidal current direction and the linear alignment orthogonal to the current direction. Turbines are equispaced (i.e., 20d, 10d) in their respective directions. |
Taking H r as 1600 h according to the distributions in Fig.7, the capacity of the tidal array at rated power can be simplified and be calculated from the product of Pavail and the quotient of hours in one year divided by H r (Eq. (15)), i.e., 11.40 MW.
| ${P_c} = {P_{{\rm{avail}}}} \cdot 8760/{H_r}.$ | (15) |
According to the previously presented tidal energy resource characteristics and the bathymetry and morphology of the PuHu Channel, a 25-turbine tidal array with a rated power of 12 MW is added to the model.
5.2 Site Selection and Layout of Tidal ArrayA suitable region for the tidal array not only has much energy potential but also other physical characteristics that allow for the construction of the farm. Several rules employed for siting of a tidal array include:
1) The maximum current velocity should be > 2.0 m s−1 (Khan and Bhuyan, 2009), the water depth should be about
20–30 m, and the distance to the coastline should be not more than 2.0 km.
2) The region should not conflict with navigation, anchorage, oil-gas pipe route, undersea cables, marine protected areas, etc.
3) The wake effects between the turbines should be minimized.
4) The demonstration region should be suitable for the transportation and setup of the tidal turbines and have sufficient area to conduct turbine testing.
Based on the above criteria and the spatial and temporal distributions of tidal current energy resources, the appointed area of approximately 0.2 km2 with 0.5 km × 0.4 km and the average depth of 22 m were selected on the north of the channel, as shown in Fig.8a. In order to minimize the effects of downstream wake, the lateral spacing between devices (the distance between axes) is set to 5 times the rotor diameter (5d), and the downstream spacing is set to 10 times the rotor diameter (10d) (Fig.8) (Legrand, 2009).
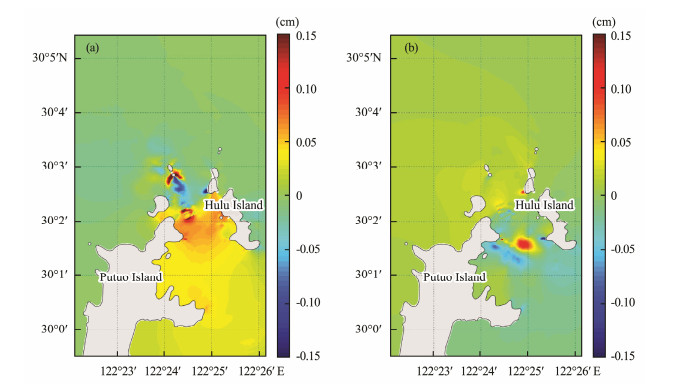
5.3 Impact on Hydrodynamic Environment 5.3.1 Water levelFig.9 illustrates the influence of the tidal array on water level, quantified by the difference of the water level before and after the installation of the tidal array at midflood tide and mid-ebb tide. As Fig.9a shows, the water level increases in the southern part of the channel at the mid-flood tide due to the hindrance of turbines array. The maximum range of water level variation is just approximately 0.18 cm, but dramatic changes from −0.15 cm to 0.16 cm appear at the south of the isle in the northern exit, possibly due to the pressure drop caused by the turbines. At the mid-ebbing tide, the water level increases in a very small range at the north of the channel. There is a roundshaped area that appears south to the tidal array, and the range of increase is approximately 0.1 cm. In general, the effects on the water level are insignificant and can be neglected in practice. Note that the differences were calculated from instantaneous water levels, which might produce array introduced phase-lag.
|
Fig. 9 Change in water level at mid-flood tide (a) and mid-ebb tide (b) due to the installation of the tidal array. |
As indicated in the previous section, the presence of the tidal array alters the flow, thereby affecting the power density distributions. The differences in the current speed at mid-flood and mid-ebb of a mean spring-tide with and without the tidal array, respectively, are shown in Figs. 10a and b. It is apparent that the impacts of the operation of the tidal array are significant, with a reduction in the tidal speed of 8 cm s−1 at both mid-flood and mid-ebb tide. The current difference can be distinguishable even a few kilometers away from the farm. Furthermore, there is an increase in the current velocity on both sides of the tidal array caused by the blockage effect (Chen et al., 2014).

|
Fig. 10 Current speed difference at mid-flood with the tidal array installed (a) and mid-ebb without the tidal array installed (b). |
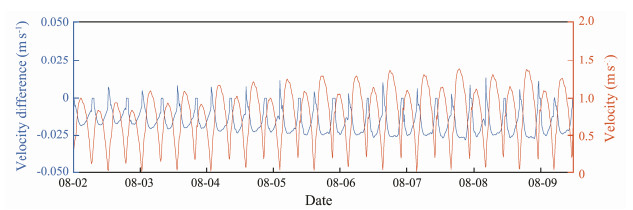
Fig.11 shows the temporal variation of current speed without turbines and the current speed difference around turbine No. 22. The speed difference changes as a sine curve along tidal process against the original tidal current speed. During a flooding and ebbing process, the maximum difference appeared at the mid-flooding tide and midebbing tide, and the difference trend gradually increases from neap tide to spring tide in the neap-spring cycle. Generally, the speed difference caused by the turbines is negligible, as it is considerably smaller compared to the background current velocity.
|
Fig. 11 Current speed difference from neap tide to spring tide at Turbine No. 22. |
As one part of the offshore general circulation, tidal residual (tidally averaged) currents govern the net exchange of material with the adjacent coastal area and are therefore of great importance for the health of the marine ecosystem (Garel and Ferreira, 2013). Fig.12a depicts the distribution of the tidal residual field before the operation of the tidal array. Overall, the residual speed is less than 0.03 m s−1 and is comparably slow on almost the entire area of this channel. However, there are still several sites on which the residual speed is greater than 0.06 m s−1; these sites are distributed at the capes of Putuo Island and Hulu Island, and the strongest residual current is approximately 0.15 m s−1, which occurs at the southwestern cape of Hulu Island.

|
Fig. 12 Temporal averaged tidal residual current without the operation of the tidal array (a) and distribution of the difference in speed (b). |
Fig.12 shows the spatial distribution of the difference between two modeling scenarios (with or without the tidal array). It can be seen that the current increase occurs at the southern part of tidal array, whereas a decrease occurs at the northern part after the deployment of the tidal array; however, there is no significant variation in the channel. The maximum change with and without turbines appears at the downstream area of the tidal farm during flooding tide and ebbing tide, with a value of approximately 2 mm s−1, and the other area of the channel is less than 1 mm s−1.
6 ConclusionsA coastal ocean numerical model FVCOM was refined and applied to simulate the hydrodynamic conditions and verified against measured data in the PuHu Channel, Zhou-shan Archipelago. The validated model was then used to estimate the tidal current energy resources of this channel.
The modeling results revealed that the PuHu Channel has 3 sites where the tidal velocities at the mid-flooding tide of a spring tide are over 1.8 m s−1. The highest power density, 3.6 kW m−2, was found at the central area of the PuHu Channel during the flooding tide, and the highest power density of 2.5 kW m−2 was found at the west coast of the channel during the ebbing tide. The spatial distributions of the generation duration, H g and H r, were found to be similar to a power density with 3 peaks, and the maximums of H g and H r located in the middle of the PuHu Channel reached to 2000 h and 5500 h, respectively.
The ocean model was modified to simulate the impacts of tidal turbines by adding a sink momentum term to the governing momentum equations. The model results demonstrated that the tidal array would not cause noticeable changes in the water level, with changes of less than 0.2 cm. The maximum decrease of the tidal current due to the operation of the tidal array is 8 cm s−1 at both midflood and mid-ebb tide in the tidal farm, but the increased velocities on both sides of the array result in the blockage effect. Moreover, the maximum change of tidal residual caused by the introduction of the tidal array that appears at the downstream area of tidal farm during flooding tide and ebbing tide is approximately 2 mm s−1, and the other area of the channel is less than 1 mm s−1; such changes are negligible in practice.
AcknowledgementsThis work was supported by the National Key R & D Program of China (Nos. 2019YFE0102500, 2019YFB150 4401, 2019YFE0102500 and 2016YFC140 1800). The authors would like to thank the FVCOM Development Group for their modeling support.
Ahmadian, R. and Falconer, R. A., 2012. Assessment of array shape of tidal stream turbines on hydro-environmental impacts and power output. Renewable Energy, 44: 318-327. DOI:10.1016/j.renene.2012.01.106 (  0) 0) |
Bai, G., Li, W., Chang, H. and Li, G., 2016. The effect of tidal current directions on the optimal design and hydrodynamic performance of a three-turbine system. Renewable Energy, 94: 48-54. DOI:10.1016/j.renene.2016.03.009 (  0) 0) |
Blunden, L. S., and Bahaj, A. S., 2007. Effects of tidal energy extraction at Portland Bill, southern UK predicted from a numerical model. Proceedings of the 7th European Wave and Tidal Energy Conference. Porto, Portugal.
(  0) 0) |
Brooks, D. A., 2006. The tidal-stream energy resource in Passamaquoddy-Cobscook Bays: A fresh look at an old story. Renewable Energy, 31(14): 2284-2295. DOI:10.1016/j.renene.2005.10.013 (  0) 0) |
Bryden, I. G., Couch, S. J., Owen, A. and Melville, G., 2007. Tidal current resource assessment. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 221(2): 125-135. DOI:10.1243/09576509JPE238 (  0) 0) |
Chen, C., Beardsley, R. C. and Cowles, G., 2006. An unstructured-grid, finite-volume coastal ocean model (FVCOM) system. Oceanography, 19(1): 78-89. DOI:10.5670/oceanog.2006.92 (  0) 0) |
Chen, C., Liu, H. and Beardsley, R. C., 2003. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries. Journal of Atmospheric and Oceanic Technology, 20(1): 159-186. DOI:10.1175/1520-0426(2003)020<0159:AUGFVT>2.0.CO;2 (  0) 0) |
Chen, W. B. and Liu, W. C., 2017. Assessing the influence of sea level rise on tidal power output and tidal energy dissipation near a channel. Renewable Energy, 101: 603-616. DOI:10.1016/j.renene.2016.09.024 (  0) 0) |
Chen, W. B., Liu, W. C. and Hsu, M. H., 2013. Modeling evaluation of tidal stream energy and the impacts of energy extraction on hydrodynamics in the Taiwan Strait. Energies, 6(4): 2191-2203. DOI:10.3390/en6042191 (  0) 0) |
Chen, Y., Lin, B. and Lin, J., 2014. Modelling tidal current energy extraction in large area using a three-dimensional estuary model. Computers and Geosciences, 72: 76-83. DOI:10.1016/j.cageo.2014.06.008 (  0) 0) |
Chen, Y., Lin, B., Lin, J. and Wang, S., 2015. Effects of stream turbine array configuration on tidal current energy extraction near an island. Computers and Geosciences, 77: 20-28. DOI:10.1016/j.cageo.2015.01.008 (  0) 0) |
Couch, S. J. and Bryden, I. G., 2004. The impact of energy extraction on tidal flow development. Proceedings of the 3rd International Conference on Marine Renewable Energy, 31(2): 133-139. DOI:10.1016/j.renene.2005.08.012 (  0) 0) |
Deng, G., Zhang, Z., Li, Y., Liu, H., Xu, W. and Pan, Y., 2020. Prospective of development of large-scale tidal current turbine array: An example numerical investigation of Zhejiang, China. Applied Energy, 264: 114621. DOI:10.1016/j.apenergy.2020.114621 (  0) 0) |
Garel, E. and Ferreira, Ó., 2013. Fortnightly changes in water transport direction across the mouth of a narrow estuary. Estuaries and Coasts, 36(2): 286-299. DOI:10.1007/s12237-012-9566-z (  0) 0) |
Hagerman, G., Polagye, B., Bedard, R., and Previsic, M., 2006. Methodology for Estimating Tidal Current Energy Resources and Power Production by Tidal in-Stream Energy Conversion (TISEC) Devices. EPRI North American Tidal in Stream
(  0) 0) |
Power Feasibility Demonstration Project. https://tethys.pnnl.gov/sites/default/files/publications/Tidal_Current_Energy_Resources_with_TISEC.pdf.
(  0) 0) |
Hou, F., Yu, H., Bao, X. and Wu, H., 2014. Analysis of tidal current energy in Zhoushan sea area based on high resolution numerical modeling. Acta Oceanologica Sinica, 35(1): 125-133. (  0) 0) |
Khan, J. and Bhuyan, G. S., 2009. Ocean energy: Global technology development status. Powertech Labs for the IEA-OES: 60-67. (  0) 0) |
Legrand, C., 2009. Assessment of Tidal Energy Resource : Marine Renewable Energy Guides. European Marine Energy Centre, London, 9-10.
(  0) 0) |
Lin, J., Lin, B., Sun, J. and Chen, Y., 2017. Numerical model simulation of island-headland induced eddies in a site for tidal current energy extraction. Renewable Energy, 101: 204-213. DOI:10.1016/j.renene.2016.08.055 (  0) 0) |
Luo, X., Xia, D., Wang, X. and Wu, H., 2017. Assessment and Characteristics of Ocean Energy in Promising Region in China. 1st edition. China Ocean Press, Beijing, 142-145.
(  0) 0) |
Mofor, L., Goldsmith, J. and Jones, F., 2014. Ocean energy: Techmology readiness, patents, deployment status and outlook. International Renewable Energy Agency IRENA, August: 76. DOI:10.1007/978-3-540-77932-2 (  0) 0) |
Nash, S., O'Brien, N., Olbert, A. and Hartnett, M., 2014. Modelling the far field hydro-environmental impacts of tidal farms – A focus on tidal regime, inter-tidal zones and flushing. Computers and Geosciences, 71: 20-27. DOI:10.1016/j.cageo.2014.02.001 (  0) 0) |
National Development and Reform Commission,, 2004. Specification of measurement and assessment for wind energy resources.. D&R Energy, 865: 1-3. (  0) 0) |
Ramos, V., Carballo, R., Álvarez, M., Sánchez, M. and Iglesias, G., 2013. Assessment of the impacts of tidal stream energy through high-resolution numerical modeling. Energy, 61: 541-554. DOI:10.1016/j.energy.2013.08.051 (  0) 0) |
Sanchez, M., Carballo, R., Ramos, V. and Iglesias, G., 2014. Floating vs. bottom-fixed turbines for tidal stream energy: A comparative impact assessment. Energy, 72: 691-701. DOI:10.1016/j.energy.2014.05.096 (  0) 0) |
The executive Committee of OES, 2019. OES Annual report: An overview of ocean energy activities in 2018. OES-TCP, Lisbon, Portugal, 7-14.
(  0) 0) |
Wang, C. and Lu, W., 2009. Ocean Energy Resources Analysis Method and the Evaluation of the Reserves. China Ocean Press, Xiamen, 1-9.
(  0) 0) |
Wang, Z., Zhou, L., Zhang, G. and Wang, A., 2010. Tidal stream energy assessment in specific channels of Zhoushan sea area. Periodical of Ocean University of China, 40(8): 27-33. (  0) 0) |
Wu, H., Wang, X., Wang, B., Bai, Y. and Wang, P., 2017. Evaluation of tidal stream energy and its impacts on surrounding dynamics in the eastern region of Pingtan Island, China. Chinese Journal of Oceanology and Limnology, 35(6): 1319-1328. DOI:10.1007/s00343-017-0187-z (  0) 0) |
Zhang, C., Zhang, J., Tong, L., Guo, Y. and Zhang, P., 2020. Investigation of array layout of tidal stream turbines on energy extraction efficiency. Ocean Engineering, 196: 106775. DOI:10.1016/j.oceaneng.2019.106775 (  0) 0) |
Zhang, D., Liu, X., Tan, M., Qian, P. and Si, Y., 2020. Flow field impact assessment of a tidal farm in the Putuo-Hulu Channel. Ocean Engineering, 208: 107359. DOI:10.1016/j.oceaneng.2020.107359 (  0) 0) |
 2021, Vol. 20
2021, Vol. 20


