2) Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China
The seabed has a significant impact on the ocean sound field because it is the lower boundary of ocean sound propagation, particularly in the shallow water environment. The studies on this kind of influence should not only consider the physical parameters of the seabed surface but also consider the strata at a certain depth below the seabed. In the study of acoustic characteristics of sediments, physical parameters of seafloor sediments, such as sound velocity, density, porosity, and other marine environmental parameters, are key indicators. It is of great significance in the territorial sea, exclusive economic zone division, military, and civil affairs (Wu, 2013).
The direct measurement of physical parameters of seabed sediment is time-consuming and expensive, yielding only the local small-scale seabed characteristics around the measurement sites. Moreover, it takes a lot of manpower and material resources to measure the physical parameters of seabed sediment in a long-distance and large range. The acoustic method can retrieve the physical parameters of the seabed sediment in the large or the whole sea area, quickly and efficiently at a low cost (Zheng, 2019). Currently, there are many inversion methods for seabed parameters, such as the inversions based on ray theory, matched field, correlation of marine environmental noise, normal wave propagation time, seabed reverberation field, and group velocity analysis (Yang and Ma, 2009; Shang, 2019; Tollefsen et al., 2020; Chandrakala et al., 2022). However, the acoustic inversion results of physical parameters of seabed sediments are uncertain due to different data acquisition instruments, different processing and inversion methods, and different models. The study on the physical parameters of seafloor sediments involves two subjects: marine acoustics and marine geophysics. In marine acoustics, the effective acquisition of seabed physical parameters has long been a hot topic, yet there are relatively few reports on the acquisition of seabed physical parameters in marine geophysics. Marine geophysical methods, such as sub-bottom profiler, multi-beam detection, and seismic exploration (streamer seismic, OBS, etc.), use the lower frequency than marine acoustics and are more commonly used for oil and gas exploration. They can also be used to evaluate the average values of physical parameters in a larger area for the deeper sediments.
This study uses the active-source data collected by OBS from the 9th and 11th CHINARE. We try to apply the active-source OBS detection technology in marine geophysics to the inversion of physical parameters of seabed sediments, and use the cost function inversion method based on the arrival time differences between the reflection and direct waves. Then the physical parameters of seabed sediments near two OBS stations in the Chukchi Sea are obtained and using active-source OBS data to invert seabed parameters is tested to be feasible. Meanwhile, the problems and deficiencies encountered in marine experiments and inversions are discussed.
2 Study SitesThe two OBS stations are located in the shelf-plateau transition zone between the Chukchi continental shelf and Chukchi margin (Fig. 1), with the water depths of 230 and 174.7 m, respectively. The distribution trend of the sediments in the Chukchi Sea from low latitude to high latitude, and from nearshore to far shore, is from coarse to fine. The coarse-grained sediments are mainly sand and silty sand, and the fine-grained sediments are mainly clay silt (Council, 1996; Gao et al., 2001; Chen, 2012; Kobayashi et al., 2016; Gamboa et al., 2017). The northeastern Siberia, the northeastern Bering Sea, and the Mackenzie River are considered to be the main sources of modern sedimentation in the Chukchi Sea (Deschamps et al., 2019). The topography, current, sea ice, and sea-level change control the type and distribution of sediments in the Chukchi Sea area (Stein et al., 2017; Deschamps et al., 2019).
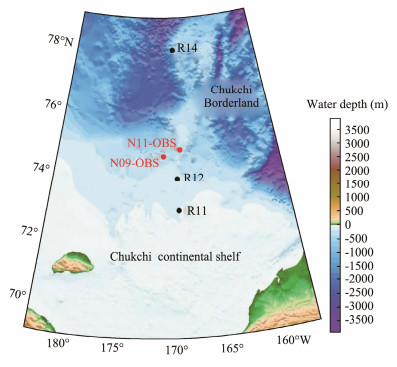
|
Fig. 1 Location map of OBS stations and sediment sampling stations. |
Based on the previous Chinese National Arctic Research Expedition, the data of three sediment collection stations R11, R12, and R14 (Meng et al., 2015) will be used as the reference for the inversion of seabed sediment parameters from OBS data (Table 1). The R12 station is closest to the two OBS stations.
|
|
Table 1 Location and character of the OBS stations and sediment sampling stations |
The 9th and 11th Chinese National Arctic Research Expedition were performed from July 20 to September 26 in 2018 and July 15 to September 28 in 2020, respectively. Active-source OBS data were acquired in the Chukchi platform (Fig. 1) by the two OBS stations (N09-OBS and N11-OBS), which are I-4C type broadband ocean bottom seismometers made by the Institute of Geology and Geophysics, CAS. In the two active-source OBS data collections, different acquisition parameters were used. More details are shown in Table 2. SIG-5 sparker sources were used as the seismic sources, while positioning was based on GPS. Shooting signals recorded by the two OBS stations can be observed on the waveform graphs (Fig. 2). When calculating the arrival time difference, the positions with the maximum waveform amplitude of direct waves and reflected waves are selected. The selection principle of reflected waves is based on the first maximum amplitude after the direct wave. The sparker shooting tracks are shown in Fig. 3.
|
|
Table 2 Collection information of two OBS data |
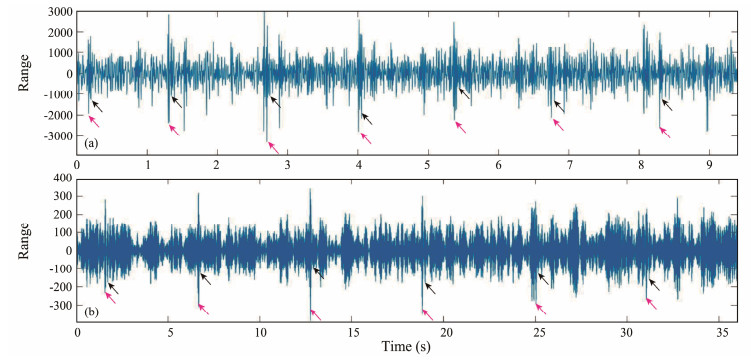
|
Fig. 2 (a) is the shooting waveform from the N09-OBS; (b) is the shooting waveform from the N11-OBS. The pink arrows indicate the direct waves; the black arrows indicate the selected reflected waves. |
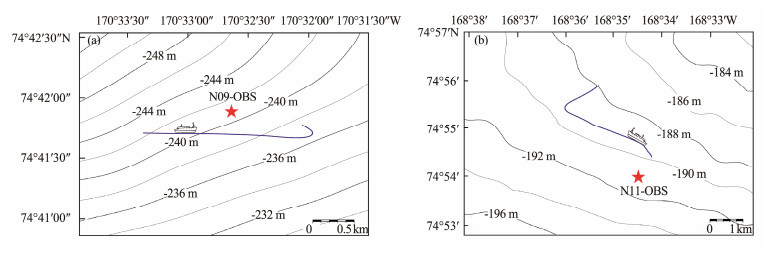
|
Fig. 3 (a) is the sparker shooting track around N09-OBS; (b) is the sparker shooting track around N11-OBS. The track direction is shown by the ship bow. The locations of the two OBS stations are shown by red stars. Water depth contours are drawn on the two figures. |
The recorded data of I-4C OBS is in RAW format, stored in a group of 12 bytes, corresponding to Z, X, Y, and hydrophone components, and each component has 3 bytes of 'int' data. The original data is converted into spectral amplitude coding (SAC) format by using a self-developed program, and the electronic distance measurement navigation data file is read to obtain the shooting information (serial number, longitude, and latitude, time), then the abnormal processing (interpolation from the points nearby) is performed. The continuous SAC data was cut and converted into SEGY data according to the shooting time interval. A common receiver gather of OBS active source data in SEGY format is formed. Obspy is used to remove the instrument response for the data. Based on the longitudes and latitudes of OBS and shooting stations, the offset is calculated. Finally, the data volume is saved as a SEGY file. Then the commercial software is used to perform the first break correction, filtering, gain, and other subsequent data processing on SEGY data to improve the resolution of the data.
3.3 Inversion MethodFor the layered seabed model, as shown in Fig. 4, assuming that the sedimentary layers are uniform and horizontal, the propagation path of the sound signals can be assumed to be the straight line when the sound signal is transmitted in close range, and the reflection and refraction of sound signals conform to the Snell Law at the interface. This study uses a cost function inversion method based on the arrival time differences between stratified reflected and direct waves in sedimentary layers; it is modified from Xu et al. (2016).
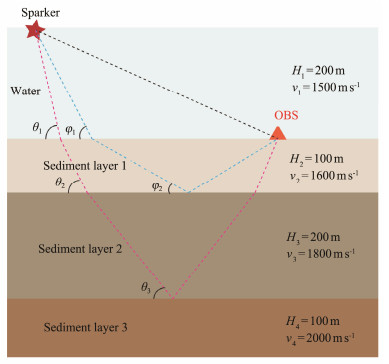
|
Fig. 4 Schematic diagram of the test model is with the parameters including thickness and velocity of water layer, and three sediment layers are given in the model. The red pentagram shows the location of the spark source. The orange triangle marks the position of OBS. |
For the reflection wave of the first sediment layer, according to the Snell Law and geometric relation, it can be concluded that:
| $ \frac{{{H_1}}}{{\tan ({\varphi _1})}} + \frac{{2{H_2}}}{{\tan ({\varphi _2})}} = R, $ | (1) |
| $ \frac{{\cos ({\varphi _1})}}{{{v_1}}} = \frac{{\cos ({\varphi _2})}}{{{v_2}}}, $ | (2) |
| $ \Delta T = \frac{{{H_1}}}{{\sin ({\varphi _1}) \cdot {v_1}}} + \frac{{2{H_2}}}{{\sin ({\varphi _2}) \cdot {v_2}}} - \frac{{\sqrt {{{({H_1})}^2} + {R^2}} }}{{{v_1}}}. $ | (3) |
For the reflection wave of the second layer of sediments, according to the Snell Law and geometric relation, it can be concluded that:
| $ \frac{{{H_1}}}{{\tan ({\theta _1})}} + \frac{{2{H_2}}}{{\tan ({\theta _2})}} + \frac{{2{H_3}}}{{\tan ({\theta _3})}} = R, $ | (4) |
| $ \frac{{\cos ({\theta _1})}}{{{v_1}}} = \frac{{\cos ({\theta _2})}}{{{v_2}}} = \frac{{\cos ({\theta _3})}}{{{v_3}}}, $ | (5) |
| $ \Delta T = \frac{{{H_1}}}{{\sin ({\theta _1}) \cdot {v_1}}} + \frac{{2{H_2}}}{{\sin ({\theta _2}) \cdot {v_2}}} + \frac{{{H_3}}}{{\sin ({\theta _3}) \cdot {v_3}}} - \frac{{\sqrt {{{({H_1})}^2} + {R^2}} }}{{{v_1}}}, $ | (6) |
where H represents the thickness, v represents the velocity, φ and θ represent the ray incidence angles. Numbers 1, 2, 3 of each physical parameters represent the water layer, the first layer, and the second layer, respectively. R stands for offset. ∆T represents the time difference of arrivals between the reflected and direct waves.
Construct the cost function as follows:
| $ CostF(v, H) = \frac{1}{{\frac{1}{N}\sum\nolimits_{n = 1}^N {\left({\Delta T(v, H, Rn) - \Delta T({\text{real}}) + b} \right)} }}, $ | (7) |
where CostF is the cost function, ∆T (v, H, Rn) and ∆T (real) represent the theoretical and actual time differences of arrivals, respectively. N represents the number of excitations of the source, b is a very small value used to improve the stability of the formula (actually taking 0.0001).
With the minimum cost, the function gets the optimal solution of the target layer. The velocity and thickness parameters can be obtained by inversion.
Based on Hamilton's empirical formula (Hamilton and Bachman, 1982) and Meng's formula (2015) for calculating the sound velocity of sediments in the Chukchi Sea and the Bering Sea, the physical parameters, such as density, porosity, and particle size of seabed strata can be further calculated. The reference formula is as follows:
| $ {V_p} = 1952.5 - 86.26{M_z} + 4.14{M_z}^2, $ | (8) |
| $ {V_p} = 2405.3 - 26.247n + 0.177{n^2}, $ | (9) |
| $ {V_p} = 2982.1 - 2107\rho + 716.26{\rho ^2}, $ | (10) |
where Vp (m s−1) is the velocity of sound, n (%) is the porosity, Mz is the particle size, ρ (g cm−3) is the density. Eq. (8) comes from Hamilton and Edwin (1982), Eqs. (9) and (10) come from Meng et al. (2015).
4 Results and Discussion 4.1 Model Validation ResultsThe forward modelling is performed to verify the effectiveness of this method on the OBS data. The established model is shown in Fig. 4. There are four layers, among which the thickness of the water layer is 200 m, and the acoustic velocity is 1500 m s−1. The thickness of the first sedimentary layer is 100 m, and the acoustic velocity is 1600 m s−1. The thickness of the second sedimentary layer is 200 m, and the acoustic velocity is 1800 m s−1. The thickness of the third sedimentary layer is 100 m, and the acoustic velocity is 2000 m s−1.
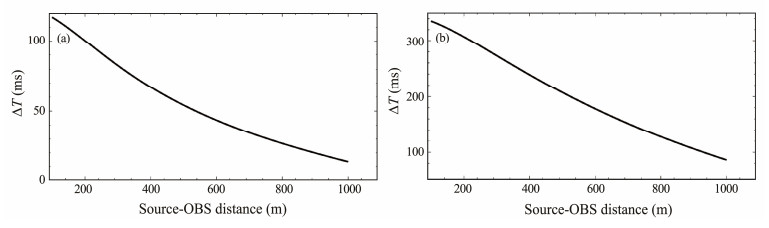
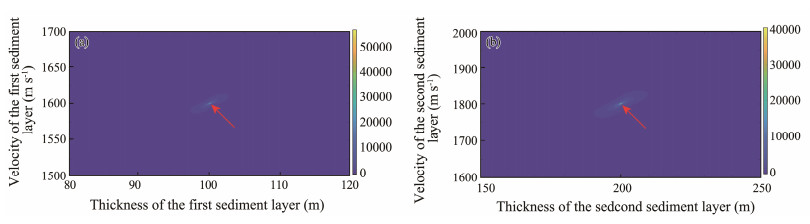
According to the model calculation, the relationship curves between the offset and the time difference between the reflected and direct waves for the first layer and the second layer are obtained, as shown in Fig. 5. The inversion results are shown in Fig. 6. The minimum value of the cost function, that is, the sound velocity and thickness corresponding to the optimal solution, is marked by the red arrow in the figure. The inversion results are as follows: the thickness of the first layer is 100 m, and the sound velocity is 1600 m s−1; the thickness of the second layer is 200 m, and the sound velocity is 1800 m s−1. The inversion results are completely consistent with the pre-set values of the model, so it can be concluded that the cost function inversion method based on the arrival time difference between the reflected and direct waves in the sedimentary layer can be used for the inversion of OBS seabed parameters. The velocity and thickness inversion results of the first and second layers converge to the pre-set parameters of the forward model. The experimental results show that as the inversion depth increases, the result becomes more divergent, as shown in Fig. 6b having a higher divergence degree than Fig. 6a. The signal-to-noise ratio of data also has a great influence on the divergence of inversion results.
|
Fig. 5 Relationship between the source-OBS distance and the time difference of direct waves and the reflection waves for the first layer (a); and the second layer (b). |
|
Fig. 6 Inversion result of cost function method for the first layer (a); the second layer (b). |
According to the sparker shooting record files, the position of direct waves and sedimentary reflection waves of each shot were picked up manually from OBS records. The arrival time difference was calculated. The offset is calculated by the OBS position and the GPS position during shooting. The inversion is carried out by using multiple groups of time differences and distances according to the formula. In the actual operation, the SIG-5 sparker was used for energy source and I-4C OBS was used for instrument reception. Due to equipment limitations, the sampling rate settings of the OBS instruments are not very suitable compared with the main frequency range of the SIG-5 spark source, which was resulting in a lower longitudinal resolution of the results.
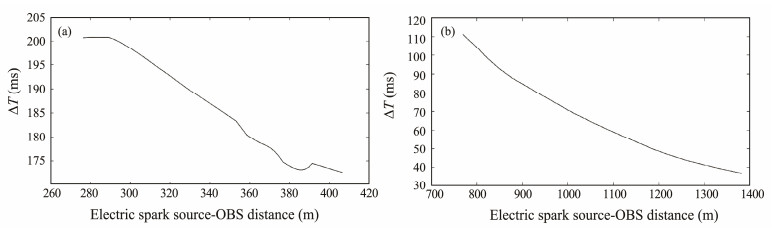
Fig. 7 shows the time difference between the reflected and direct waves identified on the SEGY section of N09-OBS and N11-OBS and the relationship between the calculated time difference and offset. Fig. 8 shows the inversion result of the cost function based on the arrival time difference between the reflected and direct waves in the sedimentary layers. Limited by the energy of the sparker source, only one layer under the seabed is identified, and the continuity of the layer is not good. The energy of the spark source used by N11-OBS is 5000 J, which is higher than the 2000 J for the spark source used by N09-OBS. According to the convergence effect shown in Fig. 8, the N11-OBS data is better than that of N09-OBS data. The cost function shown in Fig. 8a is obviously more divergent than that in Fig. 8b, which may be affected by manual picking and calculation errors. In addition, the biggest factor affecting the convergence should be the error of offset calculation. Due to the currents of the study area, there may be some deviation between the actual position of the OBSs and the recorded positions during the actual dropping of OBSs. As a result, the correlation between the calculated offset and the arrival time difference is weak and the results are more divergent.
|
Fig. 7 Relationship between the electric spark source-OBS distance and the time difference of reflected wave and direct wave identified (a) by N09-OBS data; and (b) by N11-OBS data. |

|
Fig. 8 Inversion result based on the data from (a) N09-OBS; and (b) from N11-OBS. |
The relevant physical parameters of the sediment layer with a thickness of more than 200 m near the OBS stations are calculated according to the empirical formula, and the results are listed in Table 3. The calculation results show that the physical property parameters obtained from the data inversion of the two stations are relatively close.
|
|
Table 3 Physical parameters obtained by the inversion in this paper |
Comparing the inversion results in Table 3 with the actual measurement results of samples R11, R12, and R14 in Table 1, it can be seen that the particle size obtained by inversion is close to that of R11. However, the Hamilton empirical formula used in the calculation is not the formula for the Chukchi Sea in the Arctic, which will lead to some errors due to the difference of sediment types. The density obtained by inversion is approximately equal to those of the actual samples, while the porosity is less than those of the actual samples. The reason is that the velocity used in the empirical formula is the average velocity of the whole sedimentary layer. So the physical parameters of the sedimentary layer obtained by the empirical formula are also the average values of the whole sedimentary layer, rather than the values of the sediments on the seabed surface, as measured from the samples. When the seabed is sampled and measured, if samples are taken back to the laboratory for measurement, part of the seawater will be lost in the process of sampling and preservation, resulting in a slightly larger seabed density. The above two reasons lead to the difference between the physical parameters of inversion calculation and the actual measurement. Thus, when referring to the active-source OBS data inversion of seabed physical parameters, it is important to remember that the inversion results are the average physical parameters of the sedimentary layer with a certain thickness.
Based on the experience of the active-source OBS operation accumulated by two voyages, better results will be obtained for the application of active-source OBS detection technology to the physical parameter inversions of the polar seabed. The selection of source and corresponding OBS frequency band is very important. The signal source with high energy is suggested, while the band of OBS needs to be adjusted according to the source frequency band, and the effective matching between the two parts can obtain better data quality. However, because of the complexity of international relations in the Arctic region, the selection of sources will be limited, which is also one of the factors that need to be considered. In addition, due to the influence of ice covers, the time window for active-source OBS detection is best to select the time without the ice cover on the sea surface, to reduce the influence of sea ice on the source operation and OBS recovery success rate.
4.3 Limitation of Inversion MethodIn this method, the cost function is constructed by using the relationship between the time difference of echo between the sedimentary layer interfaces and seabed surface and the offset, sound velocity and thickness of sedimentary layer. The inversion based on the sediment density parameters by Hamilton empirical formula can obtain seabed acoustic parameters quickly and with high quality, significantly reducing the impact caused by the lack of sound velocity profile and inaccurate positioning (Xu et al., 2016).
The disadvantages of this method is the gradual accumulation of the calculation error with the increase of the number of inversion sedimentary layers, which makes the deep layer inversion difficult to converge and achieve the ideal effect. Limited by the actual acquisition conditions, the active source OBS acquisition line distance is too short, the source energy is small, and the frequency is low. These will lead to low profile signal-to-noise ratio and poor continuity of in-phase axis. Due to the limitation of focal energy, sound waves cannot penetrate deep strata. The effectively identified horizon can only reach the horizon less than 200 m below the seabed. Compared with the scale of the survey line, the strata of Chukchi Sea can be considered to be relatively horizontal and uniform in the experimental area (Li et al., 2021). Therefore, based on the ideal hypothesis, the cost function and perturbation method are used to measure the proximity between the forward modeling record and the real record at a specific speed and thickness. The velocity and thickness values closest to the real seabed acoustic parameters can be obtained. This method can effectively reduce the inversion impact caused by the positioning deviation and the lack of sound velocity profile, and provide a certain accuracy guarantee. The inversion results of seabed parameters by this method are in good agreement with the actual measurement results of surface sediments (Sun et al., 2021), which proves that this method can be applied to the inversion of seabed parameters based on the active source OBS data collected in the Arctic scientific expedition.
Generally speaking, the methods for seabed acoustic parameters include the inversion method based on the vertical structure of sound field (Liu et al., 2003), the matching field processing method (Fallat and Nielson, 2000), the propagation attenuation method (Li and Zhang, 2000), etc. Different inversion methods have different effects on different inversion parameters. For example, vertical reflection coefficient is more sensitive to acoustic impedance, matched field processing is more sensitive to sound velocity, and propagation loss is more sensitive to sound attenuation. Compared with the usual vertical receiving method, this paper adopts the OBS as the receiver of acoustic signals. The OBS is arranged on the seabed, whose position is fixed and has less position disturbance than the vertical hydrophone array. Only one signal transmitting ship is needed to complete the task, which has higher economic benefits.
5 ConclusionsIn this study, the cost function inversion method based on the time difference between the reflection and direct waves in the sedimentary layers is validated in the inversion of seabed parameters based on the active-source OBS data. The method is applied in the Chukchi Sea, and the physical parameters of the sedimentary layer are obtained successfully. It provides a reference for the application of the OBS technique in the inversion of physical parameters of the polar seabed sedimentary layers.
AcknowledgementsWe thank the chief, captain, crew, and science parties of the 9th and 11th Chinese National Arctic Research Expedition. This research was supported by the National Key R & D Program of China (No. 2021YFC2801200), the National Natural Science Foundation of China (No. 420762 24), and the Fundamental Research Funds for the Central Universities (No. 201964015).
Chandrakala, K., Pandey, O. P., and Singh, S., 2022. India-Antarctica collisional ridge structure below Nellore Schist and eastern Ghats Belts as revealed by seismic studies. Geosystems and Geoenvironment: 100039. DOI:10.1016/j.geogeo.2022.100039 (  0) 0) |
Chen, Y., 2012. Late Quaternary sedimentary correlation and paleooceanographic significance of the southern and northern basins of the Bering Strait. Master thesis. First Institute of Oceanography.
(  0) 0) |
Council, N., 1996. The Bering Sea ecosystem. Committee on the Bering Sea Ecosystem the Bering Sea Ecosystem Xp. http://apbeautel.ru/nukihav.pdf.
(  0) 0) |
Deschamps, C., Montero-Serrano, J., St-Onge, G., and Poirier, A., 2019. Holocene changes in deep water circulation inferred from authigenic Nd and Hf isotopes in sediment records from the Chukchi-Alaskan and Canadian Beauport margins. Paleoceanography and Paleoclimatology, 34(7): 1038-1056. DOI:10.1029/2018PA003485 (  0) 0) |
Fallat, M. R., and Nielson, P. L., 2000. Hybrid geoacoustic inversion of broadband Mediterranean Sea data. Journal of the Acoustical Society of America, 107(4): 1967-1977. DOI:10.1121/1.428480 (  0) 0) |
Gamboa, A., Montero-Serrano, J. C., St-Onge, G., Rochon, A., and Desiage, P. A., 2017. Mineralogical, geochemical, and magnetic signatures of surface sediments from the Canadian Beaufort shelf and Amundsen Gulf (Canadian Arctic). Geochemistry, Geophysics, Geosystems, 18(2): 488-512. DOI:10.1002/2016GC006477 (  0) 0) |
Gao, A. G., Chen, R. H., Cheng, Z. B., and Li, X. Z., 2001. Progress in the study of the marine geology of the Chukchi Sea and the Bering Sea. Marine Science, 25(12): 41-45 (in Chinese with English abstract). (  0) 0) |
Hamilton, E. L., and Bachman, R. T., 1982. Sound velocity and related properties of marine sediments. Journal of the Acoustical Society of America, 72(6): 1891-1904. DOI:10.1029/JB075i023p04423 (  0) 0) |
Kobayashi, D., Yamamoto, M., Irino, T., Nam, S., Park, Y., Harada, N., et al., 2016. Distribution of detrital minerals and sediment color in western Arctic Ocean and northern Bering Sea sediments: Changes in the provenance of western Arctic Ocean sediments since the last glacial period. Polar Science, 10(4): 519-531. DOI:10.1016/j.polar.2016.07.005 (  0) 0) |
Li, F. H., and Zhang, R. H., 2000. Bottom sound speed and attenuation inverted by using pulsed waveform and transmission. Acta Acoustics, 25(4): 297-302 (in Chinese with English abstract). DOI:10.15949/j.cnki.0371-0025.2000.04.002 (  0) 0) |
Li, G. B., Zhou, Q. J., Hua, Q. F., Wang, J. Q., Liu, C. G., and Liu, B. H., 2021. Characteristics of the shallow strata structure on the northern margin of the Chukchi Sea and its significance on paleao-glaciation. Advances in Marine Science, 39(3): 393-402 (in Chinese with English abstract). (  0) 0) |
Liu, J. J., Li, F. H., and Peng, Z. H., 2003. Stochastic inversion of seabottom scattering coefficients from shallow-water reverberation. Chinese Physics Letters, 20(12): 2188-2191. DOI:10.1088/0256-307X/20/12/029 (  0) 0) |
Meng, X., Li, G., Han, G., and Kan, G., 2015. Sound velocity and related properties of seafloor sediments in the Bering Sea and Chukchi Sea. Acta Oceanologica Sinica, 34(5): 75-80. DOI:10.1007/s13131-015-0669-9 (  0) 0) |
Shang, E. C., 2019. Progress of geoacoustic inversion in underwater acoustics. Journal of Applied Acoustics, 38(4): 468-476 (in Chinese with English abstract). (  0) 0) |
Stein, R., Fahl, K., Schade, I., Manerung, A., Wassmuth, S., Niessen, F., et al., 2017. Holocene variability in sea ice cover, primary production, and Pacific-water inflow and climate change in the Chukchi and East Siberian Seas (Arctic Ocean). Journal of Quaternary Science, 32(3): 362-379. DOI:10.1002/jqs.2929 (  0) 0) |
Sun, L., Wang, J. Q., Li, G. B., Meng, X. M., Kan, G. M., and Liu, B. H., 2021. Acoustic speed properties of surface sediments in Bering Sea and Chukchi Sea. Advances in Marine Science, 39(3): 452-460 (in Chinese with English abstract). (  0) 0) |
Tollefsen, D., Dosso, S. E., and Knobles, D. P., 2019. Ship-of-opportunity noise inversions for geoacoustic profiles of a layered mud-sand seabed. IEEE Journal of Oceanic Engineering, 45(99): 189-200. (  0) 0) |
Wu, Q., 2013. Inversion of sediment characteristic parameters and measurement of geoacoustic parameters. Master thesis. Harbin Engineering University.
(  0) 0) |
Xu, D., Li, F. H., and Guo, Y. G., 2016. Inversion of deep sea acoustic parameters by pulse sound. 2016 National Acoustic Conference. Wuhan, 192-195.
(  0) 0) |
Yang, K. D., and Ma, Y. L., 2009. A geoacoustic inversion method based on bottom reflection signals. Acta Physica Sinica, 58(3): 1798-1805 (in Chinese with English abstract). DOI:10.7498/aps.58.1798 (  0) 0) |
Zheng, G. X., 2019. Inversion of seabed acoustic parameters based on propagation characteristics of shallow water acoustic field. Master thesis. Zhejiang Ocean University.
(  0) 0) |
 2023, Vol. 22
2023, Vol. 22


