2) Shandong Provincial Key Laboratory of Marine Environment and Geological Engineering, Ocean University of China, Qingdao 266100, China;
3) Laboratory for Marine Geology, Qingdao National Laboratory for Maine Science and Technology, Qingdao 266100, China
A crawler collector is the most common collecting equipment in deep-sea polymetallic nodule mining (Yang and Chen, 2010; Miller et al., 2018). Two core problems in mining system design are driving safety performance and mining operation efficiency. In 2001, during a test conducted in Fuxian Lake in Yunnan Province, China, a crawler seriously subsided because of slipping, which directly affected its normal operations (Chen, 2005). Research shows that accidents, such as slipping and subsidence, are closely related to the adhesion and mechanical properties of sedimentary soil, and a negative correlation exists between the crawler's slip ratio and soil's shear strength (Han, 2014). Accordingly, the dynamic characteristics of deep-sea sediments must be mastered to ensure crawler design reliability and safety.
The mechanical properties of soil are determined by the initial state and stress path (Wang, 1980; Liu, 2019). The stress path has a significant effect on the dynamic properties of deep-sea soft soil with a long sedimentary history, relatively stable composition, and structure. Moreover, the dynamic properties of soil are distinct under different stress paths (Shen et al., 1994; Shen et al., 2006; Zeng and Chen, 2009; Liu et al., 2018). Towhata and Ishihara (1985) performed a series of undrained tests on saturated sand and found that excess pore water pressure is generated inside the soil under the rotation path of the principal stress axis, decreasing the anti-liquefaction and strength of the soil. Shen et al. (2008) compared the failure characteristics of soil under one-amplitude and two-amplitude rotations of the principal stress axis and found significant differences, such as the need for the minimum shear stress for failure under the two-amplitude rotation. Wang et al. (2017) found that compared with the circular stress path, the cyclic strength of the soil body under non-standard elliptical stress paths was more complex and diversified. Thus, it is on an indispensable theoretical basis that the dynamic characteristics of deep-sea sediments and stress paths of sediments when driving crawlers must be explored.
A hollow cylinder apparatus is often used for sample loading in laboratory geotechnical tests of marine soil (Liu, 2010; Zhu et al., 2018; Tang, 2019). The complex stress path can be simulated by setting different parameter combinations. This method allows the research results of stress path theory to be applied to tests and practical engineering. However, in existing studies on deep-sea sediments, linear stress paths, circular and elliptical stress paths under a wave load (Wang et al., 2020), or heart-shaped stress paths under normal traffic loads (Qian et al., 2016; Wu et al., 2017) are mostly used for loading. Hence, the dynamic characteristics of the soil obtained may be quite different from the practical driving conditions of crawlers, which is attributed to two main reasons. First, although crawler collectors run on the seafloor sedimentary soil surface, the traction comes from the shear action between grousers and surface soil (Dai, 2008). Consequently, the soil produces an obvious horizontal tangential displacement in shearing. However, the horizontal shear load is not considered in the calculation of typical stress paths. Second, grousers are in direct contact with the surface soil, and the mechanical properties of the surface soil have a significant impact on the running of crawler collectors. Thus, the stress path and dynamic characteristics of the shallow soil should be further explored, but only a few targeted studies are available at present. In addition, for deep-sea sediments with high sensitivity, subtle differences in stress paths may lead to large errors in test results. Therefore, an in-depth analysis of the stress paths and principal stress rotations of deep-sea sediments under the compression-shear coupling load of the crawler collector is necessary.
On the basis of previous research results, in this study, the load of a crawler collector acting on sediments was divided into a normal compression load and horizontal shear load to evaluate the stress response of internal sedimentary soil elements. The two working conditions were superimposed under the assumption of the theory of elasticity. Then, the quasi-static stress solution of any soil element under the driving load of crawlers was obtained. A numerical simulation was performed with the Abaqus finite element software, and the results were compared and verified. On the basis of the theoretical analysis results, the effect of the horizontal shear load and the spatial rule of stress paths were analyzed. Then, an in-depth study was completed on the change of soil stress states and the rotation of the principal stress axis in the running crawler collector.
2 Deep-Sea Sediment Stress CalculationCrawler collectors travel on the surface of deep-sea sediments like land vehicles travel on roads. To study the stress of subgrade soil under land traffic loads, Ishihara (1996) deduced a heart-shaped stress path under normal loads through the quasi-static method theory and revealed the essence of the rotation of the principal stress axis of soil. Ishihara's results have been confirmed and widely recognized in subsequent theoretical studies, soil dynamics tests, and actual road engineering. Thus, this idea is used to calculate the sedimentary soil stress state and stress path under the running load of crawlers.
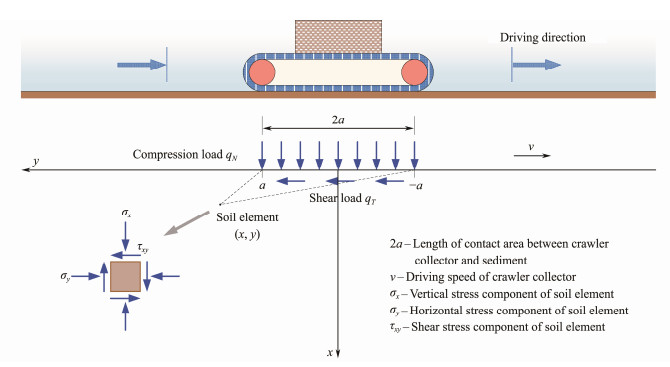
2.1 Calculation ModelAccording to the actual working conditions and theory of elasticity, a two-dimensional calculation model for the stress of sediments under the driving load of crawlers was established, as shown in Fig.1. Deep-sea sediment is often regarded as elastic-plastic (Choi et al., 2011) or viscoelastic (Xu et al., 2018) soil in the existing research, both containing elastic components. To simplify the calculation process, deep-sea sedimentary soil in this model is considered an elastic medium, and its constitutive relation is assumed to obey Hooke's law.
|
Fig. 1 Deep-sea sediment stress calculation model. |
The compression-shear coupling load acts on sediments by running crawlers. The actual scope of action is the contact area between the deep-sea sediment and the bottom surface of the crawlers. For simplification, this issue was considered a plane problem, and the acting load of crawlers was taken as the uniform load with a width of 2a on the elastic half-space surface. This load was further divided into the normal compression load qN and horizontal shear load qT. The normal compression load was perpendicular to the horizontal plane and in the downward direction, whereas the horizontal shear load was in the direction opposite to the running direction of the crawlers in the horizontal direction.
The coordinate system was established with the horizontal surface of the sediment as the y-axis and the vertical direction as the x-axis. The stress direction regulation of soil mechanics was used (the stress acting on the positive coordinate plane was positive along the negative direction of the coordinate axis, and the stress acting on the negative coordinate plane was positive along the positive direction of the coordinate axis).
2.2 Soil Stress Under the Compression-Shear Coupling LoadOnly the additional stress inside the deep-sea sedimentary soil caused by the crawler collector was calculated, and long-term loads, such as gravity and hydrostatic pressure, were not considered. On the basis of Ishihara's calculation (Ishihara, 1996), under the normal compression load qN, the solution of soil element stress is
| $ \sigma _x^N{\text{ = }}\frac{{{q_N}}}{{\text{π }}}\left\{ {\left({\arctan \frac{{y + a}}{x} - \arctan \frac{{y - a}}{x}} \right) + \left[ {\frac{{x\left({y + a} \right)}}{{{x^2} + {{\left({y + a} \right)}^2}}} - \frac{{x\left({y - a} \right)}}{{{x^2} + {{\left({y - a} \right)}^2}}}} \right]} \right\}, $ | (1a) |
| $ \sigma _y^N{\kern 1pt} = \frac{{{q_N}}}{{\text{π }}}\left\{ {(\arctan \frac{{y + a}}{x} - \arctan \frac{{y - a}}{x}) - \left[ {\frac{{x\left({y + a} \right)}}{{{x^2} + {{\left({y + a} \right)}^2}}} - \frac{{x\left({y - a} \right)}}{{{x^2} + {{\left({y - a} \right)}^2}}}} \right]} \right\}, $ | (1b) |
| $ \tau _{xy}^N = \frac{{{q_N}}}{{\text{π }}}\left[ {\frac{{{x^2}}}{{{x^2} + {{\left({y - a} \right)}^2}}} - \frac{{{x^2}}}{{{x^2} + {{\left({y + a} \right)}^2}}}} \right], $ | (1c) |
where
Based on the basic idea of the quasi-static method, the Cerruti stress solution (Xu, 2016) was calculated through an integral calculation on y∈(−a, a) in the action interval of the horizontal shear load. Thus, the soil stress under the action of the horizontal shear load qT is as follows:
| $ \sigma _x^T = \frac{{2{q_T}}}{{\text{π }}}\int_{ - a}^a {\frac{{{x^2}\left({y - \xi } \right)}}{{{{\left[ {{x^2} + {{\left({y - \xi } \right)}^2}} \right]}^2}}}{\text{d}}\xi } = \frac{{{q_T}}}{{\text{π }}}\left[ {\frac{{{x^2}}}{{{x^2} + {{\left({y - a} \right)}^2}}} - \frac{{{x^2}}}{{{x^2} + {{\left({y + a} \right)}^2}}}} \right], $ | (2a) |
| $ \sigma _y^T = \frac{{2{q_T}}}{{\text{π }}}\int_{ - a}^a {\frac{{{{\left({y - \xi } \right)}^3}}}{{{{\left[ {{x^2} + {{\left({y - \xi } \right)}^2}} \right]}^2}}}{\text{d}}\xi = \frac{{{q_T}}}{{\text{π }}}\left\{ {\ln \frac{{{x^2} + {{\left({y + a} \right)}^2}}}{{{x^2} + {{\left({y - a} \right)}^2}}} - \left[ {\frac{{{x^2}}}{{{x^2} + {{\left({y - a} \right)}^2}}} - \frac{{{x^2}}}{{{x^2} + {{\left({y + a} \right)}^2}}}} \right]} \right\}}, $ | (2b) |
| $ \tau _{xy}^T = \frac{{2{q_T}}}{{\text{π }}}\int_{ - a}^a {\frac{{x{{\left({y - \xi } \right)}^2}}}{{{{\left[ {{x^2} + {{\left({y - \xi } \right)}^2}} \right]}^2}}}{\text{d}}\xi = \frac{{{q_T}}}{{\text{π }}}\left\{ {\left({\arctan \frac{{y + a}}{x} - \arctan \frac{{y - a}}{x}} \right) - \left[ {\frac{{x\left({y + a} \right)}}{{{x^2} + {{\left({y + a} \right)}^2}}} - \frac{{x\left({y - a} \right)}}{{{x^2} + {{\left({y - a} \right)}^2}}}} \right]} \right\}}, $ | (2c) |
where
As shown in Eqs. (2) and (3), the stress value of deep-sea sediments is proportional to the external loads qN and qT. In an actual working condition, the two external load values are related to the driving state of the crawler collector, which is set as constant values that do not change with time for simplification. To facilitate the expression of results and subsequent dimensionless analysis, constant b is set as the load ratio, and has the following relationship,
| $ {q_T} = b \cdot {q_N} . $ | (3) |
Here, qT and qN refer to the normal compression load and horizontal shear load applied by the crawler, respectively. Parameter b does not represent any actual physical meaning and can be obtained by Eq. (3) only. To determine this value, load values should be determined according to the actual working conditions and research needs, and then b will be calculated.
By substituting the equivalence relation in Eq. (3) into Eq. (2) and adding Eq. (1) to Eq. (2), the soil stress solution under the total load of the crawler is obtained as follows:
| $ {\sigma _x} = \frac{{{q_N}}}{{\text{π }}}\left\{ \begin{array}{l} \left({\arctan \frac{{y + a}}{x} - \arctan \frac{{y - a}}{x}} \right) + \left[ {\frac{{x\left({y + a} \right)}}{{{x^2} + {{\left({y + a} \right)}^2}}} - \frac{{x\left({y - a} \right)}}{{{x^2} + {{\left({y - a} \right)}^2}}}} \right] \hfill \\ + b\left[ {\frac{{{x^2}}}{{{x^2} + {{\left({y - a} \right)}^2}}} - \frac{{{x^2}}}{{{x^2} + {{\left({y + a} \right)}^2}}}} \right] \hfill \\ \end{array} \right\}, $ | (4a) |
| $ {\sigma _y} = \frac{{{q_N}}}{{\text{π }}}\left\{ \begin{array}{l} (\arctan \frac{{y + a}}{x} - \arctan \frac{{y - a}}{x}) - \left[ {\frac{{x\left({y + a} \right)}}{{{x^2} + {{\left({y + a} \right)}^2}}} - \frac{{x\left({y - a} \right)}}{{{x^2} + {{\left({y - a} \right)}^2}}}} \right] \hfill \\ + b\ln \frac{{{x^2} + {{\left({y + a} \right)}^2}}}{{{x^2} + {{\left({y - a} \right)}^2}}} - b\left[ {\frac{{{x^2}}}{{{x^2} + {{\left({y - a} \right)}^2}}} - \frac{{{x^2}}}{{{x^2} + {{\left({y + a} \right)}^2}}}} \right] \hfill \\ \end{array} \right\}, $ | (4b) |
| $ {\tau _{xy}} = \frac{{{q_N}}}{{\text{π }}}\left\{ \begin{array}{l} \left[ {\frac{{{x^2}}}{{{x^2} + {{\left({y - a} \right)}^2}}} - \frac{{{x^2}}}{{{x^2} + {{\left({y + a} \right)}^2}}}} \right] \hfill \\ + b\left({\arctan \frac{{y + a}}{x} - \arctan \frac{{y - a}}{x}} \right) - b\left[ {\frac{{x\left({y + a} \right)}}{{{x^2} + {{\left({y + a} \right)}^2}}} - \frac{{x\left({y - a} \right)}}{{{x^2} + {{\left({y - a} \right)}^2}}}} \right] \hfill \\ \end{array} \right\}, $ | (4c) |
where σx, σy, and τxy refer to the vertical stress, horizontal stress, and shear stress of soil elements under the compression-shear coupling load of the crawler, respectively.
Here, qN and qT refer to the vertical compressive load and horizontal shear load of the soil, respectively. For submarine crawler collectors, the vertical positive pressure is mainly determined by the underwater weight of the crawler. Then,
| $ {F_N} = G', $ | (5) |
where FN refers to the vertical positive pressure of the soil and G′ refers to the underwater weight of the crawler. The shear action between grousers and the sediment is the traction force source of the crawler. Then,
| $ {F_T} = {F_1}, $ | (6) |
where FT refers to the horizontal shear force on the soil and F1 refers to the traction force of the collectors.
In this study, the parameters were derived from simulation experiments (Han and Liu, 2013). The underwater weight of the crawler was 11.7 t, so FN = G′ = 114.66 kN. In their study on the slip ratio of crawler collectors, Han and Liu (2013) found that the traction force sharply decreases with the increase in the slip ratio. When the slip ratio is equivalent to the expected value of 20%, the traction force of crawlers is F1 = 32.82 kN, so FT = 32.82 kN.
According to the quantity conversion relationship between the uniform distributed load and applied force of crawlers in this paper,
| $ \left\{ {\begin{array}{*{20}{c}} {{q_T} = \frac{{{F_T}}}{A}} \\ {{q_N} = \frac{{{F_N}}}{A}} \end{array} } \right., $ | (7) |
where A is the contact area between the bottom of the crawlers and sediment (constantly under the ideal driving state). Therefore, the load ratio b = qT/qN = FT/FN ≈ 0.3. Below, b = 0.3 is used for the calculation and analysis.
3 Analysis of the Horizontal Shear Load ActionStudies on the stress response of subgrade soil under a normal traffic load are abundant. Accordingly, this paper starts with the stress time-history of the sediment unit to analyze the action of the horizontal shear load.
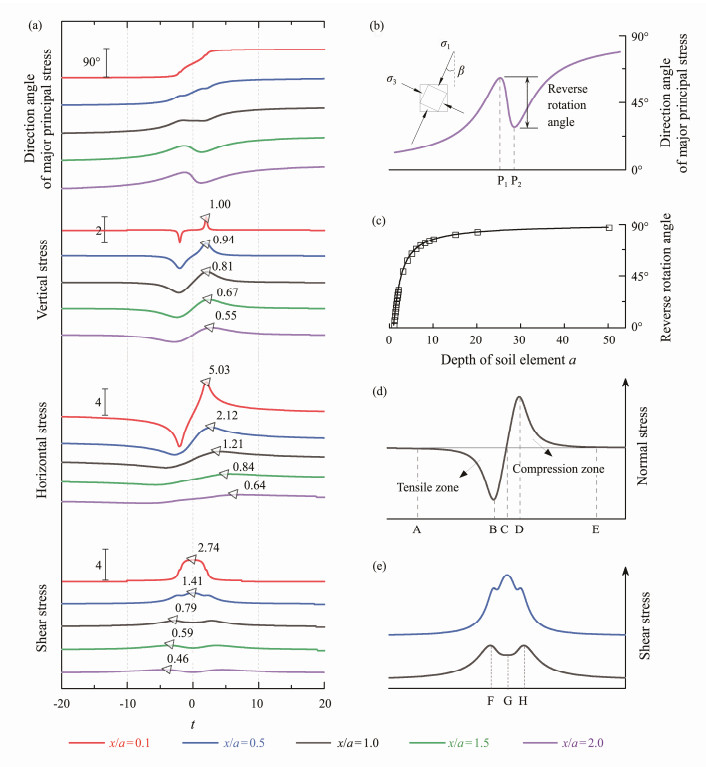
Based on mining efficiency requirements and safety considerations in deep-sea polymetallic nodule mining, the designed running speed of the crawler is 0 – 1 m s−1 and the operating running speed is 0.5 m s−1 (Feng, 2005). Thus, the crawler speed was selected as v = 0.5 m s−1. To eliminate the effect of irrelevant variables, the depth ratio is defined as the ratio of the soil depth to half the load length a. Fig.2a shows the time-history changes of each stress component and principal stress direction for soil elements with depth ratios of x/a = 0.1, 0.5, 1.0, 1.5, and 2.0 under the horizontal shear load. The time when the load center of the crawler directly reaches above the soil unit is denoted as time zero. Because of the high coincidence of some working condition curves, all curves are displayed by the dislocation to effectively show the changing trend of the stress and principal stress direction angles under various working conditions. The left axis of the coordinate (at t = −20) was set as the zero baseline (for all curves, the longitudinal coordinate value is 0 on the zero baseline). This condition is consistent with the initial stress state of the soil.
|
Fig. 2 Soil stress under a horizontal shear load. (a), Time-history variation of the direction angle of the major principal stress and three stress components of soil under a horizontal shear load. The direction angle of the major principal stress refers to the angle between the direction of major principal stress and vertical direction with the unit of degree; the unit of the stress component value is qT/π; (b), Rotation tendency of the direction angle β of the large principal stress; (c), Curve of the reverse rotation angle of the principal stress direction with the soil element depth; (d), Time-history variation trend of the normal stress component; (e), Time-history variation trend of the shear stress. |
Fig.2b shows the variation trend of the direction angle of the major principal stress of the soil at the depth ratio x/a = 2.0 under the horizontal shear load. The major principal stress direction angle of the soil is the included angle of the major principal stress direction and vertical direction (β). In a running crawler (i.e., t ∈ (−∞, +∞)), the direction angle of the large principal stress of the soil gradually rotates from 0˚ to 90˚. In addition, the axis of the major principal stress does not rotate in one direction. When the load moves to the vicinity of the x-axis (see P1 and P2 in Fig.2b), the major principal stress has a reverse rotation. In the shallow region, two reverse rotations occur in the direction of the major principal stress, and the rotation angle is small. With the increase in the soil depth, as shown in Fig.2b, the soil has an obvious reverse rotation trend in the direction of the large principal stress. The reverse rotation angles of the sedimentary soil at multiple depths were extracted and plotted according to the theoretical calculation results, as shown in Fig.2c. In particular, the reverse rotation angle of the principal stress axis increases as the depth increases, and the growth rate decreases with the depth. The maximum reverse rotation angle is 90˚, which is equivalent to two cycles.
3.2 Normal Stress ComponentThe time-history curves of the vertical stress and horizontal stress are similar in shape and waveform, as shown in Fig.2d. According to the stress state, the stress time-history of the soil element under this working condition is divided into two stages: tensile stage (A → B → C) and compression stage (C → D → E). The stress values at other moments are approximately 0 and can be ignored. As the traveling load of crawlers moved from far to near, the stress component negatively increased from A to B. It reached a negative peak at time B. In stages B to C, the absolute value of stress rapidly decreased until time C. At time C, the load center directly reached above the soil element, and the stress components, including vertical and horizontal stress, were zero due to the symmetry of the load distribution location. The load then left, and the leaving and approaching curves were symmetric about the origin. The stress reached a positive peak at time D, and the values of the positive and negative peaks were equal. Although the vertical and horizontal stresses have the same trend, their characteristic moments are significantly different. As demonstrated in Fig.2a, the vertical stress has a small fluctuation range and small peak value, whereas the horizontal stress has a wide fluctuation range and large peak value. This wide fluctuation is related to the horizontal direction of the load.
The tension of the sedimentary soil element is a special phenomenon caused by the horizontal shear load. Different from the vertical load, the normal stress components of the sedimentary soil are negative from A to C under the action of the horizontal shear load, showing a tendency to stretch. The failure form of the sedimentary soil under this stress path is one of the priorities of future works.
3.3 Shear StressFig.2e plots the time-history curve of the shear stress, in which the upper and lower curves are soil with depth ratios x/a = 0.5 and 1.0, respectively, and the initial and ending values of the shear stress of the two curves are 0. The shear stress curve was always positive in the whole movement of the load, and there were three peak points (F, G, and H). At time G, the driving load was just above the soil element, and the peak values of the shear stress at times F and H were the same. As shown in Fig.2a, the maximum shear stress of shallow soil occurs at time G, whereas the maximum shear stress of the deep soil occurs at times F and H. When the distributed load directly moved over the soil, the shallow soil was sensitive to the load movement, and its shear stress reached the maximum peak at time G. At the same time, the shear stress of the deep soil had little fluctuations. Generally, under the horizontal shear load of crawlers, the horizontal stress component of the soil element had the largest fluctuation value and widest fluctuation range.
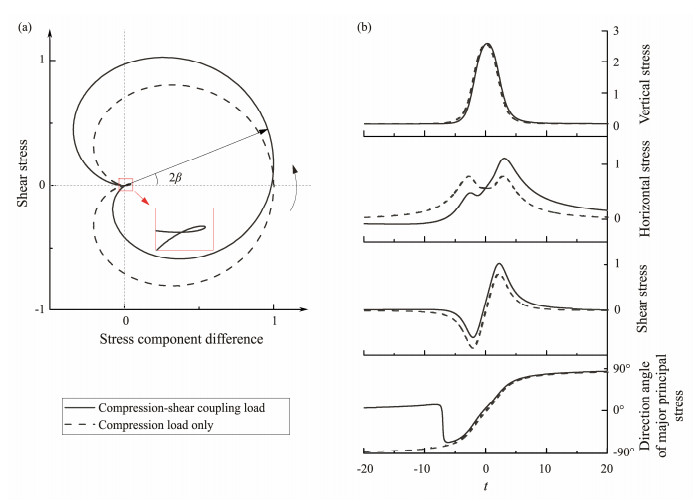
3.4 Effect of the Shear LoadThe soil element with a depth ratio x/a = 1.0 was analyzed, and its stress path diagram is given in Fig.3. The stress path diagram takes the stress component difference as the abscissa X and the shear stress as the ordinate Y, as follows:
| $ \left\{ {\begin{array}{*{20}{l}} {X = \frac{{{\sigma _x} - {\sigma _y}}}{2}} \\ {Y = {\tau _{xy}}{\kern 1pt} } \end{array} } \right., $ | (8) |
|
Fig. 3 Soil stress path at x/a = 1.0 (unit: qT/π). (a), Soil stress path curve; (b), Time-history change curve of the vertical stress, horizontal stress, shear stress and direction angle of the major principal stress of soil. |
where σx, σy, and τxy are the vertical stress, horizontal stress, and shear stress of the soil elements, respectively. Through a theoretical derivation, Ishihara (1996) concluded that the relationship between the direction angle β of the large principal stress and stress component is
| $ \beta = \frac{1}{2}\arctan \frac{{2{\tau _{xy}}}}{{{\sigma _x} - {\sigma _y}}} . $ | (9) |
To explore the effect of the horizontal shear load on the soil stress, Eqs. (1) and (4) are substituted into Eq. (8) to draw the soil stress path and time-history variation under a normal compression load and the total running load of crawlers, as shown in Fig.3. To intuitively show the rotation of the principal stress axis, the direction angle β of the large principal stress is marked in Fig.3a according to Eq. (9).
The stress path diagram of soil only under the normal compressive load is heart-shaped, and the graph is symmetric about the x-axis. When the normal compression load and horizontal shear load produced by the running load of the crawlers are comprehensively considered, the stress path diagram is no longer a symmetrical trajectory because of the effect of the shear stress. As shown in Fig.3b, considering that the horizontal shear load has little effect on the development trend of the vertical stress and shear stress of the soil elements at this depth, the peak value of the shear stress slightly increases, whereas the maximum value of the horizontal stress significantly increases. The shape of the direction angle curve of large principal stress significantly changes, and reverse rotation fluctuations appear that do not exist when only the normal load acts.
4 Numerical Simulation and Result AnalysisNumerical simulation tests were performed on the stress state of the soil elements under the action of the compression-shear coupling load with the standard module of the Abaqus software. The calculated results were compared and analyzed with the theoretical results.
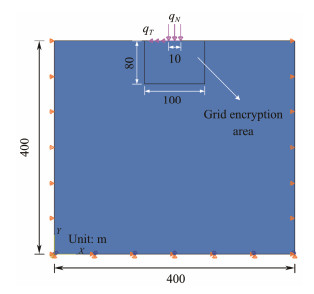
4.1 Numerical SimulationFig.4 shows the numerical calculation model of the soil stress under the compression-shear coupling load of crawlers. According to Han and Liu (2013), the length of the crawler collector is 9.2 m, which was set to 10 m in this study to simplify the subsequent processing work. Nondimensionalization is one of the data processing tasks, so the length has little effect on the results. An eight-node quadrilateral plane strain element (CPE8) was selected for the calculation. To improve the accuracy of the calculation results and facilitate subsequent data analysis, grid encryption was completed in and around the loading area. A total of 193420 elements were divided.
|
Fig. 4 Abaqus finite element analysis model. |
In the simulation, the soil is assumed to be purely elastic, and the constitutive relation obeys Hooke's law of plane strain cases (Xu, 2016), that is,
| $ \left\{ {\begin{array}{*{20}{l}} {{\varepsilon _x} = \frac{{1 - {\mu ^2}}}{E}\left({{\sigma _x} - \frac{\mu }{{1 - \mu }}{\sigma _y}} \right)} \\ {{\varepsilon _y} = \frac{{1 - {\mu ^2}}}{E}\left({{\sigma _y} - \frac{\mu }{{1 - \mu }}{\sigma _x}} \right)} \\ {{\gamma _{xy}} = \frac{{2\left({1 + \mu } \right)}}{E}{\tau _{xy}}} \end{array}} \right., $ | (10) |
where εx, εy, and γxy are the strain components, E is the elastic modulus, and μ is Poisson's ratio.
To compare and analyze the calculation with the above theoretical solution, five horizontal output paths with a depth ratio (the ratio of soil depth to half the load length) of 0.1, 0.5, 1.0, 1.5, and 2.0 were created, and the stress data S11, S22, and S12 of each path were derived. Because of the difference in the coordinate system construction and specified stress direction, the numerical simulation results were processed as follows:
| $ \left\{ {\begin{array}{*{20}{c}} {\sigma _x^s = - S22} \\ {\sigma _y^s = - S11} \\ {\tau _{xy}^s = - S12} \end{array} } \right., $ | (11) |
where σxs, σys, and τxys refer to the numerical simulation results of the vertical stress, horizontal stress, and shear stress of the soil under a total load of the crawlers, respectively.
Taking the actual operating conditions of deep-sea crawlers as an example, parameter values were calculated on the basis of Section 2.2. Table 1 shows the final parameter setting. The subsoil in the polymetallic nodule mining area is saturated clay soil dominated by silt particles (Ma et al., 2014). For soils under short-term loading conditions, the Poisson's ratio for saturated clay is 0.5 (Poulos, 1988). Therefore, the sediment was considered to have a Poisson's ratio of μ = 0.5 in this study. Among them, the vertical load and horizontal load were respectively set to 1 and 0.3 kPa; the intention is to make the stress component value dimensionless and study the objective law of the stress path. Fig.5a plots the calculation results of the example.
|
|
Table 1 Abaqus model parameters (Song, 1999) |
|
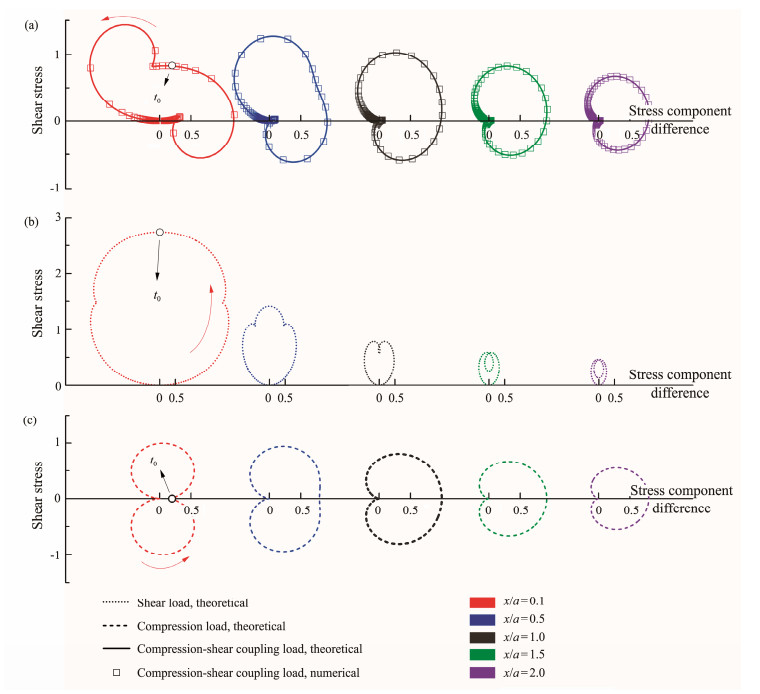
Fig. 5 Stress path of soil at different depths. (a), Theoretical and numerical solutions of the soil stress path under the compression-shear coupling load of the tracked vehicle with the stress unit of qN/π; (b), Theoretical solution of the soil stress path under the horizontal shear load with the stress unit of qT/π; (c), Theoretical solution of the soil stress path under the normal barotropic load with the stress unit of qN/π. The time when the center of the crawler reaches directly above the soil unit is represented by t0. |
The working condition studied in this work is a one-way straight running of a crawler collector. For sedimentary soil units of the same depth, different horizontal positions will only lead to a time phase difference in the soil stress change, and the stress change process remains identical. Therefore, the spatial distribution law of the stress path of soil elements is mainly aimed at the change law of the stress path with the depth of the soil. To grasp the spatial variation law of the soil stress path under the total traveling load of crawlers and explore its essence, the normal compression load and horizontal shear load were analyzed, respectively.
On the basis of the theoretical stress solution presented above, the soil stress path at depth ratios of x/a = 0.1, 0.5, 1.0, 1.5, and 2.0 is plotted with X as the abscissa and Y as the ordinate in Eq. (8), as shown in Fig.5. As the soil depth increases, the stress path diagram tends to shrink, and the stress path curve under the horizontal shear load decays the fastest (see Fig.5b). The stress response of the shallow soil is highly sensitive to a horizontal shear load. Considering that the horizontal shear load has a great effect on the stress path curve of the shallow soil and significantly increases the maximum value of shear stress, the rotation trend of the principal stress direction becomes complex.
In Fig.5c, the stress path curves of the soil are plotted at different depths under normal compressive loads only. In the existing studies (Wang and Chen, 2007; Bian et al., 2008; Wu et al., 2017; Zhang, 2019), the stress paths of soil under normal compressive loads are mostly heart-shaped. By comparing the theoretical solutions at different depths, this study found a heart-shaped stress path when the soil element is deeper. For shallow soil, through a theoretical derivation, when x/a <
Fig.5a shows the stress path diagrams of soil elements at different depths under the compression-shear coupling load of crawlers and compares the theoretical and numerical solutions of the stress when the value of the load ratio b = 0.3 (see Section 2.2). When the soil depth is large (e.g., Fig.5a, x/a = 2.0), the effect of the horizontal shear load is very small. The stress path diagram under the compression-shear coupling load is consistent with that under the normal load, and the rotation of their principal stress axes is the same. However, in shallow soil (e.g., x/a = 0.1 and 0.5), the effect of the horizontal shear load is significant, the stress path of the total load shows an obvious torsional deformation, and the principal stress axis has a complex rotation.
The numerical simulation test results take points at an equidistant horizontal distance (the spatial horizontal distance is a given value between two adjacent data points at the same depth). Therefore, the sparseness of data points in Fig.5a is related to the change rate of stress. The stress changed faster in sparse data points and slower in dense data points. From the point density, when the horizontal distance between the load and soil element was far, the stress variation range was small and the speed was slow. When the horizontal distance was relatively close between the load and soil element, the stress variation range was large, and the speed was fast. If the soil element position was relatively shallow (e.g., x/a = 0.1), when the crawler's load was directly above the soil element, the density of data points increased and the stress change speed was slightly slow. Therefore, the stress development rate is the fastest when the crawler is close to the soil but has not yet arrived or moved away from it.
5 ConclusionsIn this study, the stress state of deep-sea sediments caused by crawler collectors was analyzed and simplified to a plane problem. Through the quasi-static method, the stress path of any unit in the soil under the action of the compression-shear coupling load of a crawler collector was plotted. The stress path diagram at different depths was drawn, and the shape of the stress path diagram and the rotation of the principal stress axis were analyzed. The conclusions are presented below:
1) The stress path of sedimentary soil at various depths is quite different. Under a normal load of a crawler collector, the stress path curve of deep soil is heart-shaped, whereas that of shallow soil has a concave area. The shape of the stress path curve is often used as a technical reference index to determine the test loading scheme because the experimental instruments cannot easily simulate overly complicated stress paths when performing experiments to study the dynamic characteristics of soil under complex stress paths. Selecting the appropriate depth to perform research works according to the project needs will improve the reliability of research results.
2) The horizontal shear load has a significant effect on the stress path and rotation of the principal stress axis. The stress path of shallow soil is evident as it is close to the surface and produces obvious horizontal shear load and deflection. In addition, principal stress axes have a complex rotation. The surface soil dynamic properties are an important component of tracked vehicle design. Thus, studying the effect of the compression-shear coupling load on the soil stress path is of great engineering value.
The work in this paper was performed on the basis of the theory of elasticity, which assumes that the crawler speed and soil deformation do not affect the stress response of the sediment unit. However, because of repeated loading, the soil will show an accumulation of plastic deformation and a rise in pore water pressure (Gräbe and Clayton, 2009), which cannot be described by the theory of elasticity. Thus, selecting an effective soil constitutive model to perform relevant research more suitable to practical working conditions is the required next step.
AcknowledgementsThe study is supported by the National Natural Science Foundation of China (Nos. U1906234, 51822904, 51579082), and the Fundamental Research Funds for the Central Universities (No. 2020MS027).
Bian, X. C., Hu, T., and Chen, Y. M., 2008. Stress path in soil element of ground under moving traffic loads. China Civil Engineering Journal, 41(11): 86-92. DOI:10.3321/j.issn:1000-131X.2008.11.013 (  0) 0) |
Chen, F., 2005. Study on deep seabed mining robot vehicle motion modeling and control. PhD thesis. Central South University, Changsha.
(  0) 0) |
Choi, J. S., Hong, S., Chi, S. B., Lee, H. B., Park, C. K., Kim, H. W., et al., 2011. Probability distribution for the shear strength of seafloor sediment in the KR5 area for the development of manganese nodule miner. Ocean Engineering, 38(17-18): 2033-2041. DOI:10.1016/j.oceaneng.2011.09.011 (  0) 0) |
Dai, S. W., 2008. Study on travel control technology of deep sea mining vehicle. Master thesis. Central South University. Changsha.
(  0) 0) |
Feng, L. H., 2005. Research and virtual simulation on walking control of model car of deep sea collector. Master thesis. Central South University. Changsha.
(  0) 0) |
Gräbe, P. J., and Clayton, C., 2009. Effects of principal stress rotation on permanent deformation in rail track foundations. Journal of Geotechnical and Geoenvironmental Engineering, 135(4): 555-565. DOI:10.1061/(ASCE)1090-0241(2009)135:4(555) (  0) 0) |
Han, Q. Y., 2014. Slip and path tracking control of the deep sea tracked miner. PhD thesis. Central South University, Changsha.
(  0) 0) |
Han, Q. Y., and Liu, S. J., 2013. Slip control of deep sea tracked miner based on dynamic analysis. Journal of Central South University (Science and Technology), 44(8): 3166-3172. (  0) 0) |
Ishihara, K., 1996. Soil Behaviour in Earthquake Geotechnics. Clarendon Press, Oxford, 12.
(  0) 0) |
Liu, G. X., 2010. Study on shear behaviors of saturated marine soils under complex stress conditions. PhD thesis. Dalian University of Technology, Dalian.
(  0) 0) |
Liu, T., Zhou, L., and Chen, X. G., 2018. Study on the liquefaction properties of silt at Yellow River Delta. Journal of Ocean University of China, 17(6): 1382-1390. DOI:10.1007/s11802-018-3677-5 (  0) 0) |
Liu, Y., 2019. Fundamentals of Soil Dynamics. Tsinghua University Press, Beijing, 52.
(  0) 0) |
Ma, W. B., Rao, Q. H., Wu, H. Y., Guo, S. C., and Li, P., 2014. Macroscopic properties and microstructure analyses of deep-sea sediment. Rock and Soil Mechanics, 35(6): 1641-1646. DOI:10.16285/j.rsm.2014.06.040 (  0) 0) |
Miller, K. A., Thompson, K. F., Johnston, P., and Santillo, D., 2018. An overview of seabed mining including the current state of development, environmental impacts, and knowledge gaps. Frontiers in Marine Science, 4: 418. DOI:10.3389/fmars.2017.00418 (  0) 0) |
Poulos, H. G., 1988. Marine Geotechnics. The Academic Division of Unwin Hyman Ltd., London, 189pp.
(  0) 0) |
Qian, J. G., Wang, Y. G., Yin, Z. Y., and Huang, M. S., 2016. Experimental identification of plastic shakedown behavior of saturated clay subjected to traffic loading with principal stress rotation. Engineering Geology, 214: 29-42. DOI:10.1016/j.enggeo.2016.09.012 (  0) 0) |
Shen, R. F., Wang, H. J., Zhou, K. J., and Zhou, J. X., 1994. Building-up of pore water pressure under cyclic rotation of principle stress and evaluation of stability of seabed deposit. Chinese Journal of Geotechnical Engineering, 16(3): 70-78 (in Chinese with English abstract). (  0) 0) |
Shen, Y., Zhou, J., and Gong, X. N., 2006. Experimental progress research on influence of principle stress rotation on soils' characteristics. Chinese Journal of Rock Mechanics and Engineering, 25(7): 1408-1416. DOI:10.3321/j.issn:1000-6915.2006.07.017 (  0) 0) |
Shen, Y., Zhou, J., Zhang, J. L., and Gong, X. N., 2008. Critical properties of intact soft clay under cyclic principal stress rotation. Journal of Zhejiang University (Engineering Science), 42(1): 77-82 (in Chinese with English abstract). (  0) 0) |
Song, L. Q., 1999. Geotechnical properties of oceanic polymetallic nodule sediments. Acta Oceanologica Sinica, 21(6): 47-54. (  0) 0) |
Tang, J., 2019. Study on cyclic softening characteristics of coastal structural soft soil. Master thesis. Anhui University of Science & Technology, Huainan.
(  0) 0) |
Towhata, I., and Ishihara, K., 1985. Undrained strength of sand undergoing cyclic rotation of principle stress axes. Soils & Foundations, 25(2): 135-147. (  0) 0) |
Wang, C. J., and Chen, Y. M., 2007. Stress state variation and principle stress axes rotation of ground induced by moving loads. Chinese Journal of Rock Mechanics and Engineering, 26(8): 1698-1704. DOI:10.3321/j.issn:1000-6915.2007.08.022 (  0) 0) |
Wang, Y. K., Wan, Y. S., Fang, H. Y., Zeng, Z. N., Shi, M. S., and Wu, D., 2020. Experimental study of cyclic behavior of soft clay under circle stress paths. Rock and Soil Mechanics, 41(5): 1643-1652. DOI:10.16285/j.rsm.2019.0386 (  0) 0) |
Wang, Z. H., 1980. Stress path and stress path method. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 1980(1): 19-34. DOI:10.19760/j.ncwu.zk.1980.01.004 (  0) 0) |
Wang, Z. T., Liu, P., Jeng, D. S., and Yang, Q., 2017. Cyclic strength of sand under a nonstandard elliptical rotation stress path induced by wave loading. Journal of Hydrodynamics, 29(1): 89-95. DOI:10.1016/S1001-6058(16)60720-5 (  0) 0) |
Wu, T., Cai, Y., Guo, L., and Wang, J., 2017. Influence of shear stress level on deformation behaviour of undisturbed soft clay under traffic loading. Engineering Geology, 228: 61-70. DOI:10.1016/j.enggeo.2017.06.013 (  0) 0) |
Xu, F., Rao, Q. H., Zhang, J., and Ma, W. B., 2018. Compression-shear coupling rheological constitutive model of the deep-sea sediment. Marine Georesources & Geotechnology, 36: 288-296. DOI:10.1080/1064119X.2017.1286530 (  0) 0) |
Xu, Z. L., 2016. Elasticity. Higher Education Press, Beijing, 255pp (in Chinese).
(  0) 0) |
Yang, N., and Chen, G. G., 2010. Status quo and development trendency of deep sea minerals mining technology. Mining & Processing Equipment, 38(10): 4-9. DOI:10.16816/j.cnki.ksjx.2010.10.002 (  0) 0) |
Zeng, L. L., and Chen, X. P., 2009. Analysis of mechanical characteristics of soft soil under different stress paths. Rock and Soil Mechanics, 30(5): 1264-1270. DOI:10.16285/j.rsm.2009.05.034 (  0) 0) |
Zhang, Y., 2019. Study on stress path of foundation soil under road traffic load. Jiangsu Construction, 2019(1): 99-101, 120 (in Chinese with English abstract). (  0) 0) |
Zhu, J. F., Hong, Y., Yan, J. J., Gong, X. N., and Zhao, H. Y., 2018. Cyclic degradation of soft clay subjected to repeated wave loading and stress relief during tunnel driving through a seawall. China Civil Engineering Journal, 51(12): 111-119, 139. DOI:10.15951/j.tmgcxb.2018.12.009 (  0) 0) |
 2023, Vol. 22
2023, Vol. 22


