2) The Center for Ports and Maritime Safety (CPMS), Dalian Maritime University, Dalian 1160263, China;
3) Marine Environmental Monitoring Central Station, State Oceanic Administration, Yantai 264025, China;
4) Guangxi Key Laboratory of Marine Environmental Science, Guangxi Academy of Sciences, Nanning 530025, China
The primary driving force for waves is sea surface wind stress. The parameterization of it is necessary for the research of air-sea interaction. Many studies have been done to determine sea surface wind stress through parameterization of drag coefficient during the past decades. Wind stress can be estimated through the bulk aerodynamic method with the equation in terms of drag coefficient Cd.
| $ \tau \equiv {\rho _{\text{a}}}u_*^2 = {\rho _{\text{a}}}{C_{\text{d}}}U_{10}^2, $ | (1) |
where, ρa is the density of air, u* is the friction velocity and U10 is the wind speed at 10-meter height above mean sea level. Drag coefficient Cd was determined as constant in early research. From different field and laboratory observations, researchers obtained different linear relationships between wind speed and drag coefficient (e.g., Sheppard, 1958; Zubkovskii and Kravchenko, 1967; Smith and Banke, 1975; Smith, 1980; Wu, 1980; Donelan, 1982; Yelland and Taylor, 1996; Fairall et al., 2003; Chao et al., 2019). However, the parameterization between wind speed and drag coefficient determined by different researchers varies significantly indicated that the drag coefficient might not only depend on the wind speed, but also other factors, such as the wave development parameters containing wave age (Andreas, 2004; Makin, 2005; Liu et al., 2012a, 2012b, 2012c) and Reynolds number RB (Shi et al., 2013; Shi and Jiang, 2015). In order to get accurate Cd, some researchers also used data assimilation to optimize the parameterization (Peng et al., 2013; Peng and Li, 2015; Li et al., 2016; Li et al., 2021).
The drag coefficient has a one-to-one correspondence relationship with the aerodynamic roughness z0 through
| $ {C_{\text{d}}} = {\kappa ^2}{\left[ {\ln \left({\frac{{10}}{{{z_0}}}} \right)} \right]^{ - 2}} . $ | (2) |
Here, the reference height is 10 m, and κ = 0.4 is the von Karman constant. The sea surface roughness is widely used in numerical models to estimate sea surface wind stress. Charnock (1995) presented the famous Charnock relation
| $ g{z_0}/u_*^2 = \alpha, $ | (3) |
where g is the acceleration of gravity, and α is the Charnock parameter or nondimensional roughness length. α was taken as an constant and different researchers presented various values which indicated that sea surface roughness depended only on wind speed. As recognized, sea surface roughness depends not only on wind speed, but also on wave development. Stewart (1974) proposed an extended Charnock relation, in which the Charnock parameter was considered as a function of wave age β*:
| $ \alpha = f({\beta _*}), $ | (4) |
where β* is defined as β* = cp/u*, in which cp is the phase speed of the spectral peak. Masuda and Kusaba (1987) further gave an exponential relationship between the Charnock parameter and the wave age:
| $ g{z_0}/u_*^2 = n\beta _*^m = \alpha . $ | (5) |
As recognized, wave state has an important impact on wind stress (e.g., Toba et al., 1990; Drennan et al., 2003; Fang et al., 2015; Li et al., 2020; Rajesh et al., 2020). Concerning the relationship between the Charnock parameter α and the wave age β*, there are mainly two different, even opposite, kinds of viewpoints. One viewpoint believes that the nondimensional sea surface roughness decreases with the increasing wave age (Donelan, 1990; Drennan et al., 2003). The other viewpoint considers that the nondimensional sea surface roughness increases with the increasing wave age (Toba et al., 1990; Sugimori et al., 2000). The differences were determined by different researchers based on field and laboratory observations (Jones and Toba, 2001).
Recent research (Powell et al., 2003; Donelan et al., 2004; Powell, 2006; Potter et al., 2015) found that the drag coefficient Cd decreases under high wind speed. According to the existing field and laboratory observations, the reason why coefficient drag decreases under high wind conditions dues to the existence of sea foams. As the surface wind increases, the wave breaking and wind tearing of wave crests disrupts the air-sea interface and generates the sea sprays. There are two viewpoints explaining the influence sea spray affecting on drag coefficient Cd. Markin (2005) assumed that a thin spray droplet suspension layer prevent the air-sea momentum transportation. Andreas (2004) assumed that sea spray droplets extracts momentum from the near-surface wind and therefor slows it which causes the characteristics under high wind speed. Comparing the equations of Makin (2005) and Andreas (2004), we think that Andreas's viewpoint expresses the effect of sea spray on wind stress directly, and Troitskaya et al.(2018, 2019) approved it. Therefore, we select Andreas (2004)'s theory to do further research. It is worth noting that both Andreas (2004) and Makin (2005) did not discuss the effect of wave state on drag coefficient. We know that there is not only wind but also wave existing in the actual sea surface (Liu et al., 2012a). As an important element in the ocean, wave always exists, which will continuously affect the air-sea interaction, and then affect the parameterized expression of drag coefficient. This study thus aims to propose a new parameterization for wind stress applicable from low to high wind conditions, with both wave state and sea spray effects being taken into consideration.
2 Wave State Affected Drag Coefficient Under Low-to-Moderate WindsAs recognized, the wave stage has an important impact on the wind stress. SCOR (Scientific Committee on Oceanic Research) workgroup 101 (Jones and Toba, 2001) presented a relationship which is expressed through Eq. (2) by analyzing and synthesizing a large number of field and laboratory observations.
| $ \frac{{g{z_0}}}{{u_*^2}} = \left\{ \begin{array}{l} 0.03{\beta _*}\exp (- 0.14{\beta _*})\quad \sim 0.35 < {\beta _*} < 35 \hfill \\ 0.008\quad \quad \quad \quad \quad \quad \quad {\beta _*} \geqslant 35 \hfill \\ \end{array} \right. . $ | (6) |
The SCOR relationship contains the two viewpoints mentioned above. Using Eqs. (1) – (2) and (6), for given wind speeds U10 and wave ages β defined as β = cp/U10, the corresponding drag coefficients can be calculated through iteration and cp is the peak phase velocity. Fig.1 shows that the nondimensional sea surface roughness first increases and then decreases with the increasing wave age, and it agrees well with the field and laboratory observational data.

|
Fig. 1 The relationship between drag coefficient and wind speed under different wave age. |
It should be noted that, since the SCOR relation is determined mainly from observations under low-to-moderate wind conditions, without the consideration of other factors such as sea sprays, it is not appropriate to apply this relation to high wind conditions. This paper will extend it to extreme wind condition.
3 Sea Spray Affected Wind Stress Under High WindsAs mentioned above, the wind stress levels off or decreases when the wind speed exceeds hurricane force. Andeas (2004) assumed that sea spray droplets extract momentum from the near-surface wind and therefor cause these characteristics under high wind speed. Andreas and Emanuel (2001) and Andreas (2004) divided the total air-sea momentum flux τt into two parts: one supported by the air τa and the other supported by the sea spray τsp (Raupach, 1991), so the drag coefficient considering the effect of sea spray can be expressed through
| $ {C_{{\text{d, sp}}}} = \left({1 - \frac{{{\tau _{{\text{sp}}}}}}{{{\rho _{\text{a}}}U_*^2}}} \right){C_{\text{d}}} . $ | (7) |
In order to obtain Cd, sp, the first step is to obtain the air-sea momentum flux supported by the sea spray τsp. Andreas and Emanuel (2001) proposed the parameterization of τsp through:
| $ {\tau _{{\text{sp}}}} = \frac{{{\text{4}\pi }}}{{\text{3}}}{\rho _{\text{w}}}\int_{{r_{{\text{lo}}}}}^{{r_{{\text{hi}}}}} {{u_{{\text{sp}}}}({r_0})} r_0^3\frac{{{\text{d}}F}}{{{\text{d}}{r_0}}}{\text{d}}{r_0} . $ | (8) |
Here, ρw is the density of seawater, and rlo and rhi are the lower and upper radius limits of the droplets that are important in this process. Typically, rlo ≈ 1 μm and rhi ≈ 500 μm. usp(r0) is the speed of spray droplets before they fall back into the sea and dF/dr0 is the sea spray generation function (SSGF) which quantifies how many spray droplets with initial radius r0 are produced per square meter of surface per second per micrometer increment in droplet radius. Andreas and Emanuel (2001) assumed that all droplets with radii up to 500 μm will be essentially traveling at the local wind speed. And Schmidt (1982)'s measurements of particle speed and wind speed in blowing snow corroborate this conclusion. Therefore, usp(r0) is independent of r0, we can calculate it through
| $ U(z) = \frac{{{u_*}}}{k}{\text{ln}}\left({\frac{z}{{{z_0}}}} \right), $ | (9) |
and the roughness z0 can be modeled with Charnock's relation,
| $ {z_{\text{0}}}{\text{ = 0}}{\text{.0185}}\frac{{{u_*}}}{g} . $ | (10) |
U(z) is the wind speed at height z, Andreas (1992) estimated z as the significant wave amplitude A1/3 (A1/3 =
dF/dr0, the sea spray generation function (SSGF), which is more directly related sea spray heat fluxes is usually considered to be a function of wind speed and droplet radius (e.g., Monahan et al., 1986; Andreas, 1992) while some studies, have found that the SSGF also depends on surface wave development (Iida et al., 1992; Zhao et al., 2006; Liu et al., 2015).
Andreas et al.(2001, 2002, 2004) did not discuss the effect of wave state on SSGF. Considering the effects, we adopt Eq. (11) as the SSGF that takes the droplet radius r0 and the Reynolds number RB (
| $ \frac{{{\text{d}}F}}{{{\text{d}}{r_0}}} = \left\{ {\begin{array}{*{20}{l}} {0.506R_B^{1.09}r_0^{ - 2.95}(1 + 0.029r_0^{1.02}) \times {{10}^{1.19\exp (- B_0^2)}}}&{{\text{ }}0.8{\rm{ \mathsf{ μ} }\text{m}} < {r_0} \leqslant 20{\rm{ \mathsf{ μ} }\text{m}}} \\ {\frac{{30 - {r_0}}}{{10}}0.506R_B^{1.09}r_0^{ - 2.95}(1 + 0.029r_0^{1.02}) \times {{10}^{1.19\exp (- B_0^2)}} + \frac{{{r_0} - 20}}{{10}}(7.84 \times {{10}^{ - 3}}R_B^{1.5}r_0^{ - 1})}&{{\text{ }}20{\rm{ \mathsf{ μ} }\text{m}} < {r_0} \leqslant 30{\rm{ \mathsf{ μ} }\text{m}}} \\ {7.84 \times {{10}^{ - 3}}R_B^{1.5}r_0^{ - 1}}&{{\text{ }}30{\rm{ \mathsf{ μ} }\text{m}} < {r_0} < 75{\rm{ \mathsf{ μ} }\text{m}}} \\ {4.41 \times {{10}^1}R_B^{1.5}r_0^{ - 3}}&{{\text{ }}75{\rm{ \mathsf{ μ} }\text{m}} \leqslant {r_0} < 200{\rm{ \mathsf{ μ} }\text{m}}} \\ {1.41 \times {{10}^{13}}R_B^{1.5}r_0^{ - 8}}&{{\text{ }}200{\rm{ \mathsf{ μ} }\text{m}} < {r_0} < 500{\rm{ \mathsf{ μ} }\text{m}}} \end{array}} \right. . $ | (11) |
Taking Wu's (1980) as initial drag coefficient parameterization, according to the proposed parameterization of SSGF and using Eqs. (1) – (11), we can calculate the proportion of sea spray momentum flux to the total momentum flux (Fig.2). One can see that under all wave age conditions, the proportion of that increases with the surface wind continuously.

|
Fig. 2 the proportion of sea spray momentum flux to the total momentum flux. |
Andreas and Emanuel (2001) first suggested that sea spray momentum flux τsp goes as the fourth power of
| $ {\tau _{{\text{sp}}}} = 6.2 \times {10^{ - 5}}{\rho _{\text{w}}}u_*^4 . $ | (12) |
In our research, we find that the sea spray momentum flux τsp depends more strongly on windsea Reynolds number RB and we give the new fitting equation (Eq. (13)). Fig.3 also shows τsp as a function of RB.
| $ {\tau _{{\text{sp}}}} = 1.1 \times {10^{ - 11}}R_B^{1.8} . $ | (13) |

|
Fig. 3 The relationship between sea spray momentum flux τsp and windsea Reynolds number RB under different wage age β. |
Inserting Eqs. (1), (13) and (6) into Eq. (7) and rearranging terms, we get:
| $ {C_{{\text{d, sp}}}} = \left\{ {\begin{array}{*{20}{l}} {\left[ {1 - \frac{{1.1 \times {{10}^{ - 11}}R_B^{1.8}}}{{{\rho _{\text{a}}}u_*^2}}} \right]{{\left[ {\frac{k}{{\ln \left({10/\left[ {0.03{\beta _*}\exp (- 0.14{\beta _*})g/u_*^2} \right]} \right)}}} \right]}^2}}&{{\text{ }} \sim 0.35 < {\beta _*} < 35} \\ {\left[ {1 - \frac{{1.1 \times {{10}^{ - 11}}R_B^{1.8}}}{{{\rho _{\text{a}}}u_*^2}}} \right]{{\left[ {\frac{k}{{\ln \left({10/\left[ {0.008g/u_*^2} \right]} \right)}}} \right]}^2}}&{{\text{ }}{\beta _*} \geqslant 35} \end{array}} \right.. $ | (14) |
According to the new proposed parameterization, for given wind speeds U10 and wave ages β, the corresponding drag coefficients can be calculated through iteration. Fig.4 shows the corresponding relation between drag coefficient and wind speed under different wave developments. One can find that under high winds the drag coefficient decreases with increasing wind speed. This is in agreement with the first characteristic of the existing measurements under high wind conditions mentioned above. Sea sprays generated by wave breaking and wind tearing wave crests modify the wind profile and prevent the water surface from being dragged by the wind directly, which in turn, reduces the drag coefficient and levels off the wind stress under high winds.
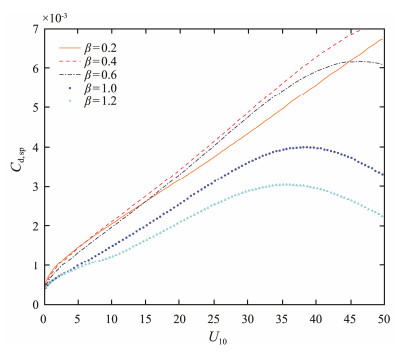
|
Fig. 4 The relation between drag coefficient and wind speed under different wave developments. |
It is also shown in Fig.4 that as for the wage state effects especially under low-to-moderate winds, there are two conditions: 1) Younger waves usually correspond to larger drag coefficients when wind speed less than 10 m s−1. 2) When wind speed more than 10 m s−1 and less than 15 m s−1, for wage age smaller than 0.4, younger waves usually correspond to smaller drag coefficients, whereas for wave age larger than 0.4, mature waves correspond to smaller drag coefficients. The later condition is consistent with the SCOR relation (Jones and Toba, 2001). However, under high wind conditions, the interaction between wave state effects and sea spray effects makes the dependence of drag coefficient on wind speed more complicated. Generally, younger waves generate less sea sprays from wave breaking, thus less impact from sea sprays on the drag coefficient; whereas older waves could be affected by sea spray obviously. We can also find that, for small wave ages (e.g., < 0.2), sea spray effects on drag coefficient are hardly seen for wind speed up to 50 m s−1.
The wind speed of drag coefficients reaching their maximum values vary under different wave developments. For wage age less than 0.6, the wind speed of the drag coefficients reaching their maximum values exceeds 50 m s−1; whereas for wage age larger than 0.6, the wind speed lies in 25 – 45 m s−1. It can also be noticed that, under most wave ages (larger than 0.1) the larger the wage age, the lower wind speed at which the drag coefficient begin to decrease or level off.
5 Validation and DiscussionAs mentioned above, the new proposed parameterization would be the same as the SCOR relation under low-to-moderate wind conditions when sea spray effects are negligible. The detailed validation for the SCOR relation can be found in Jones and Toba (2001). In this study, we will mainly focus on the behavior of the new proposed relationship under high wind conditions. Some recent laboratory (Donelan et al., 2004) and field (Powell, 2006) data sets with observations under high winds described below are used to be compared with the new relationship.
Donelan et al. (2004) utilized the Air-Sea Interaction Facility at the University of Miami to examine the wind stress under high winds. The facility includes a tank that is 15 m long and 1 m wide with its height of 1 m. It can generate winds along the centerline in the range of 0 to 30 m s−1. They adopted three methods including profile, eddy correlation, and momentum budget of water control volume to estimate wind stress and thus drag coefficient under different winds. Their results show a saturation of the drag coefficient once the wind speed exceeds 33 m s−1. From Fig.5, one can see that the new presented relation can cover the range of the existing laboratory observation well, and can explain the scatter of current measurements to some extent. The reduction of the drag coefficient under high wind conditions is shown in both the observations and the presented relation for different wave states.
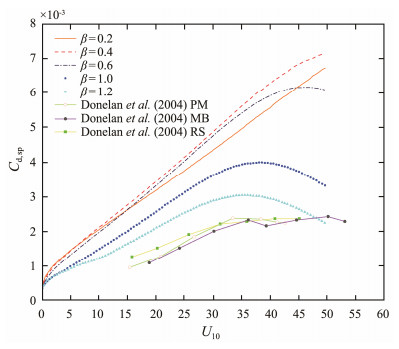
|
Fig. 5 Comparison between the drag coefficient and wind speed relations under different wave ages, corresponding to the wave age and sea spray related parameterization and laboratory observations under high winds. The red markers with dash-dotted lines are laboratory measurements from Donelan et al. (2004) through different methods. PM, profile method; MB, momentum budget method; RS, Reynolds stress method. |
Powell (2006) found that the drag coefficient increases with wind up to 41 m s−1 and then decrease with increasing wind. He also analyzed the azimuthal dependence of the drag coefficient for hurricanes. As in Black et al. (2007), a storm can be divided into three regions: 1) rear sector (151˚ – 240˚ relative to the storm motion vector) with waves moving with the wind, 2) right sector (21˚ – 150˚) with waves moving outward by up to 45˚ relative to the wind, and 3) left front sector (241˚ – 20˚) where waves travel outward at 60˚ – 90˚ to the wind. Fig.6 shows the comparison of the relation between drag coefficient and wind speed for the new presented wave state and sea spray related parameterization with the observational data for different sectors of tropical cyclones from Powell (2006) when analyzing the azimuthal dependence of the drag coefficient for hurricanes. From Fig.6, one can see that the new presented relation can cover the range of the existing field observation well, although there are some points that deviate the curve farther. This result is better than Liu (2012b)'s who extend the SCOR relation to high wind by adopting Markin (2005)'s theory.
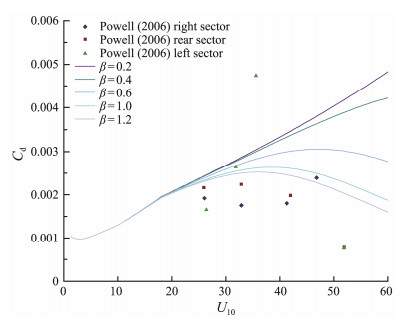
|
Fig. 6 The relation between drag coefficient and wind speed under different wave ages (β), corresponding to the wave age and sea spray related parameterization, together with the observations from Powell (2006) for different sectors. |
Parameterization of air-sea momentum flux is one of the fundamental processes that connect atmosphere, waves and ocean. In this study, a drag coefficient parameterization applicable from low to extreme winds is proposed by considering the effects of wave state and sea spray on air-sea momentum flux. According to the new presented parameterization, under low wind conditions when the effect of sea spray could be neglected, the drag coefficient increases with the increasing wind, while under high wind conditions, the drag coefficient does not increase, but decreases with the increasing wind speed due to the effect of sea spray, and this agrees well with recent observations under high winds.
As the wave state and sea spray would affect the air-sea momentum flux as well as air-sea heat and mass fluxes, the new presented parameterization could be used in coupled atmosphere-wave-ocean modeling systems. However, it should be noted that the new proposed parameterization needs to be further validated through simultaneously measured wind and wave data especially under high wind conditions. More field and laboratory experiments should also be conducted to investigate the dependence of wind stress on other factors.
AcknowledgementsThe efforts of the researchers who obtained and published the data sets used in this study as well as their funding organizations are much appreciated. This study is supported by the National Key R&D Program of China (No. 2018YFB1501901), the National Natural Science Foundation of China (Nos. 51909114, U1806227 and U1906231), and the Guangxi Key Laboratory of Marine Environmental Science, Guangxi Academy of Sciences (No. GXKLHY21-04).
Andreas, E. L., 1992. Sea spray and the turbulent air-sea heat fluxes. Journal of Geophysical Research, 97: 11429-11441. DOI:10.1029/92JC00876 (  0) 0) |
Andreas, E. L., 2004. Spray stress revisited. Journal of Physical Oceanography, 34: 1429-1440. DOI:10.1175/1520-0485(2004)034<1429:SSR>2.0.CO;2 (  0) 0) |
Andreas, E. L., and Decosmo, J., 2002. The signature of sea spray in the HEXOS turbulent heat flux data. Bound-Layer Meteor, 103: 303-333. DOI:10.1023/A:1014564513650 (  0) 0) |
Andreas, E. L., and Emanuel, K. A., 2001. Effects of sea spray on tropical cyclone intensity. Journal of the Atmospheric Sciences, 58: 3741-3751. DOI:10.1175/1520-0469(2001)058<3741:EOSSOT>2.0.CO;2 (  0) 0) |
Black, P. G., D'Asaro, E. A., Drennan, W. M., French, J. R., Niiler, P. P., Sanford, T. B., et al., 2007. Air-sea exchange in hurricanes: Synthesis of observations from the coupled boundary layer air-sea transfer experiment. Bulletin of the American Meteorological Society, 88(3): 357-374. DOI:10.1175/BAMS-88-3-357 (  0) 0) |
Chao, G. F., Shao, C. X., Wu, X. R., and Liu, K. X., 2019. Study on air-sea momentum exchange coefficient based on buoy data. Marine Information, 34(3): 35-42 (in Chinese with English abstract). (  0) 0) |
Charnock, H., 1955. Wind stress on a water surface. Quarterly Journal of the Royal Meteorological Society, 81: 639-640. (  0) 0) |
Donelan, M. A., 1982. The dependence of the aerodynamic drag coefficient on wave. The 1st International Conference on Meteorology & Air-Sea Interaction of the Coastal Zone. Boston, 381-387.
(  0) 0) |
Donelan, M. A., 1990. Air-sea interaction. In: The Sea. LéMehauté, B., and Hanes, D. M., eds., Wiley, New York, 239-292.
(  0) 0) |
Donelan, M. A., Haus, B. K., Reul, N., Plant, W. J., Stiassnie, M., Graber, H. C., et al., 2004. On the limiting aerodynamic roughness of the ocean in very strong winds. Geophysical Research Letters, 31: L18306. DOI:10.1029/2004GL019460 (  0) 0) |
Drennan, W. M., Graber, H. C., Hauser, D., and Quentin, C., 2003. On the wave age dependence of wind stress over pure wind seas. Journal of Geophysical Research, 108(C3): 8062. DOI:10.1029/2000JC000715 (  0) 0) |
Fairall, C. W., Bradley, E. F., Hare, J. E., Grachev, A. A., and Edson, J. B., 2003. Bulk parameterization of air-sea fluxes: Updates and verification for the COARE algorithm. Journal of Climate, 16: 571-591. DOI:10.1175/1520-0442(2003)016<0571:BPOASF>2.0.CO;2 (  0) 0) |
Fang, P. Z., Zhao, B. K., Zhang, S., Zeng, Z. H., and Lin, W., 2015. An observation of behavior of nearshore drag coefficient with moderate to strong wind speed. Journal of Tropical Meteorology, 31(5): 713-720. (  0) 0) |
Iida, N., Toba, Y., and Chaen, M., 1992. A new expression for the production rate of sea water droplets on the sea surface. Journal of Oceanography, 48: 439-460. DOI:10.1007/BF02234020 (  0) 0) |
Jones, I. S. F., and Toba, Y., 2001. Wind Stress Over the Ocean. Cambridge University Press, Cambridge, UK, 307pp. DOI:10.1017/CBO9780511552076
(  0) 0) |
Li, D. L., Staneva, J., Bidlot, J. R., Grayek, S., Zhu, Y. C., and Yin, B. S., 2021. Improving regional model skills during typhoon events: A case study for super typhoon Lingling over the Northwest Pacific Ocean. Frontiers in Marine Science, 8: 1-22. DOI:10.3389/fmars.2021.613913 (  0) 0) |
Li, D. L., Staneva, J., Grayek, S., Behrens, A., Feng, J. L., and Yin, B. S., 2020. Skill assessment of an atmosphere-wave regional coupled model over the East China Sea with a focus on typhoons. Atmosphere, 11(3): 1-25. DOI:10.3390/atmos11030252 (  0) 0) |
Li, F. N., Song, J. B., He, H. L., Li, S., Li, X., and Guan, S. D., 2016. Assessment of surface drag coefficient parametrizations based on observations and simulations using the weather research and forecasting model. Atmospheric and Oceanic Science Letters, 4: 327-336. (  0) 0) |
Liu, B., Guan, C. L., and Xie, L. A., 2012a. The wave state and sea spray related parameterization of wind stress applicable from low to extreme winds. Journal of Geophysical Research, 117: C00J22. DOI:10.1029/2011JC007786 (  0) 0) |
Liu, B., Guan, C. L., Xie, L. A., and Zhao, D. L., 2012b. An investigation of the effects of wave state and sea spray on an idealized typhoon using an air-sea coupled modeling system. Advances Atmospheric Sciences, 29: 391-406. DOI:10.1007/s00376-011-1059-7 (  0) 0) |
Liu, B., Guan, C. L., Xie, L. A., and Zhao, D. L., 2015. Derivation of a wave-state-dependent sea spray generation function and its application in estimating sea spray heat flux. Science China: Earth Sciences, 58: 1862-1871. DOI:10.1007/s11430-015-5169-4 (  0) 0) |
Liu, L., Fei, J. F., Huang, X. G., and Cheng, X. P., 2012c. The development of atmosphere-current-wave fully coupled model and its application during a typhoon process. Acta Physica Sinica – Chinese Edition, 61(14): 149201. DOI:10.7498/aps.61.149201 (  0) 0) |
Makin, V. K., 2005. A note on the drag of the sea surface at hurricane winds. Boundary-Layer Meteorology, 115: 169-176. DOI:10.1007/s10546-004-3647-x (  0) 0) |
Masuda, A., and Kusaba, T., 1987. On the local equilibrium of winds and wind-waves in relation to surface drag. Journal of the Oceanographical Society of Japan, 43(1): 28-36. DOI:10.1007/BF02110631 (  0) 0) |
Monahan, E. C., Spiel, D. E., and Davidson, K. L., 1986. A Model of Marine Aerosol Generation via Whitecaps and Wave Disruption. Springer, New York, 167-174.
(  0) 0) |
Peng, S., and Li, Y., 2015. A parabolic model of drag coefficient for storm surge simulation in the South China Sea. Scientific Reports, 5: 15496. DOI:10.1038/srep15496 (  0) 0) |
Peng, S., Li, Y., and Xie, L., 2013. Adjusting the wind stress drag coefficient in storm surge forecasting using an adjoint technique. Journal of Atmospheric and Oceanic Technology, 30: 590-608. DOI:10.1175/JTECH-D-12-00034.1 (  0) 0) |
Potter, H., Graber, H. C., Williams, N. J., Collins, C. O., Ramos, R. J., and Drennan, W. M., 2015. In situ measurements of momentum fluxes in typhoons. Journal of Atmospheric Sciences, 72: 104-118. DOI:10.1175/JAS-D-14-0025.1 (  0) 0) |
Powell, M. D., 2006. Drag coefficient distribution and wind speed dependence in tropical cyclones. Final report to the NOAA JHT program. Atlantic Oceanographic and Meteorological Laboratory, Miami, Florida, 26pp.
(  0) 0) |
Powell, M. D., Vickery, P. J., and Reinhold, T. A., 2003. Reduced drag coefficient for high wind speeds in tropical cyclones. Nature, 422: 279-283. DOI:10.1038/nature01481 (  0) 0) |
Rajesh, K. R., Sandeepan, B. S., and David, M. H., 2020. Impact of different sea surface roughness on surface gravity waves using a coupled atmosphere-wave model: A case of Hurricane Isaac (2012). Ocean Dynamics, 70: 421-433. DOI:10.1007/s10236-019-01327-6 (  0) 0) |
Raupach, M. R., 1991. Saltation layers, vegetation canopies and roughness lengths. Acta Mechanica, 1: 83-96. (  0) 0) |
Schmidt, R. A., 1982. Vertical profiles of wind speed, snow concentration, and humidity in blowing snow. Boundary-Layer Meteorology, 23: 223-246. DOI:10.1007/BF00123299 (  0) 0) |
Sheppard, P. A., 1958. Transfer across the Earth's surface and through the air above. Quarterly Journal of the Royal Meteorological Society, 84: 205-224. DOI:10.1002/qj.49708436102 (  0) 0) |
Shi, J., and Jiang, G. R., 2015. The influence of wind wave state on sea surface roughness. Oceanologia et Limnologia Sinica, 46(6): 1255-1262. (  0) 0) |
Shi, J., Zhou, L., and Yang, L. Y., 2013. Influence of sea spray droplets on drag coefficient in high wind speed. Acta Physica Sinica, 62(3): 1-9. (  0) 0) |
Smith, S. D., 1980. Wind stress and heat flux over the ocean in gale force winds. Journal of Physical Oceanography, 10: 709-726. DOI:10.1175/1520-0485(1980)010<0709:WSAHFO>2.0.CO;2 (  0) 0) |
Smith, S. D., and Banke, E. G., 1975. Variation of the sea surface drag coefficient with wind speed. Quarterly Journal of the Royal Meteorological Society, 101: 665-673. DOI:10.1002/qj.49710142920 (  0) 0) |
Stewart, R. W., 1974. The air-sea momentum exchange. Boundary-Layer Meteorology, 16: 151-167. (  0) 0) |
Sugimori, Y., Akiyama, M., and Suzuki, N., 2000. Ocean measurement and climate prediction-expectation for signal processing. Journal of Signal Process, 4: 209-222. (  0) 0) |
Toba, Y., Iida, N., Kawamura, H., Ebuchi, N., and Jones, L. S. F., 1990. Wave dependence of sea-surface wind stress. Journal of Physical Oceanography, 20: 705-721. DOI:10.1175/1520-0485(1990)020<0705:WDOSSW>2.0.CO;2 (  0) 0) |
Troitskaya, Y., Kandaurov, A., Ermakova, O., Kozlov, D., Sergeev, D., and Zilitinkevich, S., 2018. The 'bag breakup' spume droplet generation mechanism at high winds. Part Ⅰ: Spray generation function. Journal of Physical Oceanography, 48(9): 2167-2188. DOI:10.1175/JPO-D-17-0104.1 (  0) 0) |
Troitskaya, Y., Sergeev, D., Kandaurov, A., and Vdovin, M., 2019. The effect of foam on waves and the aerodynamic roughness of the water surface at high winds. Journal of Physical Oceanography, 49(4): 959-981. DOI:10.1175/JPO-D-18-0168.1 (  0) 0) |
Wu, J., 1980. Wind-stress coeffcients over sea surface near neutral conditions – A revisit. Journal of Physical Oceanography, 10: 727-740. DOI:10.1175/1520-0485(1980)010<0727:WSCOSS>2.0.CO;2 (  0) 0) |
Yelland, M. J., and Taylor, P. K., 1996. Wind stress measurements from the open ocean. Oceanography, 26: 541-558. (  0) 0) |
Zhao, D. L., Toba, Y., Sugioka, K. I., and Komori, S., 2006. New sea spray generation function for spume droplets. Journal of Geophysical Research, 111: C02007. (  0) 0) |
Zubkovskii, S. L., and Kravchenko, T. K., 1967. Direct measurements of some turbulence in the near-water layer. Izvestiya Atmospheric and Oceanic Physics, 3: 127-135. (  0) 0) |
 2023, Vol. 22
2023, Vol. 22


