2) National Engineering Research Center for Oceanic Fisheries, Shanghai 201306, China;
3) The Key Laboratory of Sustainable Exploitation of Oceanic Fisheries Resources, Ministry of Education, Shanghai 201306, China;
4) Department of Applied Ecology, Center for Marine Sciences and Technology, North Carolina State University, Morehead City, NC 28557, USA
Surplus production models (Schaefer, 1957), also known as biomass dynamics models (Hilborn and Walters, 1992), can easily be applied to study the population dynamics according to catch data. This type of models only considers the total biomass and ignore age structure, including recruitment, growth, and differential vulnerability to fishing gear (Hilborn and Walters, 1992). They amalgamate individual growth, recruitment, and mortality into a single model component termed surplus production (Quinn and Dersio, 1999). Biomass dynamic models have been criticized for failing to account for the size/age structure of fish populations, leading to biased and unreliable maximum sustainable yields (MSY) estimates, and even causing some fisheries management failures (Hilborn and Walters, 1992; Mace, 2001; Pauly et al., 2002). However, they are still widely used for fish stocks that have limited data available (McAllister and Kirkwood, 1998; Prager, 2002; Chen et al., 2003; Hvingel and Kingsley, 2006; Stobberup and Erzini, 2006). Biomass dynamics models with equilibrium assumptions have fallen out of favor in the 1980s, giving way to dynamic or time series fitting methods. However, their parameters are constant in time, while the environment in which the population resides undergoes continual fluctuations (Hilborn and Walters, 1992; Haddon, 2011).
In a biomass dynamics model, the surplus production is determined by two parameters, i.e., carrying capacity and intrinsic growth rate. It is only possible to estimate either of these parameters accurately if the stock size is consistently at very high levels (approaching carrying capacity) or if the intrinsic growth rate is consistently at deficient levels (Morris and Mukherjee, 2006; Tinker et al., 2021). Auxiliary information other than the time series of catch and an index of abundance data can supplement fitting these models. For instance, habitat has been commonly used to estimate the carrying capacity for fish (Sharma and Hilborn, 2001; Jacobson et al., 2005; Ayllón et al., 2012), birds (Downs et al., 2008; Donovan et al., 2012), and mammals (Gregr et al., 2008; Donovan et al., 2012).
Carrying capacity is defined as the total abundance/biomass of a fish stock that can be supported by the resources in a habitat (de Kerckhove et al., 2008). The habitat of fish species like coho salmon (Oncorhynchus kisutch) (Sharma and Hilborn, 2001), yellowfin tuna (Thunnus albacores) (Yen et al., 2012), and neon flying squid (Ommastrephes bartramii) (Tian et al., 2009) fluctuates in response to environmental conditions. Hence, carrying capacity could vary seasonally, annually, and throughout the course of a fish's lifetime to reflect typical long-term environmental conditions (Jonsson and Jonsson, 2011). The intrinsic growth rate (the growth rate when density-dependence does not play a role) can be sensitive to subtle changes in the environment and is correlated with other life history parameters such as age and size at maturity, mortality, and recruitment (Jennings, 2000). Given that carrying capacity is a balance between density-independent intrinsic growth rate and density-dependent crowding effects (α) (Haddon, 2011; Mallet, 2012), we anticipate a decline in the carrying capacity, concomitant with an increase in mortality or a decrease in birth rates, aligning with the intrinsic growth rate. Furthermore, carrying capacity as a function of habitat is influenced by environmental conditions, rendering the intrinsic growth rate that is habitat-dependent.
The habitat quality for fish species can be assessed using habitat suitability indices (HSI). The HSI model, a valuable tool in ecology (USFWS, 1981), has been widely app lied to characterize fish habitat (Rubec et al., 1999; Vadas and Orth, 2001; Vinagre et al., 2006; Tian et al., 2009). The dynamics of fish populations are affected by their habitat, as their growth, survival, and reproduction are directly affected by abiotic and biotic resources (Hayes et al., 1996). Nonetheless, incorporation of HSI model in population dynamic models remains uncommon. Jacobson et al. (2005) developed an environmentally dependent surplus production (EDSP) model that relates habitat area indices to carrying capacity and demonstrated its benefit in studying climate effects on fishery surplus production. Such models are predicated on hypothesized species-habitat correlations as opposed to statements of proven cause-and-effect relationships. A good understanding of fish habitats and their interactions with fish population dynamics is thus critical (Hayes et al., 1996; Naiman and Latterell, 2005).
Chilean jack mackerel (Trachurus murphyi), a straddling pelagic species, is widely distributed throughout the Southeast Pacific Ocean and from south-central Chile westwards to New Zealand, which is regarded as the 'jack mackerel belt' (Arcos et al., 2001; Cubillos et al., 2008; Cárdenas et al., 2009). T. murphyi has been a heavily exploited fishery resource, mainly targeted by purse seiners within the Exclusive Economic Zones (EEZ) and by international mid-water trawlers in the open waters (Li et al., 2013; Bertrand et al., 2016; Dragon et al., 2018). In Chilean waters, the habitat of Chilean jack mackerel located in the South Pacific subtropical gyre, surrounded by the northward Peru-Humboldt Current, the southwestward South Equatorial Current and the eastward Antarctic Circumpolar Current, and crossed by the eastward South Pacific Current at about 35˚S, which impacts the distribution of the main population (Yáñez et al., 2001; Ñiquen and Bouchon, 2004; Li et al., 2016). Following a dramatic increase in its annual catch since the 1970s, there was a peak catch of T. murphyi at about 4.96 million tons in 1995, followed by a significant decline until 2013. The stock started to recover as the South Pacific Regional Fisheries Management Organisation (SPRFMO) formally implemented total allowable catch (TAC) limits (SPRFMO, 2023). Multiple factors other than fishing may contribute to this abundance trajectory. For example, sea surface temperature (SST) has been widely recognized as an important environmental factor that contributes to the interannual and even multi-decade fluctuations in abundance (Espíndola et al., 2016). How the environment affects jack mackerel abundance, habitat, biological characteristics, and population genetic relationships has been the focus of a number of studies (Arcos et al., 2001; Cubillos et al., 2008; Vásquez, 2013; Li et al., 2013, 2016; Alegre et al., 2015). Comprehensive studies on how such factors affect stock assessment haven not been reported. Ignoring environmental changes may impact the accuracy of stock assessments and the effectiveness of management, especially in times of substantial decline in catches (Punt and Hilborn, 1997).
Simulation testing has often been conducted to investigate some concerns such as structural uncertainty and the impact of observation and process errors (Cao et al., 2014, 2020; Deroba et al., 2015; Perretti et al., 2020). In this study, we conducted a simulation-estimation experiment to evaluate the importance of considering the influence of environment and errors on the stock assessment of Chilean jack mackerel. Assessment models with various configurations are with respect to the assumption on the model parameters, carrying capacity and intrinsic growth rate (i.e., whether environmental impacts were considered). The primary objectives of this study were to determine the assessment performance based on different assumptions about environmental impacts using Chilean jack mackerel as an example, and to provide scientific guidance for future ecosystem-based stock assessment and management.
2 Materials and Methods 2.1 Fishery-Dependent and Fishery-Independent DataFishery-dependent and fishery-independent data were used in conditioning the operating model and developing the estimation model. The fishery-dependent data in terms of Chilean jack mackerel catch and catch per unit effort (CPUE) of high seas trawl fishery and coastal purse seine fishery during 1997 – 2014 (Table 1; Fig.1) were derived from Canales (2015), and Li and Zou (2015).
|
|
Table 1 Annual landings, original CPUE and final predicted CPUE from the operating model of coastal purse seine fishery and high seas trawl fishery, and estimated habitat area index for Chilean jack mackerel in the Southeast Pacific |
|
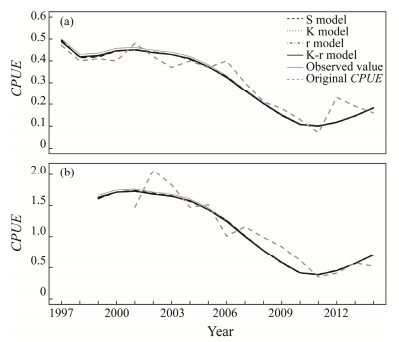
Fig. 1 Original, observed and estimated CPUEs of Chilean jack mackerel in the Southeast Pacific Ocean for four deterministic assessment scenarios from 1997 to 2014. (a), the purse seine fisheries in the coastal waters; (b), the trawl fisheries in the high seas. |
The fishery-independent data were the area of suitable habitat for Chilean jack mackerel estimated by HSI model (Li et al., 2016). HSI represents the capacity of a given habitat to support fish species, with minimum and maximum values of 0 and 1 denoting unsuitable and optimal habitat, respectively (USFWS, 1981). The HSI models with a combination of the arithmetic mean of suitability indices for SST, sea surface height (SSH), and chlorophyll-a concentration (Chl-a) developed by Li et al. (2016) were updated with additional data to provide the area of suitable habitat from 1997 to 2014. The estimated annual suitable habitat area was then rescaled between 0 and 1:
| $ {H_t} = {A_t}/\max ({A_t}), $ | (1) |
where At is the annual suitable habitat area that HSI is no less than 0.5 in year t (Li et al., 2016), Ht is index of the suitable habitat area in year t.
2.2 Description of Habitat Based Surplus Production ModelThe difference equation for the classic surplus production model is expressed by:
| $ B_{t+1}=B_t+r B_t\left(1-\frac{B_t}{K}\right)-C_t, $ | (2) |
where Bt is the biomass in year t, r is the intrinsic growth rate, K is the carrying capacity or virgin biomass, and Ct is the annual catch in year t (Hilborn and Walters, 1992).
There is a direct association, typically a linear one, between the habitat suitability index and the carrying capacity of the habitat for a particular species (Oldham et al., 2000). We assumed that K varied annually and was proportion to the area of suitable habitat:
| $ K_t=\lambda H_t . $ | (3) |
In addition, K is directly proportional to r, rather than independent, through the density-independent crowding effect parameter, that is K = r/α (Mallet, 2012). When given λα = β, the intrinsic rate of growth would be:
| $ r_t=\beta H_t . $ | (4) |
Thus, the surplus production model parameterized with the habitat index can be obtained through
| $ B_{t+1}=B_t+\beta H_t B_t\left(1-\frac{B_t}{\lambda H_t}\right)-C_t . $ | (5) |
Harvest rate (Et) and the biological reference points (BRPs), i.e., biomass (BMSY) and fishing mortality (FMSY) at maximum sustained yield (MSY) can be calculated as follow:
| $ E_t =\frac{C_t}{B_t}, $ | (6) |
| $ F_{\mathrm{MSY}, t} =\frac{r_t}{2}=\frac{\beta H_t}{2} , $ | (7) |
| $ B_{\mathrm{MSY}, t} =\frac{K_t}{2}=\frac{\lambda H_t}{2}. $ | (8) |
We assumed that error of CPUE, Iti, was multiplicative and lognormal distributed with constant variance (Haddon, 2011):
| $ \begin{aligned} \hat{I}_{t i} & =q_i \frac{B_t+B_{t+1}}{2} \exp ^{\varepsilon_{i i}} \\ \varepsilon_{t i} & \sim N\left(0, \sigma_i^2\right) \end{aligned}, $ | (9) |
| $ \sigma_i^2 =\sum\limits_t \frac{\left(\ln I_{t i}-\ln \hat{I}_{t i}\right)^2}{n}, $ | (10) |
where i is 1 for the purse seine fishery and 2 for the high seas trawl fishery,
| $ {\text{Sum}}L = \sum\limits_i {L{L_i} = \sum\limits_i {(- \frac{n}{2}(\ln (2{\rm{ \mathsf{ π}}}) + 2\ln ({{\hat \sigma }_i}) + 1))} }, $ | (11) |
where SumL refers to sum of log-likelihood, LLi is the loglikelihood for fishery i.
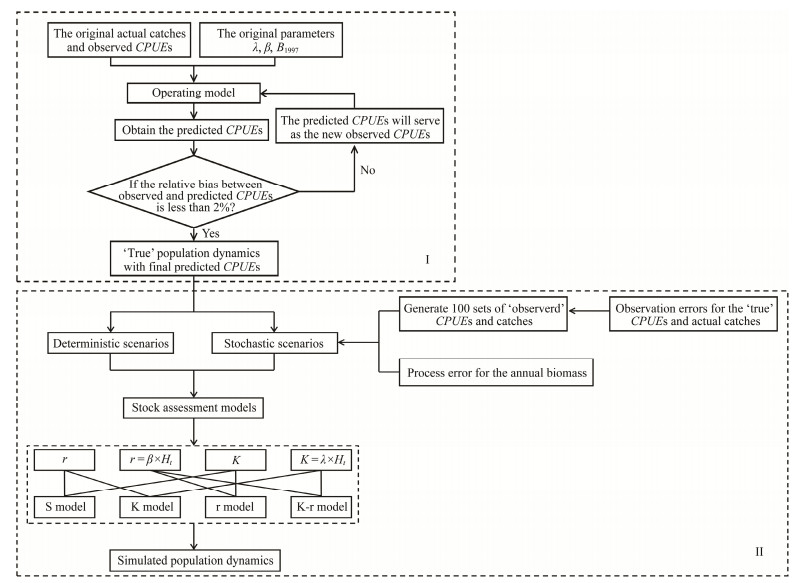
2.3 Operating Model Development and 'True' Population Dynamics SimulationWe developed a habitat based surplus production model as an operating model to simulate the 'true' population dynamics of Chilean jack mackerel. The flowchart Ⅰ shows how the accuracy of the operating model was conditioned by iterative fitting to reduce errors in the CPUE data (Fig.2), with detailed procedures for each step summarized in the following.
|
Fig. 2 Flow chart for developing operating model and stock assessment models for Chilean jack mackerel in the Southeast Pacific Ocean. |
Step 1: Substitute data into the operating model
The data included actual catches, observed CPUEs and original parameters. The initial values of B1997, β and λ were set to 9212 thousand tons (SPRFMO, 2015), 0.30 (Zou et al., 2016) and 25000 thousand tons, respectively, in which the value of K was five times the maximum historical catch (Punt and Hilborn, 2001).
Step 2: Calculate the final predicted CPUEs
Running the operating model once could address the missing CPUE in the high seas trawl fishery in 1999 and 2000. We iteratively updated the value of parameters until the relative bias (RB) between the observed and predicted CPUEs was less than 2% (the mean square error is less than 0.001; Table 1):
| $ R B_{t i}=\frac{ { predicted } \ CPUE_{t i}- { observed } \ CPUE_{t i}}{ { observed } \ CPUE_{t i}} \times 100 \% . $ | (12) |
Step 3: Obtain the 'true' population dynamics
The model would again be run to determine the 'true' population dynamics using the final predicted CPUE as the 'true' time series of abundance index data.
2.4 Stock Assessment Model ScenariosFour assessment scenarios regarding the relationships between the area of suitable habitat and the two key model parameters K and r were developed in the simulation: ⅰ) 'S' model, neither K nor r is dependent on Ht, i.e., the traditional surplus production model; ⅱ) 'K' model, only K is dependent on Ht; ⅲ) 'r' model, only r is dependent on Ht; and ⅳ) 'Joint K-r' model, both K and r are dependent on Ht. This last estimation scenario matches the assumptions on K and r specified in the operating model. For the other three scenarios, there were different model misspecifications regarding K and r to serve the purpose of examining the in-fluence of environment. The fishery data and initial values of the parameters used in each simulation scenario were set identically.
2.5 StochasticityIn addition to considering model structure and using deterministic data for the scenarios, we evaluated the effects of observation and process errors on the stock assessment. Lognormally distributed observation errors were added to the actual catch and 'true' CPUE to generate the 'observed' catch and abundance index. Annual biomass was also subjected to lognormally distributed random errors. The coefficient of variance (CVs) of annual catch, CPUE, and biomass was set to 0.05, 0.1, and 0.05, respectively. For each of the four stochastic simulation scenarios, 100 sets of 'observed' catch and CPUE data were generated with process
errors included in the annual biomass (Fig.2Ⅱ):
| $ \tau^2=\ln \left(C V^2+1\right), $ | (13) |
| $ \begin{array}{l} {B_{t + 1}} = ({B_t} + r{B_t}(1 - \frac{{{B_t}}}{K}) - {C_t}){\exp ^{{\mu _t}}} \hfill \\ {\mu _t} \sim N(0, {\tau ^2}) \hfill \end{array}, $ | (14) |
where μt is the process error of biomass in year t, τ is the standard deviation of μt.
We used relative error (RE) and relative bias to measure the disparity between the operating model and assessment models (Guan et al., 2013; Cao et al., 2014):
| $ R E_x=\frac{1}{2} \sum\limits_{t=1997}^{2014} \sqrt{\left(\frac{ { Scen }_{x, t}- { Simu }_{x, t}}{ { Simu }_{x, t}}\right)^2}, $ | (15) |
where x refers to biomass, exploitation rate and reference points, Scent is the estimated quantity of year t in the stock assessment model, Simut is the simulated value in year t from the operating model. For each of the 100 simulation runs in each year, RB and boxplot were used to quantify the influence of errors and model uncertainty:
| $ R B_{x, t}=\frac{ { Scen }_{x, t}- { Simu }_{x, t}}{{Sim}_{x, t}} \times 100 \%. $ | (16) |
The data collected were statistically analyzed using software packages, e.g., MS Excel and R.
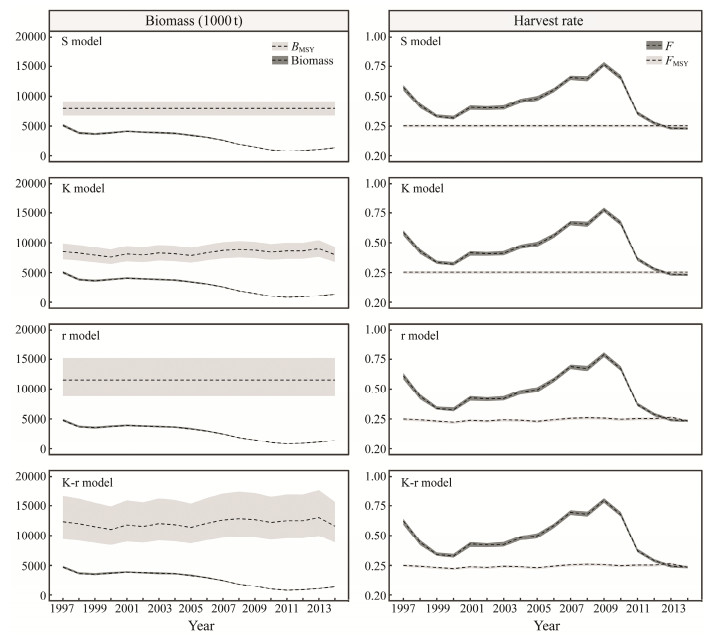
3 Results 3.1 Simulated 'True' Population DynamicsCPUEs of two fisheries were simulated in this study, one for purse seine fishery and the other for high seas trawl fishery, which had trends consistent with the 'true' biomass (Figs.1, 3). The simulated 'true' biomass and catch rate were relatively high in 1997 and then declined but maintained stable during the next five years, after which they continuously decreased and dropped to the lowest level in 2011. And then Chilean jack mackerel stock showed signs of recovery with the biomass increasing to 1303 thousand tons in 2014, and approaching the levels at 2009 (Fig.3). Estimated 'true' BMSY followed the trend of habitat area and varied between 10486 and 12400 thousand tons, 3 to 16 times the level of the biomass, which indicated that Chilean jack mackerel stock was overfished.
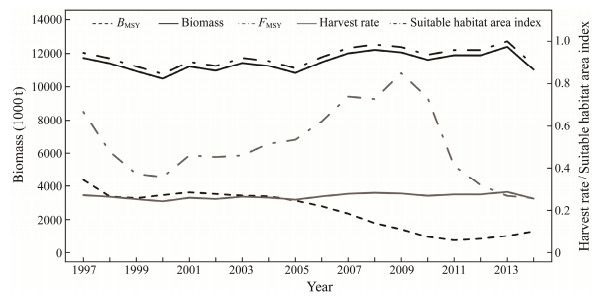
|
Fig. 3 The 'true' population dynamics for the Chilean jack mackerel stock in the Southeast Pacific from 1997 to 2014. |
Harvest rate derived from the simulation fluctuated sharply. It showed a downward trend during the period of 1997 – 2000, and then increased sharply until 2009. Afterwards, harvest rate dropped and reached the lowest value in 2013. The 'true' FMSY changed yearly and was less than the annual harvest rate except in 2013, i.e., overfishing did not occur only in the penultimate year.
3.2 Deterministic Model ScenariosThe CPUEs for the purse seine and trawl fisheries obtained from the four assessment scenarios were broadly similar, which were lower than the 'true' CPUE in the first a few years but closely matched after 2005 (Fig.1). K-r assessment model matched the operating model, so estimates such as biomass, harvest rate and reference points were identical with the true estimates when using the actual catch data and simulated CPUE data without errors. However, the outputs of the other three scenarios with model structure misspecification presented some biases (Fig.4). REs in the S model were higher than those in the other two misspecification models, suggesting that estimates from the model were more biased. On the contrary, r model was more accurate than other models because REs for biomass, BMSY, harvest rate and FMSY were 2%, 55%, 2% and 4%, respectively, which were the lowest among all the scenarios besides the K-r model (Table 2). REs for BMSY were significantly biased, especially in the S and K models, which indicated that BMSY was sensitive to ignoring the habitat effect on carrying capacity and intrinsic growth rate in the assessment.
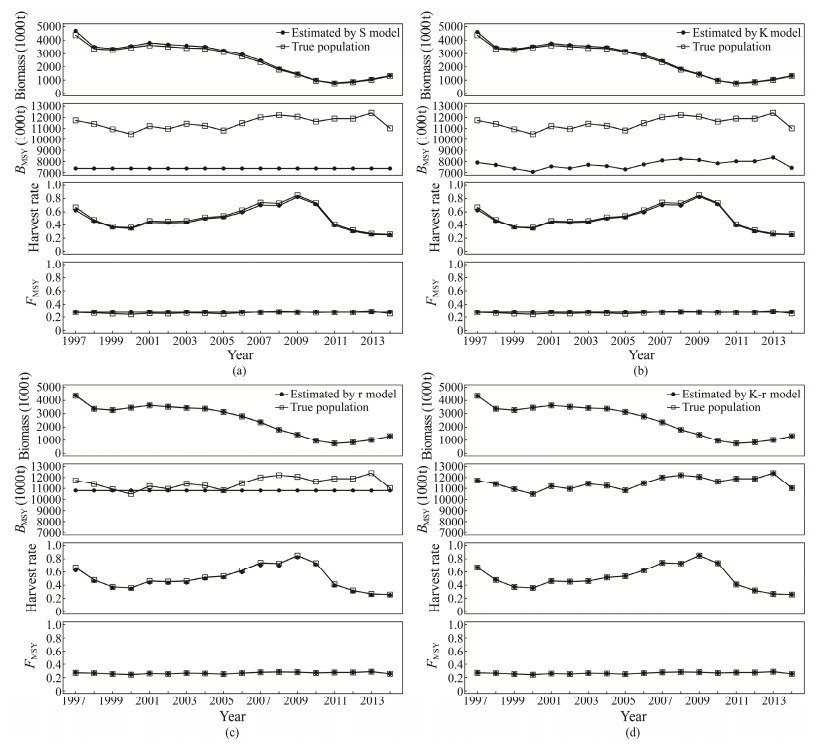
|
Fig. 4 Biomass, harvest rate, BMSY and FMSY under no stochasticity for the simulated population and estimated populations by S (a), K (b), r (c), and K-r (d) models of Chilean jack mackerel in the Southeast Pacific Ocean. |
|
|
Table 2 Relative errors (REs) for estimated biomass (B), harvest rate (F), BMSY, and FMSY of Chilean jack mackerel in the Southeast Pacific with (stochastic scenarios) and without (deterministic scenarios) observation and process errors added |
RBs of biomass, harvest rate and reference points and model parameters (K and r) were shown in Fig.5. The RBs for biomass were almost positive in all mismatched scenarios, with variations of 3% – 7% in the S model, 2% – 5% in the K model, and less than 1% in the r model, so that annual biomass was overestimated in most cases, apart from 1999 – 2000 in the r model. On the other hand, the opposite was true for the harvest rate in the r model. The absolute value of RBs for harvest rate achieved the maximum in the S model, followed by the K and r models, with seemingly minor differences between the operating model and the three misspecified models. BMSY was underestimated with negative RB values, in which it ranged from −29% to −41% in the S model, fixed at −33% in K model and ranged from −13% to −2% in the r model in all years but 2000 (Fig.5). Based on RBs value 0.41% for the r model and the same trend of fluctuating RBs between −4% and 14% for the S and K model, FMSY values were overestimated in some years and underestimated in the other years (e.g., 2007 – 2009 and 2013 in the K model scenario; Fig.5).

|
Fig. 5 Percent relative bias for biomass, harvest rate, BMSY and FMSY of Chilean jack mackerel in the Southeast Pacific Ocean under four assessment scenarios with no stochasticity. |
Estimates of model parameters, biomass, harvest rate and reference points were sensitive to model structures or ignoring the impacts of habitat in the assessment. The absolute value of RBs for these estimates in the S model were higher than those in the K and r models, suggesting that estimates from the S model were more biased, K model moderate and r model relatively robust when habitat effects were entirely or partially excluded from the assessment.
3.3 Stochastic Model ScenariosObservation and process errors were added in the stochastic scenarios to evaluate their impacts on the stock assessment and compare the performance of assessment models. Under the circumstance of stochastic scenarios, REs increased dramatically even in the K-r model, although they appeared to decrease for BMSY in the other three models (Table 2). REs for FMSY in the r and K-r model were greater than those in the S and K model, which indicated that FMSY as well as the intrinsic growth rate were sensitive to habitat changes when observation and process errors were added to the assessment. In general, the REs declined from the S model to K-r model, demonstrating that K-r model was more reliable than the mismatched model scenarios.
The variations after the inclusion of errors to the data were reflected in the RBs for each year, with notably larger values of median RBs for biomass and harvest rate. Biomass was overestimated as suggested by the positive median RBs in all scenarios, ranging from 10% to 17% for the S model, 10% to 15% for the K model, and 7% to 11% for the r model as well as K-r model, as was also found for the absolute value of median RBs for harvest rate. As for BMSY, it was underestimated in the S and K models with median RBs of −36% to −25% and fixed at −28%, respectively. However, it was overestimated in the r and K-r models, with the former being more than 0 except for 1997 and 2007 – 2013 and the latter fixed at 5%. The median RBs for FMSY were quite similar at −8% in the r and K-r models, and the errors did not cause significant bias in the other two models (i.e., the median RBs were centered around zero); however, overall FMSY tended to be underestimated (Fig.6).
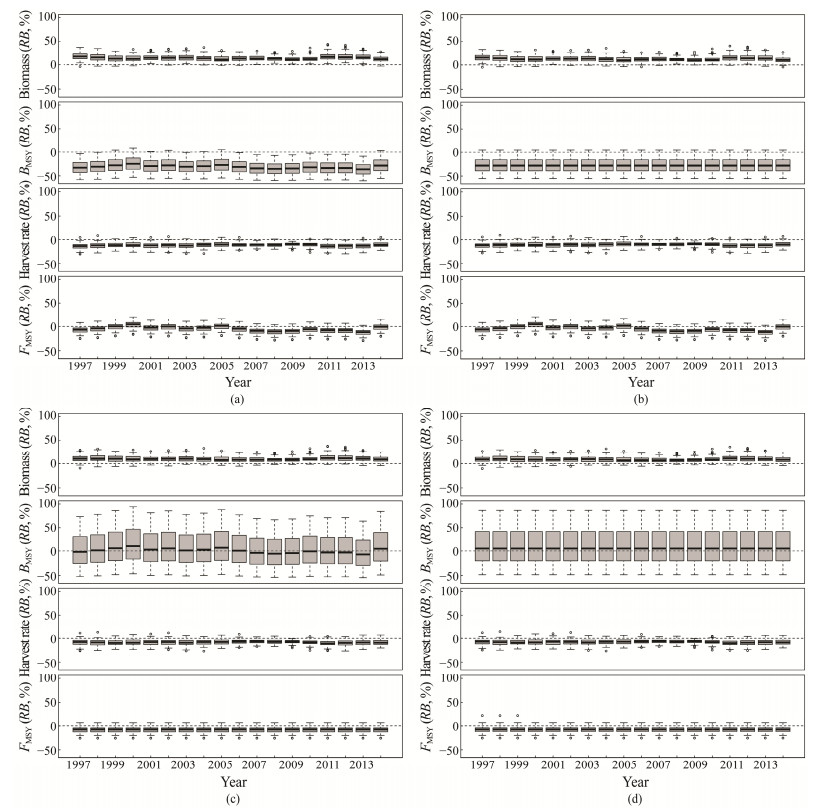
|
Fig. 6 Percent relative bias for biomass, harvest rate, BMSY and FMSY of Chilean mackerel in the Southeast Pacific Ocean of S (a), K (b), r (c), and K-r (d) models with observation and process errors. |
In this study, we have investigated the impact of suitable habitat area on biomass dynamics and estimates of reference points of Chilean jack mackerel using a surplus production model. The model parameters, i.e., carrying capacity and intrinsic growth rate, were linked to suitable habitat area. The hypothesis is that biomass as well as reference points vary with environmental conditions since the suitable habitat area estimated by the HSI model depends on environmental factors. The results indicated that ignoring habitat changes resulted in significant biases in the estimates of annual biomass, harvest rate and MSY-based reference points, which were amplified by the inclusion of observation and process errors (Fig.5). In comparison to other parameters and biological reference points, BMSY with environmental influences neglected and FMSY with observation and process errors neglected were more sensitive. Scenarios that fully considered environmental factors, with or without observation and process errors, would have brought the assessment results more in line with the 'true' population status of Chilean jack mackerel (Table 2).
Climate-driven changes in ocean conditions have direct non-lethal effects on fish growth and reproduction, in particular for pelagic fishes (Klyashtorin, 1998; Punt et al., 2021). The life history characteristics of these fishes include rapid growth, early maturity, short lifespans and small body sizes (Blaxter and Hunter, 1982; Tsikliras et al., 2019). Recruitment that determines the stock abundance depends on a large extent of conditions in the environment and/or reproductive stocks at different temporal and spatial scales (Tourre et al., 2007). Environmental change would inevitably alter habitat suitability and, in turn, population distribution and abundance patterns (Brander, 2010). For example, both chub mackerel (Scomber japonicus) and Pacific saury (Cololabis saira) in the Western Pacific experience negative effects of reduced suitable habitat area during El Niño events (Li et al., 2014; Chang et al., 2018). In the case of Chilean jack mackerel, a significant positive correlation was found between HSI and PDO indices (Feng et al., 2022), and seasonal variation in suitable habitat in latitude was consistent with the 15℃ isotherm (Li et al., 2016). Cubillos et al. (2008) suggested that suitable spawning conditions for Chilean jack mackerel were associated with SST, which had been noted as one of the major abiotic factors affecting almost all biological processes. Espíndola et al. (2016) found that incorporating SST into the stock-recruitment relationship of Chilean jack mackerel might be a promising way to examine the effects of fishing and environment conditions simultaneously. The development of an ecosystem-based model for Chilean jack mackerel to determine the extent of environmental drivers on the stock dynamics will enhance our comprehension of this population (Dragon et al., 2018).
Incorporation of various forms of auxiliary information into the surplus production model is straightforward and only involves an additional criterion onto the goodness of fit for the time series alone (Hilborn and Walters, 1992). Previous researches developed an environmental dependent surplus model to access the status of some pelagic species, but they only focused on water temperature or its proxy (Jacobson et al., 2005; Wang et al., 2016, 2018). It is well known that not just temperature, but many other environmental variables have an impact on population dynamics (Lehodey et al., 2006; Maunder and Watters, 2003). Therefore, the inclusion of a single environmental factor in the assessment model is not likely to accurately reflect the actual fishery resource status. Despite being directly based on multiple factors, the current model is only able to comprehend the composite effect of the environment on catches (Yi et al., 2017). As it combines multiple ecologically relevant environmental variables, the HSI model has the natural advantage of being able to be incorporated into the assessment model (Tanaka and Chen, 2016). Tanaka et al. (2019) used HSI to inform the recruitment dynamics of the American lobster in the size-structure model, demonstrating the potential to improve population assessment. In this study, we used the HSI model of suitable habitat area as an indicator of intrinsic growth rate and carrying capacity to investigate the suitability of different scenarios considering environmental factors to assess the resource status of Chilean jack mackerel. Our analysis found that bias typically worsened as the difference between parameters such as biomass or harvest rate and 'true' stock dynamics increases. The four assessment scenarios, from i to iv, the REs (between estimates using simulation and operating model) for each parameter and biological reference point showed a decreasing trend (Table 2), which indicated that the population dynamics of Chilean jack mackerel were influenced by environmental conditions in addition to fishing activities. With habitat-based models, dynamic BRPs that help to adjust annual regulations for fisheries management were obtained. However, resource status could not be predicted since the future proportion of area with favorable environmental conditions is unknown.
The carrying capacity of an environment is determined not only by the abundance and distribution of limited resources, but also by the methods of individuals competing for the resources (Ayllón et al., 2012). The relative role of intrinsic density-dependent factors (e.g., interand intraspecific competition, predation) that can maintain relatively stable and regular fluctuations in populations, and extrinsic, density-independent factors (environmental change) associated with irregular changes in population size is critical for population dynamics regulation (Lorenzen and Enberg, 2002; DingsØr et al., 2007). Mortality, growth and reproduction in marine fish populations are susceptible to density-independent effects and the action of density-dependent processes (Lorenzen and Camp, 2019). These processes do not occur uniformly throughout the life cycle of fishes, and density-dependent regulation determined by the size of the habitat may occur both early and late in the life history (Andersen et al., 2017). This study showed that habitat area is positively correlated with both K and densityindependent r (Figs.4, 7), implying that the higher abundance requires more space to be occupied, thus favoring the growth of Chilean jack mackerel.
Process errors in this study refer to the underlying stochasticity in the population dynamics resulting from factors other than the environment variability that cannot be describe by a surplus production model, while observation errors are certainly unavoidable when collecting data (Newman, et al., 2006). The results suggest that ⅰ) when the assessment model structure matches the operating model, observation and process error leads to an overestimation of biomass and BMSY, as opposed to harvest rate and FMSY; ⅱ) when the assessment model structure is mismatched, the bias of each estimate other than BMSY is significantly increased; ⅲ) the combined effect of observation and process error is greater than the environment acting alone (Table 2). Therefore, all types of errors need to be recognized and appropriately quantified before models are utilized (Maunder and Watters, 2003). In any scenario, good data quality can help mitigate certain biases, e.g., estimates of life history parameters can be improved by biological studies prior to their input (Zhang et al., 2015).
It is generally recognized that ignoring uncertainty associated with estimates of current stock size and potential productivity in assessment may lead to a biased view of stock status (Francis and Shotton, 1997). This is most likely to happen when the estimated biomass or harvest rate are close to the reference points. If harvest rate is underestimated and biomass is overestimated, the assessments might be overly optimistic, leading to mismanagement and stock collapse (Bouch et al., 2021). Such misjudgment can further lead to risks in decision-making, which exist objectively (Hilborn et al., 1993; Sethi, 2010). The conclusion above coincides with the final-year assessment results of the S and K models in this study. However, in the scenario where only observations and process uncertainty were studied, the interpretation for the status of Chilean jack mackerel stock was consistent with the 'true' one (Figs.3, 7). Without comparing assessment results under high and low errors, the risks in management will increase with random error (Zou et al., 2016). For this reason, it needs to be minimized through precautionary principle and ecosystembased management measures that can achieve sustainable use of fisheries resources (Kirkwood and Smith, 1996).
|
Fig. 7 Biomass, harvest rate, BMSY and FMSY of Chilean mackerel in the Southeast Pacific Ocean under four assessment scenarios with stochasticity. |
Combining climate-driven changes in suitable habitats with key parameters in assessment models can provide potential improvements in stock assessments. However, it should be noted that even in previous studies the habitatK relationship was developed as a linear relationship, though it is arbitrary. Future researches should simulate multiple different types for this relation, which is important for exploring the development of habitat-based assessment models. Additionally, the effects of errors should also be fully considered in stock assessments of Chilean jack mackerel. Our approach could be extended in the future to other similar pelagic fish stocks affected by environmental changes.
AcknowledgementThis work was supported by the National Key Research and Development Program of China (No. 2019YFD0901 404).
Author Contributions
All authors contributed to the study conception and design. Data collection was performed by Xiaorong Zou. Modeling and data analysis performed by Yangming Cao. The draft of the manuscript was written by Yangming Cao and Gang Li, and supervised by Xinjun Chen. All authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Data Availability
All data generated and analyzed during this study are included in this published article and its additional files.
Declarations
Ethics Approval and Consent to Participate
This article does not contain any studies with human participants or animals performed by any of the authors.
Consent for Publication
Informed consent for publication was obtained from all participants.
Conflict of Interests
The authors declare that they have no conflict of interests. Xinjun Chen is one of the Editorial Board Members, but he was not involved in the journal's review of, or decision related to, this manuscript.
Alegre, A., Bertrand, A., Espino, M., Espinoza, P., Dioses, T., Niquen, M., et al., 2015. Diet diversity of jack and chub mackerels and ecosystem changes in the northern Humboldt Current system: A long-term study. Progress in Oceanography, 137: 299-313. DOI:10.1016/j.pocean.2015.07.010 (  0) 0) |
Andersen, K. H., Jacobsen, N. S., Jansen, T., and Beyer, J. E., 2017. When in life does density dependence occur in fish populations?. Fish and Fisheries, 18(4): 656-667. DOI:10.1111/faf.12195 (  0) 0) |
Arcos, D. F., Cubillos, L. A., and Núnez, S. P., 2001. The jack mackerel fishery and El Niño 1997 – 98 effects off Chile. Progress in Oceanography, 49(1-4): 597-617. DOI:10.1016/S0079-6611(01)00043-X (  0) 0) |
Ayllón, D., Almodóvar, A., Nicola, G. G., Parra, I., and Elvira, B., 2012. Modelling carrying capacity dynamics for the conservation and management of territorial salmonids. Fisheries Research, 134: 95-103. DOI:10.1016/j.fishres.2012.08.004 (  0) 0) |
Bertrand, A., Habasque, J., Hattab, T., Hintzen, N. T., Oliveros-Ramos, R., Gutiérrez, M., et al., 2016. 3-D habitat suitability of jack mackerel Trachurus murphyi in the Southeastern Pacific, a comprehensive study. Progress in Oceanography, 146: 199-211. DOI:10.1016/j.pocean.2016.07.002 (  0) 0) |
Blaxter, J. H. S., and Hunter, J. R., 1982. The biology of the clupeoid fishes. Advances in Marine Biology, 20: 1-223. DOI:10.1016/S0065-2881(08)60140-6 (  0) 0) |
Bouch, P., Minto, C., and Reid, D. G., 2021. Comparative performance of data-poor CMSY and data-moderate SPiCT stock assessment methods when applied to data-rich, real-world stocks. ICES Journal of Marine Science, 78(1): 264-276. DOI:10.1093/icesjms/fsaa220 (  0) 0) |
Brander, K., 2010. Impacts of climate change on fisheries. Journal of Marine Systems, 79(3-4): 389-402. DOI:10.1016/j.jmarsys.2008.12.015 (  0) 0) |
Canales, C., 2015. Update of CPUE of Jack mackerel (Trachurus murphy) at center-south area off Chile 1983 – 2015. In: The Third Scientific Committee Meeting of SPRFMO. Port Vila, Vanuatu.
(  0) 0) |
Cao, J., Thorson, J. T., Punt, A. E., and Szuwalski, C., 2020. A novel spatiotemporal stock assessment framework to better address fine-scale species distributions: Development and simulation testing. Fish and Fisheries, 21(2): 350-367. DOI:10.1111/faf.12433 (  0) 0) |
Cao, J., Truesdell, S. B., and Chen, Y., 2014. Impacts of seasonal stock mixing on the assessment of Atlantic cod in the Gulf of Maine. ICES Journal of Marine Science, 71(6): 1443-1457. DOI:10.1093/icesjms/fsu066 (  0) 0) |
Cárdenas, L., Silva, A. X., Magoulas, A., Cabezas, J., Poulin, E., and Ojeda, F. P., 2009. Genetic population structure in the Chilean jack mackerel, Trachurus murphyi (Nichols) across the South-eastern Pacific Ocean. Fisheries Research, 100(2): 109-115. DOI:10.1016/j.fishres.2009.06.013 (  0) 0) |
Chang, Y. J., Lan, K. W., Walsh, W. A., Hsu, J., and Hsieh, C. H., 2018. Modelling the impacts of environmental variation on habitat suitability for Pacific saury in the Northwestern Pacific Ocean. Fisheries Oceanography, 28(3): 291-304. DOI:10.1111/fog.12408 (  0) 0) |
Chen, Y., Chen, L. Q., and Stergiou, K. I., 2003. Impacts of data quantity on fisheries stock assessment. Aquatic Sciences, 65(1): 92-98. DOI:10.1007/s000270300008 (  0) 0) |
Cubillos, L. A., Paramo, J., Ruiz, P., Núñez, S., and Sepúlveda, A., 2008. The spatial structure of the oceanic spawning of jack mackerel (Trachurus murphyi) off central Chile (1998 – 2001). Fisheries Research, 90(1-3): 261-270. DOI:10.1016/j.fishres.2007.10.016 (  0) 0) |
De Kerckhove, D. T., Smokorowski, K. E., and Randall, R. G., 2008. A primer on fish habitat models. Canadian Technical Report of Fisheries and Aquatic Sciences, 2817: 71. (  0) 0) |
Deroba, J. J., Butterworth, D. S., Methot Jr., R. D., De Oliveira, J. A. A., Fernandez, C., Nielsen, A., et al., 2015. Simulation testing the robustness of stock assessment models to error: Some results from the ICES strategic initiative on stock assessment methods. ICES Journal of Marine Science, 72(1): 19-30. DOI:10.1093/icesjms/fst237 (  0) 0) |
DingsØr, G. E., Ciannelli, L., Chan, K. S., Ottersen, G., and Stenseth, N. C., 2007. Density dependence and density independence during the early life stages of four marine fish stocks. Ecology, 88(3): 625-634. DOI:10.1890/05-1782 (  0) 0) |
Donovan, T. M., Warrington, G. S., Schwenk, W. S., and Dinitz, J. H., 2012. Estimating landscape carrying capacity through maximum clique analysis. Ecological Applications, 22(8): 2265-2276. DOI:10.1890/11-1804.1 (  0) 0) |
Downs, J. A., Gates, R. J., and Murray, A. T., 2008. Estimating carrying capacity for sandhill cranes using habitat suitability and spatial optimization models. Ecological Modelling, 214(2-4): 284-292. DOI:10.1016/j.ecolmodel.2008.02.006 (  0) 0) |
Dragon, A. C., Senina, I., Hintzen, N. T., and Lehodey, P., 2018. Modelling South Pacific jack mackerel spatial population dynamics and fisheries. Fisheries Oceanography, 27(2): 97-113. DOI:10.1111/fog.12234 (  0) 0) |
Espíndola, F., Quiroz, J. C., Wiff, R., and Yáñez, E., 2016. Incorporating sea surface temperature into the stockrecruitment relationship: Applications to jack mackerel (Trachurus murphyi) off Chile. Revista de Biología Marina y Oceanografía, 51(1): 137-145. DOI:10.4067/S0718-19572016000100013 (  0) 0) |
Feng, Z. P., Yu, W., and Chen, X. J., 2022. Synchronous spatio-temporal changes in potential habitats of Trachurus murphyi and Dosidicus gigas off Chile in relation to regime shift of Pacific decadal oscillation. Journal of Marine Systems, 233: 103758. DOI:10.1016/j.jmarsys.2022.103758 (  0) 0) |
Francis, R. I. C. C., and Shotton, R., 1997. 'Risk' in fisheries management: A review. Canadian Journal of Fisheries and Aquatic Sciences, 54(8): 1699-1715. DOI:10.1139/f97-100 (  0) 0) |
Gregr, E. J., Nichol, L. M., Watson, J. C., Ford, J. K., and Ellis, G. M., 2008. Estimating carrying capacity for sea otters in British Columbia. The Journal of Wildlife Management, 72(2): 382-388. DOI:10.2193/2006-518 (  0) 0) |
Guan, W. J., Cao, J., Chen, Y., and Cieri, M., 2013. Impacts of population and fishery spatial structures on fishery stock assessment. Canadian Journal of Fisheries and Aquatic Sciences, 70(8): 1178-1189. DOI:10.1139/cjfas-2012-0364 (  0) 0) |
Haddon, M., 2011. Modelling and Quantitative Methods in Fisheries. Chapman and Hall/CRC Press, London, 449pp.
(  0) 0) |
Hayes, D. B., Ferreri, C. P., and Taylor, W. W., 1996. Linking fish habitat to their population dynamics. Canadian Journal of Fisheries and Aquatic Sciences, 53(S1): 383-390. DOI:10.1139/f95-273 (  0) 0) |
Hilborn, R., and Walters, C. J., 1992. Quantitative Fisheries Stock Assessment: Choice, Dynamics and Uncertainty. Chapman and Hall, London, 570pp.
(  0) 0) |
Hilborn, R., Pikitch, E. K., and Francis, R. C., 1993. Current trends in including risk and uncertainty in stock assessment and harvest decisions. Canadian Journal of Fisheries and Aquatic Sciences, 50(4): 874-880. DOI:10.1139/f93-100 (  0) 0) |
Hvingel, C., and Kingsley, M. C., 2006. A framework to model shrimp (Pandalus borealis) stock dynamics and to quantify the risk associated with alternative management options, using Bayesian methods. ICES Journal of Marine Science, 63(1): 68-82. DOI:10.1016/j.icesjms.2005.09.002 (  0) 0) |
Jacobson, L. D., Bograd, S. J., Parrish, R. H., Mendelssohn, R., and Schwing, F. B., 2005. An ecosystem-based hypothesis for climatic effects on surplus production in California sardine (Sardinops sagax) and environmentally dependent surplus production models. Canadian Journal of Fisheries and Aquatic Sciences, 62(8): 1782-1796. DOI:10.1139/f05-095 (  0) 0) |
Jennings, S., 2000. Patterns and prediction of population reco-very in marine reserves. Reviews in Fish Biology and Fisheries, 10(2): 209-231. DOI:10.1023/A:1016619102955 (  0) 0) |
Jonsson, N., and Jonsson, B., 2011. Ecology of Atlantic Salmon and Brown Trout: Habitat As a Template for Life Histories. Fish & Fisheries Series, Volume 33. Springer, New York, 708pp.
(  0) 0) |
Kirkwood, G. P., and Smith, A. D. M., 1996. Assessing the precautionary nature of fishery management strategies. FAO Fisheries Technical Paper: 141-158. (  0) 0) |
Klyashtorin, L. B., 1998. Long-term climate change and main commercial fish production in the Atlantic and Pacific. Fisheries Research, 37(1-3): 115-125. DOI:10.1016/S0165-7836(98)00131-3 (  0) 0) |
Lehodey, P., Alheit, J., Barange, M., Baumgartner, T., Beaugrand, G., Drinkwater, K., et al., 2006. Climate variability, fish, and fisheries. Journal of Climate, 19(20): 5009-5030. DOI:10.1175/JCLI3898.1 (  0) 0) |
Li, G., and Zou, X., 2015. National report of China to the 2015 SPRFMO Science Committee Part I: The jack mackerel fishery. The Third Scientific Committee Meeting of SPRFMO, Port Vila, Vanuatu.
(  0) 0) |
Li, G., Cao, J., Zou, X. R., Chen, X. J., and Runnebaum, J., 2016. Modeling habitat suitability index for Chilean jack mackerel (Trachurus murphyi) in the South East Pacific. Fisheries Research, 178: 47-60. DOI:10.1016/j.fishres.2015.11.012 (  0) 0) |
Li, G., Chen, X. J., Lei, L., and Guan, W. J., 2014. Distribution of hotspots of chub mackerel based on remote-sensing data in coastal waters of China. International Journal of Remote Sensing, 35(11-12): 4399-4421. DOI:10.1080/01431161.2014.916057 (  0) 0) |
Li, G., Zou, X. R., Chen, X. J., Zhou, Y. Q., and Zhang, M., 2013. Standardization of CPUE for Chilean jack mackerel (Trachurus murphyi) from Chinese trawl fleets in the high seas of the Southeast Pacific Ocean. Journal of Ocean University of China, 12(3): 441-451. DOI:10.1007/s11802-013-1987-1 (  0) 0) |
Lorenzen, K., and Camp, E. V., 2019. Density-dependence in the life history of fishes: When is a fish recruited?. Fisheries Research, 217: 5-10. DOI:10.1016/j.fishres.2018.09.024 (  0) 0) |
Lorenzen, K., and Enberg, K., 2002. Density-dependent growth as a key mechanism in the regulation of fish populations: Evidence from among-population comparisons. Proceedings of the Royal Society of London. Series B: Biological Sciences, 269(1486): 49-54. DOI:10.1098/rspb.2001.1853 (  0) 0) |
Mace, P. M., 2001. A new role for MSY in single-species and ecosystem approaches to fisheries stock assessment and management. Fish and Fisheries, 2(1): 2-32. DOI:10.1046/j.1467-2979.2001.00033.x (  0) 0) |
Mallet, J., 2012. The struggle for existence. How the notion of carrying capacity, K, obscures the links between demography, Darwinian evolution and speciation. Evolutionary Ecology Research, 14: 627-665. (  0) 0) |
Maunder, M. N., and Watters, G. M., 2003. A general framework for integrating environmental time series into stock assessment models: Model description, simulation testing, and example. Fishery Bulletin, 101(1): 89-100. (  0) 0) |
McAllister, M. K., and Kirkwood, G. P., 1998. Bayesian stock assessment: A review and example application using the logistic model. ICES Journal of Marine Science, 55(6): 1031-1060. DOI:10.1006/jmsc.1998.0425 (  0) 0) |
Morris, D. W., and Mukherjee, S., 2006. Simulated and human metapopulations created by habitat selection. Evolutionary Ecology Research, 8: 1263-1275. (  0) 0) |
Naiman, R. J., and Latterell, J. J., 2005. Principles for linking fish habitat to fisheries management and conservation. Journal of Fish Biology, 67: 166-185. DOI:10.1111/j.0022-1112.2005.00921.x (  0) 0) |
Newman, K. B., Buckland, S. T., Lindley, S. T., Thomas, L., and Fernandez, C., 2006. Hidden process models for animal population dynamics. Ecological Applications, 16(1): 74-86. DOI:10.1890/04-0592 (  0) 0) |
Ñiquen, M., and Bouchon, M., 2004. Impact of El Niño events on pelagic fisheries in Peruvian waters. Deep Sea Research Part Ⅱ: Topical Studies in Oceanography, 51(6-9): 563-574. DOI:10.1016/j.dsr2.2004.03.001 (  0) 0) |
Oldham, R. S., Keeble, J., Swan, M. J. S., and Jeffcote, M., 2000. Evaluating the suitability of habitat for the great crested newt (Triturus cristatus). Herpetological Journal, 10(4): 143-155. (  0) 0) |
Pauly, D., Christensen, V., Guénette, S., Pitcher, T. J., Sumaila, U. R., Walters, C. J., et al., 2002. Towards sustainability in world fisheries. Nature, 418(6898): 689-695. DOI:10.1038/nature01017 (  0) 0) |
Perretti, C. T., Deroba, J. J., and Legault, C. M., 2020. Simulation testing methods for estimating misreported catch in a statespace stock assessment model. ICES Journal of Marine Science, 77(3): 911-920. DOI:10.1093/icesjms/fsaa034 (  0) 0) |
Prager, M. H., 2002. Comparison of logistic and generalized surplus-production models applied to swordfish, Xiphias gladius, in the North Atlantic Ocean. Fisheries Research, 58(1): 41-57. DOI:10.1016/S0165-7836(01)00358-7 (  0) 0) |
Punt, A. E., and Hilborn, R., 1997. Fisheries stock assessment and decision analysis: The Bayesian approach. Reviews in Fish Biology and Fisheries, 7(1): 35-63. DOI:10.1023/a:1018419207494 (  0) 0) |
Punt, A. E., and Hilborn, R., 2001. BAYES-SA Bayesian Stock Assessment Methods in Fisheries: User's Manual. Food and Agriculture Organization of the United Nations, Rome.
(  0) 0) |
Punt, A. E., Dalton, M. G., Cheng, W., Hermann, A. J., Holsman, K. K., Hurst, T. P., et al., 2021. Evaluating the impact of climate and demographic variation on future prospects for fish stocks: An application for northern rock sole in Alaska. Deep Sea Research Part Ⅱ: Topical Studies in Oceanography, 189: 104951. DOI:10.1016/j.dsr2.2021.104951 (  0) 0) |
Quinn, T. J., and Deriso, R. B., 1999. Quantitative Fish Dynamics. Oxford University Press, New York, 542pp.
(  0) 0) |
Rubec, P. J., Bexley, J. C., Norris, H. E. N. R. Y., Coyne, M., Monaco, M., Smith, S., et al., 1999. Suitability modeling to delineate habitat essential. American Fisheries Society Symposium, 22: 108-133. (  0) 0) |
Schaefer, M. B., 1957. A study of the dynamics of the fishery for yellow fin tuna in the eastern tropical Pacific Ocean. Bulletin of the Inter-American Tropical Tuna Commission, 2: 247-285. (  0) 0) |
Sethi, S. A., 2010. Risk management for fisheries. Fish and Fisheries, 11(4): 341-365. DOI:10.1111/j.1467-2979.2010.00363.x (  0) 0) |
Sharma, R., and Hilborn, R., 2001. Empirical relationships be-tween watershed characteristics and coho salmon (Oncorhynchus kisutch) smolt abundance in 14 western Washington streams. Canadian Journal of Fisheries and Aquatic Sciences, 58(7): 1453-1463. DOI:10.1139/f01-091 (  0) 0) |
SPRFMO, 2023. Report of the Eleventh Scientific Committee Meeting. The Eleventh Scientific Committee Meeting of SPRFMO. Panama City, Panama.
(  0) 0) |
Stobberup, K. A., and Erzini, K., 2006. Assessing mackerel scad, Decapterus macarellus, in Cape Verde: Using a Bayesian approach to biomass dynamic modelling in a data-limited situation. Fisheries Research, 82(1-3): 194-203. DOI:10.1016/j.fishres.2006.06.005 (  0) 0) |
Tanaka, K. R., Cao, J., Shank, B. V., Truesdell, S. B., Mazur, M. D., Xu, L. L., et al., 2019. A model-based approach to incurporate environmental variability into assessment of a commercial fishery: A case study with the American lobster fishery in the Gulf of Maine and Georges Bank. ICES Journal of Marine Science, 76(4): 884-896. DOI:10.1093/icesjms/fsz024 (  0) 0) |
Tanaka, K., and Chen, Y., 2016. Modeling spatiotemporal vari-ability of the bioclimate envelope of Homarus americanus in the coastal waters of Maine and New Hampshire. Fisheries Research, 177: 137-152. DOI:10.1016/j.fishres.2016.01.010 (  0) 0) |
Tian, S. Q., Chen, X. J., Chen, Y., Xu, L. L., and Dai, X. J., 2009. Evaluating habitat suitability indices derived from CPUE and fishing effort data for Ommatrephes bratramii in the northwestern Pacific Ocean. Fisheries Research, 95(2-3): 181-188. DOI:10.1016/j.fishres.2008.08.012 (  0) 0) |
Tinker, M. T., Yee, J. L., Laidre, K. L., Hatfield, B. B., Harris, M. D., Tomoleoni, J. A., et al., 2021. Habitat features predict carrying capacity of a recovering marine carnivore. The Journal of Wildlife Management, 85(2): 303-323. DOI:10.1002/jwmg.21985 (  0) 0) |
Tourre, Y. M., Lluch-Cota, S. E., and White, W. B., 2007. Global multi-decadal ocean climate and small-pelagic fish population. Environmental Research Letters, 2(3): 034005. DOI:10.1088/1748-9326/2/3/034005 (  0) 0) |
Tsikliras, A. C., Licandro, P., Pardalou, A., McQuinn, I. H., Grö-ger, J. P., and Alheit, J., 2019. Synchronization of Mediterranean pelagic fish populations with the North Atlantic climate variability. Deep Sea Research Part Ⅱ: Topical Studies in Oceanography, 159: 143-151. DOI:10.1016/j.dsr2.2018.07.005 (  0) 0) |
United States Fish and Wildlife Service (USFWS), 1981. Standards for the Development of Habitat Suitability Index Models for Use with the Habitat Evaluation Procedures. Division of Ecological Services, Washington, D. C.
(  0) 0) |
Vadas Jr., R. L., and Orth, D. J., 2001. Formulation of habitat suitability models for stream fish guilds: Do the standard methods work?. Transactions of the American Fisheries Society, 130(2): 217-235. DOI:10.1577/1548-8659(2001)130%3C0217:FOHSMF%3E2.0.CO;2 (  0) 0) |
Vásquez, S., Correa-Ramírez, M., Parada, C., and Sepúlveda, A., 2013. The influence of oceanographic processes on jack mackerel (Trachurus murphyi) larval distribution and population structure in the southeastern Pacific Ocean. ICES Journal of Marine Science, 70(6): 1097-1107. DOI:10.1093/icesjms/fst065 (  0) 0) |
Vinagre, C., Fonseca, V., Cabral, H., and Costa, M. J., 2006. Ha-bitat suitability index models for the juvenile soles, Solea solea and Solea senegalensis, in the Tagus Estuary: Defining variables for species management. Fisheries Research, 82(1-3): 140-149. DOI:10.1016/j.fishres.2006.07.011 (  0) 0) |
Wang, J. T., Chen, X. J., Staples, K. W., and Chen, Y., 2018. A stock assessment for Illex argentinus in Southwest Atlantic using an environmentally dependent surplus production model. Acta Oceanologica Sinica, 37(2): 94-101. DOI:10.1007/s13131-017-1131-y (  0) 0) |
Wang, J. T., Yu, W., Chen, X. J., and Chen, Y., 2016. Stock as-sessment for the western winter-spring cohort of neon flying squid (Ommastrephes bartramii) using environmentally dependent surplus production models. Scientia Marina, 80(1): 69-78. DOI:10.3989/scimar.04205.11A (  0) 0) |
Yáñez, E., Barbieri, M. A., Silva, C., Nieto, K., and Espíndola, F., 2001. Climate variability and pelagic fisheries in northern Chile. Progress in Oceanography, 49(1-4): 581-596. DOI:10.1016/S0079-6611(01)00042-8 (  0) 0) |
Yen, K. W., Lu, H. J., Chang, Y., and Lee, M. A., 2012. Using remote-sensing data to detect habitat suitability for yellowfin tuna in the Western and Central Pacific Ocean. International Journal of Remote Sensing, 33(23): 7507-7522. DOI:10.1080/01431161.2012.685973 (  0) 0) |
Yi, W., Chen, X. J., and Yu, W., 2017. Surplus production mo-del for Cololabis saira in the Northwest Pacific Ocean based on the environmental factors. Journal of Guangdong Ocean University, 37(4): 55-60 (in Chinese with English abstract). DOI:10.3969/j.issn.1673-9159.2017.04.009 (  0) 0) |
Zhang, C. L., Chen, Y., and Ren, Y. P., 2015. Assessing uncer-tainty of a multispecies size-spectrum model resulting from process and observation errors. ICES Journal of Marine Science, 72(8): 2223-2233. DOI:10.1093/icesjms/fsv086 (  0) 0) |
Zou, L. J., Zou, X. R., Guan, W. J., Zhang, M., and Li, G., 2016. Stock assessment and harvest control rules simulation for jack mackerel (Trachurus murphyi) in the southeast Pacific. Journal of Fisheries of China, 40(5): 807-819 (in Chinese with English abstract). DOI:10.11964/jfc.20150609934 (  0) 0) |
 2025, Vol. 24
2025, Vol. 24


