1 Introduction

The passive remote sensing of the ocean environment is important, as it provides the data of geophysical parameters, such as sea surface temperature (SST), sea surface salinity (SSS), and wind field, by satellite observations with microwave and infrared (IR) radiometers. The emissivity of a sea surface is a key quantity of retrieving ocean environment parameters from microwave brightness temperatures. The microwave emission from an ocean rough surface is related to microwave frequency and sea surface roughness, which depend on the wind vector. It is well known that the emissivity of the flat sea surface can be predicted by Fresnel reflectivity. However, it is extremely difficult to exactly calculate the emissivity of a rough sea surface due to the complex wind-generated rough surface with various random parameters, e.g., wave steepness, wave height, wavelength, and ocean whitecap.

For the wind-roughened sea surface, the waves from a few centimeters to a few meters are considered the domain contributors of sea waves (Hung and Tsai, 2009). In dealing with the emission problem of the rough sea surface, numerous theoretical and empirical studies have focused on the microwave emissivity mechanism of rough ocean surfaces based on the properties of random ocean waves. Generally, the emission theory of a rough surface results from the theory of scattering and Kirchhoff's law of thermal emission (Zavorotny and Voronovich, 2000; Voronovich and Zavorotny, 2017). For example, if the root mean square deviation (RMSD) of undulating wave height is smaller (or larger) than the radiation wavelength, the emissivity of rough surfaces can be determined by using the small perturbation method (or Kirchhoff approximation) of surface scattering coefficients (Yueh et al., 1994; Irrisov, 1997; Johnson, 2005). Related to this, two-scale scattering theory was proposed to compute the emissivity of the rough sea surface by combing the effects of large- and small-scale waves (Wu and Fung, 1972; Wentz, 1975). Furthermore, for retrieving the wind vectors and the sea surface roughness or wave spectrum, one study applied the microwave Bragg resonance of capillary gravity waves to measure the radar cross-section (Hwang et al., 2010, 2013). Emission theory of rough sea surface was developed by the small slope approximation (SSA) method of scattering cross-sections expressed as a series of surface slopes (Voronovich, 1994). This active SSA is able to produce an active, two-scale model in appropriate wavenumber limits without dividing the long and short surface wavelength scales, as in the two-scale theory (Johnson, 2005). Additionally, numerical method based on the electromagnetic model has been used to discuss the emissivity of rough sea surfaces (Burrage et al., 2019). These methods applied passive remote sensing to retrieve the geophysical parameters. However, all of these models are approximate theories of sea emissivity and have been shown to have exponentially larger computational requirements by integrating the surface bistatic scattering coefficients, including the sea surface spectrum, for higher accuracy (Fung, 1994). The empirical model has been proposed to discuss the emissions of rough sea surfaces, given the difficulty involved in obtaining the differences between the brightness temperature model calculated by the scattering coefficients and the data observed from a sea surface. For instance, emissivity models between microwave frequencies of 6 and 90 GHz were fitted by the brightness temperature data of the spaceborne microwave radiometer WindSat and the Special Sensor Microwave/Imager (SSM/I) for the wind roughened ocean surface (Meissner and Wentz, 2012). Thus, it is necessary to seek a simple theoretical method to theoretically analyze the emissive properties of a rough surface and ultimately deal with the problem of computing emissivity.

The microwave emission from the ocean surface depends on surface roughness and increases along with the increase in roughness. The contributions of surface waves to the microwave emissivity are related to the wavelength of the sea surface wave. Generally, the sea surface roughness includes large gravity waves, small gravity-capillary waves riding on top of the large-scale waves, and sea foam produced by wave breaking if the wind speeds are larger than 7 m s⁻¹. The emissivity signals produced by these mechanisms are mainly isotropic in accordance with the wind direction, given that anisotropic features give rise to small contributions to the looking direction (Meissner and Wentz, 2012). Here, the capillary gravity waves with wave-lengths that are about the same or less order of microwave wavelength play important roles in remote sensing as a major part of wind-generated ocean waves (Sasaki et al., 1988; Gentemann et al., 2010; Yueh and Chaubell, 2012). For the sea foams on the sea surface, because the air bubbles size is small (not large 1 cm) on the top and bottom interfaces of a sea foam layer, the small-scale foam rough interfaces (or meniscus transition zone) can affect the microwave emissivity of sea surfaces (Wei et al., 2014).

In this study, we deal with the problem of microwave emissivity for a rough sea surface by using effective media theory (EMT) to calculate the effective dielectric constant of a rough sea surface, which is regarded as an effective medium of air and seawater separated by the rough interface. The idea of EMT was first proposed to predict the effective physical properties of a multiphase mixture as an effective medium with average field theory, such as effective viscosity coefficient, effective conductivity and dielectric constant, thermal conductivity, and material diffusivity of two-phase mixtures, so that the macroscopic physics properties of mixtures can be easily understood (Bergman, 1978; Milton, 2002). In fact, the EMT had been used to disclose the microwave emissive mechanism of sea foams (Raizer, 2007; Wei, 2011; Anguelova and Gaiser, 2012). The permittivity of sea foam – a mixture of seawater with air-bubble structure – is calculated by the EMT of spherical composites based on the flat interfaces of a sea foam layer (Anguelova and Gaiser, 2013; Wei, 2013; Wei et al., 2018). To date, the emission mechanism induced by the rough foam interfaces under a high wind speed has not been clearly discussed despite the fact that the emissivity of sea foam surface has already been studied by EMT. Thus, in the current work, we discuss the emissivity of wind-roughened sea surface, including the effects of foam rough interface and rough sea surface.

In this paper, EMT is extended to estimate the emissivity of sea surfaces based on the solutions of electric fields of a random rough surface when the surface wave scales are not larger than the microwave wavelength (McGurn et al., 2004). The air-sea rough interface, an example of a one-dimensional (1D) Gaussian sea surface, is regarded as a layer of effective medium with effective permittivity calculated by the air and seawater dielectric constants. In our model, the emissivity of rough ocean surface is determined by the RMSD of surface wave height and correlation length of the rough surface. Furthermore, this model is applied to estimate the excess emissivities and the brightness temperature increments derived from the satellite data of wind-roughened sea surface. When the RMSD is fitted as a nonlinear function of the wind speed, we obtained good agreements upon comparing the results of our model with the satellite data at the microwave frequencies of 1.4, 6.8, 18, 21, and 37 GHz.

The rest of the paper is organized into sections. In Section 2, the effective permittivity of the Gaussian rough interface is obtained based on EMT. In the same section, the emissivity model of rough surfaces is discussed by tuning the roughness parameters. In Section 3, we estimate the excess emissivity and the brightness temperature increment of the wind-enhanced sea surface by applying the emissivity model. The model results are also discussed. Finally, Section 4 gives a brief conclusion.

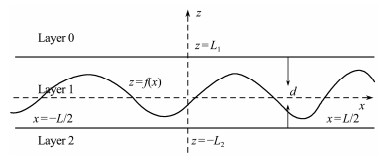
2 Emissivity of Rough Surface: EMT 2.1 Effective Permittivity of Rough Interface

We assume that the roughness of the sea surface is isotropic, and the effect of wind direction on the roughness can be neglected. Thus, the 1D rough surface is suitable for investigating the sea surface emissivity. Here, the 1D randomly rough sea surface height at a point x (see Fig.1) is defined by z = f(x), where f(x) is from a set of Gaussian stationary function {f(x)}. We determine the physical properties of the random system by averaging over the function set {f(x)}. This Gaussian function {f(x)} satisfies the following:

$ \left\langle {f(x)} \right\rangle = 0, $

(1)

$ \left\langle {f(x)f(x')} \right\rangle = {\sigma ^2}{\text{exp}}\left({ - \frac{{{{\left| {x - x'} \right|}^2}}}{{{a^2}}}} \right), $

(2)

where $ \left\langle {} \right\rangle $ denotes an average over {f(x)}, σ is the RMSD of sea surface height (i.e., from a flat surface), and a is the correlation length of the rough surface. Higher-order correlation functions of Gaussian surface roughness have been presented in McGurn et al. (2004).

Next, we consider a system of two parallel plates, as shown in Fig.1 (i.e., Layer 1), to determine the effective permittivity of a rough surface with EMT. As indicated in the figure, L₁ ≥ maxf(x) and L₂ ≥ −minf(x) for −L/2 < x < L/2, and L is very large compared to the sea surface wavelength. Between the two parallel plates, the permittivities of air and seawater are respectively denoted by ε₁ for f(x) < z ≤ L₁ and ε₂ for −L₂ ≤ z < f(x) (Klein and Swift, 1977). If an external electric field E₀ is applied to the two parallel plates along the x-direction, the electric fields and the potentials of the system can be derived with perturbation method in the quasistatic limit (McGurn et al., 2004). If the surface height f(x) is a small parameter compared to the surface wave wavelength, the effective permittivity ε_e of the effective medium between the two parallel plates is given by the first order electrical potential. Following Eq. (70) of McGurn et al. (2004), the effective dielectric constant ε_e between the two plates is given by

$ \begin{aligned} & -\varepsilon_e \frac{\phi_0}{L}=-\frac{L_1 \varepsilon_1+L_2 \varepsilon_2}{L_1+L_2} \frac{\phi_0}{L} \\ & +\frac{\phi_0}{L} \frac{4}{L_1+L_2} \frac{\left(\varepsilon_2-\varepsilon_1\right)^2}{\varepsilon_1+\varepsilon_2} \frac{\pi a \sqrt{\pi} \sigma^2}{L^2} \sum\limits_{n=0}^{\infty} n \exp \left[-\left(\frac{\pi n a}{L}\right)^2\right], \end{aligned} $

(3)

where ϕ₀ is the applied external electric potential, and the external electric field E₀ = −ϕ₀/L. Given that

$ \sum\limits_{n = 0}^\infty {n\exp \left[ { - {{\left({\frac{{{\text{π }}na}}{L}} \right)}^2}} \right]} = \frac{{{L^2}}}{{2{{\text{π }}^2}{a^2}}}, $

we now have

$ {\varepsilon _{\text{e}}} = \frac{{{L_1}{\varepsilon _1} + {L_2}{\varepsilon _2}}}{{{L_1} + {L_2}}} - \frac{2}{{{L_1} + {L_2}}}\frac{{{{({\varepsilon _2} - {\varepsilon _1})}^2}}}{{{\varepsilon _1} + {\varepsilon _2}}}\frac{{{\sigma ^2}}}{{a\sqrt {\text{π }} }}, $

(4)

where L₁ and L₂ are the parameters of the parallel plate system. Clearly, if L₁ → ∞ (or L₂ → ∞), ε_e = ε₁ (or ε_e = ε₂). This formula indicates that the RMSD σ and the correlation length a of the rough surface will give rise to the important effects of the rough interface on the effective permittivity, i.e., the effective permittivity is neither the dielectric constant of seawater nor that of air. Eq. (4) is valid for σ/a < 1. Furthermore, because of the zero-mean value of random surface height, it is possible to simplify Eq. (4). In this case, to ensure that all random wave heights between the two plates (see Fig.1) are included, we take the identical scale amplitudes crossing the x-axis (or the flat surface), i.e., L₁ = L₂ = d/2, where d is the maximum height of random waves. Then, Eq. (4) can be expressed as

$ {\varepsilon _{\text{e}}} = \frac{{{\varepsilon _1} + {\varepsilon _2}}}{2} - \frac{{2{{({\varepsilon _2} - {\varepsilon _1})}^2}}}{{{\varepsilon _1} + {\varepsilon _2}}}\frac{{{\sigma ^2}}}{{ad\sqrt {\text{π }} }} . $

(5)

Next, we will use Eq. (5) to investigate the emissivity of the rough sea surface.

2.2 Emissivity Model of Rough Surface

Given that the effective permittivity ε_e of the rough interface is determined by Eq. (5), the emissivity of a three-layer medium system having flat interfaces (see Fig.1) can be estimated by two theoretical methods. The three layers consist of the top layer constituting air (Layer 0), the bottom layer constituting seawater (Layer 2), and the middle layer constituting the rough interface (Layer 1). Meanwhile, the two methods are the incoherent approach of microwave radiative transfer theory and the wave approach method (Tsang et al., 2000). The wave approach method is adopted in the current study to calculate the emissivity $ e_{\text{p}}^{\text{r}} $ of the randomly rough surface. The emissivity formula of the two-layer model is given by

$ e_{\text{p}}^{\text{r}}(\theta) = 1 - {\left| {{R_{\text{p}}}(\theta)} \right|^2}, $

(6)

where the reflection coefficient R_p (p = V, H polarization) of the two layers of flat media is expressed as follows:

$ {R_{\text{p}}}(\theta) = \frac{{R_{\text{p}}^{01}(\theta) + R_{\text{p}}^{12}(\theta)\exp (i2h{k_{1{\text{z}}}})}}{{1 + R_{\text{p}}^{01}(\theta)R_{\text{p}}^{12}(\theta)\exp (i2h{k_{1z}})}} . $

(7)

In Eq. (7), $ R_{\text{p}}^{nm} $ denotes the Fresnel reflection coefficients from Layer n to Layer m and the incidence angle θ; $ {k_{1{\text{z}}}} = {k_0}\sqrt {{\varepsilon _{\text{e}}} - {{\sin }^2}\theta } $ with the microwave wave number k₀ of free space and the effective permittivity ε_e of Eq. (5); and h denotes the effective thickness of rough interface, which can induce important effects on the microwave radiation (this can be determined by the statistical amplitude of random surface waves). Finally, the excess emissivity ∆e_p (or the brightness temperature increment ∆e_p SST) induced by the rough surface can be calculated using Eq. (8):

$ \Delta {e_{\text{p}}} = e_{\text{p}}^{\text{r}} - e_{\text{p}}^0, $

(8)

where $ e_{\text{p}}^0 $ notes the emissivity of the flat sea surface.

We numerically discuss the emissivity of rough sea surfaces by selecting the parameters of the model in Eqs. (5) and (6) based on the statistical properties of the ocean waves. For example, the correlation length a of a sinusoidal wave is about 0.2λ_sea, i.e., a = 0.2λ_sea, where λ_sea is the wavelength of sea waves. Given that the maximum wave steepness of a random sea surface wave is less than about 0.142, the parameter d of the random wave height is not larger than 0.142λ_sea. Without losing generality, we let d = 0.142λ_sea, and the effective thickness h of the Layer 1 is about 2σ, i.e., h = 2σ, because the RMSD σ stands for the scale of statistical amplitudes of random surface waves. Here, we note that the sea surface wavelength is not larger than the microwave wavelength λ_mic according to EMT. Thus, we set λ_sea = λ_mic. Next, we use the above parameters to model the emissivity of satellite measurements.

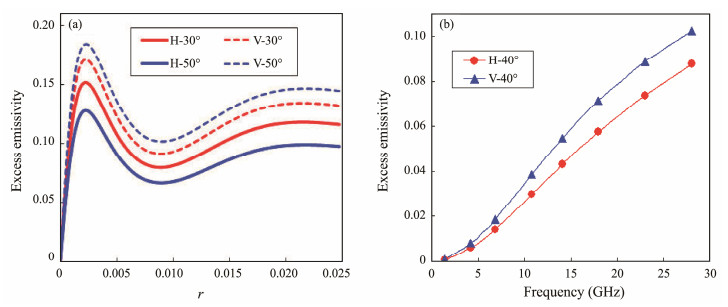
As an example, in Fig.2(a), we calculated the excess emissivity of capillary gravity waves of the wavelength 7 cm changing with the roughness parameter r = σ²/ad at a microwave frequency of 4.2 GHz for the horizontal and vertical polarizations with incidence angles 30˚ and 50˚, respectively. This indicates that, if the parameter r is less than a critical value of 0.0022, the excess emissivity increases with the parameter r (or RMSD) increase, which is related to the effective thickness and the microwave radiation frequency of the rough interface. The RMSD corresponding to the maximum excess emissivity is about 0.021λ_sea. According to Tsang et al. (2000), the fluctuation characteristic is due to the phase coherent of the effective thickness (i.e., h = 2σ) of rough interfaces. This interface coherent vanishes when the RMSD σ is large.

Fig.2(b) shows the excess emissivity of the capillary waves varying with the microwave frequency with incidence angle 40˚ if the sea surface consists of the capillary waves with a wavelength of 1.05 cm (i.e., about 28 GHz). As can be clearly seen, the excess emissivity increases with the microwave frequency increase owing to the microwave radiation resonance of the capillary gravity waves. This implies that the large excess emissivity of a rough sea surface should appear at the sea wave wavelength that matches the radiation wavelength.

3 Application and Discussion of the Emissivity Model

The emissivity model presented in Section 2 is used to estimate the excess emissivity of the rough sea surface. We compare the model results with the satellite measurement data in order to perform the validity of our model. This is achieved by fitting the RMSD as a nonlinear function of wind speed when the cost function $ \chi _{\text{p}}^2 $ (9) becomes minimum

$ \chi _{\text{p}}^2 = \sum\limits_{i = 1}^n {{{[\Delta {e_{\text{p}}}(\sigma ({u_i})) - \Delta {e_{{\text{s, p}}}}({u_i})]}^{\text{2}}}}, $

(9)

where ∆e_p denotes the excess emissivity model, ∆e_{s, p} denotes the data of excess emissivity, and u_i refers to wind speed.

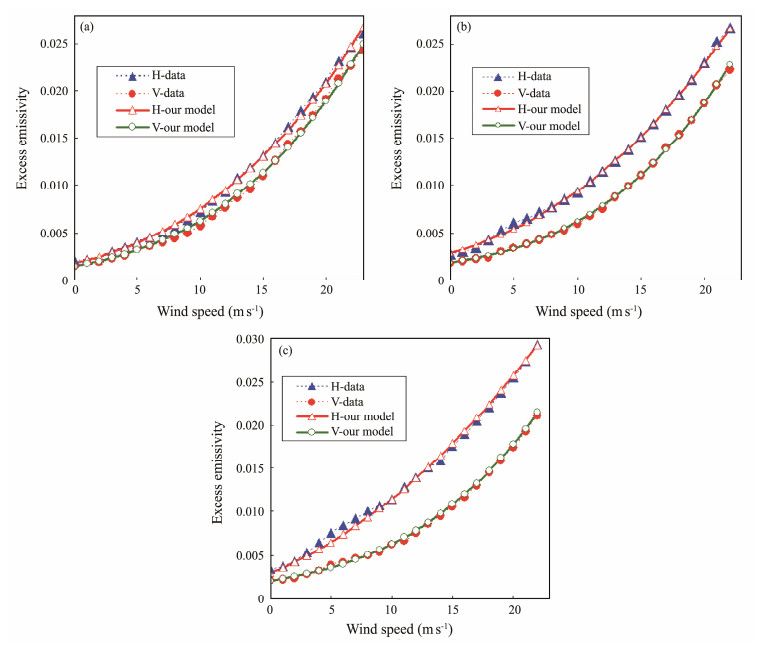
Yueh et al. (2013) used the Aquarius satellite data changing with the wind vector at L-band, i.e., 1.4 GHz for three incidence angles 29˚, 38˚, and 46˚ to derive the excess emissivity of the sea surface. Using the global total electron content product in the IONosphere map Exchange format and the International Geomagnetic Reference Field, they obtained the sea surface emissivity data from Aquarius Level-2 data files and corrected the effect of Faraday rotation angle. The dependence of excess surface emissivity on wind speed and direction was characterized with SSM/I F17 wind field, and the excess surface emissivities changing with SSM/I wind field were listed in Fig.5 in Yueh et al. (2013), who presented the isotropic components of excess surface emissivity (i.e., without wind direction) at the top row of the figure. Notably, the isotropic components of the excess surface emissivity, which are independent of wind direction, are used to validate our model, together with SSM/I wind speed, because our emissivity model is derived under the assumption of an isotropic rough surface. In Fig.3, we obtained the excellent results of the excess emissivity model compared to the isotropic excess emissivity data of microwave frequency 1.4 GHz by fitting the RMSD as a function of SSM/I wind speed u via the least squares method. The respective coefficients c_i (i = 0, 1, 2) of RMSD σ = c₀ + c₁u + c₂u² are given in Table 1 for the horizontal and vertical polarization. The results show that we were able to determine the nonlinear response of RMSD to the wind speed, which is similar to the sea wave slope as a function of wind speed (Cox and Munk, 1954; Wilheit, 1979). Fig.3 presents the root mean square error (RMSE) of the model and the observed excess emissivity values.

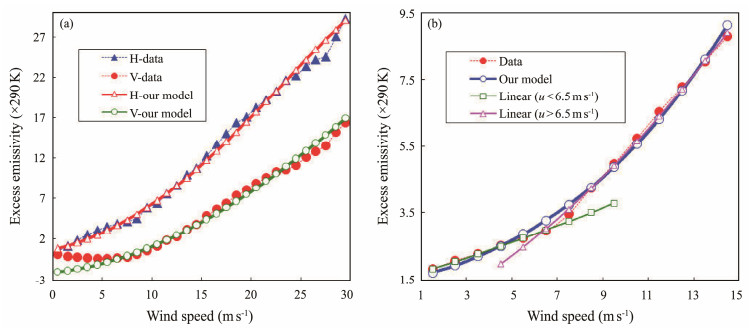
For the wind-induced ocean surface, Meissner and Wentz (2012) derived the brightness temperature increments varying with wind speed from the WindSat brightness temperature measurements for 6.8 GHz at an incidence angle of 53.8˚; they also obtained the TOPEX/Poseidon brightness temperatures for 18 GHz at a zenith angle after correcting the effects of the atmospheric path (Tran et al., 2002). These brightness temperature increments of sea surface are given in Fig.3 and Fig. 7 in Meissner and Wentz (2012) and are matched with the WindSat wind speed for 6.8 GHz and QuikSCAT wind speed for 18 GHz, respectively.

Next, we validate our emissivity model with these satellite data sets. As shown in Fig.4, we fitted the data of the brightness temperature increments with our excess emissivity model by tuning the RMSD as a function of wind speed (the coefficients of RMSD are listed in Table 1). The RMSEs of the calculated and observed excess brightness temperatures are shown in Fig.4. Generally, good agreements were obtained when we compared our model results with the satellite data. For the vertical polarization of 6.8 GHz, the incidence angle of the model decreases by about 0.9˚, which may be attributed to the slope effects of the large-scale waves on the vertical polarization. Furthermore, we used the theoretical model to estimate the respective emissivities for the low and high wind speeds. In Fig.4(b), we have modeled the brightness temperature increments of 18 GHz by fitting the RMSD as two linear functions (i.e., σ = 2.613 × 10⁻⁵ + 6.861 × 10⁻⁶u and σ = 5.025 × 10⁻⁵ + 3.081 × 10⁻⁶u, respectively) for the corresponding wind speeds of u ≥ 6.5 m s⁻¹ and u < 6.5 m s⁻¹. The results show that our model can well-simulate the emission of the sea surface with two stages of wind speed, namely, the coupling effect of surface roughness and sea foam under high wind speed and the effect of roughness for the low wind speed. This finding indicates that the radiation mechanism of the rough sea surface is different under low and high wind speeds due to the effect of sea foam.

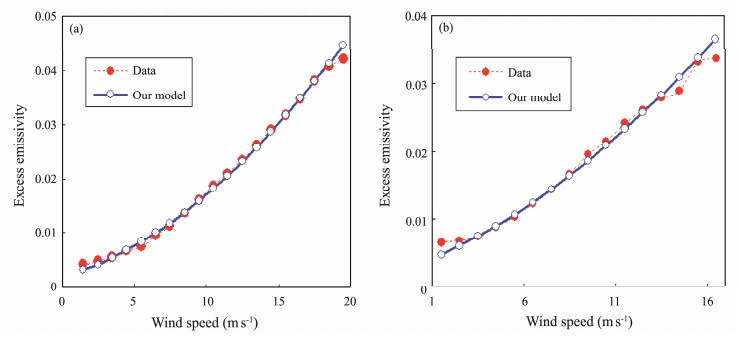
Furthermore, Tran et al. (2002) collocated the corresponding wind-induced excess emissivity values at a zenith incidence angle varying with SeaWinds wind speed (QuikSCAT satellite) from TOPEX/Poseidon brightness temperatures at 21 and 37 GHz. As shown in Fig.3 in the paper of Tran et al. (2002), the excess emissivities were averaged for each TOPEX/Poseidon microwave radiometer channel against SeaWinds wind speed using 1 m s⁻¹ bins. The nadir observations essentially eliminate a majority of surface roughness effects and leave the effects of sea foams (Wilheit, 1979). We used our model to estimate the above-mentioned excess emissivities of the sea surfaces at high microwave frequencies, and the results are shown in Fig.5. The RMSEs of the model-predicted and observed excess emissivities are also listed under Fig.5, while the coefficients of RMSD as a function of the wind speed are listed in Table 1. Good agreements imply the contributions of sea foam and capillary waves to the emissivity increase with wind speed. Furthermore, the effect of sea whitecap (or sea foam) is also important in increasing the emissivity of sea surface if the wind speed is larger than 7 m s⁻¹ (Anguelova and Gaiser, 2013; Wei, 2013). The results of our model also include the effects of whitecaps (or sea foam) even though the emission mechanism of pure rough surface is different from that of sea foam.

4 Conclusions

In this paper, we proposed a theoretical emissivity model of a 1D rough sea surface, and the emissivity of a rough sea surface is investigated with the EMT of the rough interface. In this model, the effective permittivity of the rough interface is determined by the correlation length of the rough surface and the RMSD of the rough surface height. Good agreements are obtained by comparing the model results with the satellite data. The results also show that the proposed method is valuable in calculating the emissivity of the wind-roughened ocean surface, especially when the RMSD is fitted as a function of wind speed. Furthermore, the functions of RMSD at microwave frequencies imply that the wind-induced sea surface includes the sea waves of various microwave scales even if the contributions of various small-scales waves are different from the microwave emissivity. For a high wind speed, numerous gravity-capillary waves and sea foams produced by the wave breaking can enhance the sea surface emissivities. Our model also performs well in terms of involving the effects of wave breaking (or sea foam) on the emissivity of the sea surface at a high wind speed.

The advantage of using our model is that we have provided a theoretical method with which to disclose the radiation mechanism of rough sea surfaces, although some empirical models are valuable for simulating the emissivity of the rough sea surface. Based on the emissivity formula of the EMT model, we can clearly see how the parameters of roughness (e.g., correlation length of rough surface, RMSD, effective thickness of rough interface, and maximum height of random waves) interact in the emissivity of rough surfaces. Moreover, our proposed method can be extended to retrieve the RMSD and the correlation length of the rough surface by tuning the model parameters. Finally, the emissivity of the foam layer can also be determined by our proposed model because sea foam arises as a mixture of air and water at high wind speeds.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 41676169), and the National Key R & D Program of China (No. 2016YFC1401006).