2) Laboratory for Marine Mineral Resource, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China;
3) CNOOC EnerTech-Drilling & Production Co., Data Processing Co., Zhanjiang 524057, China;
4) Key Laboratory of Submarine Geosciences and Prospecting Techniques, Ministry of Education, Qingdao 266100, China;
5) College of Marine Geo-sciences, Ocean University of China, Qingdao 266100, China;
6) National Deep Sea Center, Qingdao 266100, China
Multiples in seismic data can be generally classified into surface-related and internal types. Compared with internal multiples, surface-related multiples have obvious periodicity or apparent velocity difference. Many studies have been conducted on identifying and eliminating surface-related multiples, thereby enabling the development of feasible methods or techniques (Verschuur et al., 1992; Berkhout and Verschuur, 1997; Verschuur and Berkhout, 1997). The formation of internal multiples depends on underground geological structures. When many strong wave impedance interfaces exist under the ground, high amplitude internal multiples appear in seismic data and their velocity is generally close to that of the primary waves. Therefore, internal multiples are easily imaged, and this condition affects subsequent geological interpretation. However, the periodicity or apparent velocity difference of the internal multiples and primary waves is not obvious because underground geological interfaces that generate these multiples are typically more variable than the sea or earth's surface. Thus, these multiples and waves are difficult to identify and eliminate.
Not until the 1980s did geophysicists begin to conduct in-depth studies on internal multiples and formulated methods for prediction and attenuation. Carvalho et al. (1991) first proposed the method of attenuating internal multiples based on scattering theory. Subsequently, Carvalho et al. (1992) and Weglein et al. (1997) presented the concept of inverse scattering series and adopted the point scattering model to predict surface-related and internal multiples. According to the results of model experiments, inverse scattering series method is superior to other multiple prediction methods but is computationally intensive and costly. Therefore, this method is not yet suitable for direct application of internal multiple prediction in 2D field data. Berkhout (1982) proposed an extended surface-related multiple elimination (SRME) method for internal multiple attenuation, which extrapolates all sources and receivers to the reflecting interface that generates downward internal multiples using datum reconstruction with full wavefield; the interface then becomes a new 'surface' so that the internal multiple can be predicted and attenuated based on SRME (Verschuur et al., 1992; Berkhout and Verschuur, 1997). Berkhout and Verschuur (1997) realized only extrapolating the downward propagation part of internal multiple reflections to the interface that generates internal multiples, and then use common focus point (CPF) gathers instead of shot gathers of SRME, thereby forming a model-based extended SRME method (Berkhout and Verschuur, 2005). However, building an accurate model for field seismic data that do not eliminate multiples is extremely difficult. Jakubowicz (1998) considered that in redatuming of the sources and receivers, two inverse-propagating operators can be generated by inverse time processing of the primary event of the target interface, and the prediction process of internal multiples is decom-posed as the convolution of three reflected wavefields; Jakubowicz (1998) further proposed a data-driven extended SRME method, which avoids the establishment of an accurate seismic model but introduces additional difficult steps such as primary wave extraction of the target interface and seismic data muting. New internal multiple prediction theories and methods have also been developed, such as those based on seismic interferometry (Meles et al., 2014), suppressing internal multiples using wavepath migration (Liu et al., 2008), and suppressing internal multiples by constructing virtual events (Wu et al., 2013).
To predict internal multiples efficiently, this study proposes an internal multiple prediction method that combines imaging profile prediction and Kirchhoff demigration. The method initially predicts the prestack time migration profile, which includes the internal multiples only by inverse scattering series method based on a prestack time migration profile. Then, the method creates internal-multiple shot gathers via velocity-weighted Kirchhoff demigration. Internal multiple prediction based on the prestack time migration profile effectively reduces the computational cost. Furthermore, the internal-multiple shot records created by Kirchhoff demigration substantially reduces the complexity of the practical problem and promotes the internal multiple prediction to be applied to field data processing. Synthetic and field data tests show that the method can effectively predict the internal multiples and has considerable potential in field application, particularly in areas where internal multiples develop seriously.
2 Internal Multiple Prediction in Imaging Profile Domain by Inverse Scattering Series MethodMultiple attenuation should be applied to prestack seismic data of shot gather or common midpoint (CMP) gather to avoid primary damage of multiple subtraction in imaging profile and improve the accuracy of the prestack processing, such as migration velocity analysis, velocity inversion, and amplitude variation with offset inversion. Theoretically, the internal multiple prediction method based on the inverse scattering series method is the most accurate, but it leads to extensive calculations of 2D internal multiple prediction performed on shot or CMP gather. This situation causes difficulty in the internal multiple prediction of field seismic data. Therefore, the present study proposes an internal multiple prediction method that combines imaging profile prediction and Kirchhoff demigration. This method is based on the conventional prestack time migration profile and predicts the prestack time migration profile that only contains internal multiples using 1D inverse scattering series method. Then, this method obtains internal multiple shot records based on Kirchhoff demigration. Thus, the method avoids large computational problems of internal multiple prediction in the shotgather or CMP domain.
For conventional prestack time migration using primary velocity field, the primary wave can be well-imaged. Besides, the internal multiple is a kind of multiple reflection that occurs in the deep high-velocity layer. It can still be imaged well because its velocity is close to the primary velocity, which provides a requirement for internal multiple prediction based on the inverse scattering series. The inverse scattering series uses a point scattering model to predict internal multiples, and its input is unstacked migration result of the prestack f-k migration based on the constant velocity model. As this paper discusses internal multiple prediction based on prestack time migration profile, the single-trace data in the profile can be used independently as the input to the inverse scattering series. Therefore, internal multiple predictions can be performed via 1D inverse scattering series. In single-trace prediction mode, the prestack FK migration can be realized by 'time-depth conversion' based on the constant velocity model. In the case of 2D seismic observations, the conversion result of single trace in the profile can be expressed as
| $ b_{1}(x, z)=I M\left(x, t=\frac{2 z}{C}\right), $ | (1) |
where IM represents the prestack time migration profile, b1(x, z) denotes the input wavefield of the internal multiple prediction, C refers to constant velocity, and z refers to depth.
Adding b1(x, z) to 1D internal multiple prediction equation (Weglein et al., 1997) can obtain the following internal multiple prediction result in wave-number domain:
| $ b_{3}\left(x, k_{z}\right)=\int_{-\infty}^{\infty} \mathrm{d} z_{1}^{\prime} e^{i k_{z} z_{1}^{\prime}} b_{1}\left(x, z_{1}^{\prime}\right) \int_{-\infty}^{z_{1}^{\prime}-\varepsilon} \mathrm{d} z_{2}^{\prime} e^{-i k_{z} z_{2}^{\prime}} b_{1}\left(x, z_{2}^{\prime}\right) \int_{z_{2}^{\prime}+ \varepsilon}^{\infty}\\ \mathrm{d} z_{3}^{\prime} e^{i k_{z} z_{3}^{\prime}} b_{1}\left(x, z_{3}^{\prime}\right), $ | (2) |
where
| $ b_{3}(x, z)=\frac{1}{2 \pi} \int_{-\infty}^{+\infty} b_{3}\left(x, k_{z}\right) e^{j k z} \mathrm{d} k. $ | (3) |
When the 'depth-time conversion' can be performed based on the constant velocity model, the final internal multiple profile can be expressed as
| $ I M_{m}(x, t)=b_{3}\left(x, z=\frac{C t}{2}\right). $ | (4) |
After the prediction process of the inverse scattering series method, the primary in the input profile IM(x, t) forms the first-order internal multiple in the profile IMm(x, t), and the internal multiple (i.e., the multiple that is difficult to eliminate by conventional suppression method) whose velocity is close to the primary becomes the next-order internal multiple. Thus, the output IMm(x, t) is the prestack time migration profile that only includes the internal multiple.
In the case where the subsurface reflection interface is relatively flat, if the imaging velocity of the internal multiple is not much different from the velocity of the primary wave, then the profile IMm(x, t) would be equivalent to the imaging result of the internal multiples based on their own velocity.
3 Generation of Internal-Multiple-Shot Gather Based on Kirchhoff DemigrationIn field data processing, many problems occur in multiple adaptive subtraction based on migration profile. This condition not only limits the application effect of the multiple matching attenuation but also causes serious damage to the primary events, so the final internal multiple matching attenuation also needs to be performed on the prestack seismic data. For this reason, this paper proposes velocity-weighted Kirchhoff demigration in time domain, which generates internal-multiple shot gathers based on internal-multiple profile.
3.1 Time Kirchhoff Migration and DemigrationKirchhoff migration is the most commonly used imaging method in seismic data processing. This method, when used with the velocity model (velocity field), can generate a seismic profile using prestack data. According to the conclusions of Bleistein (1987), Schleicher et al. (1997), and Santos et al. (2000), the Kirchhoff migration can be expressed as the following equation:
| $ I M(P)=-\left.\frac{1}{2 \pi} \iint d s W_{M}(\xi, P) \frac{\partial D(\xi, t)}{\partial t}\right|_{t=\tau(\xi, P)}, $ | (5) |
where IM (P) denotes the migration profile; P is point with coordinates (x, z) in depth or (x, t) in time; ξ refers to the coordinates of a source-receiver pair (S, G); S and G are source and receiver positions, respectively; WM(ξ, P) is the weight function of the Kirchhoff migration; D(ξ, t) is the prestack seismic record; ds denotes an integral panel; and τ is the travel time from S to P to G.
To achieve high-resolution velocity-weighted factor cal-culation and Kirchhoff demigration, this paper focuses on the Kirchhoff prestack time migration in the shot-gather domain. The source-receiver pair ξ in Eq. (5) is replaced with shot records, and the migration result is a single trace of imaging gather data expressed as follows:
| $ I G(i, P)=-\left.\frac{1}{2 \pi} \sum\limits_{j=1}^{J} \iint d s W_{M}\left(S_{i}, G_{j}, P\right) \frac{\partial d_{i}(j, t)}{\partial t}\right|_{t=\tau\left(S_{i}, G_{j}, P\right)}, $ | (6) |
where the new source-receiver pair (Si, Gj) replaces ξ in Eq. (5); IG (i, P) represents a single trace of the imaging gather, which is the migration result of the shot record di of number i, and i and j are shot number and trace number, respectively.
The Kirchhoff prestack time migration conducts the ray tracing with straight-ray approximation (see Fig. 1); thus, the weight function WM(Si, Gj, P) and travel time τ(Si, Gj) in Eq. (6) are simplified considerably and can be expressed as
| $ \left\{\begin{aligned} W_{M}\left(S_{i}, G_{j}, P\right) &=\frac{\cos \theta}{v(P) r_{0} r} \\ \tau\left(S_{i}, G_{j}, P\right) &=\frac{r_{0}+r}{v(P)} \end{aligned}\right., $ | (7) |
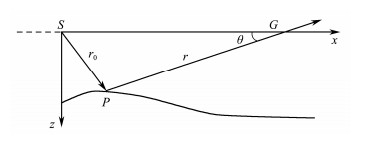
|
Fig. 1 Schematic of geometric relation in 2D prestack time migration. |
where v(P) is the migration velocity of the primary wave, cosθ is the obliquity factor, r0 is the distance from the source position to the imaging point, and r is the distance from the imaging point to the receiver position.
Santos et al. (2000) considered that the integration process of Kirchhoff demigration is similar to that of Kirchhoff migration, and they presented the following integral equation of Kirchhoff demigration:
| $ I D(\xi, t)=\left.\frac{1}{2 \pi} \iint d s W_{D}(P, \xi) \frac{\partial I M(P)}{\partial z}\right|_{\tau=t(P, \xi)}, $ | (8) |
where ID(ξ, t) represents the shot-gather record, WD(P, ξ) is the weight function of the Kirchhoff demigration, and IM (P) denotes depth migration profile.
The depth migration profile IM (P) in Eq. (8) can be replaced with the prestack time migration profile, where the derivative of the migration profile to depth z should be modified to be the derivative of that to traveling time τ. Therefore, the Kirchhoff demigration in time domain can be expressed as
| $ I D(\xi, t)=\left.\frac{1}{2 \pi} \iint d s W_{D}(P, \xi) \frac{\partial \operatorname{IM}(P)}{\partial \tau}\right|_{\tau=t(P, \xi)}. $ | (9) |
Theoretically, the shot records can be generated based on the input seismic section through Eq. (9) when the migration velocity model (velocity field) is given, and this process can be regarded as the 'reverse process' of migration imaging. However, the weight function WD(P, ξ) in the demigration process is different from that in the prestack time migration, and it should be calculated using a more precise Kirchhoff diffraction stack (see Fig. 2) as follows:
| $ W_{D}(P, \xi)=\frac{\cos \theta_{0}+\cos \theta}{v(P) r r_{0}}, $ | (10) |
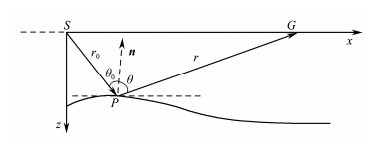
|
Fig. 2 Schematic of geometric relation in 2D Kirchhoff demigration. |
where r0 and r are the propagation distance of the incident ray and diffracted ray, θ0 is the angle between the incident ray r0 and normal vector n of reflector, and θ is the angle between the diffracted ray r and normal vector n of the reflector.
The travel time τ Eq. (9) is still calculated from ray tracing with straight-ray approximation, which can be expressed as
| $ t(P, \xi)=\frac{r_{0}+r}{v(P)}. $ | (11) |
Generating an internal-multiple shot gathers based on the internal multiple profile only by applying Eq. (9) is a difficult task. The reason is that the existing multi-velocity of internal multiples at any given time causes difficulty in recognizing and digitizing these internal multiple velocities via migration velocity analysis. To reconstruct the internal multiple events in the profile IMm(P) according to their exact velocities, the velocity-weighted factor of multiples must first be calculated and introduced into the time-domain Kirchhoff demigration. Then, the internal-multiple shot records is created through Kirchhoff demigration based on velocity amplitude weighting.
For each point P in the time migration profile, the initial migration velocity v0 and velocity interval Δv are varied with the coordinates, and a series of scanning velocities vk(P) should be
| $ v_{k}(P)=v_{0}(P)+k \Delta v(P), $ | (12) |
where 0 ≤ k ≤ K, K is the maximum number of scanning velocities.
Essentially, the velocity-weighted factor is the migration result of a series of scanning velocities. Based on the scanning velocity sequence defined in Eq. (12), Kirchhoff prestack time migration according to Eq. (6) is performed with single-shot-gather record di(j, t) as follows:
| $ I G_{k}(i, P)=-\left.\frac{1}{2 \pi} \sum\limits_{j=1}^{J} \iint d s W_{M}\left(v_{k}, S_{i}, G_{j}, P\right) \frac{\partial d_{i}(j, t)}{\partial t}\right|_{t=\tau\left(v_{k}, S_{i}, G_{j}, P\right)}, $ | (13) |
where IGk is imaging gather with given velocity vk, and weight function WM(vk, Si, Gj, P) and travel time τ(vk, Si, Gj, P) both depend on velocity vk(P), which are expressed as
| $ \left\{\begin{aligned} W_{M}\left(v_{k}, S_{i}, G_{j}, P\right) &=\frac{\cos \theta}{v_{k}(P) r_{0} r} \\ \tau\left(v_{k}, S_{i}, G_{j}, P\right) &=\frac{r_{0}+r}{v_{k}(P)} \end{aligned}\right.. $ | (14) |
Eqs. (13) and (14) provide the migration result with a single shot gather based on the scanning velocity, which has lower velocity resolution, and can seriously affect the constructed accuracy of internal multiple events. Tan et al. (2017) proposed a method for creating a high-resolution stacking velocity spectrum, in which the semblance weigh-ting process (Stoffa et al., 1981) can be introduced into the calculation of the velocity-weighted factor. The formula of the semblance-weighted factor for the imaging gather is
| $ {S_k}(P) = \frac{{\sum\limits_l {{{\left[ {\sum\limits_{i = 1}^I I {G_k}(i, P)} \right]}^\lambda }} }}{{\left({\sum\limits_l {\left[ {\sum\limits_{i = 1}^I {\left| {IG_k^\lambda (i, P)} \right|} } \right]} + \zeta } \right)}}, $ | (15) |
where λ (λ ≥ 2) indicates the order number that determines the resolution of the semblance-weighted factor Sk(P); l is the length of the time window; and ζ is the constant to ensure that the denominator is not equal to zero, generally taking the average amplitude of 0.001–0.01.
For the imaging gather that corresponds to each scanning velocity vk, the data of all the traces are stacked horizontally based on time τ and taken as an absolute value to obtain the velocity-weighted factor. Subsequently, the preceding results are weighted using the semblance factors obtained in Eq. (15). The process can be expressed as
| $ A_{k}(P)=S_{k}(P)\left|\sum\limits_{i=1}^{I} I G_{k}(i, P)\right|, $ | (16) |
where Ak(P) is a high-resolution velocity-weighted factor.
Based on the series of scanning velocities vk(P) defined in Eq. (12), the velocity-weighted factor Ak(P) calculated by Eq. (16) is introduced, and the Kirchhoff demigration is performed using Eqs. (9) and (11). The result is
| $ I D_{m}(k, \xi, t)=\frac{1}{2 \pi} \iint d s W_{D}\left(v_{k}, P, \xi\right) A_{k}(P) \frac{\partial I M_{m}(P)}{\partial t}. $ | (17) |
The demigration results of all scanning velocities are summed together to obtain the final internal multiple shotgather record, which is expressed as
| $ I D_{m}(\xi, t)=\sum\limits_{k=1}^{K} I D_{m}(k, \xi, t). $ | (18) |
The internal-multiple prediction method used in this study consists of two major steps. First, this method predicts the prestack time migration profile that only includes the internal multiples by inverse scattering series method based on a prestack time migration profile. Second, this method applies velocity-weighted Kirchhoff demigration to create the internal multiple shot gathers with the multiple profile. The flow chart of the internal multiple prediction process is presented in Fig. 3.
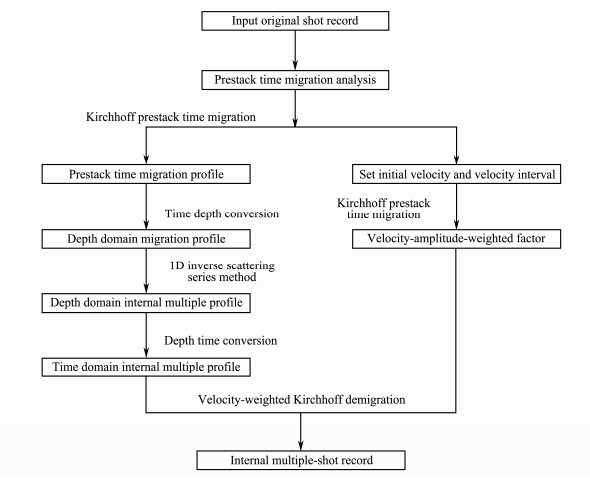
|
Fig. 3 Flow chart of internal multiple prediction process. |
The seismic data containing internal multiples are simulated based on marine-towed streamer acquisition mode. The sources and receivers are located on the sea surface (at 0 depth). A total of 200 shot gathers are in the simulated seismic record and 118 traces are in each shot gather; the shot and trace intervals are 50 m and 25 m, respectively; and the minimum offset is 25 m. For each trace data, the sampling interval is 4 ms and the maximum time reaches 5116 ms.
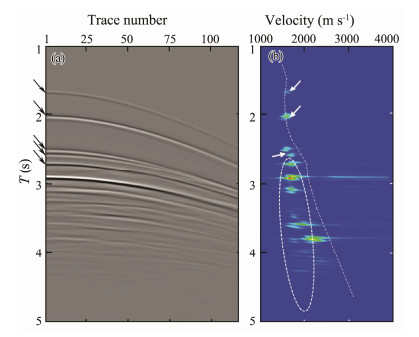
Spherical diffusion compensation processing (Yilmaz, 2001) is performed to enhance the amplitude of weak events in the deep part of the shot records. The 110th shot record of the modeling data is shown in Fig. 4a, where the arrows point to the internal multiple events that are easy to identify and whose amplitudes are weaker than those of the primary events in the same time period. In the medium-deep part of the record, the internal multiple events are mixed with the primary events. A prestack time migration velocity spectrum is generated (as shown in Fig. 4b) to analyze the velocity characteristic of the internal multiples. The velocity-time curve of the primary wave is digitized in the velocity spectrum (as shown by the dotted white line in Fig. 4b). Furthermore, the energy in the dotted ellipse region of the spectrum is multiple energy, and the velocity of the internal multiples indicated by the arrow is close to or even larger than that of the primary wave.
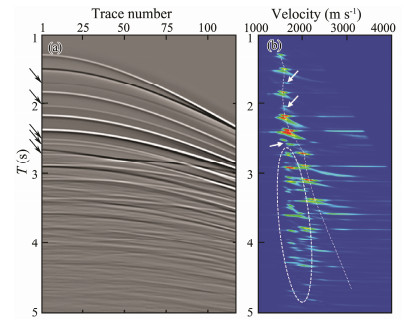
|
Fig. 4 Analysis of internal multiple characteristics in numerical record: (a) example of original shot-gather record (110th shot) and (b) example of migration velocity spectra (x = 8250 m). |
The inverse scattering series method is used to implement the internal multiple prediction for the original prestack time migration profile (as shown in Fig. 5) based on the primary velocity. The result profile of the internal multiples is shown in Fig. 6. A comparison shows that the multiple profile contains abundant internal multiples, and the travel time of the multiple events is basically the same as that in the original profile.
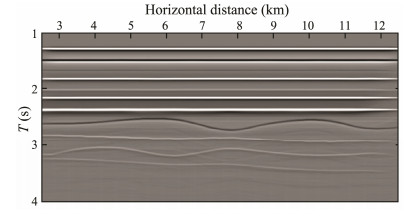
|
Fig. 5 Time migration profile based on primary velocity. |
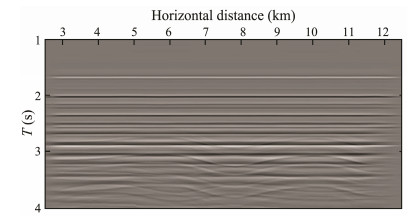
|
Fig. 6 Time migration profile only including internal multiples predicted by inverse scattering series method. |
The picked primary velocity (shown by the dashed white line in Fig. 4b) is used as the criterion for the velocity scanning in the low-velocity direction, and the semblance-weighted processing is performed on the migration results for each velocity. During velocity scanning, the velocity interval Δv changes linearly with time t. The value of the velocity interval is defined as
| $ \Delta v=\left\{\begin{array}{cc}{25} & {t <1} \\ {25+12.5(t-1)} & {1 \leq t \leq 3} \\ {50} & {t>3}\end{array}\right., $ | (19) |
where the unit of velocity interval Δv is m s-1 and the unit of travel time t is s.
The spectra of the velocity-weighted factor are generated using Eq. (16), as shown in Fig. 7. The horizontal coordinate of each spectrum is between 6 km and 8 km in the migration profile (see Fig. 5), and the velocity scanning number is from 1 to 20.
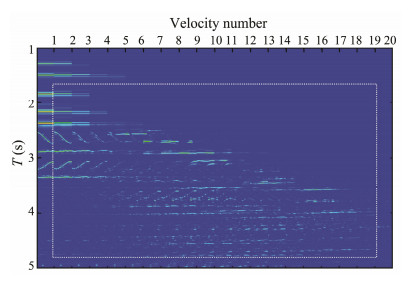
|
Fig. 7 Example of velocity scanning spectrum (1 ≤ k ≤ 20, 6 km ≤ x≤ 8 km). |
Thus, the velocity of each spectrum from left to right gradually decreases. The energy in the spectra demonstrates the velocity range of each event (including internal multiple) in the shot-gather record, in which the velocity energy of internal multiples is mainly distributed in the low-velocity region (indicated by the dotted rectangular region in Fig. 7).
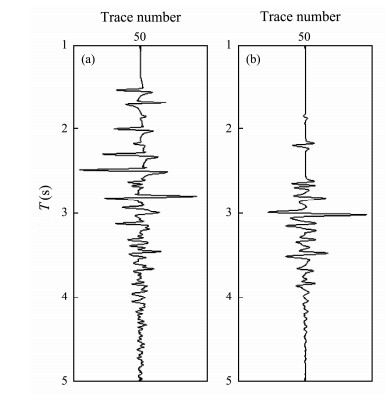
We input the internal multiple profile predicted by the inverse scattering series method (see Fig. 6) and use Kirch-hoff demigration based on the velocity-weighted factor shown in Fig. 7 to generate the internal-multiple shot records. Figs. 8a and b illustrate the predicted a single internal-multiple shot gather (110th shot) and its migration velocity spectrum, respectively. Figs. 9a and b respectively present single-trace waveform graphs of the original record and predicted internal multiples (see 50th trace in Figs. 4a and 8a). Spherical diffusion compensation processing is performed to enhance the amplitude of weak events in the deep part of the shot-gather record. Compared with the original shot gather shown in Fig. 4a, the predicted data contain abundant multiple information, and the travel time of the multiple events of strong impedance interfaces is basically the same as that in the original shot gather (as indicated by arrows in Figs. 4a and 8a).
|
Fig. 8 (a) Example of internal multiple-shot gather record (110th shot) and (b) example of its migration velocity spec-trum (x = 8250 m). |
|
Fig. 9 Waveform graphs of single-trace data: (a) original record (50th trace of 110th shot) and (b) internal multiple record (50th trace of 110th shot). |
Tan et al. (2016) proposed an adaptive multiple subtraction method based on optimized event tracing, which is particularly suited to matching attenuation of predicted multiple data with highly accurate travel time and different waveforms. The basic steps in this method are generating a multiple velocity spectrum using the predicted internal multiple record, extracting travel time information of multiple events through the event tracing technique, and correcting the errors of the predicted multiples. Finally, short-time-window FK filtering (Tan, 2017) is applied to eliminate multiple events in the original shot-gather record.
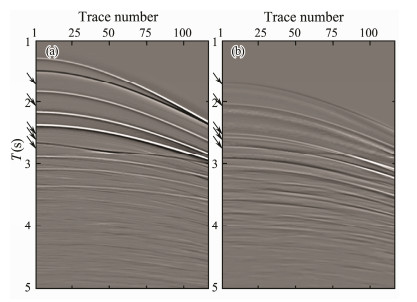
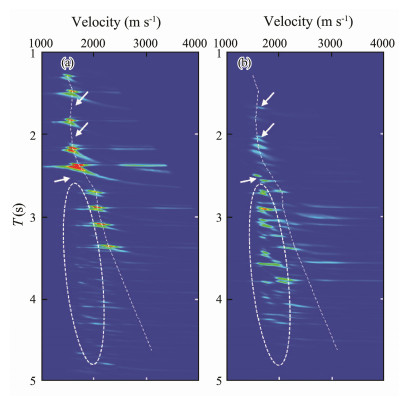
Figs. 10a and b show the shot gather after multiple subtractions and the subtracted record of internal multiples, respectively. Comparison shows that the multiple events in the original shot record (see Fig. 4) have been considerably eliminated, and no obvious primary events exist in the subtracted record of internal multiples shown in Fig. 10b. Prestack time migration velocity spectra are generated (as shown in Fig. 11) to analyze the velocity characteristics of the subtracted internal multiples. Evidently, in Fig. 11a, the internal multiple energy has been completely removed and the signal-to-noise ratio has been improved remarkably.
|
Fig. 10 (a) Example of shot record after multiple suppressions (110th shot) and (b) example of subtracted internal multiple (110th shot). |
|
Fig. 11 Examples of velocity spectra: (a) after multiple suppression and (b) subtracted internal multiple (x = 8250 m). |
The 2D seismic line ML_A located in a shallow water area is selected to test our internal multiple predication method. The original record has a total of 667 shots, and each shot gather has 324 traces. The shot and trace intervals are 50 m and 12.5 m, respectively, and the minimum offset is 150 m. Various types of multiples (e.g., surface-related multiples, ringing, and internal multiples) develop seriously because the water is shallow (approximately 100 m), and many sets of strong acoustic impedance interfaces exist (including the seafloor), and a shallow gas-bearing reservoir exists with a strong shielding effect in the middle of this seismic line. These multiples with strong energy nearly obscure the primary reflections of target interfaces. If these noises are not eliminated, then the authenticity and reliability of seismic imaging would be affected.
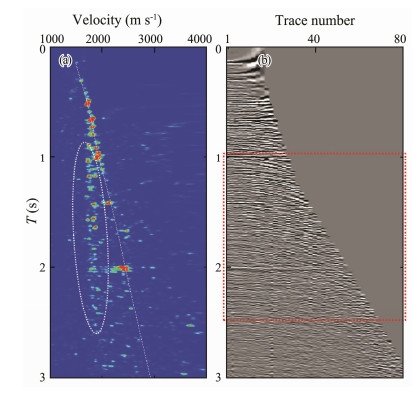
The conventional multiple suppression processing is first performed via the SRME method. Thus, a large number of strong surface-related multiples are effectively suppressed, obvious residual multiples still remain. The velocity and amplitude characteristics of the residual multiples are analyzed by combining the stacking velocity spectrum with the corresponding CMP gather after normal moveout correction (NMO). In the velocity spectrum shown in Fig. 12a, the dashed white line indicates the picked velocity-time curve of the primary wave, and a large amount of energies in the ellipse region are close to the primary velocity. The NMO is performed using the stacking velocity of the primary wave. These events of low-velocity energies, which are mainly the residual internal multiple events, exhibit a downward shape (as indicated by the red rectangular region in Fig. 12b).
|
Fig. 12 Analysis of residual multiples: (a) example of stacking velocity spectrum (x = 19350 m) and (b) CMP gather record after NMO (x = 19350 m). |
Kirchhoff prestack time migration based on the primary velocity is conducted, and then the internal-multiple profile is predicted using inverse scattering series method. Finally, the velocity-weighted Kirchhoff demigration is used to create an internal-multiple shot records. We analyze the effect of internal multiple prediction based on the predicted shot-gather record and its stacking velocity spectrum. Figs. 13a and b respectively show a set of shot gathers after SRME and predicted internal multiples, in which most of the events within the rectangular region are multiples. Figs. 14a and b present the stacking velocity spectrum generated based on the two sets of shot gathers. A comparison shows that the generated internal-multiple data contain extensive information on internal multiples, in which the velocity is less than or close to that of the primary wave (the dashed white line in the spectrum shown in Fig. 14 is the velocity-time curve of the primary wave). The travel time and stacking velocity of the main multiple events is basically the same as those of the original record (as indicated by the position of the arrow and the ellipse region in the velocity spectrum of Fig. 14).
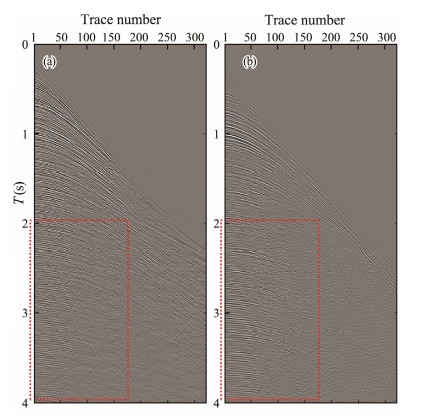
|
Fig. 13 (a) Shot gather record processed by SRME (348th shot) and (b) predicted internal multiple record (348th shot). |
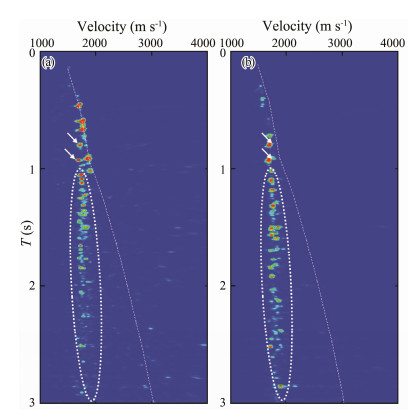
|
Fig. 14 Stacking velocity spectra (x = 20600 m) based on (a) shot gather record processed by SRME and (b) predicted internal multiple record. |
The predicted internal multiple record has certain differences in waveform and amplitude compared with the shot records after SRME, but the travel time of multiple events is basically the same; thus, multiple elimination can still be conducted through the combined adaptive multiple subtraction based on event tracing (Tan, 2016, 2017). Fig. 15 shows a group of CMP gathers before and after multiple attenuation and the removed multiple. By comparison, the internal multiple events whose velocity are close to that of the primary events in the original record are significantly suppressed and the primary events are almost undamaged.

|
Fig. 15 Examples of CMP gathers before (a) and after (b) multiple attenuation and subtracted multiples (c) (x = 20325 m). |
Using the migration velocity field of the primary wave, we performed prestack time migration on the shot gathers before and after multiple attenuation. The obtained profiles are shown in Figs. 16 and 17. The profile of the removed multiples is obtained by subtracting the two (as indicated in Fig. 18). Under the shielding effect of the gas-bearing reservoir, the amplitude of the reflections in the region below 1 s of the right side of the profile is extremely weak. After the imaging process of the primary velocity, the multiple events are effectively suppressed and their amplitude is weaker than that of the primary events. A comparison shows that the multiple events in the original profile are substantially suppressed (as in the arrow pointing position and elliptical region) in which the mid-deep geologic structure becomes clearer and the signal-to-noise ratio of the profile is improved considerably.
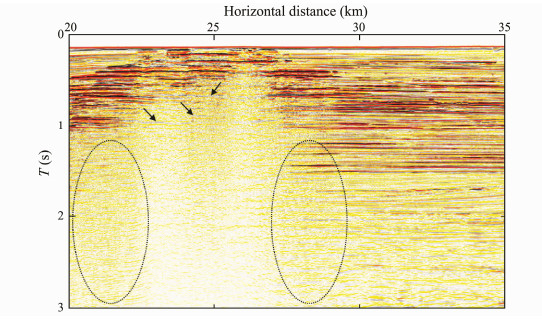
|
Fig. 16 Time migration profile based on shot-gather record processed by SRME. |
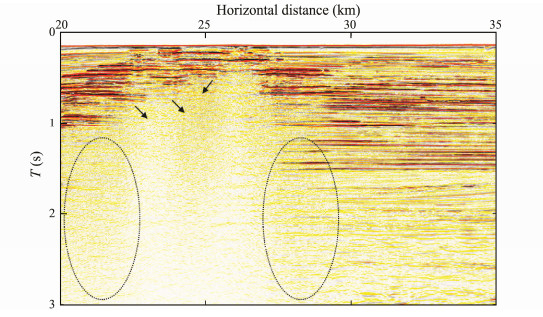
|
Fig. 17 Time migration profile based on shot-gather record after internal multiple suppression. |
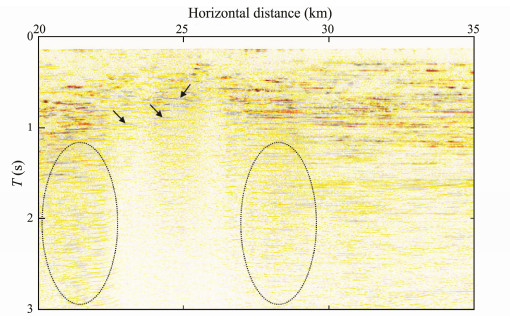
|
Fig. 18 Time migration profile of subtracted multiples. |
This paper introduces an internal multiple prediction method based on imaging profile prediction and Kirchhoff demigration. Internal multiple prediction based on prestack time migration profile effectively reduces the computational cost, and the internal-multiple shot gathers created by Kirchhoff demigration remarkably reduces the complexity of the practical problem. The results of the model and field experiments show that this method can effectively predict internal multiples. Thus, this method has potential for extensive application in the field of seismic data processing. The next focus of our research is extending this method to internal-multiple prediction in field 3D seismic data to effectively improve the accuracy of multiple elimination in this type of data.
AcknowledgementsThe authors appreciate the support of the NSFC-Shandong Joint Fund for Marine Science Research Centers (No. U1606401), the National Natural Science Foundation of China (Nos. 41704114 and 41574105), the National Science and Technology Major Project of China (No. 2016Z X05027-002), the Scientific and Technological Innovation Project financially supported by Qingdao National Laboratory for Marine Science and Technology (No. 2016 ASKJ13), Taishan Scholar Project Funding (No. tspd2016-1007), and the Latitudinal Project of Algorithm Research of Internal Multiple Prediction financially supported by CNOOC.
Berkhout, A. J., 1982. Seismic Migration: Imaging of Acoustic Energy by Wavefield Extrapolation. Elsevier Scientific Publishing Company, Amsterdam, 211-218.
(  0) 0) |
Berkhout, A. J. and Verschuur, D. J., 1997. Estimation of multiple scattering by iterative inversion, Part Ⅰ: Theoretical considerations. Geophysics, 62(5): 1586-1595. DOI:10.1190/1.1444261 (  0) 0) |
Berkhout, A. J. and Verschuur, D. J., 2005. Removal of internal multiples with the common-focus-point (CFP) approach: Part 1 – Explanation of the theory. Geophysics, 70(3): V45-V60. DOI:10.1190/1.1925753 (  0) 0) |
Bleistein, N., 1987. On the imaging of reflectors in the earth. Geophysics, 52(7): 931-942. DOI:10.1190/1.1442363 (  0) 0) |
Carvalho, F. M., Weglein, A. B., and Stolt, R. H., 1991. Examples of a nonlinear inversion method based on the T matrix of scattering theory: Application to multiple suppression. SEG Technical Program Expanded Abstracts. Houston, 1319-1322.
(  0) 0) |
Carvalho, P. M., Weglein, A. B., and Stolt, R. H., 1992. Nonlinear inverse scattering for multiple suppression: Application to real data. Part Ⅰ. SEG Technical Program Expanded Abstracts. New Orleans, 1093-1095.
(  0) 0) |
Da Costa Filho, C. A., Meles, G. A. and Curtis, A., 2017. Elastic internal multiple analysis and attenuation using Marchenko and interferometric methods. Geophysics, 82(2): Q1-Q12. DOI:10.1190/geo2016-0162.1 (  0) 0) |
Jakubowicz, H., 1998. Wave equation prediction and removal of interbed multiples. SEG Technical Program Expanded Abstracts. New Orleans, 1527-1530.
(  0) 0) |
Liu, Y. K., Chang, X., Wang, H., Lu, M. X. and Sun, H. C., 2008. Internal multiple removal and its application by wavepath migration. Chinese Journal of Geophysics, 51(2): 589-595 (in Chinese with English abstract). (  0) 0) |
Meles, G. A., L er, K., Ravasi, M., Curtis, A. and da Costa Filho, C. A., 2014. Internal multiple prediction and removal using Marchenko autofocusing and seismic interferometry. Geophysics, 80(1). (  0) 0) |
Santos, L. T., Schleicher, J., Tygel, M. and Hubral, P., 2000. Seismic modeling by demigration. Geophysics, 65(4): 1281-1289. DOI:10.1190/1.1444819 (  0) 0) |
Schleicher, J., Hubral, P., Tygel, M. and Jaya, M. S., 1997. Minimum apertures and Fresnel zones in migration and demigration. Geophysics, 62(1): 183-194. DOI:10.1190/1.1444118 (  0) 0) |
Stoffa, P. L., Buhl, P., Diebold, J. B. and Wenzel, F., 1981. Direct mapping of seismic data to the domain of intercept time and ray parameter – A plane-wave decomposition. Geophysics, 46(3): 255-267. DOI:10.1190/1.1441197 (  0) 0) |
Tan, J., Li, J. S., Song, P., Wang, L., Zhang, X. B. and Zhong, M. X., 2016. Multiple matching attenuation method based on optimized event tracing. Journal of China University of Petroleum (Edition of Natural Science), 40(6): 40-49. (  0) 0) |
Tan, J., Song, P., Li, J. S., Li, J. S., Wang, L., Zhong, M. X. and Zhang, X. B., 2017. Combined adaptive multiple subtraction based on optimized event tracing and extended wiener filtering. Journal of Ocean University of China, 16(3): 411-421. DOI:10.1007/s11802-017-3279-7 (  0) 0) |
Verschuur, D. J. and Berkhout, A. J., 1997. Estimation of multiple scattering by iterative inversion, Part Ⅱ: Practical aspects and examples. Geophysics, 62(5): 1596-1611. DOI:10.1190/1.1444262 (  0) 0) |
Verschuur, D. J. and Berkhout, A. J., 2005. Removal of internal multiples with the common-focus-point (CFP) approach: Part 2 – Application strategies and data examples. Geophysics, 70(3): V61-V72. DOI:10.1190/1.1925754 (  0) 0) |
Verschuur, D. J., Berkhout, A. J. and Wapenaar, C. P. A., 1992. Adaptive surface-related multiple elimination. Geophysics, 57(9): 1166-11770. DOI:10.1190/1.1443330 (  0) 0) |
Weglein, A. B., Gasparotto, F. A., Carvalho, P. M. and Stolt, R. H., 1997. An inverse-scattering series method for attenuating multiples in seismic reflection data. Geophysics, 62(6): 1975-1989. DOI:10.1190/1.1444298 (  0) 0) |
Wu, J., Wu, Z. Q., Hu, T. Y., He, Y. H., Wang, P., Yan, G. J. and Li, L., 2013. Seismic internal multiple attenuation based on constructing virtual events. Chinese Journal of Geophysics, 56(3): 985-994 (in Chinese with English abstract). (  0) 0) |
Yilmaz, O., 2001. Seismic Data Analysis: Processing, Inversion, and Interpretation of Seismic Data. Society of Exploration Geophysicists, Tulsa, 81-85.
(  0) 0) |
Zou, Y. L. and Weglein, A. B., 2014. An internal-multiple elimination algorithm for all reflectors for ID Earth part Ⅰ: Strengths and limitations. Journal of Seismic Exploration, 23(4): 393-404. (  0) 0) |
 2019, Vol. 18
2019, Vol. 18


